УДК 621.396
НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ИДЕНТИФИКАЦИОННЫХ ИЗМЕРЕНИЙ СПЕКТРОВ СИГНАЛОВ
А. А. Горшенков, Ю. Н. Кликушин
Омский государственный технический университет
Получена 22 января 2011 г.
Аннотация. Описаны основные инструменты, предназначенные для количественного анализа формы и когерентности спектров сигналов. Выявлен ряд закономерностей, присущих идентификационным измерениям спектров сигналов, что позволяет расширить функциональные возможности спектрального анализа.
Ключевые слова: закономерность, идентификационные измерения, инструменты анализа, классификация, когерентность, форма, спектры сигналов.
Abstract. Describes the basic tools for quantitative analysis of shape and coherence spectra of the signals. Identified a number of regularities inherent in the identification of measuring the spectra of signals that can extend the functionality of the spectral analysis.
Keywords: pattern, identification of measurement tools of analysis, classification, coherence, shape and the spectra of signals.
ВВЕДЕНИЕ
Спектральный анализ является важной и вполне самостоятельной областью многих физических исследований. Достаточно сказать, что в радиотехнике с помощью спектральных методов решаются такие задачи, как обнаружение, фильтрация, преобразование и генерация сигналов. В теоретическом плане, знание спектров сигналов позволяет относительно простыми средствами оценивать их временные и корреляционные характеристики, что, в конечном итоге, позволяет получать большее количество полезной информации об объектах исследований.
Очевидно, что качественные показатели спектрального анализа во многом зависят от совершенства используемых инструментов (средств, методов, технологий). В свою очередь, совершенство этих инструментов определяется тем, насколько правильно (адекватно) производится измерение (количественное оценивание) тех или иных свойств спектров исследуемых сигналов.
В настоящее время ситуация в спектральном анализе сигналов может быть охарактеризована следующим образом.
Во-первых, хотя мы умеем измерять амплитуды и частоты отдельных гармонических составляющих исследуемого спектра, однако до сих пор не знаем, как измерять спектр. В данном случае, под спектром понимается некоторое единое и неделимое свойство сигнала, а не произвольный набор гармоник. В нашем понимании – сочетание «измерить спектр» - означает дать качественную, например, классификационную, характеристику спектра по результатам измерения распределения гармонических составляющих. Например, результат измерения спектра некоторого сигнала может быть выражен лингвистически в виде суждения «Сигнал имеет непрерывный равномерный спектр, что характерно для стационарных случайных сигналов». Естественно, что кроме качественной, в результат измерения должна входить и количественная характеристика, например, в виде совокупности верифицируемых параметров.
Во-вторых, хотя в спектральном анализе существует устоявшаяся система понятий, характеризующих различные свойства спектров сигналов, некоторые из них не имеют средств физического отображения и, соответственно, количественной оценки. В частности, речь идет о понятии «когерентность» сигнала. В физике и теории сигналов [1-4] понятие когерентности имеет несколько определений.
1. Когерентность рассматривается как согласованное протекание во времени нескольких колебательных или волновых процессов.
2. Колебания называются когерентными, если разность их фаз остается постоянной или изменяющейся закономерно.
3. Когерентными считаются сигналы, имеющие одинаковую частоту и, колебания в которых, совершаются вдоль одного и того же направления.
4. Когерентность интерпретируется как мера спектральной ширины сигнала. При этом, чем меньше спектральная ширина сигнала, тем выше степень его когерентности.
Важность понятия когерентности заключается в том, что с его помощью можно оценивать способность сигналов к взаимодействию (интерференции).
В данной работе предлагается решение вопроса измерения спектров сигналов, основанное на количественной оценке свойства когерентности. Исследование особенностей проявления данного свойства в отношении различных групп сигналов позволило установить ряд новых закономерностей, которые можно использовать для расширения функциональных возможностей спектрального анализа. В частности, авторам удалось сформировать ряд алгоритмов, решающих задачи объективной, автоматической классификации спектров сигналов.
МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЙ
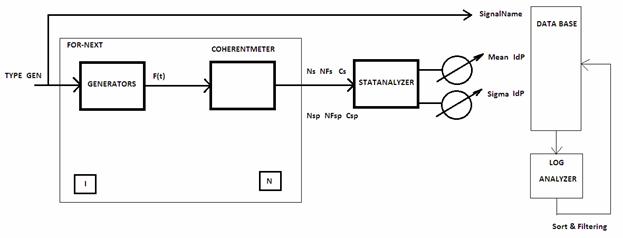
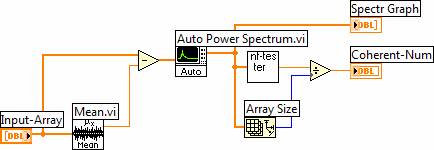
Методика и инструменты исследований основаны на теории идентификационных измерений (ИИ), систематически изложенной в [5,6]. Применительно к задаче спектрального анализа, методология ИИ поясняется структурной схемой измерителя когерентности, представленной на рис. 1.
Рис. 1. Структурная схема измерителя когерентности.
Модель измерителя когерентности выполнена в среде LabVIEW-7.1 и содержит: блок автоматического смещения, состоящий из модуля Mean.vi и вычитающего устройства, модуля Auto Power Spectrum.vi преобразования временной реализации сигнала F(t) в спектр F(ω), идентификационного тестера (NF-tester.vi), определителя (Array Size.vi) размера N массива спектра и делительного устройства.
Временная реализация сигнала в форме массива подается на вход Input Array. С помощью блока автоматического смещения из входного сигнала исключается постоянная составляющая. В модуле Auto Power Spectrum.vi производится быстрое преобразование Фурье (БПФ) временной функции F(t) в амплитудный спектр F(ω). Здесь символами t и ω обозначены время и круговая частота, соответственно. Основным блоком измерителя когерентности является идентификационный тестер NF-типа, который преобразует спектр F(ω) в специальное число, называемое идентификационным (IdP).
Математическая модель данного тестера связана с вычислением отношения размаха спектра сигнала к среднеквадратическому отклонению (СКО) спектра:
где xi – амплитуда i-ой гармоники спектра на входе тестера, X – среднее значение (математическое ожидание) спектра сигнала, N – объем выборки спектра (количество гармоник спектра), Kf – параметр, который можно трактовать, как коэффициент пропорциональности между шириной N спектра на входе тестера и виртуальной шириной NF спектра на его выходе. Поскольку при идентификационных измерениях временных функций сигналов, показатель NF служит количественной оценкой формы [7] сигнала, то, по аналогии, в данной модели этот показатель выступает в качестве количественной оценки формы спектра.
В основу проведенных исследований была положена гипотеза о том, что именно Kf параметр (1) может служить количественной оценкой когерентности спектра F(ω). В частности, поэтому для формирования информативной величины (Coherent-Num) в структуре (рис. 1) выходная величина NF тестера делится на значение N.
Таким образом, в данной модели свойство когерентности отображается в виде комплексной, интегральной оценки формы и ширины спектра. В дальнейшем, Kf параметр будем называть степенью когерентности, полагая, что численные значения этого параметра лежат, для всех возможных сигналов, в диапазоне от 0 до 1.
Для проверки данного предположения, с помощью имитационного моделирования, авторами был проведен ряд исследований, целями которых являлось:
1) создание базы данных (БД) результатов измерения формы и когерентности типовых сигналов;
2) анализ полученной базы данных на предмет выявления закономерностей, объединяющих (или разделяющих) группы типовых сигналов;
3) применение установленных закономерностей к анализу спектров не типовых сигналов (т.е. сигналов, не входящих в синтезированную БД).
В качестве типовых были использованы следующие классы сигналов:
1) периодические (синусоидальной – sin, треугольной – tri, прямоугольной – squ, пилообразной – saw формы);
2) случайные, стационарные с симметричными распределениями (двумодальным – 2mod, арксинусным – asin, биномиальным – binom, равномерным – even, треугольным – simp, нормальным – gaus, двусторонним экспоненциальным – lapl и Коши – kosh);
3) случайные, стационарные с асимметричными распределениями (экспоненциальным – expn, Рэлея – rele, Пуассона - pois, Бернулли – bern);
4) фрактальные, с показателем Херста, равным нулю (fract-0), одной второй (fract-0,5) и единице (fract-1);
5) композитные (SNR), представляющие собой бинарные аддитивные смеси периодического синусоидального сигнала и нормального «белого» шума с варьируемым отношением сигнал-шум (0≤SNR≤1, где SNR – SignalNoiseRelation);
6) композитные (Comp), представляющие собой аддитивные смеси периодических синусоидальных сигналов одинаковой амплитуды, но разной частоты.
Выбор указанных классов типовых сигналов был обусловлен следующими соображениями. Во-первых, применительно к радиотехническим источникам, абсолютно когерентными могут считаться только те из них, которые генерируют строго периодические синусоидальные сигналы. У таких сигналов ширина спектра минимальна, поскольку спектр состоит из одной гармоники. Степень когерентности для синусоидального сигнала должна быть максимальной из всех возможных сигналов и, соответственно, равна 1.
Во-вторых, к частично когерентным, относятся генераторы периодических сигналов несинусоидальной, например, треугольной, формы. В спектре такого сигнала содержатся несколько гармоник, распределенных определенным образом. Частично когерентными являются также сигналы, представляющие собой смесь периодической синусоидальной компоненты и случайного шума, если при этом интенсивность шума много меньше интенсивности полезной компоненты. Если же интенсивность шума много больше интенсивности полезной компоненты, то когерентность таких сигналов будет мала и их спектр по форме должен приближаться к спектрам чисто случайных сигналов. Степень когерентности для частично когерентных сигналов должна быть меньше 1.
В-третьих, абсолютно некогерентными считаются генераторы случайных сигналов, имеющие сплошной спектр в некотором диапазоне частот. При этом спектральная плотность мощности случайного сигнала может иметь разную форму распределения. В частности, случайный сигнал, имеющий равномерную спектральную плотность, называется «белым шумом». Случайный сигнал, имеющий произвольную, неравномерную спектральную плотность, называется «окрашенным шумом». Степень когерентности для некогерентных сигналов должна быть близка к 0.
В-четвертых, фрактальные сигналы были выбраны с целью проверки гипотезы о наличии статистической связи между показателем Херста [8], и степенью когерентности. Поскольку фрактальные сигналы выглядят как случайные, а по физическим свойствам похожи на регулярные, то ожидается, что степень когерентности для них будет лежать в диапазоне от 0 до 1.
Структурная схема эксперимента, изображенная на рис. 2, состоит из блока
модельных генераторов (Generators) типовых сигналов, указанных выше классов, измерителя (CoherentMeter) когерентности и статистического
анализатора (StatAnalyzer).
Рис. 2. Структурная схема эксперимента.
Генераторы и измеритель когерентности помещались в цикл типа For-Next, чтобы реализовать возможность многократного повторения эксперимента. Измерялось 6 основных параметров, относящихся к форме распределения временной функции F(t) сигнала (Ns, NFs, Cs) и к форме спектрального распределения F(ω) (Nsp, NFsp, Csp). Все параметры усреднялись по совокупности сгенерированных реализаций в результате чего статистический анализатор формировал оценки средних значений (Mean IdP) и среднеквадратического отклонения (Sigma IdP). Имена сигналов (SignalName) и указанные оценки идентификационных параметров записывались в базу данных (DataBase). Совокупность записей БД анализировалась в интерактивном режиме с помощью операций сортировки и фильтрации (Sort&Filtering) на предмет выявления латентных закономерностей в структуре сгенерированного множества сигналов. Некоторые характерные примеры измерения формы и когерентности спектров отдельных сигналов даны на рис. 3-5. Каждый сигнал представлен 4 графиками временной (Time), вероятностной (Hist), корреляционной (Corr) и спектральной (Spectr) функциями, расположенными в порядке слева – направо, сверху – вниз. В нижней части рисунков изображены фрагменты таблицы БД с указанием имени сигнала и его идентификационных параметров.
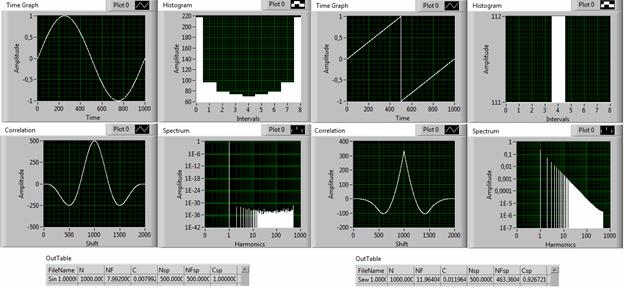
Рис. 3. Временная (Time), вероятностная (Hist), корреляционная (Corr) и спектральная (Spectr) характеристики синусоидального и пилообразного сигналов.
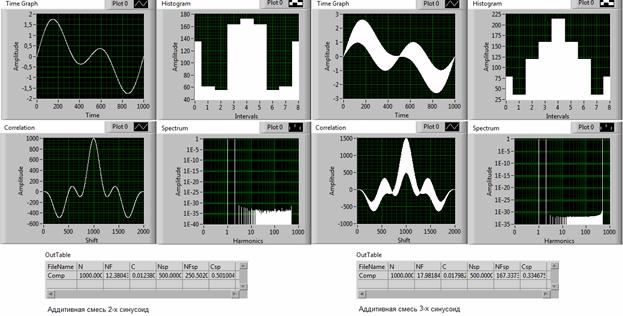
Рис. 4. Временная (Time), вероятностная (Hist), корреляционная (Corr) и спектральная (Spectr) характеристики смесей двух и трех синусоидальных сигналов.
Параметры формы и когерентности временной функции сигнала обозначены в таблицах как NF и С. Параметры формы и когерентности спектральной функции сигнала обозначены в таблицах как NFsp и Сsp.
Рис. 5. Примеры тестовых сигналов, имеющих одинаковое число (2) значимых гармоник, но разную когерентность (сигнал слева Ssp=0,666, сигнал справа Ssp=0,41).
Физический смысл параметров когерентности (С, Сsp) состоит в том, что они характеризуют концентрированность, соответственно, вероятностной и спектральной функций сигнала.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
В соответствии со структурной схемой (рис. 2) эксперимента, результаты анализа сигналов сосредоточены в БД.
Упрощенный вариант БД в виде табл. 1 содержит 6 полей (колонок). Измеренные значения оценок степени когерентности временной и спектральной характеристик записаны в 3 и 4 колонках, соответственно. Для удобства сравнения и классификации сигналов в 5 и 6 колонках представлены вычисленные значения величин S и Ssp, обратные к значениям степеней когерентности и округленные до целых. Такое представление позволяет выделить в структуре БД несколько классов сигналов. Необходимо только договориться о значениях критериев раздела классов. В частности, в самом простом случае сигналы можно разделить на 3 группы по критерию Ssp следующим образом (табл. 2).
В вою очередь, внутри каждого класса сигналы можно разделить по критерию формы S.Так, например, хаотические сигналы по форме распределения мгновенных значений разделяются так, как показано в табл. 3.
Физический смысл параметра Ssp состоит в том, что он определяет количество значимых (наибольших по амплитуде) гармоник в спектре сигнала. Именно поэтому, для сигналов аддитивной смеси с ОСШ≥0,5, значение этого параметра равно 1. Что касается периодических сигналов, содержащих в спектре ряд гармоник, то, до тех пор, пока преобладающей является лишь одна гармоника, оценка Ssp будет близка к 1. Если же в спектре сигнала появляются несколько равнозначных по амплитуде гармоник, то когерентность Csp уменьшается от 1 до значений 1/n, где n – число одинаковых гармоник. Это обстоятельство как раз и отражено на рис. 4, где левый сигнал имеет Ssp=2 и, соответственно, содержит 2 значимые гармоники. Правый сигнал, имеющий Csp=0,334, содержит 3 значимые гармоники. Если мы хотим выяснить, является ли данный сигнал периодическим и какое число значимых гармоник он содержит, то должны оценивать значение Ssp. В случае, когда необходимо различить сигналы, имеющие одинаковое значение Ssp, необходимо анализировать значение Csp (табл. 4). Примером этому является рис. 3, где сравниваются два периодических (синусоидальный и треугольный) сигнала с параметром Ssp, равным 1.
Фрагмент базы данных результатов измерения формы и когерентности спектров сигналов
|
№ |
FileName |
C |
Csp |
S=1/C |
Ssp=1/Csp |
|
1 |
compose\gaus+sin-100-0,1.txt |
0,005407 |
0,139675 |
185 |
7 |
|
2 |
compose\gaus+sin-100-0,2.txt |
0,005192 |
0,639821 |
193 |
2 |
|
3 |
compose\gaus+sin-100-0,5.txt |
0,005322 |
0,98966 |
188 |
1 |
|
4 |
compose\gaus+sin-100-1.txt |
0,005245 |
1 |
191 |
1 |
|
5 |
compose\gaus+sin-100-10.txt |
0,001429 |
1 |
700 |
1 |
|
6 |
compose\gaus+sin-100-100.txt |
0,000849 |
1 |
1178 |
1 |
|
7 |
rnd\2mod.txt |
0,0004 |
0,013725 |
2500 |
73 |
|
8 |
rnd\asin.txt |
0,000802 |
0,016151 |
1247 |
62 |
|
9 |
rnd\even.txt |
0,001187 |
0,024657 |
842 |
41 |
|
10 |
rnd\gaus.txt |
0,005615 |
0,027594 |
178 |
36 |
|
11 |
rnd\kosh.txt |
0,866046 |
0,0072 |
1 |
139 |
|
12 |
rnd\lapl.txt |
0,027256 |
0,014635 |
37 |
68 |
|
13 |
rnd\simp.txt |
0,002411 |
0,011277 |
415 |
89 |
|
14 |
saw\saw-1.txt |
0,0012 |
0,924216 |
833 |
1 |
|
15 |
saw\saw-10.txt |
0,0012 |
0,924222 |
833 |
1 |
|
16 |
saw\saw-100.txt |
0,0012 |
0,924782 |
833 |
1 |
|
17 |
saw\saw-1000.txt |
0,0012 |
0,924216 |
833 |
1 |
|
18 |
sin\sin-1.txt |
0,0008 |
1 |
1250 |
1 |
|
19 |
sin\sin-10.txt |
0,0008 |
1 |
1250 |
1 |
|
20 |
sin\sin-100.txt |
0,0008 |
1 |
1250 |
1 |
|
21 |
sin\sin-1000.txt |
0,0008 |
1 |
1250 |
1 |
|
22 |
squ\squ-1.txt |
0,0004 |
0,985633 |
2500 |
1 |
|
23 |
squ\squ-10.txt |
0,0004 |
0,985636 |
2500 |
1 |
|
24 |
squ\squ-100.txt |
0,0004 |
0,985879 |
2500 |
1 |
|
25 |
squ\squ-1000.txt |
0,0004 |
0,979213 |
2500 |
1 |
|
26 |
tri\tri-1.txt |
0,0012 |
0,999851 |
833 |
1 |
|
27 |
tri\tri-10.txt |
0,0012 |
0,999851 |
833 |
1 |
|
28 |
tri\tri-100.txt |
0,001199 |
0,999849 |
834 |
1 |
|
29 |
tri\tri-1000.txt |
0,0012 |
0,999851 |
833 |
1 |
В тоже время, более точная оценка по степени когерентности указывает на различие этих сигналов Csp(sin)=1, Csp(tri)=0,99985 (табл. 4).
На рис. 5 представлены графики и результаты измерения двух сложных сигналов, не входящих в БД (табл. 1). Эти сигналы содержат одинаковое число (Ssp=2) значимых гармоник в спектре, что определяет свойство их похожести. Однако, формы спектров у этих сигналов довольно значительно отличаются, на что указывают оценки когерентности (сигнал слева Csp=0,667, сигнал справа Csp=0,41). Следовательно, степень различия формы спектров составляет для этих сигналов: µ = Csp1/Csp2 = 0,667/0,41 ≈ 1,6 раза.
Таким образом, общим классифицирующим параметром, определяющим похожесть сигналов по спектральному содержанию, может служить оценка вида Ssp = int[1/Csp] = (1;∞), где символом int обозначена операция округления до ближайшего целого. Внутри одного класса идентифицирующим параметром, определяющим различие сигналов по форме спектра, может служить оценка вида Csp = (0; 1).
Классификация сигналов БД по критерию Ssp
|
№ п/п |
Имя класса |
Качественная характеристика класса |
Имя сигнала |
Критерии принадлежности к классу |
||||||||||||||||||||
|
1 |
Регулярные сигналы |
Все периодические сигналы, сигналы аддитивных смесей вида «сигнал-шум» с ОСШ≥0,5. |
|
S=833 S=1250
Ssp = 1
|
||||||||||||||||||||
|
2 |
Частично регулярные сигналы |
Сигналы, не имеющие явных визуальных признаков регулярности |
|
1<Ssp<30 |
||||||||||||||||||||
|
3 |
Хаотичные (нерегулярные) сигналы |
Все стационарные случайные сигналы |
|
S=178
S=842
S=1247
S=37
S=2500
S=415
S=1 |
Классификация хаотических сигналов по критерию S
|
Критерий (N=10000) |
Формы распределения хаотических сигналов |
||||||
|
2mod |
asin |
even |
simp |
gaus |
lapl |
kosh |
|
|
S |
2500 |
1247 |
842 |
415 |
178 |
37 |
1 |
Классификация периодических сигналов
|
Критерий
|
Форма периодических сигналов |
|||
|
sin |
tri |
squ |
saw |
|
|
Ssp |
1 |
1 |
1 |
1 |
|
Csp |
1 |
0,99985 |
0,98 |
0,92 |
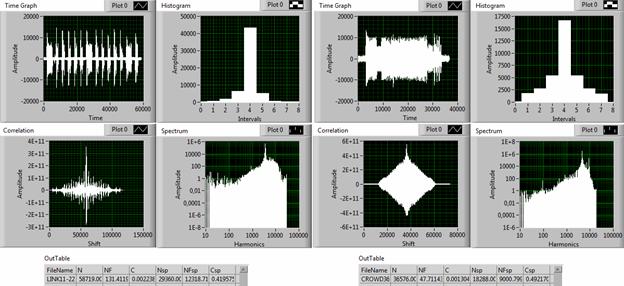
Рис. 6. Примеры сигналов, имеющих похожие спектры, но отличающиеся временными реализациями.
Физический смысл понятия когерентности применительно к временным реализациям сигналов можно пояснить следующим образом. Чем меньше когерентность C временной (Time) функции, тем более размытой (менее концентрированной) является вероятностная (Hist) характеристика сигнала. Отсюда следует, что сигналы с похожими спектрами и относящиеся к одному и тому же классу по параметру Ssp, (как например, сигналы на рис. 6, у которых Ssp1 = Ssp2 =2), могут иметь различные формы временных реализаций. В частности, для рассматриваемых (рис. 6) сигналов, различие в форме временной функции выражается в оценках S1 = (1/С1) = 447 и S2 = (1/С2) = 767 или в 1,7 раза.
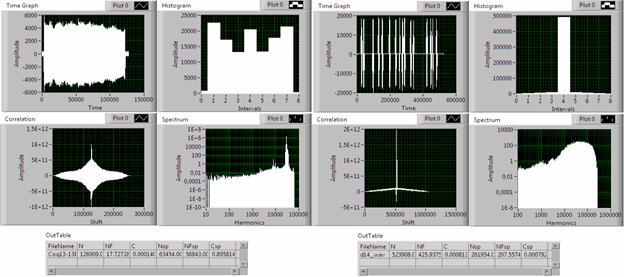
Рис. 7. Примеры тестовых сигналов, относящихся к классу регулярных (слева) и хаотических (справа).
В качестве примера, подтверждающего «правильность» (адекватность) предлагаемого подхода при решении задач спектрального анализа, на рис. 7 даны характеристики двух реализаций, относящихся к противоположным классам регулярных (слева) и хаотических (справа) сигналов. Сравнение спектров показывает, что сигнал, классифицируемый, как регулярный, имеет в спектре явно выраженные и сосредоточенные в узком диапазоне, периодические компоненты. В тоже время, второй сигнал имеет сплошной, «окрашенный» спектр, характерный для чисто случайных сигналов. Эти же сигналы имеют существенные различия и по когерентности временной функции, что хорошо видно на графиках гистограмм распределений.
Опыт применения спектральных идентификационных измерений показывает, что наибольшее количество сигналов может быть отнесено к классу частично регулярных. Поэтому, для увеличения разрешающей способности системы автоматической классификации рекомендуется разделить класс частично регулярных сигналов на несколько подклассов. Следует отметить еще одну особенность идентификационных измерений спектров сигналов, относящихся к классам частично регулярных и хаотических. Для подобных сигналов следует учитывать зависимость измеренных значений когерентности от объема N выборочной реализации. Общий характер этой зависимости следует из (1): чем больше объем выборки, тем меньше значение оценки степени когерентности при прочих равных условиях. Поэтому сравнение сложных сигналов желательно проводить для выборочных реализаций сигналов одинакового объема. В тех случаях, когда объемы выборок сравниваемых сигналов отличаются, анализ необходимо проводить и по абсолютным, и по относительным параметрам когерентности.
Таким образом, предложенная методология идентификационных измерений позволила, во-первых, выявить общую закономерность эволюции спектров сигналов от регулярных до хаотических. Во-вторых, удалось создать инструмент количественной оценки интегральных свойств спектров (формы, ширины, гармонического содержания) сигналов и предложить на этой основе технологию решения задач их автоматической классификации. В-третьих, выявлены условия, позволяющие оценивать свойства «похожести – различия» сигналов, как в спектральной, так и во временной области. В-четвертых, установлено соответствие (физический смысл) количественных оценок когерентности с качественным состоянием сигналов. Это открывает перспективу построения интеллектуальных систем автоматического распознавания сложных процессов, каковыми, например, являются сигналы медицинской и технической диагностики, сейсмосигналы и др.
ЛИТЕРАТУРА
1. Савельев И.В. Курс физики. В 3-х томах. Том 2. Электричество. Колебания и волны. Волновая оптика. Изд. 3-е, стереотип. - М.: Изд-во Лань, 2007. - 480 с.
2. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000. - 462 с.
3. Большой Энциклопедический словарь. Электронная версия: http://dic.academic.ru.
4. Универсальная энциклопедия. Интернет ресурс. http://ru.wikipedia.org
5. Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов: Монография. – Петропавловск: Изд-во СКГУ им. М. Козыбаева, 2007. – 186 с.
6. Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: Монография. – Омск: Изд-во ОмГТУ, 2010. – 216 с.
7. Klikushin Y.N., Koshekov K.T. New technology for signals recognition //Proceedings III International Conference Strategy of Quality in Industry and Education. – Varna, Bulgaria, 2007. – V.2. – C. 503 – 505.
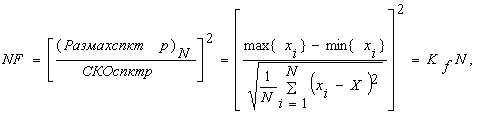 (1)
(1)