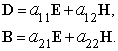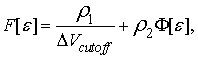УДК 519.63, 537.87
СИНТЕЗ СЛОИСТОГО КИРАЛЬНО-ДИЭЛЕКТРИЧЕСКОГО ВОЛНОВОДА
Н. А. Боголюбов, И. А. Буткарев, Ю. В. Мухартова
Московский государственный университет имени М.В.Ломоносова, физический факультет
Статья получена 14 марта 2015 г.
Аннотация. Рассмотрено решение одной из весьма важных задач синтеза прямоугольного волновода с кирально – диэлектрическим заполнением, обладающего максимальной полосой одномодового режима. При данном режиме работы в волноводе существует только одна мода и не существует межмодовой дисперсии, вносящей искажения в распространяемый по волноводу сигнал.
Ключевые слова: регулярный волновод, метаматериалы, киральные среды, дисперсионная характеристика, задача синтеза, метод конечных элементов.
Abstracts: The solution of one of the very important task of synthesis of a rectangular waveguide with chiral – dielectric filling, which has a maximum band width of single-mode, is given. When this mode in the waveguide, there is only one mode and there is no modal dispersion, which introduces distortion in the signal propagating in waveguides.
Keywords: regular waveguide, metamaterials, chiral media, the dispersion characteristic, the synthesis problem, finite element method.
Введение
В настоящее время большие перспективы в высокочастотной электродинамике, волновой и интегральной оптике связывают с устройствами, построенными с использованием мезоскопических систем. Мезоскопические системы – это искусственно созданные структурированные материалы (метаматериалы) с характерными размерами структурных элементов от единиц до сотен нанометров.
Для произвольной линейной среды связывающие векторы электрического и магнитного полей материальные уравнения имеют следующий вид [1]:
Материальные параметры ![]() и
и ![]() зависят от выбора конкретной модели
среды. Линейные среды общего вида называются би-анизотропными. Если
материальные параметры являются скалярами или псевдоскалярами, то
соответствующие среды носят название би-изотропных. Киральные среды
характеризуются тремя параметрами: диэлектрической проницаемостью
зависят от выбора конкретной модели
среды. Линейные среды общего вида называются би-анизотропными. Если
материальные параметры являются скалярами или псевдоскалярами, то
соответствующие среды носят название би-изотропных. Киральные среды
характеризуются тремя параметрами: диэлектрической проницаемостью ![]() магнитной проницаемостью
магнитной проницаемостью ![]() и параметром киральности
и параметром киральности ![]() . При стремлении параметра киральности к
нулю среда вырождается в диэлектрик или магнетик.
. При стремлении параметра киральности к
нулю среда вырождается в диэлектрик или магнетик.
Постановка задачи синтеза
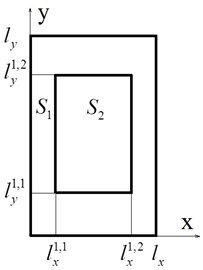
Рассмотрим регулярный волновод прямоугольного сечения с идеально проводящей стенкой и слоистым кирально-диэлектрическим заполнением (рис. 1).
Рис. 1. Поперечное сечение кирально-диэлектрического волновода.
Задачи синтеза (математического проектирования) волноведущих систем составляют специальный класс обратных задач математической физики и состоят в определении таких значений оптимизационных параметров, определяющих геометрию данной волноведущей системы и свойства применяемого в ней материала заполнения, при которых данная система обладает требуемыми свойствами.
Наиболее полный и универсальный подход к решению задач синтеза волноведущих систем был предложен в работах А.Г. Свешникова и А.С. Ильинского [2], [3]. Алгоритм основан на многократном решении прямой задачи с направленно изменяемыми оптимизационными параметрами. Такая методика решения задачи синтеза определяет структуру программы решения задачи синтеза, которая состоит из трех блоков: блока решения прямой задачи, блока оптимизации и вспомогательного блока. Построенная по данной методике программа обладает большой универсальностью, так как для перехода к решению новой задачи синтеза достаточно только заменить блок решения прямой задачи.
Поскольку в процессе решения задачи синтеза происходит многократное решение прямой задачи, то к алгоритму решения прямой задачи предъявляются весьма жесткие требования. Для решения прямой задачи используется алгоритм, основанный на методе конечных элементов с использованием лагранжевых элементов. Однако, как это хорошо известно, при использовании лагранжевых конечных элементов для расчета волноведущих систем при решении спектральных задач возможно появление не имеющих физического смысла посторонних решений, так называемых «духов», борьба с которыми сильно снижает эффективность используемых алгоритмов [4]. В работе [5] была предложена новая постановка спектральной краевой задачи, при применении которой с использованием лагранжевых конечных элементов для численного расчета не возникают нефизические решения.
Рассмотрим решение одной из весьма важных задач синтеза прямоугольного волновода с диэлектрической сердцевиной и киральной оболочкой, обладающего максимальной полосой одномодового режима. При данном режиме работы в волноводе существует только одна мода в частотном диапазоне от первой (основной) моды до второй (следующей) моды. Таким образом, в одномодовом режиме не существует межмодовой дисперсии, вносящей искажения в распространяемый по волноводу сигнал.
В оптимизационном блоке осуществляется решение задачи минимизации функционала:
где ![]()
![]() — i-я частота отсечки,
— i-я частота отсечки, ![]() и
и ![]() —
весовые множители,
—
весовые множители, ![]() — стабилизатор.
— стабилизатор.
Поскольку рассматриваемая задача синтеза представляет собой задачу с нелинейным и несамосопряженным оператором, для которой достаточно подробно исследован только случай квадратичной целевой функции, то большинство эффективных методов, используемых для минимизации функционала в рассматриваемом случае неприменимо. В данной работе используется метод Нелдера-Мида, предложенного Нелдером и Мидом в 1964 году [6] и называемый также методом поиска по деформируемому многограннику. Метод Нелдера-Мида является развитием симплексного метода Спендли, Хекста и Химсфорта [7]. В случае отсутствия дополнительной информации о свойствах минимизируемого функционала этот метод является одним из наиболее надежных и универсальных методов минимизации функционала. Так как при решении рассматриваемой задачи синтеза встает вопрос о необходимости минимизации функционалов в ограниченных областях, в работе применяется основанный на методе Нелдера-Мида метод скользящего допуска, позволяющий искать минимум при наличии ограничений на область, как в виде неравенств, так и в виде равенств.
Оптимизационная
задача состоит в определении таких значений оптимизационных параметров,
определяющих геометрию данного волновода и свойства применяемого в нем
материала заполнения, при которых частотный диапазон одномодового режима будет
максимальным. Причем предполагается, что оптимальный режим достигается при
постоянных значениях параметров, определяющих физические свойства заполнения
волновода. При решении задачи синтеза волокна с киральной оболочкой в качестве
оптимизационных выбирались следующие параметры (см. рис. 1): ![]() =
=![]() — мнимая
часть параметра киральности.
— мнимая
часть параметра киральности.
Результаты синтеза
Проведенные численные эксперименты позволяют сделать следующие выводы.
1) Добиться решения рассматриваемой
оптимизационной задачи получения максимальной полосы одномодового режима для
чисто диэлектрического (без использования метаматериалов) волновода в
однородной оболочке ![]() (
(![]() )
при постоянных значениях параметров сердцевины волновода
)
при постоянных значениях параметров сердцевины волновода ![]() (
(![]() )
возможно в том случае, когда сердцевина исчезает и получается однородное по
сечению волокно со значением диэлектрической проницаемости, равной значению
диэлектрической проницаемости оболочки.
)
возможно в том случае, когда сердцевина исчезает и получается однородное по
сечению волокно со значением диэлектрической проницаемости, равной значению
диэлектрической проницаемости оболочки.
Значительное увеличение частотной полосы одномодового режима в случае чисто диэлектрического заполнения можно добиться, если рассматривать волокно с переменными параметрами сердцевины, как это сделано в работе [8], посвященной синтезу градиентного волокна, обладающего максимальной полосой одномодового режима.
2) Аналогичные выводы можно сделать
относительно волновода с би-изотропной сердцевиной![]() и
оболочкой
и
оболочкой ![]() из обычного диэлектрика при тех же значениях
диэлектрических проницаемостей.
из обычного диэлектрика при тех же значениях
диэлектрических проницаемостей.
3) Наибольший эффект достигается для
волновода, обладающего диэлектрической сердцевиной![]() и
би-изотропной оболочкой
и
би-изотропной оболочкой![]() .
.
Пример. При габаритах сечения волновода,
определяемых параметрами ![]() и
и ![]() , и
значениях диэлектрической проницаемости
, и
значениях диэлектрической проницаемости ![]() =1,5 в
оболочке
=1,5 в
оболочке ![]() и
и ![]() =2,1, а
также
=2,1, а
также ![]() =0 в сердцевине
=0 в сердцевине ![]() волновода
оптимизация достигается при следующих значениях оптимизационных параметров:
волновода
оптимизация достигается при следующих значениях оптимизационных параметров: ![]() =0,
=0, ![]() =0,3678,
=0,3678,
![]() =1,3713 в оболочке
=1,3713 в оболочке ![]() .
При этом частоты отсечки двух первых мод имеют следующие значения:
.
При этом частоты отсечки двух первых мод имеют следующие значения: ![]() =1,5068 и
=1,5068 и ![]() =2,6348.
Таким образом, частотная полоса одномодового режима имеет величину:
=2,6348.
Таким образом, частотная полоса одномодового режима имеет величину: ![]() =1,1280.
=1,1280.
Для диэлектрической оболочки,
когда в области оболочки ![]() параметр киральности
равен нулю (
параметр киральности
равен нулю (![]() =0), при тех же габаритах волновода и той
же геометрии вставки отсечки двух первых мод имеют следующие значения:
=0), при тех же габаритах волновода и той
же геометрии вставки отсечки двух первых мод имеют следующие значения: ![]() =1,4746 и
=1,4746 и ![]() =2,3154,
что дает значение для частотной полосы одномодового режима
=2,3154,
что дает значение для частотной полосы одномодового режима ![]() =0,8408.
=0,8408.
Если теперь положить ![]() =
=![]() =1.5
(однородное волокно), то получаются следующие значения частот и полосы одномодовости:
=1.5
(однородное волокно), то получаются следующие значения частот и полосы одномодовости:![]() =1,7119,
=1,7119, ![]() =2,5693
и
=2,5693
и ![]() =0,8574, что соответствует значению
для чисто диэлектрического волокна.
=0,8574, что соответствует значению
для чисто диэлектрического волокна.
Если рассмотреть однородное
волокно с ![]() =
=![]() =2,1,
то получаются следующие значения частот и полосы одномодовости:
=2,1,
то получаются следующие значения частот и полосы одномодовости: ![]() =1,4473,
=1,4473, ![]() =2,1719
и полоса одномодовости равна
=2,1719
и полоса одномодовости равна ![]() =0,7246, что меньше,
чем в случае
=0,7246, что меньше,
чем в случае ![]() =
=![]() =1,5.
=1,5.
Полученные результаты позволяют
сделать вывод о том, что наличие киральной оболочки позволяет существенно (на
34% по сравнению с диэлектрическим волноводом с оболочкой и на 32% по сравнению
с однородным диэлектрическим волноводом) увеличить полосу одномодового режима.
Несколько неожиданным является тот факт, что оптимальное при данных габаритах
волновода увеличение полосы одномодового режима достигается при значении ![]() =0, то есть по существу мы уже имеем не
волновод с оболочкой, а трехслойный волновод типа «сэндвич», построенный по
типу кирал-диэлектрик-кирал.
=0, то есть по существу мы уже имеем не
волновод с оболочкой, а трехслойный волновод типа «сэндвич», построенный по
типу кирал-диэлектрик-кирал.
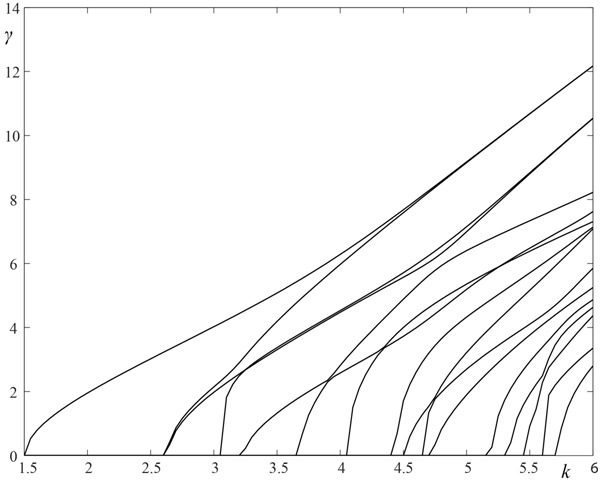
Рис.
2. Дисперсионные кривые трехслойного волокна кирал-диэлектрик-кирал типа
«сэндвич», рассмотренного в примере. По оси абсцисс отложены значения волнового
числа k , а по оси
ординат значения постоянной распространения ![]() .
.
Полученные результаты позволяют сделать вывод о том, что наличие киральных слоев (волокно типа «сэндвич») позволяет существенно (на 27% по сравнению с диэлектрическим волноводом с диэлектрической оболочкой и на 33% по сравнению с однородным диэлектрическим волноводом) увеличить полосу одномодового режима.
Заключение
Проведенные исследования позволяют сделать следующий вывод: введение киральных элементов позволяет решить задачу увеличения ширины полосы одномодового режима, причем эффективность решения этой проблемы существенно зависит от стратегии введения киральных элементов в структуру волновода.
Заметим также, что наличие четырех
оптимизируемых параметров-коэффициентов ![]() и
и ![]() в формуле (1) позволяет использовать
разработанную методику для синтеза волновода с би-изотропным заполнением
наиболее общего вида. Задавая конкретный диапазон изменения параметров и
накладывая необходимые связи между ними, можно моделировать любое заполнение.
в формуле (1) позволяет использовать
разработанную методику для синтеза волновода с би-изотропным заполнением
наиболее общего вида. Задавая конкретный диапазон изменения параметров и
накладывая необходимые связи между ними, можно моделировать любое заполнение.
Литература
1. Laszlo Solymar and Ekaterina Shamonina. Waves in Metamaterials. Oxford University Press. 2009.
2. Свешников А.Г. Прямые и обратные задачи электродинамики // Проблемы математической физики и вычислительной математики. 1979. С. 287-297.
3. Свешников А.Г., Ильинский А.С. Задачи проектирования в электродинамике // ДАН СССР, 1972, т.204, №5, с.1077-1080.
4. Боголюбов А.Н, Боголюбов Н.А., Свешников А.Г. Математическое моделирование волноведущих систем методом конечных разностей и конечных элементов // Физические основы приборостроения. 2013. Т.2, №1. С.10-17.
5. Боголюбов Н.А., Мухартова Ю.В. Спектральная задача в волноводе с однородным би-изотропным заполнением // Журнал вычислительной математики и математической физики, 2014, т.54, №6, с.969-976.
6. Nelder J.A., Mead R. A method of function optimization // The Comp. J., 1965, v.7, p.308-313.
7. Spendly W., Hext G.R., Himsworth F.R. Sequential applications of simplex designs in optimization and evolutionary operation // Technometric, 1962, v.4, p.441-461.
8. Свешников А.Г., Боголюбов А.Н., Красильникова А.В. Задача синтеза круглых диэлектрических волноводов // Вестник Моск. ун-та. Серия 3. Физика. Астрономия, 1996, т.37, №5, с.12-17.