| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 1999 |
Г.А. Ерохин, В.Г. Кочержевский, А.А.
Петровский
Московский Технический Университет Связи и
Информатики
Получена 5 марта 1999 г.
Анализируются общие тенденции, связанные с характером изменения амплитуды поля при перемещении точки наблюдения из дальней зоны в зону Френеля. Приведены также результаты расчета указанных зависимостей для различных типов проволочных антенн и угловое распределение электрического и магнитного полей на различных расстояниях от источника.Интерес, проявляемый в настоящее время к структуре поля в промежуточной и ближней зонах излучающих устройств, связан прежде всего с решением ряда вопросов электромагнитной экологии, в частности, с расчетом геометрии санитарно-защитных зон и зон ограничения застройки вблизи передающих центров. При размещении антенн на крышах жилых домов или административных зданий (что характерно, например, для систем сотовой связи) указанная проблема возникает даже при использовании сравнительно слабонаправленных излучателей, поскольку здесь приходится рассчитывать поле в точках, весьма близко расположенных к антеннам.
В литературе весьма ограничены сведения как о пространственной структуре ближнего поля конкретных типов антенн, так и общих тенденциях (среди которых главная – характер изменения амплитуды), присущих электромагнитному полю произвольных антенн при переходе из дальней зоны, где зависимость амплитуды поля от расстояния в любом направлении описывается функцией 1/r, в промежуточную и, тем более, в ближнюю зону.
В теории излучения давно и хорошо известны общие формулы, позволяющие осуществить расчет поля в промежуточной зоне (зоне Френеля). Известно также, что для антенн апертурного типа граница дальней зоны в области бокового излучения располагается значительно ближе к антенне, чем эта же граница в области главного лепестка ( здесь указанная граница определяется как
r0 = 2D2/l , где D – максимальный размер антенны ); в случае же антенн осевого излучения (например антенн типа "волновой канал") закономерности формирования дальней зоны оказываются прямо противоположными. Однако получить четкий ответ на вопрос, как же с расстоянием меняются поля произвольных излучателей, не удается. Известны лишь общие соображения [1,2], что в зоне Френеля "на монотонное убывание поля по закону 1/r накладывается осциллирующее затухающее колебание".Исключение составляют, пожалуй, только результаты исследования ближнего поля квадратных и круглых апертур, детально описанные, например, в
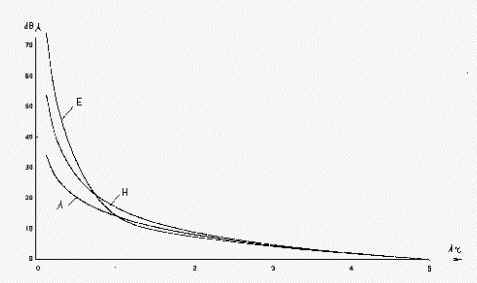
[3, 4]. Что касается антенн проволочного типа, то здесь детально проанализировано [5] только излучение элементарного электрического вибратора ( ЭЭВ ), поле которого, помимо компоненты, пропорциональной 1/r, имеет составляющие, определяемые зависимостями 1/r2 и 1/r3. Именно наличие последних компонент обуславливает резкий (по сравнению с 1/r) рост амплитуды поля при приближении к излучателю, что проиллюстрировано на рис.1, где дано распределение амплитуды электрического и магнитного полей в зависимости от расстояния до ЭЭВ в направлении максимального излучения, т.е. перпендикулярно оси вибратора. Обычно предполагается, (см. например, [6]), что подобные же закономерности имеют место и для других проволочных антенн, поскольку поле этих антенн определяется интегрированием полей соответствующих ЭЭВ. Однако оказывается, что это далеко не так. Результаты исследования структуры ближнего поля ЭЭВ не позволяют, к сожалению, судить о ближнем поле, по крайней мере, в направлении максимума излучения реальных антенн, даже таких простых как симметричные вибраторы.Для рассмотрения вопроса о поведении амплитуды поля проволочных антенн при переходе из дальней зоны в зону Френеля исследуем дискретную систему из
N изотропных излучателей, произвольно расположенных в пространстве. Для такой системы в зоне Френеля справедливо![]()
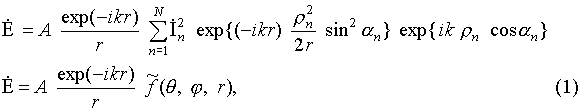
где
r – расстояние, отсчитываемое от начала координат, In – ток в n-ом излучателе,амплитуды поля ![]() определяется совместным действием
функций 1/
определяется совместным действием
функций 1/
Выявить характер зависимости
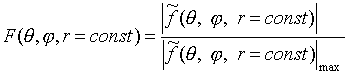 , (2)
, (2)
нормированную к максимальному значению поля при данном значении
r. В дальней зоне, т.е. при r > r0, функцияИзвестно, что оценить отличие функции
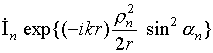 (зависящее от положения точки
наблюдения) и находя для него диаграмму
направленности по обычным формулам дальней зоны.
Ограничимся рассмотрением систем,
сфокусированных на бесконечности. В простейшем
случае, для линейной антенной решетки,
эквивалентное распределение токов отличается от
истинного квадратичным (относительно середины
решетки) изменением фазы, максимальная величина
которого, зависящая от r, соответствует положению
точек наблюдения на перпендикуляре к оси решетки
и убывает до нуля для точек, находящихся на ее
оси. Соответственно, максимальное отличие
(зависящее от положения точки
наблюдения) и находя для него диаграмму
направленности по обычным формулам дальней зоны.
Ограничимся рассмотрением систем,
сфокусированных на бесконечности. В простейшем
случае, для линейной антенной решетки,
эквивалентное распределение токов отличается от
истинного квадратичным (относительно середины
решетки) изменением фазы, максимальная величина
которого, зависящая от r, соответствует положению
точек наблюдения на перпендикуляре к оси решетки
и убывает до нуля для точек, находящихся на ее
оси. Соответственно, максимальное отличие D(r) < D0
при r < r0 , (3)где
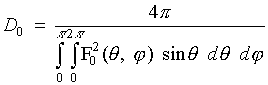
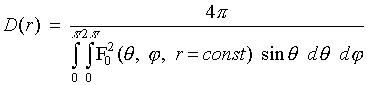
уверенности можно утверждать, что подобное же соотношение (3) имеет место для любых антенных систем, сфокусированных на бесконечности.
Вернемся теперь к радиальной зависимости поля в зоне Френеля. Рассмотрим сначала направление максимального излучения. Представляя модуль напряженности электрического поля в произвольной точке в виде
![]() . (4)
. (4)
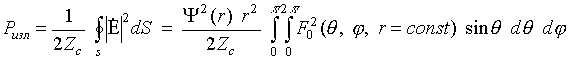 . (5)
. (5)
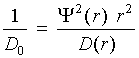 , (6)
, (6)
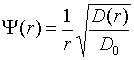 . (7)
. (7)
![]() (8)
(8)
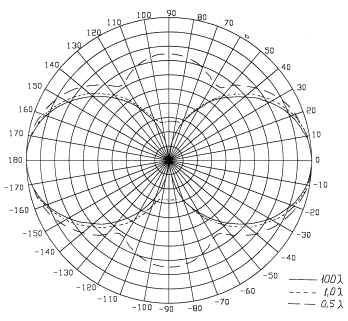
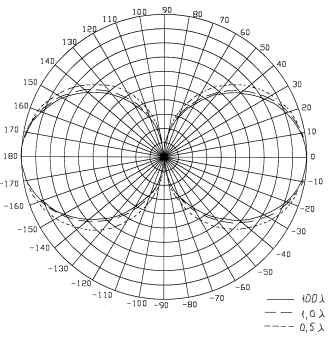
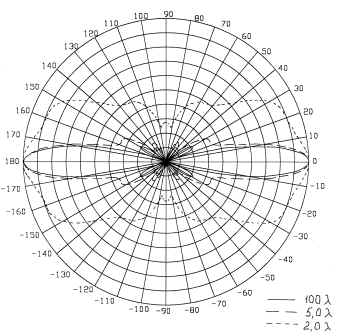
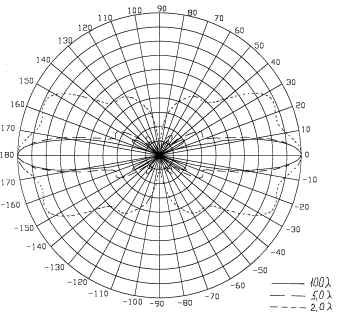
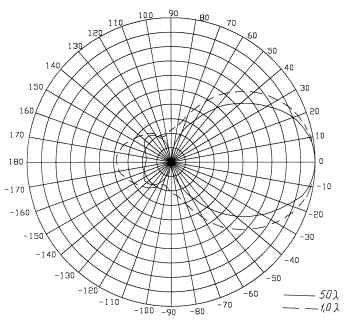
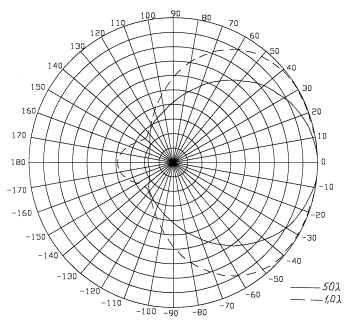
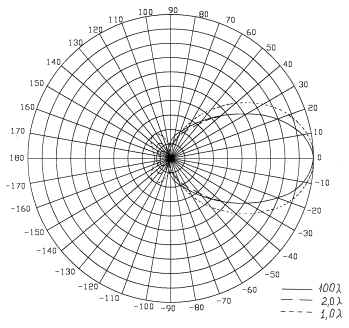
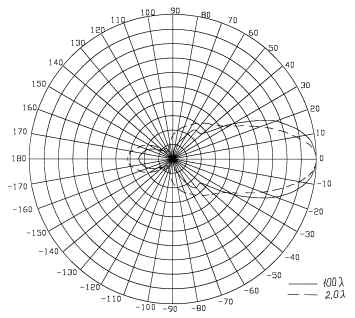
На рис.8 и 9 приведены серии диаграмм
направленности для электрического и магнитного
полей соответственно решетки из четырех
коллинеарных вибраторов резонансной длины,
расположенных с шагом ![]() . Здесь, как и в предыдущем случае,
обращает внимание появление электрического поля
в точках на оси решетки при малых
. Здесь, как и в предыдущем случае,
обращает внимание появление электрического поля
в точках на оси решетки при малых
Графики функции
Результаты исследований позволяют сделать следующие выводы:
Литература:
|
|
|
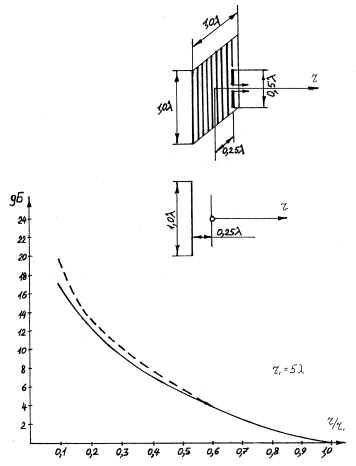 Рис. 4 Рис. 4
|
|
|
|
|
|
|
|
 |
 |
Авторы:
Ерохин Густав Арсентьевич
Кочержевский Вадим Георгиевич
Петровский Андрей Александрович