УДК 519.216
МЕТОД МЕДЛЕННО МЕНЯЮЩЕЙСЯ ЧАСТОТЫ В РАДИОВОЛНОВЫХ ИЗМЕРЕНИЯХ
В. К. Игнатьев, А.
В. Никитин
Волгоградский государственный университет, кафедра радиофизики
Получена 17 октября 2011 г., после доработки - 21 ноября 2011 г.
Аннотация. Показано, что если для волны существует квазигармоническое представление с ограниченной медленно меняющейся частотой, то оно единственно. Необходимым и достаточным условием существования волны с медленно меняющимися амплитудой и частотой является медленное изменение параметров среды, в которой распространяется волна, и то, что источником волны является осциллятор с медленно меняющимися параметрами.
Ключевые слова: волна, квазигармоническое представление, медленно меняющаяся частота, единственность.
Abstract. It is shown that if the quasiharmonious representation for a wave with the limited slowly varying frequency exists, then it is unique. Necessary and sufficient condition for the wave’s with slowly varying amplitude and frequency existence is a slow varying parameters of the environment through the wave propagates, and that the wave’s source is the oscillator with slowly varying parameters.
Key words: wave, quasiharmonious representation, slowly varying frequency, uniqueness.
Введение
Наиболее точно измеряемой физической величиной является частота, современные атомные часы имеют относительную нестабильность порядка 10–15 и ожидается создание квантовых стандартов частоты с нестабильностью на уровне 10–17 [1]. В радиоволновых измерениях частотный метод заключается в извлечении информации об измеряемой величине из мгновенной частоты квазигармонической волны вида
x(r, t) = А(r, t)cos[q(r, t)], (1)
причем частная производная по времени полной фазы q(r, t) называется мгновенной частотой w(r, t) = ¶q(r, t)/¶t, а ее градиент – волновым вектором k(r, t) = ¶q(r, t)/¶r [2]. Однако спектр квазигармонической волны может меняться при ее распространении, например, из-за движения среды, в которой волна распространяется [3]. В результате мгновенная частота, регистрируемая приемником, будет отличаться от мгновенной частоты излучателя. Поэтому при извлечении информации из распространяющегося электромагнитного поля с точностью, которая обеспечивается современными квантовыми стандартами частоты [4] и требуется для систем радиоастрономии, радиоэлектронного противодействия, радиоволновых датчиков и контролируемых с помощью электромагнитных волн параметров технологических процессов [5, 6], необходимо определять динамику не только мгновенной частоты, но и волнового вектора квазиграмонической волны, например, с помощью радиоинтерферометров [7].
Волны с медленно меняющейся мгновенной частотой
Рассмотрим для примера задачу акустической локации. Пусть в системе координат, связанной с приемником по траектории r0(t) движется точечный источник гармонического сигнала с частотой ω0, а однородная несжимаемая среда перемещается со скоростью V(t) = dr1(t)/dt, где r1(t) – координата элемента среды в системе отсчета, связанной с приемником. В системе отсчета, связанной со средой, волновое уравнение будет иметь вид [8]
![]() , (2)
, (2)
где j(r¢, t) – потенциал колебательной скорости u(r¢, t) = –Ñj, c – скорость звука в неподвижной среде, r0¢(t) = r0(t) – r1(t) – координата источника в системе отсчета, связанной со средой.
Решение волнового уравнения (2) имеет вид [8]
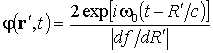 , (3)
, (3)
где R¢ – положительный корень уравнения
f(R¢) = |r¢ – r¢0(t – R¢/c)|2 – R¢2 = 0. (4)
Возвращаясь в систему координат, связанную с приемником, положим в уравнениях (3) и (4) r¢(t) = r – r1(t):
f(R) = |r – r1(t) – r0(t – R/c) + r1(t – R/c)|2 – R2 = 0. (6)
Мгновенная частота и волновой вектор, регистрируемые приемником, будут при этом иметь вид
Дифференцируя уравнение (6) по времени и по координатам и полагая, что скорость среды V меняется медленно и много меньше скорости звука с, получим, что в дальней зоне можно положить R » r0, тогда в начале координат при r = 0 получаем:
Здесь n = r0/r0, a = dV/dt, значение скорости источника v берется в момент времени t – r0/c, а скорости среды V и ее ускорения a – в момент времени t.
Из формул (7) и (8), в свою очередь, следует, что приемник, расположенный в начале координат, зафиксирует следующие мгновенную частоту и волновой вектор:
Здесь v = vn, V = Vn, a = an – радиальные компоненты скорости источника v, скорости среды V и ее ускорения a.
Из формул (9) следует, что независимо от движения источника и среды волновой вектор k(t) = – k(t)n в любой момент времени направлен от источника к приемнику, что соответствует приближению геометрической акустики [8]. Для однородной среды с медленно меняющимися параметрами, в данном случае – скоростью, условия этого приближения выполняются. Кроме того, ω(t) = k(t)(c – V), то есть скорость звука в движущейся среде, измеренная неподвижным приемником, составляет c – V, что соответствует правилу сложения скоростей.
Для неподвижной среды из первой
формулы (9) при V = 0 получается классическая формула
эффекта Доплера ![]() .
Если же источник покоится относительно приемника, а среда движется
неравномерно, приемник зафиксирует частоту
.
Если же источник покоится относительно приемника, а среда движется
неравномерно, приемник зафиксирует частоту
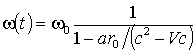 ,
,
а вычисление скорости источника по классической формуле Доплера покажет величину v = – ar0/c. Эта величина – погрешность измерения скорости частотным методом – растет с увеличением расстояния до источника и может оказаться существенной в «порывах» ветра. Даже равномерное движение среды между движущимся источником и приемником вносит относительную погрешность в измерение скорости источника частотным методом, равную V/c.
Все эти погрешности можно исключить, если приемник фиксирует не только мгновенную частоту волны, но и мгновенное значение ее волнового вектора. Тогда из формул (9) получаем
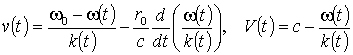 . (10)
. (10)
Первое уравнение (10) можно переписать в виде линейного дифференциального уравнения первого порядка:
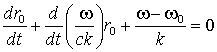 ,
,
решение которого при известном начальном положении источника имеет вид:
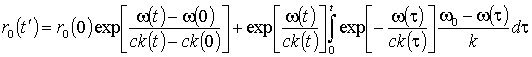 ,
(11)
,
(11)
где t¢ = t – r0/c. Соответственно,
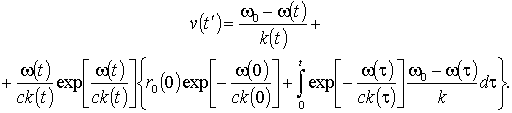 (12)
(12)
Второе слагаемое в формуле (12) представляет вносимую движением среды поправку к измеренной частотным способом скорости источника, вычисляемую по измеренным значениям волнового вектора. Если скорость источника меняется медленно, в формуле (11) можно положить r0(t¢) = r0(t)(1 – v(t)/c).
Заметим, что полученные результаты для звукового поля движущегося источника во многих отношениях сходны с потенциалами Ленарда – Вихерта электромагнитного поля движущегося в вакууме точечного заряда е [9]:
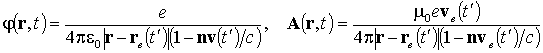 ,
,
где момент времени t¢, в который берется координата заряда re и его скорость ve, связаны с моментом измерения t соотношением ct¢ = ct – |r – re(t¢)|. Если заряд совершает гармонические колебания с частотой ω0 около положения равновесия r0, то есть re(t) = r0 + r1exp(iω0t), |r1| << |r0|, в дальней зоне переменная часть электрического поля будет равна
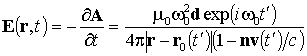 , (13)
, (13)
где d = er1, v = dr0/dt. Нетрудно видеть, что уравнение (13) для проекций электрического поля аналогично уравнению (5) для акустического поля с учетом соотношений (6) и (8).
Влияние движения среды на распространение электромагнитной волны вида (13) можно качественно учесть с помощью известного результата Физо. В движущемся со скоростью u диэлектрике с коэффициентом преломления n скорость света составляет c¢ = c/n + u(1 – 1/n2) [10]. Поэтому в формулу (9) вместо скорости V следует подставить u(n – 1/n). Таким образом, относительная погрешность, вносимая движением среды в частотный метод радиоволновых измерений, составит u(n – 1/n)/c. Для тропосферы n – 1 » 3×10–4 [3], и при скорости ветра 30 м/c эта погрешность составит 6×10–11 и может проявиться лишь в предельных измерениях. Однако для ионосферной плазмы со сложным законом дисперсии соответствующая погрешность может оказаться существенно больше и, например, увеличить погрешность в опыте по измерению скорости нейтрино [11]. Устранить эту погрешность можно измерением волнового вектора в точках синхронизации часов по сигналам GPS [12].
Радиоэлектронные системы локации и связи в большинстве случаев находятся на поверхности Земли и движутся с ней в пространстве, поэтому развитие методов траекторных измерений космических объектов и космической навигации, анализ работы высокоточных доплеровских геодезических систем и ряд других задач требует строгого учета преобразования мгновенной частоты радиосигналов за счет вращения и поступательного движения как радиопередающего и радиоприемного звеньев, так и объекта локации, а также гравитационного поля в пространстве между ними. Так, строгое решение задачи о рассеянии монохроматической (в неподвижной системе отсчета) плоской электромагнитной волны вращающимся телом показывает, что спектр поля рассеяния зависит от отношения периода вращения к времени измерения и электродинамических свойств тела, а отраженная волна является квазигармонической [13] вида (1).
В рамках общей теории относительности неинерциальность системы отсчета может быть учтена введением дополнительных локальных гравитационных полей, гравитация же в отношении своего воздействия на электромагнитное поле играет роль среды с переменными электрической и магнитной проницаемостями [14]. Таким образом, в неинерциальных системах отсчета и с учетом гравитации даже вакуум следует рассматривать как неоднородную среду, формирующую сложную зависимость между волновым вектором и частотой распространяющейся в нем волны (1). В современный радионавигационных системах обычно учитывается влияние гравитационного поля только на мгновенную частоту, но не на волновой вектор электромагнитной волны [4, 12].
Для однозначного описания волны (1) с помощью двух функций – амплитуды (огибающей) А(r, t) и полной фазы q(r, t) необходимо то или иное дополнительное условие. Если в любой точке пространства полная фаза определяется как аргумент аналитического сигнала
z(r,t) = А(r, t)exp[iq(r, t)] = x(r, t) + iy(r, t),
построенного на основе исследуемой волны x(r, t) с помощью преобразования Гильберта [15]:
то огибающая А(r, t) и мгновенная частота w(r, t) волны (1) равны
Можно показать [16, 17], что преобразование Гильберта (14) является единственным непрерывным линейным преобразованием, связывающим функции x(r, t) и y(r, t). Применяются и другие определения полной фазы [18], которые, как и определение Габора [15], являются формально-математическими и могут приводить к физическим противоречиям [19].
Отметим, что вопрос о единственности представления волны в форме (1) существенен, если огибающей и (или) мгновенной частоте сопоставляются измеряемые физические величины, например, огибающая определяет энергию волны, а мгновенная частота связана со скоростью объекта, как в задаче доплеровской локации.
Рассмотрим модельную задачу. Пусть излучателем является электрический диполь, ориентированный вдоль оси y и движущийся равномерно и прямолинейно вдоль оси x со скоростью v << c. Если дипольный момент совершает гармонические колебания с постоянной частотой ω0 и постоянной амплитудой p0, то напряженность магнитного поля в начале координат в приближении дальней зоны и без учета релятивистских эффектов в будет равна [9]
Здесь x(t) – текущая координата диполя и принято, что в момент времени t = 0 излучатель проходит точку x = 0 с нулевой начальной фазой колебания. Если диполь движется с постоянной скоростью, то x(t) = vt, при v << c можно пренебречь доплеровским сдвигом частоты и вычислить преобразование Гильберта (14) для сигнала (16) аналитически:
![]() ,
,
Для огибающей и полной фазы в этом случае по формулам (15) получим
![]() (17)
(17)
Если полагать, что мгновенная частота сигнала, регистрируемого приемником, определяется источником колебаний, а огибающая – расстоянием до приемника, то представление сигнала в форме (17) приводит к физически неправильному результату – источник совершает сложное колебательное движение относительно начала координат, а частота принятого сигнала вдвое меньше, чем частота излученного. Таким образом, в представлении (16) огибающая и мгновенная частота связаны с физическими параметрами системы, а в представлении (17) – нет.
В этом случае нужны физические условия однозначного определения огибающей и полной фазы. Как показано в Приложении, при естественных предположениях, что в любой точке пространства огибающая А(r, t) и мгновенная частота w(r, t) – положительные и непрерывные функции, а w(r, t) ограничена как сверху, так и снизу
одним из таких условий может быть ограниченность носителя спектра мгновенной частоты w(r, t). Заметим, что представление (6) этим условиям удовлетворяет, а основанное на преобразовании Гильберта (14) представление (17) со знакопеременной огибающей – нет.
Пусть в любой точке пространства r мгновенная частота может быть представлена интегралом Фурье:
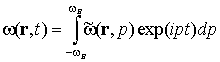 .
.
Тогда для производных мгновенной частоты справедлива оценка
Квазигармоническую волну (1), для которой выполняются условия (18) и (19), естественно назвать волной медленно меняющейся мгновенной частотой (МММЧ).
Существование квазигармонических волн МММЧ
На практике существование квазигармонического представления (1) с медленно меняющейся мгновенной частотой можно обосновать, например, связью параметров волны с медленно меняющимися параметрами среды, в которой распространяется волна, или породившей ее физической системы. Покажем, что для среды с медленно меняющимися во времени параметрами нормальной является волна вида (1) с медленно меняющейся мгновенной частотой. Волновое уравнение для электромагнитной волны в однородной среде без дисперсии с переменными проводимостью s(t), диэлектрической e(t) и магнитной m(t) проницаемостями имеет вид [9]
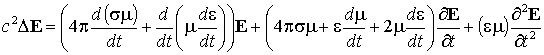 . (20)
. (20)
Будем искать решение уравнения (20) в виде волны с линейной поляризацией, положив E(r, t) = eR(r)T(t). Подставляя это выражение в уравнение (20), с помощью стандартной процедуры разделения переменных получим
![]() , (21)
, (21)
где k – волновое число и обозначено
медленно меняющиеся коэффициенты.
Решение уравнения (21) можно записать в виде
где введен волновой вектор k = km, m – единичный вектор. Уравнение (22), описывающее осциллятор с переменными параметрами, подстановкой
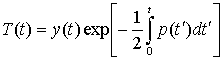 (25)
(25)
приводится к виду
где
Условие медленности изменения параметров осциллятора можно выразить соотношением 1/Ω0τ = μ, μ << 1, или записать следующим образом:
![]() , μ << 1. (28)
, μ << 1. (28)
Если уравнение (22) описывает линейный осциллятор с малыми потерями, то с учетом физических допущений p2(t) ~ μq(t). При таких условиях с математической точки зрения уравнение (26) с медленно меняющимся коэффициентом эквивалентно уравнению с малым параметром μ при старшей производной. Такие уравнения решают с помощью асимптотических методов разложения по малому параметру [2, 20 – 22]. Такая процедура приводит к асимптотическому ряду, который расходится при увеличении количества его членов: при фиксированном μ, начиная с некоторого номера n, следующие слагаемые оказываются больше предыдущих [2, 23]. Поэтому ограничиваются конечным отрезком ряда, например, при использовании приближения ВКБ [21] двумя его членами. При заданных начальных условиях можно представить решение в тригонометрической форме:
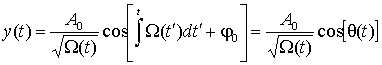 ,
,
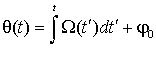 .
.
Здесь A0 и φ0 – константы, определяемые из начальных условий. Возвращаясь к функции T(t), получим
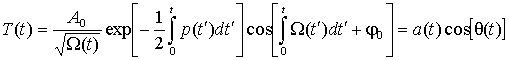 , (29)
, (29)
где
Видно, что введенная ранее как производная полной фазы θ(t) частота ω(t) [2] совпадает с Ω(t). Соотношения (23) и (27) определяют при этом закон дисперсии МММЧ волны. Записывая условие медленного изменения параметров среды и малых потерь в ней в виде
![]() , (31)
, (31)
получим ω(t) = сk/n(t),
где ![]() –
переменный коэффициент преломления. С учетом соотношений (24), (29) и (30) волновой
процесс можно записать в форме (1), где
–
переменный коэффициент преломления. С учетом соотношений (24), (29) и (30) волновой
процесс можно записать в форме (1), где
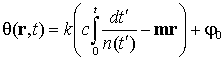 .
(32)
.
(32)
Источником волн МММЧ может быть осциллятор с медленно меняющимися параметрами. К примеру, в ЯМР известны уравнения Блоха для поперечных проекций магнитного момента [24]:
![]() Bx = 0, By = 0,
Bz = B(t),
Bx = 0, By = 0,
Bz = B(t),
из которых легко получается уравнение вида (22) для
свободной прецессии поперечной намагниченности в медленно меняющемся продольном
магнитном поле B(t),
где T(t) = Mx или My,
![]() ,
, ![]() .
.
В волновой зоне
магнитно-дипольное излучение описывается векторным потенциалом [9] ![]() . В дальней зоне волну
можно считать плоской, распространяющейся вдоль оси z.
С учетом формулы (32) волновой процесс можно записать в форме (1):
. В дальней зоне волну
можно считать плоской, распространяющейся вдоль оси z.
С учетом формулы (32) волновой процесс можно записать в форме (1):
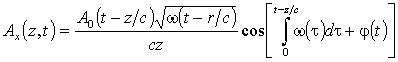 , (33)
, (33)
где
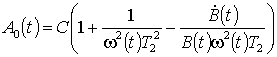 ,
,
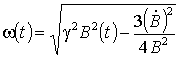 ,
,
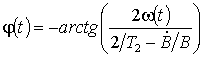 .
.
Из формулы (33) видно, что если магнитное поле медленно меняется во время свободной прецессии, то есть |dB/dt| << w(t)B(t), то магнитно-дипольное излучение будет волной ММЧ. Если возможно по измеренному, например спиновым детектором [24], сигналу (33) динамику мгновенной частоты и амплитуды, можно проследить за динамикой изменения продольного магнитного поля B(t) и времени поперечной релаксации Т2(t), что важно в задачах спектроскопии, томографии, исследовании геомагнитного поля и т. д. Аналогичный результат можно получить для электрического дипольного перехода с помощью оптических уравнений Блоха [24], а так же для любого мультипольного излучения [9].
Зафиксируем в пространстве точку r0, например, координату приемника, в котором квазигармоническая волна (1) создаст колебание
y(t) = x(r0, t) = a(t)cos[j(t)], (34)
где обозначено a(t) = А(r0, t), j(t) = q(r0, t). Рассмотрим колебание вида (34) медленно меняющимися амплитудой и мгновенной частотой (ММАМЧ), условие медленного изменения по аналогии с условием МММЧ (19) можно сформулировать в виде
При выполнении условий ММАМЧ вида (35) любая производная ММАМЧ процесса тоже будет ММАМЧ процессом. Найдем первообразную колебания (34). Интегрируя по частям и полагая, что a(t ® – ¥) ® 0, получаем
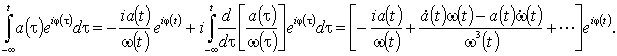
Нетрудно видеть, что при выполнении условий ММАЧ (35) все слагаемые в квадратный скобках являются медленно меняющимися функциями, удовлетворяющими условию (35), а каждое последующее слагаемое имеет порядок малости m по отношению к предыдущему. Поэтому ряд в квадратных скобках быстро сходится к медленно меняющейся функции (амплитуде). Следовательно, первообразная ММАЧ процесса – тоже ММАЧ процесс. Поскольку напряженности полей в волновой зоне пропорциональны первой или второй производной дипольного (или мультипольного) момента [9], для того, чтобы квазигармоническая волна в дальней зоне была волной ММАЧ, необходимо и достаточно, чтобы дипольный момент излучателя был ММАЧ колебанием.
С другой стороны, подстановкой функции (34) в уравнение (22) можно показать, что любое колебание ММАМЧ удовлетворяет дифференциальному уравнению второго порядка с медленно меняющимися коэффициентами вида
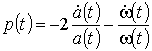 ,
,
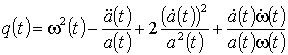 . (36)
. (36)
Таким образом, между медленно меняющимися мгновенной частотой и амплитудой колебания (34) и медленно меняющимися коэффициентами уравнения (22) существует взаимно однозначная связь вида (30) и (36), и можно сформулировать необходимое и достаточное условие того, что квазигармоническая волна была волной ММАЧ – источником волны является осциллятор с медленно меняющимися параметрами, а параметры среды, в которой распространяется волна, медленно меняются во времени.
Аппаратная реализация цифровых параметрических алгоритмов оценивания огибающей и мгновенной частоты квазигармонического сигнала по короткой выборке и эксперименты с реальными электромеханическими системами [25 – 28] подтверждают высокие метрологические характеристики метода медленно меняющейся мгновенной частоты при исследовании нестационарных систем. Отличительной особенностью этого метода является малое количество операций при вычислении огибающей и мгновенной частоты, не зависящее от длительности скользящего окна, в рамках которого производится оценка [28]. Это позволяет реализовать измерительную систему на базе сигнальных процессоров и добиться высокой скорости оценивания огибающей и мгновенной частоты. Дальнейшим совершенствованием этого метода является разработка быстрых алгоритмов для оценивания волнового вектора.
Заключение
Основные мировые производители промышленного оборудования, такие как Siemens, Mitsubishi, Allen-Bradley, Emerson и другие в своих последних разработках и решениях широко используют беспроводные средства измерения и передачи данных. Если для передачи данных, в основном, используют наборы стандартов IEEE 802.11 и 802.15, то для измерений таких стандартов не существует, а датчики и вторичные измерительные приборы постоянно модифицируются в сторону увеличения класса точности и скорости измерений. Важнейшим условием для этого является минимизация методических и динамических погрешностей. Весьма перспективным в задачах дистанционного контроля является частотный метод радиоволновых измерений [6]. Доказанные условия существования и единственности квазигармонического представления волнового процесса позволяют установить взаимно однозначную связь огибающей и мгновенной частоты сигнала приемника с медленно меняющимися физическими параметрами породившей волну системы или среды, в которой она распространяется, без предположений об узкополосности волнового процесса.
Приложение. Единственность квазигармонического представления МММЧ волны
Предположим, что квазигармоническое представление (1) для волны ММЧ не единственно, то есть помимо функций А(r, t) и q(r, t) существуют еще функции B(r, t) и J(r, t) такие, что x(r, t) = B(r, t)cos[J(r, t)], причем и функция q(r, t), и функция J(r, t) удовлетворяют условиям (18) и (19) во всех точках пространства, но при этом J(r, t) не равна тождественно q(r, t). Это значит, что существует, по крайней мере одна, точка r0, такая, что в какой-то момент времени t = t¢ имеет место неравенство J(r0, t¢) ≠ q(r0, t¢). Из непрерывности функций q(r, t) и J(r, t) следует, что это неравенство выполняется и в некоторой окрестности момента времени t¢.
Зафиксируем в пространстве точку r0 и рассмотрим колебание вида (34)
y(t) = x(r0, t) = a(t)cos[j(t)] = b(t)cos[y(t)], (37)
где обозначено a(t) = А(r0, t), j(t) = q(r0, t), b(t) = B(r0, t), y(t) = J(r0, t). По предположению о не единственности квазигармонического ММЧ представления j(t) ≠ y(t), но обе мгновенные частоты w(t) = dj(t)/dt и w1(t) = dy(t)/dt удовлетворяют условиям (18) и (19).
Пусть функция y(t) вида (37) имеет нули в моменты времени tk, образующие монотонную последовательность без конечных предельных точек. Из непрерывности и положительности функций a(t) и b(t) следует, что
j(tk) = y(tk) = qk = pk – p/2. (38)
Здесь принято, что в момент времени t = t0 = 0 функция y(t) проходит через ноль с положительной производной. Таким образом, нахождение полной фазы j(t) сводится к решению интерполяционной задачи для неэквидистантной последовательности точек (узлов интерполяции) tk.
Задача интерполяции (35) всегда имеет решение, не обязательно в виде ряда Лагранжа, в классе целых аналитических функций, какими бы ни были действительные числа tk и qk [29]. Это решение не является единственным. Пусть целые функции j(z) и y(z), где z = t + iu, являются решением интерполяционной задачи (38). Из условия (18) положительности мгновенной частоты следует, что в точках z = tk функция cos[j(z)] имеет простые нули. Тогда функция
c(z) = [y (z) – j(z)]/cos[j(z)]
тоже является целой аналитической, так как нули ее знаменателя совпадают с нулями числителя. Поэтому общее решение интерполяционной задачи (38) в классе целых функций имеет вид
y(z) = j(z) + c(z)cos[j(z)], (39)
где c(z) – произвольная целая функция.
Покажем, что решение интерполяционной задачи (38) единственно в классе целых функций с финитным спектром. Пусть существует конечный предел
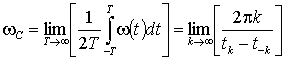 . (40)
. (40)
Естественно, что wm £ wС £ wM. Из ограниченности мгновенной частоты следует, что полная фаза q(t) растет при |t| ®¥ не быстрее чем t. Если носителем спектра функции q(t) является отрезок [–wВ, wВ], причем wВ < wС, то в силу теоремы Винера – Палея – Шварца [30, 31] ее аналитическое продолжение j(z) является целой функцией конечной степени (типа), меньшей чем wС.
Целая функция конечной степени имеет первый порядок. Из теоремы о порядке произведения целых функций [32] следует, что для того чтобы функция y(z), не равная тождественно j(z), также имела конечную степень, меньшую wС, необходимо, чтобы и функция cos[j(z)] имела порядок не выше первого. Целая функция cos(z) имеет первый порядок, поэтому сложная функция cos[j(z)] может иметь первый порядок только в случае, если j(z) – многочлен [33]. Но многочлен степени выше первой растет на действительной оси быстрее, чем |t|, что противоречит условию (15) ограниченности мгновенной частоты.
Таким образом, различные решения интерполяционной задачи (38) возможны лишь при j(t) = w0t – p/2. Но спектр функции вида (39)
y(t) = w0t – p/2 + c(t)cos(w0t – p/2) (40)
ограничен сверху частотой w0 + wc ≥ wС > wВ, где wc – верхняя граничная частота спектра функции c(t), так как для колебания (37) с полной фазой (9) из условия (40) следует wС = w0. Таким образом, при c(t) не равной тождественно нулю спектр функции y(t) не является финитным, что и доказывает единственность решения интерполяционной задачи (35) в классе целых функций с финитным спектром. При этом финитности спектра амплитуды a(t) и самого колебания y(t) не требуется.
Если предел (40) не существует, класс единственности решения интерполяционной задачи (38) определяется условием wВ < wm. Условие положительности амплитуды a(t) также можно ослабить. Достаточно того, чтобы функция a(t) имела нули в счетном множестве точек tm, которые полагаются известными. Тогда из множества узлов интерполяции tk следует исключить простые нули сигнала x(t), совпадающие с числами tm.
Поскольку производная целой функции имеет тот же порядок и степень, что и сама функция [32], мгновенная частота в силу теоремы Винера – Палея – Шварца [30, 31] также должна быть целой функцией с финитным спектром, удовлетворяющей условию (19).
С другой стороны, при выполнении
условия (19) коэффициенты разложения cn
аналитической функции w(t)/wC в ряд Тейлора в произвольной точке удовлетворяют
условию ![]() .
Тогда для степени a этой функции получаем
[32]
.
Тогда для степени a этой функции получаем
[32] ![]() и по
теореме Винера – Палея – Шварца [30, 31] мгновенная частота w(t) имеет
финитный спектр, ограниченный частотой wB < wC. Таким образом, если для колебания существует
представление (37) с медленно меняющейся частотой, удовлетворяющей условиям (18)
и (19), то оно единственно. В общем случае это представление может не являться
аналитическим сигналом. Но из единственности квазигармонического представления
ММЧ колебания (37) следует, что y(t) ≡ j(t), что, в свою очередь, противоречит предположению о не единственности
представления (1) квазигармонической волны с медленно меняющейся частотой.
и по
теореме Винера – Палея – Шварца [30, 31] мгновенная частота w(t) имеет
финитный спектр, ограниченный частотой wB < wC. Таким образом, если для колебания существует
представление (37) с медленно меняющейся частотой, удовлетворяющей условиям (18)
и (19), то оно единственно. В общем случае это представление может не являться
аналитическим сигналом. Но из единственности квазигармонического представления
ММЧ колебания (37) следует, что y(t) ≡ j(t), что, в свою очередь, противоречит предположению о не единственности
представления (1) квазигармонической волны с медленно меняющейся частотой.
Вопрос об условиях, которым должен удовлетворять волна, чтобы для нее существовало квазигармоническое представление (1) с медленно меняющейся частотой, сводится к задаче об условиях, которым должна удовлетворять последовательность tk нулей функции x(t), чтобы числа qk = pk – p/2 могли быть значениями функции с финитным спектром, взятыми в моменты tk [34]. Поскольку последовательность qk бесконечно большая, эти условия могут быть излишне ограничительными или не иметь ясного физического смысла [35]. Например, может быть усилено условие (40) [34]:
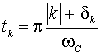 ,
,
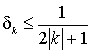 ,
, ![]()
Работа поддержана грантом РФФИ 10-07-9713р_а.
Литература
1. Риле Ф. Стандарты частоты. Принципы и приложения / Пер. с англ. – М.: ФИЗМАТЛИТ, 2009. – 512 с.
2. Трубецков Д. И., Рожнев А. Г. Линейные колебания и волны: Учеб. пособие. – М.: Физматлит, 2001. – 416 с.
3. Яковлев О. И., Якубов В. П., Урядов В. П., Павельев А. Г. Распространение радиоволн. – М.: ЛЕНАНД, 2009 – 496 с.
4. Ashby N. Relativity in the Global Positioing System. [Электронный ресурс]. – Режим доступа: http://relativity.livingreviews.org/Articles/lrr-2003-1
5. Перунов Ю. М., Фомичев К. И., Юдин Л. М. Радиоэлектронное подавление информационных каналов систем управления оружием. – М.: Радиотехника, 2003. – 416 с.
6. Викторов В. А., Лункин Б. В., Совлуков А. С. Радиоволновые измерения. – М.: Энергоатомиздат, 1989. – 208 с.
7. Томпсон Р., Моран Дж., Свенсон Дж. Интерферометрия и синтез в радиоастрономии. – М.: ФИЗМАТЛИТ, 2003. – 624 с.
8. Блохинцев Д. И. Акустика неоднородной движущейся среды. – М.: Наука, 1981. – 208 с.
9. Бредов М. М., Румянцев В. В., Топтыгин И. Н. Классическая электродинамика. – М.: Физматлит, 1985. – 400 с.
10. Бутиков Е. И. Оптика. – М.: Высшая школа, 1986. С. 395.
11. Measurement of the neutrino velocity with OPERA detector in the CNGS beam. Adam T. at all. [Электронный ресурс]. – Режим доступа: http://arxiv.org/ftp/arxiv/papers/1109/1109.4897.pdf.
12. Одуан К. Гино. Б. Измерение времени. Основы GPS. – М.: Техносфера, 2002 – 400 с.
13. Петров Б. М. Прикладная электродинамика вращающихся тел. – М.: Горячая линия – Телеком, 2009. – 288 с.
14. Ландау Л. Д., Лифшиц Е. М. Теория поля. – М.: Наука, 1973. – с. 328.
15. Gabor D. // JIEE. – 1946. – V. 93. – P. 429 – 457.
16. Вакман Д. Е. // Радиотехника и электроника. – 1972. – Т. 17. – № 5. – С. 972 – 978.
17. Титчмарш Э. Ч. Введение в теорию интегралов Фурье. – М.: ОГИЗ, 1948. – С. 159 – 161.
18. Cohen L. // Proc. IEEE. 1989. – V. 46. – № 7. – P. 941 – 981.
19. Вайнштейн Л. А., Вакман Д. Е. Разделение частот в теории колебаний и волн. – М.: Наука, 1983. – 288 с.
20. Островский Л. А., Потапов А. И. Введение в теорию модулированных волн. – М.: Физматлит, 2003. – 400 с.
21. Федорюк М. В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. – М.: Наука, 1983. – 352 с.
22. Ломов С. А. Введение в общую теорию сингулярных возмущений. – М.: Наука, 1981. – 400 с.
23. Ландау Л. Д., Лифшиц Е. М. Квантовая механика. Нерелятивистская теория. – М.: Физматлит, 2004. – 800 с.
24. Квантовая радиофизика / под ред. В. И. Чижика. СПб.: Изд-во СПбГУ, 2004. – 689 с.
25. Игнатьев В. К., Никитин А. В., Юшанов С. В. // Изв. вузов. Электромеханика. – 2009. – № 2. – С. 28.
26. Игнатьев В. К., Никитин А. В., Юшанов С. В. // Известия вузов. Радиофизика. – 2010. – Т. LIII – № 2. – C. 145 – 159.
27. Игнатьев В. К., Никитин А. В., Хоружий Д. Н., Юшанов С. В. // Измерительная техника. – 2011. – № 1. – С. 32 – 36.
28. Игнатьев В. К., Никитин А. В., Юшанов С. В. // Журнал Радиоэлектроники [Электронный ресурс]. – 2011. – № 8. – 14 с. – Режим доступа: http://jre.cplire.ru/jre/aug11/7/text.pdf, свободный. – Загл. с экрана.
29. Гельфонд А. О. Исчисление конечных разностей. – М.: Физматгиз, 1959. – 212 с.
30. Хургин Я. И, Яковлев В. П. Финитные функции в физике и технике. – М.: Наука, 1971. – 408 с.
31. Гельфанд И. М., Шилов Г. Е. Обобщенные функции и действия над ними. – М.: Физматгиз, 1958. – 276 с.
32. Леонтьев А. Ф. Целые функции. Ряды экспонент. – М.: Наука, 1983. – 176 с.
33. Polya G. // Journal London Math. Soc. – 1926. – V. 1. – P. 12 – 15.
34. Евграфов М. А. Асимптотические оценки и целые функции. – М.: Наука, 1979. – 320 с.
35. Левин Б. Я. Распределение корней целых функций. – М.: Гостехтеориздат, 1956. – 632 с.
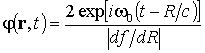 , (5)
, (5)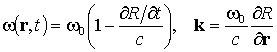 . (7)
. (7)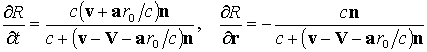 . (8)
. (8)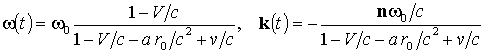 . (9)
. (9)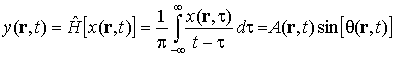 , (14)
, (14)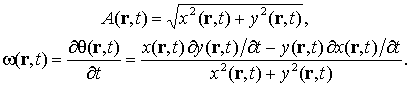
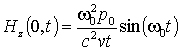
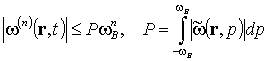 .
(19)
.
(19)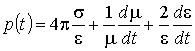 ,
,
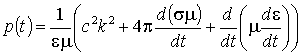 – (23)
– (23)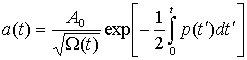 ,
,
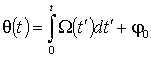 . (30)
. (30)