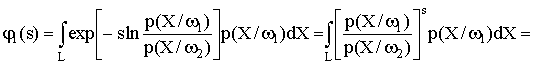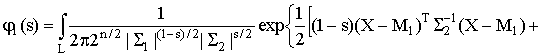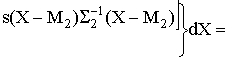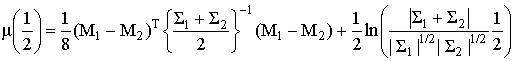| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4, 2006 |
|
УДК 621.396.96
Применение байесовского классификатора для распознавания классов целей
С. В. Субботин,
Д. Ю.
Большаков
ОАО "Научно-исследовательский электромеханический
институт" (ОАО "НИЭМИ")
Получена 11 октября 2006 г.
На основе минимизации верхней границы Чернова для вероятности ошибки и расстояния Бхатачария синтезирован байесовский классификатор для распознавания классов целей. Проведено сравнение данного классификатора с существующими методами распознавания классов целей, позволяющее установить его преемственность. Рассмотрен пример использования предлагаемого классификатора.
Один из способов распознавания классов целей основан на байесовском подходе к решению поставленной задачи [1].
Пусть в процессе радиолокационного наблюдения получено некое множество измеренных признаков объекта, составляющих вектор наблюдений. Предположим, что вектор наблюдений представляет собой случайный вектор с условной плотностью вероятности, зависящей от принадлежности его к определенному классу целей. Если условная плотность вероятности известна для каждого класса целей, то задача распознавания классов целей сводится к статистической проверке гипотез.
Предположим, что вектор Х - вектор наблюдений объекта. Необходимо определить принадлежность этого объекта классу
или
с учетом решающего правила, которое можно выразить через логарифм отношения правдоподобия [1]:
где
- условная плотность вероятности вектора Х при определении его принадлежности к классу
,
- априорная вероятность i-го класса,
- пороговое значение отношения правдоподобия.
Уравнение (1) называют байесовским критерием, минимизирующим ошибку отнесения объекта к данному классу.
Для нахождения вероятности ошибки в замкнутой форме может быть использовано выражение для верхней границы вероятности (граница Чернова) [2]. Минимизация выражения для верхней границы вероятности ошибки приводит к минимаксному критерию. Этот критерий сводит к минимуму не средний риск, а максимально возможное значение условного риска. Из определения минимаксного критерия следует, что он обеспечивает наилучшее решение для наихудшего случая. Любое минимаксное решение есть байесовское [3]. Введем для класса целей
характеристическую функцию
решающего правила
:
где
- условная плотность решающего правила.
Можно получить производящую функцию решающего правила
, заменяя комплексный аргумент
в формуле (2) на действительное число
:
Логарифмируем производящую функцию, берем логарифм со знаком минус и получаем
Введем новую случайную величину
, имеющую следующую плотность вероятности:
Случайная величина
имеет следующие математическое ожидание и дисперсию:
Учитывая, что вероятность ошибки
объектов первого класса равна
(7)
и принимая во внимание, что при
справедливо неравенство
выражение (7) при
можно представить в виде
Так как интеграл в выражении (9) меньше 1, получаем
Поскольку верхнюю границу вероятности ошибки, определяемую уравнением (10), при оптимальном значении s называют границей Чернова, то оптимальное значение s должно удовлетворять равенству
Соотношения (6) и (11) показывают, что значение s выбрано так, чтобы математическое ожидание случайной величины g было равно величине порога.
Формулы (6) – (11) позволяют определить верхнюю границу вероятности ошибки
объектов второго класса
Из выражения (12) следует, что верхняя граница вероятности ошибки при
равна
где
- оптимальное значение, которое можно получить из уравнения (11).
Вероятность суммарной ошибки равна
Из-за трудности нахождения оптимального значения s и малой чувствительности аргумента
вблизи оптимума, как правило, выбирают значение
, с помощью которого можно решить уравнение (11) при
. В этом случае выражение (14) принимает вид
Величину
называют расстоянием Бхатачария [2].
Для того, чтобы найти расстояние Бхатачария, выразим производящую функцию в выражении (3) через условные плотности вероятностей
где L - область определения функций условных плотностей вероятностей.
В случае нормального закона распределения признаков распознавания производящая функция в некоррелированной системе равна [2]
(17)
где
,
- матрицы математических ожиданий набора признаков первого и второго классов соответственно;
,
- ковариационные матрицы набора признаков первого и второго класса соответственно.
Подставляя выражение (17) в формулу (4), имеем
(18)
Соотношение (18) при
равно
В качестве классификатора для распознавания целей будем использовать правую часть формулы (19).При независимости признаков в соответствующих векторах объектов первого и второго классов, т.е. при
, i = 1,2, где I - единичная матрица, из выражения (19) следует, что предлагаемый классификатор может быть отнесен к классификаторам основанным на принципе вычисления минимума расстояния в непараметрических одноэтапных методах многоальтернативного распознавания. Эти классификаторы предусматривают принятие решения о классе объекта i =1,M по минимуму расстояния
или их квадратов
от точки многомерного пространства признаков, определяемой оценочным вектором
до точек
, соответствующих условным средним значениям векторов признаков для объектов i различных классов. В нашем случае речь идет о квадрате расстояния между средними значениями векторов признаков для объектов первого и второго классов. Могут использоваться евклидово расстояние, расстояние в пространстве обобщенных признаков или расстояние Махалонобиса [3]. Последнее определяется, исходя из того, что известны как условные средние значения векторов признаков, так и соответствующие корреляционные матрицы Фi для векторов признаков объектов различных классов
Выражение (20) с точностью до значения элементов ковариационных матриц совпадает с первым слагаемым правой части соотношения (19). Кроме того, выражение (20) с точностью до логарифмического слагаемого совпадает с оптимальным байесовским методом для признаков с гауссовой статистикой, где признаками служат отсчеты принимаемой выборки.
Проведенное выше сопоставление предлагаемого классификатора для распознавания классов целей с разработанными ранее методами [1] свидетельствует об их тождественности в частных случаях и подтверждает преемственность классификатора.
Предлагаемый классификатор для распознавания целей при произвольном числе объектов выполняет следующие действия:
- выбор эталонного класса объектов и соответствующего ему набора признаков;
- попарное сравнение набора признаков данного класса и эталонного класса, т.е. вычисление расстояния Бхатачария между любым из предъявленных к распознаванию классов и эталонным классом, в соответствии с выражением (19);
- выбор минимального расстояния Бхатачария для одного из классов целей, т.е. идентификация этого класса с эталонным.
К несомненному преимуществу предлагаемого классификатора относится отсутствие сравнения условных плотностей вероятностей (1) с порогом, величина которого в общем случае будет разной для каждой пары сопоставляемых классов целей.
Рассмотрим пример реального распознавания трех классов целей, основанный на данных натурных экспериментов. В результате радиолокационных наблюдений за объектами получены дискретные вейвлет-спектры этих объектов [4]. Отметим, что в отличие от преобразования Фурье, вейвлет-преобразование обеспечивает двумерную развертку исследуемого одномерного сигнала, при этом частотная и временная оси являются независимыми, что дает возможность проводить анализ свойств сигнала одновременно в частотном и временном пространствах.
Для построения каждого дискретного вейвлет-спектра использовалось 512 временных отсчетов нормально распределенного сигнала.
В качестве признаков распознавания классов выберем математическое ожидание, дисперсию и коэффициенты ковариации дискретных вейвлет-спектров объектов классов A, B, C.
Проверка предлагаемого классификатора для распознавания целей осуществлялась для случая, когда эталонным последовательно считался каждый из рассматриваемых трех классов. Это дало возможность оценить работу классификатора не только по разграничению классов целей, но и по объединению однотипных целей в один класс.
Результаты расчета вероятностей распознавания классов целей с помощью предлагаемого классификатора представлены в таблице. Отметим, что число независимых экспериментов (выборок) составило 51, что обеспечивает достоверность расчета 95% [5].
|
Вероятность распознавания класса цели |
|||
|
Распознаваемый класс |
Эталонный класс |
||
A |
B |
C |
|
|
A |
0.725 |
0.118 |
0.157 |
|
B |
- |
0.824 |
0.098 |
|
C |
- |
- |
0.784 |
Матрица вероятностей
распознавания классов целей имеет симметричный относительно главной диагонали
вид, поэтому элементы ниже главной диагонали в таблице не представлены.
Из таблицы следует, что, например, вероятность правильного распознавания объекта класса B при эталонном классе B составляет 0.824, а вероятность ошибочного принятия объекта класса A за объект класса B составляет 0.118.
Предлагаемый классификатор для распознавания классов целей обеспечивает достаточно высокие вероятности правильного распознавания: 0.7-0.8, а вероятности ошибочного распознавания не превышают 0.2. Это свидетельствует о целесообразности практического использования данного классификатора.
ЛИТЕРАТУРА
1. ПАТРИК Э. Основы теории распознавания образов. /Пер. с англ; Под ред. Б.Р. Левина. – М.: Сов. Радио, 1980.
2. ФУКУНАГА. К. Введение в статистическую теорию распознавания образов. /Пер. с англ. – М.: Наука, 1979.
3. ШИРМАН Я.Д., Горшков С.А., Лещенко С.П. и др. Методы радиолокационного распознавания и их моделирование. - Зарубежная электроника. – 1996. - № 11. c. 3-63.
4. СУББОТИН С.В., Большаков Д.Ю. Сравнительный анализ фильтрации сложного сигнала при малом отношении сигнал - шум с помощью дискретного вейвлет-преобразования и быстрого преобразования Фурье. – Вычислительные устройства и ПО РЛС (тематический сборник, вып. 2) ОАО "Концерн ПВО "Алмаз-Антей", 2005, - c. 108-112
5. ПУГАЧЕВ В.П. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. – М.: Мир, 1995.
Авторы: Субботин Сергей Валентинович, Большаков Денис Юрьевич zuml@mail.ru, ОАО "Научно-исследовательский электромеханический институт" (ОАО "НИЭМИ")
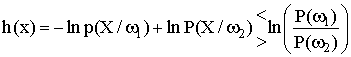
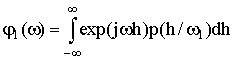 . (2)
. (2)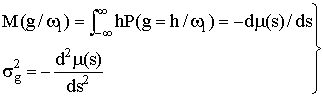 (6)
(6)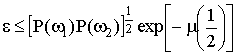 . (15)
. (15)