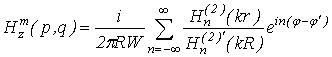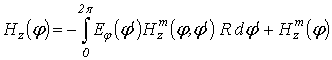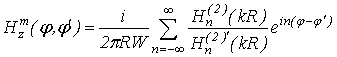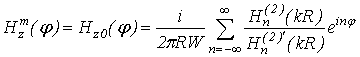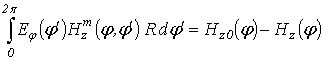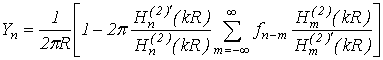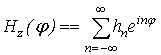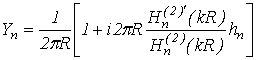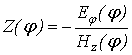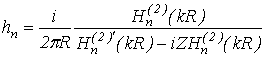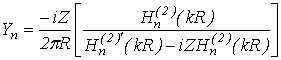synthesis of impedance cylinder
Jean-François D. Essiben
University of Douala (Ecole Normale Supérieure d`Enseignement Technique),
Department of Electrical Engineering, B.P. 1872 Douala-Cameroon
Received March 27, 2007The problem of synthesis for an infinite circular impedance cylinder is theoretically/numerically investigated. The obtained law of impedance distribution must provide, with higher speed, the electromagnetic field attenuation along the structure, as compared with an ideally conducting cylinder. Numerical simulations are presented.
I. Introduction
Artificially soft and hard surfaces have received increased attention in recent years [1]. The concept of artificially soft and hard surfaces has been introduced to generally characterize how loaded surfaces interact with electromagnetic (EM) waves. It has been shown that such surfaces can be used systematically to control the radiation, scattering and propagation characteristics of the waves and, thereby, they can be used to design better antennas. The most common soft surface is the quarter wavelength deep, transversely corrugated surface [2]. It is also possible to realize the soft boundary condition by other means, e.g., by coating a metal surface with a strip-loaded dielectric or magnetic material, which even may be anisotropic or lossy [2]. The soft surface can also be used to reduce coupling between antennas [3]−[9], and to improve the performance of element antennas on ground planes [10]. There are also exists other applications. As the review of articles shows [2]−[9], most of the authors also consider the influence of different structure parameters (or their combination) on their characteristics, i.e., only the problems of analysis are solved. However, effective design of these metamaterials (periodic structures) requires to set and solve the problem of synthesis. The purpose of the present paper is the solution of the problem of synthesis of a circular impedance cylinder, with the purpose of creation on their basis effective decoupling structures.
II. Formulation of the problem
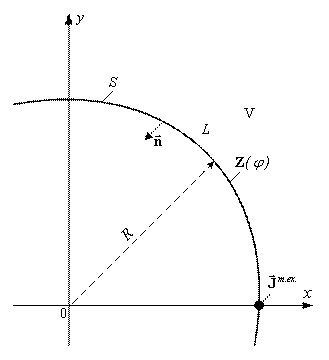
Let us consider the solution of the two-dimensional problem of synthesis in the following statement. On the circular impedance cylinder
with radius
, let there be located an antenna in the shape of infinite thread of in-phase magnetic current, directed along axis
(Fig. 1).
The opening of a narrow parallel-plate waveguide can serve as a physical model of such a radiator. The environment, which fills up the unlimited space, is homogeneous, isotropic and linear [11].
On the surface
It is necessary to define the distribution law of passive impedance
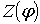
, by the stated law of magnetic field alteration
on the surface
Fig. 1. Geometry of the problem.
III. Solution of the synthesis problem
For the solution of the problem, we will use the Lorentz lemma in the integral form [11]:
where
are vectors of intensity required of the electric and magnetic fields, respectively in volume
;
are vectors of intensity of the electric and magnetic fields of the auxiliary source in volume
are complex amplitudes of densities of currents of the auxiliary electric and magnetic sources in volume
are amplitudes of densities of linear currents of by-side source threads;
is an external normal to a surface
is the region of placement of an external source.
In accordance with the stated polarization of the radiated field, we will choose the thread of in-phase magnetic current parallel to axis
where
is a two-dimensional delta-function;
are the points of arrangement of an auxiliary source and observation, respectively;
is a current amplitude.
To simplify the solution of the stated problem, in the integral correlation (3), we will impose the boundary conditions on the auxiliary fields:
In this case, for the magnetic field of the thread of current (4) on the surface of the ideally conducting cylinder (Fig. 1), we will obtain:
where
an imaginary unit;
is the characteristic resistance;
is the Hankel function of the second kind and
order, and
its derivative;
are the points of observation and integration.
IV. Integral equation
From the Lorentz lemma (3), placing the subsidiary source
on the surface of the cylinder, we will obtain the integral equation:
where
is the field of the thread of current (1) on the surface of the ideally conducting cylinder.
Let us next consider that the complete magnetic field
on the surface of the cylinder is stated, then from (7) relative to the complete electric field
, we will obtain the Fredholm integral equation of the first kind:
The solution of the equation (10) relative to
In this case, the realizability of the required impedance is not imposed any limitations. It can be checked in the process of calculations and thus, the class of the realized passive impedance decoupling structures is defined.
In order to find analytically the complete field along the impedance structure, we will present
the following way:
where
is the function specifying the law of the complete field behavior on the surface of the cylinder.
Solution of the integral equation (10), taking into account (8), (9) can be written in the manifest form:
where
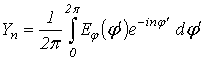
are the coefficients of vector decomposition
on the surface of the cylinder;
.
If the stated complete magnetic field presented immediately as a complex Fourier series:
then the solution of integral equation (10) is the following:
The solution of integral equation (10) can be presented as a sum of two functions:
,
where in accordance with (14)
;
.
The required impedance we will find from the boundary conditions (2)
In (15) the impedance can acquire any values depending on the stated field
. The condition of physical realizability of the passive impedance
, will define the class of the realized decoupling structures.
If the decoupling structure is a homogeneous comb, it can be presented as homogeneous surface impedance
.
The solution of integral equation in this case is the following:
V. Numerical Results and Discussion
Below we present the results of decoupling for the homogeneous surface impedance and the synthesized law of impedance.
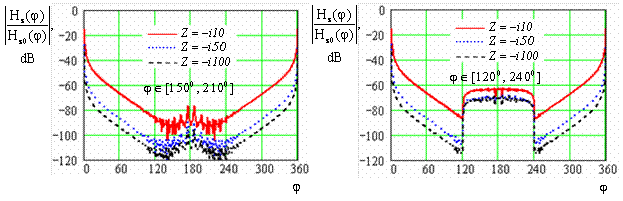
Fig. 2 (a) shows the dependences
on the surface of the circular cylinder with electric radius
, calculated for the constant reactive impedance (normalized to
)
(solid line),
(dotted line) and
(dashed line). As we can see, on the surface of the cylinder, as compared with a plane, the same levels of field reduction can be obtained with smaller values of reactance. In the space of deep shadow
the influence of impedance is reduced.
The analysis of numeric research results showed that with big negative values of the impedance «pushing» the field from the surface of the cylinder, the complete field along the impedance structure reduced by the law
where
.
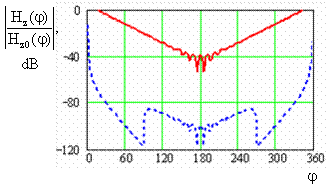
Fig. 2 (b) shows examples of behavior of the complete field on the surface of the same cylinder, at which only the shadow part of
surface of the cylinder is ideally conducting. Curves in Figs. 2 (b) and 3 correspond with other. As we can see, the presence of the ideally conducting part of a shadow surface practically has not affected the field in its impedance part.
(a) (b)
Fig. 2 Behaviors of the magnetic field along the structure, calculated for different values of the homogeneous surface impedance
with
(a) and
(b).
As an example, Fig. 3 shows the behavior of fields of completely ideally conducting cylinder (solid line) and the cylinder, at which ideally conducting is only the part of
surface (dashed line).
Fig. 3. Behavior of the magnetic field along the structure with
.
Let us now state the complete magnetic field on the impedance part as:
where
is the coefficient of attenuation
.
The synthesized impedance has to provide with a higher speed, the electromagnetic field attenuation along the structure, as compared with the ideally conducting cylinder. The speed of attenuation is defined by the value of
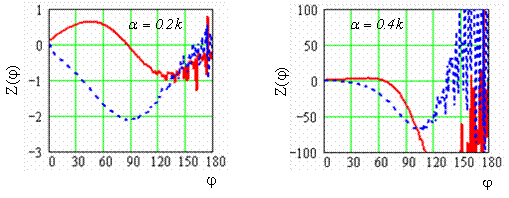
(a) (b)
Fig. 4. Laws of the synthezised impedance, calculated for
(a) and
(b).
As an example, Figs. 4 (a) and (b) show the laws of the synthesized impedance distribution about the surface of the cylinder
(solid line) and
(dashed line), calculated for the attenuation coefficients
(Fig. 4 (a)) and
(Fig. 4 (b)). As we can see, the synthesized impedance, as it was anticipated above, has spaces with negative real parts in the shadowed surface of the cylinder
. As the further research and calculations results in Figs. 3, 4 and 5 showed, on these spaces real parts of the impedance can be eliminated.
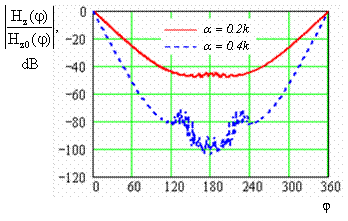
Fig. 5 shows the dependences
Fig. 5. Behavior of the magnetic field along the structure, calculated for
and
.
Numerical research showed that the questions of synthesis of impedance structures, which provides decoupling of antennas on a cylinder, to a great extent correspond with the analogical problems for a plane. Many of the found regularities have the same character for both surfaces.
VI. Conclusion
Thus, the problem of synthesis of the circular impedance cylinder with the purpose of creation on his basis decoupling structure is solved. However, during the solution of the problem of synthesis the interaction between antennas was not taken into account. It is evident that the presence of the receiving aperture antenna will lead to undesirable reduction of antennas decoupling, by means of inhomogeneous character, created by the aperture of the receiving antenna. That is why it is required to research this question as well.
Acknowledgment
The author wishes to thank Prof. Yu.V. Yukhanov, of Taganrog (Russia) State University of Radio Engineering, for helpful discussions
References
George Goussetis, Alexandros P. Feresidis, and Panagiotis Kosmas, “Efficient Analysis, Design, and Filter Applications of EBG Waveguide with Periodic Resonant Loads”, IEEE Transactions on Microwave Theory and Techniques, vol. 54, No. 11, November 2006, pp. 3885–3892.
Zhinong Ying, Per-Simon Kildal, Ahmed A. Kishk, “Study of Different Realizations and Calculation Models for Soft Surfaces by Using a Vertical Monopole on a Soft disk as a Test Bed”, IEEE Transactions on Antennas and Propagation, vol. 44, pp. 1474-1481, No. 11, Nov. 1996.
Ruey Bing Hwang, Song Tsuen Peng, “Surface-Wave Suppression of Resonance-Type Periodic Structures”, IEEE Transactions on Antennas and Propagation, vol. 51, No. 6, June 2003, pp. 1221–1229.
A.G. Kurkchan, M.Kh. Zimnov, “Coupling between Antennas on a Cylinder in the Presence of Corrugated Structures”, Radiotechnics and Electronics, Vol. 12, No. 9, pp. 2308 -2315, 1985.
D. Sievenpiper and E. Yablonovitch, “Eliminating Surface Currents with Metallodielectric Photonic Crystals”, IEEE International Microwave Symposium Digest, Baltimore, MD, vol. 2, June 7-12, 1998, pp. 663–666.
R. Kim and H.Y.D. Yang, “Surface Waves and Leaky Waves in Integrated Circuit Structures with Planar Periodic Dipole Loading”, IEEE APS-International Symposium Digest, salt Lake city, UT, vol. 1, July 17–21, 2000, pp. 346-349.
R. Coccioli and T. Itoh, “Design of Photonic Bandgap Substrates for Surface-Wave Suppression”, IEEE International Microwave Symposium Digest, Baltimore, MD, vol. 3, June 7-12, 1998, pp. 1259–1262.
Dan Sievenpiper, L. Zhang, R.F.J. Broas, N.G. Alexopolous and E. Yablonovitch, “High-Impedance Electromagnetic Surfaces with a Forbidden Frequency Band”, IEEE Transactions on Microwave Theory and Techniques, vol. 47, No. 11, November 1999, pp. 2059–2074.
Brian A. Lail, Steven P. Castillo, “Coupling Through Narrow Slot Apertures to Thin Wire Structures”, IEEE Transactions on Electromagnetic Compatibility, vol. 42, No. 3, August 2000, pp. 276–283.
Z. Ying and P-S. Kildal, “Improvements of dipole, helix, spiral, Microstrip patch and aperture antennas with ground planes by using corrugated soft surfaces,”, IEE Proc. Microwaves, Antennas, Propagation, vol. 143, No. 3, June 1996, pp. 244–248.
B.M. Petrov, Electrodynamics and propagation of Radio waves, Moscow, Hot Line – Telecom press, 2003.
Author:
Jean-François D. Essiben, Ph.D. in Electrical Engineering, University of Douala (ENSET), Department of Electrical Engineering, B.P. 1872 Douala-Cameroon, jessibencm@yahoo.fr.
