ВОЗБУЖДЕНИЕ ПЛАНАРНОГО ЕBG-ВОЛНОВОДА ПРЯМОУГОЛЬНЫМ МЕТАЛЛИЧЕСКИМ ВОЛНОВОДОМ
В.А. Калошин, Е.А. Скородумова
Институт радиотехники и электроники им. В.А. Котельникова РАН
Получена 31 марта 2009 г.
Рассматривается задача о стыке прямоугольного металлического волновода и ЕBG- волновода, две стенки которого выполнены в виде металлических плоскостей, а две других – в виде двухмерных решеток из круговых металлических цилиндров. Найдены расстояния от фланца до первого ряда цилиндров и между первым и вторым рядом цилиндров, обеспечивающие малые потери на отражение в полосе частот. Исследование проводится на основе моделирования методом конечных элементов.
Ключевые слова: планарный EBG-волновод, численное моделирование в электродинамике.
Введение
Для построения планарных интегральных схем СВЧ используются, как правило, полосковые или микрополосковые линии. При больших размерах схем, например, при построении планарных антенных решеток, в коротковолновой части сантиметрового диапазона и миллиметровом диапазоне потери могут стать недопустимо большими. В этом случае в качестве линий используют полые металлические волноводы. Известны различные технологии изготовления волноводных схем: фрезерование, литье под давлением, литье по выплавляемым моделям. Все эти технологии требуют больших затрат. В качестве альтернативы можно использовать планарные ЕBG волноводы, стенками которых в плоскости вектора электрического поля являются двумерные периодические решетки из металлических цилиндров [1]. Однако при возбуждении такого волновода стандартным металлическим волноводом возникает отражение, связанное со скачком граничных условий на стенках. В данной работе исследуется возможность уменьшения отражения от стыка за счет изменения расстояния T0 между первым (от стыка) и вторым рядом цилиндров и расстояния T1 от фланца до первого ряда цилиндров (см. рис. 1).
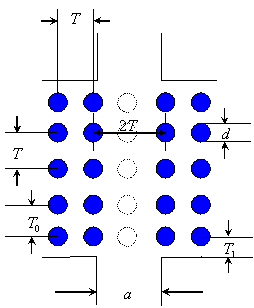
Рис. 1
Описание математической модели
Рассмотрим ЕBG-волновод, образованный удалением одного ряда цилиндров с диаметром d в двумерной периодической решетке с периодом T (рис. 1). Удаленные цилиндры показаны на рис. 1 пунктиром. На расстоянии T1 от центров цилиндров первого ряда расположен фланец возбуждающего металлического волновода шириной a, в котором распространяется TE-мода. С другой стороны расположен аналогичный волновод, который предполагается нагруженным на согласованную нагрузку. Будем искать численное решение для коэффициента отражение от стыка возбуждающего металлического волновода и ЕBG-волновода на основе метода конечных элементов.
Результаты численных исследований
Численные исследования проводились для следующих параметров модели: T = 12.5 мм, d = 5 мм, a = 23 мм.
Исследования проводились в два этапа. Сначала исследовалось влияние расстояния между центрами цилиндров первого и второго ряда на коэффициент отражения. При этом расстояние от фланца до центров цилиндров второго ряда оставалось неизменным и равным 1.5T (T1 = 0.5T). Результаты приведены на рис. 2. В качестве начального расстояния использовался период решетки T. На рисунке это соответствует значению 0. Остальные кривые описывают влияние на КСВ уменьшения расстояния между первым и вторым рядом, соответственно, на 0.5, 1, 1.5 и 2 мм.
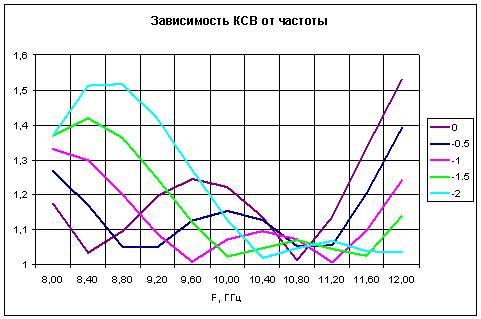
Рис .2
Как видно из рисунка, оптимальное расстояние с точки зрения максимальной ширины полосы частот по уровню КСВ, равного 1.1, является значение T0 = T – 1.5 мм.
На втором этапе подбиралось расстояние от фланца до первого ряда цилиндров, обеспечивающее минимум КСВ в выбранной полосе частот при заданном (оптимальном) значении T0. Результаты приведены на рис. 3.
Таким образом, в результате подбора параметров удалось без использования согласующих элементов уменьшить уровень КСВ до 1.04 в полосе частот 2 ГГц. Колебание КСВ в этой полосе частот определяется интерференцией отраженной ТЕ моды от двух стыков. При этом максимальное отражение мы наблюдаем в центре полосы (КСВ=1.04), где коэффициент отражения является суммой коэффициентов отражения от двух стыков. При этом КСВ одного стыка в данной точке будет в два раза меньше и равен 1.02.
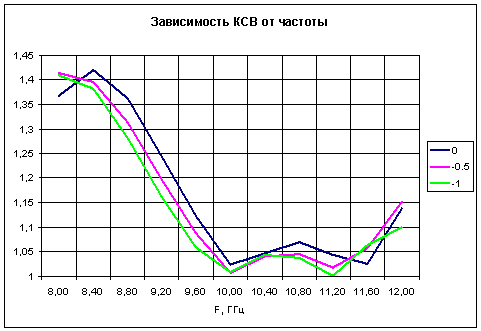
Рис. 3
Работа выполнена при поддержке РФФИ (проект №08-08-12200).
Литература