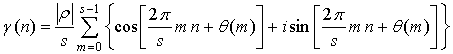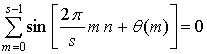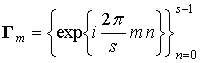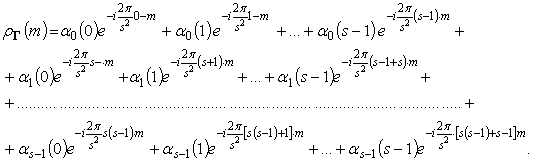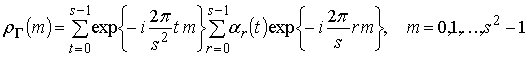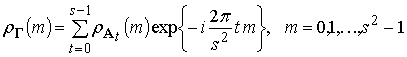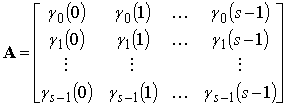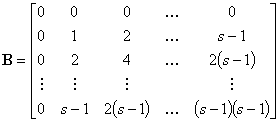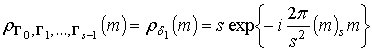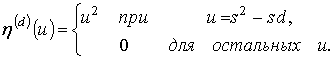УДК 621.396
2D и 4D векторные сигналы с хорошими корреляционными свойствами
Я. А. Фурман, И. Л. Егошина, Р. В. Ерусланов
Марийский государственный технический университет, г. Йошкар-Ола
Получена 12 марта 2012 г.
Аннотация.
Рассмотрены дискретные модулирующие последовательности для получения фазокодированных
зондирующих сигналов. Векторы этих последовательностей являются элементами
унитарного Cs
и кватернионного Hs
пространств. Показано, что некоторые виды таких сигналов могут обладать идеальными
корреляционными свойствами. Описаны два класса подобных сигналов, компонентами
которых являются векторы, образующие ортогональные базисы в ![]() и
и ![]() .
.
Ключевые слова: дискретный комплекснозначный сигнал, дискретный кватернионный сигнал, равномерный энергетический спектр, идеальные корреляционные свойства, унитарное кватернионное пространство, элементарный контур, композиционный контур, обработка фазокодированных сигналов, циклическая согласованная фильтрация, алгоритм «через s шаговое суммирование».
Abstract.
The discrete modulating sequence for phase-coded probing signal obtaining are
considered. The vectors of these sequences are the elements of unitary space ![]() s
and quaternion space
s
and quaternion space ![]() .
It is shown that some types of these signals can to have the ideal correlate
properties. Two classes of such signals the components of which are the vectors
which are form the orthogonal basis in
.
It is shown that some types of these signals can to have the ideal correlate
properties. Two classes of such signals the components of which are the vectors
which are form the orthogonal basis in ![]() and
and ![]() are
described.
are
described.
Keywords: discrete complex valued signal, discrete quaternion signal, uniform energy spectrum, ideal correlate properties, unitary vector space, quaternion vector space, elementary contour, composition contour, phase-coded signal processing, cyclic matched filtration, "by S-step incremental summing" algorithm.
Принятые сокращения:
АКФ – автокорреляционная функция, ВКФ – взаимокорреляционная функция, ИКС –
идеальные корреляционные свойства, КТС – кватернионный сигнал, РЭС –
равномерный энергетический спектр, СП – скалярное произведение, ЭВ –
элементарный вектор, ЭК – элементарный контур, ЭКС – элементарный кватернионный
сигнал, ЧСШС – «через s
шаговое суммирование».
1. Введение. Об ограничении вида функций для получения сигналов с равномерным энергетическим спектром
Пусть
![]() – дискретный комплекснозначный сигнал в
виде последовательности элементарных сигналов (элементарных векторов (ЭВ))
– дискретный комплекснозначный сигнал в
виде последовательности элементарных сигналов (элементарных векторов (ЭВ)) ![]() , а
, а ![]() ,
, ![]() , – его спектр. Если он имеет равномерный
энергетический спектр (РЭС), т.е.
, – его спектр. Если он имеет равномерный
энергетический спектр (РЭС), т.е. ![]() ,
, ![]() , то обратное ДПФ принимает вид
, то обратное ДПФ принимает вид
Отсюда
следует, что вещественный сигнал будет обладать РЭС лишь в том случае, если
его фазочастотный спектр ![]() удовлетворяет
следующему специфическому условию:
удовлетворяет
следующему специфическому условию:
Если
дополнительно потребовать, чтобы сигнал Г обладал единичным пик-фактором,
то вещественный сигнал с РЭС будет достаточно редким сигналом. Примером такого
сигнала является кодирующая последовательность ![]() .
Другие сигналы в виде кода Баркера будут обладать РЭС лишь в том случае, если
изменить у них одну компоненту, например,
.
Другие сигналы в виде кода Баркера будут обладать РЭС лишь в том случае, если
изменить у них одну компоненту, например, ![]() на
на ![]() . Но после этого пик-фактор у них становится
отличным от единицы. АКФ сигналов с РЭС состоит лишь из одной ненулевой компоненты.
Такие сигналы обладают идеальными корреляционными свойствами (ИКС) и представляют
значительный интерес в качестве кодирующих последовательностей для модуляции
высокочастотных несущих сигналов. Как следует из (1) и (2), сигналы с подобными
свойствами целесообразно рассматривать в качестве элементов не действительных
линейных пространств
. Но после этого пик-фактор у них становится
отличным от единицы. АКФ сигналов с РЭС состоит лишь из одной ненулевой компоненты.
Такие сигналы обладают идеальными корреляционными свойствами (ИКС) и представляют
значительный интерес в качестве кодирующих последовательностей для модуляции
высокочастотных несущих сигналов. Как следует из (1) и (2), сигналы с подобными
свойствами целесообразно рассматривать в качестве элементов не действительных
линейных пространств ![]() , а унитарных
, а унитарных ![]() и кватернионных
и кватернионных ![]() векторных
пространств. Впервые такой подход применительно к пространству
векторных
пространств. Впервые такой подход применительно к пространству ![]() был описан в работах [1,2], а в данной
работе он будет распространен на сигналы, заданные в кватернионном пространстве
был описан в работах [1,2], а в данной
работе он будет распространен на сигналы, заданные в кватернионном пространстве
![]() .
.
2. Дискретно-кодированные сигналы с ИКС, заданные в
пространстве ![]() .
.
В
унитарном пространстве существует ортогональный базис ![]() ,
где
,
где ![]() – базисный векторный сигнал порядка m,
имеющий вид [3]:
– базисный векторный сигнал порядка m,
имеющий вид [3]:
Векторные
диаграммы таких сигналов при ![]() образуют правильные фигуры
(рис. 1) и поэтому названы элементарными контурами (ЭК). АКФ ЭК
образуют правильные фигуры
(рис. 1) и поэтому названы элементарными контурами (ЭК). АКФ ЭК ![]() , состоит из s
комплекснозначных
отсчетов с единичным модулем,
, состоит из s
комплекснозначных
отсчетов с единичным модулем,
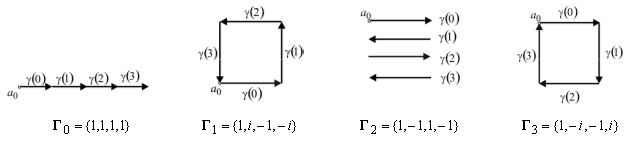
Рис. 1. Семейство элементарных контуров размерности s=4
образующих ЭК ![]()
![]() . Произвольный
дискретный комплекснозначный сигнал
. Произвольный
дискретный комплекснозначный сигнал ![]() служит адекватной
математической моделью дискретно-кодированного сигнала с постоянным значением
частоты гармонического сигнала внутри кодового интервала, количество которых
равно s. Амплитуда синусоиды
внутри n-го кодового интервала
равна
служит адекватной
математической моделью дискретно-кодированного сигнала с постоянным значением
частоты гармонического сигнала внутри кодового интервала, количество которых
равно s. Амплитуда синусоиды
внутри n-го кодового интервала
равна ![]() , а ее начальная фаза –
, а ее начальная фаза – ![]() . Базисные векторные сигналы (3) задают фазокодированные
сигналы
. Базисные векторные сигналы (3) задают фазокодированные
сигналы ![]() , у которых начальная фаза синусоиды n-го
кодового интервала равна
, у которых начальная фаза синусоиды n-го
кодового интервала равна ![]() , а амплитуды синусоид
во всех кодовых интервалах одинаковы и равны 1.
, а амплитуды синусоид
во всех кодовых интервалах одинаковы и равны 1.
Рассмотрим подход к
получению алфавита дискретных комплекснозначных сигналов с ИКС в виде композиционных
контуров из полного семейства ЭК [4]. Пусть ![]() ,
, ![]() , произвольные кодовые
последовательности из состава композиционной кодовой последовательности
, произвольные кодовые
последовательности из состава композиционной кодовой последовательности ![]() . Через
. Через ![]() ,
, ![]() , обозначены ЭВ последовательностей
, обозначены ЭВ последовательностей ![]() , а через
, а через ![]() ,
, ![]() , те же ЭВ, но уже в составе
композиционной последовательности. Спектр последовательности
, те же ЭВ, но уже в составе
композиционной последовательности. Спектр последовательности ![]() обозначим как
обозначим как ![]() .
Получим теперь выражение для спектра
.
Получим теперь выражение для спектра ![]() . В общем случае ДПФ
последовательности
. В общем случае ДПФ
последовательности ![]() , имеет вид
, имеет вид
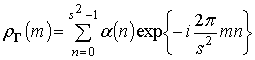 ,
,
![]() ,
,
или в развернутом виде
Данная сумма состоит из
![]() строк и
строк и ![]() столбцов.
Рассмотрим в транспонированном виде только один,
столбцов.
Рассмотрим в транспонированном виде только один, ![]() -й
столбец:
-й
столбец:
Для выявления закономерностей экспоненту в каждом слагаемом выражения (5) представим произведением двух экспонент. В результате выражение (5) примет вид
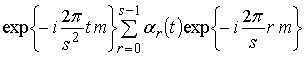 ,
,
а компонента спектра композиционной последовательности будет равна
Пусть теперь ЭВ
последовательностей ![]() ,
, ![]() ,
обладают свойством эргодичности, т.е.
,
обладают свойством эргодичности, т.е. ![]() ,
, ![]() . Тогда внутренняя сумма в (5) есть
. Тогда внутренняя сумма в (5) есть ![]() -я компонента спектра
-я компонента спектра ![]() последовательности
последовательности ![]() и выражение (6) примет вид
и выражение (6) примет вид
Рассмотрим случай,
когда последовательности ![]() ,
, ![]() , образуют алфавит сигналов, эффективный
для решения задачи различения, т.е. их спектры не пересекаются, а объем
алфавита равен
, образуют алфавит сигналов, эффективный
для решения задачи различения, т.е. их спектры не пересекаются, а объем
алфавита равен ![]() . Такому условию отвечают
комплекснозначные последовательности в виде ЭК (3).
. Такому условию отвечают
комплекснозначные последовательности в виде ЭК (3).
Семейство ЭК можно
задать ортогональной матрицей ![]() порядка
порядка ![]() ,
, ![]() -ая
строка которой состоит из ЭВ
-ая
строка которой состоит из ЭВ ![]() контура
контура ![]() . В соответствии со свойством эргодичности
матрица
. В соответствии со свойством эргодичности
матрица ![]() будет симметрической. Ей можно
сопоставить матрицу
будет симметрической. Ей можно
сопоставить матрицу ![]() индексов ЭВ полного семейства
ЭК, взятых по модулю
индексов ЭВ полного семейства
ЭК, взятых по модулю ![]() . Эта матрица также имеет
порядок
. Эта матрица также имеет
порядок ![]() и является симметрической.
и является симметрической.
Например, для ![]() (см.
рис.2) эти матрицы будут равны
(см.
рис.2) эти матрицы будут равны
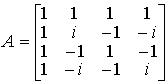 ;
;
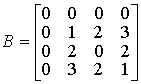 .
.
Так как спектры ЭК разных порядков не пересекаются, последнее выражение для спектра базового композиционного контура, полученного конкатенацией ЭК с последовательным возрастанием индексов, примет следующий вид:
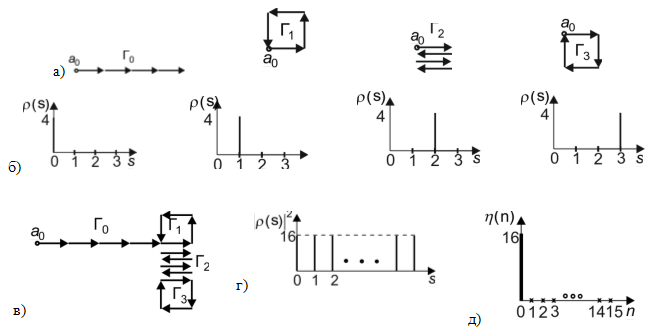
Рис. 2. Композиционный контур для ![]() : а) семейство
элементарных контуров; б) энергетические спектры элементарных контуров; в)
композиционный контур
: а) семейство
элементарных контуров; б) энергетические спектры элементарных контуров; в)
композиционный контур ![]() ; г) энергетический спектр
композиционного контура
; г) энергетический спектр
композиционного контура ![]() ; д) циклическая АКФ
контура
; д) циклическая АКФ
контура ![]()
Из (10) вытекает, что
при ![]() компонента спектра базового контура
строго веществена и равна
компонента спектра базового контура
строго веществена и равна ![]() . Отсюда же следует,
что базовый контур характеризуется РЭС вида
. Отсюда же следует,
что базовый контур характеризуется РЭС вида ![]() (рис.2г).
(рис.2г).
Из полного семейства ЭК
размерности ![]() можно составить
можно составить ![]() композиционных
контуров, однако не все они будут обладать РЭС. Для определения комбинации из
полного семейства ЭК, обеспечивающих данное свойство композиционных контуров,
найдем связь ЭК с кратным значением аргумента, т.е. когда
композиционных
контуров, однако не все они будут обладать РЭС. Для определения комбинации из
полного семейства ЭК, обеспечивающих данное свойство композиционных контуров,
найдем связь ЭК с кратным значением аргумента, т.е. когда 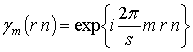 , с ЭК, содержащими ЭВ, задаваемые
выражениями (8) и (9). Из свойства эргодичности элементарных векторов ЭК
следует, что эти векторы для контуров порядка
, с ЭК, содержащими ЭВ, задаваемые
выражениями (8) и (9). Из свойства эргодичности элементарных векторов ЭК
следует, что эти векторы для контуров порядка ![]() с
аргументами кратности
с
аргументами кратности ![]() образуют ЭК порядка
образуют ЭК порядка ![]() . Поэтому
. Поэтому ![]() -ая
строка матрицы
-ая
строка матрицы ![]() ,
, ![]() ,
задает ЭК
,
задает ЭК ![]() с элементарными векторами кратности
с элементарными векторами кратности ![]() .
.
Свойство суммы (4),
состоящее в том, что каждый ее столбец задает выражение для спектра ЭК, будет
сохраняться лишь при следующих условиях, предъявляемых к матрице ![]() :
:
1. Симметричность
матрицы ![]() , а значит, и матрицы
, а значит, и матрицы ![]() . Только в этом случае можно
воспользоваться свойством эргодичности ЭК при преобразовании суммы (4). Данное
условие выполняется при умножении матрицы
. Только в этом случае можно
воспользоваться свойством эргодичности ЭК при преобразовании суммы (4). Данное
условие выполняется при умножении матрицы ![]() на
любое целое число
на
любое целое число ![]() . При этом сумма элементов
. При этом сумма элементов ![]() -го столбца в (4) будет равна спектру
контура
-го столбца в (4) будет равна спектру
контура ![]() со сдвинутой начальной точкой. В
результате суммы всех столбцов станут нулевыми за исключением одной суммы, по
модулю равной
со сдвинутой начальной точкой. В
результате суммы всех столбцов станут нулевыми за исключением одной суммы, по
модулю равной ![]() .
.
2. Матрицы ![]() и
и ![]() должны
содержать элементарные векторы всех ЭК. В них не должно быть повторяющихся
строк или столбцов. В противном случае в сумме (4) одни спектральные компоненты
будут повторяться несколько раз, а другие будут отсутствовать, что приведет к
неравномерности энергетического спектра композиционного контура. Это будет
иметь место, если при умножении матрицы
должны
содержать элементарные векторы всех ЭК. В них не должно быть повторяющихся
строк или столбцов. В противном случае в сумме (4) одни спектральные компоненты
будут повторяться несколько раз, а другие будут отсутствовать, что приведет к
неравномерности энергетического спектра композиционного контура. Это будет
иметь место, если при умножении матрицы ![]() на
на ![]() появятся строки с одинаковой (по модулю
появятся строки с одинаковой (по модулю ![]() ) кратностью, т.е.
) кратностью, т.е.
![]() ,
,
где ![]() и
и ![]() – номера
строк. Тогда
– номера
строк. Тогда ![]() ,
, ![]() ,
, ![]() . Для целых
. Для целых ![]() ,
, ![]() , данное условие может выполняться только
в случае, если числа
, данное условие может выполняться только
в случае, если числа ![]() и
и ![]() содержат
множители, кратные
содержат
множители, кратные ![]() , т.е. не являются взаимно
простыми с
, т.е. не являются взаимно
простыми с ![]() . Следовательно, чтобы получить последовательность
ЭВ композиционных контуров с РЭС достаточно умножить матрицу
. Следовательно, чтобы получить последовательность
ЭВ композиционных контуров с РЭС достаточно умножить матрицу ![]() на число, взаимно простое с
на число, взаимно простое с ![]() , и взять ее элементы по модулю
, и взять ее элементы по модулю ![]() . Тогда для семейства ЭК размерностью
. Тогда для семейства ЭК размерностью ![]() существует
существует ![]() композиционных
контуров с РЭС, где
композиционных
контуров с РЭС, где ![]() ‑ число Эйлера.
‑ число Эйлера.
3. Анализ дискретно-кодированных сигналов в виде композиционных контуров
Получим выражение для
спектра любого из базовых композиционных контуров порядка ![]() . Так как такой контур состоит из ЭК,
элементарные векторы которых имеют аргументы кратности
. Так как такой контур состоит из ЭК,
элементарные векторы которых имеют аргументы кратности ![]() ,
то выражение (7) примет вид:
,
то выражение (7) примет вид:
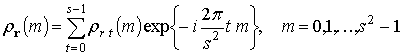 . (11)
. (11)
Здесь
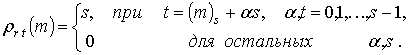
Отсюда следует, что в
сумме (4) необходимо учитывать только ненулевые компоненты, которые получаются
при целом ![]() , т.е.
, т.е.
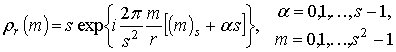 . (12)
. (12)
Полученное выражение позволяет сделать следующие выводы о свойствах спектра композиционного контура.
1. Амплитудный и энергетический спектры равномерны
![]() .
.
2. Фазочастотный спектр в общем случае имеет вид
![]() .
.
Новые композиционные контуры на основе базовых можно получить, проводя преобразования, не затрагивающие форму их энергетических спектров. Преобразуя компоненты спектра по закону
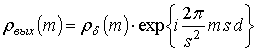 , (13)
, (13)
получаем контуры со сдвинутой на ![]() ЭК начальной точкой. Величина
ЭК начальной точкой. Величина ![]() может изменяться в диапазоне
может изменяться в диапазоне ![]() . Таким образом, алфавит содержит
. Таким образом, алфавит содержит ![]() композиционных контуров из полного
семейства ЭК с РЭС. Этот алфавит можно разбить на
композиционных контуров из полного
семейства ЭК с РЭС. Этот алфавит можно разбить на ![]() группы
по s контуров в каждой группе. Контуры одной
группы образуются циклическим сдвигом базового композиционного контура.
Например, отдельную группу
группы
по s контуров в каждой группе. Контуры одной
группы образуются циклическим сдвигом базового композиционного контура.
Например, отдельную группу ![]() ,
, ![]() и
и ![]() образуют
композиционные контуры размерности
образуют
композиционные контуры размерности ![]() .
.
Все ![]() композиционных контуров алфавита
характеризуются равномерностью своих энергетических спектров. Но при этом ВКФ
контуров внутри одной группы отличается от ВКФ контуров из других групп.
композиционных контуров алфавита
характеризуются равномерностью своих энергетических спектров. Но при этом ВКФ
контуров внутри одной группы отличается от ВКФ контуров из других групп.
Определим вид ВКФ
композиционных контуров внутри отдельной группы алфавита. Пусть ![]() – базовый контур группы, а
– базовый контур группы, а ![]() контур, полученный циклическим сдвигом ЭК
базового контура. Если
контур, полученный циклическим сдвигом ЭК
базового контура. Если ![]() , — компонента спектра
базового контура, то соответствующая компонента спектра контура
, — компонента спектра
базового контура, то соответствующая компонента спектра контура ![]() с учетом выражения (3) равна
с учетом выражения (3) равна
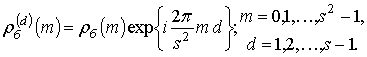 (14)
(14)
ВКФ ![]() , контуров
, контуров ![]() и
и ![]() связана со взаимным энергетическим
спектром этих контуров
связана со взаимным энергетическим
спектром этих контуров ![]() преобразованием
Фурье, т.е.
преобразованием
Фурье, т.е.
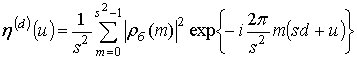 .
.
Так как ![]() , то
, то
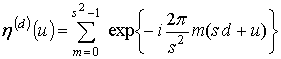 . (15)
. (15)
Данная сумма при любом u
равна нулю, кроме значения ![]() (рис. 3а). При этом
значение u-ого отсчета ВКФ равно
(рис. 3а). При этом
значение u-ого отсчета ВКФ равно ![]() . Следовательно,
. Следовательно,
Покажем теперь, что ВКФ композиционных контуров из разных групп алфавита композиционных контуров с РЭС может иметь ненулевые отсчеты.
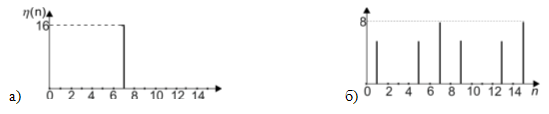
Рис.3. Примеры ВКФ композиционных контуров: а) для
контура ![]() и
и ![]() , полученного
циклическим сдвигом контура
, полученного
циклическим сдвигом контура ![]() ; б) для контура
; б) для контура ![]() и контура
и контура ![]() ,
полученного циклическим сдвигом контура
,
полученного циклическим сдвигом контура ![]()
Строки матрицы B, номера которых являются вместе с s взаимно простыми числами, задают комбинации ЭК в композиционном контуре. Так как первыми в базовых композиционных контурах всегда будут ЭК нулевого порядка, имеющие вид {1,1,…,1}, ВКФ которых равна s, а ВКФ последующих ЭК равна 0, то, по крайне мере, один отсчет ВКФ двух базовых композиционных контуров не будет равен 0. Следовательно, два композиционных контура, взятые из разных групп, не является ортогональными (рис. 3б).
4. Примеры синтеза кодовых последовательностей с РЭС в виде композиционных контуров из полного семейства элементарных контуров
В качестве примера
получения алфавита композиционных контуров с РЭС рассмотрим случай, когда ![]() . Существует шесть чисел, взаимно простых
с числом
. Существует шесть чисел, взаимно простых
с числом ![]() : 1,2,4,5,7,8. Следовательно имеются шесть
базовых композиционных контуров, образующих шесть групп кодовых
последовательностей с РЭС, по
: 1,2,4,5,7,8. Следовательно имеются шесть
базовых композиционных контуров, образующих шесть групп кодовых
последовательностей с РЭС, по ![]() контуров в каждой. Запишем
последовательность чисел от 0 до 9, т.е. 0,1,2,3.4,5,6.7.8, умножим эти
последовательность на одно из чисел
контуров в каждой. Запишем
последовательность чисел от 0 до 9, т.е. 0,1,2,3.4,5,6.7.8, умножим эти
последовательность на одно из чисел ![]() и перейдем к значениям
по модулю 9. В результате получаем конкретные комбинации порядков ЭК,
образующих базовые контуры с РЭС:
и перейдем к значениям
по модулю 9. В результате получаем конкретные комбинации порядков ЭК,
образующих базовые контуры с РЭС:
0,1,2,3,4,5,6,7,8; 0,2,4,6,8,1,3,5,7;
0,4,8,3,7,2,6,1,5; 0,5,1,6,2,7,3,8,4;
0,7,5,3,1,8,6,4,2; 0,8,7,6,5,4,3,2,1.
Выполняя циклический
сдвиг порядков ЭК в каждом из шести базовых контуров, получаем 54 кодовых последовательностей
с РЭС, имеющих размерность ![]() . На рис.4 представлен
базовый композиционный контур
. На рис.4 представлен
базовый композиционный контур ![]() .
.
Рис.
4. Базовый композиционный контур ![]()
С каждым из ЭК ![]() ,
, ![]() ,
составляющих композиционный контур, можно связать периодический процесс с
некоторой круговой частотой
,
составляющих композиционный контур, можно связать периодический процесс с
некоторой круговой частотой ![]() . Отсюда следует, что
базовый композиционный контур
. Отсюда следует, что
базовый композиционный контур ![]() , у которого порядки составляющих
его ЭК последовательно возрастают от
, у которого порядки составляющих
его ЭК последовательно возрастают от ![]() до
до ![]() , является аналогом дискретного линейного
, является аналогом дискретного линейного ![]() – образного ЧМ сигнала. Остальные пять
базовых композиционных контуров задают аналоги ЧМ колебаний с более сложным,
чем линейный, законом. Тем не менее каждый из них при сжатии будет иметь
нулевые боковые лепестки.
– образного ЧМ сигнала. Остальные пять
базовых композиционных контуров задают аналоги ЧМ колебаний с более сложным,
чем линейный, законом. Тем не менее каждый из них при сжатии будет иметь
нулевые боковые лепестки.
5. Обработка кодовых последовательностей с равномерным энергетическим спектром
Обработка подобных сигналов должна выполняться циклическим согласованным фильтром в момент совпадения окна фильтра с положением сигнала. Не выполнение этих условий для существующих сигналов и устройств для их обработки приводит к возникновению боковых лепестков.
Для контура,
обладающего спектром ![]() ,
, ![]() ,
частотный коэффициент передачи контурного согласованного фильтра равен [4]:
,
частотный коэффициент передачи контурного согласованного фильтра равен [4]:
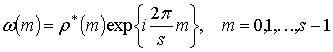 .
.
Если фильтр согласован с базовым композиционным контуром, то
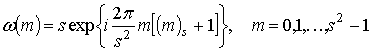 . (17)
. (17)
Видно, что АЧХ фильтра является равномерной, т.е.
![]() . (18)
. (18)
Спектр выходного сигнала будет равен
![]() (19)
(19)
Из (19) следует, что
амплитудно-частотный спектр выходного контура остается равномерным, а отсчеты
фазочастотного спектра линейно нарастают в пределах от 0 до 2![]() с шагом
с шагом ![]() .
Выходной контур, вычисленный путем обратного ДПФ от спектра (19), равен
.
Выходной контур, вычисленный путем обратного ДПФ от спектра (19), равен
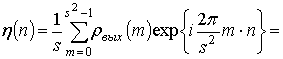
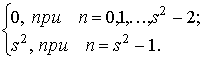 (20)
(20)
Таким образом, в
отличие от кодов Баркера, М – последовательностей и др., сигнал в виде базового
композиционного контура после обработки при любом значении ![]() не имеет боковых лепестков, т.е. допускает
идеальное сжатие и концентрирует всю энергию в пределах одного кодового
интервала.
не имеет боковых лепестков, т.е. допускает
идеальное сжатие и концентрирует всю энергию в пределах одного кодового
интервала.
При прохождении через
фильтр, согласованный с композиционным контуром, произвольного контура ![]() , имеющего спектр
, имеющего спектр ![]() ,
спектр выходного контура и сам выходной контур
,
спектр выходного контура и сам выходной контур ![]() будут
равны:
будут
равны:
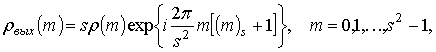 (21)
(21)
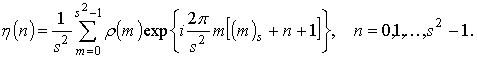 (22)
(22)
Как следует из (21),
при фильтрации несогласованного сигнала амплитудно-частотный спектр выходного
сигнала, равный ![]() ,
, ![]() ,
является функцией
,
является функцией ![]() и становится неравномерным.
Следствием этого будет появление боковых лепестков в выходном сигнале фильтра.
и становится неравномерным.
Следствием этого будет появление боковых лепестков в выходном сигнале фильтра.
Как уже было отмечено
выше, для идеального разрешения незашумленных выходных сигналов фильтра должны
выполняться три условия: 1) совпадение окна фильтра с сигналом, 2) циклический
характер обработки и 3) равномерность энергетического спектра сигнала.
Выполнение последнего условия обеспечивается свойствами композиционного
контура. Особенность первого условия объясняется тем, что установить момент
совпадения окна фильтра с положением всего фильтруемого сигнала достаточно
сложно. В работе [4] для получения совместного эффекта циклической фильтрации и
совпадения окна фильтра с сигналом использован алгоритм ЧСШС (через s2
шагового суммирования). При работе алгоритма ЧСШС операция циклической
фильтрации заменяется на операцию ациклической фильтрации, а выходной сигнал
получается суммированием отсчетов ациклического
фильтра, разнесенных на ![]() позиций.
позиций.
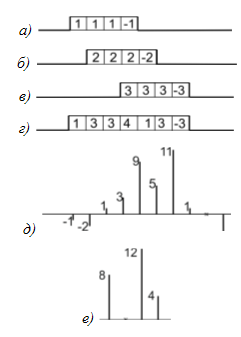
Рис.
5. Разрешение трех перекрывающихся сигналов ![]() с
разными амплитудами: а, б, в) исходные сигналы; г) суммарный сигнал (локус); д)
результат ациклической согласованной фильтрации, е) результат обработки по алгоритму
ЧКШС.
с
разными амплитудами: а, б, в) исходные сигналы; г) суммарный сигнал (локус); д)
результат ациклической согласованной фильтрации, е) результат обработки по алгоритму
ЧКШС.
Проиллюстрируем
процедуру сжатия перекрывающихся сигналов в виде композиционных контуров с использованием
алгоритма ЧСШС. Пусть, например, три контурных сигнала ![]() с
масштабами один, два и три расположены как показано на рис. 5а,б,в.
Суммарный контурный сигнал
с
масштабами один, два и три расположены как показано на рис. 5а,б,в.
Суммарный контурный сигнал ![]() и результат
ациклической согласованной фильтрации
и результат
ациклической согласованной фильтрации ![]() равны
(рис. 5г,д)
равны
(рис. 5г,д) ![]() ,
, ![]() .
.
По виду дискретной
последовательности ![]() достаточно сложно принять правильное
решение о том, что имеются три сигнала и оценить их масштаб и их взаимное
положение. Применение алгоритма ЧКШС для
достаточно сложно принять правильное
решение о том, что имеются три сигнала и оценить их масштаб и их взаимное
положение. Применение алгоритма ЧКШС для ![]() дает
следующие результаты:
дает
следующие результаты:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Таким образом,
результаты циклической фильтрации ![]() дают
дают
четкое представление о взаимном положении и масштабах входных сигналов.
На рис. 6 и рис.7 представлены результаты обработки отраженных от целей
фазокодированных сигналов. На рис. 6
показаны этапы обработки одиночного сигнала Фрэнка, который является частным
случаем композиционного контура, в данном случае контура ![]() . Обратим внимание на рис. 6е. На нем
показан выходной сигнал при ациклической согласованной фильтрации. Видно, что
кроме основного лепестка имеются хорошо заметные боковые лепестки [7]. Ниже, на
рис. 6ж дан вид сигнала, полученный с помощью алгоритма ЧСШС: боковые лепестки
полностью подавлены и достигнуто идеальное сжатие сигнала.
. Обратим внимание на рис. 6е. На нем
показан выходной сигнал при ациклической согласованной фильтрации. Видно, что
кроме основного лепестка имеются хорошо заметные боковые лепестки [7]. Ниже, на
рис. 6ж дан вид сигнала, полученный с помощью алгоритма ЧСШС: боковые лепестки
полностью подавлены и достигнуто идеальное сжатие сигнала.
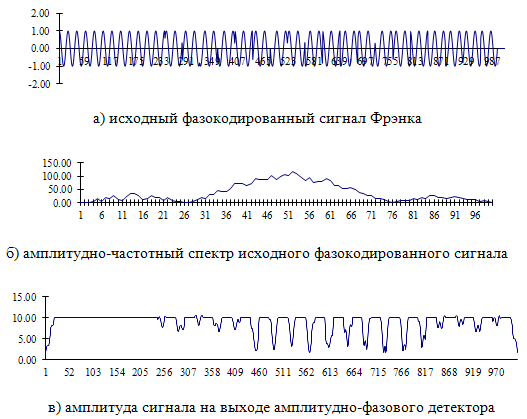
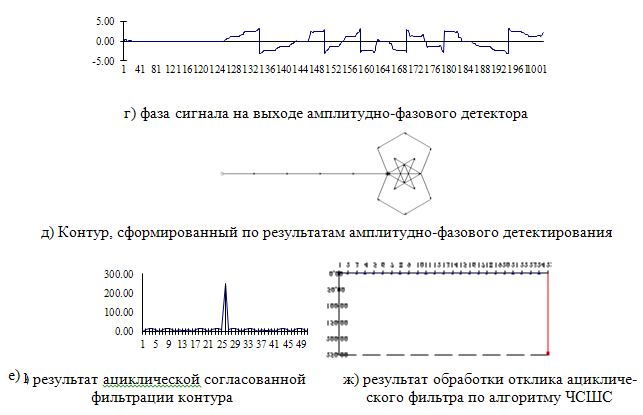
Рис.6. Пример обработки сигнал Фрэнка с эффектом идеального сжатия.

а – взаимное расположение сигналов

б – суммарный сигнал на входе амплитудно-фазового детектора
в – амплитудный спектр суммарного сигнала

г – амплитуда сигнала на выходе амплитудно-фазового детектора
![]()
д – фаза сигнала на выходе амплитудно-фазового детектора
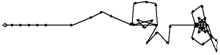
е – контур, сформированный по результатам амплитудно-фазового детектирования
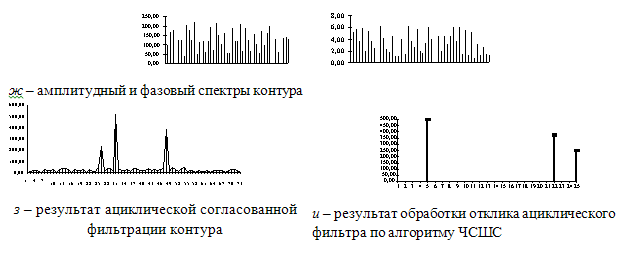
Рис. 7. Обработка трех пересекающихся фазокодированных сигналов.
На рис.7 показаны диаграммы поэтапной обработки пересекающихся во времени трех фазокодированных отраженных сигналов с разными амплитудами. На вход амплитудно-фазового детектора поступает суммарный сигнал, по виду которого сложно определить количество, взаимный сдвиг сигналов и их размахи. После амплитудно-фазового детектирования и ациклической согласованной фильтрации возникают боковые лепестки, способные замаскировать сигнал от цели с малой ЭПР. После применения алгоритма ЧСШС боковые лепестки оказываются полностью подавленными и достигается эффект идеального разрешения сигналов.
6. Дискретно-кодированные
сигналы с ИКС, заданные в пространстве ![]()
Удобный
математический аппарат для описания и преобразования различных сигналов должен
допускать выполнение 4-х арифметических операций – сложение/вычитание и
умножение/деление. В соответствии с теоремой Фробениуса существуют только три
ассоциативных алгебры с делением – алгебра действительных чисел, алгебра
комплексных чисел и алгебра кватернионов [5]. Поскольку комплексные числа
применяются для сигналов, представленных на плоскости, многомерные 3D
и 4D сигналы можно задавать только с
помощью вещественных чисел или кватернионов. Полный кватернион q
определяет
в ![]() точку с координатами
точку с координатами ![]() и записывается как
и записывается как ![]() , где
, где ![]() – мнимые
единицы. Алгебра кватернионов рассмотрена, например, в [5,6]. Группу из s
точек, каждая из которых задана кватернионом
– мнимые
единицы. Алгебра кватернионов рассмотрена, например, в [5,6]. Группу из s
точек, каждая из которых задана кватернионом ![]() ,
,![]() , будем рассматривать в качестве
дискретного кватернионного сигнала (КТС)
, будем рассматривать в качестве
дискретного кватернионного сигнала (КТС) ![]() . Если
. Если
![]() , то кватернион q
задает точку в 3D пространстве и
называется векторным (рис. 8).
, то кватернион q
задает точку в 3D пространстве и
называется векторным (рис. 8).
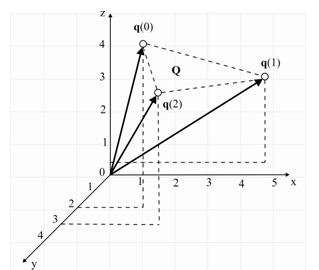
Рис. 8. 3D дискретный кватернионный сигнал
![]()
Преимущество задания 3D
и 4D сигналов
с помощью кватернионов по сравнению с заданием их вещественными числами
заключается в более высокой информативности скалярного произведения векторов в ![]() по сравнению с заданием скалярного
произведения в
по сравнению с заданием скалярного
произведения в ![]() [4,5]. Скалярное произведение
сигналов, заданных векторными кватернионами, имеет вид:
[4,5]. Скалярное произведение
сигналов, заданных векторными кватернионами, имеет вид:
![]() . (23)
. (23)
Здесь ![]() и
и ![]() – s-мерные
сигналы, представленные векторными кватернионами,
– s-мерные
сигналы, представленные векторными кватернионами, ![]() –
реальная часть скалярного произведения, равная скалярному произведению
векторных сигналов, представленных в
–
реальная часть скалярного произведения, равная скалярному произведению
векторных сигналов, представленных в ![]() ,
, ![]() – гиперкомплексная часть произведения,
задающая усредненную нормаль к собственным плоскостям ЭВ
– гиперкомплексная часть произведения,
задающая усредненную нормаль к собственным плоскостям ЭВ ![]() и
и ![]() ,
, ![]() . Более высокая информативность СП
. Более высокая информативность СП ![]() по сравнению с
по сравнению с ![]() объясняется
наличием дополнительной гиперкомплексной части
объясняется
наличием дополнительной гиперкомплексной части ![]() .
Благодаря этому в кватернионном пространстве возможно различение сигналов с одинаковыми
значениями скалярного произведения в линейном действительном
пространстве.
.
Благодаря этому в кватернионном пространстве возможно различение сигналов с одинаковыми
значениями скалярного произведения в линейном действительном
пространстве.
В соответствии с
процедурой Кэли-Диксона [5] кватернионы могут быть получены удвоением
комплексных чисел. Например, ![]() , где
, где ![]() ,
, ![]() . При таком подходе КТС можно рассматривать
как сумму двух комплекснозначных сигналов, заданных во взаимно перпендикулярных
плоскостях.
. При таком подходе КТС можно рассматривать
как сумму двух комплекснозначных сигналов, заданных во взаимно перпендикулярных
плоскостях.
7. Кватернионные композиционные сигналы.
В
кватернионном пространстве H
существует ортогональный базис ![]() [4], получаемый с
помощью процедуры удвоения базиса
[4], получаемый с
помощью процедуры удвоения базиса ![]() в
в ![]() из дискретных комплексных сигналов, где
из дискретных комплексных сигналов, где
![]() ,
, ![]() . (24)
. (24)
Векторные
сигналы (24) называются элементарными кватернионными сигналами (ЭКС). Например,
ортогональный базис в ![]() размерности
размерности ![]() имеет вид
имеет вид
![]() ;
; ![]() ;
;
(25)
![]() ;
; ![]() .
.
Из
условия ортогональности ЭКС следует, что как реальная, так и гиперкомплексная
части их скалярного произведения ![]() ,
, ![]() , равны нулю. Спектр произвольного
дискретного КТС Q, полученный
разложением сигнала в базисе (24), определяется как
, равны нулю. Спектр произвольного
дискретного КТС Q, полученный
разложением сигнала в базисе (24), определяется как
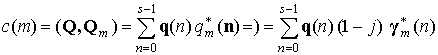 ,
,
![]() . (26)
. (26)
Сформируем
теперь из ЭКС ![]() аналог композиционного контура:
аналог композиционного контура:
![]() . Полученный сигнал назовем кватернионным
композиционным сигналом. Его спектр, найденный в соответствии с (26) и с учетом
представления кватернионов комплексными числами, будет равен
. Полученный сигнал назовем кватернионным
композиционным сигналом. Его спектр, найденный в соответствии с (26) и с учетом
представления кватернионов комплексными числами, будет равен
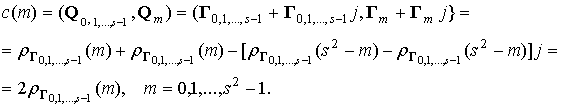
Используя (10), окончательно получим
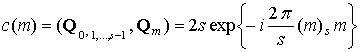 ,
, ![]() . (27)
. (27)
Видно, что энергетический спектр этого кватернионного сигнала является равномерным и поэтому результат его циклической согласованной фильтрации будет иметь вид символа Кронекера.
Остальные
свойства кватернионных композиционных контуров аналогичны свойствам
комплекснозначных композиционных контуров. Из полного семейства ЭКС размерности
![]() можно получить
можно получить ![]() групп кватернионных композиционных
контуров по
групп кватернионных композиционных
контуров по ![]() контуров в каждой группе. В каждой группе
имеется один базовый контур, в котором первый ЭКС равен
контуров в каждой группе. В каждой группе
имеется один базовый контур, в котором первый ЭКС равен ![]() ,
а остальные
,
а остальные ![]() контуров получаются циклическим сдвигом остальных
его ЭКС. ВКФ контуров внутри одной группы являются дельтовидными (аналогично
(16)), а ВКФ контуров из разных групп таким свойством не обладают. Обработка
кватернионных композиционных контуров должна выполняться циклическим согласованным
фильтром в момент совпадения окна фильтра с положением сигнала. В результате
такой обработки боковые лепестки сжатого сигнала равны нулю. Как и при
обработке комплекснозначного композиционного контура процедуру циклической
фильтрации можно заменить ациклической фильтрацией с последующим применением
алгоритма ЧСШС.
контуров получаются циклическим сдвигом остальных
его ЭКС. ВКФ контуров внутри одной группы являются дельтовидными (аналогично
(16)), а ВКФ контуров из разных групп таким свойством не обладают. Обработка
кватернионных композиционных контуров должна выполняться циклическим согласованным
фильтром в момент совпадения окна фильтра с положением сигнала. В результате
такой обработки боковые лепестки сжатого сигнала равны нулю. Как и при
обработке комплекснозначного композиционного контура процедуру циклической
фильтрации можно заменить ациклической фильтрацией с последующим применением
алгоритма ЧСШС.
8. Пример обработки 4D дискретно-кодированного сигнала в виде кватернионного композиционного контура
Кватернионный
композиционный сигнал ![]() имеет вид:
имеет вид:
![]()
![]()
![]()
![]() . (28)
. (28)
Его спектр, вычисленный по формуле (26), равен
![]()
![]()
![]()
![]() .
.
Энергетический
спектр контура ![]() и результат его циклической
согласованной фильтрации представлены в следующем виде:
и результат его циклической
согласованной фильтрации представлены в следующем виде:
![]() ;
;
![]() .
.
Получим
полное семейство кватернионных композиционных сигналов с РЭС размерности ![]() . Для
. Для ![]() существуют
два числа, взаимно простые с числом 4:
существуют
два числа, взаимно простые с числом 4: ![]() и
и ![]() . Отсюда следует, что при этой размерности
имеются два базовых композиционных сигналов. Первый из них
. Отсюда следует, что при этой размерности
имеются два базовых композиционных сигналов. Первый из них ![]() задается выражением (28). Для определения
второго базового сигнала необходимо каждое число последовательности {0,1,2,3}
умножить на
задается выражением (28). Для определения
второго базового сигнала необходимо каждое число последовательности {0,1,2,3}
умножить на ![]() и полученные произведения взять по модулю
и полученные произведения взять по модулю
![]() . В результате второй базовый сигнал будет
равен
. В результате второй базовый сигнал будет
равен
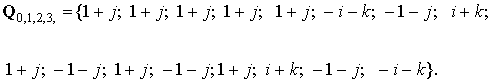
Таким
образом, для ![]() существуют две группы кватернионных
композиционных контуров с базовыми контурами
существуют две группы кватернионных
композиционных контуров с базовыми контурами
![]() и
и ![]() .
.
В
каждой группе содержатся по ![]() контура, обладающих
РЭС.
контура, обладающих
РЭС.
Полное
семейство кватернионных композиционных сигналов с РЭС для ![]() имеет вид:
имеет вид:
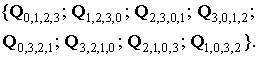
Проиллюстрируем
на примере контура ![]() применение алгоритма ЧСШС.
Пусть поступивший для обработки сигнал является суммой сигнала
применение алгоритма ЧСШС.
Пусть поступивший для обработки сигнал является суммой сигнала ![]() и сигнала
и сигнала ![]() ,
причем второй сигнал запаздывает на две позиции. В результате суммарный сигнал
имеет вид
,
причем второй сигнал запаздывает на две позиции. В результате суммарный сигнал
имеет вид
![]() .
.
Ациклическая ВКФ для данного случая равна
![]() .
.
При
суммировании элементов этой последовательности, разнесенных на ![]() шагов, получим следующий результат:
шагов, получим следующий результат: ![]() . Из него следует, что на входе было два
перекрывающихся сигнала вида
. Из него следует, что на входе было два
перекрывающихся сигнала вида ![]() , причем один из них
имел удвоенный масштаб и сдвиг на 2 шага.
, причем один из них
имел удвоенный масштаб и сдвиг на 2 шага.
Заключение
В статье рассмотрены кодирующие последовательности зондирующих сигналов, интерпретированных как заданные на плоскости и в 4D пространстве контуры. Показано, что для обеспечения идеального временного разрешения сигналов их энергетические спектры должны обладать свойством равномерности, выполняемая обработка – циклической и согласованной, а сами кодирующие последовательности, как правило, должны быть комплекснозначными или кватернионными. Синтезированы обладающие подобными свойствами комплекснозначные и кватернионные сигналы в виде композиционных контуров, представляющие собой последовательности следующих друг за другом элементарных контуров, образующих одно полное семейство. Подобное семейство элементарных контуров обладает свойствами ортогональности в 2D пространстве – для комплекснозначных и в 4D пространстве – для кватернионных композиционных контуров.
Литература
1. Фурман Я.А. Помехоустойчивые символы для передачи сообщений // Автометрия. 1996. №1. С. 42-51.
2. Фурман Я.А., Роженцов А.А., Хафизов Р.Г. Дискретно-кодированные сигналы на базе композиционных контуров /Автометрия. 1996. №1. С72-79.
3. Фурман Я.А. О двух замечательных видах замкнутых контуров изображений // Радиотехника и электроника, 1993. – Т. 36. №6. – С.1054-1061.
4. Введение в контурный анализ и его приложения к обработке изображений и сигналов / Я.А. Фурман, А.В. Кревецкий, А.К. Передреев [и др.]; под ред. Я.А. Фурмана. – 2-е изд., испр. – Москва: ФИЗМАТЛИТ, 2003. – 592 с.
5. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М.: Наука, 1973.
6. Арнольд В.И. Геометрия комплексных чисел, кватернионов и спинов. – М.: МЦНМО. 2002.
7. Кук Ч., Бернфельд М. Радиолокационные сигналы / Пер. с англ. Под ред. Кельзона В.С. – М.: Сов. Радио. 1971.
8. Я.А. Фурман, И.Л. Егошина, Р.В. Ерусланов. 2D и 4D векторные сигналы с хорошими корреляционными свойствами / Труды V Всероссийской конференции «Радиолокация и радиосвязь», 21-25 ноября 2011г. С. 286-291.