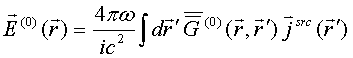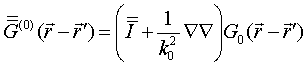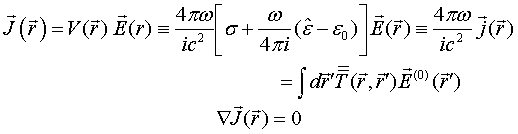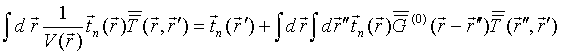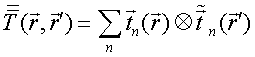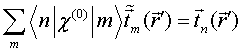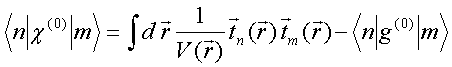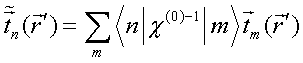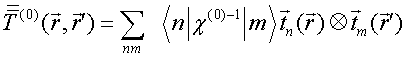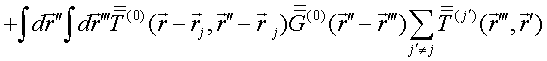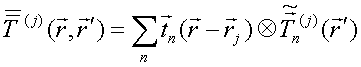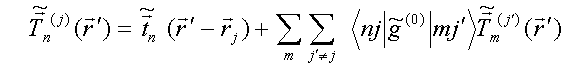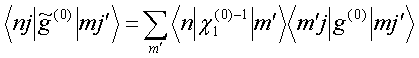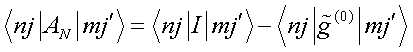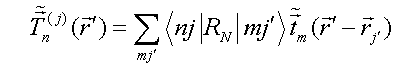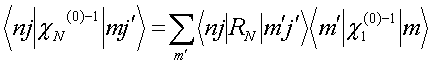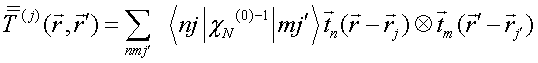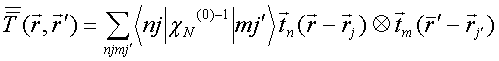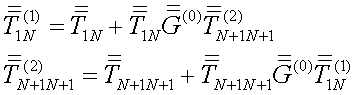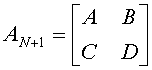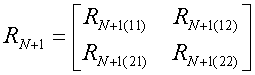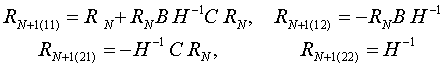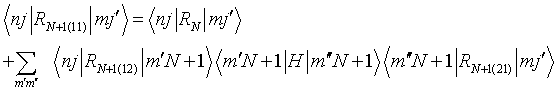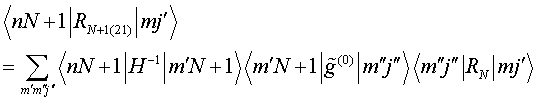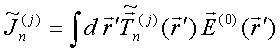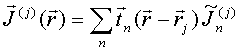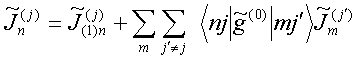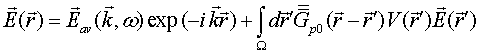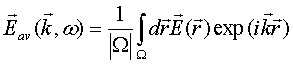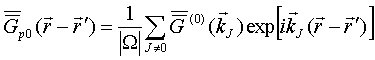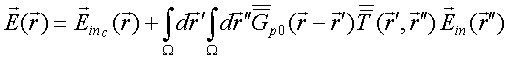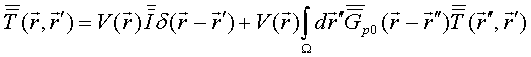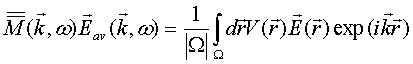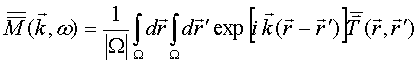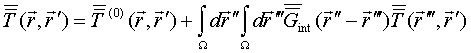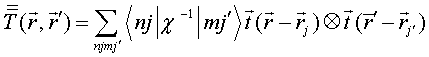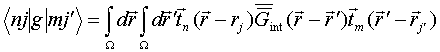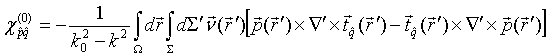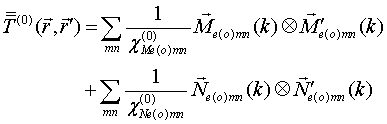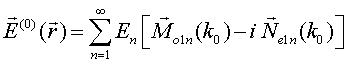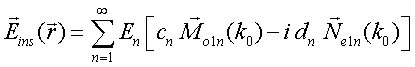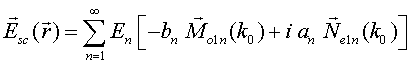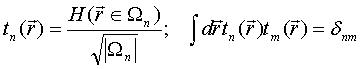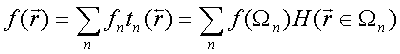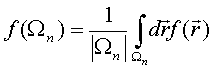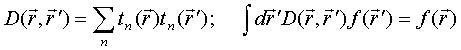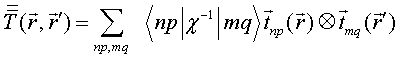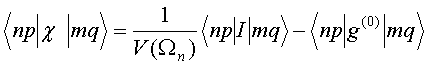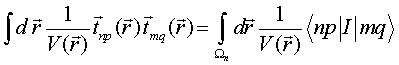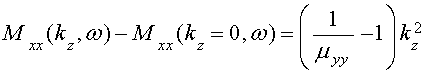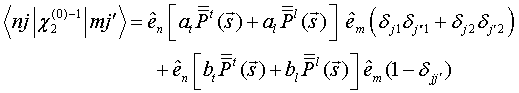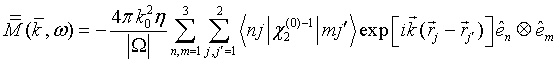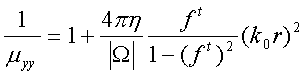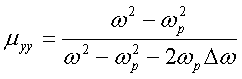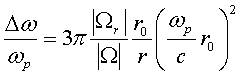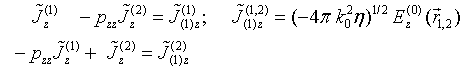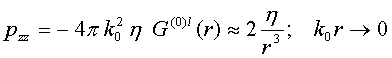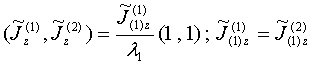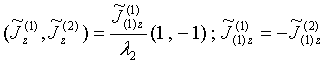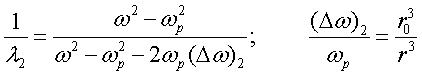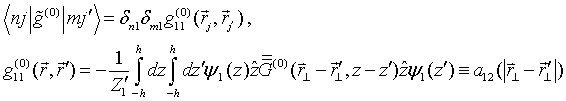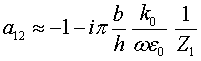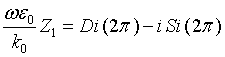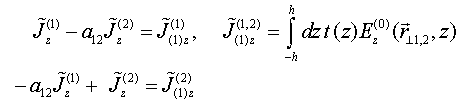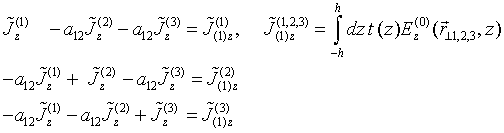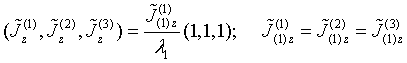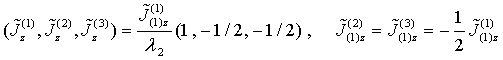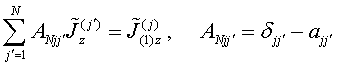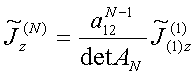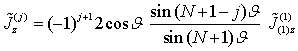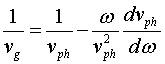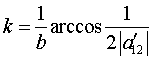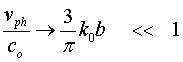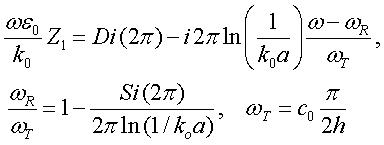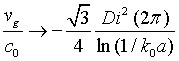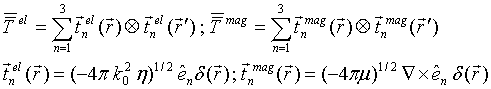QUASI-SEPARABLE T-SCATTERING OPERATOR APPROACH TO LOCAL FIELD DIRECT CALCULATIONS IN MULTIPLE SCATTERING PROBLEMS
Yu. N. Barabanenkov 1, M. Yu. Barabanenkov 2
1 V.A. Kotelnikov Institute of Radioengineering and Electronics of RAS, Moscow
2 Institute of Microelectronics Technology of RAS, Chernogolovka, Moscow Region
Received April 10, 2013
Abstract. We present analytic solution to fundamental in wave multiple scattering theory Lippmann-Schwinger (LS) integral equation for electric field quantum mechanical type tensor T- scattering operator by nonmagnetic arbitrary shaped particle with given scalar dielectric permittivity and specific conductivity in free space. The solution is obtained with the aid of a vector expansion functions’ basis and Galerkin method and written as sum of separable scattering operators weighted by inverse of a generating matrix, which is expressed through matrix describing wave coupling between the particle elements. Similar quasi-separable (QS) form is obtained for T-scattering operator of coupled particles’ ensemble, when generating matrix is related with matrix describing wave coupling between particles; an equations’ system for self consistent currents excited inside coupled particles is derived on this way also. Having given directly the current excited inside particle, T-scattering operator should be closed connected with wave spatial dispersion effect in homogenized electromagnetic crystal structure. Really, we show the rigorously defined a periodic structure effective dielectric permittivity tensor is exactly expressed by unit cell QS T- scattering operator, with generating matrix related to matrix of wave coupling between unit cell particles directly and via crystal. In order to test and apply the QS T-scattering operator approach, some different choosing the vector expansion functions are considered. In the case of vector spherical wave functions’ basis the QS T-scattering operator gives the Mie solution for incident plane wave scattering from and transmitted into a spherical particle. The another basis vector expansion functions defined on finite elements of particle volume is consistent with QS approximation of particle scattering potential operator, for which the LS equation is resolved exactly. Next, an asymptotic formula is obtained for contribution of spatially resonant coupling between two small spherical plasmonic particles inside unit cell of electromagnetic crystal into the structure effective magnetic permeability. We study at last some simple low dimensional ordered periodic arrays of particles, with particles’ coupling matrix obeying a stochastic property for the case of specifically linearly polarized wave electric field, and find corresponding stochastic and overtone eigenmodes and method of their excitation. Exact and asymptotic formulas are found also for standing and propagating wave transfer of currents’ exciting along a strait linear chain of particles with Jacobi’s coupling matrix.
Keywords: electromagnetic wave field, arbitrary shaped nonmagnetic coupled particles, multiple scattering, T-scattering operator, Lippmann-Schwinger integral equation, analytic solution, currents excited inside particles, electromagnetic crystal structures, low dimension arrays of particles.
1. Introduction
Theory of electromagnetic waves’ multiple scattering by dielectric and conducting nonmagnetic particles appears at present as tool for numerous studies of artificial materials and especially of microsized particles’ assemblies, which are useful in variety of optical applications because of their resonant interaction with a visible and infrared light. Between these studies there are the following interesting examples. Microstructured periodic materials known as “metamaterials”, with negative effective dielectric permittivity and/or negative effective magnetic permeability being derived either by spatially averaging the Maxwell equations on base of a self-consistent rigorous approach [1]or via so called full-wave dispersion relation [2,3] describing small nanoparticles in terms of their dipolar polarizability and using the local field approach. Contribution of coupled magnetic dipole resonances in small dielectric spheres’ clusters into the effective permittivity and permeability, being evaluated with the aid of classical Clausius-Mossotti homogenization formula [4]. Previously space-group resonance in clusters of nonresonant particles was considered [5, 6].The coupling between optical waveguides and high-quality resonators, which can being created within a photonic crystal structure with modified some unit cells [7]. High quality optical modes in low dimensional arrays of dielectric nanoparticles studies within the coupled dipole approach [8, 9]. Earlier similar modes were studied in theory of coupled parallel antennas [10].
Turn directly to main subject of our paper concerning with itself theory of electromagnetic waves’ multiple scattering by dielectric and conducting particles. This theory can be started with Lippmann-Schwinger (LS) integral equation for electric wave field tensor (dyadic) T- scattering operator by a particle, written similarly to the quantum mechanical case [11-14]. Having given directly the field and current excited inside a particle [15] as well as the field scattered by the particle, the T-scattering operator technique has been applying successfully for a long time. As early as 1967, a derivation was proposed [16] (see also [17,18]) of the phenomenological radiative transfer equation in a discrete randomly inhomogeneous medium, with due regard for correlation of particles in all orders and wave coupling between particles within the same cluster of particles. The Dyson and Bethe–Salpeter equations were used in the single- group approximation. Latter there were derived [19] exact self-consistent Dyson and Bethe-Salpeter equations (relations) for evaluating the ensemble averaged wave electric field and coherence function of wave electric field inside dense discrete random media, with random mass and intensity operators having been under averaging sign and written in terms of the particles’ correlations functions of all orders and particles’ cluslers random group T-scattering operators. A group T-scattering operator was constructed via special group operation from T-scattering operators of cluster particles, with T-scattering operator of a particle set having been satisfied a self consistent LS equation, integral term of which included exact random Green function and described particle coupling via the random medium. These self-consistent Dyson and Bethe-Salpeter equations gave all known approximations for wave multiple scattering in random media including the single group approximation. Ward-Takahashi identity for two-frequency combination of T-scattering operators was proved [20] to derive the radiative transfer equation with time delay via effect of pulse entrapping in a resonant random media. Mentioned above [7] scattering theory analysis of waveguide-resonator coupling was based on T-scattering operator, actually. Artificial magnetism in theory of wave multiple scattering by random discrete nonmagnetic conducting media [21] was considered with the aid of Dyson equation technique and generalized Lorentz –Lorenz formula including the Fourier transform of T-scattering operator of a particle. Referred to metamaterial effective permittivity derivation by spatially averaging the Maxwell equations [1] was performed with the aid of Lippmann-Schwinger integral equation for electric wave field inside periodic media that directly connected , actually, to a T-scattering operator of a periodically structure cell. Recently [22] the T-scattering operator technique was used to phenomenon study of virtual singular scattering of electromagnetic wave on a dielectric scatterer embedded into a flat left handed material slab (Veselago lens). Watson composition rule [12,17] of T-scattering operators was reformulated [23] in terms of virtual splitting the volume or surface inhomogeneous dielectric structure into a stack of elementary layers and the system of recurrent equations of invariant imbedding method [24] type obtained for changing the reflection and transmission coefficients of stack of N layers at (N+1)-st layer attachment.
Despite of enumerated T-scattering operator direct applications, to the best of our knowledge, there is no still sufficient attention on systematic method of solution to LS equation for this operator and instead that the Waterman transition matrix [14, 25-27] in the form, as one can verify, a simple combination from electric wave field dyadic Green function in free space and T-scattering operator widely has been using. The transition matrix technique expands the incident and the scattered electromagnetic waves by a particle in vector spherical wave functions, with expressing the expanding coefficients of scattered wave through the expanding coefficients of incident wave with the aid of the transition matrix. As making so, the transition matrix is written with the help of the extended boundary condition technique in terms of surface integrals from vector spherical functions’ bilinear combinations along the particle surface. A substantial progress has been achieved during last one and half decade in the form of new recursive transition matrix method for calculating local electromagnetic fields inside of spheres, system of which is subject to strong dependent scattering [28,29]. Though this achieving, the transition matrix technique needs in some improvement at present that is returning our attention to T-scattering operator. Really, using the spherical wave functions in the case of particles with complicate shape becomes nonrational, evidently. T-scattering operator gives directly the field inside a particle, whereas the transition matrix technique implies additional application of Mie internal field coefficients for evaluating the field in the interior of a particle [29]. Application the transition matrix technique can be difficult for rigorous evaluating an electromagnetic crystal structure effective dielectric permittivity [1] that directly connected with T-scattering operator of the structure unit cell.
The aim of our paper consists in considering a systematic method on
practical solution to LS equation for electric wave field dyadic T-scattering
operator in the form of quasi–separable (QS) approach. This approach adopted
from the quantum mechanical scattering potential approximation as sum of
separable potentials in nuclear physics [30]. In electromagnetics the separable
approximation for small particle scattering potential was used at study the radiative
transfer with time delay via effect of pulse entrapping in resonant random
media [20] as well as the wave virtual singular scattering by scatterer inside
Veselago lens [22]. We apply a vector expansion functions’ basis and Galerkin
technique [28,31,32] exploited [1] to evaluate a metamaterial effective dielectric
permittivity and employ by us to solve the LS equation for dyadic T-scattering
operator in QS form as sum of separable scattering operators weighted by
inverse of a generating matrix, which is expressed through wave coupling
between the particle elements’ matrix. One can apply various vector expansion
functions’ bases. In the case of vector spherical wave functions the QS T-
scattering operator gives the well known Mie solution for incident plane wave
scattering from and transmitted into a spherical particle. We show that a basis
vector expansion functions defined on finite elements of particle volume in
spirit of general finite element method [33] and used more earlier by Haar [34]
enables one to verify that QS T-scattering operator corresponds really to a QS
approximation of particle scattering potential operator, for which the LS
equation is resolved exactly. Next our goal consists in constructing the QS T-scattering
operator for coupled particles’ ensemble with generating matrix related with
wave coupling between particles, that we make by exact solving the Watson
composition rule [12] of T-scattering operators. On this way we exploit the
invariant imbedding method idea [23,24] to a recursive procedure creation for
QS T- scattering operator generating matrix inversion, by attaching to N
coupled particles a (N+1)-st particle and using the Frobenius formula
[35] for inversion of ![]() block’s matrix. Side by side with this recursive procedure for
inversion of the QS-T-scattering operator generating matrix, we consider an
equations’ system for self consistent currents excited inside coupled particles
and apply this system to study new effects for some simple low dimensional
ordered particles’ arrays in the form of periodic polygon chain [9,10] as well
as strait linear chain [3]. We show the particles’ coupling matrix of periodic
polygon chain obeys a stochastic property [35] and find corresponding stochastic eigenmodes and overtone ones and method of their excitation. For strait linear
chain [3] with Jacobi’s particles’ coupling matrix rising to Rayleigh’s book
[36] yet we derive exact and asymptotic formulas for standing and propagating
wave transfer of currents’ exciting along the strait linear chain. Our last general
result concerns the deriving an electromagnetic crystal structure unit cell QS
T-scattering operator, with generating matrix related with matrix of wave
coupling between the unit cell particles directly and via crystal electric
field dyadic Green function. This QS T-scattering operator we apply to analytic
consideration of space–group resonance effect [5,6] between the unit cell small plasmonic particles contribution into the structure effective magnetic permeability,
without applying a priory of Clausius-Mossotti homogenization formula.
block’s matrix. Side by side with this recursive procedure for
inversion of the QS-T-scattering operator generating matrix, we consider an
equations’ system for self consistent currents excited inside coupled particles
and apply this system to study new effects for some simple low dimensional
ordered particles’ arrays in the form of periodic polygon chain [9,10] as well
as strait linear chain [3]. We show the particles’ coupling matrix of periodic
polygon chain obeys a stochastic property [35] and find corresponding stochastic eigenmodes and overtone ones and method of their excitation. For strait linear
chain [3] with Jacobi’s particles’ coupling matrix rising to Rayleigh’s book
[36] yet we derive exact and asymptotic formulas for standing and propagating
wave transfer of currents’ exciting along the strait linear chain. Our last general
result concerns the deriving an electromagnetic crystal structure unit cell QS
T-scattering operator, with generating matrix related with matrix of wave
coupling between the unit cell particles directly and via crystal electric
field dyadic Green function. This QS T-scattering operator we apply to analytic
consideration of space–group resonance effect [5,6] between the unit cell small plasmonic particles contribution into the structure effective magnetic permeability,
without applying a priory of Clausius-Mossotti homogenization formula.
The organization of the paper is as follows. In Section 2 the starting LS equation for dyadic T-scattering operator of a particle is resolved in QS form. Section 3 contains deriving the QS T-scattering operator for ensemble of N coupled particles, by resolving the Watson composition rule of T-scattering operators. The recursive procedure for QS T-scattering operator generating matrix inversion is created in Section 4. Section 5 includes consideration an equations’ system for self consistent currents excited inside ensemble of coupled particles The QS T-scattering operator for electromagnetic crystal unit cell is derived in Section 6, with getting an exact formula for metamaterial effective dielectric permittivity in terms of the unit cell QS T-scattering operator. Applications of the QS T–scattering operator are placed in the Section 7. In Section 8 we conclude. Appendices A, B and C consist of details related to spherical particle QS T-scattering operator generating matrix, finite element vector expansions’ functions and strait linear chain with Jacobi’s particles’ coupling matrix, respectively. Some preliminary results of this paper were reported to recent PIERS symposium [37].
2. Quasi-separable T-scattering operator of particle in free space
2.1. Lippmann-Schwinger equation
We start with Lippmann-Schwinger (LS) integral equation for total electric
field ![]() of monochromatic electromagnetic wave
outside and inside of a nonmagnetic particle with given scalar dielectric permittivity
of monochromatic electromagnetic wave
outside and inside of a nonmagnetic particle with given scalar dielectric permittivity
![]() and specific conductivity
and specific conductivity ![]() , the particle being placed in homogeneous
nonmagnetic background (free space) with dielectric permittivity
, the particle being placed in homogeneous
nonmagnetic background (free space) with dielectric permittivity ![]() and the electromagnetic field source
volume current density
and the electromagnetic field source
volume current density ![]() . The LS equation for the total
electric field has in dyadic denotation form
. The LS equation for the total
electric field has in dyadic denotation form
Here ![]() denotes the incident on particle electric
field given by
denotes the incident on particle electric
field given by
The symbol ![]() denotes the electric field dyadic Green
function in free space of a form
denotes the electric field dyadic Green
function in free space of a form
with
![]() and
and ![]() and
and ![]() being the unit dyad and free space wave
number and free space scalar Green function, respectively. The quantity
being the unit dyad and free space wave
number and free space scalar Green function, respectively. The quantity ![]() is named as particle scattering potential
and defined in terms of particle complex permittivity
is named as particle scattering potential
and defined in terms of particle complex permittivity ![]() by
by
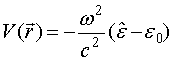 . The Gaussian system of units is used and
. The Gaussian system of units is used and
![]() denotes the light speed in vacuum and
denotes the light speed in vacuum and ![]() denotes wave
frequency. The magnetic permeability is supposed to be
denotes wave
frequency. The magnetic permeability is supposed to be ![]() everywhere.
The LS-equation derivation from Maxwell equations has been given in [14,38]
with the aid of vector Green theorem and accounting the boundary conditions.
everywhere.
The LS-equation derivation from Maxwell equations has been given in [14,38]
with the aid of vector Green theorem and accounting the boundary conditions.
Solution to the LS equation (1) for total electric field is written in terms of dyadic T–scattering operator as
Comparison of this equality with integral Eq. (1) gives LS integral equation for T-scattering operator
From equations (1) and (5) one gets [15] the following physically transparent relations
These
relations show that one can evaluate the total electric field ![]() as well as the complete current
as well as the complete current ![]() excited inside particle, having known the
particle T-scattering operator. We see also from Eq. (4) that convolution
excited inside particle, having known the
particle T-scattering operator. We see also from Eq. (4) that convolution ![]() of the electric wave field dyadic Green
function in free space with T-scattering operator gives, actually, the Waterman
transition matrix [14, 25-27]. The last divergence Eq.(6) imposes a solenoidal
restriction on T-scattering operator, provided the complex dielectric
permittivity has constant value inside particle.
of the electric wave field dyadic Green
function in free space with T-scattering operator gives, actually, the Waterman
transition matrix [14, 25-27]. The last divergence Eq.(6) imposes a solenoidal
restriction on T-scattering operator, provided the complex dielectric
permittivity has constant value inside particle.
2.2. Quasi-separable solution to Lippmann-Schwinger equation
Let
us apply to solution of LS integral equation (5) for T-scattering operator a
Galerkin technique [1,28]. With this aim we choose a vector expansion
functions’ basis![]() ,
, ![]() . Dividing
dyadic Eq.(5) by potential
. Dividing
dyadic Eq.(5) by potential ![]() and multiplying result
on vector
and multiplying result
on vector ![]() from the left side and integrating with
respect to
from the left side and integrating with
respect to ![]() gives
gives
We seek a solution to obtained equation in a form of dyadic expansion
with
![]() being a set of unknown vectors and symbol
being a set of unknown vectors and symbol
![]() denoting the dyadic product of two
vectors. Substituting (8) into Eq. (7) leads to an algebraic equations’ system
for unknown vectors
denoting the dyadic product of two
vectors. Substituting (8) into Eq. (7) leads to an algebraic equations’ system
for unknown vectors
The
generating matrix ![]() under left hand side (LHS) sum
of Eq. (9) is defined by expression of two terms
under left hand side (LHS) sum
of Eq. (9) is defined by expression of two terms
the second of which describes wave coupling between the particle elements in free space according to
Resolving equations’
system (9) with the aid of inverse matrix ![]() as
as
and
substituting the resolution result into dyadic expansion (8) right hand side
(RHS) leads us to quasi-separable (QS) solution to LS integral equation (5) for
T-scattering operator of a particle ![]() in free space
in free space
The reciprocity of the electric field dyadic Green function in free
space ![]() =
= ![]() where
the superscript
where
the superscript ![]() refers to the transpose dyadic,
leads to the symmetrical property of the particle coupling matrix elements
refers to the transpose dyadic,
leads to the symmetrical property of the particle coupling matrix elements ![]() =
= ![]() and
the generating matrix
and
the generating matrix ![]() =
= ![]() . The
inverse matrix symmetry property
. The
inverse matrix symmetry property ![]() =
= ![]() agrees with the T-scattering operator
reciprocity
agrees with the T-scattering operator
reciprocity ![]() =
= ![]() .
.
3. Quasi-separable T-scattering operator of particle’s ensemble in free space
Having obtained QS T-scattering operator (13) of a single particle,
one can get automatically QS T-scattering operator of ![]() coupled
particles’ ensemble, with their centers being placed at
coupled
particles’ ensemble, with their centers being placed at ![]() points.
To this end we start with Watson composition rule [12] for T-scattering operators
in a form
points.
To this end we start with Watson composition rule [12] for T-scattering operators
in a form
and
Here
![]() and
and ![]() are self
consistent and single T-scattering operators of ensemble
are self
consistent and single T-scattering operators of ensemble ![]() -th particle, respectively.
-th particle, respectively.
Substituting QS T-scattering operators (13) into Eqs. (15) RHS leads to exact solution of this equations’ system. We seek such solution in a form of dyadic expansion
similar
to (8). For unknown vectors ![]() ,
, ![]() , one gets an equations’ system
, one gets an equations’ system
with inhomogeneous terms being defined by (12) and matrix elements under double sum given by
where the matrix of particles’ coupling
is similar to (11).
The quantity ![]() denotes the generating matrix (10) of
single particle.
denotes the generating matrix (10) of
single particle.
The dyadic expansion (16) and relations (6) show that Eqs.(17) system
is basic one to evaluate the total electric fields and complete currents
excited inside coupled particles. To avoid in the second sum of Eqs.(17) system RHS restriction ![]() one can put conditionally
one can put conditionally ![]() = 0 if
= 0 if ![]() and
introduce next unit matrix
and
introduce next unit matrix ![]() and matrix
and matrix ![]() with elements
with elements
that is the Eqs.
(17) system matrix. With the aid of resolvent matrix ![]() the
solution to Eqs. (17) system is written as
the
solution to Eqs. (17) system is written as
Substituting this solution into dyadic expansion (16) RHS and denoting
gives the self
consistent T-scattering operator of ensemble ![]() th
particle
th
particle
The last step with using the Eq. (14) leads to desired QS T-scattering operator of particles’ ensemble in free space
The inverse ![]() to the matrix (22) is the generating
matrix for
to the matrix (22) is the generating
matrix for ![]() coupled particles’ ensemble.
coupled particles’ ensemble.
Note while particles’ coupling matrix (19) is symmetrical one ![]() =
= ![]() the
transformed particles’ coupling matrix (18) is not symmetrical unless the
matrices (10) and (19) commute.
the
transformed particles’ coupling matrix (18) is not symmetrical unless the
matrices (10) and (19) commute.
4. Quasi-separable recursive procedure for resolvent matrix evaluation
4.1. Recurrent equations with a particle attachment
Return to Watson composition rule for T-scattering operators in Eqs.
(14) and (15) and consider a special case of two “particles”, with first
complicate particle consisting , actually, the![]() coupled
particles’ ensemble, the T- scattering operator of which (24) we denote
temporally
coupled
particles’ ensemble, the T- scattering operator of which (24) we denote
temporally ![]() , and a single
, and a single ![]() -st
particle, the T –scattering operator of which we denote temporally
-st
particle, the T –scattering operator of which we denote temporally ![]() . In this special
. In this special ![]() case
Watson composition rule takes a form
case
Watson composition rule takes a form
and
Eqs.
(25) and (26) system describes physically a changing T-scattering operator of ![]() coupled particles’ ensemble at
attachment a single
coupled particles’ ensemble at
attachment a single ![]() -st particle to this ensemble. These
equations’ system was used in Ref. [23] to study of changing the reflection and
transmission coefficients of
-st particle to this ensemble. These
equations’ system was used in Ref. [23] to study of changing the reflection and
transmission coefficients of ![]() layers’ stack at
layers’ stack at ![]() -st infinitesimal thin layer
attachment. One can recognize a using the Eqs. (25) and (26) system in Refs.
[28,29] at elaborating the recursive transition matrix method for calculating
local electromagnetic fields inside of coupled spheres. Nevertheless, analytic
investigation of Eqs. (25) and (26) system shows that there is not more
complicate and perhaps more simple alternative recursive method to evaluate
T-scattering operator
-st infinitesimal thin layer
attachment. One can recognize a using the Eqs. (25) and (26) system in Refs.
[28,29] at elaborating the recursive transition matrix method for calculating
local electromagnetic fields inside of coupled spheres. Nevertheless, analytic
investigation of Eqs. (25) and (26) system shows that there is not more
complicate and perhaps more simple alternative recursive method to evaluate
T-scattering operator ![]() of
of ![]() coupled
particles at attachment a single
coupled
particles at attachment a single ![]() -st particle to known T
scattering operator
-st particle to known T
scattering operator ![]() of
of ![]() coupled
particles. The alternative method is based on the basic Eqs. (17) system matrix
(20)
coupled
particles. The alternative method is based on the basic Eqs. (17) system matrix
(20)![]() block splitting and the Frobenius formula
[34] application for the block matrix inversion.
block splitting and the Frobenius formula
[34] application for the block matrix inversion.
4.2. Matrix ![]() block
splitting
block
splitting
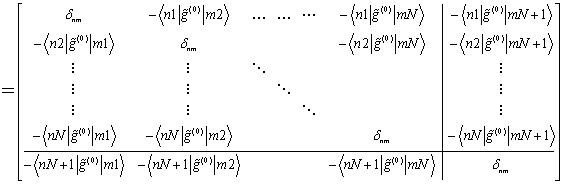
Turn to matrix (20) in the case of ![]() coupled
particles and write of this one in details as a table matrix
coupled
particles and write of this one in details as a table matrix
According
to vertical and horizontal lines one can understand this matrix as ![]() block matrix of the form
block matrix of the form
Here
the left up corner block matrix is appeared to be ![]() and the
right down corner block matrix coincides with matrix element
and the
right down corner block matrix coincides with matrix element ![]() of unit matrix. The block one column
of unit matrix. The block one column ![]() and one row
and one row ![]() matrices
are given by
matrices
are given by
and
Next
we are interesting in resolvent matrix ![]() corresponding
to the case of
corresponding
to the case of ![]() particles and obtaining by the
matrix (28) inversion. According to the Frobenius formula [35], the seeking resolvent matrix has
particles and obtaining by the
matrix (28) inversion. According to the Frobenius formula [35], the seeking resolvent matrix has ![]() block matrix structure similar
to (28) that we write as
block matrix structure similar
to (28) that we write as
with blocks given by
Here the block matrix of principle ![]() is defined by
is defined by ![]() and
has due to Eqs. (29) and (30) the right down corner block matrix form
and
has due to Eqs. (29) and (30) the right down corner block matrix form
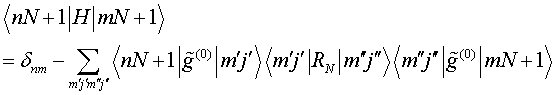 (33)
(33)
The inverse matrix ![]() has
similar right down corner block form . The nonzero elements of block matrices
(32) can be evaluated as follows
has
similar right down corner block form . The nonzero elements of block matrices
(32) can be evaluated as follows
Eqs. (34)--(37) enables one to evaluate the blocks of resolvent
matrix (31) in the case of ![]() particles, provided
one knows the resolvent matrix for
particles, provided
one knows the resolvent matrix for ![]() particles. That is a recursive
procedure based on Frobenius formula in matrix algebra.
particles. That is a recursive
procedure based on Frobenius formula in matrix algebra.
5. Self consistent currents excited inside coupled particles in quasi-separable approach
As was mentioned in Sec.3, Eqs. (17) system is basic one to evaluate the currents excited inside coupled particles, in the framework of quasi-separable approach. Consider this notice in more details.
According
to Eqs. (6), (14) and (15) the self consistent current ![]() excited
inside of ensemble
excited
inside of ensemble ![]() -th particle is defined
by
-th particle is defined
by
with
the ensemble incident electric field ![]() giving in Eq. (2).The QS
self consistent T-scattering operator of ensemble
giving in Eq. (2).The QS
self consistent T-scattering operator of ensemble ![]() -th
particle
-th
particle ![]() is presented as dyadic expansion (16) .
Therefore denoting
is presented as dyadic expansion (16) .
Therefore denoting
enables one to write
We
get a physically transparent representation for the self consistent current
excited inside of ensemble ![]() th particle as
expansion along vector basis functions, with expansion coefficients being equal
to the quantities (39). These expansion coefficients satisfy the equations’
system
th particle as
expansion along vector basis functions, with expansion coefficients being equal
to the quantities (39). These expansion coefficients satisfy the equations’
system
which is originated from Eqs. (17) system. An inhomogeneous term in the new obtained equations’ system RHS is defined by
and
presents expansion coefficient along vector basis functions of current excited
inside single ![]() -th particle.
-th particle.
The matrix of obtained Eqs. (41) system coincides with matrix ![]() defined by Eq. (20) and hence this system
can be resolved with the help of the resolvent matrix
defined by Eq. (20) and hence this system
can be resolved with the help of the resolvent matrix ![]() and
recursive procedure of preceding section. At the same time, the Eqs. (41)
system is interesting itself in special cases of low dimensional ordered arrays
of particles.
and
recursive procedure of preceding section. At the same time, the Eqs. (41)
system is interesting itself in special cases of low dimensional ordered arrays
of particles.
6. Quasi-separable T-scattering operator for electromagnetic crystal unit cell
In previous Secs.2-5 we considered T–scattering operators in QS approach for single particle as well as coupled particles’ ensemble arbitrarily placed without overlapping in free space. The aim of this section is to show that QS approach can be used also at evaluating the homogenized electromagnetic crystal structure effective dielectric permittivity tensor (dyadic).
The way of QS application on this area is opened by the principal
observation that above effective dielectric permittivity dyadic is simple
expressed via crystal structure unit cell T-scattering operator. The scattering
potential ![]() of crystal structure has periodic
property
of crystal structure has periodic
property ![]() where
where ![]() is lattice
point, with
is lattice
point, with ![]() and
and ![]() being
the primitive vectors and generic multi-index of integers, respectively. The
incident electric field
being
the primitive vectors and generic multi-index of integers, respectively. The
incident electric field ![]() is supposed after [1]
to have the Floquet property, i.e.,
is supposed after [1]
to have the Floquet property, i.e., ![]() is periodic in the
crystal, for example, constant vector as we imply in the future. Under this
condition a solution to LS equation (1) for the total electric field
is periodic in the
crystal, for example, constant vector as we imply in the future. Under this
condition a solution to LS equation (1) for the total electric field ![]() has Floquet property also, becoming a
Bloch (Floquet) wave field with wave vector
has Floquet property also, becoming a
Bloch (Floquet) wave field with wave vector ![]() [39]. LS
equation (1) for the Floquet electric field is transformed [1,
40] to a
productive form
[39]. LS
equation (1) for the Floquet electric field is transformed [1,
40] to a
productive form
Here
the RHS inhomogeneous term represents the averaged over crystal structure unit
cell ![]() Floquet electric field given by
Floquet electric field given by
with
![]() denoting the unit cell volume. In Eq.(43)
RHS integral term one sees integration over structure unit cell and an electric
field reduced lattice dyadic Green function defined [1] as
denoting the unit cell volume. In Eq.(43)
RHS integral term one sees integration over structure unit cell and an electric
field reduced lattice dyadic Green function defined [1] as
In
this definition the multi-index ![]() components must not be
all equal to zero simultaneously; the vector
components must not be
all equal to zero simultaneously; the vector ![]() , where
, where
![]() and
and ![]() ,
, ![]() ,
, ![]() are
reciprocal lattice primitive vectors;
are
reciprocal lattice primitive vectors; ![]() =
= ![]() denotes the spatial Fourier transform of
the electric field dyadic Green function (3) in free space. The averaged
electric field (44) satisfies the Dyson equation
denotes the spatial Fourier transform of
the electric field dyadic Green function (3) in free space. The averaged
electric field (44) satisfies the Dyson equation
The
dyadic mass operator ![]() is related to the effective
dielectric permittivity dyadic
is related to the effective
dielectric permittivity dyadic ![]() via well known
relation (see, e.g., [21])
via well known
relation (see, e.g., [21]) ![]() =
= ![]() .
.
Return now to transformed LS Eq.(43) for Floquet electric field and write its solution similar to Eq. (4) in a form
where
we denote ![]() . The dyadic
. The dyadic ![]() in the
Eq. (47) RHS has physical sense of the crystal structure unit cell T-scattering
operator. Comparison Eqs. (43) and (47) leads to LS integral equation for unit
cell T-scattering operator
in the
Eq. (47) RHS has physical sense of the crystal structure unit cell T-scattering
operator. Comparison Eqs. (43) and (47) leads to LS integral equation for unit
cell T-scattering operator
that is obtained also from LS integral equation (5) for single particle in free space T-scattering operator by formal replacing the electric field dyadic Green function in free space to electric field reduced lattice dyadic Green function.
Now we are ready to resolve the main problem of this section,
concerning the application of crystal structure unit cell T-scattering operator
for structure effective dielectric permittivity dyadic evaluation. The problem
is resolved with the aid of identity for dyadic mass operator ![]() in a form
in a form
This identity, being actually definition for structure effective dielectric permittivity dyadic, jointly with Eqs.(47) and (48) lead to desired result
The got result shows that dyadic mass operator can be written as double Fourier transform over crystal structure unit cell from the unit cell dyadic T-scattering operator.
Side by side with the unit cell T-scattering operator satisfied the
LS Eqs. (48) we introduce T-scattering operator of a virtual unit cell in free
space satisfied LS Eqs. (5), solution to which we denote ![]() . One can exclude scattering potential of
unit cell from LS Eqs. (48) RHS, via replacing its by T-scattering operator of
unit cell in free space. After that one gets a LS equation for crystal
structure unit cell T-scattering operator in transformed form
. One can exclude scattering potential of
unit cell from LS Eqs. (48) RHS, via replacing its by T-scattering operator of
unit cell in free space. After that one gets a LS equation for crystal
structure unit cell T-scattering operator in transformed form
where
![]()
![]() denotes [1] electric
field lattice dyadic Green function interaction part defined as difference
between electric field reduced lattice dyadic Green function (45) and electric
field dyadic Green function in free space (3). QS solution to transformed LS Eqs. (51) we seek in a form
denotes [1] electric
field lattice dyadic Green function interaction part defined as difference
between electric field reduced lattice dyadic Green function (45) and electric
field dyadic Green function in free space (3). QS solution to transformed LS Eqs. (51) we seek in a form
with
inversion to an unknown generating matrix ![]() .
Direct substituting representations (24) for
.
Direct substituting representations (24) for ![]() and (52)
into transformed LS Eqs.(51) determines the seeking generating matrix as
difference of two matrices
and (52)
into transformed LS Eqs.(51) determines the seeking generating matrix as
difference of two matrices
first of which coincides with inversion to matrix in Eqs. (22) LHS and second is given by
and describes coupling between particles of a unit cell via crystal structure. The obtained exact expression (50) for mass operator in terms of unit cell T-scattering operator and QS representation (52) for this unit cell T-scattering operator enable one to evaluate contribution effects of coupling between unit cell particles into crystal structure effective dielectric permittivity tensor, without relating a priory to Clausius-Mossotti homogenization formula.
7. Quasi-separable T-scattering operator applications
In this section we consider several applications of QS technique for T-scattering operator. Fist of all one should show how this technique gives classical Mie result on plane wave scattering by homogeneous dielectric sphere.
7.1. Plane wave scattering from and transmitting into spherical particle
Apply the QS T-scattering operator (13) to the case of homogeneous
spherical particle of radius ![]() in free space. We
choose a vector expansion functions’ basis
in free space. We
choose a vector expansion functions’ basis ![]() in the
form of infinite set of regular at the origin spherical vector wave functions [41,42,43]
denoted in spherical coordinates
in the
form of infinite set of regular at the origin spherical vector wave functions [41,42,43]
denoted in spherical coordinates ![]() ,
, ![]() ,
, ![]() as
as ![]() and
and ![]() . In
these denotations indices
. In
these denotations indices ![]() and
and ![]() mean even and odd spherical harmonics
with respect to latitude angle
mean even and odd spherical harmonics
with respect to latitude angle ![]() , respectively, and
indices
, respectively, and
indices ![]() number spherical harmonics with respect
to azimuth angle
number spherical harmonics with respect
to azimuth angle ![]() and
and ![]() again.
Argument
again.
Argument ![]() denotes wave number inside the spherical
particle,
denotes wave number inside the spherical
particle, ![]() . Introducing a multi-index
. Introducing a multi-index ![]()
![]() or
or ![]() we write below
we write below ![]() or
or
![]() . Note that these vector expansions’
functions satisfy the solenoidal restriction in the last Eq.(6) automatically
due to definition of vector spherical wave functions.
. Note that these vector expansions’
functions satisfy the solenoidal restriction in the last Eq.(6) automatically
due to definition of vector spherical wave functions.
We need evaluating the generating matrix (10). To this end one can previously make a productive identical transformation of coupling matrix (11), using differential wave equations for electric field dyadic Green function Eq. (3) in free space and for spherical vector wave functions and applying then vector Green theorem [41]. The described transformation of coupling matrix (11) permits one to rewrite the generating matrix (10) as follows
where
a vector ![]() The out and inner integrations in the
rewritten generating matrix expression RHS are performed along the spherical
particle volume
The out and inner integrations in the
rewritten generating matrix expression RHS are performed along the spherical
particle volume ![]() and surface
and surface ![]() , respectively, with
, respectively, with ![]() being volume element and
being volume element and ![]() and
and ![]() being
surface element and unit normal to surface element.
being
surface element and unit normal to surface element.
The detailed integrations in the Eq. (55) RHS is not difficult in
the main and gives the diagonal generating matrix![]() after
that the QS T-scattering operator (13) takes a form
after
that the QS T-scattering operator (13) takes a form
where
the primed spherical vector wave functions are related to primed spherical
coordinates ![]() ,
, ![]() ,
, ![]() . The elements
. The elements ![]() of
diagonal generating matrix (55) are presented in terms of Mie scattering
coefficients and special bilinear
of
diagonal generating matrix (55) are presented in terms of Mie scattering
coefficients and special bilinear ![]() -functionals of
spherical vector wave functions on spherical particle volume ( see Appendix A).
-functionals of
spherical vector wave functions on spherical particle volume ( see Appendix A).
Let the incident on spherical particle electric field has form [43] of transversal plane wave
with
denoting ![]() . The electric field
. The electric field ![]() transmitted inside spherical particle is
evaluated with the aid of general Eqs.(6) and expression (56) for QS T-
scattering operator of spherical particle. The evaluation result is as follows
transmitted inside spherical particle is
evaluated with the aid of general Eqs.(6) and expression (56) for QS T-
scattering operator of spherical particle. The evaluation result is as follows
where
transmitting coefficients ![]() and
and ![]() coincide with usual for Mie theory (see
Ref. [43], page 128). The electric field
coincide with usual for Mie theory (see
Ref. [43], page 128). The electric field ![]() scattered
by spherical particle is evaluated automatically with the aid of LS equation
(1) for total electric field, provided one knows the electric field transmitted
inside the particle. The result is as follows
scattered
by spherical particle is evaluated automatically with the aid of LS equation
(1) for total electric field, provided one knows the electric field transmitted
inside the particle. The result is as follows
where scattering
coefficients ![]() and
and ![]() coincide
with usual for Mie theory (see Ref. [43], pages 129 and 130).
coincide
with usual for Mie theory (see Ref. [43], pages 129 and 130).
7.2. Pre-Haar basis of vector functions defined on particle finite elements
Having applied the QS T-scattering operator (13) for homogeneous
spherical particle in the preceding subsection, we chose a vector expansion
functions’ basis ![]() in the form of infinite set of
spherical vector wave functions defined over whole particle volume
in the form of infinite set of
spherical vector wave functions defined over whole particle volume ![]() . Consider now another choosing for vector
expansion functions’ basis consisting the functions defined on finite elements
of particle volume in spirit of general finite element method [33]. Such
choosing may be useful in the case of particle with complicate shape and leads
to QS approximation of particle scattering potential operator when LS equation
for T-scattering operator is resolved exactly.
. Consider now another choosing for vector
expansion functions’ basis consisting the functions defined on finite elements
of particle volume in spirit of general finite element method [33]. Such
choosing may be useful in the case of particle with complicate shape and leads
to QS approximation of particle scattering potential operator when LS equation
for T-scattering operator is resolved exactly.
Subdivide the particle volume ![]() into
set of not overlapping subdomains
into
set of not overlapping subdomains ![]() ;
; ![]() , so that
, so that ![]() and
and ![]() as
as ![]() . Define
the orthogonal and normalized set of functions
. Define
the orthogonal and normalized set of functions
where
![]() is a subdomain
is a subdomain ![]() characteristic
function equal to unite as point
characteristic
function equal to unite as point ![]() belongs to the
subdomain and equal to zero if point not belong the subdomain. The set of
functions in Eqs. (60), which can be used as first step on the way to construct
the Haar bases [34], we conditionally call as pre-Haar basis. This basis creates
the piecewise constant functions defined on the particle volume as
belongs to the
subdomain and equal to zero if point not belong the subdomain. The set of
functions in Eqs. (60), which can be used as first step on the way to construct
the Haar bases [34], we conditionally call as pre-Haar basis. This basis creates
the piecewise constant functions defined on the particle volume as
with ![]() denoting the function
denoting the function ![]() averaged over subdomain
averaged over subdomain ![]() according to
according to
On set of functions (61) an analog of Dirac delta-function has a form
Turn now to LS integral Eqs (5) for T-scattering operator. Its RHS
inhomogeneous term has a factor ![]() with particle
scattering potential
with particle
scattering potential ![]() . We replace this factor approximately
as
. We replace this factor approximately
as
and
obtain QS particle scalar scattering potential ![]() operator.
Going to get QS particle dyadic scattering potential
operator.
Going to get QS particle dyadic scattering potential ![]() operator,
we generalize the basis of scalar functions
operator,
we generalize the basis of scalar functions ![]() in
Eqs. (60) to basis of vector functions
in
Eqs. (60) to basis of vector functions
Here
![]() denotes a three–valued vector function of
integer index
denotes a three–valued vector function of
integer index ![]() = 1, 2, 3, equal to unit
vectors
= 1, 2, 3, equal to unit
vectors ![]() ,
, ![]() ,
, ![]() along the
along the ![]() ,
, ![]() ,
, ![]() axes
of the Cartesian coordinate system, respectively. Using identity
axes
of the Cartesian coordinate system, respectively. Using identity ![]() we find similarly with Eqs.(64) an
approximation
we find similarly with Eqs.(64) an
approximation
that is really QS
particle dyadic scattering potential ![]() operator. The LS Eqs.
(5) for T-scattering operator with QS scattering potential operator (66) is
resolved exactly as follows
operator. The LS Eqs.
(5) for T-scattering operator with QS scattering potential operator (66) is
resolved exactly as follows
with generating matrix
where the second matrix element in the RHS describing wave coupling between the particle elements is defined as in Eq. (11), i.e.
The unit matrix ![]() is the same with one before Eq.(20).
is the same with one before Eq.(20).
There is a formal difference between the first terms in the RHS of Eqs. (10) and (68). In details the first term in the Eq. (10) RHS should seen in the case of basis vector functions (65) as
The
integral in the RHS of this equation tends to the quantity ![]() in the RHS first term of Eq.(68) in the
limit of infinitesimally small subdomains of the particle volume, i.e. when
in the RHS first term of Eq.(68) in the
limit of infinitesimally small subdomains of the particle volume, i.e. when ![]() and mentioned formal difference is
dissipated.
and mentioned formal difference is
dissipated.
The vector expansions’ functions (65) satisfy with corresponding accuracy to solenoidal restriction in the last Eq.(6) as is shown in Appendix B. It would be interesting also to compare the pre-Haar basis functions in Eqs.(60) and (65) with position of the electric and magnetic field vector components about a cubic unit cell of the Yee space lattice [44] in computational electrodynamics of the finite-difference time-domain method [45]. But such comparison is out of our paper aim.
7.3. Artificial double diamagnetic-paramagnetic narrow peak in metamaterial with unit cell of coupled plasmonic particles
In Ref.[21] the Dyson equation technique for averaged wave electric field over statistical ensemble of random discrete media was used to evaluate the medium effective dielectric permittivity with spatial dispersion and then via Lindhard rule [46] the corresponding effective magnetic permeability. In details, the effective diamagnetic property was demonstrated in limit of independent strongly reflected nonmagnetic small spherical particles, which possessing individual high dielectric permittivity or conductivity. The physical base for effective magnetic permeability appearance consisted in circular currents created inside a single particle via magnetic dipole scattering.
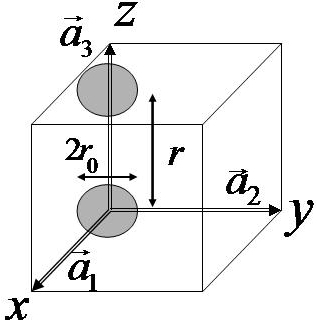
Figure1. A sketch to illustrate an unit
cell in a 3D crystal structure (![]() is the Cartesian
coordinate system,
is the Cartesian
coordinate system, ![]() are primitive vectors) with two
small coupled plasmonic spherical particles (
are primitive vectors) with two
small coupled plasmonic spherical particles (![]() and
and ![]() is a diameter and distance between particles,
respectively).
is a diameter and distance between particles,
respectively).
Now we are going to apply the Dyson Eq.(46) for averaged over electromagnetic crystal structure unit cell wave electric field to evaluate the structure effective dielectric permittivity and then via Linhard rule again the corresponding effective magnetic permeability. In particular, we intend to demonstrate a specific parametric resonance effect as narrow in frequency band double diamagnetic-paramagnetic peak coursed by space-grope resonance effect [5,6] between unit cell coupled small plasmonic spherical particles. The physical base for double diamagnetic-paramagnetic peak appearance consists in circular currents around coupled particles (see Fig.1) via electric dipole scattering by a single particle.
We start with generalized [1] on the anisotropic case the Linhard
rule for effective magnetic permeability dyadic ![]() evaluation,
which in our denotations and geometry on Fig.1 has for the component
evaluation,
which in our denotations and geometry on Fig.1 has for the component ![]() a form
a form
The dyadic mass
operator is given by exact formula (50), with unit cell T-scattering operator
double Fourier transform being in the RHS. As our investigation has shown, the
space-grope resonance effect between unit cell coupled small plasmonic spherical
particles can be considered in tight binding approximation, when direct wave
coupling between init cell particles is substantially grater their coupling via
crystal structure. The unit cell T-scattering operator satisfies the
transformed LS Eq. (51) and can be approximated in the tight binding limit by
the first term of this equation RHS that is by T-scattering operator of unit
cell in free space ![]()
![]() . But
T-scattering operator of two coupled electric dipole scatterers is evaluated in
Ref. [6] and is written out, actually, as QS T-scattering operator (24) for two
coupled particles, with inverse generating matrix and vector expansion
functions being defined as
. But
T-scattering operator of two coupled electric dipole scatterers is evaluated in
Ref. [6] and is written out, actually, as QS T-scattering operator (24) for two
coupled particles, with inverse generating matrix and vector expansion
functions being defined as
and ![]() in Eq.(A9). We denote here
in Eq.(A9). We denote here ![]() and
and ![]()
![]() . The dyadics
. The dyadics ![]() and
and ![]() are, respectively, transversal and
longitudinal projectors on unit vector
are, respectively, transversal and
longitudinal projectors on unit vector ![]() along
vector
along
vector ![]() connecting two coupled particles inside
unit cell. The quantities
connecting two coupled particles inside
unit cell. The quantities ![]() where transversal and
longitudinal components
where transversal and
longitudinal components ![]() of the electric field
dyadic Green function (3) in free space are defined by the following identity and
have the values
of the electric field
dyadic Green function (3) in free space are defined by the following identity and
have the values
where
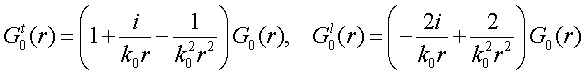
The electric susceptibility ![]() of
small spherical particle with radius
of
small spherical particle with radius ![]() and dielectric
permittivity
and dielectric
permittivity ![]() is given according Ref. [43] by
is given according Ref. [43] by ![]() . Substituting the inverse generating
matrix (72) and vector expansion functions (A9) into QS T-scattering operator
(24) and the last into formula (50) for mass operator results in
. Substituting the inverse generating
matrix (72) and vector expansion functions (A9) into QS T-scattering operator
(24) and the last into formula (50) for mass operator results in
Substituting the obtained dyadic mass operator (74) into Linhard rule (71) gives the expression for inverse effective magnetic permeability component evaluation
We apply this expression to study the space-grope resonance effect
on effective magnetic permeability. According to Ref. [5,6], the space-grope
resonance is characterized by condition ![]() that can
give in general for resonance distant
that can
give in general for resonance distant ![]() between
small spherical particles a value close and even smaller their diameter
between
small spherical particles a value close and even smaller their diameter ![]() , provided that unit cell dimensions being
smaller the wavelength in free space. In the case of plasmonic particles, whose
dielectric permittivity
, provided that unit cell dimensions being
smaller the wavelength in free space. In the case of plasmonic particles, whose
dielectric permittivity ![]() , the resonance distant
between particles can be more their diameter and in vicinity of space grope
resonance the expression (75) for effective magnetic permeability is rewritten as
, the resonance distant
between particles can be more their diameter and in vicinity of space grope
resonance the expression (75) for effective magnetic permeability is rewritten as
We denote here ![]() the plasmonic
resonance frequency related to particle dielectric permittivity by identity
the plasmonic
resonance frequency related to particle dielectric permittivity by identity ![]() . A quantity
. A quantity ![]() measures
a difference between the plasmonic resonance frequency and a space group
resonance frequency and is defined according to
measures
a difference between the plasmonic resonance frequency and a space group
resonance frequency and is defined according to
where
![]() is volume of a sphere with radius equal
to distance between two particles in the unit cell. Fig.2 demonstrates the
resonance dependence (76) in the form of diamagnetic-paramagnetic narrow peak
near plasmonic resonance frequency. The parameters values are taken close to
ones in Ref. [48]
is volume of a sphere with radius equal
to distance between two particles in the unit cell. Fig.2 demonstrates the
resonance dependence (76) in the form of diamagnetic-paramagnetic narrow peak
near plasmonic resonance frequency. The parameters values are taken close to
ones in Ref. [48] ![]() =
1/100,
=
1/100, ![]() = 1/10,
= 1/10, ![]() = 1/1000,
= 1/1000, ![]() = 1/2.
= 1/2.
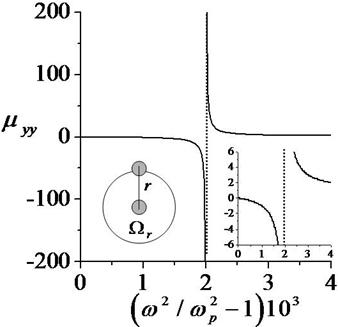
Figure 2. Calculated effective magnetic
permeability (76) versus the normalized frequency of electromagnetic wave near plasmonic resonance frequency ![]() (vertical dotted line is given as a reference
for eyes). The right inset presents dia- -paramagnetic peak in more details.
The left inset illustrates the quantity
(vertical dotted line is given as a reference
for eyes). The right inset presents dia- -paramagnetic peak in more details.
The left inset illustrates the quantity ![]() (see Eq.(77)).
(see Eq.(77)).
7.4. Simple low dimensional ordered periodic and linear arrays of particles with coupling matrix of specific properties
As was noticed in Sec.5, the Eqs.(41) system for self consistent
currents excited inside coupled particles can be peculiarly interesting in
special cases of low dimensional ordered arrays of particles. Let us consider
some such cases when the transformed particles’ coupling matrix ![]() gets property of stochastic matrix or
Jacobi’s matrix for arrays in the form of periodic polygon chain or a strait
linear chain, respectively.
gets property of stochastic matrix or
Jacobi’s matrix for arrays in the form of periodic polygon chain or a strait
linear chain, respectively.
7.4.1. Periodic arrays of particles with coupling matrix of stochastic property
Note that inverse generating matrix (72) of two small coupling
spherical particles can be obtained from general formula (22) for inverse
generating matrix of coupling arbitrarily particles ensemble if one takes the
small spherical particle single T-scattering operator (13) in approximation (A9)
of electric dipole single scattering when the generating matrix (10) of single
particle becomes unit one ![]() . In this electrical
dipole approximation Eqs.(41) system for expansion coefficients
. In this electrical
dipole approximation Eqs.(41) system for expansion coefficients ![]() along vector expansion functions (A9) of
self consistent longitudinal currents
along vector expansion functions (A9) of
self consistent longitudinal currents ![]() excited
inside two coupled small spherical particles drawn on Fig.1 and considered now
in free space takes a form
excited
inside two coupled small spherical particles drawn on Fig.1 and considered now
in free space takes a form
The longitudinal
component ![]() =
= ![]() of
transformed two small spherical particles’ coupling matrix is given by
of
transformed two small spherical particles’ coupling matrix is given by
The matrix of obtained Eqs.(78) system obeys a property of
stochastic matrix that is its both rows have the same sum of their elements ![]() . Though the true stochastic matrix [35]
has positive elements, the mentioned stochastic property of Eqs.(78) system
matrix enables one to find its eigenmode, which we call conditionally
stochastic one
. Though the true stochastic matrix [35]
has positive elements, the mentioned stochastic property of Eqs.(78) system
matrix enables one to find its eigenmode, which we call conditionally
stochastic one
As
one can see, the found stochastic eigenmode (80), corresponding to eigenvalue ![]() , describes the excited longitudinal
currents in both coupling small spherical particles oriented in the same direction
of propagation. The matrix of Eqs.(78) system has also another eigenmode (overtone)
corresponding to eigenvalue
, describes the excited longitudinal
currents in both coupling small spherical particles oriented in the same direction
of propagation. The matrix of Eqs.(78) system has also another eigenmode (overtone)
corresponding to eigenvalue ![]() and getting a form
and getting a form
and describing the excited longitudinal currents in both coupling small spherical particles in the opposite directions of propagations. The both found eigenmodes (80) and (81) can be created at special choice of incident electric field. Resolving Eqs.(78) system gives
and
Thus, the stochastic mode (80) and overtone (81) are created by incident electric field excited currents of the same direction and opposite directions inside single particles, respectively.
Consider some details in frequency dependence of eigenvalues ![]() and
and ![]() for
stochastic and overtone eigenmodes supposing two small spherical particles to
be plasmonic ones. Substituting the electric susceptibility
for
stochastic and overtone eigenmodes supposing two small spherical particles to
be plasmonic ones. Substituting the electric susceptibility ![]() from Subs.7.3 into particles’ coupling
matrix longitudinal component (79) leads to following formula for overtone
inverse eigenvalue
from Subs.7.3 into particles’ coupling
matrix longitudinal component (79) leads to following formula for overtone
inverse eigenvalue
and
similar formula for stochastic mode inverse eigenvalue that is obtained by
replacing ![]() in Eq.(84) RHS. Comparison shows that
formula (84) for overtone inverse eigenvalue is different from the formula (76)
for effective magnetic permeability only in definition of its plasmonic resonance
in Eq.(84) RHS. Comparison shows that
formula (84) for overtone inverse eigenvalue is different from the formula (76)
for effective magnetic permeability only in definition of its plasmonic resonance
![]() width. Physically such close connection
between formulas (76) and (84) means that effective magnetic permeability in metamaterial
with unit cell of coupled plasmonic particles is coursed by circular currents
around coupled particles, as was mentioned above, that corresponds to currents
excited inside coupled particles according Eq.(83).This physical reason is
illustrated on Fig.3.
width. Physically such close connection
between formulas (76) and (84) means that effective magnetic permeability in metamaterial
with unit cell of coupled plasmonic particles is coursed by circular currents
around coupled particles, as was mentioned above, that corresponds to currents
excited inside coupled particles according Eq.(83).This physical reason is
illustrated on Fig.3.
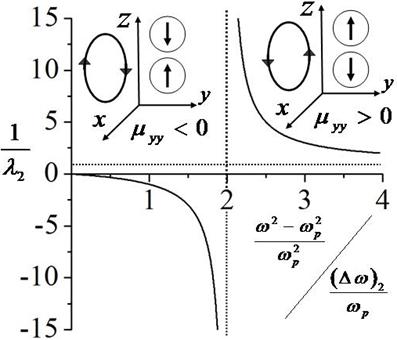
Figure 3. Illustration to correspondence
between circular currents around two coupled plasmonic particles and currents
excited inside these particles according to Eq.(83), in the cases of positive ![]() and negative
and negative ![]() effective
magnetic permeability component. Dotted lines are given as a reference for
eyes.
effective
magnetic permeability component. Dotted lines are given as a reference for
eyes.
Returning to the start of this Subs. 7.4.1 we would recognize that did
not consider a periodic array of particles yet, though having revealed an
interesting stochastic property of two particles’ coupling matrix. In order to
generalize this stochastic property on the case of a periodic array of
particles one could study an ensemble of small spherical particles placed along
parallel cylindrical domains when cylinders themselves centered at the corners
of ![]() sided equilateral polygon as in Fig.4.
Nevertheless we prefer to consider here more simpler model of
sided equilateral polygon as in Fig.4.
Nevertheless we prefer to consider here more simpler model of ![]() coupled parallel wire vibrator–dipoles
turned to half wavelength.
coupled parallel wire vibrator–dipoles
turned to half wavelength.
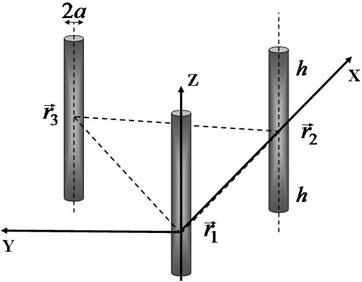
7.4.1.1. N coupled parallel wire vibrator–dipoles tuned to half wavelength
We consider an ensemble of ![]() coupled
parallel thin wire vibrator-dipoles of length
coupled
parallel thin wire vibrator-dipoles of length ![]() each tuned
to half wavelength in free space
each tuned
to half wavelength in free space ![]() ,
, ![]() and centered at the corners of
and centered at the corners of ![]() sided equilateral polygon (Fig.4). The
polygon plane coincides with the
sided equilateral polygon (Fig.4). The
polygon plane coincides with the ![]() plane and the wire
vibrator-dipoles are oriented along the
plane and the wire
vibrator-dipoles are oriented along the ![]() axis
of the Cartesian coordinate system.
axis
of the Cartesian coordinate system.
Figure 4. Schematic showing of coupled
parallel wire (diameter ![]() ) half wavelength
) half wavelength ![]() vibrator-dipoles which are extended along
the
vibrator-dipoles which are extended along
the ![]() axis of the Cartesian coordinate system
axis of the Cartesian coordinate system ![]() and whose centre positions in the
and whose centre positions in the ![]() plane are defined by radius vectors
plane are defined by radius vectors ![]() ,
, ![]() .
.
QS T-scattering operator of single wire vibrator-dipole turned to half wavelength is given according to [15, 48] by Eq. (13), with generating matrix and vector expansion functions being defined approximately as
In these equations ![]() describes harmonics of current
distribution, accurate with an amplitude, along the single wire vibrator-dipole
excited by incident electric field and
describes harmonics of current
distribution, accurate with an amplitude, along the single wire vibrator-dipole
excited by incident electric field and ![]() is
evaluated via double integral
is
evaluated via double integral
and
related to single wire vibrator-dipole input impedance [15] ![]() by
by ![]() . The
formulas (85) are obtained in approximation of “big logarithm”
. The
formulas (85) are obtained in approximation of “big logarithm” ![]() >>1, with
>>1, with ![]() being
the cylindrical vibrator radius. Substituting Eqs. (85) into Eqs. (18) and (19)
results in
being
the cylindrical vibrator radius. Substituting Eqs. (85) into Eqs. (18) and (19)
results in
where
index ![]() notes a projection on the
notes a projection on the ![]() plane. The dimensionless quantity
plane. The dimensionless quantity ![]() was introduced in Ref. [15] as specific
coupling factor of two vibrator-dipoles with distant
was introduced in Ref. [15] as specific
coupling factor of two vibrator-dipoles with distant ![]() between
them (see Fig. 5).
between
them (see Fig. 5).
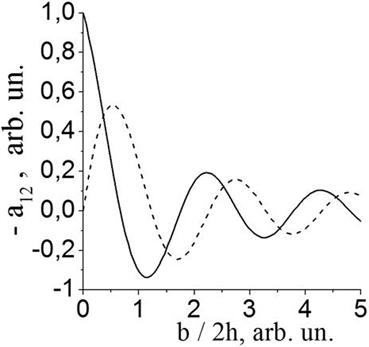
Figure 5. Calculated dependence (87) of
the real (solid line) and imaginary (dashed line) parts of the specific
coupling factor ![]() of two half wavelength
of two half wavelength ![]() vibrator - dipoles versus normalized
distance
vibrator - dipoles versus normalized
distance ![]() between vibrator-dipoles.
between vibrator-dipoles.
As
one sees from this figure the coupling factor ![]() as
as ![]() that agrees the Eq.(86) and Eq.(87)
second. The more exact asymptotics for coupling factor at small distances
that agrees the Eq.(86) and Eq.(87)
second. The more exact asymptotics for coupling factor at small distances ![]() between vibrator-dipoles has a form
between vibrator-dipoles has a form
Here
![]() is the integral sine [49] and regular
function
is the integral sine [49] and regular
function ![]() relates to the integral cosine
relates to the integral cosine ![]() and Euler constant
and Euler constant ![]() 0.5772 by
0.5772 by ![]() =
= ![]() .
.
With expression (87) for transformed particles’ coupling matrix the Eqs.(41)
system for expansion coefficients ![]() along vector expansion
functions (85) of self consistent longitudinal currents
along vector expansion
functions (85) of self consistent longitudinal currents ![]() excited
inside two coupled parallel thin wire vibrator-dipoles turned to half
wavelength takes a form
excited
inside two coupled parallel thin wire vibrator-dipoles turned to half
wavelength takes a form
being
similar to Eqs.(78) system in the case of two coupled small spherical
particles. The matrix of obtained Eqs.(89) system obeys a property of
stochastic matrix and has two eigenmodes, stochastic of type (80) with eigenvalue ![]() and overtone of type (81) with eigenvalue
and overtone of type (81) with eigenvalue
![]() . At creating these eigenmodes by special
choice of incident electric field, as in Eqs.(82) and (83), the amplitudes of
stochastic and overtone eigenmodes 1/
. At creating these eigenmodes by special
choice of incident electric field, as in Eqs.(82) and (83), the amplitudes of
stochastic and overtone eigenmodes 1/![]() and 1/
and 1/![]() tend to finite limit and infinity,
respectively, as distance between two coupled parallel thin wire
vibrator-dipoles becomes too small
tend to finite limit and infinity,
respectively, as distance between two coupled parallel thin wire
vibrator-dipoles becomes too small
These limits means that at close spacing two coupled parallel thin wire vibrator-dipoles the overtone eigenmode with opposite excited currents direction of propagations is created more preferably compared to stochastic eigenmode with the same excited currents directions of propagations.
Consider now three coupled parallel thin wire vibrator-dipoles
centered at the corners of equilateral triangle (Fig.4). In this case Eqs.(41)
system for expansion coefficients ![]() along vector expansion
functions (85) of self consistent longitudinal currents
along vector expansion
functions (85) of self consistent longitudinal currents ![]() excited
inside three coupled parallel thin wire vibrator-dipoles, with accounting
symmetry relations
excited
inside three coupled parallel thin wire vibrator-dipoles, with accounting
symmetry relations ![]() , takes a form
, takes a form
The
matrix of this system obeys a property of stochastic matrix and has two
eigenvalues ![]() with stochastic eigenmode
with stochastic eigenmode
and
degenerated ![]() with two linearly independent overtone eigenmodes
written for example as
with two linearly independent overtone eigenmodes
written for example as
The eigenmodes (92) and (93) can be created at special choice of incident electric field. Resolving Eqs.(91) system gives
and
The
amplitudes of stochastic and overtone eigenmodes 1/![]() and 1/
and 1/![]() tend to finite limit and infinity,
respectively, as distances between three coupled parallel thin wire
vibrator-dipoles become too small, with
tend to finite limit and infinity,
respectively, as distances between three coupled parallel thin wire
vibrator-dipoles become too small, with ![]() /
/![]() and 1/
and 1/![]() going
to infinity as in Eq.(90). These limits means that at close spacing three
coupled parallel thin wire vibrator-dipoles the overtone eigenmodes with not
the same excited currents direction of propagations are created more preferably
compared to stochastic eigenmode with the same excited currents directions of propagations
in all three wire vibrator-dipoles.
going
to infinity as in Eq.(90). These limits means that at close spacing three
coupled parallel thin wire vibrator-dipoles the overtone eigenmodes with not
the same excited currents direction of propagations are created more preferably
compared to stochastic eigenmode with the same excited currents directions of propagations
in all three wire vibrator-dipoles.
7.4.2. Linear array of parallel wire vibrator–dipoles with coupling matrix of Jacobi’s property
Consider again the ensemble of ![]() coupled
parallel thin wire vibrator-dipoles of length
coupled
parallel thin wire vibrator-dipoles of length ![]() each
turned to half wavelength and centered now along a strait line coincided with
the
each
turned to half wavelength and centered now along a strait line coincided with
the ![]() axis and oriented along the
axis and oriented along the ![]() axis of the Cartesian coordinate system
(Fig.4). We are interesting in extinction rate of currents’ exciting along wire
vibrator-dipoles when this exciting is transfered from the first vibrator-dipole
to one with the number
axis of the Cartesian coordinate system
(Fig.4). We are interesting in extinction rate of currents’ exciting along wire
vibrator-dipoles when this exciting is transfered from the first vibrator-dipole
to one with the number ![]() .
.
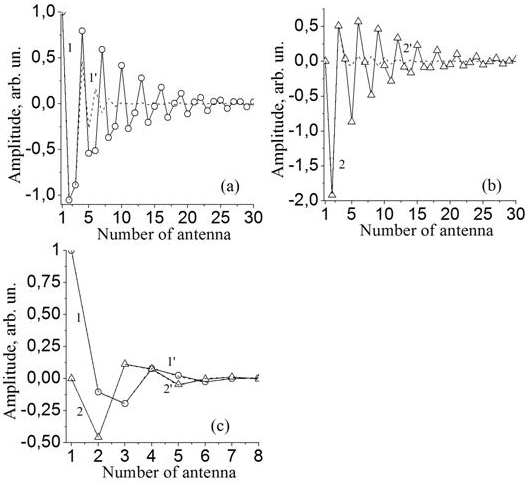
The Eqs.(41) system for expansion coefficients ![]() along vector expansion functions (85) of
self consistent longitudinal currents
along vector expansion functions (85) of
self consistent longitudinal currents ![]() excited
inside linear array of
excited
inside linear array of ![]() coupled parallel thin wire vibrator-dipoles
we are writing in a form
coupled parallel thin wire vibrator-dipoles
we are writing in a form
where
a specific coupling factor ![]() of two
vibrator-dipoles with numbers
of two
vibrator-dipoles with numbers ![]() and
and ![]() is defined by Eq.(87) again. Our task
consists in evaluating the expansion coefficient
is defined by Eq.(87) again. Our task
consists in evaluating the expansion coefficient ![]() of
current excited inside the vibrator-dipole with number
of
current excited inside the vibrator-dipole with number ![]() ,
provided the incident electric field excites the current inside the fist single
vibrator-dipole only
,
provided the incident electric field excites the current inside the fist single
vibrator-dipole only ![]() and
and ![]() = 0,
= 0, ![]() .
.
To simplify the problem we use a closest neighbour interaction
aproach putting ![]() as
as ![]() and
making the matrix
and
making the matrix ![]() of Jacobi’s property one (Jacobi’s
approximation). Under this simplification our problem is resolved by formula
of Jacobi’s property one (Jacobi’s
approximation). Under this simplification our problem is resolved by formula
Determinant of
matrix ![]() is evaluated with the aid of recurrent
relation
is evaluated with the aid of recurrent
relation
For rough estimations one can use an asymptotic solution to this recurrent relation in the form
The
numerical evaluation results of current exciting inside vibrator-dipole with
number ![]() relatively to exciting the first vibrator
dipole
relatively to exciting the first vibrator
dipole ![]() is depicted in Fig.6.
is depicted in Fig.6.
|
Fig.6. Relative current |
According to these figures the current exciting is transferred from
the first vibrator-dipole to one with the number ![]() along
strait line of vibrator-dipoles with substantial oscillation in dependence on
along
strait line of vibrator-dipoles with substantial oscillation in dependence on ![]() and experienced extinction at
and experienced extinction at ![]() on level 0.25, with normalized distance
between next vibrator-dipoles being
on level 0.25, with normalized distance
between next vibrator-dipoles being ![]() = 0.1. The asymptotics
(99) gives for curves on Fig.6(a,b) not enough in accuracy approximation yet.
This accuracy is enough for curves on Fig.6(c) where spacing between next
vibrator dipoles becomes bigger
= 0.1. The asymptotics
(99) gives for curves on Fig.6(a,b) not enough in accuracy approximation yet.
This accuracy is enough for curves on Fig.6(c) where spacing between next
vibrator dipoles becomes bigger ![]() = 0.5 and current
exciting is transferred along strait line of vibrator-dipoles to
= 0.5 and current
exciting is transferred along strait line of vibrator-dipoles to ![]() only.
only.
7.4.2.1. Standing and propagating waves of currents’ exciting along linear array of vibrator-dipoles and particles at all
According to Fig.6 the currents’ exciting is transfered from the
first vibrator-dipole to the ![]() th one along strait
line of vibrator-dipoles with substantial oscillations in dependence on
th one along strait
line of vibrator-dipoles with substantial oscillations in dependence on ![]() . The physical reason for these
oscillations consists in specific property of Eqs.(96) system matrix
. The physical reason for these
oscillations consists in specific property of Eqs.(96) system matrix ![]() in Jacobi’s approximation. Namely, the
middle
in Jacobi’s approximation. Namely, the
middle ![]() rows of this matrix have sum of their
elements equal to
rows of this matrix have sum of their
elements equal to ![]() whereas the first and
whereas the first and ![]() -th rows have sum of their elements
equal to
-th rows have sum of their elements
equal to ![]() . Because of that the first and
. Because of that the first and ![]() -th equations of system (96) play
role of specific boundary conditions for the rest middle
-th equations of system (96) play
role of specific boundary conditions for the rest middle ![]() equations and solution to the Eqs.(96)
system becomes similar to elastic string oscillations [36], being rather
standing wave of currents’ exciting along linear array of vibrator-dipoles than
propagating wave. Nevertheless in the middle part of a long array the solution
under study is approximately a propagating wave. Next we give analytic
confirmation for predicted physical feature of Eqs.(96) system solution.
equations and solution to the Eqs.(96)
system becomes similar to elastic string oscillations [36], being rather
standing wave of currents’ exciting along linear array of vibrator-dipoles than
propagating wave. Nevertheless in the middle part of a long array the solution
under study is approximately a propagating wave. Next we give analytic
confirmation for predicted physical feature of Eqs.(96) system solution.
Recurrent relation (98) for determinant of Eqs.(96) system matrix in Jacobi’s approximation enables one to get solution to this system analytically, provided the incident electric field excites the current inside the fist single vibrator-dipole only
(see some details to solution in Appendix C)
The second Eq.(100)
is dispersion equation for the complex variable ![]() . In
the middle part of a long linear array of vibrator-dipoles, when
. In
the middle part of a long linear array of vibrator-dipoles, when ![]() and vibrator position number
and vibrator position number ![]() is fixed, Eq.(100) gives asymptotically
is fixed, Eq.(100) gives asymptotically
where
![]()
![]() and
and ![]() is a wave number. Having known the wave
number, one can evaluate as usually [41] corresponding phase velocity
is a wave number. Having known the wave
number, one can evaluate as usually [41] corresponding phase velocity ![]() and group velocity
and group velocity ![]() putting
putting
The
frequency dependence of wave number is obtained by solution of dispersion
Eq.(100). Being complicate in general, this dispersion equation is simple resolved
analytically in physically interesting case of ![]() and
and ![]() when wave number takes a form
when wave number takes a form
Apply the obtained form (103) for dispersion equation to the limit
of small distances between linear array vibrator-dipoles tuned to half
wavelength when according Eq.(88) the coupling factor ![]() approximates
to minus one and wave phase velocity in Eq.(102) due to Eq.(103) is given by
approximates
to minus one and wave phase velocity in Eq.(102) due to Eq.(103) is given by
where
![]() denotes the light speed in free space. To
evaluate the group velocity one
denotes the light speed in free space. To
evaluate the group velocity one
needs
considering the case of weakly detuned vibrator-dipoles, which length is
lightly different from half wavelength and vibrator-dipole input impedance ![]()
![]() is defined according
to [48] via relations
is defined according
to [48] via relations
As
one can verify at resonance frequency ![]() the
input impedance becomes pure real and at tuned frequency
the
input impedance becomes pure real and at tuned frequency ![]() the input impedance value is consistent
with Eq.(88). Substituting now the weakly detuned vibrator-dipole impedance (105)
into expression for
the input impedance value is consistent
with Eq.(88). Substituting now the weakly detuned vibrator-dipole impedance (105)
into expression for ![]() in Eq.(88) and the last into Eq.(102) with accounting Eq.(103) gives for group velocity at resonance
frequency a value
in Eq.(88) and the last into Eq.(102) with accounting Eq.(103) gives for group velocity at resonance
frequency a value
The obtained value shows that group velocity of currents’ exciting propagation between close packed resonance vibrator-dipoles is negative in sign and small in magnitude compared with light speed in vacuum.
Return to analytic solution (100) to Eq.(96) system. Bearing in mind
definition (101) for wave number, this solution describes rather standing wave
of currents’ exciting along linear array of vibrator-dipoles than propagating
wave, though asymptotics (101) for the middle part of a long linear array of vibrator-dipoles
when ![]() and
and ![]() is
fixed describes propagating wave. Consider now a limit for the right end part
of the long linear array
is
fixed describes propagating wave. Consider now a limit for the right end part
of the long linear array ![]() corresponding to
solution in Eq.(97). Asymptotics of analytic solution (100) for the right end
describes a standing wave, with exponentially decreasing amplitude as
corresponding to
solution in Eq.(97). Asymptotics of analytic solution (100) for the right end
describes a standing wave, with exponentially decreasing amplitude as ![]() in accordance to Fig. 6(c). Especially
interesting from physical point of view to note a special case
in accordance to Fig. 6(c). Especially
interesting from physical point of view to note a special case ![]() , which realized for dispersion equation
(103) and when above amplitude exponentially decreasing effect is canceled. In
this case the asymptotics for expansion coefficient (97) of current excited
inside the vibrator-dipole with number
, which realized for dispersion equation
(103) and when above amplitude exponentially decreasing effect is canceled. In
this case the asymptotics for expansion coefficient (97) of current excited
inside the vibrator-dipole with number ![]() takes
a form
takes
a form
![]() (107)
(107)
This asymptotics
substantially oscillates in dependence on ![]() as was
noticed on the Fig.6.
as was
noticed on the Fig.6.
8. Conclusion
In this work, we have presented obtained for the first time analytic solution to fundamental in electromagnetic wave multiple scattering theory Lippmann-Schwinger (LS) integral equation for T-scattering operator of electric wave field by dielectric and conducting nonmagnetic particle of arbitrary size and shape. The solution is derived with the aid of a chosen vector expansion functions’ basis and written as sum of separable scattering operators weighted by inverse of a generating matrix and named quasi–separable (QS) T-scattering operator. The QS solution to LS equation is generalized for ensemble of coupled particles in free space as well as for coupled particles inside unit cell of electromagnetic crystal. An equations’ system for self consistent currents excited inside coupled particles was derived also in QS form.
In the case of a single spherical particle we have verified that vector expansion functions’ basis chosen as vector spherical wave functions the QS T-scattering operator gives the Mie solution for incident transverse plane wave scattered from particle and transmitted inside particle. The elements of diagonal generating matrix are presented for this case in terms of Mie scattering coefficients and special bilinear functionals of spherical vector wave functions on spherical particle volume. We considered also a principally another choosing the vector expansion functions’ defined on finite elements of particle volume and named conditionally pre-Haar basis. It was shown that such “basis”, even including finite number of expansions’ functions, leads to QS simplified scattering potential operator and automatically to a corresponding exact solution to LS equation, which tends to solution of LS equation with actual, not simplified scattering potential operator when number expansions’ function of pre-Haar basis becomes infinite.
Mentioned above equations’ system for self consistent currents excited inside coupled particles can be resolved in general case with the aid of recursive procedure, which is appeared at a particle attachment in spirit of invariant imbedding method. But for some interesting special cases this system is resolved via simple methods analytically. On this way were considered such phenomena as artificial double diamagnetic-paramagnetic narrow peak in metamaterial with unit cell of coupled plasmonic particles; creation for eigenmodes with overtones in periodic arrays of particles with coupling matrix of stochastic property; extinction rate for transfer of currents’ exciting in linear array of particles with coupling matrix of Jacobi’s property and standing and propagation wave phenomenon for such transfer.
APENDIX A. Diagonal generating matrix (55) in terms of Mie
scattering coefficients and bilinear ![]() -functional of spherical vector wave
functions
-functional of spherical vector wave
functions
Let us denote ![]() a bilinear functional
of spherical vector wave functions on spherical particle volume
a bilinear functional
of spherical vector wave functions on spherical particle volume ![]() defined by
defined by
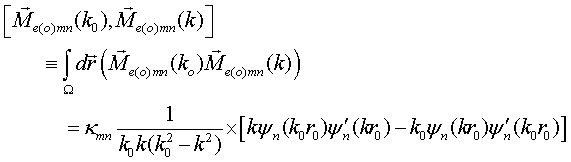 (A1)
(A1)
and similarly
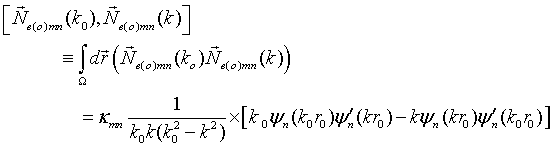 (A2)
(A2)
Here an auxiliary matrix is used
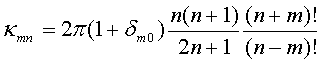 (A3)
(A3)
and ![]() is Riccati-Bessel function (see [43],
page 129). The basic result of this Appendix A consists in the following
formulas for diagonal generating matrix (55) elements
is Riccati-Bessel function (see [43],
page 129). The basic result of this Appendix A consists in the following
formulas for diagonal generating matrix (55) elements
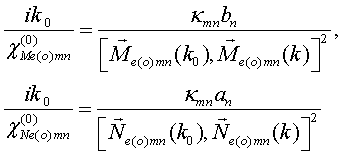 (A4)
(A4)
There are also simple relations between Mie scattering and transmission coefficients
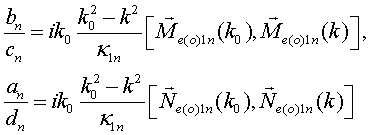 (A5)
(A5)
that can help to understand the derivation of Eqs.(58) and (59) with the aid of QS T-scattering operator (56).
In electric and magnetic dipole approximation the QS T-scattering operator (56) becomes equal to a sum
![]() (A6)
(A6)
where the RHS
first “electric” and second “magnetic” terms are created by Eq.(56) second and
first terms, respectively, taken in approximation ![]() = 1,
= 1, ![]() = 0, 1. For the case of small spherical
particle
= 0, 1. For the case of small spherical
particle ![]() ,
, ![]() we
find
we
find
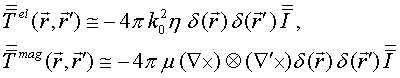 (A7)
(A7)
with ![]() and
and ![]() being the spherical particle electric and
magnetic susceptibilities, respectively.
being the spherical particle electric and
magnetic susceptibilities, respectively.
In the first formula (A7) for QS T-scattering electric dipole approximation a Dirac delta-function is appeared, actually, as expression
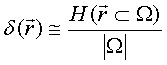 (A8)
(A8)
and similarly
when argument ![]() is replaced to
is replaced to ![]() , in accordance with Dirac delta-function analog
definition in Eqs.(63) by considering functions defined on particle finite
elements. Formulas (A7) were obtained in ref.[17] via the Hertz’s vector of
electric dipole and magnetic dipole scattering study. One can rewrite the electric
and magnetic dipole approximations (A7) for T-scattering operator in QS form
(13) as
, in accordance with Dirac delta-function analog
definition in Eqs.(63) by considering functions defined on particle finite
elements. Formulas (A7) were obtained in ref.[17] via the Hertz’s vector of
electric dipole and magnetic dipole scattering study. One can rewrite the electric
and magnetic dipole approximations (A7) for T-scattering operator in QS form
(13) as
where unit
vectors ![]() are defined in subsection 7.2. Note that electric
dipole vector expansion function
are defined in subsection 7.2. Note that electric
dipole vector expansion function ![]() in Eq.(A9) with analog Dirac
delta-function (A8) satisfies automatically the solenoidal restriction in the
last Eq.(6) for points laying strictly inside spherical particle domain. With
accounting points on spherical particle surface or in the case of true Dirac
delta-function the selenoidal restriction on electric dipole vector expansion
function is verified with the aid of generalized function theory (see next
Appendix B). Magnetic dipole vector expansion function in Eq.(A9) satisfies the
solenoidal restriction automatically.
in Eq.(A9) with analog Dirac
delta-function (A8) satisfies automatically the solenoidal restriction in the
last Eq.(6) for points laying strictly inside spherical particle domain. With
accounting points on spherical particle surface or in the case of true Dirac
delta-function the selenoidal restriction on electric dipole vector expansion
function is verified with the aid of generalized function theory (see next
Appendix B). Magnetic dipole vector expansion function in Eq.(A9) satisfies the
solenoidal restriction automatically.
APENDIX B. Solenoidal restriction on finite element vector expansions’ functions (65)
Let us verify that vector expansions’ functions (65) defined on finite elements of particle volume satisfy with corresponding accuracy to solenoidal restriction in the last Eq. (6) in weak sense of theory of generalized functions [51]. For points lying strictly inside particle volume domain the solenoidal restriction is satisfied exactly.
Take
divergence of a vector function (65) and integrate this differential operation
with product by a test smooth function ![]() of
compact support. We obtain
of
compact support. We obtain
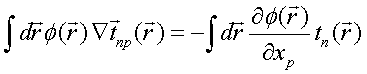 (B1)
(B1)
We suppose for
simplicity that all subdomains ![]() have form of cubes
with their edges being parallel to the axes of the Cartesian coordinate system.
Denoting
have form of cubes
with their edges being parallel to the axes of the Cartesian coordinate system.
Denoting ![]() the test function averaged over cube 2D
section
the test function averaged over cube 2D
section ![]() perpendicular to
perpendicular to ![]() axis
one can transform
axis
one can transform
![]()
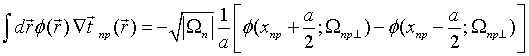 (B2)
(B2)
where ![]() is subdomain centre coordinate and
is subdomain centre coordinate and ![]() denotes the cube edge length, with
denotes the cube edge length, with ![]() . In the limit of
. In the limit of ![]() Eq.(B2)
RHS tends to zero as
Eq.(B2)
RHS tends to zero as ![]()
APENDIX Ñ. Analytic solution to Eqs.(96) system in Jacobis’ approximation
Turn to recurrent relation (98) for Eqs.(96) system matrix determinant. One can directly verify the following solution to this recurrent relation
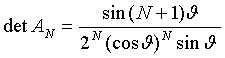 (C1)
(C1)
Solution in Eq.(100) to Eqs.(96) system is written out first as
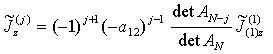 (C2)
(C2)
that is verified directly again. Transformation of solution (C2) to the form in Eq.(100) is performed using Eq.(C1).
References
1. M. Silveirinha, Metamaterial homogenization approach with application to the characterization of microstructured composites with negative parameters // Phys. Rev. B 75, 115104, 2007.
2. P. A. Belov, C. R. Simovsky, Homogenization of electromagnetic crystals formed by uniaxial resonant scatterers // Phys. Rev. E 72, 026615, 2005.
3. A. Alu, N. Engheta, Three-dimensional nanotransmission lines at optical frequencies: A recipe for broadband negative-refraction optical metamaterials // Phys. Rev. B 75, 024304, 2007.
4. M. S. Wheeler, J. S Aitchison, M. Mojahedi, Coupled magnetic dipole resonances in sub-wavelength dielectric particle clusters // J. Opt. Soc. Am. B 21, 1083, 2010.
5. Yu. N. Barabanenkov, V. V. Shlypin, Space group resonance in electromagnetic wave multiple scattering // Phys. Lett. A 170, 239, 1992.
6. Yu. N. Barabanenkov, V. V. Shlypin, Space-group resonance effect in scattering of light by a small volume of individually nonresonant dipoles // Phys. Rev. B 58, 3034, 1998.
7. Y. Xu, Y. L. Reginald, K. Lee, A. Yariv, Scattering-theory analysis of waveguide-resonator coupling // Phys. Rev. E 62, 7389, 2000.
8. A. L. Burin, H. Cao, G. C. Schatz, M. A. Ratner, High-quality optical modes in low-dimensional arrays of nanoparticles: application to random lasers //J. Opt. Soc. Am. B 21, 121, 2004.
9. A. L. Burin, Bound whispering gallery modes in circular arrays of dielectric spherical particles //Phys. Rev. E 73, 066614, 2006.
10. R. King, The Theory of N Coupled Parallel Antennas //J. Appl. Phys. 21, 94 (1950).
11. B. A. Lippmann, J. Schwinger, Variational principles for scattering processes. I. //Phys. Rev. 79, 469, 1950.
12. M. L. Goldberger, K. M. Watson. Collision Theory (Wiley, New York, 1964).
13. J. R. Taylor, The Quantum Theory on Nonrelativistic Collisions (John Wiley, New York, 1972).
14. L. Tsang, J. A. Kong, R. T. Shin, Theory of Microwave Remote Sensing (John Wiley, New York, 1985).
15. Yu. N. Barabanenkov, M. Yu. Barabanenkov, V. A. Cherepenin, Near – field coherent effects at thermal microwave radiation receiving on coupled linear wire antennas // Journal of Radio Electronics, N 12, 2011, http://jre.cplire.ru/jre/dec11/3/text.html
16. Yu. N. Barabanenkov, V. M. Finkel’berg, Radiation transport equation for correlated scatterers // Zh. Eksp. Teor. Fiz. 53, 978 (1967) [Sov. Phys. JETP 26, 587 (1968)]
17. Yu. N. Barabanenkov, Multiple scattering of waves by ensemble of particles and the radiative transport // Usp. Fis. Nauk 117 ,49, 1975 [Sov. Phys. Usp. 18, 673 (1975)].
18. Yu. N. Barabanenkov, Asymptotic limit of the radiative transfer theory in problems of multiple wave scattering in randomly inhomogeneous media // Phys.-Usp. 52, 502, 2009.
19. Yu. N. Barabanenkov, M. I. Kalinin, Weakly nonuncoupled relations in wave multiple scattering theory for dense discrete random media // Phys. Lett. A 163, 241, 1992.
20. Yu. N. Barabanenkov, M. Yu. Barabanenkov, Radiative transfer theory with time delay for effect of a pulse imprisonment in a resonant random media : general transfer equation and point-like scatterer model //Waves in Random Media 7, 607, 1997.
21. Yu. N. Barabanenkov, M. Yu. Barabanenkov, S. A. Nikitov, Artificial magnetism in theory of wave multiple scattering by random discrete non-magnetic conducting media // arXiv:1009.4770 v 1[cond-mat.dis-nn] 24 Sep 2010.
22. Yu. N. Barabanenkov, M. Yu. Barabanenkov, S. A. Nikitov, Virtual singular scattering of electromagnetic waves in transformation media concept // Advanced Electromagnetism, 1, No. 1, 38, 2012.
23. Yu. N. Barabanenkov, V. L. Kounetsov, M. Yu. Barabanenkov, Transfer relations for electromagnetic wave scattering from periodic dielectric one-dimensional interface // Progress in Electromagnetic Research , PIER, Ed by J.A. Kong (EMW, Cambridge, 1999).
24. R. Bellman and G.M. Wing. An Introduction to Invariant Imbedding (Wiley-Interscience, New York, 1975).
25. P.C. Waterman. Proc. IEEE 53, 805, 1965.
26. P. C. Waterman, Symmetry, Unitarity, and Geometry in Electromagnetic Scattering // Phys. Rev. D 3, 825. 1971.
27. M. I. Mishchenko, J. W. Hovenier, L. D. Travis, Lignt Scattering by Nonspherical Particles (Acad. Press, New York, 2000).
28. W. C. Chew. Waves and Fields in Inhomogeneous Media (IEEE, 1995).
29. B. Stout, J. C. Auder, J. Lafait, A transfer matrix approach to local field calculations in multiple-scattering problems // J. Mod. Opt. 49, 2129, 2002.
30. C. Lovelace, Practical Theory of Three-Particle States. I. Nonrelativistic // Phys. Rev. 135, B1225, 1964.
31. B. G. Galerkin, Eng. Bull. (Vestn. Inzh .Tech.) 19, 897 (1915) (Russian).
32. R. E. Collin, Field Theory of Guided Waves, 2 nd ed.(IEEE, New York, 1991).
33. G. Strang, G. J. Fix. An Analysis of the Finite Element Method (Englewood Gliff, New York, 1973).
34. A. Haar, Zur theorie der orthogonalen funktionensysteme // Math. Ann. 69, 1910.
35. P. Lankaster, Theory of Matrices (Academic Press, New York, 1969).
36. J. W. S. Rayligh, Theory of Sound (MacMillan, London, 1894).
37. Yu. N. Barabanenkov, M. Yu. Barabanenkov, I. Lisenkov. Progress In Electromagnetic Research Symposium Abstract, Moscow, Russia, August 19-23, 2012, p. 814.
38. L. Tsang, J. A. Kong, Multiple scattering of electromagnetic waves by random distributions of discrete scatterers with coherent potential and quantum mechanical formalism // J. Appl. Phys. 51, 3465, 1980.
39. A. Yariv. Optical waves in crystals (John Wiley, New York, 1987).
40. J.M. Ziman. The Calculation of Bloch Functions (New York, 1971).
41. J.A. Stratton. Electromagnetic Theory (McGraw-Hill, New York, 1941),
(J. Wiley, New York,1983).
42. C.T. Tai. Dyadic Green’s Function in Electromagnetic Theory (International Textboo, Scranton, PA, 1971).
43. C.F.Bohren and D.R.Huffman. Absorption and Scattering of Light by Small Particles (J. Wiley, New York, 1983).
44. K.S. Yee. IEEE Trans. Antennas and Propagation. 14, 302 (1966).
45. A. Teflove. Computational Electrodynamics: The Finite-Difference Time
46. J.Lindhard, On the properties of a gas of charged particles // Dan. Mat. Fys. Medd., 28. No. 8, 3, 1954.
47. M. Silveirinha, Generalized Lorentz-Lorenz formulas for microstructured materials // Phys. Rev. B 75, 245117, 2007.
48. M.A.Leontovich and M.L. Levin. Journ. Thechn. Phys. 14, 481 (1944).
49. G.A. Korn and T.M. Korn. Mathematical Handbook(for scientists and engeneers) (McGray-Hill, New York, 1961).
50. I.M. Gelfand and G.E. Shilov. Generalized functions. Vol. I.Properties and Operations (Acad. Press, Boston, 1964).