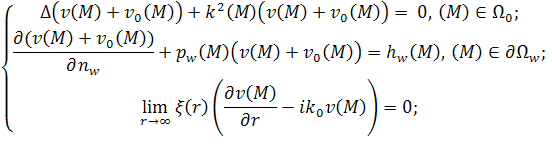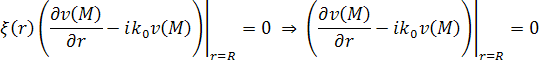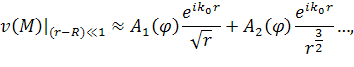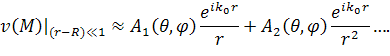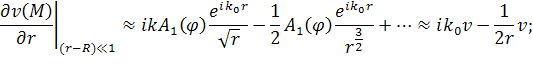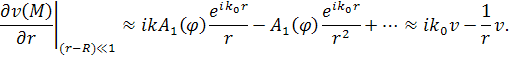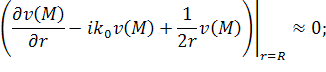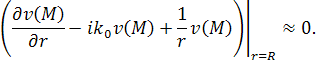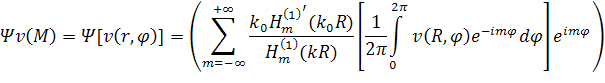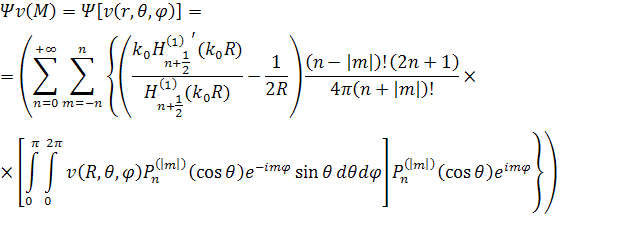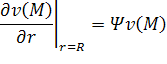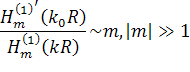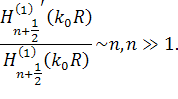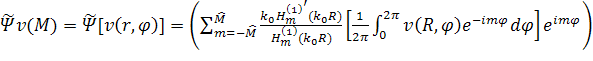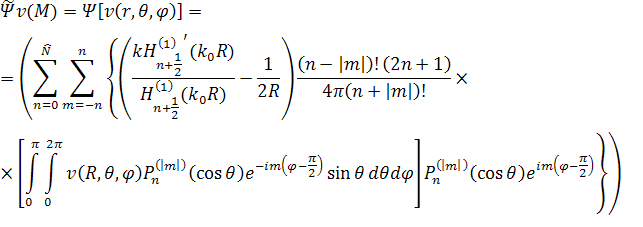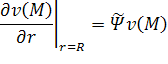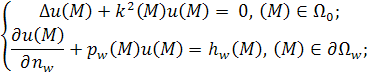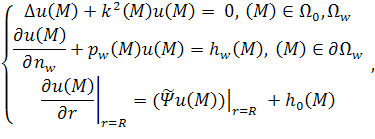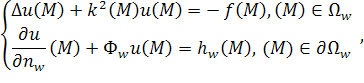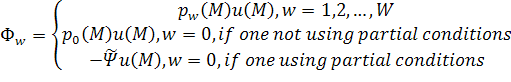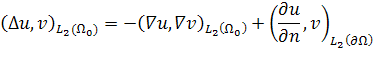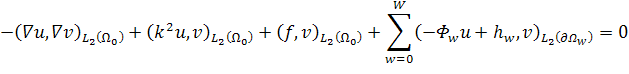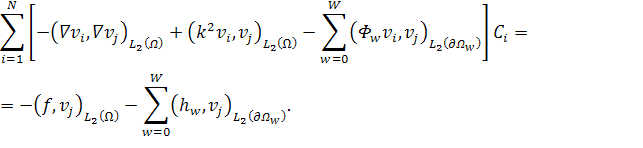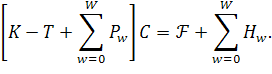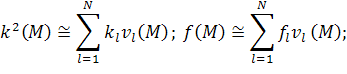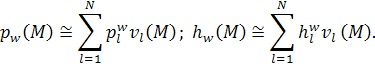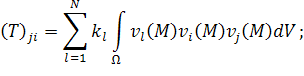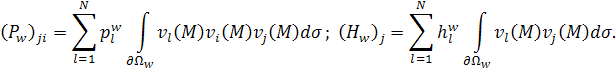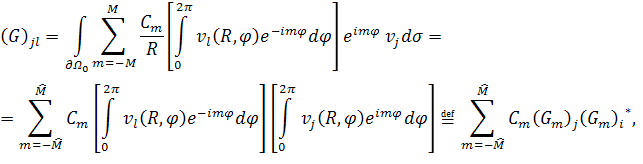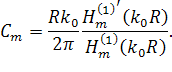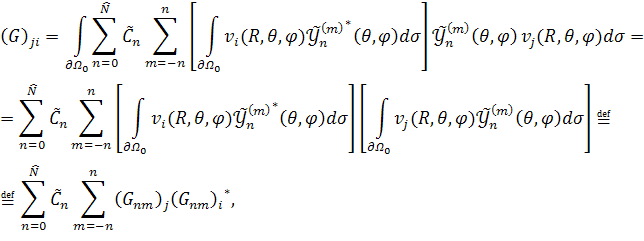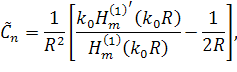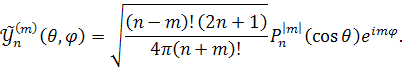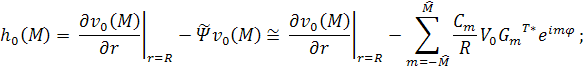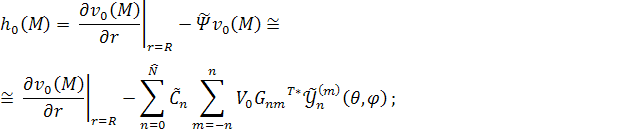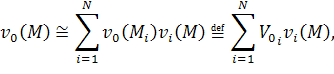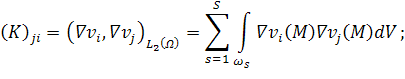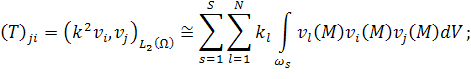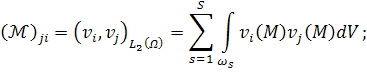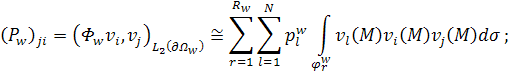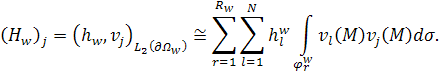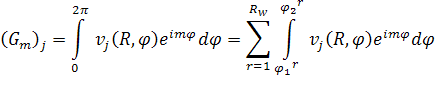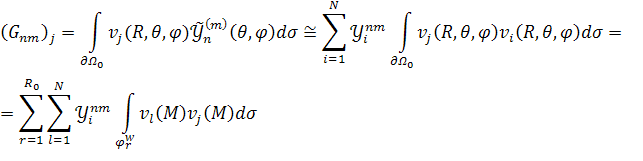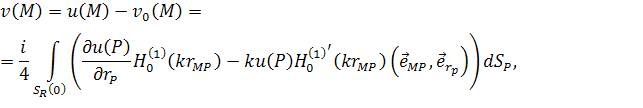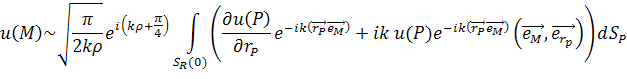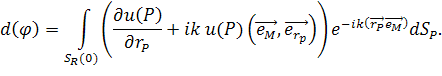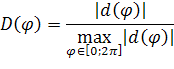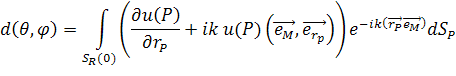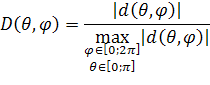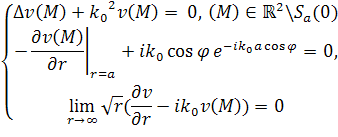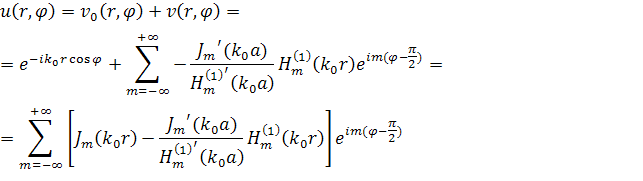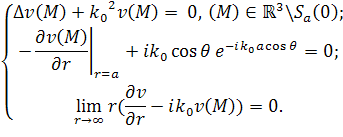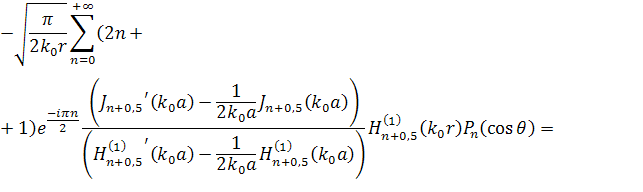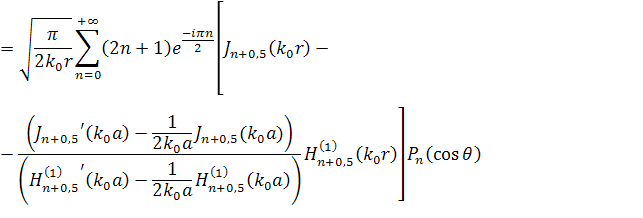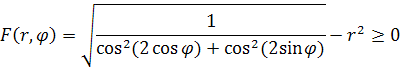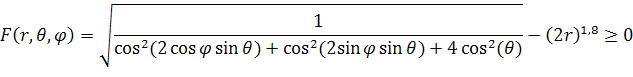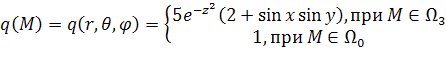МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИФРАКЦИИ АКУСТИЧЕСКИХ И ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА СЛОЖНЫХ РАССЕИВАТЕЛЯХ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Д. А. Коняев, А. Л. Делицын
МГУ им. М. В. Ломоносова, Физический факультет, кафедра математики
Статья получена 31 марта 2014 г.
Аннотация. Данная работа посвящена конечно-элементному анализу скалярной задачи дифракции на двумерных и трёхмерных рассеивателях сложной структуры с использованием парциальных условий излучения. В работе представлены основные результаты тестирования реализованного программного комплекса. Проведённые тесты показали хорошее согласие численных и аналитических решений задачи дифракции на канонических рассеивателях: на бесконечном цилиндре в двумерном случае и на сфере в трёхмерном случае. Также, для демонстрации возможностей разработанной программы представлен ряд расчётов для дифракции на сложных рассеивателях.
Ключевые слова: задача дифракции, метод конечных элементов, парциальные условия излучения.
Abstract: This article is devoted to finite element analysis of scalar diffraction problem on two-dimensional and three-dimensional complex scatterers using partial radiation conditions. The article presents the main results of testing the proposing program. Tests have shown good agreement between the numerical and analytical solutions of the diffraction problem on canonical scatterers: on an infinite cylinder in the two-dimensional case and sphere in the three-dimensional case. Also, to demonstrate the capabilities of the developed program, number of calculations for diffraction on complex scatterers was presented.
Key words: diffraction problem, finite element method, partial radiation conditions.
Введение.
Математическое моделирование волновых полей в сложных средах является актуальной задачей в связи с проблемами радиолокации, антенной техники, электроразведки, различными биомедицинскими и другими применениями. А, как известно, для решения обратных задач и задач синтеза необходимо иметь надёжный алгоритм решения прямых задач [1,2].
При решении краевых задач в сложных областях наиболее универсальным является метод конечных элементов [3]. Однако, в связи с тем, что задача дифракции ставится в неограниченной области, применение этого метода требует серьёзных затрат вычислительных ресурсов. Задача ограничения области и постановки оптимальных граничных условий на фиктивной границе, позволяющих достичь максимальной точности результатов при минимальных вычислительных затратах, сама по себе является весьма сложной. В работе [4] рассматривается вопрос постановки неотражающих условий на границах расчётной области, обеспечивающих поглощение падающих на них волн. Основным недостатком этих условий является отсутствие универсальности их построения.
Парциальные условия излучения [5,6] в каком-то смысле можно считать выполняющими ту же роль, что и неотражающие. Дело в том, что парциальные условия в точной постановке (в виде ряда) позволяют выделить необходимое решение, то есть являются точными. При этом фиктивную границу можно расположить достаточно близко к рассеивателям. Стоит отметить, что парциальные условия излучения представляет собой интегро-дифференциальный оператор, поэтому их использование требует адаптации к методу конечных элементов.
2. Постановка задачи.
На практике часто трёхмерная
задача дифракции может быть сведена к двумерной задаче дифракции [7], поэтому рассмотрение двумерной задачи также целесообразно [8,9]. В данной работе рассматривается стационарная, с временной зависимостью ![]() , задача
дифракции скалярных волновых полей в двумерной и трёхмерной постановках.
, задача
дифракции скалярных волновых полей в двумерной и трёхмерной постановках.
Будем рассматривать
рассеиватели, состоящие из нескольких тел. Обозначим эти тела за ![]() , где
индекс
, где
индекс ![]() является
номером тела рассеивателя. Границы этих
тел обозначим соответственно за
является
номером тела рассеивателя. Границы этих
тел обозначим соответственно за ![]() . Также
введём обозначение области пространства, в которой отсутствуют рассеиватели:
. Также
введём обозначение области пространства, в которой отсутствуют рассеиватели: ![]() .
.
Введём следующие ограничения
на границы тел рассеивателей. В каждой точке границы существует касательная
плоскость в трёхмерном случае и прямая в двумерном случае. В двумерном случае
также потребуем звёздность границ тел рассеивателей. Впрочем, это требование не
является принципиальным и может быть устранено при незначительной модификации
разработанного приложения. Потребуем также связность областей тел
рассеивателей. В противном случае можно просто разделить тело рассеивателя на
два новых рассеивателя. Также, потребуем, чтобы ![]() . То есть
рассеиватели отделены друг от друга внешним пространством. Ранее двумерная
задача уже была рассмотрена в [8,9]. Пример
допустимой совокупности тел рассеивателей в двумерном случае изображён на
рисунке 1.
. То есть
рассеиватели отделены друг от друга внешним пространством. Ранее двумерная
задача уже была рассмотрена в [8,9]. Пример
допустимой совокупности тел рассеивателей в двумерном случае изображён на
рисунке 1.
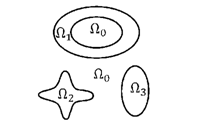
Рисунок 1. Пример конфигурации тел рассеивателей.
Тела рассеивателей могут
иметь различную внутреннюю структуру. Это могут быть проницаемые рассеиватели с
неоднородным заполнением, абсолютно непроницаемые рассеиватели, а также
рассеиватели с сильным поглощением, которые приближённо можно считать
непроницаемыми, так как поле проникает лишь в небольшой слой близ границы
рассеивателя [6,5]. На границах проницаемых
рассеивателей следует поставить условия сопряжения, а именно в случае дифракции
скалярного поля условия непрерывности неизвестной функции и её нормальной
производной. При этом решение необходимо искать как вне, так внутри
рассеивателя. Заметим, что при применении метода конечных элементов для этого
достаточно лишь аппроксимировать границы таких рассеивателей элементами сетки [9]. Поэтому для изложения материала удобно исключить из списка тел рассеивателей
проницаемые рассеиватели, произведя при этом перенумерацию проницаемых
рассеивателей. Далее будем считать, что ![]() – число непроницаемых рассеивателей. На границах
абсолютно непроницаемых рассеивателей следует поставить условие Дирихле, или
Неймана. В представленной программе используется лишь условие Неймана, как
частный случай условия третьего рода. На границах тел с большим поглощением
необходимо поставить условия третьего рода, то есть импедансные граничные
условия [6,5].
– число непроницаемых рассеивателей. На границах
абсолютно непроницаемых рассеивателей следует поставить условие Дирихле, или
Неймана. В представленной программе используется лишь условие Неймана, как
частный случай условия третьего рода. На границах тел с большим поглощением
необходимо поставить условия третьего рода, то есть импедансные граничные
условия [6,5].
Известно, что для выделения единственного решения уравнения Гельмгольца также необходимо использовать дополнительные условия – условия излучения на бесконечности, в качестве которых, как правило, используются условия излучения Зоммерфельда [6,5,10]. Запишем строгую математическую постановку задачи дифракции скалярного поля [6,5,10].
|
(1) |
где ![]() – заданные
функции,
– заданные
функции, ![]() – волновое
число, соответствующее однородной среде, заполняющей
– волновое
число, соответствующее однородной среде, заполняющей ![]() ,
, ![]() ,
, ![]() – падающая
волна,
– падающая
волна, ![]() в
двумерном случае и
в
двумерном случае и ![]() – в
трёхмерном случае, а
– в
трёхмерном случае, а ![]() – точка
двумерного пространства в двумерном случае, или
– точка
двумерного пространства в двумерном случае, или ![]() – точка
трёхмерного пространства в трехмерном случае. Условимся, что вектора нормали
– точка
трёхмерного пространства в трехмерном случае. Условимся, что вектора нормали ![]() , при
, при ![]() , направлены внутрь областей
, направлены внутрь областей ![]() .
.
3. Ограничение области.
Основной трудностью при
применении метода конечных элементов к задаче дифракции является неограниченная
область, в которой рассматривается исходная краевая задача. То есть для
применения этого метода необходимо разумно ограничить область [4], в которой ставится задача. Для этого в двумерном случае рассмотрим круг, полностью содержащий
все тела рассеивателей [8,9], а в трёхмерном случае сферу, также включающую все
тела рассеивателей. Будем называть вновь введённую границу фиктивной, а также
введём для неё обозначение ![]() , а её
радиус обозначим как
, а её
радиус обозначим как ![]() . Для изображённого
на рисунке 1 примера
рассеивателя на рисунке 2 представлен
пример введения фиктивной границы.
. Для изображённого
на рисунке 1 примера
рассеивателя на рисунке 2 представлен
пример введения фиктивной границы.
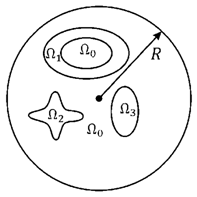
Рисунок 2. Ограничение внешней по отношению к рассеивателям области в двумерном случае.
Наиболее очевидным и простым
способом постановки граничных условий на фиктивной границе является
использование условий излучения Зоммерфельда при фиксированном ![]() . При этом, очевидно, надо потребовать, чтобы
. При этом, очевидно, надо потребовать, чтобы ![]() было достаточно велико [4,8,9]. То есть должны быть выполнены условия
было достаточно велико [4,8,9]. То есть должны быть выполнены условия ![]() и
и ![]() , где
, где ![]() – длина
волны падающего излучения, а
– длина
волны падающего излучения, а ![]() –
минимальный радиус фиктивной границы, при котором внутри неё содержатся все
рассеиватели. Тогда граничное условие примет вид.
–
минимальный радиус фиктивной границы, при котором внутри неё содержатся все
рассеиватели. Тогда граничное условие примет вид.
|
|
(2) |
Накладываемые
на ![]() требования
сильно увеличивают вычислительные затраты при численном решении задачи, и как
показала практика, даже в двумерном случае применение этих условий
нецелесообразно.
требования
сильно увеличивают вычислительные затраты при численном решении задачи, и как
показала практика, даже в двумерном случае применение этих условий
нецелесообразно.
Получим другие приближённые условия излучения [4]. Можно показать, что в двумерном случае имеет место представление
|
|
(3) |
аналогичное полученному в [11] для трёхмерного случая:
|
|
(4) |
Тогда, дифференцируя (3) и (4), получим в двумерном случае (5) и в трёхмерном случае (7)
|
|
(5) |
|
|
(6) |
Подставив в (5) и (6) выражения (3) и (4), сохранив при этом только первые члены разложения, получим (7) и (8) соответственно для двумерного и трёхмерного случаев.
|
|
(7) |
|
|
(8) |
Эти
условия весьма популярны среди исследователей, так как фактически являются
граничными условиями третьего рода. Будем называть эти условия радиационными
граничными условиями первого порядка [4].
Используя эти условия на фиктивной границе, удаётся получить неплохие
результаты при существенно меньших ![]() , чем в
предыдущем случае [8]. Однако,
требование, чтобы
, чем в
предыдущем случае [8]. Однако,
требование, чтобы ![]() было
велико, всё ещё сохраняется. Избавиться от этого требования позволяют
парциальные условия излучения [9].
было
велико, всё ещё сохраняется. Избавиться от этого требования позволяют
парциальные условия излучения [9].
Следуя [6,5], заменим исходную задачу дифракции эквивалентной, используя парциальные условия на фиктивной
границе ![]() . Для
удобства введём оператор
. Для
удобства введём оператор ![]() , который в
двумерном случае определяется равенством (9), а в
трёхмерном случае равенством (10).
, который в
двумерном случае определяется равенством (9), а в
трёхмерном случае равенством (10).
|
|
(9) |
|
|
(10) |
Тогда парциальные условия излучения можно записать в следующем виде как для двумерного, так и трёхмерного случаев.
|
|
(11) |
Это граничное условие
представляет собой бесконечный ряд, который при численном решении задачи
придётся заменить конечной суммой. Здесь на радиус фиктивной границы необходимо
наложить лишь одно условие, а именно ![]() . Однако,
при детальном рассмотрении коэффициентов ряда в операторе
. Однако,
при детальном рассмотрении коэффициентов ряда в операторе ![]() нетрудно
заметить, что этот ряд сходится довольно медленно, так как
нетрудно
заметить, что этот ряд сходится довольно медленно, так как
|
|
(12) |
и
|
|
(13) |
То
есть, коэффициенты ряда Фурье, входящие в оператор ![]() , убывают очень медленно.
, убывают очень медленно.
Отсюда следует, что для численного решения задачи дифракции с использованием парциальных условий излучения на фиктивной границе возможны два подхода.
Первый подход заключается в
поиске способа ускорения сходимости ряда в операторе ![]() , а второй – эвристический подход, в замене ряда в
операторе
, а второй – эвристический подход, в замене ряда в
операторе ![]() его частичной
суммой, и, исходя из результатов сравнения численных решений задачи дифракции
на рассеивателях, для которых аналитическое решение известно, с этими
аналитическими решениями, можно определить диапазоны значений параметров
его частичной
суммой, и, исходя из результатов сравнения численных решений задачи дифракции
на рассеивателях, для которых аналитическое решение известно, с этими
аналитическими решениями, можно определить диапазоны значений параметров ![]() и
и ![]() ,
определяющих число слагаемых в частичных суммах в двумерном и трёхмерном
случаях соответственно, при которых соответствующая ошибка минимальна. Использование
второго подхода оправдано, если значение полученной ошибки невелико, в
противном случае необходимо пользоваться первым подходом.
,
определяющих число слагаемых в частичных суммах в двумерном и трёхмерном
случаях соответственно, при которых соответствующая ошибка минимальна. Использование
второго подхода оправдано, если значение полученной ошибки невелико, в
противном случае необходимо пользоваться первым подходом.
В данной работе используется
второй подход. Обозначим оператор, получаемый при замене ряда в операторе ![]() за
за ![]() . Тогда
оператор
. Тогда
оператор ![]() можно
записать в виде равенств (14) и (15)).
можно
записать в виде равенств (14) и (15)).
|
|
(14) |
|
|
|
|
|
(15)) |
Теперь приближённые парциальные условия излучения можно записать в следующем виде.
|
|
(16) |
Итак, были рассмотрены три
варианта постановки граничных условий на фиктивной границе. В реализованной
программе имеется возможность использовать любой из этих вариантов, однако, как
показала практика, первый вариант даже в двумерном случае не позволяет получить
какие-либо результаты. Использование
второго варианта в двумерном случае было описано в [8]. Однако, в трёхмерном
случае использование этого варианта весьма затратно в плане вычислительных
ресурсов из-за требования больших ![]() . Вариант
использования парциальных условий в двумерном случае также представлен в [9]. Первые два варианта постановки граничных
условий на фиктивной границе удобны тем, что представляют собой условия
третьего рода, и поэтому задачу можно переписать в следующей форме:
. Вариант
использования парциальных условий в двумерном случае также представлен в [9]. Первые два варианта постановки граничных
условий на фиктивной границе удобны тем, что представляют собой условия
третьего рода, и поэтому задачу можно переписать в следующей форме:
|
|
(17) |
где
введены следующие обозначения: ![]() – полное
волновое поле,
– полное
волновое поле, ![]() ,
, ![]() и
и ![]() ,
, ![]() для приближённых условий Зоммерфельда и радиационных
граничных условий первого порядка соответственно,
для приближённых условий Зоммерфельда и радиационных
граничных условий первого порядка соответственно, ![]() в двумерном случае и
в двумерном случае и ![]() в трёхмерном случае.
в трёхмерном случае. ![]() . В случае
использования приближённых парциальных условий излучения задача дифракции
принимает несколько более сложный вид.
. В случае
использования приближённых парциальных условий излучения задача дифракции
принимает несколько более сложный вид.
|
|
(18) |
где ![]() .
.
Задача переписана в форме задачи поиска полного волнового поля неслучайно, поскольку при этом сильно упрощается задание граничных условий на границах сложной формы.
4. Метод конечных элементов.
Следуя [3], рассмотрим применение метода конечных элементов к задаче дифракции. Запишем задачу дифракции в следующем виде.
|
|
(19) |
где введено обозначение:
|
|
(20) |
Рассмотрим задачу поиска слабого решения этой задачи:
|
|
(21) |
Обозначим
за ![]() границу
области
границу
области ![]() ,
представляющую собой объединение границ
,
представляющую собой объединение границ ![]() . Воспользуемся первой формулой Грина и преобразуем
первое слагаемое:
. Воспользуемся первой формулой Грина и преобразуем
первое слагаемое:
|
|
(22) |
Здесь
![]() – элемент
площади в двумерном случае и элемент объёма в трёхмерном случае, а
– элемент
площади в двумерном случае и элемент объёма в трёхмерном случае, а ![]() – элемент длины кривой в двумерном случае и элемент
площади в трёхмерном случае. Вспомним, что вектора нормали
– элемент длины кривой в двумерном случае и элемент
площади в трёхмерном случае. Вспомним, что вектора нормали ![]() , при
, при ![]() , направлены внутрь областей
, направлены внутрь областей ![]() . Поэтому
вектор
. Поэтому
вектор ![]() совпадает
с соответствующими векторами
совпадает
с соответствующими векторами ![]() . В связи с
этим, пользуясь граничными условиями,
получим:
. В связи с
этим, пользуясь граничными условиями,
получим:
|
|
(23) |
Построим теперь в
рассматриваемой области треугольную в двумерном случае и тетраэдрическую в
трёхмерном случае сетку методом граничной коррекции [12,13,14]. С существующими методами построения треугольных и тетраэдрических сеток можно ознакомиться в [13,15,14]. Области тел рассеивателей задаются при
помощи неравенств: ![]() в
двумерном случае и
в
двумерном случае и ![]() в
трёхмерном случае, при этом на их границы
в
трёхмерном случае, при этом на их границы
![]() накладываются следующие требования. Будем
предполагать, что функция в левой части неравенства является гладкой, что
обеспечивает отсутствие «рёбер» и «особых точек» на границе. А также
предположим, что начало координат – точка
накладываются следующие требования. Будем
предполагать, что функция в левой части неравенства является гладкой, что
обеспечивает отсутствие «рёбер» и «особых точек» на границе. А также
предположим, что начало координат – точка ![]() лежит внутри фиктивной границы, то есть известно, что
лежит внутри фиктивной границы, то есть известно, что
![]() . Все функции, используемые в постановке задачи,
задаются в виде символьных формул, вводимых с клавиатуры. При этом в программе
используется несколько видов функций: функции, заданные одной формулой;
функции, заданные формулами на промежутках значений аргументов; а также функции,
заданные формулами на различных областях задачи.
. Все функции, используемые в постановке задачи,
задаются в виде символьных формул, вводимых с клавиатуры. При этом в программе
используется несколько видов функций: функции, заданные одной формулой;
функции, заданные формулами на промежутках значений аргументов; а также функции,
заданные формулами на различных областях задачи.
Обозначим за ![]() элементы
этой сетки. Введём теперь набор конечных
элементов заданного порядка. Обозначим набор конечных элементов через
элементы
этой сетки. Введём теперь набор конечных
элементов заданного порядка. Обозначим набор конечных элементов через ![]() , где
, где ![]() , где
, где ![]() – количество
узлов заданной сетки. Как известно, результирующая ошибка приближённого
решения по отношению к точному зависит как от порядка конечных элементов, так и
от аппроксимации границы области, в которой решается задача [3,12,16]. Так как в программе не используются сетки, допускающие наличие элементов с
криволинейной границей, нет смысла требовать высокий порядок конечных
элементов. Поэтому будем использовать линейные конечные элементы.
– количество
узлов заданной сетки. Как известно, результирующая ошибка приближённого
решения по отношению к точному зависит как от порядка конечных элементов, так и
от аппроксимации границы области, в которой решается задача [3,12,16]. Так как в программе не используются сетки, допускающие наличие элементов с
криволинейной границей, нет смысла требовать высокий порядок конечных
элементов. Поэтому будем использовать линейные конечные элементы.
|
|
(24) |
где ![]() в
двумерном случае и
в
двумерном случае и ![]() в трёхмерном случае. Тогда уравнение перейдёт в
следующую систему линейных алгебраических уравнений:
в трёхмерном случае. Тогда уравнение перейдёт в
следующую систему линейных алгебраических уравнений:
|
|
(25) |
Введём следующие матрицы и столбцы:
|
|
(26) |
Тогда систему можно переписать в виде:
|
|
(27) |
5. Сборка матриц.
Перед построением матриц проделаем некоторые упрощения. А именно, приблизим конечными элементам функции, стоящие под интегралами [3].
|
|
(28) |
Теперь введём матрицы:
|
|
(29) |
где ![]() – узел
треугольной сетки с номером j. Тогда искомые матрицы можно переписать в следующем
виде [3]:
– узел
треугольной сетки с номером j. Тогда искомые матрицы можно переписать в следующем
виде [3]:
|
|
(30) |
Несложно
заметить, что для построения матрицы ![]() достаточно
построить матрицу массы
достаточно
построить матрицу массы ![]() , затем
вычислить столбец
, затем
вычислить столбец ![]() , тогда
, тогда ![]()
![]() [3]
[3]![]() .
.
Для матрицы ![]() ,
соответствующей парциальным условиям излучения, введём дополнительное
обозначение
,
соответствующей парциальным условиям излучения, введём дополнительное
обозначение ![]() . Равенства
(29)
и (33)(30 задают элементы матриц, соответствующих парциальным
условиям излучения в двумерном и трёхмерном случаях соответственно.
. Равенства
(29)
и (33)(30 задают элементы матриц, соответствующих парциальным
условиям излучения в двумерном и трёхмерном случаях соответственно.
|
|
(31) |
где
|
|
(32)(32) |
|
|
(33)(30 |
где
|
|
(34) |
|
(35) |
Элементы
матриц ![]() в случае
использования парциальных условий излучения вычисляются так же, как и элементы
матриц
в случае
использования парциальных условий излучения вычисляются так же, как и элементы
матриц ![]() , только
функции
, только
функции ![]() вычисляются
при помощи равенств (33) и (34)
соответственно в двумерном и трёхмерном случаях.
вычисляются
при помощи равенств (33) и (34)
соответственно в двумерном и трёхмерном случаях.
|
|
(36) |
|
(37) |
где ![]() – столбец,
составленный из коэффициентов
– столбец,
составленный из коэффициентов ![]() :
:
|
|
(38) |
где ![]() – узел
треугольной сетки.
– узел
треугольной сетки.
Будем вычислять интегралы в (28) по элементам
сетки [3]. Будем использовать ранее введённое обозначение ![]() для
элементов треугольной сетки, а также введём новое обозначение
для
элементов треугольной сетки, а также введём новое обозначение ![]() – границы
элементов треугольной сетки, принадлежащие границе области номер
– границы
элементов треугольной сетки, принадлежащие границе области номер ![]() . Поясним значение индекса
. Поясним значение индекса ![]() . При построении треугольной сетки, дополнительно
формируется массив границ элементов, принадлежащих границам областей. Первый
индекс данного массива соответствует номеру границы, второй индекс является
порядковым номером, уменьшенным на единицу, элемента границы некоторого
элемента
. При построении треугольной сетки, дополнительно
формируется массив границ элементов, принадлежащих границам областей. Первый
индекс данного массива соответствует номеру границы, второй индекс является
порядковым номером, уменьшенным на единицу, элемента границы некоторого
элемента ![]() , принадлежащего соответствующей границе области. Этот
индекс, увеличенный на единицу, и обозначен через
, принадлежащего соответствующей границе области. Этот
индекс, увеличенный на единицу, и обозначен через ![]() . Полезно также ввести обозначение
. Полезно также ввести обозначение ![]() ,
обозначающее максимальное значение индекса
,
обозначающее максимальное значение индекса ![]() для границы номер
для границы номер ![]() . Теперь формулы можно переписать в следующем виде [3].
. Теперь формулы можно переписать в следующем виде [3].
|
|
(39) |
|
|
(40) |
|
|
(41) |
|
|
(42) |
|
|
(43) |
|
|
(44) |
где ![]() – меньшая
дуга окружности, стягиваемая элементом
– меньшая
дуга окружности, стягиваемая элементом ![]() .
.
|
|
(45) |
где ![]() , где
, где ![]() – узел
треугольной сетки.
– узел
треугольной сетки.
Необходимо отметить, что поскольку в двумерном случае граница аппроксимируется отрезками, то направления этих отрезков должны быть согласованы (заданы в соответствии с направлением обхода границы) [9]. Впрочем, последнее, в силу звёздности областей, достигается отслеживанием полярных углов концов отрезка. Разность углов должна иметь всегда один и тот же знак, за исключением отрезка, один конец которого лежит в первой четверти системы координат, а второй в четвёртой. Последний случай легко отработать, так как только в этом случае разность углов будет превышать 180о [9].
Так как ![]() является
конечными элементами, то интегралы по
является
конечными элементами, то интегралы по ![]() или
или ![]() будут
отличны от нуля лишь в том случае, если индексы всех конечных элементов,
стоящих под интегралом, являются номерами узлов треугольной сетки,
принадлежащих
будут
отличны от нуля лишь в том случае, если индексы всех конечных элементов,
стоящих под интегралом, являются номерами узлов треугольной сетки,
принадлежащих ![]() или
или ![]() соответственно.
Следовательно, для сборки представленных выше матриц достаточно для каждого
элемента
соответственно.
Следовательно, для сборки представленных выше матриц достаточно для каждого
элемента ![]() и
и ![]() вычислить
значения соответствующих интегралов для всех возможных комбинаций индексов
конечных элементов, удовлетворяющих требованию: индексы всех конечных
элементов, стоящих под интегралом, являются номерами узлов треугольной сетки,
принадлежащих
вычислить
значения соответствующих интегралов для всех возможных комбинаций индексов
конечных элементов, удовлетворяющих требованию: индексы всех конечных
элементов, стоящих под интегралом, являются номерами узлов треугольной сетки,
принадлежащих ![]() или
или ![]() соответственно, при этом добавляя полученные значения к
соответствующим ячейкам матрицы. Естественно, при этом изначально матрицы
необходимо инициализировать как нулевые.
соответственно, при этом добавляя полученные значения к
соответствующим ячейкам матрицы. Естественно, при этом изначально матрицы
необходимо инициализировать как нулевые.
Часто для реализации
последней операции используют так называемые элементные матрицы. [3]. Действительно, если рассмотреть конкретный элемент ![]() или
или ![]() , то
используя локальную нумерацию узлов, принадлежащих этому элементу, можно
построить плотную матрицу малой размерности по представленным выше формулам. Затем
полученные элементные матрицы «встраиваются» соответствующие ячейки глобальной
матрицы.
, то
используя локальную нумерацию узлов, принадлежащих этому элементу, можно
построить плотную матрицу малой размерности по представленным выше формулам. Затем
полученные элементные матрицы «встраиваются» соответствующие ячейки глобальной
матрицы.
Из рассмотренного выше
правила построения матриц можно сделать вывод. Ненулевыми ячейками ранее
введённых квадратных матриц будут лишь те ячейки, номера строки и столбца
которых являются номерами узлов, принадлежащих одному элементу ![]() или
или ![]() , в
зависимости от рассматриваемой матрицы. Поэтому получаемые матрицы являются
сильно разреженными, в связи с чем можно выбрать более экономный, нежели
естественный, формат хранения матриц. Одним из наиболее популярных форматов
хранения разреженных матриц является разреженный строчный формат хранения
матриц [17]. Данный формат, как раз и используется в программе для хранения
матриц в программе. При этом для сложения
и умножения матриц используются параллельные варианты алгоритмов рассмотренных
в [17].
, в
зависимости от рассматриваемой матрицы. Поэтому получаемые матрицы являются
сильно разреженными, в связи с чем можно выбрать более экономный, нежели
естественный, формат хранения матриц. Одним из наиболее популярных форматов
хранения разреженных матриц является разреженный строчный формат хранения
матриц [17]. Данный формат, как раз и используется в программе для хранения
матриц в программе. При этом для сложения
и умножения матриц используются параллельные варианты алгоритмов рассмотренных
в [17].
Поскольку матрица системы является разреженной, её решение осуществляется итерационным методом, а именно, обобщённым методом минимальных невязок (GMRES) [18] c предобусловливанием в виде неполного LU разложения [18]. При этом для построения матрица предобусловливателя используется параллельная версия алгоритма, представленного в [19]. Решив данную систему, получаем приближённое решение задачи дифракции, которое можно записать в следующем виде.
|
|
(46) |
6. Диаграмма рассеяния.
По аналогии с [7], рассмотрим третью формулу Грина в двумерном случае.
|
|
(47) |
где, ![]() .
.
Устремим
![]() к
бесконечности:
к
бесконечности: ![]() , тогда
третью формулу Грина можно переписать в следующем виде.
, тогда
третью формулу Грина можно переписать в следующем виде.
|
|
(48) |
Введём обозначение:
|
|
(49) |
По аналогии с [7] определим диаграмму рассеяния следующим образом.
|
|
(50) |
Аналогично в трёхмерном случае получим:
|
|
(51) |
Диаграмму рассеяния по аналогии с [7] определим следующим образом.
|
|
(52) |
7. Тестирование программы.
Начнём тестирование программы
с двумерного случая, а затем перейдём к трёхмерному случаю. Во всех далее
рассмотренных примерах предполагается ![]() . Эту
величину
. Эту
величину ![]() будем
называть шагом исходной сетки.
будем
называть шагом исходной сетки.
Рассмотрим тестовую задачу дифракции на бесконечном непроницаемом цилиндре радиуса a. Решение данной задачи можно найти, например в [10], где для этого используется метод интегральных уравнений. В связи с бесконечной протяжённостью рассеивателя вдоль оси OZ декартовой системы координат, эту задачу можно рассматривать как двумерную задачу дифракции на круге радиуса a.
В качестве падающей волны будем рассматривать плоскую волну, приходящую с положительного направления оси OX декартовой системы координат.
|
|
(53) |
Тогда, задача, поставленная в §1, примет следующий вид.
|
|
(54) |
Поскольку численно решается задача, сформулированная в терминах поиска полного волнового поля, запишем решение тестовой задачи также в терминах поиска полного поля.
|
|
(55) |
Введём фиктивную границу в виде окружности радиуса R с центром в начале координат. На рисунке 3 представлена область, в которой находится численное решение задачи дифракции.
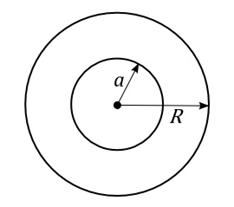
Рисунок 3. Иллюстрация тестовой задачи.
Для удобства положим ![]() .
Суммирование в точном решении будем проводить от
.
Суммирование в точном решении будем проводить от ![]() до
до ![]() , при этом
порядок следующих членов ряда точного решения существенно меньше сеточных норм
получаемых решений.
, при этом
порядок следующих членов ряда точного решения существенно меньше сеточных норм
получаемых решений.
Перейдём к тестированию
программы в случае использования приближённых парциальных условий излучения. При
тестировании необходимо определить область допустимых значений ![]() , при
которых рост ошибки, связанный с накапливанием ошибок при суммировании конечной
суммы ряда из приближённого оператора
, при
которых рост ошибки, связанный с накапливанием ошибок при суммировании конечной
суммы ряда из приближённого оператора ![]() ,
незначителен. На рисунках 4 и 5 представлены
зависимость относительной ошибки от
,
незначителен. На рисунках 4 и 5 представлены
зависимость относительной ошибки от ![]() при
при ![]() и
и ![]() и
соответственно
и
соответственно ![]() и
и ![]() .
.
Заметим, что при ![]() , как и
следовало ожидать, ошибка больше 100%. Однако, при
, как и
следовало ожидать, ошибка больше 100%. Однако, при ![]() ошибка уже
становится меньше 100% и очень быстро спадает до значений около 0,36% при
ошибка уже
становится меньше 100% и очень быстро спадает до значений около 0,36% при ![]() , и 0,39%
при
, и 0,39%
при ![]() , при этом
осциллируя с очень маленькой амплитудой. Рост ошибки, связанный с накоплением
ошибок при суммировании становится заметным лишь при
, при этом
осциллируя с очень маленькой амплитудой. Рост ошибки, связанный с накоплением
ошибок при суммировании становится заметным лишь при ![]() . Стоит
отметить, что при
. Стоит
отметить, что при ![]() этот рост
менее заметен на фоне большей ошибки, связанной с уменьшением числа элементов,
приходящихся на длину волны.
этот рост
менее заметен на фоне большей ошибки, связанной с уменьшением числа элементов,
приходящихся на длину волны.
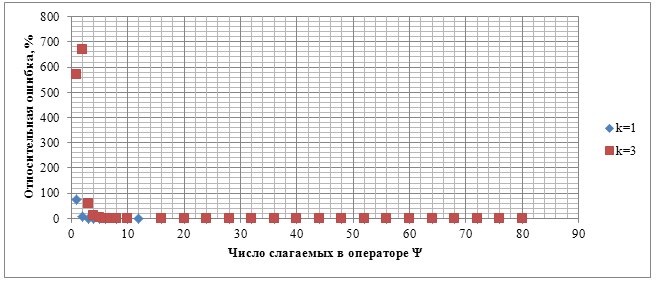
Рисунок 4. Зависимость относительной ошибки от числа положительных слагаемых в частичной сумме приближённых парциальных условий излучения при использовании этих условий на фиктивной границе.
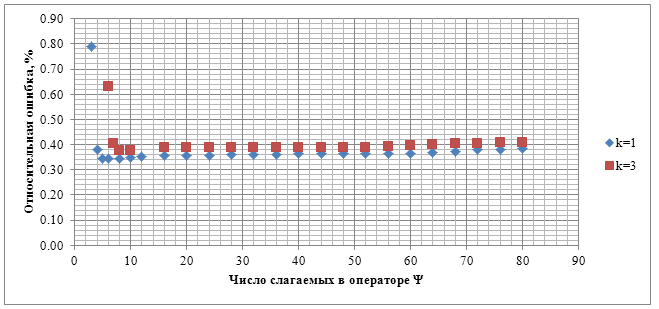
Рисунок 5. Зависимость относительной ошибки от числа положительных слагаемых в частичной сумме приближённых парциальных условий излучения при использовании этих условий на фиктивной границе.
На рисунке 6 проиллюстрирована зависимость относительной ошибки от шага исходной сетки.
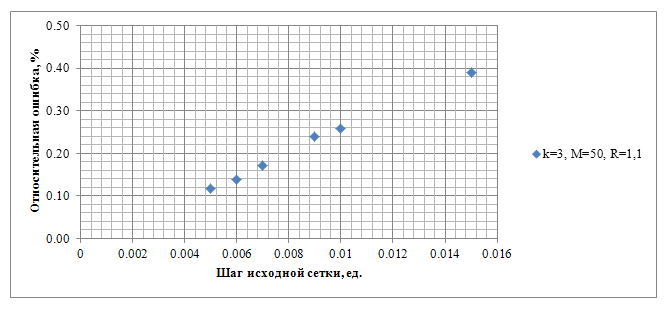
Рисунок 6. Зависимость относительной ошибки от шага исходной сетки при использовании приближённых парциальных условий излучения на фиктивной границе.
Как и ожидалось, относительная ошибка уменьшается при уменьшении шага исходной сетки.
На рисунке 7 представлена зависимость относительной ошибки от ![]() .
.
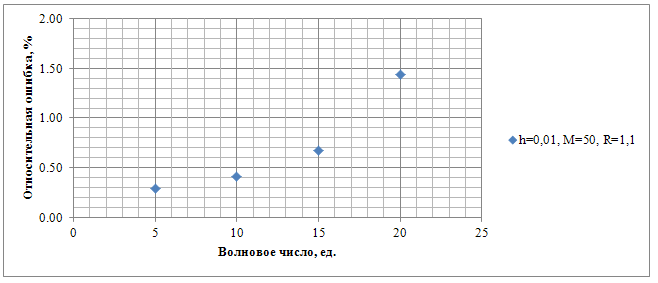
Рисунок 7. Зависимость относительной ошибки от волнового числа, при использовании приближённых парциальных условий излучения на фиктивной границе.
Нетрудно
заметить, что, как и ожидалось, ошибка растёт, при этом достаточно быстро. Этот
рост связан с уменьшением числа элементов сетки, приходящихся на одну длину
волны. Однако заметим, что из-за возможности максимально приблизить фиктивную
границу к рассеивателям, можно выбрать весьма малый шаг исходной сетки.
Вследствие чего, можно достичь большей точности при использовании приближённых
парциальных условий излучения, чем при использовании радиационных граничных
условий первого порядка. А следовательно, можно решать задачу дифракции при
больших ![]() , чем те,
при которых адекватный результат можно получить, используя радиационные граничные условия первого порядка. Однако отметим, что ограничение на
, чем те,
при которых адекватный результат можно получить, используя радиационные граничные условия первого порядка. Однако отметим, что ограничение на ![]() также
накладывает ограничение и на
также
накладывает ограничение и на ![]() .
.
Перейдём к тестированию трёхмерного случая. Рассмотрим тестовую задачу дифракции на сфере радиуса a. Решение этой задачи известно [10]. В качестве падающей волны будем рассматривать плоскую волну, приходящую с положительного направления оси OZ декартовой системы координат.
|
(56) |
Тогда задача (1) примет следующий вид.
|
|
(57) |
Аналитическое решение этой задачи имеет вид.
|
|
(58) |
Введём
фиктивную границу в виде сферы радиуса R с центром
в начале координат. Для удобства положим ![]() .
Суммирование в точном решении будем проводить от
.
Суммирование в точном решении будем проводить от ![]() до
до ![]() , при этом
порядок следующих членов ряда точного решения существенно меньше сеточных норм
получаемых решений.
, при этом
порядок следующих членов ряда точного решения существенно меньше сеточных норм
получаемых решений.
На рисунках 8 и 9 представлены зависимость относительной ошибки от
величины ![]() , при
, при
![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
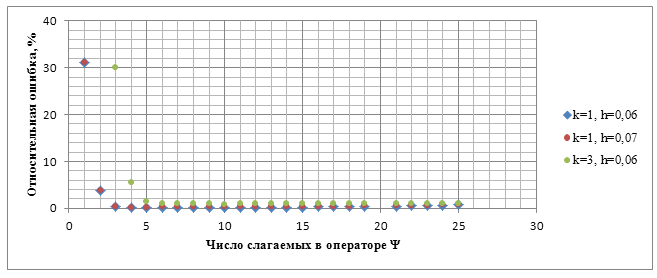
Рисунок 8. Зависимость относительной ошибки от числа слагаемых в частичной сумме приближённых парциальных условий излучения при использовании этих условий на фиктивной границе.
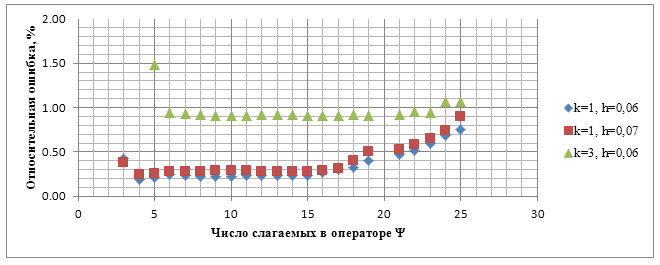
Рисунок 9. Зависимость относительной ошибки от числа слагаемых в частичной сумме приближённых парциальных условий излучения при использовании этих условий на фиктивной границе.
Рассмотрев эти зависимости,
можно сделать следующие выводы. При ![]() относительная
ошибка меньше 100%, однако ещё достаточно велика, а при
относительная
ошибка меньше 100%, однако ещё достаточно велика, а при ![]() быстро
спадает до некоторого значения, затем слабо осциллирует близ этого значения.
Однако, заметим, что при
быстро
спадает до некоторого значения, затем слабо осциллирует близ этого значения.
Однако, заметим, что при ![]() уже
начинается рост относительной ошибки. Это связано с наличаем двойного
суммирования в операторе
уже
начинается рост относительной ошибки. Это связано с наличаем двойного
суммирования в операторе ![]() в
трёхмерном случае, то есть при
в
трёхмерном случае, то есть при ![]() число
слагаемых в этом операторе уже равно 255. Рост ошибки при больших
число
слагаемых в этом операторе уже равно 255. Рост ошибки при больших ![]() менее
заметен на фоне общего увеличения ошибки за счёт уменьшения числа элементов
сетки на длину волны падающего излучения. Итак, оптимальными значениями
менее
заметен на фоне общего увеличения ошибки за счёт уменьшения числа элементов
сетки на длину волны падающего излучения. Итак, оптимальными значениями ![]() являются
значения от 1 до 15, при этом возникает и ограничение на допустимые значения
являются
значения от 1 до 15, при этом возникает и ограничение на допустимые значения ![]() :
: ![]() , где
, где ![]() . Разумно
выбрать
. Разумно
выбрать ![]() . Однако,
заметим, что, несмотря на рост относительной ошибки при
. Однако,
заметим, что, несмотря на рост относительной ошибки при ![]() , значения
этой ошибки всё ещё не велики, так что можно использовать и
, значения
этой ошибки всё ещё не велики, так что можно использовать и ![]() . При таком
выборе следует вычислить несколько приближённых решений для близких
. При таком
выборе следует вычислить несколько приближённых решений для близких ![]() и
посмотреть, на сколько они отличаются друг от друга. Если это отличие невелико,
то можно использовать эти значения
и
посмотреть, на сколько они отличаются друг от друга. Если это отличие невелико,
то можно использовать эти значения ![]() .
.
В заключение, рассмотрим тесты, иллюстрирующие зависимость относительной ошибки от шага исходной сетки. Эти тесты представлены на рисунке 10.
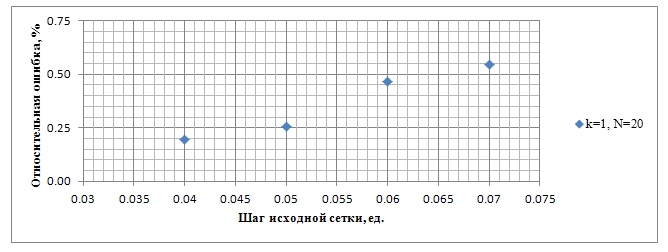
Рисунок 10. Зависимость относительной ошибки от шага исходной сетки, при использовании приближённых парциальных условий излучения на фиктивной границе.
Из
графика видно, что точность растёт с уменьшением шага исходной сетки, даже при ![]() ,
хотя, как было отмечено выше, при таком выборе
,
хотя, как было отмечено выше, при таком выборе ![]() уже
наблюдается рост относительной ошибки, связанный с накоплением ошибок при
суммировании.
уже
наблюдается рост относительной ошибки, связанный с накоплением ошибок при
суммировании.
8. Результаты работы программы.
Примеры решения задачи
дифракции на различных сложных рассеивателях представлены в [9]. Рассмотрим здесь лишь один пример решения задачи дифракции в двумерном случае. Исходя из
результатов тестирования программы, выберем ![]() . Будем
считать, что внешние источники отсутствуют, то есть
. Будем
считать, что внешние источники отсутствуют, то есть ![]() . На границах непроницаемых рассеивателях поставим
однородные граничные условия второго рода (условия Неймана). В качестве
падающей волны возьмём плоскую волну, распространяющуюся вдоль оси OX
декартовой системы координат в направлении от
. На границах непроницаемых рассеивателях поставим
однородные граничные условия второго рода (условия Неймана). В качестве
падающей волны возьмём плоскую волну, распространяющуюся вдоль оси OX
декартовой системы координат в направлении от ![]() к
к ![]() . Рассмотрим
рассеиватель, состоящий из проницаемого
эллипса с центром в точке
. Рассмотрим
рассеиватель, состоящий из проницаемого
эллипса с центром в точке ![]() и
полуосями
и
полуосями ![]() и
и
![]() и двух
непроницаемых фигур заданных неравенством (56) с центрами
в точках (0;2,5) и (0;-2,5).
и двух
непроницаемых фигур заданных неравенством (56) с центрами
в точках (0;2,5) и (0;-2,5).
|
|
(59) |
Возьмём
![]() ,
, ![]() и
и ![]() . При этом положим:
. При этом положим:
|
|
(60) |
Полученные треугольная сетка, численное решение задачи дифракции и диаграмма рассеяния представлены на рисунке 11.
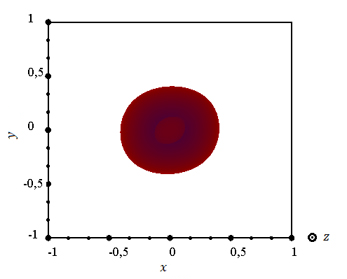
Рассмотренный рассеиватель симметричен относительно оси OX декартовой системы координат, поэтому диаграмма рассеяния также должна быть симметричной относительно этой координатной оси. Указанную симметрию нетрудно заметить на рисунках.
Перейдём к рассмотрению
примеров численного решения задачи дифракции в трёхмерном случае. Исходя из
результатов тестирования, положим ![]() . Будем считать,
что внешние источники отсутствуют, то есть
. Будем считать,
что внешние источники отсутствуют, то есть ![]() . На границах непроницаемых рассеивателях поставим
однородные граничные условия второго рода (условия Неймана). В качестве
падающей волны будем использовать плоские волны (35) и (37).
. На границах непроницаемых рассеивателях поставим
однородные граничные условия второго рода (условия Неймана). В качестве
падающей волны будем использовать плоские волны (35) и (37).
|
|
(61) |
|
|
(62) |
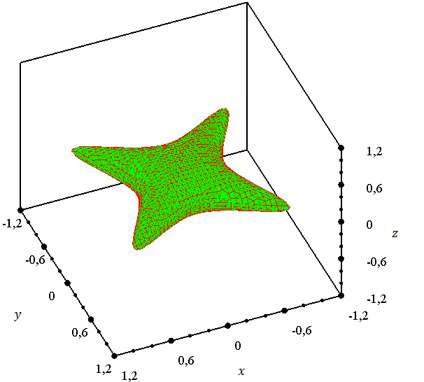
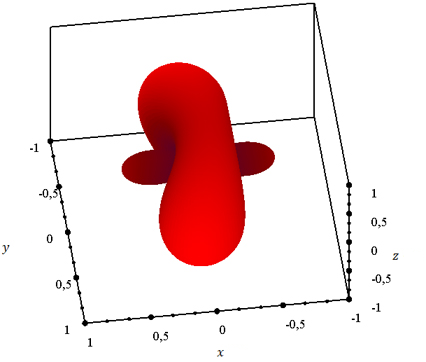
В качестве первого примера рассмотрим рассеиватель, состоящий из одного тела, а именно непроницаемой фигуры, заданной неравенством, с центром в начале декартовой системы координат.
|
|
(63) |
Возьмём
![]() ,
, ![]() и
и ![]() . В
качестве падающей волны выберем
. В
качестве падающей волны выберем ![]() Рассеиватель,
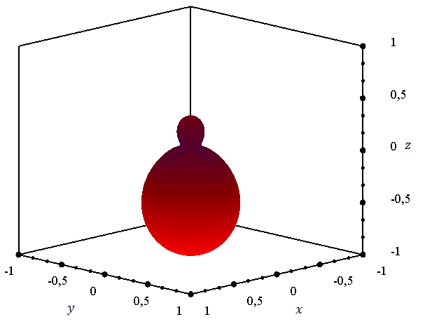
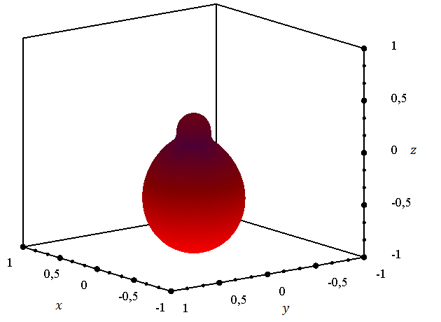
а также полученная диаграмма рассеяния представлены на рисунках 12 – 14. Так как
рассеиватель симметричен относительно плоскостей OXY и OXZ декартовой системы координат, то диаграмма рассеяния также должна быть
симметричной относительно этих плоскостей. Указанную симметрию нетрудно
заметить на рисунках.
Рассеиватель,
а также полученная диаграмма рассеяния представлены на рисунках 12 – 14. Так как
рассеиватель симметричен относительно плоскостей OXY и OXZ декартовой системы координат, то диаграмма рассеяния также должна быть
симметричной относительно этих плоскостей. Указанную симметрию нетрудно
заметить на рисунках.
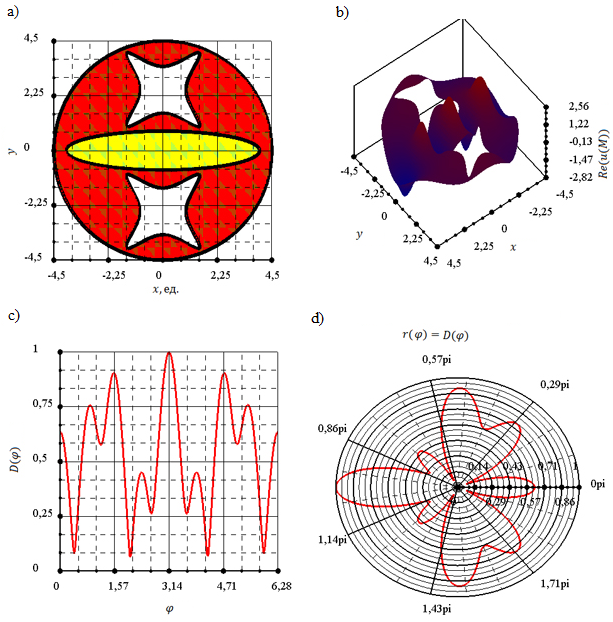
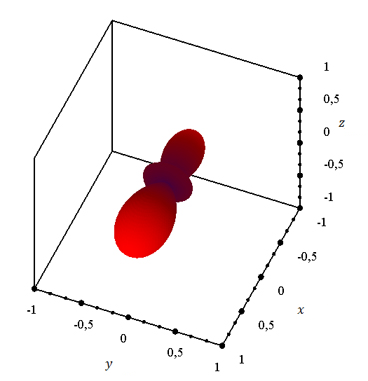
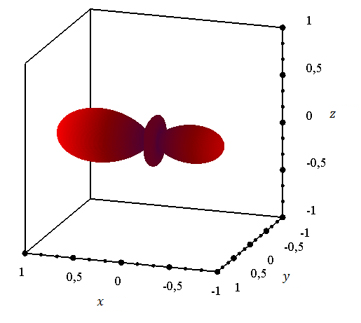
Рисунок 11. a) – треугольная сетка, b) – действительная часть полного волнового поля, c), d) – диаграмма рассеяния.
Рисунок 12. Рассеиватель.
|
Рисунок 13. Диаграмма рассеяния. |
Рисунок 14. Диаграмма рассеяния. |
В качестве второго примера
рассмотрим девятнадцать непроницаемых шаров с центрами в точках ![]() и
радиусами
и
радиусами ![]() , значения
которых представлены в таблице Таблица 1.
, значения
которых представлены в таблице Таблица 1.
Таблица 1. Параметры рассеивателей.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
0 |
-1 |
1 |
1 |
-1 |
0 |
1 |
0 |
-1 |
0 |
0 |
1 |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
1 |
-1 |
-1 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 |
-1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
|
|
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
Возьмём
![]() ,
, ![]() и
и ![]() . В
качестве падающей волны выберем
. В
качестве падающей волны выберем ![]() Рассеиватель,
а также полученная диаграмма рассеяния представлены на рисунках Рисунок 15 – Рисунок 17. Так как
рассеиватель симметричен относительно плоскостей OXY и OXZ
декартовой системы координат, то диаграмма рассеяния также должна быть
симметричной относительно этих плоскостей. Указанную симметрию нетрудно
заметить на рисунках 15 – 17.
Рассеиватель,
а также полученная диаграмма рассеяния представлены на рисунках Рисунок 15 – Рисунок 17. Так как
рассеиватель симметричен относительно плоскостей OXY и OXZ
декартовой системы координат, то диаграмма рассеяния также должна быть
симметричной относительно этих плоскостей. Указанную симметрию нетрудно
заметить на рисунках 15 – 17.
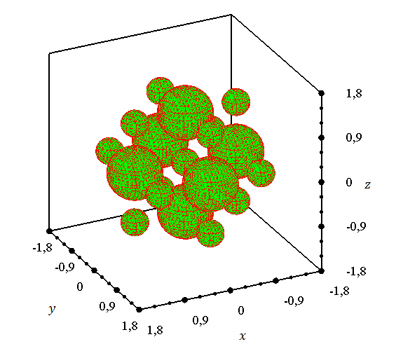
Рисунок 15. Рассеиватель.
В качестве последнего,
третьего примера рассмотрим рассеиватель, состоящий из двух непроницаемых шаров с центрами в точках ![]() и
и ![]() с
радиусами
с
радиусами ![]() , а также
проницаемой фигуры, заданной неравенством.
, а также
проницаемой фигуры, заданной неравенством.
|
|
(64) |
Зададим
функцию ![]() следующим
образом.
следующим
образом.
|
|
(65) |
Возьмём
![]() ,
, ![]() и
и ![]() . В
качестве падающей волны выберем
. В
качестве падающей волны выберем ![]() Рассеиватель,
а также полученная диаграмма рассеяния представлены на рисунках 18 – 21. Так как
рассеиватель симметричен относительно плоскостей
Рассеиватель,
а также полученная диаграмма рассеяния представлены на рисунках 18 – 21. Так как
рассеиватель симметричен относительно плоскостей ![]() и
и ![]() декартовой
системы координат, то диаграмма рассеяния также должна быть симметричной
относительно этих плоскостей. Указанную симметрию нетрудно заметить на рисунках
18 – 21.
декартовой
системы координат, то диаграмма рассеяния также должна быть симметричной
относительно этих плоскостей. Указанную симметрию нетрудно заметить на рисунках
18 – 21.
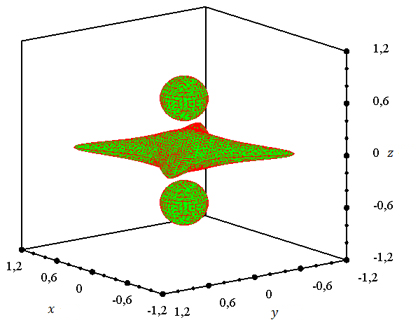
Рисунок 18. Рассеиватель.
Заключение.
В данной работе представлена программа, позволяющая использовать конечно-элементный анализ, с применением парциальных условий излучения на фиктивной границе, к двумерным и трёхмерным задаче дифракции акустических волн на рассеивателях сложной структуры, включающих несколько тел, природа которых может быть различной. Также, представленные в двумерном случае результаты можно трактовать как некоторые частные случаи трёхмерной задачи дифракции электромагнитных волн на сложных рассеивателях.
Литература
|
Еремин Ю.А., Свешников А.Г. Задачи распознавания и синтеза в теории дифракции // Журнал вычислительной математики и математической физики. 1992. Т. 32. № 10. С. 1594-1607. |
|
|
Еремин Ю.А., Свешников А.Г. Обоснование метода неортогональных рядов и решение некоторых обратных задач дифракции // Журнал вычислительной математики и математической физики. 1983. Т. 23. № 3. С. 738-742. |
|
|
Стренг Г., Фикс Д. Теория метода конечных элементов. Москва: Издательство «МИР», 1977. |
|
|
Ильгамов М.А., Гильманов А.Н. Неотражающие условия на границах расчётной области. Москва: ФИЗМАТЛИТ, 2003. |
|
|
Свешников А.Г., Могилевский И.Е. Избранные математические задачи теории дифракции. Москва: Физический факультет МГУ, 2012. |
|
|
Ильинский А.С., Кравцов В.В., Свешников А.Г. Математические модели электродинамики. Москва: «ВЫСШАЯ ШКОЛА», 1991. |
|
|
Галишникова Т.Н., Ильинский А.С. Численные методы в задачах дифракции. Издательство Московского Университета, 1987. |
|
|
Коняев Д.А. Метод конечных элементов для решения скалярной задачи дифракции на двумерных рассеивателях сложной структуры // ВМУ. Серия 3. Физика. Астрономия. 2012. № 4. С. 30-36. |
|
|
Коняев Д.А., Делицын А.Л. Метод конечных элементов с учётом парциальных условий излучения для задачи дифракции на рассеивателях сложной структуры // Матем. моделирование. Принята в печать. |
|
|
Хёнл К., Мауэ А., Вестпфаль К. Теория дифракции. Москва: Издательство «МИР», 1964. |
|
|
Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. Москва: Издательство «МИР», 1987. |
|
|
Шайдуров В.В. Многосеточные методы конечных элементов. Москва: Наука, 1989. |
|
|
Галанин М.П., Щеглов И.А. Разработка и реализация алгоритмов трёхмерной триангуляции сложных пространственных областей: итерационные методы // Препринты Института прикладной математики им. МВ Келдыша РАН. 2006. № 0. С. 9-32. |
|
|
Frey P.J., George P.L. Mesh Generation Application to Finite Elements. HERMES Science Europe Ltd., 2000. |
|
|
Галанин М.П., Щеглов И.А. Разработка и реализация алгоритмов трёхмерной триангуляции сложных пространственных областей: прямые методы // Препринты ИПМ им. МВ Келдыша. 2006. № 10. |
|
|
Rao S.S. The finite element method in engineering. Butterworth-heinemann, 2005. |
|
|
Писсанецки С. Технология разреженных матриц. Москва: Издательство «МИР», 1988. |
|
|
Баландин М.Ю., Шурина Э.П. Методы решения СЛАУ большой размерности. Новосибирск: Издательство НГТУ, 2000. |
|
|
Ахунов Р.Р., Куксенко С.П., Салов В.К., Газизов Т.Р. Усовершенствование алгоритма ILU(0)-разложения, использующего разреженный строчный формат // Записки научных семинаров ПОМИ. 2012. Т. 405. № 0. С. 40-53. |