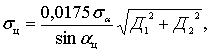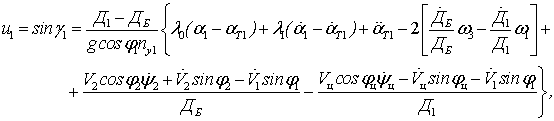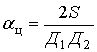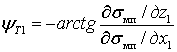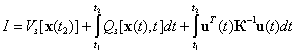УДК 629.7.05

МЕТОДЫ ТРАЕКТОРНОГО УПРАВЛЕНИЯ НАБЛЮДЕНИЕМ В ИНТЕГРИРОВАННЫХ МНОГОДАТЧИКОВЫХ ДВУХПОЗИЦИОННЫХ СИСТЕМАХ РАДИОМОНИТОРИНГА ВОЗДУШНОГО БАЗИРОВАНИЯ

 

В. И. Меркулов, Д. А. Миляков, О. Е. Радоминов, В. С. Чернов

Акционерное общество «Концерн радиостроения «Вега»

 

Статья поступила в редакцию 30 марта 2016 г.

 

Аннотация. Рассмотрены различные методы траекторного управления наблюдением, используемые в интегрированных многодатчиковых двухпозиционных системах радиомониторинга воздушного базирования и проведен их анализ. Предложен модифицированный метод проекции градиента, обеспечивающий эффективное траекторное наблюдение в интегрированных многодатчиковых двухпозиционных системах радиомониторинга воздушного базирования при наличии запретных зон для полетов летательных аппаратов информационной поддержки.

Ключевые слова: траекторное управление наблюдением, угломерные двухпозиционные системы, источник радиоизлучения, позиция информационной поддержки, ведущая позиция, ортогональное наведение, градиентный метод наведения.

Abstract. Various methods of trajectory control of observations for airborn integrated multisensor biposition radiomonitoring systems (AIMBRS) are observed and their analysis are conducted. A modified method of gradient projection, providing efficient trajectory monitoring in AIMBRS in the presence of radio monitoring restricted areas to flights of aircraft information support, is offered.

Keywords: trajectory control of observation, goniometric biposition radio-monitoring systems, radiation source, infotainment position, leading position, orthogonal directing, gradient directing method.

 

Введение

Развитие бортовых радиоэлектронных систем летательных аппаратов различного назначения неразрывно связано с возрастанием роли пассивных режимов их функционирования, что обусловлено действием ряда факторов
[1-4].

Во-первых, в процессе ведения боевых действий для предотвращения поражения воздушных, наземных и морских целей будут широко использоваться средства радиоэлектронной борьбы. При современном состоянии техники радиоэлектронного противодействия вероятны ситуации, когда на летательных аппаратах каналы дальности и скорости однопозиционных бортовых РЛС будут подавлены. При этом бортовые РЛС смогут измерять лишь угловые координаты источников помеховых радиосигналов.

Во-вторых, в настоящее время большая роль отводится системам контроля (радиомониторинга) источников радиоизлучения, основу которых составляют средства радио- и радиотехнической разведки (РРТР) летательных аппаратов (ЛА). Данные средства в однопозиционном варианте также могут измерять лишь угловые координаты ИРИ.

В третьих, объединение информации, полученной в активных и пассивных режимах функционирования бортовых радиоэлектронных комплексов позволяет существенно повысить степень ситуационной осведомленности об окружающей обстановке.

В то же время для обеспечения ситуационной осведомленности об окружающей обстановке и формирования команд наведения летательными аппаратами на неподвижные и движущиеся радиоизлучающие источники необходимо иметь достаточно точные оценки дальностей до них, скоростей сближения, углов пеленгов и угловых скоростей линий визирования в вертикальной и горизонтальной плоскостях. Из-за отсутствия в пассивных режимах информации о времени излучения непосредственное измерение дальности до источника излучения по запаздыванию радиосигнала невозможно. Поэтому для определения дальности до радиоизлучающей цели и скорости сближения с ней применяются методы косвенного оценивания при приеме сигналов в нескольких разнесенных точках пространства. Такие точки могут быть получены при использовании многопозиционных систем определения координат цели, основанных на пеленгационных (угломерных) методах [1-4].

Следует отметить, что в указанных условиях нормальное функционирование информационно-управляющих систем летательных аппаратов может быть обеспечено за счет объединения их в многопозиционные пассивные системы на базе бортовых РЛС, функционирующих в режиме пассивной пеленгации источников радиоизлучений, или средств РРТР в рамках децентрализованной системы либо с использованием центра сбора, обработки информации и управления, базирующегося, в частности, на самолете авиационного комплекса радиолокационного дозора и наведения. В подобной централизованной системе информационно-управляющая система центра сбора, обработки информации и управления осуществляет связь с наводимыми ЛА, принимает и обобщает радиолокационную и иную информацию, поступающую от летательных аппаратов, а также формирует и передает команды целеуказания и наведения на ЛА. По своей сути данная система является многопозиционной системой командного радиоуправления, в состав которой входят наводимые ЛА и пункт управления, выполняющий функции центра сбора, обработки информации и управления. Здесь под позициями понимаются наводимые с пункта управления летательные аппараты. От известных систем командного радиоуправления первого вида эта система отличается тем, что источники первичной информации о цели располагаются на самих наводимых ЛА и представляют собой пассивные угломерные системы (измерители).

В децентрализованных многопозиционных системах центр сбора, обработки информации и управления отсутствует. В этих системах задачи траекторного управления самостоятельно решаются на самих летательных аппаратах, обменивающихся информацией о внешних источниках радиоизлучения, полученных установленной на них аппаратурой.

Таким образом, для решения задач помехозащиты, радиомониторинга и информационного обеспечения процесса наведения ЛА от пунктов управления (ПУ) необходимо выполнять радионаблюдение целей на базе многопозиционных пассивных радиосистем: многопозиционных средств РРТР и/или многопозиционных пассивных бортовых РЛС. В этих системах оценивание координат целей производится достаточно быстро. Кроме того, они обладают высокой скрытностью и живучестью [1, 3]. В то же время в многопозиционных пассивных системах приходится решать сложные задачи, связанные с обменом информацией между позициями и отождествлением результатов измерений, полученных от разных позиций.

Наиболее простым вариантом пассивных многопозиционных радиосистем являются угломерные двухпозиционные радиосистемы, позволяющие достаточно быстро оценивать дальности до радиоизлучающих целей и скорости сближения с ними либо прямоугольные координаты целей и их производные. Поскольку в угломерных двухпозиционных радиосистемах осуществляется траекторное управление ЛА, то часто такие системы называют угломерными двухпозиционными системами наведения.

Цель статьи – анализ современных и разработка новых методов и алгоритмов управления пространственным положением информационных датчиков, обеспечивающих высококачественное формирование двухпозиционной интегрированной многодатчиковой системой радиомониторинга воздушного базирования в различных условиях ее применения ситуационной осведомленности о состоянии окружающей среды.

Отметим, что под методом наведения понимается закон формирования требуемой фазовой траектории подвижного объекта управления. Координаты требуемого движения находят путем преобразования фазовых координат относительного и абсолютного движения цели и объекта управления. Правило формирования управляющих сигналов, именуемых также параметрами рассогласования Δ, по которому определяется несоответствие реальных фазовых координат  объекта управления (ОУ) их требуемым значениям  (), называется алгоритмом траекторного управления [1]. 

 

1. Принципы построения угломерной двухпозиционной системы наведения

В состав угломерной двухпозиционной системы наведения (ДПСН) входят два наводимых ЛА и пункт управления, выполняющий функции командного пункта наведения. В качестве ЛА для конкретности будем рассматривать самолеты-истребители. Бортовые пассивные радиосистемы этих самолетов объединяются в группу, образуя пассивную угломерную двухпозиционную систему, работающую по источникам радиоизлучений (ИРИ).

Для эффективного функционирования двухпозиционной системы командного наведения, использующей угломерные радиосистемы двух приемных позиций, должны быть решены следующие задачи:

– пеленгация ИРИ (измерение угловых координат ИРИ) на приемных позициях (ПП);

– оценка прямоугольных координат и параметров движения измерительных позиций;

– передача результатов измерений с измерительных позиций на пункт управления;

– отождествление на ПУ пеленгов ИРИ, поступающих от разных измерительных позиций;

– построение траекторий ИРИ;

– формирование параметров требуемого движения самолетами и передача их значений на борт наводимых самолетов.

В общем случае необходимо организовать наведение самолетов в двух плоскостях: горизонтальной и вертикальной. В дальнейшем для простоты будем рассматривать управление только в горизонтальной плоскости, поскольку на этапе самонаведения дальности между самолетами и радиоизлучающей целью значительно превышают высоту их полета. Двухпозиционная система наведения, обеспечивающая оценивание координат ИРИ и формирование параметров управления самолетами в горизонтальной плоскости, функционирует следующим способом.

В состав ДПСН входят первая и вторая наводимые приемные позиции (рисунок 1). Приемные позиции являются подвижными и размещаются на самолетах С₁ и С₂. Каждая приемная позиция содержит одинаковый состав оборудования, включающий угломер бортовой РЛС (средств РРТР), навигационную систему, аппаратуру передачи данных, командную радиолинию управления (КРУ) и вычислительную систему.

Источник излучения, пространственно совпадающий с целью, формирует радиосигналы, принимаемые в первой и второй приемных позициях. Источниками радиоизлучения могут быть станции активных помех либо РЛС, установленные на цели, а также другие радиоэлектронные средства цели.

 

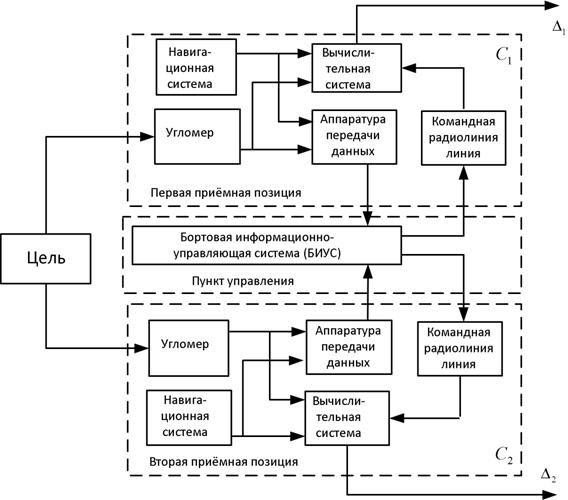
Рисунок 1. Структурная схема угломерной двухпозиционной системы наведения

Угломеры, называемые часто пеленгаторами, измеряют бортовые пеленги цели  и  в каждой из двух приемных позиций. Навигационные системы счисляют местоположение приемных позиций ( и ) в прямоугольной системе координат и измеряют курсы ,  самолетов. Предпочтительным вариантом для определения координат самолетов является использование спутниковой радионавигационной системы как наиболее точной. Указанные координаты и параметры движения образуют минимально необходимый набор измеряемых величин. Измеренные значения пеленгов цели, прямоугольных координат приемных позиций и курсов самолетов с помощью аппаратуры передачи данных передаются с приемных позиций на ПУ. Результаты измерения пеленгов цели в двух разных позициях, прямоугольных координат и курсов самолетов поступают в вычислительную систему ПУ, где формируются оценки координат и параметров движения цели на основе одного из известных алгоритмов [3, 4]. Вместо данных о бортовых пеленгах цели и курсах ЛА на ПУ могут передаваться азимуты цели, что позволяет сократить объем передаваемой на ПУ информации. Кроме того, в случае решения задачи пространственного местоопределения могут передаваться углы места цели и высоты самолетов. В вычислительной системе ПУ вырабатываются параметры требуемого движения наводимых самолетов, передаваемые на самолеты, где формируются параметры рассогласования Δ_1,2.

Таким образом, в угломерной двухпозиционной системе при наведении ЛА на ИРИ необходимо решать две задачи: задачу синтеза алгоритмов оценивания дальности до ИРИ и скорости сближения с ним либо его прямоугольных координат и их производных и задачу синтеза алгоритмов траекторного управления отдельными приемными позициями.

Способы построения различных алгоритмов оценивания дальности и скорости ИРИ в угломерных двухпозиционных системах достаточно подробно рассмотрены в [3, 4]. Особенностью задачи построения алгоритмов траекторного управления отдельными приемными позициями является возможность реализации концепции траекторного управления наблюдением. Суть концепции состоит в том, что наряду с решением основной задачи - перехвата движущихся радиоизлучающих целей, двухпозиционные пассивные системы наведения способны за счет целенаправленного управления пространственным положением одной или обеих приемных позиций обеспечить наивысшую точность определения координат и параметров движения ИРИ, а соответственно и наивысшую точность наведения [1].

Ниже приведена классификация методов наведения ДПСН, выполнен анализ ранее разработанных и новых методов, а также рассмотрены особенности реализации алгоритмов траекторного управления приемными позициями. Отметим, что методы траекторного управления наблюдением определяют закономерности формирования процедуры оптимизации пространственной конфигурации (топологии) расположения движущихся приемных позиций в двухпозиционных системах наведения.

 

2. Общая характеристика методов наведения угломерными двухпозиционными системами

В пассивных двухпозиционных системах наведения улучшение условий наблюдения ИРИ за счет траекторного управления ЛА направлено на достижение высокой точности определения ее координат и параметров движения [1, 3].

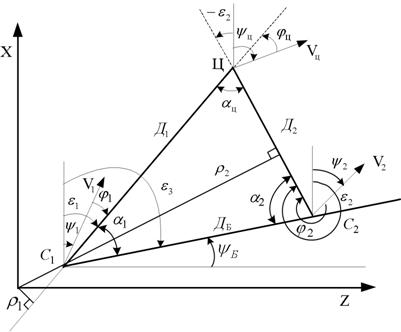
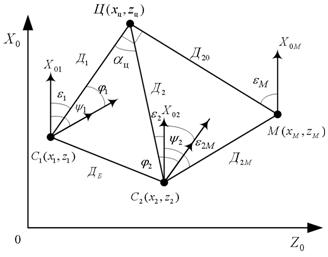
Для формирования координат и параметров движения цели на ПУ предварительно выполняют косвенные измерения координат радиоизлучающей цели триангуляционным способом [1-4]. При этом местоположение цели определяется точкой пересечения двух прямых, каждая из которых является линией положения, т.е. геометрическим местом точек возможного местонахождения источника излучения. Для определения пространственных координат цели достаточно измерить азимуты a₁ и a₂ в двух пунктах (точках пеленгации).

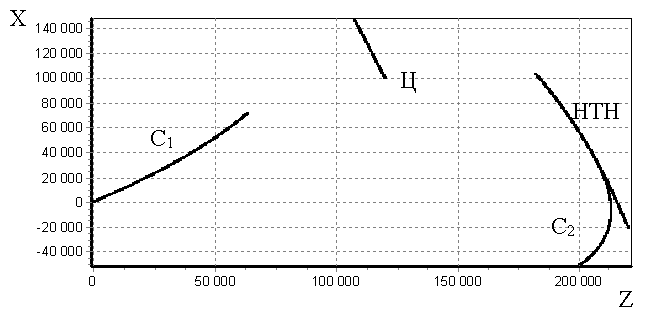
Принцип определения координат ИРИ в угломерной двухпозиционной системе иллюстрируется рис. 2, на котором показана схема взаимного расположения элементов угломерной ДПСН (приемных позиций и источника радиоизлучения). При пеленгации источника радиоизлучения, расположенного в точке Ц, из двух точек С₁ и С₂, отстоящих друг от друга на расстояние Д_б, координаты ИРИ в угломерной двухпозиционной системе определяются путем решения треугольника С₁ЦС₂ по двум углам ,  и основанию (базе) Д_б с помощью соотношений [3, 4]:

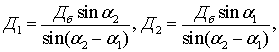                           (1)

где углы  и  отсчитываются в точках С₁ и С₂ относительно направления базы пеленгации.

 

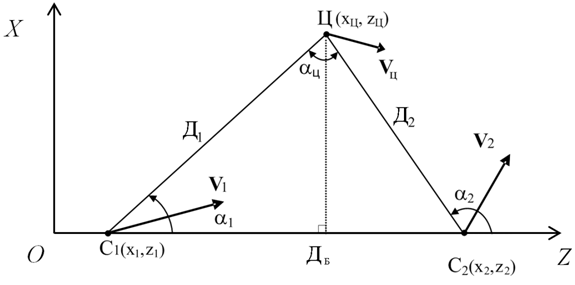
Рисунок 2. Схема взаимного расположения элементов угломерной двухпозиционной системы наведения

На рисунке введены следующие обозначения: Д₁ и Д₂ – расстояния от ИРИ (точка Ц) до приемных позиций С₁ и С₂, оборудованных пеленгаторами (угломерами);  – угол пересечения линий визирования (пеленгов); Д_б – база пеленгации (линия, соединяющая приемные позиции); , ,  – векторы скорости ПП и ИРИ; , ,  ,  и  ,  - текущие координаты первой и второй приемных позиций (ПП) и ИРИ.

Наряду с оцениванием расстояний Д₁ и Д₂ в угломерных ДПСН может выполняться оценивание прямоугольных координат ,  источника радиоизлучения. Прямоугольные координаты цели связаны с азимутами цели  и прямоугольными координатами позиций пеленгации следующими соотношениями  [4]:

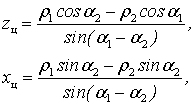
где ,  – расстояния от начала прямоугольной системы координат до прямых, проходящих через точки С₁ (z₁,x₁) и С₂ (z₂,x₂) в направлениях, определяемых линиями визирования С₁Ц и С₂Ц соответственно.

При условии, что начало прямоугольной системы координат совмещено с точкой С₁:

х_ц=0,5Д_б - 0,5 Д_б sin(a₁+a₂)/sin(a₂-a₁),

z_ц=Д_б sina₁ sina₂ /sin(a₂-a₁).

В угломерных двухпозиционных системах ошибки измерителей азимутов  и  ИРИ относительно двух ПП и ошибки измерения собственных прямоугольных координат ПП приводят к погрешностям формирования (расчета) оценок расстояний Д₁ и Д₂ и прямоугольных координат  и  ИРИ. Анализ точности определения местоположения радиоизлучающей ИРИ при функционировании ДПСН, проведенный в [5], показал, что ошибки определения местоположения ИРИ зависят от пространственной конфигурации («геометрии») системы местоопределения, т.е. от размеров базы и положения ИРИ относительно базы, а также от погрешностей измерения пеленгов, прямоугольных координат ПП и курсов ПП.

Точность определения местоположения радиоизлучающих целей на плоскости характеризуется линейной ошибкой. При случайных ошибках пеленгации и при использовании в качестве показателя точности средней квадратичной ошибки (СКО) местоопределения  в случае одинаковых ошибок пеленгаторов  имеет место соотношение [5]:

                                  (2)

где  – СКО измерения пеленгов цели с позиций С₁ и С_2.

Из (2) следует, что ошибка  определяется значениями , Д₁ и Д₂ и ошибками пеленгации . Из (2) видно, что точность оценивания наиболее высока, если угол  пересечения линий положения (пеленгов) достаточно близок к прямому углу, и заметно снижается, если линии положения пересекаются под острым углом.

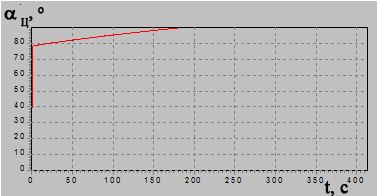
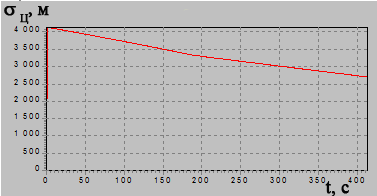
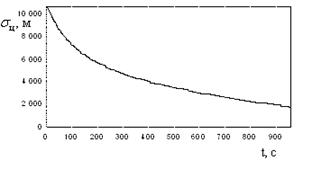
Рисунок 3 иллюстрирует зависимость СКО  от геометрии решения задачи определения местоположения.

 

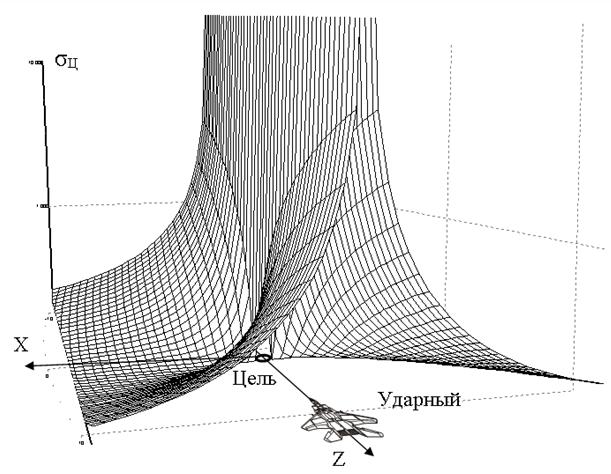
Рисунок 3. Иллюстративный пример зависимости ошибки  от геометрии решения задачи местоопределения

 

На рисунке взаимное положение ИРИ (цели) и самолета С₁ (ударного самолета) на плоскости является неизменным, что предполагает постоянство величины Д₁. Положение второго самолета С₂ на плоскости является произвольным. Для каждого заданного положения самолета С₂ рассчитаны дальность Д₂ между ним и ИРИ, а также значение ошибки  (2). Значение этой ошибки приведено на графике для каждой точки расчетного местонахождения самолета С₂.

Отметим, что все рассмотренные ниже алгоритмы пассивного двухпозиционного наведения базируются на следующих допущениях:

– на каждой позиции измеряются собственные координаты в той или иной прямоугольной системе, курсы и бортовые пеленги ИРИ;

– на каждой позиции имеется система передачи данных, с помощью которой передаются результаты первичных измерений на ПУ;

– рассматривается наведение самолетов только в горизонтальной плоскости.

В общем случае задача формирования управления обеими позициями, одновременно обеспечивающего и повышение точности определения местоположения радиоизлучающей цели и ее уничтожение, является достаточно сложной. Обусловлено это рядом причин.

Во-первых, для повышения точности оценивания местоположения радиоизлучающей цели необходимо, чтобы пеленгаторы двигались по отношению к ней под некоторыми, достаточно большими углами φ₁ и φ₂, поскольку при малых углах возрастают относительные ошибки пеленгации  и . В то же время для поражения цели линия пути самолетов должна проходить через цель или упрежденную точку встречи с ней.

Во-вторых, задача одновременного управления двумя позициями становится многокритериальной, что предопределяет усложнение процедуры синтеза оптимального управления.

Задача оптимизации управления пассивной ДПСН, как указывалось выше, существенно упрощается, если функции перехвата излучающей цели и обеспечения максимальной точности определения ее местоположения разделить между носителями С₁ и С₂. При таком подходе одна из позиций, например, наиболее близкая к цели, решает задачу наведения, используя тот или иной метод, а вторая – целенаправленно изменяет свое положение в пространстве, обеспечивая на обеих позициях максимально высокую точность определения местоположения перехватываемого объекта.

Ниже на основе указанного подхода приводится синтез алгоритмов управления одной из позиций пассивной ДПСН, обеспечивающих максимально высокую точность оценивания местоположения радиоизлучающей цели, при условии, что другая позиция наводится на нее одним из известных способов [1]. Первая позиция обычно называется позицией информационной поддержки (информационного обеспечения), а вторая – ударной позицией. Ниже основное внимание будет уделено вопросам траекторного управления наблюдением.

Как видно из формулы (2), одним из способов снижения ошибок оценивания местоположения ИРИ является поддержание угла , близким к 90^о. Для реализации этого условия разработано несколько методов наведения летательных аппаратов [6-11]: метод ортогонального наведения на основе нелинейных моделей состояния, метод ортогонального наведения на основе линейных моделей состояния, метод наведения в наилучшую точку наблюдения, выбираемую с учетом безопасности самолета информационной поддержки. Для первого метода задача выбора траекторного управления решена на основе концепции обратных задач динамики, для второго метода - на основе статистической теории оптимального управления, а для третьего метода – на основе эвристических соображений.

Общим недостатком данных методов наведения является то обстоятельство, что до выхода ПП информационной поддержки в произвольную точку, лежащую на перпендикуляре к линии ИРИ - ведущая (ударная) ПП, или в заданную точку этого перпендикуляра по существу не предъявляется никаких требований к текущим значениям ошибок определения местоположения ИРИ. В то же время процесс наведения ведущей ПП может закончиться еще до момента выхода ПП информационной поддержки на указанный перпендикуляр, когда ошибки определения местоположения ИРИ становятся минимальными.

Так как обеспечение одновременного выхода ведущей ПП в точку окончания наведения, а ПП информационной поддержки на заданную линию (точку) представляет собой довольно сложную задачу, то управление ПП информационной поддержки можно организовать таким образом, чтобы ошибка определения местоположения ИРИ в любой момент времени была минимально возможной. Для выполнения данного условия ПП информационной поддержки должна двигаться по специальной траектории, параметры которой определяются алгоритмом, полученным на основе теории оптимального управления динамическими процессами. В качестве целевой функции при этом выбирается зависимость ошибки (2) определения местоположения ИРИ от погрешностей пеленгаторов и «геометрии» решения задачи местоопределения.

Для вычисления оптимальных траекторий могут использоваться две группы методов:

косвенные методы, использующие необходимые условия оптимальности;

прямые методы, определяющие оптимальное управление непосредственным решением оптимизируемого функционала без использования необходимых условий.

Из косвенных методов наибольшее распространение получили принцип максимума Л.С. Понтрягина и динамическое программирование Беллмана. При этом следует отметить, что разработанная до настоящего времени техника оптимизации, позволяющая получить аналитически оптимальное управление из необходимых условий, применима к ограниченному типу задач.

В [12] рассмотрена возможность применения теории оптимального управления на базе принципа динамического программирования для разработки алгоритмов траекторного управления ПП информационной поддержки в угломерной двухпозиционной системе. Для вычисления оптимального управления с использованием принципа динамического программирования необходимо решить уравнение Беллмана, представляющее собой нелинейное уравнение в частных производных.

Конкретизация постановки задачи нахождения оптимального управления применительно к приемной позиции информационной поддержки связана с выбором целевой функции, в качестве которой в [12] использована зависимость ошибки (2) определения местоположения ИРИ. Поскольку в минизируемом функционале средняя квадратичная ошибка местоопределения  нелинейно зависит от прямоугольных координат, то аналитическое определение оптимального управления не представляется возможным. Для отыскания оптимального управления приемной позицией информационной поддержки необходимо воспользоваться приближенными способами решения задачи: численной формой динамического программирования, построением разностных схем, методом рядов и методом характеристик [12].

Рассмотрим возможности прямых методов оптимизации для нахождения алгоритма траекторного управления ПП информационной поддержки.

В классе прямых методов наиболее популярны градиентные методы. Из классических градиентных методов наиболее известны метод наискорейшего спуска и метод Ньютона-Рафсона. Ко второму поколению градиентных методов относятся метод сопряженного градиента и метод с переменной метрикой, которые характеризуются простотой и хорошей сходимостью. Оптимальное управление при использовании прямых методов является итерационной процедурой, основанной на информации о градиенте функционала качества.

При разработке алгоритмов траекторного управления по курсу на основе прямых методов параметры траектории приемной позиции информационной поддержки могут рассчитываться по формулам, полученным на основе теории принятия решений в одношаговых задачах оптимального управления с использованием градиентных методов нелинейного программирования. В качестве целевой функции обычно выбирается зависимость ошибки (2) определения местоположения ИРИ. В этом случае движение по требуемой траектории ПП информационной поддержки приводит к максимально быстрому уменьшению ошибки (2) на каждом шаге управления. Такой подход использован при разработке градиентного метода наведения по курсу в [13, 14].

Указанные выше методы траекторного управления ПП информационной поддержки, подробно рассмотренные в [6-16], обладают существенным недостатком, который проявляется в ситуациях, когда к моменту начала оценивания координат ИРИ подвижные приемные позиции находятся на относительно небольших расстояниях друг от друга (т.е. при малых углах ), что не позволяет достаточно точно оценивать координаты ИРИ. В этом случае необходимо определенное время для занятия приемными позициями требуемого взаимного пространственного положения. Из-за отсутствия достаточно точных сведений о координатах ИРИ в течение достаточно продолжительного времени, необходимого для построения требуемой геометрии определения местоположения, будет затруднено функционирование систем, использующих информацию угломерной двухпозиционной системы о координатах ИРИ, например, системы управления перехватом носителя ИРИ ведущей (ударной) ПП. Это может привести к нежелательным последствиям при их функционировании, в том числе к снижению показателей эффективности систем управления и даже к срыву их работы, особенно при возможном выключении ИРИ или прерывистой его работе.

Для устранения указанного недостатка необходимо, чтобы заблаговременно еще до начала работы пеленгаторов по сигналам от ИРИ приемные позиции заняли требуемое для точного определения координат ИРИ пространственное положение. Решение данной задачи может быть достигнуто за счет введения этапа предварительного наведения, на котором организуется процесс управления движением ПП с помощью пункта управления. Команды управления приемными позициями могут быть выработаны на ПУ на основе знания координат и параметров движения носителя ИРИ и наводимых ПП, получаемых от активной радиолокационной системы или других источников информации, входящих в состав ПУ. Этот этап должен быть закончен к моменту начала оценивания координат ИРИ, выполняемого непосредственно по результатам приема радиосигналов ИРИ пеленгаторами приемных позиций.

В то же время разработанные ранее методы траекторного управления подвижными позициями изначально не предусматривают такую возможность для реализации указанной выше концепции заблаговременного построения требуемой «геометрии» угломерной ДПСН. Поэтому необходимо было разработать методы траекторного управления приемной позицией информационной поддержки для заблаговременного построения требуемой пространственной конфигурации ДПСН.

Как показывает анализ, наиболее подходящим для решения данной задачи является использование метода градиентного наведения ПП информационной поддержки [13, 14], так как при его применении имеет место наименьшее удаление приемных позиций друг от друга и обеспечивается максимально быстрое уменьшение ошибок местоопределения ИРИ на каждом шаге управления.

Однако при реализации градиентного метода может наблюдаться существенное искривление траектории ПП информационной поддержки, а также может потребоваться ее движение с большей скоростью по сравнению со скоростью ведущей (ударной) ПП, что необходимо для обеспечения приблизительно одинаковой дальности до ИРИ в момент начала обнаружения его сигналов пеленгаторами обеих приемных позиций. Объясняется это тем, что для решения задачи минимизации ошибки определения местоположения ИРИ на начальном этапе наведения с ПУ необходимо обеспечить значительное удаление ПП информационной поддержки от ведущей ПП. В процессе наведения по мере сближения ведущей ПП и ИРИ это удаление будет уменьшаться. В результате траектория ПП информационной поддержки может значительно искривляться и соответственно удлиняться. Это приводит к излишним затратам топлива, расходуемого двигательной установкой ПП информационной поддержки. Кроме того, движение ПП информационной поддержки с бóльшей скоростью по отношению к скорости ведущей ПП не всегда возможно. В этом случае дальности до ИРИ от ведущей ПП и ПП информационной поддержки в момент окончания этапа предварительного наведения могут существенно отличаться, что ухудшит точностные характеристики угломерной двухпозиционной системы, как это следует из выражения (2).

Для преодоления отмеченных недостатков в [17] предложено использовать модифицированный вариант градиентного метода, который предполагает наведение информационной ПП на вспомогательный движущийся объект (цель), выступающий в качестве виртуальной (фиктивной) радиоизлучающей цели. При реализации разработанного метода процедуру формирования требуемого курса можно выполнять не только на ПУ, но и на самой ПП информационной поддержки при условии, что оценки прямоугольных координат носителя ИРИ передаются с ПУ на приемные позиции. При этом оценки координат приемных позиций также можно передавать с ПУ либо в случае измерения собственных координат на самих приемных позициях обмениваться ими между собой посредством аппаратуры передачи данных.

При боевом применении угломерной ДПСН возможны ситуации, когда на траекторию полета самолета информационной поддержки накладываются определенные ограничения в виде неравенств. Как правило, эти ограничения задаются допустимой областью нахождения самолета информационной поддержки. В этом случае алгоритмы траекторного управления могут быть найдены на основе метода проекции градиента целевой функции либо метода штрафных функций. В работе приведены алгоритмы, разработанные с использованием обоих этих методов.

Общим недостатком концепции управления позициями ДПСН, основанной на разделении функций между ЛА на ударные и информационные, является достаточно большое время, необходимое для достижения минимума ошибки (2), а соответственно, и низкая точность определения местоположения ИРИ на начальных участках траектории наведения в случае малых начальных значениях угла . Для устранения данного недостатка на основе статистической теории оптимального управления разработаны метод и соответствующие алгоритмы траекторного управления обеими позициями, направленные на обеспечение наивысшей точности определения координат ИРИ, и лишь после этого на решение задачи наведения [16].

Ниже приводится краткий анализ известных методов траекторного управления ДПСН: ортогонального наведения на основе нелинейных и линейных моделей состояния, наведения в наилучшую точку наблюдения, градиентных методов наведения, метода на основе принципа динамического программирования, метода одновременного управления обеими позициями, обеспечивающих повышенную точность определения местоположения ИРИ.

 

3. Современные методы и алгоритмы наведения с использованием пассивных режимов и их информационного обеспечения

3.1. Метод ортогонального наведения на основе нелинейных моделей состояния

Как указывалось, задача оптимизации управления ДПСН существенно упрощается, если функции перехвата радиоизлучающей цели и обеспечения максимальной точности определения ее местоположения разделить между носителями. При таком подходе одна из позиций решает задачу наведения, а вторая – обеспечивает на обеих позициях максимально высокую точность определения местоположения перехватываемого объекта.

В общем случае представляет интерес синтез управления информационной позицией на основе нелинейных представлений с полным учетом всех видов пространственных связей между позициями и радиоизлучающей целью. В такой постановке задача управления может быть решена на основе концепции обратных задач динамики [9]. Геометрия взаимного расположения радиоизлучающего воздушного объекта  и приемных позиций  и  в прямоугольной системе координат показана на рис. 4.

 

Рисунок 4. Схема взаимного расположения радиоизлучающего объекта и пеленгаторов

На этом рисунке: , и  – курсовые углы самолетов-носителей ,  и цели;  и  – углы визирования цели с носителей в выбранной системе координат;  и  – бортовые пеленги цели с позиций  и ; , и  – углы триангуляционного треугольника .

Если позиция  является ударной, а  – информационной позицией, то сигнал управления , обеспечивающий минимизацию функционала

,

где  – коэффициент штрафа за величину сигнала управления, вычисляется по формуле [9]

      (3)

в которой: , , ,  – требуемое значение угла между направлением на пеленгатор  и линией визирования ,  – первая и вторая производные данного угла;  – угловые скорости линии визирования, соответствующие производным углов визирования ;  – угол крена самолета С₁,  – ускорение свободного падения,  – положительные числа, обеспечивающие устойчивость его решения.

Анализ (3) позволяет прийти к следующим заключениям.

Полученный закон управления относится к пропорционально-дифференциальному типу, поскольку его правая часть включает пропорциональное слагаемое  и слагаемые с производными  и .

Для реализации (3) в состав ДПСН должны входить фильтры, формирующие оценки , , , , , , , , , , , , , , , , , , , , . Заметим, что координаты местоположения ,,, ,, и высота  непосредственно не используются в законе управления, однако они применяются при вычисление  и ,  [9].

При перечислении состава оцениваемых координат было учтено, что, в общем случае, любой из самолетов может использоваться как для наведения, так и для улучшения точности оценивания используемых в (3) фазовых координат.

Вес ошибок управления ,  и  зависит как от условий применения, определяемых значениями , , , так и от требований обеспечения устойчивости, предопределяющих значения  и .

Область применения закона (3) ограничена условиями

, .                                             (4)

При невыполнении первого условия (4) сигнал управления тождественно равен нулю. Это обусловлено тем, что любой маневр самолета  в горизонтальной плоскости приводит к одинаковому изменению угловых скоростей  и , а следовательно, к нулевым приращениям .

В свою очередь, полет самолета  под углом  потребует для реализации условия (4) бесконечно большого сигнала управления [9].

Следует подчеркнуть, что обычно двухпозиционная пассивная система наведения используется на больших дальностях ,  и . В такой ситуации последние три слагаемых в (3) примерно равны нулю и процедура формирования сигнала управления

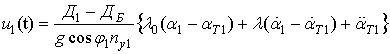                    (5)

 

и его информационного обеспечения существенно упрощается.

Конкретные значения  и , обеспечивающие минимум функционала качества I, могут быть получены в процессе решения уравнений ,  после подстановки в них полученного управления [9].

Точность управления при использовании (3) и (5) при наличии больших первоначальных ошибок  во многом будет зависеть от скорости сходимости алгоритмов оценивания , ,  и их производных, , ,  и располагаемого времени наведения (наблюдения) [9].

Анализируя вышеприведенные соотношения, можно прийти к заключению, что алгоритм (5) достаточно сложен и накладывает определенные ограничения на геометрию ДПСН.

3.2. Метод ортогонального наведения на основе линейных моделей состояния

В связи со сложностью вычисления сигналов управления (3), (5), его информационного обеспечения и большим объемом информации, которым должны обмениваться приемные позиции, представляет интерес синтез более простых законов управления, базирующихся на использовании линейных моделей состояния. В результате появляется возможность использовать для синтеза хорошо отработанные алгоритмы статистической теории оптимального управления.

В [6, 10] на основе этой теории выполнен синтез управления одной из позиций ДПСН, обеспечивающего максимально высокую точность оценивания местоположения радиоизлучающей цели, при условии, что другая позиция наводится на нее одним из известных способов.

Задача синтеза решена при условии, что выполняются следующие допущения:

– на цель наводится вторая, наиболее близкая к ней, позиция, а первая управляется для повышения точности определения ее местоположения (рис. 4);

– на каждой позиции измеряются собственный курс (ψ₁, ψ₂), бортовые пеленги (φ₁,φ₂), счисляются собственные координаты x₁, z₁ и x₂, z₂ и скорость их изменения ;

– на каждой позиции одним из известных методов [4] оцениваются дальности Д₁ и Д₂  до цели и скорости их изменения ;

– в течение времени формирования оценок дальностей и скоростей цель не изменяет скорости и направления полета;

– на каждом борту имеется система обмена данными, через которую все измеряемые и оцениваемые фазовые координаты передаются на другую позицию.

Последняя особенность дает возможность вычислять на каждой позиции базу Д_Б и угол ее наклона =90^о-(рис. 4).

Кроме того, предполагается, что алгоритмы управления позициями в вертикальной и горизонтальной плоскостях не влияют друг на друга. В связи с этим рассмотрены алгоритмы управления только в горизонтальной плоскости в предположении, что цель и оба пеленгатора находятся на одной высоте.

Используя процедуру формирования сигнала управления j_г1, оптимального по минимуму локального функционала качества, в [10] получен алгоритм траекторного управления самолетом С₁, определяемый несоответствием требуемого и фактического ускорений, в виде

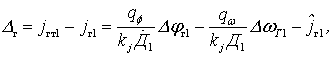                         (6)

 

в котором  ,  – угловая скорость линии визирования С₁Ц;  – скорость изменения дальности Д₁;  – поперечное ускорение самолета С₁ в горизонтальной плоскости, рассматриваемое в качестве управляющего сигнала;  и  – требуемые значения бортового пеленга и угловой скорости линии визирования; q_φ и q_ω – коэффициенты штрафа за ошибки управления по  и , а k_j – коэффициент штрафа за величину сигнала управления ;  – оценка собственного поперечного ускорения.

Из геометрии рис. 4 следует, что

           (7)

При этом угловая скорость линии визирования рассчитывается по формуле 

                                (8)

Анализ соотношений (6) – (8) позволяет прийти к следующим заключениям.

Управляющее поперечное ускорение самолетом С₁ определяется ошибками по угловой координате  и ошибками по угловой скорости .

Вес этих ошибок обусловлен соотношениями штрафов  и  и условиями применения, определяемыми значениями Д₁ и . При этом на больших расстояниях, предопределяющих малые значения угловых скоростей, преобладающее значение имеет управление по угловым ошибкам. В то же время на малых расстояниях, при достаточно больших значениях угловых скоростей основным является управление по угловым скоростям. Расстояние, на котором происходит перераспределение сигналов управления, определяется соотношением штрафов  и .

В общем случае, любой из самолетов может использоваться как для наведения на цель, так и для улучшения точности оценивания ее фазовых координат. В связи с этим для информационного обеспечения алгоритма траекторного управления (6) – (8) необходимо на борту каждого самолета формировать оценки собственного курса, угловой скорости линии визирования, собственного поперечного ускорения, дальности до цели и скорости ее изменения. Следует подчеркнуть, что такой набор оценок позволяет реализовать практически все существующие методы наведения.

 

а)
б)
в)

Рисунок 5. Пример траекторий движения цели и самолетов (а),
график изменения угла  в процессе наведения (б),
график изменения ошибки  в процессе наведения (в)

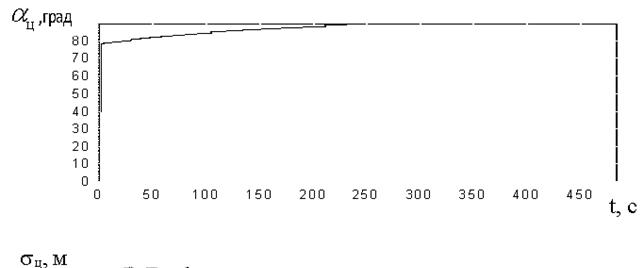
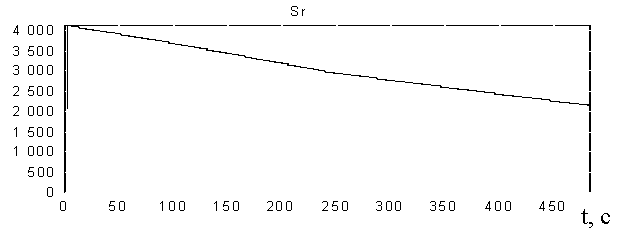
Пример траекторий полета цели Ц, ударного самолета С₂, наводимого по методу пропорционального наведения, и самолета информационной поддержки С₁ показаны на рисунке 5а, а законы изменения угла  и СКО ошибки оценивания на рис.5б и 5в [6, 10].

Из рисунков видно, что самолет С₁ информационной поддержки движется по такой траектории, что , а СКО уменьшается, что свидетельствует о повышении точности определения местоположения цели в процессе наведения.

Спецификой функционирования рассмотренной пассивной угломерной двухпозиционной системы наведения является необходимость обмена между позициями непосредственно или через ПУ информацией о собственном курсе, бортовом пеленге цели и их производных.

Следует отметить, что полученный закон управления является инвариантным к методам наведения ударного самолета и взаимному расположению цели и позиций.

3.3. Метод наведения в наилучшую точку наблюдения

Суть этого метода состоит в том, что в то время как ударный самолет наводится на радиоизлучающую цель одним из известных способов, самолет информационного поддержки выводится в заданную точку на прямой, ортогональной линии визирования ударный самолет – цель, при полете по которой создаются наилучшие условия для радиолокационного наблюдения (2). Разработаны два варианта реализации данного метода [7, 8].

Согласно [7] самолет информационной поддержки наводится по кривой погони в наилучшую точку наблюдения (НТН), находящуюся на перпендикуляре ударный самолет – ИРИ на удалении от ИРИ, равном расстоянию ИРИ от ударного самолета. Этот способ предусматривает совмещение продольной оси самолета информационной поддержки в процессе наведения с направлением на НТН. Положение НТН в пространстве непрерывно изменяется за счет сближения ударного самолета и ИРИ. Поэтому предусмотренная данным способом процедура наведения в определенных тактических ситуациях может потребовать от самолета информационной поддержки выполнения разворота с поперечными перегрузками, лежащими вне допустимого диапазона. Кроме того, при реализации этого способа наведения не всегда обеспечивается плавный выход самолета информационной поддержки на линию ИРИ-НТН. Отмеченные недостатки приводят к снижению эффективности ДПСН. Указанные недостатки устранены в разработанном в [8] способе наведения самолета информационной поддержки, рассмотренном ниже.

Геометрия взаимного положения приемных позиций и ИРИ при реализации метода наведения в наилучшую точку наблюдения в горизонтальной плоскости показана на рис. 6 [8, 11].

 

Рисунок 6. Схема взаимного расположения объектов при методе наведения в НТН

С учетом обеспечения безопасности самолета информационной поддержки  наименьшая ошибка оценивания местоположения цели соответствует случаю, когда линии визирования цели с двух точек пеленгации пересекаются под прямым углом (), а самолет С₂ находится на удалении от цели на расстоянии =, где  – заданное расстояние до цели от наилучшей точки наблюдения, большее или равное расстоянию до цели от ударного самолета . Такой геометрии взаимного расположения приемных позиций и цели соответствует точка  (рис. 6) требуемого нахождения второго самолета . Условно данную точку называют наилучшей точкой наблюдения с заданной дальностью до цели. Ее положение непрерывно изменяется в пространстве, так как цель движется и изменяется угловое положение линии визирования  и дальность до цели . При необходимости максимально быстрого выхода на перпендикуляр к линии визирования  в качестве наилучшей точки наблюдения может задаваться проекция самолета информационной поддержки на данный перпендикуляр [8, 11].

Независимо от способа выбора НТН при известном угле визирования цели  в точке  угол визирования цели относительно наилучшей точки наблюдения , а угловая скорость линии цель – НТН равна угловой скорости лини визирования :. Для выхода в НТН параметр управления самолетом  рассчитывается по формуле [8, 11]:

, если ,                     (9)

, если <,  (10)

где  – угол визирования НТН относительно самолета ;  – требуемый угол упреждения самолета ;  – пеленг цели, измеряемый на самолете С₂;  – расстояние до НТН от самолета ;  – расстояние, после достижения которого осуществляется дополнительный разворот самолета ;  – весовые коэффициенты алгоритма наведения самолета  по курсу, углу и угловой скорости линии визирования соответственно;  – весовой коэффициент угла упреждения.

Для нахождения угла  необходимо знать прямоугольные координаты , НТН и  самолета . Угол  находится по формуле [8, 11]:

.

 

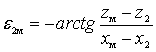Координаты самолета  оцениваются по результатам проведения навигационных измерений, а координаты НТН вычисляются из условия достижения наилучших результатов наблюдения на основе полученных оценок прямоугольных координат цели и заданного положения НТН относительно цели. Для нахождения прямоугольных координат НТН к оцененным координатам цели добавляют прямоугольные проекции вектора , соединяющего цель с НТН. Расчетные соотношения для прямоугольных координат НТН следуют из рис. 6:

,                                          (11)

,                                       (12)

где , .

Расстояние  до НТН от самолета  определяется по известным координатам местонахождения НТН и самолета :

.

Таким же образом рассчитываются расстояния до цели от самолетов  и :

, .

Следует отметить, что в зависимости от метода наведения ударного самолета на цель закон перемещения НТН может быть достаточно сложным. В связи с этим для управления самолетом информационной поддержки целесообразно использовать методы наведения с упреждением. Методика нахождения требуемых углов упреждения хорошо известна [1, 8, 11]. В работе [8, 11] для угла упреждения (рис. 6) использовано соотношение

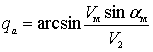,                                        (13)

соответствующее методу параллельного сближения [1], где  – скорость перемещения НТН, ,  – составляющие скорости  по осям прямоугольной системы координат;  – угол между вектором скорости  и линией ;  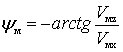– курсовой угол перемещения НТН.

Алгоритм траекторного управления самолетом  описывается выражениями (9) и (10). Параметр управления (9) обеспечивает наведение самолета  в НТН, лежащую на перпендикуляре к линии визирования цель – самолет . При выборе 0<<1 он соответствует прямому методу наведения со смещением. Выбором весового коэффициента  добиваются уменьшения влияния ошибок определения местоположения НТН на процедуру формирования параметра управления самолетом , а подбором весового коэффициента  уменьшают кривизну траектории, присущей прямому способу наведения [1, 11].

Использование параметра управления в виде (9) может приводить к ситуациям, когда на конечном участке наведения самолет  будет пересекать линию , не выходя при этом на указанную линию. Это означает, что траектория самолета  после выхода в НТН не будет совпадать с линией . Для предотвращения подобных явлений при подлете самолета  к НТН на расстояние  параметр управления рассчитывается по (10). При этом в (11) и (12)  уменьшается на величину . В результате под действием второго и третьего слагаемых параметра управления (10) самолет  на конечном участке сближения дополнительно разворачивается и плавно выходит на линию . Следует отметить, что углы и угловые скорости линий визирования могут оцениваться с высокой точностью, что позволяет при соответствующем выборе весовых коэффициентов выводить самолет  на линию  с малыми ошибками [1, 8, 11].

Пример наведения самолетов С₁ и С₂ на цель для одного из исследовавшихся гипотетических вариантов приведен на рис. 7а [18]. Цель движется под углом к оси ОX₀, одновременно удаляясь от оси абсцисс OZ₀. Самолет С₁ летит в упрежденную точку встречи с НТН.

 

а) Пример траекторий полета цели и самолетов

б) График изменения угла  в процессе наведения

в) График изменения ошибки  в процессе наведения

 

Рисунок 7. Наведения самолетов С₁ и С₂ на цель

На рис.7б приведен график изменения угла  в процессе наведения. При выходе самолета на указанный выше перпендикуляр угол  становится равным 90⁰, как это и требуется по условиям наведения.

На рис. 7в показан график, иллюстрирующий эволюцию ошибки  определения местоположения цели во времени. Из графика видно, что по мере сближения самолета С₂ с НТН ошибка  уменьшается.

Результаты моделирования свидетельствуют о возможности существенного уменьшения ошибок определения местоположения цели в процессе наведения, что должно повысить эффективность применения пассивной угломерной двухпозиционной системы наведения. Таким образом, данный способ управления позволяет наводить самолет информационной поддержки в заданную точку с выходом на линию, обеспечивающую наилучшие условия для радиолокационного наблюдения цели.

Недостатком метода является сложность формирования закона управления при наведении на маневрирующую радиоизлучающую цель.

3.4. Градиентный метод наведения

Одним из перспективных методов наведения является градиентный метод, основанный на поиске минимума целевой функции. Под градиентом функции , обозначаемым  или , понимают вектор, величина которого определяет скорость изменения функции , а направление совпадает с направлением наибольшего возрастания этой функции  [19].

Вектор , указывающий направление наибольшего убывания функции , называется антиградиентом функции .

Пусть -мерный векторный аргумент  определяет состояние управляемого объекта (самолета информационной поддержки). Тогда градиент функции будет представлять вектор-столбец вида

.

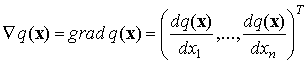Стратегия градиентного метода представляет собой последовательность шагов, каждый из которых содержит две операции [19]:

1) определение направления наибольшей крутизны спуска, т.е. направления антиградиента функции ;

2)перемещение в выбранном направлении на заданное расстояние.

Математически стратегия градиентного метода получается, если перемещение  на каждом шаге вдоль каждой из осей будет пропорционально составляющей градиента  в направлении этой оси:

, .

 

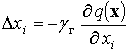При этом поправка на  шаге решения задачи может быть представлена в виде

. (14)

Стратегия, выражаемая соотношением (14), задает движение с переменным шагом, так как значение шага определяется значением градиента . Организовать полет самолета с переменным шагом достаточно сложно. Поэтому используют градиентную стратегию с постоянным шагом, значение которого , где  – скорость самолета. В этом случае поправка на каждом шаге определяется по формуле

,

получаемой из (14) заменой вектора градиента  на вектор направления градиента

,

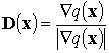где 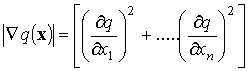 – модуль градиента .

 

В угломерных двухпозиционных системах обеспечивается оценивание координат цели ,  в горизонтальной плоскости, углов визирования  и  относительно двух самолетов и расстояний до цели от самолетов  и . Вектор первичных наблюдаемых параметров наряду с углами визирования цели в точках пеленгации содержит также прямоугольные координаты ,  и , , скорости   и  и курсы ,  самолетов , .

Как указывалось, при траекторном управлении самолетом информационной поддержки в качестве целевой функции целесообразно выбрать среднюю квадратичную ошибку местоопределения  (2). В этом случае переменными состояния (компонентами вектора состояния) являются прямоугольные координаты ,  самолета  информационной поддержки. Выражение (2) в явном виде не зависит от этих координат, поэтому его преобразуют к виду, удобному для нахождения градиента целевой функции. Необходимые для этого соответствующие уравнения связи определяются соотношениями [13]

, ,                    (15)

где  – площадь треугольника ;  – полупериметр этого треугольника;

 – расстояние между приемными позициями (база пеленгации).

Если подставить указанные выражения в (2), то получим зависимость целевой функции от прямоугольных координат цели и самолетов. Для нахождения аналитического выражения градиента целевой функции необходимо взять частные производные  и  целевой функции  по прямоугольным координатам ,  самолета информационного поддержки .

После вычисления частных производных требуемый курс самолета информационного обеспечения и параметр управления им рассчитывают по формулам

, .                          (16)

 

Если в качестве самолета информационного поддержки выбран самолет , то  может быть найден на основании следующих выражений:

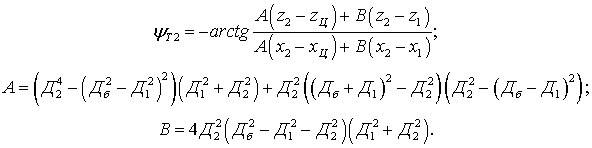
На практике можно воспользоваться численным способом нахождения частных производных.

Алгоритм (16) траекторного управления самолетом информационной поддержки обеспечивает получение наибольшего убывания среднего квадрата ошибки местоопределения радиоизлучающей цели и, тем самым, удовлетворяет предъявленным требованиям.

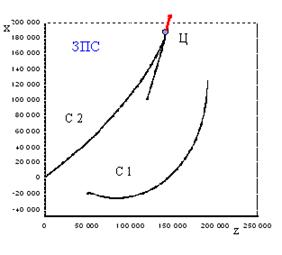
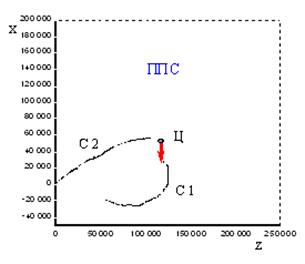
На рисунке 8а,в приведены траектории движения ударного самолета С₂, самолета информационного обеспечения С₁ и цели в горизонтальной плоскости для гипотетических вариантов перехвата цели в заднюю (ЗПС) и переднюю (ППС) полусферы, а на рисунке 8б,г – эволюции во времени ошибки  определения местоположения цели [18].

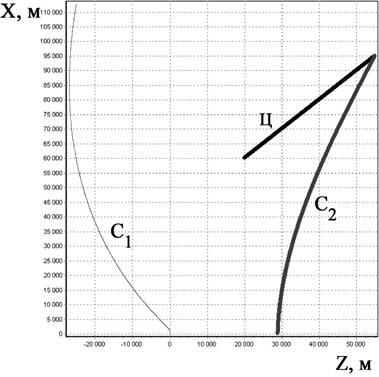
В начальный момент времени самолеты С₂ и С₁  находятся в точках с координатами x₂(0)=0, z₂(0)=0 и x₁(0)=-20 км, z₁(0)=50 км соответственно, а цель – в точке 100 км,125 км. Из графиков, иллюстрирующих эволюцию ошибок  определения местоположения цели во времени, видно, что по мере сближения самолета С₁, наводимого согласно алгоритму (16), с целью ошибка  уменьшается.

 

а)	б)
в)	г)

Рисунок 8. Эволюции взаимного расположения самолетов и цели при наведении в ЗПС (а) и ППС (в) и ошибок оценивания  (б) и (г)

         Результаты имитационного моделирования показали, что алгоритмы траекторного управления самолетом информационной поддержки на основе разработанных методов являются работоспособными. Они обеспечивают успешное наведение в различных условиях боевого применения. Траектории полета самолета представляют собой плавные кривые. Ошибки определения местоположения радиоизлучающей цели с течением времени убывают. По сравнению с методом наведения в наилучшую точку наблюдения градиентный метод наведения позволяет получить некоторый выигрыш в точности определения координат цели, величина которого зависит от начальных условий наведения. По данным моделирования эта величина составляет примерно 10…20 % [18]. При методе наведения в наилучшую точку наблюдения пеленг цели изменяется в больших пределах, чем при градиентном методе. При наличии ограничений на пределы измерения угла пеленга это может привести к необходимости корректировки алгоритмов траекторного управления самолетом информационной поддержки в случае превышения углом пеленга предельного значения.

3.5. Градиентный метод наведения на виртуальную цель

Как указывалось выше, градиентный метод траекторного управления приемной позицией информационной поддержки можно применять для заблаговременного построения по командам с ПУ требуемой пространственной конфигурации угломерной ДПСН.

Для этого вводится вспомогательный движущийся объект, который выступает в качестве виртуальной (фиктивной) цели [17, 20]. Геометрическое положение виртуальной цели (ВЦ) выбирается на линии визирования ИРИ – ведущая ПП на удалении от ведущей ПП на расстоянии, равном дальности обнаружения Д_об ИРИ бортовыми системами радиотехнической разведки или бортовыми РЛС приемных позиций при их работе в пассивном режиме. При таком выборе виртуальная цель должна совпасть в пространстве с фактическим положением ИРИ в момент его обнаружения на приемных позициях.

Геометрия взаимного положения всех объектов, участвующих в процессе наведении, показана на рис. 9, где точки С₁, С₂, ВЦ, ПУ и Ц соответствуют положениям на плоскости ведущей ПП, ПП информационной поддержки, виртуальной цели, пункта управления и ИРИ;  ,  и   - скорости наводимых ведущей ПП, ПП информационной поддержки и движущегося ИРИ; , ,  , ,  ,  и  ,  - текущие координаты ведущей ПП, ПП информационной поддержки, ВЦ и ИРИ.

 

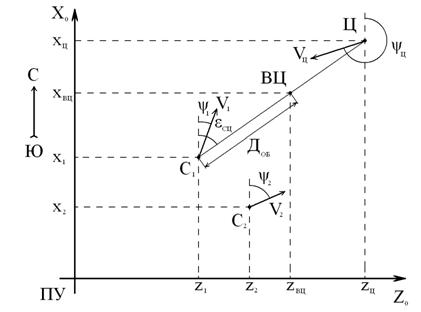
Рисунок 9. Схема взаимного расположения объектов при наведении на виртуальную цель

Прямоугольные координаты ВЦ определяются соотношениями:

,                                     (17)

,                                    (18)

где  – угол визирования ИРИ с ведущей ПП, связанный с прямоугольными координатами соответствующих точек Ц и С₁ следующей зависимостью:

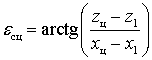.                                            (19)

Рассчитанные координаты используются для формирования требуемого курса ПП информационной поддержки путем подстановки в алгоритм траекторного управления (16) и связанных с ним соотношений (15) значений координат виртуальной цели (17) и (18) вместо текущих координат ИРИ. При этом следует иметь в виду, что показатель точности  – средняя квадратичная ошибка местоопределения (2) применительно к ВЦ носит искусственный характер, так как пеленгация виртуальной цели реально не осуществляется.

Таким образом, совокупность ведущей и информационной позиций на этапе наведения с ПУ можно рассматривать как некоторую «виртуальную» угломерную двухпозиционную систему, обеспечивающую организацию и поддержание требуемого пространственного положения ПП информационной поддержки до момента обнаружения ИРИ пеленгаторами приемных позиций. Данная совокупность приемных позиций образует реальную угломерную двухпозиционную систему при условии, что сигналы ИРИ начинают приниматься пеленгаторами ПП и, следовательно, появляется возможность самостоятельно формировать оценки координат ИРИ.

Из изложенного выше следует, что для реализации модифицированного варианта градиентного метода траекторного управления приемной позицией информационной поддержки в угломерной двухпозиционной системе необходимо выполнять следующую последовательность действий:

– с помощью активной радиолокационной системы пункта управления измерять координаты носителя ИРИ и приемных позиций, 

– оценивать на ПУ прямоугольные координаты носителя ИРИ и приемных позиций,

– определять значение требуемого курса  движения ПП информационной поддержки градиентным методом с использованием расчетных значений координат ВЦ,

– передавать значение  с ПУ на ПП информационной поддержки, 

– на ПП информационной поддержки измерять его текущий курс  и определять параметр управления ,

– в соответствии с параметром  осуществлять управление траекторией движения ПП информационной поддержки.

При реализации разработанного метода процедуру формирования требуемого курса  можно выполнять не только на ПУ, но и на ПП информационной поддержки при условии, что прямоугольные координаты ИРИ передаются с ПУ на приемные позиции. При этом оценки координат приемных позиций также можно передавать с ПУ либо в случае измерения собственных координат на самих приемных позициях обмениваться ими между собой посредством аппаратуры передачи данных.

Для оценки эффективности разработанного метода и алгоритма траекторного управления ПП информационной поддержки было проведено имитационное моделирование процесса наведения, осуществляемого с ПУ [17]. В качестве показателя эффективности рассматривалась ошибка  (2) определения местоположения ВЦ и ИРИ. При моделировании полагалось, что как ИРИ, так и ПУ движутся равномерно и прямолинейно. Ведущая ПП наводится на цель по методу перехвата [1]. Приемная позиция информационной поддержки управляется согласно модифицированному градиентному методу. Координаты виртуальной цели рассчитываются на основе соотношений (17), (18).

Результаты моделирования приведены на рис. 10, 11. На рисунках показаны траектории движения ведущей ПП С₁, ПП информационной поддержки С₂, ВЦ, ПУ и ИРИ в горизонтальной плоскости для одного из гипотетических вариантов применения, а также график поведения во времени СКО  определения местоположения ВЦ и ИРИ. На рис. 10 показаны примеры траекторий движения ПП при наведении на ИРИ, движущийся с постоянным курсом =260°, при использовании виртуальной цели и без ее использования. Для ПП информационной поддержки показаны две траектории. Из рис. 10 следует, что траектория ПП информационной поддержки при наведении согласно разработанному способу близка к прямолинейной. Траектория ПП информационной поддержки при наведении в соответствии с известным градиентным способом, при котором в качестве третьей точки треугольника наведения выступает ИРИ, является криволинейной.

В процессе моделирования проверялось влияние ошибок измерения дальности и азимутов ИРИ и наводимых ПП, получающихся на выходе РЛС пункта наведения, на качество наведения и ошибки определения местоположения виртуальной цели. При реальных ошибках измерения это влияние оказалось незначительным и приводит к небольшим флуктуациям траекторий полета наводимых ПП и некоторому росту ошибок оценивания местоположения виртуальной цели.

Анализ результатов моделирования показывает, что применение предлагаемого метода траекторного управления позволяет заранее до начала приема сигналов ИРИ пеленгаторами сформировать угломерную двухпозиционную систему, что обеспечивает в дальнейшем успешное решение стоящих перед угломерной ДПСН задач. Предлагаемый алгоритм траекторного управления ПП информационной поддержки, использующий концепцию «виртуальной» цели, приводит также к уменьшению кривизны траектории полета ПП информационной поддержки и, следовательно, сокращению длины пролетаемого пути и времени построения требуемой геометрии взаимного положения ПП для достижения заданной точности местоопределения ИРИ угломерной двухпозиционной системой и снижению затрат топлива.

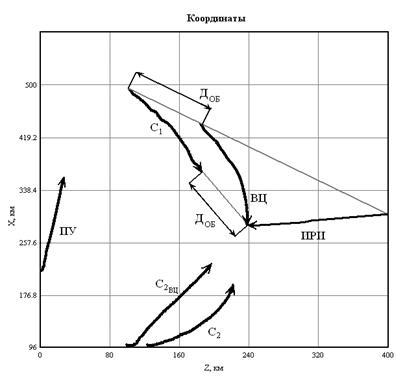
Рисунок 10. Пример траекторий движения объектов при наведении на виртуальную цель

 

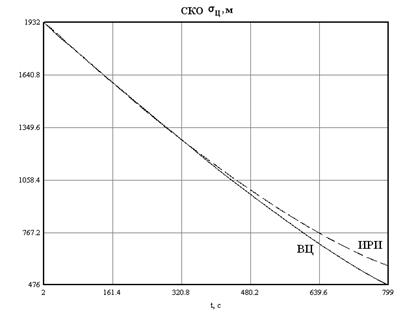
Рисунок 11. График изменения ошибок оценивания  в процессе наведения

Рассмотренный метод наведения может использоваться и на этапе пассивного самонаведения самолетов, когда необходимо получить максимально возможную точность определения местоположения цели в момент применения оружия. В этом случае в качестве виртуальной цели можно использовать виртуальную точку пуска, удаленную от ударного самолета на максимальную расчетную дальность применения оружия.

Следует отметить, что при боевом применении угломерной ДПСН возможны ситуации, когда на траекторию полета самолета обеспечения накладываются определенные ограничения в виде неравенств. В этом случае алгоритмы траекторного управления могут быть найдены на основе метода проекции градиента целевой функции либо метода штрафных функций. В работе использованы оба метода.

3.6. Алгоритм траекторного управления самолетом информационной поддержки на основе метода проекции градиента

Данный метод применяется в задачах оптимизации с ограничениями в виде неравенств [21]. В нашем случае эти ограничения задаются допустимой областью нахождения самолета информационной поддержки.

Под допустимой областью  понимается область -мерного пространства, в которой выполняются ограничения, наложенные на переменные . В начальный момент времени самолет находится в допустимой области . При нахождении самолета в допустимой области рассматриваемый метод является обычным градиентным методом. После выхода на границу области  в некоторой граничной точке , , движение в направлении антиградиента – может вывести самолет за пределы допустимого множества. Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки . Двигаясь в направлении проекции вектора – на многообразие М, отыскивают новую точку , в которой , принимают  за исходное приближение и продолжают процесс. Опишем данную процедуру более подробно.

В точке  часть ограничений-неравенств удовлетворяются как равенство:

,                                    (20)

где  – общее число ограничений-неравенств.

Такие ограничения называются активными.

Обозначим через  набор индексов  этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области  в окрестности точки . В общем случае эта граница является нелинейной. Ограничения , аппроксимируются гиперплоскостями, касательными к ним в точке :

.

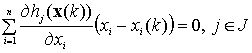Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область  в окрестности точки .

Проекция  антиградиента – на многогранник вычисляется по формуле

.    (21)

Здесь Р – оператор ортогонального проектирования, определяемый выражением

,                                      (22)

где  – единичная матрица размером ;  – матрица размеров . Она образуется транспонированными векторами-градиентами , активных ограничений. Далее осуществляется спуск в выбранном направлении:

.

Метод проекции градиента можно использовать для нахождения алгоритма траекторного управления в ситуациях, когда на полет самолета информационной поддержки С₂ накладываются определенные ограничения. В частности, они могут быть обусловлены требованием к самолету С₂ не находиться в зоне возможных пусков ракет с самолета противника либо в зоне поражения зенитно-ракетных комплексов [22, 23].

Для упрощения решаемой задачи будем полагать, что известна дальность  стрельбы самолетом противника, которая может меняться в зависимости от ракурса сближения с целью. Данное допущение позволяет считать, что самолет С₂ не должен приближаться к цели на расстояние меньшее, чем . Тогда допустимая область  для самолета С₂ может быть охарактеризована ограничением-неравенством вида

.                                            (23)

Активное ограничение имеет форму

или

.                                            (24)

В результате сравнения (20) и (24) приходим к выводу, что в данном случае , а матрица А представляет собой вектор

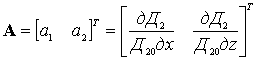,                           (25)

где , .

 

На основе (22) и (25) может быть найден оператор Р ортогонального проектирования 

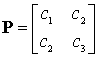,                                                (26)

в котором  , , .

 

Используя (21), (25) и (26), получим выражение для проекции р вектора антиградиента на границу допустимой области:

,

где , .

Требуемый курс для самолета С₂ рассчитывается аналогично (16)

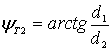.                                         (27)

 

Таким образом, полученный алгоритм траекторного управления самолетом информационной поддержки, использующий метод проекции градиента, предотвращает вход самолета в опасную зону. Недостаток алгоритма состоит в том, что проекция градиента начинает рассчитываться, когда самолет С₂ находится в точке, где выполняется равенство (24). В силу инерционности самолета он может выйти из допустимой области. Поэтому алгоритм траекторного управления должен быть доработан либо можно воспользоваться алгоритмом траекторного управления, полученным ниже на основе метода штрафных (барьерных) функций.

3.7. Алгоритм траекторного управления самолетом информационной поддержки на основе метода внутренних штрафных функций

Методы штрафных функций преобразуют задачу нелинейного программирования с ограничениями в задачу безусловной оптимизации некоторых вспомогательных функций. В общем случае вспомогательная функция имеет вид [21]

.

Здесь  – целевая функция задачи оптимизации;  – «штрафная» функция, связанная с функциями-ограничениями; параметр >0.

При наличии ограничений в виде неравенств, , для решения задачи нелинейного программирования применяют методы внутренних штрафных, или барьерных, функций, подбираемых таким образом, чтобы их значения неограниченно возрастали при приближении к границе допустимой области G. Иными словами, приближение к границе «штрафуется» резким увеличением функции . Тем самым на границе G строится барьер, препятствующий нарушению ограничения в процессе безусловной минимизации функции .

Поиск минимума вспомогательной функции  осуществляется каким-либо известным методом, например, градиентным методом. При этом в процессе минимизации траектория спуска никогда не выйдет за пределы допустимой области.

При решении задачи нелинейного программирования, как и в п. 3.6, будем полагать, что ограничение-неравенство определяется выражением (23). На основе рекомендаций, приведенных в [6], в качестве внутренних штрафных (барьерных) функций целесообразно использовать функции вида

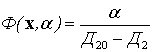                                             (28)

и

.                                      (29)

 

Обоснованный выбор вида штрафной функции (28) либо (29) и численного значения параметра  может быть осуществлен по результатам моделирования алгоритма траекторного управления самолетом информационной поддержки, полученного на основе решения задачи безусловной минимизации функции  аналогично тому, как это сделано в п. 3.4.

3.8. Метод управления информационной позицией на основе принципа динамического программирования

Из косвенных методов наибольшее распространение получили принцип максимума Л.С. Понтрягина и динамическое программирование Беллмана.

Рассмотрим возможности применения теории оптимального управления на базе принципа динамического программирования для разработки алгоритмов траекторного управления ПП информационной поддержки в угломерной двухпозиционной системе. Предварительно приведем необходимые математические соотношения [1, 19, 21].

Пусть управляемый процесс описывается детерминированным уравнением общего вида:

.

Здесь  – полная производная вектора состояния  по времени ,  – векторная функция векторных аргументов  и скалярного аргумента ,  – вектор управления.

Как известно, для вычисления оптимального управления с использованием принципа динамического программирования решается уравнение Беллмана. Решение этого уравнения упрощается в определенных случаях, в частности, для процесса с линейно входящим управлением 

                                           (30)

и функционала с аддитивной квадратичной функцией затрат на управления [1, 19]:

,                           (31)

 

где  – заданная скалярная функция конечного состояния процесса ;

 – заданная функция; К – диагональная невырожденная матрица заданных коэффициентов;  – матричная функция размера  аргументов .

Интегрирование в (31) осуществляется от текущего момента времени t₁=t до конечного t₂=t_к. Первая часть функционала, называемая терминальной, отражает конечную ошибку, вторая (подинтегральная) – требования к точностным характеристикам системы и третья – ограничения на управляющие воздействия.

Уравнение Беллмана и оптимальное управление имеют вид [1, 19]:

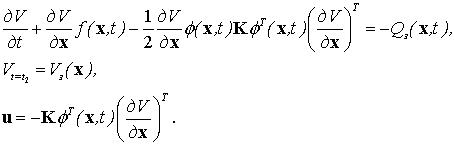           (32)

Здесь «Т» – символ транспонирования.

Уравнение Беллмана представляет собой нелинейное уравнение в частных производных. Решение этого уравнения при граничном условии  должно определять оптимальное управление. Аналитическое построение точных решений существуют лишь для линейно-квадратичных задач. Для нелинейных систем возможны различные способы приближенного решения уравнений Беллмана, которые могут оказаться полезными при решении задач синтеза для динамических процессов невысокой размерности. При этом используют численную форму динамического программирования, построение разностных схем, метод рядов и метод характеристик [19, 21].

В общем случае управляемый процесс является стохастическим. Следует заметить, что для нелинейных систем задача управления стохастическими процессами путем минимизации функционалов еще намного сложнее, чем для детерминированных процессов. В то же время для нелинейных задач применительно к функционалу (31) приближенно справедлива теорема разделения, согласно которой можно раздельно синтезировать систему оценивания и идентификации и систему собственно управления. Ниже предполагается, что процедура оценивания фазовых координат и идентификации параметров в угломерной ДПСН произведена.

Конкретизируем постановку задачи нахождения оптимального управления применительно к приемной позиции информационной поддержки угломерной ДПСН. В качестве целевой функции выберем зависимость ошибки (2) определения местоположения ИРИ

.

 

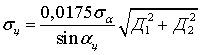Введем обозначение переменных вектора состояния х, полагая в качестве управления u угол  отклонения элеронов и учитывая его связи с углом крена и курсом летательного аппарата [1, 22]:  – прямоугольные координаты ведущей приемной позиции по оси X_о  неподвижной в пространстве горизонтальной системе координат ОX_о Z_о;  – производная по времени прямоугольной координаты ведущей ПП по оси X_о;  – прямоугольные координаты ПП информационной поддержки по оси Z_о;  – производная по времени прямоугольной координаты ПП информационной поддержки по оси Z_о;  – курс ПП информационной поддержки С₂;  – скорость изменения курса ПП информационной поддержки С₂;  – крен ПП информационной поддержки С₂;  – скорость изменения угла крена;  и  – коэффициент эффективности и угол отклонения элеронов.

Отсюда следует, что уравнения состояния можно записать следующим образом:

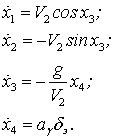                                                 (33)

Применительно к рассматриваемому случаю минимизируемый функционал (31) имеет вид:

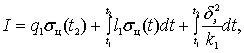                                (34)

 

где , ,  – коэффициенты штрафов.

В минимизируемом функционале (34) член с квадратичным управлением u = служит для ограничения управляющего воздействия.

Если рассматривать в  качестве управления u боковое ускорение j_б, то уравнения состояния могут быть упрощены. Действительно, скорость изменения курса приемной позиции С₂ [1]

.

 

Для этого случая уравнения состояния приобретают вид:

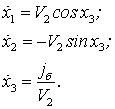                                               (35)

Из (35) видно, что размерность вектора состояния x меньше, чем в динамической системе (33). Минимизируемый функционал имеет тот же вид (34), но при условии подстановки j_б вместо .

Поскольку в минизируемом функционале средняя квадратичная ошибка местоопределения  нелинейно зависит от прямоугольных координат, то аналитическое определение оптимального управления не представляется возможным. Для отыскания оптимального управления приемной позицией информационной поддержки необходимо воспользоваться указанными выше приближенными способами решения задачи.

3.9. Алгоритмы траекторного управления самолетами пары на основе использования корреляционной матрицы ошибок измерений

Как отмечалось, на практике возникают ситуации, когда задача повышения точности оценивания координат радиоизлучающей цели может решаться одновременно двумя самолетами, входящими в состав двухпозиционной системы наведения.

В частности, известен способ управления движением двух самолетов по курсу в горизонтальной плоскости [24], позволяющий повысить точность оценивания координат и параметров движения цели, перемещающейся линейно и равномерно. На каждом из самолетов измеряют угловые координаты цели и собственные прямоугольные координаты. Измерения содержат ошибки. По полученным на текущий момент времени измерениям формируют оценки координат и параметров движения цели, затем по этим оценкам вырабатывают сигналы оптимального управления движением самолетами. Задача управления фактически сводится к формированию управлений самолетами, обеспечивающих в каждый момент времени минимум нормы корреляционной матрицы ошибок искусственно формируемых (косвенных) измерений прямоугольных координат ИРИ и их производных. Основой предложенного способа является достаточно сложная процедура нахождения векторного поля оптимальных перемещений самолетов (приемных позиций), позволяющая определять направление движения, при котором достигается максимально быстрое убывание нормы корреляционной матрицы ошибок измерений.

При реализации данного способа управления траекториями самолетов может быть достигнуто двукратное увеличение точности оценивания местоположения цели [24]. Вместе с тем нелинейности преобразований накладывают существенные ограничения на допустимые максимальные ошибки в измерениях пеленгов: при среднеквадратической ошибке измерения пеленга больше 15 угловых минут возможны срывы управления. К недостаткам данного способа также можно отнести достаточно жесткие требования к характеру движения цели: допускается лишь равномерное и прямолинейное движение цели.

Отмеченные недостатки стимулируют разработку новых алгоритмов траекторного управления самолетами. В частности, рассмотренные выше алгоритмы траекторного управления самолетом информационного обеспечения на основе ортогональных методов могут быть использованы и при решении задачи минимизации ошибок местоопределения цели за счет управления самолетами пары.

Кроме того, для управления самолетами пары можно воспользоваться алгоритмом градиентного метода наведения, полученным в п. 3.4 при использовании в качестве целевой функции выражения (2). Однако для оценки эффективности такого варианта градиентного метода управления необходимо проведение дополнительных исследований.

3.10. Метод одновременного управления обеими позициями на основе линейных моделей состояния

Одним из возможных приемов наведения ДПСН является метод, в котором обе позиции используются для повышения точности оценивания координат и параметров движения радиоизлучающей цели за счет поддержание угла , близким к 90^о.

Алгоритм такого одновременного траекторного управления самолетами  и имеет вид [16]:

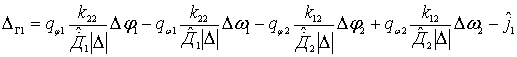;        (36)

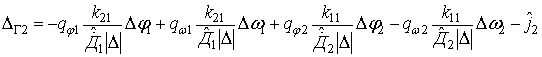,   (37)

 

где , , , , а  – определитель матрицы  штрафов за величину сигналов управления; ,  – бортовые пеленги радиоизлучающей цели; ,  – угловые скорости линий визирования , ; ,  – скорости изменения дальностей , ; ,  – поперечные ускорения пеленгаторов ,  в горизонтальной плоскости, рассматриваемые в качестве управляемых сигналов,  и ,  – требуемые значения бортовых пеленгов и угловых скоростей линий визирования; , , ,  – коэффициенты штрафов за ошибки управления по ,  и ,  [16].

В (36), (37) ,  – оценки собственных поперечных ускорений приемных позиций; ,  и ,  – оценки дальностей , и скоростей их изменения.

Из геометрии взаимного расположения (см. рис. 4) следует, что

,         (38)

.    (39)

В свою очередь на участке повышения точности определения местоположения радиоизлучающей цели

,                                         (40)

.                                  (41)

Анализ выражений (36) – (41) позволяет сделать следующие заключения.

Сигналы траекторного управления  и  зависят как от ошибок по углу и угловой скорости своей позиции, так и от соответствующих ошибок другой позиции. При этом эти сигналы направляют самолеты  и  в противоположные стороны, что приводит к более быстрому выполнению условия , обеспечивая наивысшую точность определения местоположения радиоизлучающей цели.

Если самолеты С₁ и С₂ имеют различную маневренность (k₁₁k₂₂, k₁₂k₂₁), то предпочтение в решении общей задачи достижения  отдается более маневренному самолету.

Качественно траектории полета цели и самолетов С₁ и С₂ при использовании (36), (37) показаны на рис. 12.

 

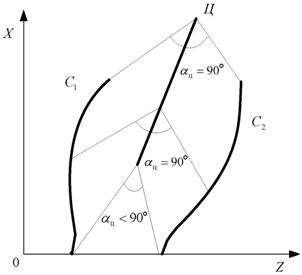
Рисунок 12. Пример траекторий полета цели и самолетов при одновременном управлении приемными позициями

Вес ошибок управления Δφ₁, Δω₁, Δφ₂, Δω₂ зависит от выбора штрафов q_φ1, q_ω1, q_φ2, q_ω2 и k_11, k₁₂, k₂₁, k₂₂ и условий применения, определяемых значениями ,  и , . При этом на больших расстояниях, предопределяющих малые значения угловых скоростей, преобладающим является управление по угловым ошибкам, в то время как ошибки по угловым скоростям играют роль корректирующих сигналов в процессе приближения  к . На малых расстояниях при достаточно больших значениях угловых скоростей основным является управление по ошибкам угловых скоростей. Эта особенность дает возможность на одной или обеих позициях перейти к наведению на ИРИ при условии ω_г1,2=0, обеспечивающему минимизацию промаха 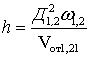 [1], где V_от1,2 – относительная скорость позиций С₁, С₂ и цели.

 

Для информационного обеспечения (36) – (41) необходимо на борту каждого самолета формировать оценки собственного курса, бортового пеленга, угловой скорости линии визирования, собственного поперечного ускорения, дальности до ИРИ и скорости ее изменения. Кроме того, необходимо осуществлять обмен между позициями информацией о собственном курсе, бортовом пеленге и их производных, а также о требуемых значениях пеленгов и угловых скоростей линии визирования, либо соответствующих ошибках наведения Δφ₁, Δω₁, Δφ₂, Δω₂.

Недостатком данного метода является сложность взаимного обмена информацией.

Необходимо отметить, что в рамках разработанной процедуры синтеза алгоритмов траекторного управления могут быть получены и более простые законы управления, при которых k₁₂=k₂₁=0, в меньшей степени учитывающие взаимное влияние позиций друг на друга.

 

4. Разработка модифицированного метода проекции градиента

Как следует из изложенного выше, основной задачей метода проекции градиента является обеспечение полета ЛА информационной поддержки вблизи запретной зоны. Результаты исследований показывают, что при управлении по методу проекции градиента наблюдается неустойчивое положение ЛА на границе запретной (опасной) зоны полета, представляющей круг с заданным радиусом . Это приводит к тому, что ЛА периодически оказывается внутри запретной зоны полета, хотя и недалеко от ее границы. Поэтому необходимо разработать такой алгоритм управления, который бы обеспечивал движение ЛА информационной поддержки без захода в запретную зону полета.

В принципе, для полета по окружности можно воспользоваться идеей, положенной в основу маршрутного метода наведения летательных аппаратов по курсу по фиксированной траектории. В качестве такой траектории обычно используется участок ортодромии, проходящей через два пункта маршрута. Напомним, что ортодромия определяет кратчайшее расстояние между двумя точками на сфере [1].

Траектория управления при маршрутном методе наведения сводится к удержанию ЛА на выбранной ортодромии. В качестве параметра рассогласования, реализующего цель маршрутного метода наведения, может быть использована величина бокового отклонения ЛА от ортодромии. Для повышения точности и устойчивости управления обычно в выражение для параметра рассогласования вводится слагаемое, пропорциональное скорости изменения бокового отклонения ЛА от ортодромии. В нашем случае вместо бокового отклонения от ортодромии предлагается использовать боковое отклонение от окружности с радиусом , центр которой совпадает с ИРИ. Применительно к рассматриваемой ситуации параметр рассогласования для маршрутного метода наведения имеет вид 

,                                              (42)

где  – боковое отклонение ЛА от окружности, отсчитываемое по линии, соединяющей центр окружности и ЛА информационной поддержки; - скорость изменения бокового отклонения;  – весовой коэффициент.

Для реализации алгоритма (42) необходимо оценивать  и . Расстояние от ЛА информационной поддержки до центра окружности рассчитывается по формуле

,

а скорость  изменения бокового отклонения определяется как производная его по времени.

Для нахождения бокового отклонения необходимо оценивать прямоугольные координаты , ИРИ и измерять прямоугольные координаты , ЛА .

В соответствии с методом проекции градиента параметр управления ЛА, характеризующий несоответствие требуемого и фактического курсов, определяется выражением

,                                                 (43)

в котором  – требуемое значение курса, рассчитываемое по формуле (27);  – текущее значение курса ЛА.

Объединяя (42) и (43), для участка полета ЛА в районе границы запретной зоны окончательно получим

,                        (44)

где  – весовой коэффициент по курсу;  – весовой коэффициент по боковому отклонения и скорости его изменения.

Таким образом, алгоритм (44) обеспечивает реализацию модифицированного метода траекторного управления наблюдением, начиная с момента достижения границы запретной зоны летательным аппаратом информационной поддержки, т.е. при выполнении условия . При этом полет ЛА до границы запретной зоны должен осуществляться по градиентному методу в соответствии с алгоритмом (16).

В принципе переход на модифицированный метод наведения может быть выполнен несколько раньше, чем наступит момент времени, когда . Момент такого перехода может быть определен, если задать условие перехода в виде , где  – пороговое расстояние от ЛА информационной поддержки до окружности по линии визирования ИРИ-ЛА информационной поддержки (боковое отклонение). При этом  должно быть много меньше, чем . В результате будет обеспечен плавный выход ЛА информационной поддержки на границу запретной зоны, что предотвратит вход ЛА в эту зону из-за инерционности процесса управления. Численное значение  может быть найдено экспериментальным путем по результатам имитационного моделирования процесса наведения ЛА.

 

Заключение

Изложенное выше позволяет сделать следующие выводы:

1.       В интегрированных многодатчиковых двухпозиционных системах радиомониторинга могут использоваться разнообразные методы траекторного управления наблюдением, каждый из которых имеет свои достоинства, недостатки и предпочтительные условия применения.

2.       В состав угломерной двухпозиционной системы наведения входят два наводимых ЛА и пункт управления, выполняющий функции командного пункта наведения. В качестве информационных датчиков используются угломеры бортовых РЛС, работающих в пассивных режимах, либо систем РРТР наводимых самолетов. В угломерной двухпозиционной системе при наведении ЛА на ИРИ необходимо решать две задачи: задачу синтеза алгоритмов оценивания дальности до ИРИ и скорости сближения с ним либо его прямоугольных координат и их производных и задачу синтеза алгоритмов траекторного управления отдельными приемными позициями. Особенностью задачи построения алгоритмов траекторного управления отдельными приемными позициями является возможность реализации концепции траекторного управления наблюдением.

3.       Ключевыми алгоритмами функционирования угломерных двухпозиционных систем наведения являются алгоритмы целенаправленного управления пространственным положением отдельных позиций. Задача оптимизации управления угломерной ДПСН существенно упрощается, если функции перехвата излучающей цели и обеспечения максимальной точности определения ее местоположения разделить между различными позициями. При таком подходе одна из позиций решает задачу наведения, используя тот или иной известный метод, а вторая – целенаправленно изменяет свое положение в пространстве, обеспечивая на обеих позициях максимально высокую точность определения местоположения перехватываемого объекта.

4.     Наибольшее число разработанных алгоритмов траекторного управления наблюдением в пассивных угломерных двухпозиционных системах базируются на условии, что оптимальное положение самолета информационной поддержки лежит на перпендикуляре к линии ударный самолет-цель. Одна группа алгоритмов обеспечивает вывод самолета поддержки в произвольную точку перпендикуляра, а вторая группа алгоритмов – в заданную точку перпендикуляра, выбираемую с учетом безопасности самолета информационной поддержки.

5.     Алгоритм траекторного управления самолетом информационной поддержки, разработанный на основе градиентного метода минимизации целевой функции, позволяет сформировать требуемую траекторию самолета информационной поддержки, движение по которой приводит к максимально быстрому уменьшению ошибок местоопределения радиоизлучающей цели на каждом шаге управления. Для вычисления требуемого курса самолета информационной поддержки целесообразно воспользоваться численным способом нахождения частных производных целевой функции по прямоугольным координатам.

6.                Модифицированный градиентный метод наведения обеспечивает возможность  заблаговременно до начала приема сигналов ИРИ пеленгаторами приемных позиций сформировать необходимую пространственную конфигурацию угломерной двухпозиционной системы, при этом достигается минимизации ошибок определения местоположения ИРИ. Разработанный алгоритм траекторного управления ПП информационной поддержки, использующий концепцию «виртуальной» цели, приводит также к уменьшению кривизны траектории полета ПП информационной поддержки и, следовательно, к сокращению длины траектории и времени построения требуемой геометрии взаимного положения ПП, а также к снижению затрат топлива. Рассмотренный метод наведения может использоваться и на этапе пассивного самонаведения самолетов, когда необходимо получить максимально возможную точность определения местоположения цели в момент применения оружия.

7.                Разработанные перспективные алгоритмы траекторного управления самолетом информационной поддержки, использующие метод проекции градиента и метод барьерных функций, повышают эффективность боевого применения угломерной двухпозиционной системе наведения, предотвращая вход самолета в запретную (опасную) зону.

8.                Метод траекторного управления самолетом информационной поддержки, разработанный на основе принципа динамического программирования, позволяет сформировать требуемую траекторию самолета информационной поддержки с использованием, в отличие от градиентных методов, необходимых условий оптимизации. Движение по такой траектории приводит к максимально быстрому уменьшению ошибок местоопределения радиоизлучающей цели на каждом шаге управления. Но поскольку в минимизируемом функционале средняя квадратичная ошибка местоопределения нелинейно зависит от прямоугольных координат, то аналитическое определение оптимального управления не представляется возможным. Для отыскания оптимального управления приемной позицией информационной поддержки необходимо воспользоваться известными приближенными способами решения задачи.

9.                Методы одновременного управления обеими позициями, направленные на получение наивысшей точности определения координат ИРИ, обеспечивают более быстрое достижение минимума ошибки определения местоположения и соответственно получение более высокой точности на начальных участках траектории наведения по сравнению с пассивной ДПСН, основанной на разделении функций между позициями на ударные и информационные.

10.           При совместном решении задачи минимизации ошибок местоопределения цели обоими самолетами пары в качестве алгоритмов траекторного управления на каждом из них могут быть использованы градиентные алгоритмы управления, полученные с использованием корреляционной матрицы ошибок искусственно формируемых (косвенных) измерений прямоугольных координат ИРИ и их производных. При реализации данного способа нелинейности преобразований накладывают существенные ограничения на допустимые максимальные ошибки в измерениях пеленгов. К недостаткам градиентных алгоритмов управления также можно отнести достаточно жесткие требования к характеру движения цели: допускается лишь равномерное и прямолинейное движение цели. Для управления самолетами пары можно воспользоваться также алгоритмом градиентного метода наведения, полученным при использовании в качестве целевой функции выражения (2). Однако для оценки эффективности такого варианта градиентного метода управления необходимо проведение дополнительных исследований.

11.           При ортогональном методе одновременного управления обеими позициями на основе линейных моделей состояния сигналы траекторного управления самолетами зависят как от ошибок по углу и угловой скорости своей позиции, так и от соответствующих ошибок другой позиции. При этом эти сигналы направляют самолеты  и  в противоположные стороны, что приводит к более быстрому выполнению условия , обеспечивая наивысшую точность определения местоположения радиоизлучающей цели. Недостатком данного метода является сложность взаимного обмена информацией.

12.           Модифицированный метод проекции градиента для траекторного управления ПП информационной поддержки разработан с учетом использования основных положений, положенных в основу методов проекции градиента и маршрутного. Он обеспечивает бóльшую безопасность для летательных аппаратов информационной поддержки при наличии запретных зон полетов, чем обычный метод проекции градиента. Для оценки эффективности модифицированного метода проекции градиента необходимо проведение дополнительных исследований.

13.           Особенностью траекторного управления наблюдением в угломерных двухпозиционных системах является возможность перехода с одного алгоритма наведения на другой на разных этапах применения.

14.           В общем случае для информационного обеспечения алгоритмов траекторного управления необходимо на борту каждого самолета формировать оценки собственного курса, углов пеленга, угловой скорости линии визирования, собственного поперечного ускорения, дальности до цели и скорости ее изменения, либо прямоугольные координаты цели и скорости их изменения. Следует подчеркнуть, что такой набор оценок позволяет реализовать практически все существующие методы наведения.

15.           Результаты имитационного моделирования разработанных алгоритмов траекторного управления наблюдением для методов ортогонального наведения на основе нелинейных и линейных моделей состояния, метода наведения в наилучшую точку наблюдения, градиентного метода наведения, градиентного метода наведения на виртуальную цель, метода проекции градиента, метода одновременного управления обеими позициями на основе линейных моделей состояния показали достаточно высокую эффективность и могут быть использованы на практике при создании интегрированных многодатчиковых двухпозиционных систем радиомониторинга воздушного базирования для различных условий их применения.

Работа выполнена при поддержке РФФИ, проект № 15-08-04000-а.

 

Литература

1.                Меркулов В.И., Чернов В.С., Гандурин В.А., Дрогалин В.В., Савельев А.Н. Авиационные системы радиоуправления: учебник для военных и гражданских ВУЗов и научно-исследовательских организаций. / Под ред. В.И. Меркулова. – М.: Изд. ВВИА им. проф. Н.Е. Жуковского. 2008.

2.                Меркулов В.И., Миляков Д.А., Чернов В.С. Уровни и варианты объединения информации в мобильных интегрированных комплексах мониторинга окружающего пространства. // Журнал радиоэлектроники [электронный журнал]. 2015. №4.  URL: http://jre.cplire.ru/jre/na/12/10/text.html.

3.                Верба В.С., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч.3. / Под ред. В.С. Вербы, В.И. Меркулова. – М.: Радиотехника. 2010.

4.                Дрогалин В.В., Меркулов В.И., Чернов В.С. и др. Алгоритмы оценивания координат и параметров радиоизлучающих целей в угломерных двухпозиционных бортовых радиолокационных системах. // Информационно-измерительные и управляющие системы. 2003. №1.

5.                Дрогалин В.В., Меркулов В.И., Чернов В.С. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. // Успехи современной радиоэлектроники. Зарубежная радиоэлектроника. 2003. №5.

6.                Способ наведения летательных аппаратов в двухпозиционной радиолокационной системе. Патент РФ на изобретение № 2262649 от 20.10.2005.

7.                Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе. Патент РФ на изобретение №2256870 от 20.07.2005.

8.                Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе. Патент РФ на изобретение №2308093 от 10.10.2007.

9.                Меркулов В.И., Харьков В.П., Чернов В.С. Алгоритмы управления позициями в пассивной двухпозиционной радиолокационной системе. // Радиотехника. 2004. №10.

10.           Меркулов В.И. Управления пассивными двухпозиционными РЛС в режиме наведения на радиоизлучающую цель. // Радиотехника. 2005. №6.

11.           Бирина Н.О., Меркулов В.И., Чернов В.С. и др. Способ управления самолетами в угломерной двухпозиционной радиолокационной системе. // Радиотехника. 2005. №6.

12.           Меркулов В.И., Миляков Д.А., Чернов В.С. Траекторное управление наблюдением в распределенных угломерных радиоэлектронных системах управления воздушного базирования. // Материалы 2-й Всероссийской конференции «Суперкомпьютерные технологии СКТ-2012» (24-29 сентября 2012 г. Дивноморское, Геленджик).

13.           Меркулов В.И., Суворов Н.Н., Чернов В.С. и др. Алгоритмы управления и адаптивной фильтрации в угломерной двухпозиционной радиолокационной системе. // Радиотехника. 2006. №7.

14.           Меркулов В.И., Харьков В.П., Чернов В.С. и др. Алгоритмы траекторного управления самолетами в угломерной двухпозиционной радиолокационной системе. // Юбилейная научно-техн. конф. «Авиационные системы 21 века». ФГУП ГосНИИАС. 2006.

15.           Меркулов В.И., Чернов В.С., Юрчик И.А. Авиационные многопозиционные системы радиоуправления. // Успехи современной радиоэлектроники. 2006. №12.

16.           Меркулов В.И., Чернов В.С., Куимов А.М. Траекторное управление пассивными двухпозиционными системами. // Информационно-измерительные и управляющие системы. 2008. №12.

17.           Меркулов В.И., Чернов В.С., Чербаев С.Г. и др. Способы траекторного управление наблюдением в угломерной двухпозиционной системе. // Информационно- измерительные и управляющие системы. 2012. №4.

18.           Абатуров В.А., Меркулов В.И., Чернов В.С. Авиационные системы радиоуправления. Многопозиционные системы радиоуправления. Учебное пособие. – М.: ВВИА им. проф. Н.Е Жуковского, 2008.

19.           Коршунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Энергия, 1980.

20.           Меркулов В.И., Чернов В.С. Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения // Успехи современной радиоэлектроники. 2013. №7.

21.           Фурунжиев Р.И., Бабушкин Ф.М., Варавко В.В. Применение математических методов и ЭВМ: Практикум: Учеб. пособие для вузов. – Мн.: Выш. шк., 1988.

22.           Меркулов В.И., Миляков Д.А., Чернов В.С. Траекторное управление наблюдением в подвижных пассивных системах воздушного базировании. // Журнал радиоэлектроники [электронный журнал]. 2012. №11. URL: http://jre.cplire.ru/jre/na/12/10/text.html.

23.           Меркулов В.И., Миляков Д.А., Чернов В.С. Градиентные методы траекторное управление летательными аппаратами в двухпозиционных системах наведения воздушного базирования с повышенной точностью определения местоположения источников радиоизлучения. // Информационно-измерительные и управляющие системы. 2015. №54.

24.           Катулев А.Н., Тухватулин В.В. Формирование управлений движением пеленгаторов угломерной системы. // Радиотехника. 1989. №10.