УДК 621.396

Квазиплоскостной метод обеспечения объектовой ЭМС РЭС для всенаправленных по азимуту антенн

 

А. А. Мозоль ¹, В. А. Головской ²

¹ФКУ «НПО «Специальная техника и связь» МВД России

²Краснодарское высшее военное училище

 

Статья поступила в редакцию 6 апреля 2016 г.

 

Аннотация. В статье предложен метод решения задачи объектовой ЭМС в действующей группировке радиосредств для всенаправленных по азимуту антенн. Метод заключается в использовании классического критерия ЭМС для определения места установки размещаемого радиоэлектронного средства в горизонтальной плоскости, определяемой требуемым значением высоты установки. При этом задача решается относительно внеосевого угла антенны парным способом расчета для детерминированного подхода.

Ключевые слова: электромагнитная совместимость, размещаемое радиоэлектронное средство, эмиттер радиопомехи, угол места.

Abstract. This paper proposes a method for solving the problem of on-site EMC in the current group of radio for omnidirectional antennas in azimuth. The method lies in the use of classic EMC criteria for determining a location of electronic device in a horizontal plane determined by the required value of the installation height. This problem is solved with respect to the off-axis angle of the antenna pair of calculation method for deterministic approach.

Key words: electromagnetic compatibility, allocated radio-electronic device, emitter of interference, elevation.

 

Введение

Интенсивное развитие информационно-телекоммуникационных технологий является одной из реалий современности. Следствием этого явилось возрастание актуальности научно-практической задачи обеспечения электромагнитной совместимости (ЭМС) технических средств (ТС), оснащенных радиоприемниками (РПМ) и (или) радиопередатчиками (РПД). Такие ТС далее будем называть радиоэлектронными средствами (РЭС). Особенно остро данная задача стоит в контексте обеспечения объектовой ЭМС, когда для нескольких РЭС, размещенных на одном объекте, требуется обеспечить совместное функционирование с заданным качеством [1]. При этом в самом общем случае временные, частотные, энергетические, поляризационные и пространственные параметры, их характеризующие, могут быть сколь угодно различными в контексте как детерминированного, так и вероятностного подходов. Широким классом среди объектовых РЭС представлены РЭС со всенаправленными по азимуту антеннами. К ним относятся РЭС теле- и радиовещания, РЭС подвижной радиосвязи и услуг широкополосного беспроводного доступа.

В отличие от классического определения ЭМС [2] для упрощения расчетов в данной статье предполагается, что размещаемое РЭС (РРЭС) не создает непреднамеренных радиопомех (НРП) для РЭС, функционирующих на объекте, т.е. РРЭС является рецептором радиопомех (РРП), а все остальные РЭС, размещенные на объекте, – эмиттерами радиопомех (ЭРП) [1, 3]. Тогда решение задачи объектовой ЭМС РЭС ищется относительно значений пространственных координат точки установки РРЭС, обеспечивающих выполнение критерия ЭМС за счет пространственного разноса. Классическим критерием ЭМС является условие, при котором уровень НРП на входе РПМ РРП (РРЭС) не превышает допустимый уровень [4–7].

Задача обеспечения объектовой ЭМС РЭС решается, как правило, путем реализации парного метода расчета в вероятностной или детерминированной постановке [8–13]. Однако получение классического решения задачи объектовой ЭМС РЭС сопряжено с рядом принципиальных и вычислительных трудностей:

-                   нерационально большие вычислительные затраты, требующие соответствующих программно-аппаратных ресурсов;

-                   существенно нелинейный характер уравнения ЭМС относительно координат места установки размещаемого РЭС (РРЭС);

-                   три неизвестных в одном исходном нелинейном уравнении ЭМС, составленном применительно к одному дуэльному сочетанию РРЭС-ЭРП;

-                   высокая сложность точного аналитического представления функций, характеризующих пространственно-избирательные свойства антенн РРП и ЭРП, а также другие трудности.

Вследствие указанных трудностей возникает необходимость синтеза нового метода решения задачи объектовой ЭМС РЭС применительно к всенаправленным по азимуту антеннам, базирующегося на классическом критерии ЭМС РЭС и свободного от указанных недостатков.

 

Постановка и ограничения задачи

Предположим, что на некотором объекте расположены  (), функционирующие с требуемым качеством в каждый момент времени. Таким образом, в исходной группировке РЭС обеспечена их ЭМС. Необходимо установить на этот объект на мачту высотой  некоторое РРЭС с известными тактико-техническими характеристиками. Т.е. требуется определить значения координат местоположения РРЭС, для которых выполнялся бы классический критерий ЭМС в рамках детерминированного подхода и парного метода расчета. Иными словами, требуется найти все области пространства, при расположении в каждой точке которых фазового центра антенны РРЭС уровни помех, создаваемых всеми ЭРП объекта и в любом частотном канале приема РРЭС, не превышают соответствующих допустимых значений. При этом рассматриваются только всенаправленные по азимуту антенны. В качестве математической модели радиотрассы НРП примем простейшую модель – модель свободного пространства [14].

Решение задачи (основные соотношения метода)

Классическим критерием ЭМС РЭС является условие [4–7, 11]

 ,                                                 

 где  – допустимое значение НРП, дБВт;  – расчетное значение НРП, дБВт.

Допустимое значение для основного и побочных частотных каналов воздействия, а также по блокированию и перекрестным искажениям определяется из следующего выражения [4–7]:

 ,                          

 где  – уровень допустимой по признаку  НРП на входе РПМ, дБВт;  – признак воздействия НРП, определяемый значениями набора параметров : для основного канала приема – , для побочного – , для нелинейных эффектов блокирования и перекрестных искажений – ;  – уровень реальной чувствительности РПМ РРЭС, дБВт;  – уровень пороговой чувствительности РПМ РРЭС, дБВт;  – избирательность РПМ РРЭСпо побочному каналу приема, дБ;  – динамический диапазон РПМ РРЭС по блокированию и перекрестным искажениям, дБ;  – величина защитного отношения полезного сигнала к помехе, дБ.

Расчетное  значение НРП от  (предположим, что , ) в основном и побочных частотных каналах приема РРЭС определяется из выражения [3–13]

 

          

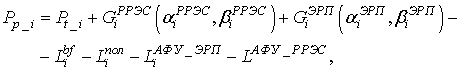
 где  – мощность передатчика , , дБВт;  – значение коэффициента усиления (КУ) антенны РРЭС от значений внеосевых углов в горизонтальной и вертикальной плоскостях в направлении на , дБ;  – значение КУ антенны  от значений внеосевых углов в горизонтальной и вертикальной плоскостях в направлении на РРЭС, дБ;  –ослабление за счет основных потерь при распространении в свободном пространстве, дБ;  – поляризационное ослабление, дБ;  – ослабление в антенно-фидерном устройстве (АФУ) , дБ;  – ослабление в АФУ РРЭС, дБ.

Значения параметров ,  и  задаются в исходных данных задачи. Величина поляризационного ослабления  для каждого дуэльного сочетания выбирается из таблицы [7] по известным типам поляризации  и максимальным значениям их КУ . Аналитический вид функций  и , описывающих значение КУ от направления в пространстве, может быть задан с помощью моделей типовых антенн, рекомендуемых в [15–17]. Функция  основных потерь в свободном пространстве имеет вид [18]

 ,                                

 где  – частота радиоизлучения , МГц;  – расстояние между  и РРЭС, м, определяемое трехмерной арифметической евклидовой метрикой [19] .

Для пространственной координатной сетки объекта и с учетом требования азимутальной всенаправленности антенн основные потери в свободном пространстве будут иметь вид функций дискретных пространственных координат места установки РРЭС  (, , , , , ,  – шаг сетки) и внеосевых углов места антенн , .

С учетом , представим выражение в виде

                          

 где  – константа для фиксированного дуэльного сочетания РЭС; .

Выражение представляет собой модифицированный критерий ЭМС РЭС для детерминированного подхода и парного метода оценки ЭМС.

Теперь рассмотрим представленную на рис.1 геометрию задачи.

 

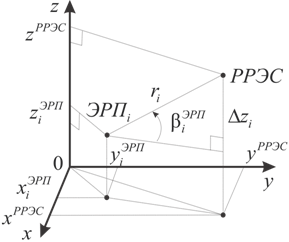
Рис.1. Геометрия задачи

Из рис.1 видно, что  , где .

С учетом выражения , а также принимая во внимание, что , преобразуем относительно переменной  к виду

 .           

 

Выражение представляет собой критерий ЭМС для детерминированного подхода и парного метода оценки ЭМС относительно одной переменной  и параметра , определяемого исходными требованиями к высоте установке антенны РРЭС . Решая неравенство , получаем значения , для которых критерий ЭМС выполняется в заданной плоскости  ( – требуемая высота установки антенны РРЭС) относительно фиксированного .

Однако неравенство может оказаться неразрешимым в явном аналитическом виде для требуемой высоты  установки антенны РРЭС. В таком случае можно использовать предложенный ниже алгоритм, основанный на исследовании поведения функции ЭМС с помощью производной:

-                   на основе критерия ЭМС составляем «функцию ЭМС» вида

 ,           

 где , ;

-                   определяем нули  функции ЭМС , , – количество нулей функции ЭМС, составленной для дуэльного сочетания РРЭС и , . Для этого можно использовать специальные встроенные функции различных программ для математических вычислений или графический метод [20].

-                   для каждого дуэльного сочетания (для каждого ) ранжируем полученные значения  и составляем интервалы ,…,,…, значений аргумента , соответствующие положительным и отрицательным участкам функции;

-                   определяем знак производной  в точках ;

-                   для каждого -го дуэльного сочетания РРЭС-ЭРП формируем линейные множества , содержащие решения неравенства для -го дуэльного сочетания в виде значений угла места , путем проверки выполнения условий:

если 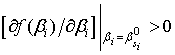, то ;

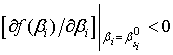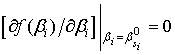если , то ; если , то ;

 

-                   множеству  решений, содержащему удовлетворяющие критерию ЭМС значения угла места  для -го дуэльного сочетания, ставим в соответствие множество  решений по радиусам  окружностей, построенных в требуемой плоскости  установки РРЭС из проекции точки расположения  на плоскость . Для отображения элементов  множества  в элементы  множества  используем правило

 .                                                

 В результате реализации приведенного алгоритма мы имеем набор из  решений задачи объектовой ЭМС для всех  дуэльных сочетаний    РРЭС-ЭРП, представляющий собой в геометрической интерпретации набор участков назначенной плоскости  в форме колец, ограниченных «разрешенными» значениями радиусов либо в форме линии окружности «разрешенного» в смысле критерия радиуса.

Результирующее решение задачи, учитывающее помеховые воздействия всех , размещенных и функционирующих на объекте, определяется как результат пересечения в требуемой плоскости  всех  решений задачи объектовой ЭМС для всех  дуэльных сочетаний, и представляет собой участок плоскости  в форме пересечения всех колец, ограниченных «разрешенными» для каждого -го дуэльного сочетания значениями радиусов либо в форме общей точки пересечения  окружностей разрешенных радиусов. Эту процедуру в общем случае можно представить выражением

 ,                        

 где 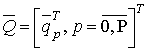 – вектор решений задачи, содержащий пары значений, соответствующих абсциссе и ординате места установки РРЭС в плоскости , ;  – оператор, который значениям плоских координат  размещения , значениям элементов  множества  и любому заданному значению абсциссы (ординаты)  места установки РРЭС в плоскости , ставит в соответствие значение ординаты (абсциссы) точки в плоскости . При решении задачи на ЭВМ наличие оператора  в аналитической форме не обязательно.

 

Иллюстративный пример

Предположим, что на некотором объекте, представляющем собой прямоугольную крышу (длиной  и шириной ) высотного здания, размещены и непрерывно функционируют в условиях обеспеченности ЭМС  РЭС. Каждое  () по своим частотным характеристикам является источником НРП в основной и побочные частотные каналы приема РРЭС. Необходимо определить место установки РРЭС на крыше таким образом, чтобы для РРЭС была обеспечена ЭМС со всеми  ().

Исходными данными задачи являются значения следующих параметров и характеристик:  м;  дБ;  дБВт;  дБ;  дБи; координаты размещения :  м,  м,  м;  ГГц;  дБ;  дБВт;  дБи;  м; значения поляризационного ослабления для каждого дуэльного сочетания назначим произвольным образом  дБ; значения ширины луча в вертикальной плоскости для ДНА РРЭС  и всех   () определялись по выражению [17]  в предположении, что углы места главных осей ДНА РРЭС и всех  () равны нулю, и равны  град.,  град.; ДНА всех ЭРП и РРЭС были описаны с использованием рекомендованной в [17] модели

 

 

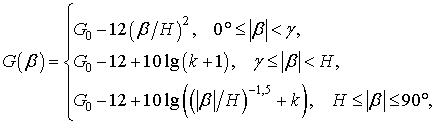
где  (для улучшенных антенн в диапазоне от 400 МГц до 3 ГГц); параметр , град., определяется из выражения .

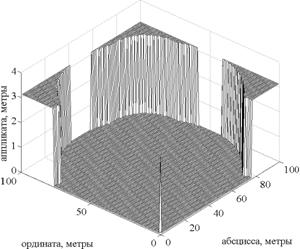
«Функции ЭМС», построенные по формуле для каждого дуэльного сочетания, показаны на рис.2.

 

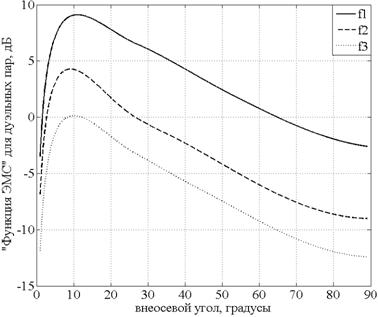
Рис. 2. «Функции ЭМС»

 

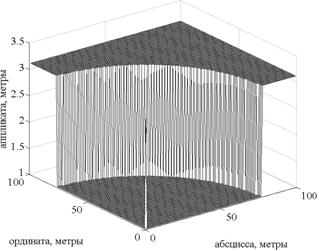
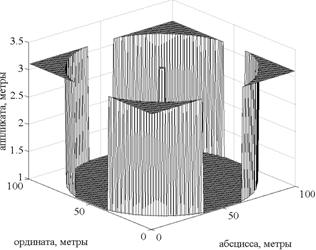
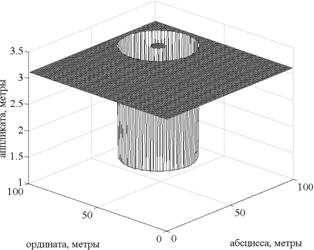
Решения для каждого дуэльного сочетания показаны в виде участков требуемой плоскости, ограниченной размерами объекта, на рис.3-5 соответственно. Общее решение задачи показано на рис.6.

 

Рис. 3. Решение для РРЭС и

Рис. 4. Решение для РРЭС и

 

Рис. 5. Решение для РРЭС и

Рис. 6. Общее решение

 

В результате решения получена  точка, пригодная для установки РРЭС с точки зрения ЭМС в требуемой плоскости .

 

 

Анализ точностных характеристик метода

Выражение , позволяющее определять значения «разрешенных» в смысле критерия в требуемой плоскости  установки радиусов  окружностей или образуемых ими колец, содержит параметры, которые могут быть известны с некоторой степенью точности. К таким параметрам относятся значение аппликаты  места установки ЭРП и значения «разрешенных» углов места . Если рассматривать  и  как случайные величины с математическими ожиданиями ,  и дисперсиями , , а функцию  – как случайную, то с помощью дисперсии  можно оценить точность определения значений «разрешенных» радиусов по известной формуле [21]

 ,

 

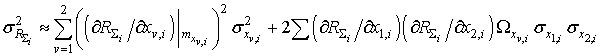где  – коэффициент корреляции случайных величин  и ;  и  – среднеквадратические отклонения (СКО) случайных величин и  соответственно.

Если случайные величины , , , некоррелированы, то

 

             

 

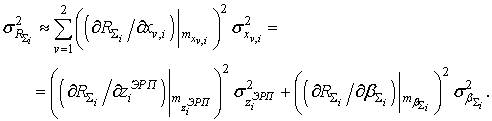
Применительно к выражению дисперсия примет вид

 .                         

 

Анализ выражения показывает, что точность оценивания разрешенных радиусов, характеризуемая его дисперсией, носит сложную функциональную зависимость, определяемую комбинацией квадратов тригонометрических функций. Кроме того, она прямо пропорциональна квадрату высоты установки РРЭС относительно антенны ЭРП. Это объясняется тем, что одни и те же погрешности определения разрешенных значений угла места приводят на больших относительных высотах  к большим погрешностям в определении разрешенных радиусов. Это легко понять из геометрических построений. В выражении сомножитель  выступает, своего рода, весовым коэффициентом характеристики точности разрешенного угла места . Следовательно, максимальная погрешность определения разрешенных значений радиусов для группировки ЭРП будет определяться погрешностью, которая рассчитывается для наибольшего значения , .

 

Выводы

Таким образом, в статье в рамках детерминированного подхода и парного способа расчетов предложен новый метод решения известной задачи объектовой ЭМС РЭС для всенаправленных по азимуту антенн. Отличительной особенностью метода является реализованное в нем свойство декомпозиции классического критерия ЭМС, которое позволяет с учетом принятых ограничений существенно упростить вычислительный процесс задачи. Принципиальным требованием метода является необходимость априорного задания аппликаты места установки РРЭС, что видится вполне логичным, учитывая ограниченные практические возможности мачтового размещения. Метод основан на решении нелинейного уравнения ЭМС, построенного по классическому критерию, относительно внеосевого угла места. При этом предложен альтернативный вычислительный алгоритм, основанный на исследовании поведения функции ЭМС с помощью производной. Характерной особенностью метода является процедура однозначного перехода от «дуэльных решений» в виде значений внеосевого угла к общему решению задачи в виде точек для установки в требуемой плоскости путем проецирования и пересечения «дуэльных решений».

 

Литература

1.       Головской В.А., Мозоль А.А. Проблемные вопросы обеспечения объектовой электромагнитной совместимости радиоэлектронных средств // Технологии электромагнитной совместимости. 2015. № 3(54). С. 3–10.

2.       Совместимость технических средств электромагнитная. Термины и определения: ГОСТ Р 50397-2011. – Введ. 2012–09–01. – М.: Стандартинформ, 2013.

3.       Головской В.А., Мозоль А.А. Отдельные вопросы обеспечения электромагнитной совместимости технических средств в условиях сложной радиообстановки // Материалы международной научно-практической конф. «Охрана, безопасность, связь – 2014». ч. 1. Воронеж. 2014. С. 100–105.

4.       Ефанов В.И., Тихомиров А.А. Электромагнитная совместимость радиоэлектронных средств и систем: учебное пособие. Томск.: ТГУ систем управления и РЭ, 2012. 228 с.

5.       Основы управления использованием радиочастотного спектра. Т. 2: Обеспечение электромагнитной совместимости радиосистем / Под ред. М.А. Быховского. М.: КРАСАНД, 2012. 553 с.

6.       Управление радиочастотным спектром и электромагнитная совместимость радиосистем / Под ред. М.А. Быховского. М.: Экотрендз, 2006. 376 с.

7.       Феоктистов Ю.А., Матасов В.В, Башурин Л.И. Теория и методы оценки электромагнитной совместимости радиоэлектронных средств / Под ред. Ю.А. Феоктистова. М.: Радио и связь, 1988. 216 с.

8.       Методика расчета электромагнитной совместимости земных станций фиксированной спутниковой службы и радиорелейных станций фиксированной службы гражданского назначения в полосах частот совместного использования от 1 ГГц до 40 ГГц. ч. 1. Методика расчета / Решение ГКРЧ от 26 сентября 2005 года № 05-08-02-001. [Электронный ресурс]. URL: http://docs.cntd.ru/document/901985364

9.       Методика расчета ЭМС основных типов (групп) РЭС систем СПС с другими типами (группами) РЭС гражданского назначения, работающими в общих полосах частот в диапазонах 160 МГц, 450 МГц, 900 МГц и 2 ГГц. [Электронный ресурс]. URL: http://minsvyaz.ru/common/upload/docs/20060228164040.pdf

10.  Методика расчета ЭМС систем абонентского радиодоступа и беспроводной передачи данных с другими РЭС гражданского применения на территории Российской Федерации, работающими в общих полосах частот в диапазоне от 1 ГГц до 30 ГГц. [Электронный ресурс]. URL:

http://minsvyaz.ru/common/upload/docs/20060228163741.pdf

11.  Технические средства радиосвязи. Взаимные радиопомехи в локальной группировке. Методы расчета: ГОСТ Р 55898-2013. – Введ. 2014-07-01.

12.  Альтер Л.Ш., Подманков И.И., Свириденко М.В. Расчет взаимных помех между проектируемыми и действующими радиосредствами на локальном объекте // T-Comm: Телекоммуникации и транспорт. 2009. Т. 3. № 1. С. 23–25.

13.  Бабкин А.Н., Шерстюков С.А. Исследование электромагнитной совместимости радиотехнических средств, расположенных в непосредственной близости друг от друга // Вестник Воронежского государственного технического университета. 2012. Т. 8, № 6. С. 14–16.

14.  Петров Б.М. Электродинамика и распространение радиоволн: учебник для вузов. М.: Радио и связь, 2000. 559 с.

15.  Рекомендация МСЭ-Р F.699-5. Эталонные диаграммы излучения антенн радиорелейных систем прямой видимости для использования при изучении вопросов координации и оценки помех в диапазоне частот от 1 до примерно 40 ГГц. [Электронный ресурс]. URL: http://www.itu.int/rec/R-REC-F.699-7-200604-I/en

16.  Рекомендация МСЭ-R F.1245-2. Математическая модель усредненных и родственных диаграмм направленности излучения антенн систем фиксированной беспроводной связи прямой видимости для связи пункта с пунктом, предназначенная для использования при изучении определенных вопросов координации и оценке помех в диапазоне частот от 1 ГГц примерно до 70 ГГц [Электронный ресурс]. URL: http://www.itu.int/rec/R-REC-F.1245-2-201203-I/en

17.  Recommendation ITU-R F.1336-4. Reference radiation patterns of omnidirectional, sectoral and other antennas for the fixed and mobile services for use in sharing studies in the frequency range from 400 MHz to about 70 GHz [Электронный ресурс]. URL: http://www.itu.int/rec/R-REC-F.1336-4-201402-I/en

18.  Рекомендация МСЭ-R P.525-2. Расчет ослабления в свободном пространстве [Электронный ресурс]. URL: http://www.itu.int/rec/R-REC-P.525-2-199408-I/en

19.  Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. 7-е изд. М.: ФИЗМАТЛИТ, 2004. 572 с.

20.  MATLAB. Exponenta. [Электронный ресурс]. URL: http://matlab.exponenta.ru/optimiz/book_4/5/fzero.php

21.  Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения: учеб. пособие для студ. втузов. 3-е изд., перераб. и доп. М.: Издательский центр «Академия», 2003. 464 с.