УДК 621.396.969

Метод обработки сигнала РЛС планового обзора, обеспечивающий повышенную разрешающую способность по азимуту

 

Е. В. Бессонова, В. И. Ирхин

Акционерное общество "Федеральный научно-производственный центр "Нижегородский научно-исследовательский институт радиотехники"

 

Статья поступила в редакцию 22 марта 2016 г., после доработки – 19 апреля 2016 г.

 

Аннотация. Исследован вопрос получения высокой разрешающей способности по угловым координатам в движущихся РЛС переднего и планового обзора. Рассмотрен метод обработки сигналов в подобных РЛС, позволяющий улучшить разрешающую способность по азимуту и сократить габариты антенной системы. Приведены результаты обработки рассмотренным методом данных, полученных экспериментально.

Ключевые слова: плановый обзор, разрешающая способность РЛС по азимуту, синтезированная апертура.

Abstract. The problem of obtaining high angle resolution of moving radars of forward and planned review is described. The method of signal processing in such radars which permits to improve the azimuth resolution and to reduce dimensions of antenna system is considered. Results of experimental data processing by given method are shown.  

Key words: planned review, azimuth resolution of radar, synthetic aperture.

 

Введение

Радиолокационные системы с синтезированной апертурой имеют широкое применение при решении задач инженерной разведки местности для обнаружения и определения координат малоразмерных объектов с габаритами порядка десятков сантиметров. В частности, могут применяться в радиолокационных системах (РЛС), позиционирующихся на беспилотных летательных аппаратах (БЛА) либо наземных шасси, для разведки минных полей. РЛС для решения таких задач должны обеспечивать хорошее разрешение в передней зоне обзора (вблизи линии пути) и непосредственно под носителем в случае с БЛА. Известно [1], что в РЛС с синтезированной апертурой при приближении зоны обзора к линии пути резко ухудшается разрешающая способность по азимуту. Устранить данный недостаток позволило использование РЛС планового обзора, основные преимущества которой достигались за счет длинной вдоль крыльевой антенной решетки в сочетании и с синтезированием апертуры (СА) вдоль линии пути (рис.1), что в результате давало высокую разрешающую способность по обеим угловым координатам [1, 2].

 

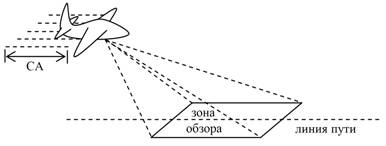
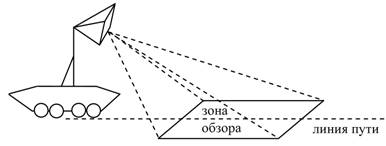
Рис.1 Варианты базирования РЛС планового обзора.

Однако размеры современных БЛА и требования к уменьшению массогабаритных характеристик РЛС не позволяют использовать антенные решетки, состоящие из большого числа элементов, что затрудняет получение высокой разрешающей способности по азимутальной координате. Поэтому целесообразно рассмотреть возможности дополнительной обработки сигнала, принимаемого малогабаритной РЛС планового обзора, в пределе состоящей из одного приемо-передающего элемента, для получения высокого разрешения по азимуту.

В данной работе представлен метод обработки эхо-сигнала от цели, в результате которой улучшается разрешающая способность по азимуту в малогабаритных РЛС планового обзора.

1. Постановка задачи

Пусть малогабаритная РЛС, в предельном случае состоящая из одного приемо-передающего элемента, ширина диаграммы направленности (ДН) которого составляет Δθ ≈ 90⁰, равномерно движется со скоростью v за счет носителя (рис.1) в заданном направлении на постоянной высоте H. Зондирующий сигнал РЛС представляет пачку импульсов с тактовой частотой следования F_такт. Длительность импульса, внутриимпульсная частота и вид модуляции зондирующего сигнала выбираются исходя из заданных требований к разрешающей способности РЛС по дальности, которые в настоящей работе не имеют принципиального значения. Поэтому полагаем, что на выходе оптимального приемника сигнал является простым с шириной спектра Δf.

Рассмотрим случай, когда цель расположена на поверхности земли на прямой, совпадающей с линией пути носителя РЛС, прямая дальность до цели составляет величину R. Особенность принимаемого сигнала в движущейся РЛС от неподвижной цели заключается в изменении фазы сигнала в соответствии с изменением взаимного расположения цели и РЛС. Сигнал, принятый за N тактов и сохраненный в устройстве обработки, может быть описан вектором S с компонентами , где – частота Доплера,  – временное положение m-го импульса пачки относительно её первого импульса, j – мнимая единица, m=1, 2,…,N. Фаза сигнала при переходе от (n-1)-го импульса к n-му импульсу описывается выражением

φ_n = 2πfτ_такт∙n,

где

,

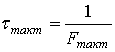F_такт – тактовая частота следования импульсов.

Будем считать, что за время, соответствующее N тактам, равное τ_такт∙N, носитель РЛС проходит расстояние D, много меньшее дальности до цели: D << R.

Это означает, что проекция скорости носителя РЛС на прямую, соединяющую РЛС и цель – наклонную дальность, v_r меняться практически не будет, соответственно, доплеровский сдвиг частоты сигнала, отраженного от цели в пределах отрезка D, останется неизменным.

Используя известное соотношение для доплеровского сдвига, можно переписать выражение для фазы φ_n в виде:

φ_n = 2k∙v_rτ_такт∙n = 2k∙d_r∙n,

где k = 2π/λ – волновое число, v_r – радиальная скорость движения РЛС относительно цели, d_r – проекция расстояния, на которое перемещается РЛС за время, равное длительности такта, на наклонную дальность. Само перемещение РЛС d можно найти, используя формулу .

 

Расстояние d≈d_r в случае, когда выполняется условие R>>H.

Рассматриваемая модель РЛС имеет достаточно широкую ДН антенны для увеличения сектора обзора пространства без механического или электронного сканирования по азимуту. Разность фаз между принятыми сигналами в соседних тактах соответствует разности фаз между соседними элементами антенной решетки с осевым излучением [3], причем расстояние между элементами подобной решетки составляет 2d_r. Теоретически при соответствующих параметрах простое суммирование принятых в разных тактах сигналов с учетом, что цель не выходит за элемент разрешения по дальности, может привести к обужению ДН антенны по азимуту до разме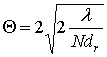ров , где N – число суммируемых тактов (элементов решетки), а при увеличении угла между направлением на цель и траекторией движения РЛС данная величина уменьшается до размеров 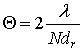, в соответствии с ДН аналогичных антенных решеток.

 

2. Модель сигнала, принимаемого плановой РЛС

Рассмотрим случай, когда проекция траектории движения РЛС на земную поверхность не проходит через точку, в которой расположена цель (рис.2а). Импульсы зондирующего сигнала, отраженные от цели, попадают на антенну под углом θ  в каждом такте в пределах расстояния D при выполнении условия D << R. Азимутальным направлением на цель можно считать угол θ_n – проекцию угла θ на поверхность земли, причем углы θ и θ_n связаны соотношением

.

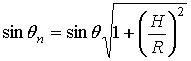При выполнении условия R>>H угол θ_n≈θ. Для упрощения дальнейших расчетов примем, что условие R>>H всегда выполняется. Тогда совокупность эхо-сигналов от цели, принятых за N тактов, эквивалентна совокупности сигналов, принимаемых одновременно N элементами линейной антенной решетки, на которую падает плоская электромагнитная волна, отраженная от цели, под углом θ (рис.2б).

 

        

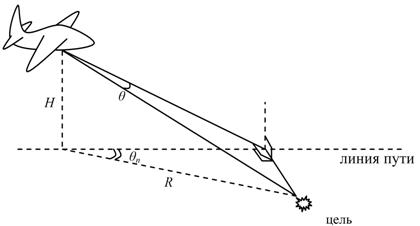
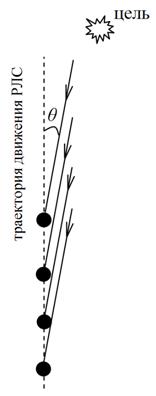
(а)                                                               (б)

Рис.2 Формирование эхо-сигнала от цели, сдвинутой относительно

 траектории движения РЛС

 

В этом случае сигнал, принятый за N тактов, может быть описан вектором S с компонентами

,                                                                               (1)

где θ – угол между траекторией РЛС и направлением на цель. Данное описание действительно в предположении, что сигнал, отраженный от цели, представляет собой плоскую волну в пределах отрезка Nd. Среди параметров фазы сигнала S_m неизвестен только угол θ, определение которого позволит улучшать азимутальное разрешение РЛС при соответствующей обработке последовательности принятых импульсов.

В общем виде, принятая за N тактов последовательность импульсов может быть записана в виде двумерной функции. Данная функция представляет зависимость амплитуды принятого эхо-сигнала от времени задержки эхо-сигнала и времени прихода очередного такта S(t_з, t_m). Время t_з определяет дальность до цели R в каждом такте по мере движения РЛС S_r(R), а время t_m, как показано выше, выражается зависимостью от угла θ и описывается выражением под экспонентой в (1). В силу независимости R и θ эхо-сигнал от цели в m-ом такте может быть представлен в виде произведения S_r(R_m)S_m, где R_m – дальность до цели в момент прихода m-го такта. Сигнал, принятый за N тактов, запишем в виде матрицы

.

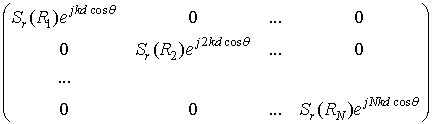Нулевые значения данной матрицы означают отсутствие сигнала от цели на данной дальности. Для неподвижных целей закон изменения дальности описывается уравнением движения носителя РЛС, поэтому, компенсируя миграцию цели по дальности и с учетом (1), получаем сигнал от цели, который описывается вектором S_S = S_r(R)S, S_r(R) – амплитуда сигнала, которую при небольшом N будем считать неизменной от такта к такту.

 

3. Метод обработки сигнала, принимаемого плановой РЛС

Для определения угла θ, выполним операцию матричного умножения вектор-строки S_S на вектор-столбец S₀ с компонентами , где , и нормируем полученное выражение на амплитуду сигнала. В результате получим функцию

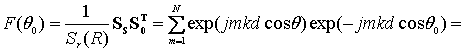
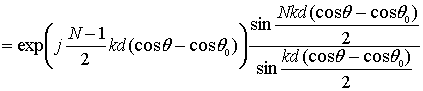                                                           (2)

где θ – искомый угол между траекторией РЛС и направлением на цель. Максимум функции F(θ₀) находится в точке θ, сама функция, как известно, представляет собой главный максимум, окруженный боковыми лепестками, амплитуда которых значительно меньшей главного максимума (рис.3).

 

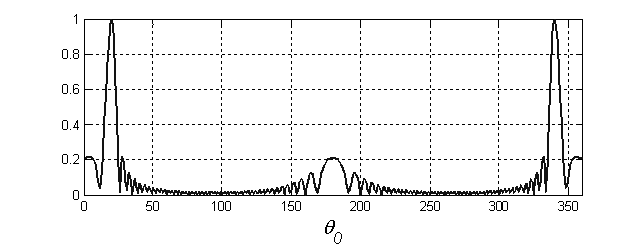
Рис.3 Функция F(θ₀) при θ = 20⁰.

         С учетом ДН антенной системы, максимум которой направлен по направлению движения РЛС, область углов [0⁰+Δθ/2, 360⁰-Δθ/2], не засвечиваемых ДН, можно исключить из рассмотрения. Неоднозначность на 2π‑θ возникает из-за осевой симметрии данных направлений относительно траектории РЛС (рис.4).

 

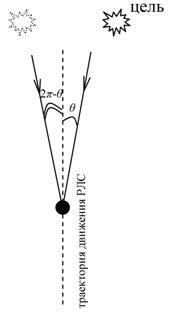
Рис.4 Симметричные относительно осевого направления цели, полученные в результате преобразования эхо-сигнала

 

         Способом устранения данного недостатка может служить применение интерферометра.

         Сходство функции F(θ₀) с формулой для ДН антенной решетки с электронным сканированием луча [4] доказывает, что точность измерения азимутальной координаты не имеет систематической ошибки измерения, связанной со способом обработки (при условии разделения истинного и симметричного ему лучей), а будет ограничиваться лишь шумовой ошибкой, определяемой как отношение величины элемента разрешения к отношению сигнал-шум [5].

 

4. Результаты компьютерного моделирования

         Оценим разрешающую способность РЛС по азимуту, получающуюся в результате данной обработки. Обрабатываемую последовательность импульсов, принимаемых движущейся РЛС в течение N тактов, в силу аналогии с обработкой сигналов в линейной антенной решетке (АР), назовем синтезируемой АР. С помощью компьютерного моделирования была получена зависимость ширины ДН по уровню 0.7 синтезируемой АР от азимута цели θ (рис.5) для отрезка перемещения РЛС L = Nd = 10м и длины волны зондирующего сигнала λ = 1.5м. Синтезируемая АР с данными параметрами имеет ДН по уровню 0.7 θ_0.7 = 33⁰ при θ близком к нулю (то есть цель расположена на линии пути), а для больших θ ≈ 40⁰-45⁰ - θ_0.7 = 6⁰.

 

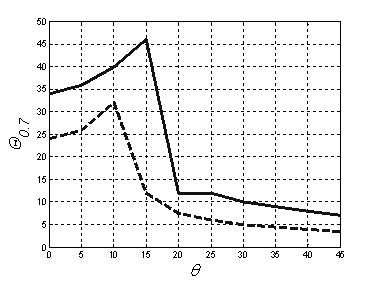
Рис.5 График зависимости элемента разрешения синтезированной АР θ_0.7

от угла между траекторией РЛС и направлением на цель θ

для различных размеров синтезированной АР:

L = 10м - сплошная, L = 20м – штриховая.

 

Более точную оценку ширины ДН по нулям θ₀ можно оценить из анализа выражения (2), находя θ₀ при F(θ₀)=0. Ширина главного максимума будет равна:

 

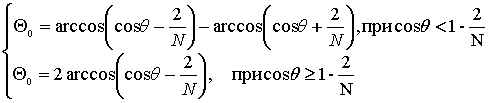      (3)

 

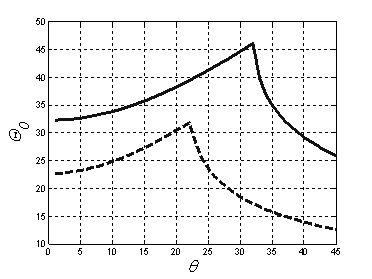
Рис.6 График зависимости выражения (3) θ₀(θ) для различных размеров синтезированной АР: L = 10м - сплошная, L = 20м – штриховая.

Излом графиков зависимостей Θ_0.7(θ) (рис.5) и Θ₀(θ) (рис.6) определяется углом θ, в котором элемент разрешения по азимуту имеет максимальное значение, когда симметричные максимумы функции F(θ₀) невозможно разделить по уровню 0.7 для Θ_0.7(θ) и по нулям для Θ₀(θ). При малых углах θ происходит ухудшение элемента разрешения, связанное с невозможностью разделить два максимума, которые получаются вследствие неоднозначности измерения азимута предложенным способом. То есть максимумы функции F(θ₀), соответствующие истинной и симметричной ей целей, при малых углах начинают раздвигаться, но из-за недостаточно малой ширины еще не разделяются (рис.7).

 

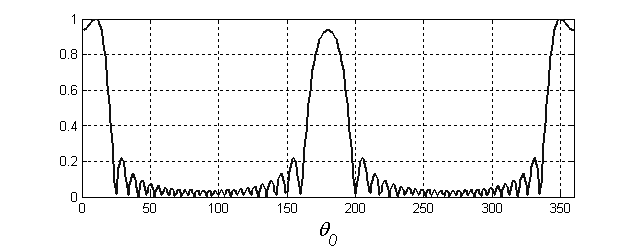
Рис.7 Иллюстрация эффекта увеличения ДН синтезированной АР при небольших углах
между траекторией РЛС и направлением на цель θ (θ = 10⁰, L = 20м)

         Анализ зависимостей, изображенных на рис.5 и рис.6, показывает, что для увеличения разрешения, в том числе для разрешения целей при малых углах θ₀, необходимо увеличивать длину синтезируемой АР L, что на практике достигается путем увеличения времени синтезирования.

 

5. Результаты обработки данных, полученных в натурном эксперименте

Обработка эхо-сигналов от реальных целей показывает возможность применения предлагаемого метода формирования и обработки синтезированной АР на практике. На рис.7 показаны результаты обработки с различной длиной синтезируемой АР.

 

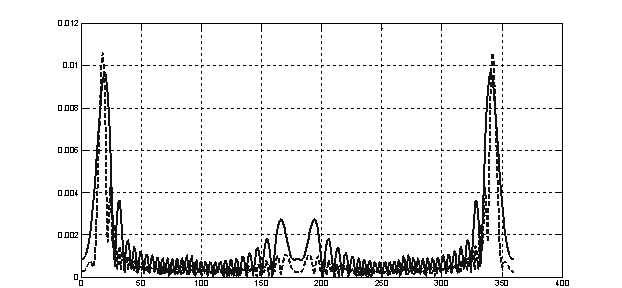
Рис.7 Экспериментальные результаты синтезирования АР вдоль линии пути

при L = 6м - сплошная, L = 14м – штриховая.

Данные результаты совпадают с теоретическими выводами, то есть увеличение размеров синтезируемой АР обеспечивает увеличение разрешающей способности РЛС по азимуту.

Выводы

Таким образом, предложенный в данной работе метод обработки эхо-сигналов от цели, расположенной вблизи линии пути движущейся РЛС, позволяет добиться высокой разрешающей способности по азимуту, не прибегая к увеличению габаритов антенны.

 

Литература

1       Кондратенков Г.С., Потехин В.А., Реутов А.П., Феоктистов Ю.А. Радиолокационные станции обзора Земли. М.: Радио и связь, 1983, 272с.

2       Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли. М.: Радиотехника, 2005, 368с.

3       Никольский В.В. Антенны. М.: Связь, 1966, 367с.

4       Шифрин Я.С. Антенны. Издание академии, 1976, 407с.

5       Бартон Д. Радиолокационные системы. М.: Военное издательство, 1967, 480с.