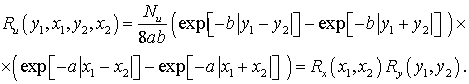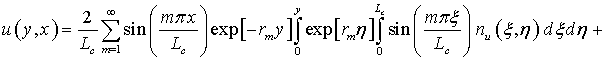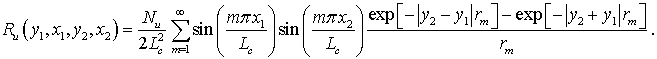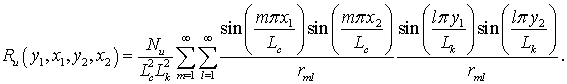УДК 621.391

Модели радиолокационных изображений на основе дифференциальных уравнений в частных производных

 

С. А. Лепешкин, А. П. Кадочников, В. Я. Пророк

Военно-космическая академия имени А.Ф.Можайского

 

Статья поступила в редакцию 8 апреля 2016 г.

 

Аннотация. Представлены результаты выбора параметров и анализа моделей радиолокационных изображений, полученных в результате решения линейных дифференциальных уравнений в частных производных второго порядка: гиперболического, параболического, эллиптического.

Ключевые слова: система радиовидения, дифференциальные уравнения в частных производных.

Abstract. The results of experimental selection of parameters and analysis of models of radar images are presented. The results have been obtained by solution of boundary problems of mathematical physics on the basis of differential equations in partial derivatives.

Key words: the system of radio vision, differential equation in partial derivatives.

 

Введение

В настоящее время существует тенденция представления изображений различной природы, в том числе и радиолокационных изображений (РЛИ), в виде случайных полей.

Выбор математической модели в виде случайного поля, отражающей свойства РЛИ, является необходимым этапом при разработке устройств предварительной обработки таких изображений в системах радиовидения [1]. С одной стороны, выбираемая модель должна быть достаточно простой, чтобы обеспечить возможность технической реализации устройства обработки, с другой  –  математическая модель должна как можно полнее отражать свойства РЛИ, чтобы обеспечить высокое качество обработки. Системы радиовидения позволяют получать РЛИ независимо от времени суток, освещенности, в сложных метеорологических условиях. Существует два метода формирования РЛИ: прямое и обратное синтезирование апертуры антенны [2], которые предполагают движение либо носителя системы зондирования, либо объекта наблюдения.

Следует отметить, что формирование (восстановление) РЛИ на основе принимаемого траекторного сигнала [3] является задачей в математическом смысле некорректной [4, 5], т.е. бесконечно малым приращениям входного воздействия (траекторного сигнала) могут соответствовать бесконечно большие приращения результата восстановления. При этом возникает необходимость регуляризации решения – существенного уменьшения разброса решений относительно истинного значения.

В [6] предложен метод оптимальной обработки случайных полей применительно к задачам восстановления изображений в радиолокационных системах мониторинга земной поверхности, основанный на байесовском подходе, где в качестве регуляризирующей функции используется априорная корреляционная функция модели восстанавливаемого РЛИ.

Таким образом, задача выбора и обоснование адекватности математической модели РЛИ в виде случайного поля с требуемыми вероятностными характеристиками является актуальной.

 

1. Постановка задачи

Исходя из физических соображений, плоское РЛИ можно представить в виде поля значений яркости. Такое поле можно задать функцией трех переменных , где  – время;  – пространственные координаты. Значения функции  определяют меняющуюся во времени яркость изображения в каждой точке пространства [7].

Для описания математической модели поля РЛИ  целесообразно воспользоваться аппаратом стохастических дифференциальных уравнений в частных производных, который непосредственно указывает способ генерации реализаций поля, а также позволяет производить анализ вероятностных характеристик получаемых моделей. Исходя из этого, целесообразно ограничиться хорошо изученными уравнениями математической физики [8, 9]. Известно, что к основным уравнениям математической физики относятся три типа линейных дифференциальных уравнений в частных производных второго порядка: гиперболические, параболические, эллиптические.

В ходе исследований, проведенных в работе [7], установленно, что с помощью трех типов моделей (на основе гиперболического, параболического и эллиптического дифференциальных уравнений в частных производных) можно описать различные по характеру оптические изображения, а также выявлена связь между типом изображения и вероятностными характеристиками модели.

Однако специфика дифракции электромагнитных волн радиодиапазона на поверхности искусственных объектов сложной формы определяет особенности РЛИ. К данным особенностям относятся [10]:

– «дробление» РЛИ распределенных объектов, вызываемое зеркальным отражением падающих под малыми углами радиоволн в сторону от системы радиовидения большинством плоских поверхностей искусственных объектов;

– затенение части поверхности распределенных объектов их выступающими по высоте деталями;

– блики на РЛИ, образующиеся за счет очень интенсивных отражений, которые дают зеркальные плоские поверхности при нормальном падении на них электромагнитных волн, а также выпуклые и вогнутые поверхности объектов;

– интерференционные искажения, обусловленные флуктуациями яркости элементов изображений по площади распределенных объектов (спекл-изображения), образуются в силу когерентности отраженных сигналов РЛИ;

– появление ложных отметок на РЛИ, к которым приводят ошибки дискретизации сигналов в системе радиовидения.

В силу отмеченных особенностей необходимо провести выбор параметров и анализ адекватности моделей РЛИ на основе дифференциальных уравнений в частных производных.

 

2. Анализ дифференциальных уравнений в частных производных

Гиперболическое уравнение

В [11] для описания моделей двумерных случайных полей предлагается использовать дифференциальные уравнения в частных производных гиперболического типа. Рассмотрим, как один из вариантов этих моделей, краевую задачу вида

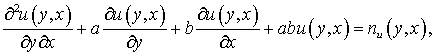                    (1)

где

Здесь  – белое гауссовское шумовое поле с известными характеристиками

,                                                                                (2)

;                             (3)

где .

Для решения уравнения (1) применен метод замены переменных [11]. В результате решение краевой задачи (1) будет иметь вид

      (4)

 

Поскольку входное воздействие  является гауссовским, а уравнение (1) – линейным, то и поле  также будет гауссовским. Следовательно, исчерпывающими статистическими характеристиками  являются математическое ожидание и корреляционная функция.

С учетом (2) и (4) определим математическое ожидание поля :

                                   (5)

Тогда корреляционная функция модели изображения будет определяться как

         (6)

Подставив (4) в (6) и выполнив операцию усреднения, получим

               (7)

Из (7) видно, что корреляционная функция  факторизуется и может быть представлена в виде произведения двух корреляционных функций по различным координатам, т.е. для данной модели значения поля по координатам  и  независимы. Кроме того, выражение (7) свидетельствует о наличии причинных связей между значениями поля по обеим координатам, так как корреляционная функция убывает с увеличением расстояния между значениями поля по каждой координате.

Таким образом, гиперболическое уравнение относится к классу каузальных моделей.

Параболическое уравнение

Рассмотрим одну из краевых задач для уравнения параболического типа

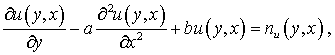                                          (8)

где  – длина строки изображения.

Используя метод функций Грина [12], получено решение краевой задачи (8), которое определяться выражением

 

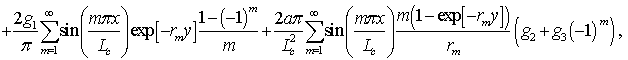    (9)

 

где

 

Определяя статистические характеристики, получим, что математическое ожидание поля равно сумме второго и третьего членов в правой части (9), а корреляционная функция будет иметь вид

  (10)

 

Из анализа (10) можно сделать вывод об отсутствии у параболических моделей причинных связей между значениями поля изображения по координате , так как степень корреляционной зависимости значений поля определяется не столько расстоянием между этими значениями по координате , сколько их взаимным расположением на этой координате. Следовательно, параболические уравнения относятся к классу полукаузальных моделей.

Эллиптическое уравнение

Из широкого круга краевых задач для эллиптических уравнений рассмотрим краевую задачу, которая по своей физической сути может быть использована для описания РЛИ

                                     (11)

где  и  – длина строки и длина кадра изображения соответственно.

Для решения краевой задачи (11) используем метод Фурье. В результате получим

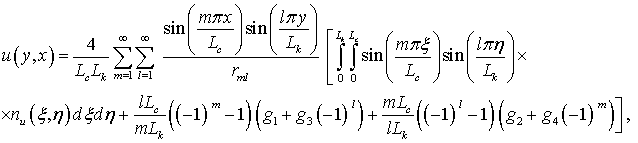(12)

где

 

Определяя по аналогии с предыдущими случаями корреляционную функцию эллиптической модели, получим

         (13)

Как видно из (13), эллиптические модели являются некаузальными по обеим координатам. Для полей, описываемых такими моделями, характерным является то, что наиболее коррелированными являются те значения поля, которые расположены ближе к центру плоскости .

Понятие каузальности тесно связано с типом изображения. Так, для каузальных изображений наличие причинно-следственных связей во всех направлениях обеспечивает однородность всего изображения, т.е. отсутствие особенностей в каком-либо направлении. К таким изображениям можно отнести, например, РЛИ лесного массива, морской поверхности и др. Отсутствие каузальности приводит к возникновению неоднородностей (особенностей) в изображении на каких-либо участках. Изображениями некаузального типа будут являться, например, РЛИ одиночных и групповых объектов (самолеты, танки, пусковые установки и др.), РЛИ крупномасштабных объектов на различных фонах (корабли, авианосцы), РЛИ, полученные системами радиовидения с обратным синтезированием апертуры антенны и т.п.

Таким образом, установлено, что с помощью трех типов моделей можно описать различные по характеру РЛИ, а также установлена связь между типом РЛИ и статистическими характеристиками модели.

 

3. Выбор параметров моделей радиолокационных изображений

Более точный выбор моделей и их параметров осуществлялся путем сравнения статистических характеристик РЛИ и моделей. Так, на основе моделирования в свободно распространяемой интегрированной среде разработки MATLAB, был проведен анализ соответствия предлагаемых моделей некоторым реальным РЛИ. Для этого использовались два изображения различного типа: РЛИ земной поверхности (полученное методом прямого синтезирования апертуры антенны), рисунок 1а и РЛИ космического объекта (полученное методом обратного синтезирования апертуры антенны), рисунок 1б. Эти изображения были представлены в цифровом виде размером 500 500 пикселов для обработки на ЭВМ.

 

  

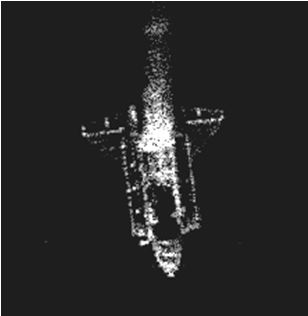
а)                                                       б)

Рис. 1. РЛИ, полученные методами прямого и обратного синтезирования апертуры антенны

Так как в данном случае речь идет о конкретном изображении, то в качестве его статистической характеристики использовано следующее определение корреляционной функции

                                                         (14)

 

где .

Здесь  – значение «яркости» n-го РЛИ в точке с координатами
 – количество элементов изображения по вертикали и горизонтали соответственно;  – операция усреднения по всем N изображений в точке с координатами  N – количество частей РЛИ (реализаций модели), используемых при статистической обработке.

Количество частей РЛИ (реализаций моделей), применяемых для расчета статистической корреляционной функции , было рассчитанно путем моделирования. Для расчета N было выбрано параболическое уравнение.

Степень соответствия статистической  и аналитической  корреляционной функции параболической модели определялась методом среднеквадратичной ошибки (СКО) [13]

                                                       (15)

 

На рисунке 2 приведены примеры реализаций параболической модели, полученной на основе решения уравнения (9). Рисунок 2а с параметрами модели a=0,01; b=2,23. Рисунок 2б с параметрами модели a=0,10; b=2,34.

 

  

а)                                                         б)

Рис. 2. Примеры реализаций модели РЛИ в виде случайного поля

 

Результаты математического моделирования представлены в таблице 1 и на рисунке 3.

Таблица 1. Значения СКО аналитической и статистической корреляционных функций параболической модели

№	1	2	3	4	5	6	7	8	9	10
N	16	32	64	128	256	512	1024	2048	4096	8192
	0,4591	0,2910	0,1429	0,0865	0,0537	0,0259	0,0150	0,0132	0,0124	0,0113

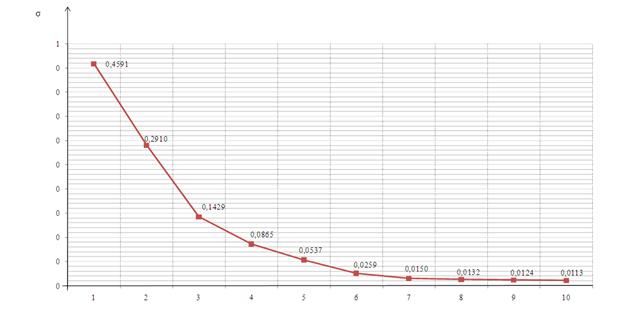
Рис. 3. Зависимость значений СКО аналитической и статистической корреляционных функций полукаузальной модели от количества реализаций.

 

Внешний вид корреляционной функции, рассчитанной статистически, для различных значений N (согласно таблице 1) показан на рисунке 4. Внешний вид аналитической и статистической корреляционной функции  параболической модели при количестве реализаций N=8192 представлен на рисунке 5.

 

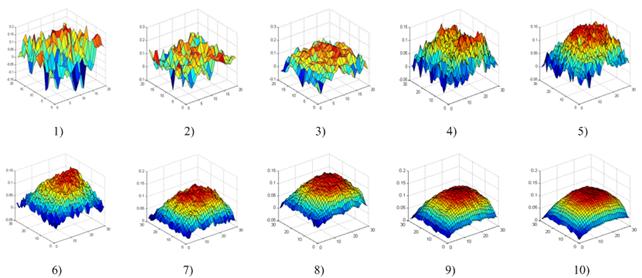
Рис. 4. Внешний вид статистической корреляционной функции  полукаузальной модели в зависимости от количества реализаций.

 

 

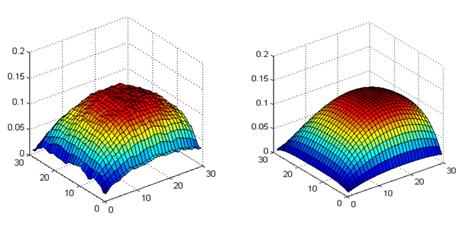
а)                                                       б)

Рис.5. Внешний вид статистической и аналитической корреляционной функции полукаузальной модели при количестве реализаций N=8192.

 

При N=1024...8192 значение СКО аналитической и статистической корреляционных функций параболической модели становится практически неизменным. Таким образом, при математическом моделировании количество частей РЛИ, применяемых для расчета корреляционной функции , было выбрано равным N=1024.

Для обработки на ЭВМ статистический материал по РЛИ земной поверхности (рисунок 1а) и РЛИ космического объекта (рисунок 1б) был представлены числовым массивом данных размером  пикселей (в виде трехмерной матрицы), каждый из которых определялся градацией яркости из диапазона [0;255]. Порядок набора статистического материала по РЛИ показан на рисунках 6, 7.

 

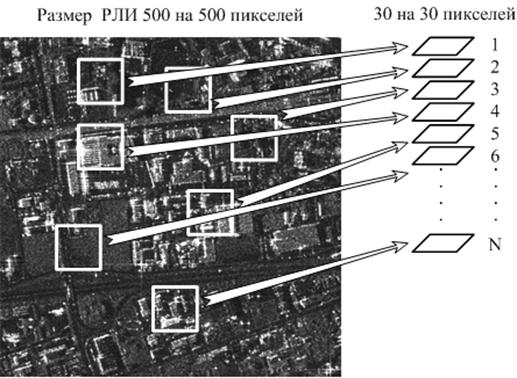
Рис. 6. Порядок набора статистического материала по РЛИ, полученному методом прямого синтезирования апертуры антенны

 

Рис. 7. Порядок набора статистического материала по РЛИ, полученному методом обратного синтезирования апертуры антенны

 

На основе критерия (15) производилось сравнение корреляционных функций математических моделей (7, 10, 13) и РЛИ (14). Минимизация  производилась по параметрам моделей (рисунок 8а, б, в). Результаты расчета приведены в таблице 2.

 

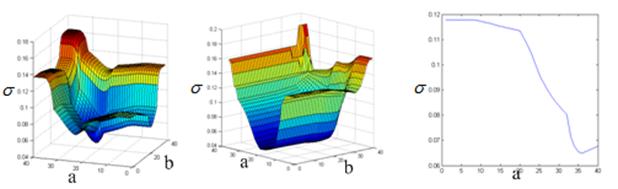
Рис.8. Минимизация СКО  по параметрам моделей a и b: гиперболической (а), параболической (б), эллиптической (в).

 

Таблица 2. Параметры математических моделей РЛИ при минимальном СКО

Тип изображения	Тип модели	Параметры модели
РЛИ полученное методом прямого синтезирования апертуры антенны (рисунок 1а)	каузальная	a=b=0,07	0,0436
	полукаузальная	a=0,11; b=2,03	0,0427
	некаузальная	a=1,21	0,0650
РЛИ полученное методом обратного синтезирования апертуры антенны (рисунок 1б)	каузальная	a=b=0,09	0,2262
	полукаузальная	a=0,14; b=1,11	0,1619
	некаузальная	a=0,81	0,0728

 

Из анализа результатов математического моделирования, приведенных в таблице 2, следует, что они не противоречат теоретическим положениям. Так, полукаузальная и каузальная модели достаточно хорошо описывают РЛИ, полученные методом прямого синтезирования апертуры антенны, а некаузальная модель – РЛИ, полученные методом обратного синтезирования апертуры антенны.

 

Выводы

Таким образом, приведенные рассуждения и результаты имитационного моделирования позволяют сделать несколько выводов:

1.   С помощью трех типов моделей можно описать различные по характеру РЛИ.

2.   Модели на основе гиперболического и параболического дифференциальных уравнений в частных производных достаточно хорошо описывает РЛИ, полученные методом прямого синтезирования апертуры антенны.

3.   Модель на основе эллиптического дифференциального уравнения в частных производных достаточно хорошо описывает РЛИ, полученные методом обратного синтезирования апертуры антенны.

4.   Модели, полученные в результате решения линейных дифференциальных уравнений в частных производных второго порядка: гиперболического, параболического, эллиптического, целесообразно использовать при разработке устройств оптимального восстановления изображений в системах радиовидения.

5.   Возможность подбора параметров модели для минимизации СКО позволяет синтезировать адаптивные алгоритмы восстановления изображений в системах радиовидения.

 

Литература

1. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли. Учебное пособие для вузов / Под ред. Г.С. Кондратенкова. – М.: Радиотехника, 2005. – 368 с.

2. Антипов В.Н. Радиолокационные станции с цифровым синтезированием апертуры антенны / В.Н. Антипов, В.Т. Горяинов [и др.]. – М.: Радио и связь, 1988. – 304 с.

3. Фалькович С.Е., Пономарев В.И., Шкварко Ю.В. Оптимальный прием пространственно-временных сигналов в радиоканалах с рассеянием / Под ред. С.Е. Фальковича. – М.: Радио и связь, 1989. – 296 с.

4. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Учебное пособие для вузов. Изд. 3-е, исправленное.– М.: Наука, 1986. – 288 с.

5. Василенко Г.И., Тараторин А.М. Восстановление изображений. – М.: Радио и связь, 1986. – 304 с.

6. Коренной А.В., Лепёшкин С.А. Оптимальное восстановление изображений в радиолокационных системах мониторинга земной поверхности // Радиотехника. – 2010. – № 11.– C. 6-9.

7. Коренной А.В. Математические модели полутоновых изображений // Радиотехника. – 2007. – № 8. – С. 79-81.

8. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Издательство МГУ, 1999. – 799 с.

9. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. – М.: Высшая школа, 1970. – 712 с

10. Школьный Л.А., Радиолокационные системы воздушной разведки, дешифрирование радиолокационных изображений. – М.: изд. ВВИА им. проф. Н.Е. Жуковского, 2008. – 531 с.

11. Ярлыков М.С., Моисеенко Ю.Н. Математические модели гауссовских  случайных полей в виде стохастических дифференциальных уравнений  в частных производных // Авиационные радиоэлектронные комплексы и их эксплуатация. Научно-методические материалы. - М.: ВВИА, 1988.

12. Бутковский А.Г. Характеристики систем с распределенными параметрами. – М.: Наука, 1979. – 114 с.

13. Кокошкин, А. В. Сравнение объективных методов оценки качества изображений [Электронный ресурс] / Кокошкин А.В., Коротков В.А., Коротков К.В., Новичихин Е.П. – М.: Журнал радиоэлектроники [электронный журнал]. – 2015. – №6. – Режим доступа: http://jre.cplire.ru/jre/jun15/15/text.pdf.