| "JOURNAL OF RADIOELECTRONICS" N 8, 2000 |
INTERACTION OF SUPER STRONG ELECTROMAGNETIC PULSE WITH DENSE PLASMA LAYER.
Anton
S. Il'in![]() , Victor
V. Kulagin
, Victor
V. Kulagin![]() , Vladimir
A. Cherepenin
, Vladimir
A. Cherepenin![]() and S.L. Ziglin1
and S.L. Ziglin1
![]() Institute
of Radioengineering and Electronics RAS, Moscow, Russia
Institute
of Radioengineering and Electronics RAS, Moscow, Russia
![]() Sternberg Astronomical
Institute, Moscow State University, Moscow, Russia
Sternberg Astronomical
Institute, Moscow State University, Moscow, Russia
Received August 16, 2000
An interaction of a super strong linear-polarized electromagnetic wave with a dense plasma layer is investigated with the help of a self-consistent method of the analysis. It is shown that at falling a powerful harmonic wave at a thin plasma layer the reflected field can be in the form of ultrashort pulses of radiation with amplitude considerably larger than an amplitude of an incident wave. A process of interaction of a plasma layer with a standing electromagnetic wave is considered also and a generalization of classical results about character of an electron motion in an electromagnetic field is obtained for a case of a strong field and large radiation friction. In a strong field a minimum of an effective potential splits into two new that results in violation of a mirror symmetry of plasma layer radiation.
Keywords: Ultrashort pulse, plasma layer, laser-plasma interaction, radiation friction, radiation field
Introduction.
Recently large attention is given to the problems of
generation of powerful ultrashort pulses and coherent electromagnetic radiation
of high (up to x-ray) frequency through an interaction of a superstrong laser
radiation with a solid target [1-6]. The
reason for occurrence of high harmonics in a spectrum of reflected wave is the
following: at falling a powerful electromagnetic wave with intensity ![]() on a target the electron plasma with large density (about the order of
on a target the electron plasma with large density (about the order of ![]()
![]() )
is formed on its boundary, the electrons of this plasma layer move not only in
transversal direction but also commit the longitudinal vibrations at a double
frequency under the action of magnetic component of the incident wave. There are
two approaches now to the solution of such problems. First is based on a direct
numerical simulation of Maxwell equations for process of interaction of plasma
and powerful electromagnetic wave by a particle-in-cell method [2,4]
and has all known lacks intrinsic to numerical experiments of such kind:
technical complexity, difficulty of interpretation and selection of the physical
solutions etc. In the second approach the simplified description permitting to
receive analytical expressions is used. The model of an oscillating mirror is
usually considered [1], in which the high harmonics in the
reflected wave arise due to the periodic modulation of its phase:
)
is formed on its boundary, the electrons of this plasma layer move not only in
transversal direction but also commit the longitudinal vibrations at a double
frequency under the action of magnetic component of the incident wave. There are
two approaches now to the solution of such problems. First is based on a direct
numerical simulation of Maxwell equations for process of interaction of plasma
and powerful electromagnetic wave by a particle-in-cell method [2,4]
and has all known lacks intrinsic to numerical experiments of such kind:
technical complexity, difficulty of interpretation and selection of the physical
solutions etc. In the second approach the simplified description permitting to
receive analytical expressions is used. The model of an oscillating mirror is
usually considered [1], in which the high harmonics in the
reflected wave arise due to the periodic modulation of its phase: ![]() ,
where
,
where ![]() - is a
frequency of an incident wave and
- is a
frequency of an incident wave and ![]() is its initial phase. The incompleteness of such approach is due to the facts
that, at first, the mirror is supposed to be absolutely reflecting, secondly,
the time dispersion and dynamic relativistic effects are omitted. Besides the
form of mirror oscillations in such approach is supposed to be harmonic that,
generally speaking, does not correspond to the precise solution of
self-consistent equations of motion for the plasma layer. At the same time at
ultra relativistic amplitude of an external field when the work of a field on
the wavelength becomes considerably larger than the rest energy of the electron
(accelerating parameter
is its initial phase. The incompleteness of such approach is due to the facts
that, at first, the mirror is supposed to be absolutely reflecting, secondly,
the time dispersion and dynamic relativistic effects are omitted. Besides the
form of mirror oscillations in such approach is supposed to be harmonic that,
generally speaking, does not correspond to the precise solution of
self-consistent equations of motion for the plasma layer. At the same time at
ultra relativistic amplitude of an external field when the work of a field on
the wavelength becomes considerably larger than the rest energy of the electron
(accelerating parameter ![]() ),
the indicated effects should play an essential role. Actually at reflection of a
wave from a mirror moving towards with constant speed the reflected amplitude is
proportional to the factor
),
the indicated effects should play an essential role. Actually at reflection of a
wave from a mirror moving towards with constant speed the reflected amplitude is
proportional to the factor![]() ,
where
,
where ![]() is the
ratio of mirror speed to the speed of light in vacuum
is the
ratio of mirror speed to the speed of light in vacuum ![]() [7]. In essentially relativistic regimes of interaction of the
electromagnetic wave with the plasma layer (
[7]. In essentially relativistic regimes of interaction of the
electromagnetic wave with the plasma layer (![]() ,
,![]() )
the form of the reflected field can evidently has a strong dependence on the
amplitude factor
)
the form of the reflected field can evidently has a strong dependence on the
amplitude factor ![]() .
.
The essential results describing the process of reflection of the powerful (ultra relativistic) electromagnetic wave from the plasma layer can be obtained within the framework of electron sheets model [8]. This model gives the consistent microscopic description of plasma layer interaction with electromagnetic waves and allows to solve many self-consistent problems about interaction of fields with charged medium. Especially simple equations of motion can be obtained in the case of small width of the plasma layer (considerably less than the wavelength of the incident radiation) when in the model it is possible to use one sheet only. Just this case will be considered in the present paper.
In particular it will be shown that at ultra relativistic
amplitudes of the external field the reflected wave has essentially nonharmonic
character: there is a synchronous radiation of harmonics of the incident wave
frequency. Namely the sinusoidal incident wave can be converted into a sequence
of short pulses of electromagnetic radiation with large amplitude. Thus due to
the enrichment with the harmonics the decrease of each pulse duration takes
place and the amplitude of pulses can essentially exceed the amplitude of the
incident wave. The process of interaction of the plasma layer with a standing
linear-polarized electromagnetic wave will be considered also and the
generalization of the classical results about the character of electron motion
in electromagnetic field [9] for the case of the strong field
and large electron concentration (large radiation friction) will be obtained. It
appears that in the strong electromagnetic field (![]() )
each minimum of an effective potential splits into two new minima. It results in
violation of a mirror symmetry of plasma layer radiation and dependence of the
stationary state on the initial conditions due to essentially non-linear
character of electron’s oscillations.
)
each minimum of an effective potential splits into two new minima. It results in
violation of a mirror symmetry of plasma layer radiation and dependence of the
stationary state on the initial conditions due to essentially non-linear
character of electron’s oscillations.
For simplicity in the following analysis we shall consider that an ion background is fixed and electron concentration in plasma is large enough, so that the frequency of an external field will be much less than plasma characteristic frequency. Besides we shall consider that the initial velocity of the electrons is zero (approximation of a cold plasma).
1. Model and main equations.
Let consider a charged medium homogeneous in directions
perpendicular to Oz axis. In this case the densities of charge ![]() and current
and current ![]() depend only on
depend only on ![]() and are independent on
and are independent on ![]() and
and ![]() . Formal
solutions of Maxwell equations can be in this case obtained by a method of a
Green function and look like [8]:
. Formal
solutions of Maxwell equations can be in this case obtained by a method of a
Green function and look like [8]:
Here [ , ] is the sign of a vector product.
Let now consider a thin layer of electrons extended in x and
y-direction with the width considerably smaller than the wavelength of the
incident radiation. In this case the layer is equivalent to an infinitely thin
charged sheet the dynamics of which can be described by 3 + 1 functions of time:
three components of speed ![]() and one space coordinate
and one space coordinate ![]() (fig.1).
(fig.1).
Figure. 1. (3 + 1) - model of electron sheet.
The densities of charge and current of such sheet have the form:
where ![]() is the surface density of charge.
is the surface density of charge.
Substituting now expressions (2) in
equations (1) and integrating over ![]() and
and ![]() , one can obtain the
following expressions for the components of electromagnetic field:
, one can obtain the
following expressions for the components of electromagnetic field:
where ![]() ,
,
![]() ,
, ![]() and the "delaying" time
and the "delaying" time ![]() is determined from the equation
is determined from the equation ![]() .
.
It is worth to mention that the expressions (3)
are one dimensional (or, more precisely, 3 + 1 dimensional) analogues of the
classic Lienar-Wihert solutions [7] and give the exact
expressions for the field created by the infinite plane. Here the component ![]() can be interpreted as a near field and component
can be interpreted as a near field and component ![]() as a field of radiation.
as a field of radiation.
Let consider an expression for a spectral component of the
radiation field ![]() .
Substituting into equation
.
Substituting into equation
the expressions for the field (1), one can receive
where ![]() and
and ![]() . Then
using expression for the current density according to (2) one
can obtain:
. Then
using expression for the current density according to (2) one
can obtain:
For periodic (with period ![]() )
motion of the plane the spectral decomposition of the radiation field contains
only components at frequencies
)
motion of the plane the spectral decomposition of the radiation field contains
only components at frequencies ![]() with values
with values
Let consider now an influence of the radiation field (3) on the motion of the electron sheet. It follows from expressions (3) that the interaction of the electron sheet with the own radiation field results in appearance of a specific self-action force [8]:
I.e. there is effective viscous force (8)
with a constant coefficient of viscosity 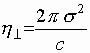 for transversal motion and non-linear coefficient of viscosity
for transversal motion and non-linear coefficient of viscosity 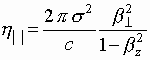 for longitudinal motion.
for longitudinal motion.
The equations of motion for a separate electron of the sheet in homogeneous along x and y fields look like:
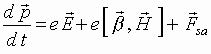 ,
,
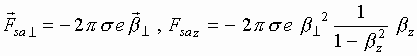 (9)
(9)
Here ![]() is the relativistic momentum of the electron and
is the relativistic momentum of the electron and ![]() is its charge.
is its charge.
2. Given longitudinal motion of the plasma sheet.
Let at first consider a given longitudinal motion ![]() of the sheet. For transversal motion of the sheet in a field
of the sheet. For transversal motion of the sheet in a field ![]() (normal falling of the linear-polarized wave at the plasma layer) one has from
equations (9):
(normal falling of the linear-polarized wave at the plasma layer) one has from
equations (9):
Let for simplicity the surface density of charge ![]() is large enough. In this case the sheet is practically an ideal mirror and, as
was shown in Ref. [8], it is possible to neglect the inertial
(dispersion) term
is large enough. In this case the sheet is practically an ideal mirror and, as
was shown in Ref. [8], it is possible to neglect the inertial
(dispersion) term ![]() in equation (10) (strictly speaking, the larger
in equation (10) (strictly speaking, the larger ![]() the greater should be the surface density
the greater should be the surface density ![]() for the sheet be the ideally reflecting mirror). Under these conditions the
expression for the reflected wave has according to (3) the
following form:
for the sheet be the ideally reflecting mirror). Under these conditions the
expression for the reflected wave has according to (3) the
following form:
Note that the expression for the amplitude Doppler factor ![]() in this case appears valid not only for uniform motion but also for arbitrary
dependence
in this case appears valid not only for uniform motion but also for arbitrary
dependence ![]() with replacement of t by the delaying time
with replacement of t by the delaying time ![]() .
.
Let now the dependence of the longitudinal velocity on time
is determined by an expression ![]() (a phase difference between the mirror oscillations and electromagnetic wave is
determined by the value
(a phase difference between the mirror oscillations and electromagnetic wave is
determined by the value ![]() ).
From (11) it follows that for
).
From (11) it follows that for ![]() the function A has a form of infinitely high pulses at the double
frequency. The amplitude modulation of the reflected field due to the factor
the function A has a form of infinitely high pulses at the double
frequency. The amplitude modulation of the reflected field due to the factor ![]() (cf. (11)) essentially enriches for
(cf. (11)) essentially enriches for ![]() the radiation spectrum so the shape of the reflected wave considerably differs
from a sine wave. In fig. 2 the time dependence of the reflected field is
displayed for different values of
the radiation spectrum so the shape of the reflected wave considerably differs
from a sine wave. In fig. 2 the time dependence of the reflected field is
displayed for different values of ![]() .
.
Figure. 2. Reflected field ![]() for
for ![]() (à) ;
0.9 (b); 0.99 (c).
(à) ;
0.9 (b); 0.99 (c).
There is a large number of odd harmonics of base frequency ![]() in the reflected wave and the closer is
in the reflected wave and the closer is ![]() to unit the more harmonics is involved in the formation of the reflected wave.
The principle point is the rigid binding for the phases of all harmonics to the
phase of the incident wave. As a result all harmonics are added synchronously
and the reflected field has the form of short pulses of radiation following with
frequency
to unit the more harmonics is involved in the formation of the reflected wave.
The principle point is the rigid binding for the phases of all harmonics to the
phase of the incident wave. As a result all harmonics are added synchronously
and the reflected field has the form of short pulses of radiation following with
frequency ![]() with the amplitude directly proportional to the number of harmonics and with
duration inversely proportional to that number. For relative complex amplitude
of 2p + 1 harmonic one can obtain substituting the solution (11)
into the spectral decomposition of the radiation field (7)
with the amplitude directly proportional to the number of harmonics and with
duration inversely proportional to that number. For relative complex amplitude
of 2p + 1 harmonic one can obtain substituting the solution (11)
into the spectral decomposition of the radiation field (7)
where the coefficients A and B are defined by the following expressions:
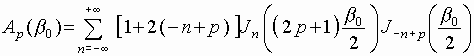
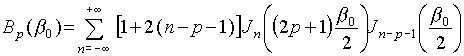 ,
,
Here ![]() is the Bessel function of the n-th order. Thus the expression (12)
gives the precise analytical solution to the problem of reflection of the sine
wave with frequency
is the Bessel function of the n-th order. Thus the expression (12)
gives the precise analytical solution to the problem of reflection of the sine
wave with frequency ![]() from the ideally reflecting mirror oscillating in the longitudinal direction
with arbitrary amplitude
from the ideally reflecting mirror oscillating in the longitudinal direction
with arbitrary amplitude ![]() and frequency
and frequency ![]() .
It is worth to mention that similar formulas can be obtained for the general
case with dispersion.
.
It is worth to mention that similar formulas can be obtained for the general
case with dispersion.
The analysis of expression (12) gives not only a numerical value for a conversion coefficient of the incident wave power into harmonics, but also displays its strong dependence on the phase difference between the oscillations of the electron sheet and the wave.
3. Radiation of the sheet in the field of monochromatic wave.
Let proceed now to the self-consistent analysis of the
reflected field in the case when the sheet moves under the action of the
linear-polarized incident wave ![]() .
Here contrary to the case considered in section 2 the dispersion of electron
medium (inertial term) and highly nonharmonic character of electron oscillations
will be taken into account. The trajectory of the electron sheet in this case
can be presented as the sum of three components:
.
Here contrary to the case considered in section 2 the dispersion of electron
medium (inertial term) and highly nonharmonic character of electron oscillations
will be taken into account. The trajectory of the electron sheet in this case
can be presented as the sum of three components:
1). Transversal oscillations at the frequency of the incident wave.
2). Longitudinal oscillations at the double frequency of the incident wave.
3). Longitudinal drift under the action of a radiation pressure force.
At relativistic intensities the radiation pressure force
acting on the sheet will be very large that will cause fast longitudinal
acceleration of the sheet to about the speed of light; after that the sheet
practically will stop to reflect the incident radiation. Therefore it is
necessary to compensate the mean radiation pressure by, for example, an external
electrostatic field ![]() (in real experiment such field can be produced by positive charge of heavy ions,
for example. Actually for
(in real experiment such field can be produced by positive charge of heavy ions,
for example. Actually for ![]() ,
where
,
where ![]() , the
force of the electrostatic attraction from the ionic background appears to be
larger than the force of light pressure, and the steady state regime is possible
in the system). At
, the
force of the electrostatic attraction from the ionic background appears to be
larger than the force of light pressure, and the steady state regime is possible
in the system). At ![]() for the full compensation of the radiation pressure force it is necessary to put
for the full compensation of the radiation pressure force it is necessary to put
![]() [8].
In this case equations of motion (3) for the electron sheet
have the following form:
[8].
In this case equations of motion (3) for the electron sheet
have the following form:
where ![]() is a dimensionless compensatory force. A numerical analysis of the system (13)
displays that the longitudinal oscillations of the electron sheet have
essentially nonharmonic character for large
is a dimensionless compensatory force. A numerical analysis of the system (13)
displays that the longitudinal oscillations of the electron sheet have
essentially nonharmonic character for large ![]() that differs from the usually supposed sinusoidal law of motion. Besides there
are parts of trajectory where the mirror moves towards to the incident wave with
the speed close to the speed of light. According to expressions (3)
just from these parts there is the radiation of large amplitude pulses
(generation of high harmonics).
that differs from the usually supposed sinusoidal law of motion. Besides there
are parts of trajectory where the mirror moves towards to the incident wave with
the speed close to the speed of light. According to expressions (3)
just from these parts there is the radiation of large amplitude pulses
(generation of high harmonics).
The most effective increase of reflected pulses’ amplitude and enrichment
by harmonics occur according to (3) for the motion of the
sheet towards the incident wave with the speed close to ![]() .
For the oncoming acceleration of the electron sheet a swinging wave with
frequency considerably smaller than the frequency of the incident radiation can
be used in addition to the constant compensating field. Then the constant
electrostatic field compensates the radiation pressure force of the incident
wave and the swinging field provides at some moments the counter speed of the
sheet close to the speed of light. Let, for example, the external field is
selected in the form
.
For the oncoming acceleration of the electron sheet a swinging wave with
frequency considerably smaller than the frequency of the incident radiation can
be used in addition to the constant compensating field. Then the constant
electrostatic field compensates the radiation pressure force of the incident
wave and the swinging field provides at some moments the counter speed of the
sheet close to the speed of light. Let, for example, the external field is
selected in the form 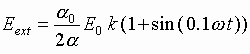 ,
where the factor
,
where the factor ![]() is introduced
for the regime to be quasistationary. For this case the shape of the reflected
field
is introduced
for the regime to be quasistationary. For this case the shape of the reflected
field ![]() is
shown in fig. 3 for
is
shown in fig. 3 for ![]() and different values of
and different values of ![]() and
and ![]() . The
reflected field represents a set of trains following with frequency of the
swinging wave (
. The
reflected field represents a set of trains following with frequency of the
swinging wave (![]() in fig. 3) and each train consists of the short pulses with
large amplitude which are radiated from the parts of trajectory where
in fig. 3) and each train consists of the short pulses with
large amplitude which are radiated from the parts of trajectory where ![]() .
The duration of each train is about the half of the swinging field period and
there is a nonuniform effective compression of the train due to the Doppler
conversion of the frequency. Distance between different trains in the set
practically does not change because these segments correspond to the instants
when
.
The duration of each train is about the half of the swinging field period and
there is a nonuniform effective compression of the train due to the Doppler
conversion of the frequency. Distance between different trains in the set
practically does not change because these segments correspond to the instants
when ![]() and the
Doppler frequency conversion is inessential. Note that here contrary to the
approximation utilized in section 3 (fig. 2) accounting the
inertial term results in the two-polar shape of each pulse.
and the
Doppler frequency conversion is inessential. Note that here contrary to the
approximation utilized in section 3 (fig. 2) accounting the
inertial term results in the two-polar shape of each pulse.
Figure. 3. Radiation field of the
plasma layer at the presence of the swinging field for ![]() (à) and
(à) and ![]() (b).
(b).
4. Radiation of the sheet in the field of two counter propagating waves.
It was already noted that the electron sheet commits finite oscillations in the field of the powerful electromagnetic wave when the radiation pressure force is compensated. In the previous section the force of radiation pressure was compensated by the homogeneous electrostatic field. However for the interaction of the electron sheet with the high-power electromagnetic wave the realization of such field in real experiment can be impossible. A more attractive scheme exists in which there are two waves of equal amplitudes running towards one another. Thus the problem of interaction of the electron sheet with a standing electromagnetic wave arises.
For electric and magnetic components of the standing linear-polarized wave one has:
![]() ;
;
![]() .
(14)
.
(14)
The equations of motion (9) will be recorded now in the following way:
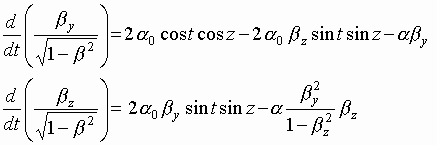 .
(15)
.
(15)
The normalized dimensionless variables ![]() are introduced here.
are introduced here.
Let at first ![]() .
In this case equations (15) become:
.
In this case equations (15) become:
In the equation for ![]() the term
the term ![]() should be taken into account despite of the smallness of longitudinal and
transversal velocities of the electron sheet because the factor
should be taken into account despite of the smallness of longitudinal and
transversal velocities of the electron sheet because the factor ![]() and this term can be about the order of remaining terms in the second equation
of the system (16).
and this term can be about the order of remaining terms in the second equation
of the system (16).
One can conclude that equations (16)
belong to the well known type of particle’s equations of motion in a high
frequency electromagnetic field when the force of the sheet self-action
(radiation friction) described by the last term in (16) is neglected. The
classical result [9] is that in the absence of radiation
friction the longitudinal motion of particles represents fast oscillations at
frequency ![]() and
slow drift in an effective Gaponov-Miller potential
and
slow drift in an effective Gaponov-Miller potential ![]() (here character
(here character ![]() means time-averaging operation). It is natural to suppose that if there is a
dissipation of energy due to the radiation the particles after some time will
occur in a minimum of the potential energy
means time-averaging operation). It is natural to suppose that if there is a
dissipation of energy due to the radiation the particles after some time will
occur in a minimum of the potential energy ![]()
![]() ),
i.e. in a node of the wave. At this points the electric field is equal to zero
so the particles will stay at rest and will not radiate. Rigorous analysis of
the system (16) displays that the inclusion of the non-linear
radiation friction terms can essentially change the situation.
),
i.e. in a node of the wave. At this points the electric field is equal to zero
so the particles will stay at rest and will not radiate. Rigorous analysis of
the system (16) displays that the inclusion of the non-linear
radiation friction terms can essentially change the situation.
Let, for example, the condition ![]() is valid (this condition does not limit the analysis to a case of small
amplitudes, since for any accelerating parameter
is valid (this condition does not limit the analysis to a case of small
amplitudes, since for any accelerating parameter ![]() it is possible to take rather large density for the sheet charge so that the
condition
it is possible to take rather large density for the sheet charge so that the
condition ![]() remains valid). Retaining in equations (16) the terms of the
first and second order in
remains valid). Retaining in equations (16) the terms of the
first and second order in ![]() one can obtain for the slow longitudinal drift
one can obtain for the slow longitudinal drift ![]() the following equation (see Appendix):
the following equation (see Appendix):
and for an effective potential energy and effective friction coefficient the expressions:
 ,
,
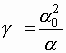 .
(18)
.
(18)
The first term in (18) corresponds to the Gaponov-Miller
potential, the second one describes the effect of non-linear radiation friction.
It can be shown that at ![]() the drift corresponds to the motion in the Gaponov-Miller potential: the steady
state equilibrium position is in the node of the standing wave electric
component (
the drift corresponds to the motion in the Gaponov-Miller potential: the steady
state equilibrium position is in the node of the standing wave electric
component (![]() ).
However for
).
However for ![]() the former equilibrium position becomes unstable, each effective potential
minimum splits into two adjacent minima which for large
the former equilibrium position becomes unstable, each effective potential
minimum splits into two adjacent minima which for large ![]() tend to
tend to ![]() (fig.
4).
(fig.
4).
Figure. 4. Dependence of the
normalized effective potential energy of the slow drift on longitudinal
coordinate for different values of acceleration parameter: curve 1 - ![]() ;
curve 2 -
;
curve 2 - ![]() (point of bifurcation) and 3 -
(point of bifurcation) and 3 -![]() .
.
Comparing for ![]() an
effective oscillation frequency near the minima of the potential energy with
damping (cf. (18)) one can conclude that the drift of the
sheet has a character of aperiodic motion to a new equilibrium position. At new
equilibrium positions the amplitudes of electric and magnetic fields of the
standing wave are nonzero so the electron sheet commits intensive oscillations
at frequency
an
effective oscillation frequency near the minima of the potential energy with
damping (cf. (18)) one can conclude that the drift of the
sheet has a character of aperiodic motion to a new equilibrium position. At new
equilibrium positions the amplitudes of electric and magnetic fields of the
standing wave are nonzero so the electron sheet commits intensive oscillations
at frequency ![]() in transverse direction and at frequency
in transverse direction and at frequency ![]() in longitudinal direction radiating the electromagnetic waves. Thus the
effective radiation of the plasma layer in the field of standing wave is
possible only for powerful enough fields ensuring
in longitudinal direction radiating the electromagnetic waves. Thus the
effective radiation of the plasma layer in the field of standing wave is
possible only for powerful enough fields ensuring ![]() (note that the analytical solution is obtained under condition of
(note that the analytical solution is obtained under condition of ![]() ).
The numerical analysis for the complete set of equations of motion displays that
taking into account the relativistic factors in the system (15)
does not change qualitatively the character of the longitudinal drift. For large
enough intensity of the standing wave the amplitude of the relativistic velocity
).
The numerical analysis for the complete set of equations of motion displays that
taking into account the relativistic factors in the system (15)
does not change qualitatively the character of the longitudinal drift. For large
enough intensity of the standing wave the amplitude of the relativistic velocity
![]() of fast
longitudinal anharmonic oscillations at frequency
of fast
longitudinal anharmonic oscillations at frequency ![]() aims to unit and the radiation takes the form of a sequence of powerful pulses
following at the double frequency of the wave. The shape of the radiation field
is shown in the fig. 5 and 6. The
essential point here is the dependence of the radiated field on the initial
conditions. Actually if the initial value of the longitudinal coordinate is
close to the equilibrium position then the steady-state amplitude of the
radiation field is achieved practically during one-two periods of the incident
wave. If initial position is far from equilibrium then at first one or two
pulses are radiated with amplitude larger than the steady-state values (fig.
5) then a long period follows when the pulses have rather small amplitude
and further the steady-state regime is achieved. Last case can be interesting to
a problem of generation of ultra broadband single optical pulse.
aims to unit and the radiation takes the form of a sequence of powerful pulses
following at the double frequency of the wave. The shape of the radiation field
is shown in the fig. 5 and 6. The
essential point here is the dependence of the radiated field on the initial
conditions. Actually if the initial value of the longitudinal coordinate is
close to the equilibrium position then the steady-state amplitude of the
radiation field is achieved practically during one-two periods of the incident
wave. If initial position is far from equilibrium then at first one or two
pulses are radiated with amplitude larger than the steady-state values (fig.
5) then a long period follows when the pulses have rather small amplitude
and further the steady-state regime is achieved. Last case can be interesting to
a problem of generation of ultra broadband single optical pulse.
Figure. 5. Non-stationary
radiation field of the plasma layer in the transient regime: ![]() ;
normalized initial coordinate of the layer
;
normalized initial coordinate of the layer ![]() .
.
Figure. 6. Radiation field of the
plasma layer in positive (a) and negative (b) directions of ![]() axis for
axis for ![]() .
The motion is near the left equilibrium position (with regard to the node of
electrical component of standing wave).
.
The motion is near the left equilibrium position (with regard to the node of
electrical component of standing wave).
Let mark another interesting effect arising due to a
bifurcation in the considered system. For ![]() the radiation of the plasma layer acquires an asymmetrical character (fig.
6), i.e. fields radiated to the left and to the right are different. In this
case not only the transient process of steady-state achievement but also the
stationary state itself becomes dependent on the initial conditions. In fig.
7 the steady-state trajectories of an electron in the ultra relativistic
case (
the radiation of the plasma layer acquires an asymmetrical character (fig.
6), i.e. fields radiated to the left and to the right are different. In this
case not only the transient process of steady-state achievement but also the
stationary state itself becomes dependent on the initial conditions. In fig.
7 the steady-state trajectories of an electron in the ultra relativistic
case (![]() and
and ![]() )
are shown for some initial position of the layer.
)
are shown for some initial position of the layer.
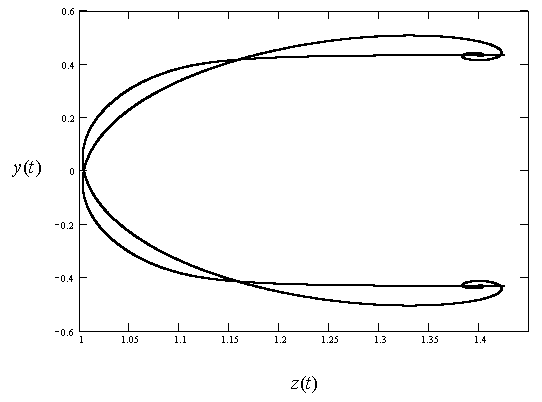
Figure. 7. Stationary
trajectories of the plasma layer motion for ![]() (à) and 150 (b). The motion is near the left equilibrium position.
(à) and 150 (b). The motion is near the left equilibrium position.
The asymmetry of the curves indicates asymmetry of radiation in the positive and negative directions of z axis. For other initial conditions the trajectory can be mirror reflected with regard to the node of electric component of the standing wave. The parameters of the layer radiation in this case change to the opposing.
5. Discussion of results.
Above considerations show that during interaction of the powerful electromagnetic wave with the dense plasma layer the sequence of ultrashort pulses with amplitude much greater than the amplitude of the incident wave can be generated.
Let estimate the value of acceleration parameter which can be
realized experimentally now. From expression (8) one has ![]() for a power density of an incident radiation
for a power density of an incident radiation ![]() W/cm
W/cm![]() and a wavelength of 2
microns. The increase in the amplitude of the reflected pulses with regard to
the amplitude of the incident wave is more than 15 times (see fig.
3a). Further advance in super-power laser pulses generation will allow to
increase the acceleration parameter. For values
and a wavelength of 2
microns. The increase in the amplitude of the reflected pulses with regard to
the amplitude of the incident wave is more than 15 times (see fig.
3a). Further advance in super-power laser pulses generation will allow to
increase the acceleration parameter. For values ![]() (fig.3b) the intensity of the pumping wave about
(fig.3b) the intensity of the pumping wave about ![]() W/cm
W/cm![]() is necessary that does not
seem inaccessible. An alternative way for the increase of efficiency of powerful
ultrashort pulses generation during the reflection from the plasma layer can be
the usage of cascaded reflection process that will be considered elsewhere.
is necessary that does not
seem inaccessible. An alternative way for the increase of efficiency of powerful
ultrashort pulses generation during the reflection from the plasma layer can be
the usage of cascaded reflection process that will be considered elsewhere.
Let estimate the value of parameter ![]() accessible in modern experiments. The surface density
accessible in modern experiments. The surface density ![]() is determined by a volume concentration of electrons
is determined by a volume concentration of electrons ![]() and by a thickness of the sheet. Let the wavelength of radiation falling at the
sheet is
and by a thickness of the sheet. Let the wavelength of radiation falling at the
sheet is ![]() . Then
for the thickness of the sheet smaller than
. Then
for the thickness of the sheet smaller than![]() all points of the sheet will move practically along the same trajectories. For
such case all expressions obtained for indefinitely thin sheet are valid (if the
width of the medium is larger than
all points of the sheet will move practically along the same trajectories. For
such case all expressions obtained for indefinitely thin sheet are valid (if the
width of the medium is larger than ![]() then for the correct solution of the problem it is necessary to take into
account the difference of velocities for different layers inside the sheet so
the set of equations becomes more complicated though the proposed method is
still usable). Thus for the electron concentration
then for the correct solution of the problem it is necessary to take into
account the difference of velocities for different layers inside the sheet so
the set of equations becomes more complicated though the proposed method is
still usable). Thus for the electron concentration ![]() of the order of
of the order of ![]() cm
cm![]() and the sheet width equal to
and the sheet width equal to ![]() one can obtain for parameter
one can obtain for parameter ![]() the value from 10 to 100 depending on the wavelength. It is obvious that for
more thin sheets the value of
the value from 10 to 100 depending on the wavelength. It is obvious that for
more thin sheets the value of ![]() can be made smaller.
can be made smaller.
In the present paper the perpendicular falling of the
electromagnetic wave at the plasma sheet is considered. The obtained results can
be easily generalized for the case of oblique falling using the method
considered in Ref. [3]. Besides the proposed technique allows
to find not only the reflected field but also the transmitted wave. For example
in Ref. [8] the expression up to the third order in parameter ![]() is analytically retrieved for radiation passing through the thin plasma sheet.
is analytically retrieved for radiation passing through the thin plasma sheet.
For simplicity the ionic background was not considered in the above calculations. However one can easily take into account the effects of ions with the help of the approach used here for electrons. This is valid also if there is nontrivial initial distribution of electrons with velocity - for each value of velocity it is necessary to use the separate electron sheet with partial charge density, in this case the effective force of radiation reaction can be calculated by integrating over the velocity distribution function.
In experiment the thin plasma sheet model can be realized by evaporation of the freely suspended thin (about several microns or less) film by the powerful laser radiation. Probably this problem can be solved most naturally in the field of two counter propagating waves. It is necessary to note that the analogue of longitudinal low frequency swinging of the sheet considered in section 3 is evidently the case when one of the waves or both are modulated.
It is worth to mention in conclusion that the experimental confirmation of a capability of electromagnetic pulses’ generation can be obtained in interferometric experiments, for example, using the division of a wave front [11] already for a moderate value of incident radiation power. Also the optical nonlinearities can be used for demonstration in the scheme based on the effects of two-photon (multiphoton) luminescence [12,13].
Appendix.
In this appendix the analytical results concerning the character of the electron sheet motion in the field of two counter propagating waves used without proof in section 4 will be justified.
The equations (16) can be written as the system of three first order equations:
Let introduce the following dimensionless parameter
(hereinafter we shall suppose that it is small): 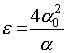 .
Then the equations (A.1) can be written in the following way:
.
Then the equations (A.1) can be written in the following way:
The solution of the first equation of a system (A.2) can be
obtained with the method of sequential approximations, using for the transversal
velocity the series expansion ![]() and
equating factors with identical powers of
and
equating factors with identical powers of ![]() .
For the solution to within
.
For the solution to within ![]() one has
one has
For the second bracket in the r.h.s. one can omit all terms
proportional to ![]() and
and 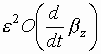 .
Substituting equation (A.3) into the system (A.2)
one can obtain two equations of the first order:
.
Substituting equation (A.3) into the system (A.2)
one can obtain two equations of the first order:
Introducing ![]() one has
one has
The equations (A.5) can be solved by the averaging method [14,15],
for what it is necessary to write them in a canonical form: ![]() .
With this purpose we shall make a change of variables
.
With this purpose we shall make a change of variables ![]() ,
where the function
,
where the function ![]() is choosen
so that to compensate in the first equation of the system (A.5)
the term
is choosen
so that to compensate in the first equation of the system (A.5)
the term ![]() . It
is easy to test that for this purpose it is enough to put
. It
is easy to test that for this purpose it is enough to put ![]() .
.
The system (A.5) in new variables has the form:
Making now in (A.6) time-averaging operation one can obtain for the drift component of the longitudinal coordinate the following equation:
whence equation (17) directly follows.
According to the averaging theorem [15] the error due to the
replacement of the solutions of equations (A.6) by the solution of the average
equation (A.7) have the order of ![]() evenly for the times of the order of
evenly for the times of the order of ![]() .
.
References
Authors:
Anton
S. Il'in, Victor
V. Kulagin, Vladimir
A. Cherepenin and S.L. Ziglin