|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2006 |
|
УДК 530.12:539.12:621.396
ПРОСТРАНСТВО – ВРЕМЯ И ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ СВЯЗАННЫХ ЗАРЯДОВ
к.ф.- м.н. Подосенов С.А.
SPACE-TIME AND ELECTROMAGNETIC FIELDS OF BOUND CHARGES
Podosenov S.A., Ph. D.
Работа выполнена во Всероссийском научно-исследовательском институте оптико-физических измерений (ВНИИОФИ)
Получена 28 июля 2006
От редакции
Редакция журнала считает развиваемый в настоящей статье подход дискуссионным и не вполне согласна с выводами автора по результатам настоящей работы. Тем не менее, учитывая репутацию С.А.Подосенова как физика-теоретика, имеющего значительное число работ, редакция сочла возможным опубликовать данную работу на страницах журнала "Журнал радиоэлектроники".
Содержание
Электрическое поле связанных зарядов
Поле со сферической симметрией
Поле с цилиндрической симметрией
Электромагнитное поле бегущей волны, созданное током связанных зарядов
Краткая биографическая справка
Аннотация
На основе точного решения для поля заряда в равноускоренной неинерциальной системе отсчета (НСО) и сформулированного автором "положения об эквивалентных ситуациях" построена нелинейная электромагнитная теория связанных (не свободных) зарядов. Предложенный метод требует выхода за рамки плоского пространства - времени, однако кривизна другой природы, не связанной с теорией тяготения Эйнштейна. Метод устраняет расходимость собственной энергии поля зарядов и делает классическую электродинамику внутренне непротиворечивой при переходе к любым достаточно малым расстояниям. Предсказаны новые эффекты, которые доступны проверке на современном уровне развития науки и техники.
Введение
Основной
трудностью классической (и квантовой) теории электромагнитного поля является
противоречие между точечностью эаряженных частиц и их бесконечной собственной
энергией. Попытки устранения этой трудности были связаны с развитием нелинейных
теорий Г. Ми (1912 г.), М. Борна и Л. Инфельда (1934 г.) [1]. Однако основания этих теорий базируются на произвольном выборе лагранжиана и не
обоснованы экспериментом. Необходимость нелинейной электродинамики возникла в
связи с открытием позитрона и образования пар, т.е. одновременного
возникновения электрона и позитрона под действием жестких ![]() - лучей. Линейные уравнения
Максвелла в принципе не могли привести к такому рассеянию, что непосредственно
следует из принципа суперпозиции полей. Две волны должны были проникнуть одна
через другую. Поэтому эксперимент требует некоторого изменения уравнений
Максвелла в сторону их нелинейности [1].
- лучей. Линейные уравнения
Максвелла в принципе не могли привести к такому рассеянию, что непосредственно
следует из принципа суперпозиции полей. Две волны должны были проникнуть одна
через другую. Поэтому эксперимент требует некоторого изменения уравнений
Максвелла в сторону их нелинейности [1].
Предлагаемая здесь модель нелинейной теории основывается на учете взаимодействия зарядов, создающих поле, с созданным зарядами полем. Учитывается и поле связей. Однако подход требует выхода за рамки плоского пространства - времени. Исходными уравнениями теории являются уравнения Максвелла, записанные в общековариантной четырехмерной форме [2]. Для нахождения метрики используются выведенные автором уравнения структуры, устанавливающие связь между кинематическими характеристиками системы отсчета (СО), такими как тензор скоростей деформаций, тензор угловой скорости вращения, 4-ускорения с метрическим тензором СО. Как и в общей теории относительности (ОТО), под СО понимаем "совокупность бесконечного числа тел, заполняющих все пространство, наподобие некоторой "среды" [2]".
Исходим из доказанной нами в [3], [4], [5], [21] теоремы, что переход в жесткую глобально равноускоренную НСО приводит к искривлению пространства - времени. Позднее эти результаты (без ссылки на [3]) повторены в [6], [7]. Более подробно вопросы СО и физический смысл перехода от одной СО к другой изложены автором в монографиях [5] и [21]. Развитие нетрадиционного подхода к НСО привело к кругу задач, которые на первый взгляд не имеют никакого отношения к НСО, но на самом деле оказались с ними тесно связанными.
Возникла совершенно новая область исследований, связывающих геометрию пространства - времени с классическими (неквантовыми) полями связанных зарядов. Сформулируем [4], [5], [21] "положение об эквивалентных ситуациях".
Поле от точечного заряда, находящегося в равновесии в постоянном электрическом поле, эквивалентно полю от этого заряда закрепленного в равноускоренной НСО, если силы реакции связей, удерживающие заряд в НСО и в поле неподвижным, равны. Этого положения нет в классической электродинамике, где считается, что поле, покоящегося в инерциальной системе отсчета (ИСО) точечного заряда, является кулоновым сферически-
-симметричным вне зависимости от того является ли заряд свободным или сумма сил, действующих на заряд, равна нулю. Например, поле от точечного заряда, закрепленного нитью между обкладками плоского конденсатора, считается кулоновым, сферически симметричным. С другой стороны, поле от этого же заряда, закрепленного на нити с одинаковым натяжением (что и в конденсаторе) в равноускоренной системе отсчета, в согласии с классической электродинамикой для наблюдателя в НСО будет аксиально-симметричным вне зависимости от того или иного метода перехода в НСО [2].
Итак, одинаковая физическая ситуация, в которой находятся заряды (одинаковые силы реакции связи), приводит к полям с разной симметрией! Попытка разрешения парадокса предпринята в данной работе.
Более подробное обсуждение дано нами в монографиях [5], [21]. Предлагаемая работа дополняет идеи автора рассмотренные в [22], [23].
Уравнения структуры НСО
В релятивистской теории не существует общепризнанного аналитического определения как систем отсчета, так и правил, устанавливающих переход между ними [8]. В работах [4], [5], [21] построена теория релятивистской жесткой равноускоренной НСО, которая реализуется в римановом пространстве постоянной кривизны. Подход при построении НСО базируется на очевидном требовании отсутствия деформаций и напряжений в твердом теле при его поступательном движении в однородном силовом поле. Получены следующие соотношения:
Для
движущейся сплошной среды в четырехмерном пространстве - времени с сигнатурой ![]() справедливо разложение
справедливо разложение
![]() (1)
(1)
где Vm - поле 4 - скорости, удовлетворяющее условию нормировки
![]() (2)
(2)
gmn - метрический тензор в системе отсчета Эйлера,
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Здесь Smn - тензор скоростей деформаций, Wmn - тензор угловой скорости вращения, Fm - векторы первой кривизны мировых линий частиц среды.
Круглые скобки, окружающие индексы, служат знаком симметрирования, а квадратные - знаком альтернирования. Греческие индексы могут принимать значения от нуля до трех, латинские от единицы до трех. Разложение (1) можно трактовать с двух точек зрения:
1. Считать, что поле 4 - скорости Vm известно, например, в результате интегрирования релятивистского уравнения Эйлера или Навье - Стокса при заданной плоской метрике. В этом случае характеристики континуума Smn, Wmn, Fm могут быть получены по формулам (3-5), а разложение (1) выступает как математическое тождество.
2. Считать заданными функциями Smn, Wmn, Fm. В этом случае разложение (1) превращается в систему дифференциальных уравнений относительно Vm и gmn. Так как число уравнений системы (1) и (2) превосходит число неизвестных функций, то должны выполняться условия интегрируемости. Условием интегрируемости для компонент 4 - скоростей будет соотношение
![]()
![]() (6)
(6)
из которого следует, что
![]() (7)
(7)
Интегрирование системы (1), (7), где Rmes,n - тензор кривизны, выражаемый через метрический тензор обычным образом, дает решение задачи о геометрии пространства - времени, в которой реализуется НСО с заданной структурой. Уравнения (7) назовем уравнениями структуры НСО [3 – 5, 21].
Из (7) следует, что жесткое глобально равноускоренное движение можно реализовать в римановом пространстве постоянной кривизны с метрикой [3 – 5, 21]
![]() (8)
(8)
где ускорение a0 направлено вдоль оси y1. Одна независимая компонента тензора кривизны, вычисленная по метрике (8), имеет вид
![]() (9)
(9)
Для компонент тензора Риччи Rbd = gagRab,gd имеем
![]()
![]()
![]() (10)
(10)
Для скалярной кривизны получаем
![]() (11)
(11)
Электрическое поле связанных зарядов
Используем "положение об эквивалентных ситуациях" и математический аппарат НСО для нахождения электрического поля заряженных проводников. Заряды на поверхности проводника испытывают силы отрицательного давления со стороны внешнего поля. Со стороны решетки металла на заряды действует сила, препятствующая зарядам покинуть поверхность тела. Таким образом, поле от рассматриваемой системы эквивалентно полю системы зарядов "движущихся" равноускоренно с ускорениями направленными внутрь проводника. Для нахождения суммарного поля заряженного проводника нужно просуммировать поля от зарядов элементов поверхности.
Следует особо отметить, что в отличие от пространства Минковского, в пространстве Римана, покоящиеся на поверхности проводника заряды, имеют отличное от нуля ускорение (поэтому слово... "движущихся" в кавычках). При ликвидации реакции связи они будут двигаться по геодезической линии (т.е. без ускорения!). Сила реакции связи сбивает частицу с геодезической, искривляя ее мировую линию, и создавая отличный от нуля вектор первой кривизны (4-ускорение).
Следовательно, между рассмотрением движения заряженных частиц в электростатическом поле пространства Минковского и движением в поле связанных зарядов в пространстве Римана имеется принципиальное различие.
В пространстве Минковского искривлена мировая линия движущейся в поле частицы, а в пространстве Римана искривлена мировая линия закрепленной в поле частицы.
Таким образом, в римановом пространстве-времени второй закон Ньютона оказался несправедливым, так как равенство нулю сил, действующих на частицу, привело к ненулевому ускорению.
С аналогичной ситуацией сталкиваемся и в ОТО. Например, для наблюдателя, покоящегося на поверхности гравитирующей сферы, с точки зрения механики Ньютона сумма сил равна нулю, что приводит и к нулевому ускорению. С точки зрения ОТО, тело, покоящееся на поверхности этой сферы, имеет отличный от нуля вектор первой кривизны, что, например, следует из решения Шварцшильда [2]. Ускорение направлено вдоль "радиуса-вектора" от центра сферы.
Уравнение для скалярного потенциала A0 точечного заряда, вмороженного в начало координат НСО (8) имеет вид
![]() (12)
(12)
Это уравнение можно получить из уравнений Максвелла, записанных в общековариантной форме [2]. Решение уравнения приводит к соотношению
![]() (13)
(13)
Для
напряженности электрического поля ![]() имеем
имеем
![]() (14)
(14)
где r
- трехмерное (евклидово) расстояние от начала координат, совпадающим с зарядом,
до точки наблюдения, q - угол между радиусом - вектором ![]() и
и ![]() ,
, ![]()
Формулы (12), (13) и (14) являются ключевыми для расчета электростатических полей связанных зарядов.
В качестве примера на основе [4], [5], [21] приведем выражения для поля, создаваемого заряженной бесконечной металлической пластиной и определим геометрию пространства-времени для пробных зарядов q, подвешенных на нитях в поле пластины и неподвижных относительно ее. Значение напряженности поля заряженной плоскости дает
![]() (15)
(15)
где s0 - поверхностный заряд плоскости. Определим метрику пространства - времени, выбрав в качестве базиса НСО невзаимодействующую заряженную пыль над одноименно заряженной плоскостью. Пусть каждая из частиц связана с заряженной плоскостью невесомой и нерастяжимой нитью. Заряженная пыль в данной модельной задаче задает базис системы отсчета, структура которого определяется совместным решением уравнений "движения" и уравнений Максвелла, решение которого дается формулой (15). Частицы пыли будут взаимно неподвижны, так что тензор скоростей деформаций и тензор угловой скорости вращения равен нулю, а натяжения нитей отличны от нуля. Примем, что плоскость бесконечна, плотность заряда на ней постоянна, а отношения зарядов к массам для всех частиц базиса одинаковы. По определению считаем, что пыль поля не создает, а поле определяется только зарядами плоскости в согласии с (15). Очевидно, что физическая ситуация для частиц пыли в верхнем полупространстве эквивалентна ситуации в некоторой НСО "движущейся" вниз в направлении плоскости, что математически описывается метрикой (8) с отрицательным знаком в экспоненте, т.е. заменой a0®-a. Величины a0 и a требуется вычислить. Вычисления, проведенные в [5], [21] приводят к элементу интервала вида
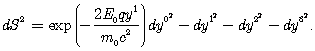 (16)
(16)
Из (16) видно, что эта формула аналогична (8) с отрицательным ускорением
a = - E0q /m, направленным к плоскости, если заряд плоскости и пробный заряд q одного знака и положительным ускорением при разноименных зарядах. Пространство - время будет плоским, если пробная частица не заряжена. Если для частиц базиса отношение пробных зарядов к массам для всех частиц одинаково, а заряды плоскости и пробных частиц разноименны, то метрика (16) тождественна с (8) при a = a0.
Для
сравнения теории с экспериментом нужно выразить поля в "физических"
или тетрадных компонентах вне заряженной плоскости. Сопутствующие тетрады для
метрики удобно выбрать так, что вектор ![]() направлен вдоль линии времени, а триада
направлен вдоль линии времени, а триада ![]() вдоль координатных осей
yk (калибровка Ламе [9], [10]). Тетрадные индексы будем
заключать в скобки. Выражение для тетрад в согласии с (16), будет иметь вид:
вдоль координатных осей
yk (калибровка Ламе [9], [10]). Тетрадные индексы будем
заключать в скобки. Выражение для тетрад в согласии с (16), будет иметь вид:
![]()
![]()
![]()
![]()
![]() (17)
(17)
где суммирование по a отсутствует. Для "физических" компонент тензора поля находим
![]() (18)
(18)
Из (18) следует, что в локальных тетрадах поле заряженной плоскости точно такое же, как и при обычном рассмотрении в декартовых координатах. Это приводит к одинаковым значениям силы, действующей на пробный заряд, при различных рассмотрениях.
Однако геометрия пространства-времени, обусловленная электростатическим полем, оказалась псевдоримановой, а не псевдоевклидовой, как при обычном рассмотрении. Неевклидовость пространства-времени другой природы, чем в ОТО. Она связана с совместным решением уравнений Максвелла, уравнений структуры (7) и уравнений "движения".
Для учета реальных поправок к полю отрицательно заряженных проводников, проведем "экзотический" расчет поля, создаваемого электроном, "подвешенным" на нити в однородном электрическом поле. Ситуация с "подвешенным" электроном массы m и зарядом e эквивалентна его помещению в НСО (8), движущуюся с ускорением, направленным вдоль оси y1 и равным по величине a0 = eE/m. Расчет по формуле (14) при напряженности поля плоскости E = 100 кВ/м дает для точек в направлениях по полю к точкам поперек поля на расстоянии 1 м от заряда разность значений, отличающихся на 10 %. При стандартном расчете поле электрона должно быть изотропным и кулоновым, таким же как и поле свободного электрона.
Рассмотрим проводник, заряженный отрицательно. На его поверхность действует сила "отрицательного давления", значение которой на единицу поверхности равно
F = 0.5s0 E [11], где E - величина напряженности у поверхности металла, а s0 = Ne/S. Здесь
N -
число электронов заряда, e на площади S. Поэтому со стороны поля
на каждый из электронов действует сила Fe = 0.5eE. Сила со
стороны решетки металла направлена в обратную сторону и ее действие
эквивалентно силе реакции со стороны тела, "движущегося с ускорением"
a0 = 0.5eE/m, в которое "вморожен"
электрон. Отсюда следует, что на проводниках, заряженных отрицательно,
поверхностные электроны испытывают лишь в два раза меньшую силу со стороны
решетки, чем электроны "подвешенные" на нити ![]() . Поэтому поправки к полю у
отрицательно заряженных проводников значительны.
. Поэтому поправки к полю у
отрицательно заряженных проводников значительны.
Для проводников, заряженных положительно, на поверхности находятся не электроны, а положительные ионы с массой значительно большей, чем у электронов. Поэтому их эффективное "ускорение" а0, а, следовательно, и поправка для поля будет гораздо меньше.
Тензор энергии-импульса электромагнитного поля в криволинейных координатах имеет вид [2]
![]() (19)
(19)
где тетрадные компоненты тензора вычисляются по правилу
![]() (20)
(20)
Энергию поля от плоскости можно вычислить по формуле [10]
![]() (21)
(21)
где g - определитель метрического тензора, dSm = VmdV. dSm - геометрический объект равный произведению элемента площади гиперповерхности ортогональной мировым линиям базиса, построенной на базе трех бесконечно малых смещений, на единичный вектор нормали (т.е. 4-скорость Vm). Ввиду важности соотношения (21) обсудим его более подробно.
Так как мы рассматриваем тензор энергии импульса электромагнитного поля вне зарядов, создающих поле, то должно выполняться соотношение
![]() (22)
(22)
В плоском пространстве - времени в галилеевых координатах это соотношение выражает закон сохранения энергии - импульса электромагнитного поля. В римановом пространстве - времени это соотношение в общем случае не выражает никакого закона сохранения, так как вместо частной производной от тензора энергии - импульса стоит ковариантная. Это обстоятельство хорошо известно в литературе по ОТО.
При вычислении энергии в (21) мы фактически используем не "закон сохранения" (22), а истинный закон сохранения, напоминающий внешне закон сохранения заряда.
Это вытекает из равенства
![]() (23)
(23)
При выводе (23) мы учли, что конгруенция мировых линий частиц базиса СО является безвихревой и жесткой, что векторы Vm и Fm ортогональны и что равна нулю свертка антисимметричного тензора поля Fmn с произведением векторов первой кривизны.
Соотношение (23) можно переписать в форме
![]() (24)
(24)
Проинтегрируем выражение (24) по инвариантному 4 – объему
![]() (25)
(25)
Используя теорему Гаусса и полагая, что на "боковой" временноподобной охватывающей пространственный объем гиперповерхности интеграл стремится к нулю, (что имеет место в задачах с зарядами, расположенными в конечном объеме), получаем
![]() (26)
(26)
Откуда имеет место закон сохранения величины типа "заряда"
![]() (27)
(27)
в которой V1 и V2 - трехмерные объемы занимаемые полем в разные моменты времени.
Сравнение (21) с (27) говорит о тождественности этих величин, которые представляют энергию электромагнитного поля.
Вычислим энергию поля отрицательно заряженной плоскости. При стандартном вычислении энергия поля плоскости напряженности E, заключенная в цилиндре с площадью основания S и высоты h по обе стороны плоскости с образующими, перпендикулярными плоскости, очевидно равна
![]()
![]() (28)
(28)
При h ® ¥, W0 ® ¥.
Для нашего случая энергия поля в указанном объеме
![]() (29)
(29)
где E = 2ps0.
Очевидно, что при малых расстояниях h от плоскости, т.е. при
![]()
энергия поля в объеме, вычисленная в согласии с (29), совпадает с классическим выражением (28). Однако, если при классическом рассмотрении при h ® ¥, W0 ® ¥, то в нашем случае энергия поля внутри бесконечно длинного цилиндра остается конечной величиной, определяемой равенством
![]() (30)
(30)
Итак:
Энергия электрического поля внутри бесконечно длинного цилиндра оказалась равной энергии покоя N электронов, расположенных на заряженной поверхности площади S внутри цилиндра. В эту энергию не входит величина заряда Q элемента площади.
Формула (30) остается в силе и для плоскости, заряженной положительно. В этом случае роль массы играет масса атома проводника, потерявшего один электрон.
Таким образом, собственная энергия зарядов на плоскости оказалась равной их энергии покоя!
Учитывая, что пространственное сечение для метрики (8) является плоским, а ускорение отрицательным для тензора энергии - импульса в сопутствующих тетрадах находим выражение
![]()
![]()
![]()
![]() (31)
(31)
Последнее соотношение в локальных тетрадах совпадает с тензором энергии-импульса постоянного однородного поля в ИСО пространства Минковского в галилеевых координатах.
Поле со сферической симметрией
Рассмотрим электростатическое поле, обладающее центральной симметрией. Такое поле может быть создано заряженным сферическим телом или точечным зарядом. В предыдущем разделе показано, что электростатическое поле связанных зарядов отличается от поля свободных зарядов. Рассмотрим заряженный проводящий шар радиуса R, заряженный зарядом Q. Требуется найти напряженность электрического поля E и определить геометрию пространства-времени вне шара.
Каждый из зарядов на проводнике будет находиться на поверхности шара и испытывать со стороны создаваемого ими поля силу "отрицательного давления", направленную по внешней нормали к поверхности [11]. Эта сила компенсируется силой со стороны решетки, удерживающей заряды на поверхности сферы. Таким образом, рассматриваемая физическая ситуация эквивалентна ситуации, в которой находятся заряды, связанные невесомыми нитями длины R, закрепленными в общем центре. Следовательно, поле, создаваемое каждым из зарядов будет таким же, как если бы каждый из зарядов двигался равноускоренно с ускорением направленным к центру шара. Итак, в согласии с (13) и (8) потенциал dA0 в точке наблюдения имеет вид
![]() (32)
(32)
где r'
- трехмерное (евклидово) расстояние от заряда dQ до точки наблюдения, q - угол
между радиусом - вектором ![]() и
и ![]() ,
, ![]()
![]() для каждого элемента заряда dQ
направлен к центру сферы. Величина "ускорения" a0
для зарядов отрицательно заряженной сферы (электронов) вычисляется по формуле
для каждого элемента заряда dQ
направлен к центру сферы. Величина "ускорения" a0
для зарядов отрицательно заряженной сферы (электронов) вычисляется по формуле
![]() (33)
(33)
вывод которой приведен ранее. Здесь e - величина заряда, m - масса электрона, E - напряженность поля на поверхности сферы. Для шара, заряженного положительно, "релятивистский" эффект будет значительно менее выражен, т.к. под массой m, будет выступать масса положительного иона, значительно превышающая массу электрона. Поэтому поле от положительно заряженного шара практически совпадает с классическим, а для отрицательно заряженного шара "релятивистские" поправки могут оказаться значительными.
В согласии с (8) каждый из электронов на поверхности сферы принадлежит касательному плоскому пространству, но риманову пространству - времени. Поэтому операция интегрирования по сфере происходит в плоском пространстве и является корректной. Выполнив интегрирование в (32), получим
![]() ,
, ![]() (34)
(34)
В (32) r - расстояние от центра шара до точки наблюдения, F(iz) - интеграл вероятности мнимого аргумента, определяемый как
![]()
С другой стороны, совокупность электронов на поверхности сферы не принадлежит конгруенции мировых линий базиса НСО (8), а включаются в совокупность мировых линий, принадлежащих сферически – симметричной лагранжевой сопутствующей НСО с метрикой
![]() (35)
(35)
Функции n(r) и l(r) нуждаются в определении. Для их нахождения воспользуемся решением сферически-симметричных статических уравнений Максвелла с использованием метрики (35), аналогичных по записи уравнениям электродинамики в "заданном гравитационном поле" [2]. Затем сравним полученное решение с выражением для поля, получаемом из (34).
Для отличной от нуля радиальной компоненты "индукции" D1 имеем уравнение
![]() (36)
(36)
решением которого будет
![]() (37)
(37)
В (36) и (37) между "индукцией" D1 напряженностью поля E1 и компонентой тензора поля F01 существуют известные [2] соотношения
![]()
![]()
![]() (38)
(38)
где gkl - пространственный метрический тензор с определителем равным g.
Из (36) и (37) следует, что уравнения Максвелла не определяют функций n(r) и l(r).
В согласии с (34) и (35) тензор электромагнитного поля Fmn имеет отличные от нуля компоненты F01 = -F10
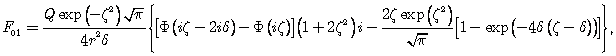
![]() (39)
(39)
Приравнивая (39) выражению F01 из (38), находим уравнение связи на функции n(r) и l(r).
![]()
![]()
![]() (40)
(40)
Для нахождения второго уравнения, связывающего эти функции, рассмотрим силу со стороны поля, действующую на пробный заряд q, закрепленный в точке с координатой r от центра шара. Пусть масса пробного заряда m0. Тогда вектор первой кривизны F1 мировой линии этого заряда можно найти из соотношения
![]()
и из силы, действующей на заряд со стороны связи, удерживающей заряд в поле неподвижным. Эта сила численно равна силе со стороны поля и противоположна ей по знаку
![]() (41)
(41)
Из (39)-(41) находим
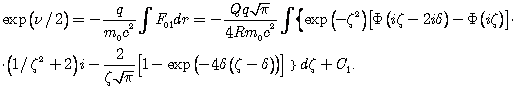 (42)
(42)
Постоянную интегрирования C1 определим из требования евклидовости пространства на бесконечности.
Выполнить интегрирование в (42) аналитически не представляет труда, т.к. по определению
![]()
где A0 определяется из (34). В результате получим
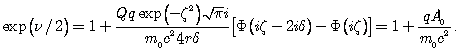 (43)
(43)
Из (40) и (43) находим
 (44)
(44)
Проведем
анализ (43), (44), раскладывая выражения в ряд по безразмерному параметру d.
Отметим, что для заряженного отрицательно металлического шара ![]() = - 50 кВ соответствует
d = 0.11,
для электрона с классическим радиусом r0 = e2/mc2, d =
0.35355, для протона d = 0.015.
= - 50 кВ соответствует
d = 0.11,
для электрона с классическим радиусом r0 = e2/mc2, d =
0.35355, для протона d = 0.015.
Разложение в ряд по d c сохранением членов пропорциональных первой степени d (в числителе (44) раскладываем в ряд, удерживая члены с d 2) приводит к соотношению
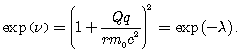 (45)
(45)
В формуле (45) заряды Q и q могут иметь как одинаковые, так и противоположные знаки.
В отличие от ОТО метрика пространства - времени зависит как от заряда, создающего поле Q, так и от величины пробного заряда q. Дальнейший анализ полученных соотношений подробно описан в [5], [21] и выходит за рамки настоящей статьи. Отметим, однако, что при формальной замене констант взаимодействия в законе Кулона на константы взаимодействия в законе всемирного тяготения Ньютона Qq ® -kMm, соотношение (45) для слабых полей эквивалентно точному решению уравнения Эйнштейна в форме метрики Шварцшильда [2].
Попытаемся предсказать возможные эксперименты, которые бы позволили подтвердить или опровергнуть предлагаемую схему.
Произведем расчет емкости заряженного металлического шара радиуса R. При классическом рассмотрении емкость C = R.
Вычислим емкость по формуле
![]() (46)
(46)
Плотность
энергии r соответствует ![]() компонентам тензора энергии-импульса.
Очевидно, что
компонентам тензора энергии-импульса.
Очевидно, что
![]()
Используя выражения (45), (46), находим для плотности энергии r соотношение
![]() (47)
(47)
которое совпадает с выражением для плотности энергии поля вне заряженной сферы в пространстве Минковского.
Однако для нахождения полной энергии поля вне заряженного шара нужно производить интегрирование по пространству в римановом пространстве - времени с метрикой (35), определяемой из (43), (44). Для этого воспользуемся формулой (21), из которой имеем
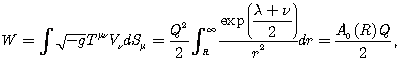 (48)
(48)
где A0(R) определяется из (34) при r = R.
В результате получим для емкости C
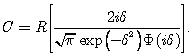 (49)
(49)
Считая d малой величиной, из (49) находим
![]() (50)
(50)
Например, при потенциале -50 кВ добавка к емкости должна составлять 0.8 %.
Для вычисления емкости шара можно вместо формулы (46) определить емкость обычным способом по формуле
![]() (51)
(51)
где A0 вычисляется из (34) при r = R.
Таким образом, обе формулы (46) и (51) оказались эквивалентными, как и при классическом рассмотрении.
Как известно, [2] в классической (неквантовой) релятивистской механике элементарным частицам нельзя приписывать конечных размеров и они должны рассматриваться как точечные. С другой стороны, заряженная частица при таком рассмотрении обладает бесконечной собственной энергией, а следовательно и массой. Физическая бессмысленность такого результата требует ограничить основные принципы самой электродинамики определенными пределами.
Докажем, что в предлагаемой нами модели указанной выше трудности не возникает и собственная энергия отрицательного точечного заряда Q, содержащего в себе N электронов, соответствует конечной величине W = 2Nmc2.
Для доказательства воспользуемся выражением (60) и (46) при R ® 0. Полагая в (60) Q = Ne и воспользовавшись известной асимптотической формулой [12]
![]() (52)
(52)
находим при z = d >>1 выражение
![]()
![]()
Откуда при R ® 0 имеем
W = 2Nmc2. (53)
Величина энергии точечной частицы оказалась независимой от знака и величины заряда. Из (53) следует, что энергия поля отрицательно заряженной частицы с зарядом
Q = Ne определяется суммарной энергией покоя ее 2N электронных масс.
В частности, для одного электрона "размазанного" на сфере радиуса R ® 0 собственная энергия поля совпадает с его удвоенной энергией покоя W = 2mc2. Любопытно отметить, что емкость точечного электрона Ce = r0/4, что в четыре раза меньше его классического радиуса.
Основной вопрос о природе электрона остается до сих пор не выясненным. Как говорил Эйнштейн, "электрон является чужаком в электродинамике". Из электродинамики трудно понять, как может конечный заряд электрона e, рассматриваемый как точечный или находящийся в очень малом объеме, сохраняться в качестве стабильного образования, вопреки действующими между его элементами кулоновыми силами отталкивания. Природа сил, препятствующих взрыву электрона под действием кулоновых сил, нам неизвестна. На решение этой проблемы можно надеяться лишь в общей теории элементарных частиц.
Пуанкаре [1] "в 1906 году ввел поверхностное давление неизвестного происхождения, которое должно было действовать на электрон со всех сторон, как равномерно натянутая пленка".
Эта пленка эквивалентна нашей модели упругих нитей, закрепленных в центре и сдерживающих элементы заряда электрона от разбегания за счет кулоновых сил. В этом давлении Пуанкаре (или силах упругой деформации) должна, по-видимому, скрываться часть энергии покоя электрона. Поэтому электромагнитная масса электрона оказалась больше массы покоя. Часть электромагнитной массы оказалась ответственной за его устойчивость.
Аналогичное удвоение энергии имеет место и в ОТО при рассмотрении полной энергии материи и постоянного гравитационного поля (т.е. полной массы тела), выражаемой через тензор энергии импульса одной только материи [2], [5], [21]. В нашем случае роль гравитационного поля выполняет поле сил связей, (давление Пуанкаре) которые препятствуют кулоновским силам отталкивания и сохраняют жесткость заряженной частицы. По этой причине в формуле (53) происходит удвоение энергии.
Хотя потенциал A0 и энергия W поля точечного заряда оказались конечными, однако выражение для закона Кулона, оказалось справедливым в тетрадах для всей области значений радиуса. Для отличных от нуля тетрадных компонент следует выражение
![]()
которое в точности совпадает с классическим выражением для напряженности поля точечного заряда для любых n и l.
Поле с цилиндрической симметрией
Рассмотрим поле, обладающее цилиндрической симметрией, создаваемое бесконечно длинным заряженным металлическим цилиндром.
Совместим
ось z с осью цилиндра, выбрав начало координат в центре цилиндра. Расчет
поля будем производить в цилиндрической системе координат, воспользуясь для
нахождения потенциала формулой (32), где r' - трехмерное (евклидово)
расстояние от заряда dQ до точки наблюдения, q - угол
между радиусом - вектором ![]() и
и ![]() ,
, ![]()
![]() для каждого элемента заряда dQ
направлен к центру цилиндра перпендикулярно его поверхности. Величина
"ускорения" a0 для зарядов отрицательно заряженной
цилиндрической поверхности (электронов) вычисляется по формуле (33).
для каждого элемента заряда dQ
направлен к центру цилиндра перпендикулярно его поверхности. Величина
"ускорения" a0 для зарядов отрицательно заряженной
цилиндрической поверхности (электронов) вычисляется по формуле (33).
Каждый из зарядов на проводнике будет находиться на поверхности цилиндра и испытывать со стороны создаваемого ими поля силу "отрицательного давления", направленного по внешней нормали к поверхности [11]. Эта сила компенсируется силой со стороны решетки, удерживающей заряды на поверхности цилиндра. Таким образом, рассматриваемая физическая ситуация эквивалентна ситуации, в которой находятся заряды, связанные невесомыми нитями длины R, равной радиусу цилиндра, закрепленные вдоль оси цилиндра. Следовательно, поле, создаваемое каждым из зарядов будет таким же, как если бы каждый из зарядов двигался равноускоренно с ускорением, направленным к оси цилиндра. В согласии с (8) каждый из электронов на поверхности цилиндра принадлежит касательному плоскому пространству, но риманову пространству - времени. Поэтому операция интегрирования по цилиндру происходит в плоском пространстве и является корректной. Интегрируя, как и в случае сферической симметрии, имеем:
![]() (54)
(54)
Найденная формула справедлива при r > R, т.е. для потенциала вне цилиндра. Для потенциала внутри цилиндра при r < R формула примет вид
![]() (55)
(55)
Здесь введены обозначения
![]()
![]()
![]() (56)
(56)
Kk, Ik - цилиндрические функции Бесселя в общепринятых обозначениях [12], g - линейная плотность зарядов. При выборе знака в формулах мы учитываем две возможности. Верхний знак означает, что заряды находятся на поверхности цилиндра с "ускорением", направленным к центру цилиндра (например, на внутреннем электроде цилиндрического конденсатора). Нижний знак соответствует зарядам, находящимся на внутренней поверхности цилиндрической трубы (например, на наружном электроде цилиндрического конденсатора). Очевидно, что "ускорения" зарядов, направленные всегда внутрь металла на внутренней и внешней обкладках конденсатора имеют диаметрально противоположные направления, с чем и связан выбор знаков. На границе цилиндра при r = R обе формулы очевидно совпадают.
Найдем поведение потенциала (54) на больших расстояниях от цилиндра, т.е. полагая r >> R. Используя известное асимптотическое разложение [9], применимое для больших z
![]()
а также известную формулу суммирования
![]() (57)
(57)
находим
![]() (58)
(58)
где m - масса электрона, если цилиндр заряжен отрицательно, или масса ядра металла, при положительном заряде, e - заряд электрона, принимающий отрицательное значение при отрицательном заряде цилиндра и положительное значение (по величине равное заряду электрона) при положительном заряде цилиндра. Очевидно, что при r ® ¥ потенциал стремится к нулю, а не логарифмически расходится, как имеет место при классическом рассмотрении. Таким образом, поведение потенциала на бесконечности резко отличается от классического аналога, что в конечном итоге и приводит к устранению расходимости для энергии электромагнитного поля.
Формула (58) применима не только для больших расстояниях от провода. Величины r1, R1 могут быть очень большими и на самой поверхности цилиндра малого радиуса, если плотности зарядов на проводе велики. Итак, для больших плотностей зарядов потенциал на поверхности цилиндра конечного радиуса из (58) имеет вид
![]() (59)
(59)
Энергия электрического поля вне цилиндрической оболочки может быть вычислена по общей формуле (30) и приводит к соотношению
W = Nmc2. (60)
Величина энергии поля вне проводящей при большой плотности зарядов на оболочке оказалась независимой от знака и величины заряда. Из приведенной формулы следует, что энергия поля отрицательно заряженной оболочки с зарядом Q = Ne на длине h определяется суммарной энергией покоя ее N электронных масс. Для положительно заряженной оболочки роль массы играет масса ядра.
При классическом рассмотрении энергия поля вне оболочки стремится к бесконечности.
Обратим внимание на то, что для поля цилиндра и плоскости в отличие от поля сферы, удвоения энергии не происходит. Причина связана с характером рассматриваемых моделей распределения зарядов и подробно рассмотрена в [5], [21].
Как известно, при классическом рассмотрении потенциал внутри оболочки постоянен и равен потенциалу оболочки, а напряженность электрического поля равна нулю. В поле связанных зарядов это не так. Как видно из решения (55) потенциал внутри оболочки не является постоянной величиной. Отношение внутренней напряженности Eвнутр. внутри цилиндра к внешней напряженности на границе Eвнеш.= Е0 дается формулой
![]() (61)
(61)
Очевидно, что это отношение равно нулю в центре цилиндра и максимально на границе раздела при r = R. Рассмотрим пример. Пусть цилиндр заряжен отрицательно и величина
Е0 = 106 B/м, а радиус цилиндра R = 0.05 м. Тогда
![]() (62)
(62)
Для цилиндра, заряженного положительно, это отношение при тех же параметрах ~ 10-6. При классическом рассмотрении это отношение равно нулю и не зависит от знака заряда. В [5], [21] в разделе "трудности теории связанных зарядов и возможные пути выхода" показано, что эффект является "чисто классическим" и использование квантовой механики, в которой "голая" масса электрона должна заменяться на эффективную массу, уменьшают эффект в несколько десятков раз [13]. Однако существование электрического поля внутри замкнутой металлической оболочки - принципиальное предсказание теории связанных зарядов. В [5], [21] вычислена метрика пространства - времени вне и внутри цилиндра, однако мы этим заниматься не будем. В тетрадах (17) F(0)(1) компонента тензора электромагнитного поля совпадает с классической.
![]() (63)
(63)
Итак, для трех видов симметрии (плоской, сферической и цилиндрической), энергия поля, создаваемая точечными зарядами, не расходится, как это имеет место при классическом рассмотрении, а определяется энергией покоя зарядов, создающих поле. При этом величина заряда выпадает из формул для энергии.
Таким образом, предлагаемый нами подход расширяет область применимости классической теории поля при переходе к достаточно малым расстояниям.
Электромагнитное поле бегущей волны, созданное током связанных зарядов
В работах [15 - 19] нами разработан новый метод для исследования полей излучения бегущих волн тока для системы тонких криволинейных проводов, основанный на непосредственном нахождении тензора электромагнитного поля без промежуточного вычисления запаздывающих потенциалов. При рассмотрении электромагнитного поля излучения не учитывалось, что заряды на поверхности провода испытывают силу отрицательного давления со стороны создаваемого ими поля. Представляет интерес учесть это взаимодействие. Уравнения Максвелла в общем случае совместно с условиями Лоренца будут иметь вид
![]()
![]()
![]() (64)
(64)
Ввиду того, что
![]()
другие уравнения Максвелла
![]()
выполняются тождественно для любой метрики.
В соотношении (64) метрический тензор не известен. Поэтому эти уравнения нельзя непосредственно интегрировать.
В [5], [21] были получены уравнения для нахождения статической плотности зарядов на проводниках произвольной формы, геометрии пространства-времени и электростатического поля, создаваемого такими проводниками.
Аналогичная
процедура применима и при рассмотрении поля от нестационарного тока, но условия
стационарности уже не будут выполнены. Компоненты метрического тензора должны
удовлетворять еще и уравнениям структуры (7). Из сказанного следует, что
решение поставленной задачи в общем виде аналитически затруднительно, поскольку
переменный в пространстве и во времени ток обуславливает (в согласии с
постулатом эквивалентных ситуаций) помимо нестационарного электромагнитного
поля и поле нестационарного неоднородного метрического тензора. Поэтому
предельно упростим задачу, считая, что бегущая волна тока постоянной амплитуды J
распространяется по бесконечному тонкому прямому цилиндрическому проводу. Пусть
провод расположен на оси y3 = z. Требуется вычислить
напряженность электрического ![]() и магнитного
и магнитного ![]() полей вне провода.
полей вне провода.
Без учета взаимодействия зарядов на проводе с создаваемым ими электрическим полем решение тривиально. Напряженность магнитного поля определяется формулой
![]()
![]() (65)
(65)
Для электрического поля имеем
![]()
![]() (66)
(66)
где связь между линейной плотностью заряда g и током J дается простым соотношением
![]()
![]() (67)
(67)
Попытаемся ответить на вопрос: "Что нового по сравнению с (65) и (66) дает тот факт, что заряды на поверхности провода являются связанными?"
1. Связанные заряды изменяют геометрию пространства - времени, что подробно исследовано в [5], [21].
2. Так как магнитное поле не действует на покоящиеся пробные заряды, то оно не изменяет силы реакции связи, удерживающие эти заряды неподвижными в электрическом поле. Однако, созданное током магнитное поле, окружающее проводник, действует на поверхность проводника, сжимая провод вдоль радиуса. Так как мы считаем проводник идеально проводящим, то текущий по проводнику ток является поверхностным током [11].
Плотность заряда g считаем отрицательной, так что по поверхности проводника движутся электроны, средняя скорость v которых ничтожно мала по сравнению с фазовой скоростью распространения бегущей волны тока, равной скорости света c. На каждый из электронов со стороны магнитного поля тока будет действовать сила Лоренца. Как известно [11], сжимающее давление определяется формулой
![]() (68)
(68)
где ![]() - единичный вектор,
направленный вдоль радиуса провода, He = Hf -
магнитное поле снаружи провода у его поверхности. Таким образом, сжимающее
давление по величине равно плотности энергии магнитного поля. Величина силы F,
действующей на кусок цилиндрического провода площади S, на которой
размещены N электронов равна очевидно
- единичный вектор,
направленный вдоль радиуса провода, He = Hf -
магнитное поле снаружи провода у его поверхности. Таким образом, сжимающее
давление по величине равно плотности энергии магнитного поля. Величина силы F,
действующей на кусок цилиндрического провода площади S, на которой
размещены N электронов равна очевидно
![]() (69)
(69)
Отсюда в согласии с (67) на каждый электрон действует сила
![]() (70)
(70)
При
выводе (70) учли, что Er = 4ps, где s -
поверхностная плотность заряда. Итак, сила со стороны магнитного поля на
поверхностные электроны с точностью до знака совпала с силой со стороны
электрического поля. Таким образом, если в электростатике силой реакции связи,
удерживающей создающие поле заряды на поверхности проводника неподвижными, была
сила со стороны металлической решетки, то в магнитостатике эту роль выполняет
сила Лоренца. В согласии с "постулатом эквивалентных ситуаций",
решение для электрического поля от бегущей ступенчатой волны тока, будет такое
же, как и для электростатического поля заряженной нити. Так как компоненты
метрического тензора входят в уравнения Максвелла, то магнитное поле зависит от
метрики. Из (54) при R![]() имеем для тонкой нити
имеем для тонкой нити
![]()
![]() (71)
(71)
![]()
![]() (72)
(72)
На
поверхности цилиндра величина поля ![]() совпадает с тетрадной компонентой F(0)(1).
Поэтому для величины
совпадает с тетрадной компонентой F(0)(1).
Поэтому для величины ![]() имеем
имеем
![]()
![]() (73)
(73)
E0 -
напряженность поля на поверхности цилиндра. Основываясь на работе [5], [21],
для величины векторного потенциала ![]() имеет вид
имеет вид
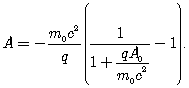 (74)
(74)
Тензор
электромагнитного поля для рассматриваемой задачи имеет отличные от нуля
компоненты ![]()
![]() и
и ![]() , для которых имеем
, для которых имеем
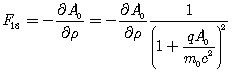 . (75)
. (75)
Для отличных от нуля тетрадных компонент тензора поля с помощью тетрад (17) находим
![]()
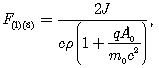
![]() . (76)
. (76)
Итак, напряженность электрического поля в тетрадах в точности совпадает с классическим выражением, а напряженность магнитного поля содержит релятивистскую поправку. Найдем отличные от нуля тетрадные компоненты тензора энергии-импульса.
![]()
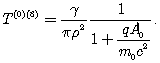 (77)
(77)
Вычислим энергию поля от элемента заряженной нити длины h:
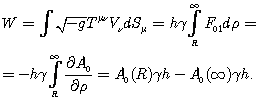 (78)
(78)
Так
как по доказанному в [5] A0(![]() )=0, а нить по условию имеет радиус R
)=0, а нить по условию имеет радиус R![]() 0, то соотношение
(78) примет вид
0, то соотношение
(78) примет вид
![]() (79)
(79)
Для больших расстояний от нити можно воспользоваться известными асимптотическими разложениями для функций Бесселя [14]:
![]() ,
, ![]() . (80)
. (80)
Из последних формул следует, что энергия электромагнитного поля внутри цилиндра длины h и бесконечного радиуса является конечной величиной, что резко отличается от классического значения электромагнитной энергии поля бегущей волны которая бесконечно
велика.
При очень большой плотности зарядов на нити, т.е. при выполнении условия
![]() (81)
(81)
имеем для энергии выражение
![]() , (82)
, (82)
где N - число электронов на длине h нити. Неравенство (81) эквивалентно неравенству
![]() , (83)
, (83)
где ток выражен в амперах.
Для больших токов предельная энергия электромагнитного поля внутри цилиндра высоты и бесконечного радиуса равна удвоенной массе покоя N электронов, создающий ток на нити. Энергия электромагнитного поля поровну распределяется между энергиями электрического и магнитного полей.
В реальном случае справедливо другое неравенство
![]() (84)
(84)
Для слабых полей при условии (84), используя известные разложения для функций Бесселя [14], имеем:
![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]() (85)
(85)
где C = 0.577215... - есть постоянная Эйлера.
Выражение (85) с точностью до значения постоянных в потенциале совпадает с классическим выражением. Однако метрика пространства-времени даже в случае слабого поля остается римановой.
Итак, как для сильного, так и для слабого полей энергия электрического поля от бегущей волны тока We равна энергии магнитного поля Wm. Приравнивая соответствующие соотношения для энергий их классическим аналогам,
![]()
![]() (86)
(86)
находим погонную индуктивность Lm и погонную емкость Ce бесконечно тонкого провода
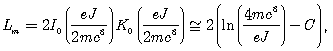
![]() (87)
(87)
Вычисление погонной индуктивности и емкости бесконечно тонкого провода при классическом рассмотрении приводит к принципиальным трудностям, связанным с бесконечной энергией поля точечного заряда [1]. В нашем случае таких трудностей не возникает как для слабого, так и для сильных полей. Рассмотрим причины возникновения трудностей.
Индуктивность единицы длины бесконечно длинного провода зависит от длины провода h и вычисляется в наших обозначениях по формуле из [1]:
![]()
![]() (88)
(88)
Для погонной индуктивности коаксиальной линии имеем из [20] соотношение
![]()
![]() (89)
(89)
где b - внешний, а R - внутренний радиус коаксиальной линии.
Для бесконечной коаксиальной линии погонная индуктивность не зависит от длины провода. Переход к однопроводной линии от коаксиальной должен получиться при стремлении внешнего радиуса к бесконечности. Однако этого не происходит, индуктивность в согласии с (89) стремится при этом к бесконечности.
Из анализа видно, что зависимость погонной индуктивности длинного провода от длины провода - явная трудность классической теории поля.
Рассмотрим формулу (87), для слабых полей (малых токов) в виде удобном для сравнения с экспериментом:
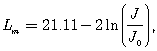
![]()
![]()
где J0 равен одному амперу и ток J измеряется в амперах. Рассчитаем по формуле (90) погонную емкость провода длиной 10 метров и радиуса 0.06 миллиметра при токе J = 0.1 А. Для этого случая имеем Lm = 25.715. Увеличив ток в десять раз, получим Lm = 21.11.
Расчет по формуле (88) дает Lm=24.048. Таким образом, несмотря на принципиально разные формулы расчета индуктивности, результаты оказались близкими.
В [5] показано, что для малых токов параметры для коаксиальной линии совпадают с классическими.
Для сильных токов будут проявляться различия. Общая формула для погонной индуктивности коаксиального кабеля будет иметь вид:
![]() (91)
(91)
Для больших токов можно воспользоваться известными асимптотическими разложениями для функций Бесселя (80), что приводит к соотношению
![]() . (92)
. (92)
Энергия магнитного поля на единице длины в коаксиальной линии между центральным проводом и внешней оболочкой для сильных токов имеет вид
![]() (93)
(93)
При b![]() или R
или R![]() 0 энергия магнитного
поля совпадает с энергией покоя масс зарядов на единице длины центрального
провода. При этом заряды и токи из рассмотрения выпадают. Таким образом, очень
сильные токи (J >> 105 A) создают в пространстве
магнитное поле внутри цилиндра длины h и бесконечного радиуса, энергия
которого определяется произведением числа зарядов на длине h на энергию
массы покоя заряда. При классическом рассмотрении магнитная энергия стремится к
бесконечности, что лишено физического смысла и является принципиальной
трудностью классической теории поля.
0 энергия магнитного
поля совпадает с энергией покоя масс зарядов на единице длины центрального
провода. При этом заряды и токи из рассмотрения выпадают. Таким образом, очень
сильные токи (J >> 105 A) создают в пространстве
магнитное поле внутри цилиндра длины h и бесконечного радиуса, энергия
которого определяется произведением числа зарядов на длине h на энергию
массы покоя заряда. При классическом рассмотрении магнитная энергия стремится к
бесконечности, что лишено физического смысла и является принципиальной
трудностью классической теории поля.
Заключение
Перечислим основные результаты, полученные в работе.
1. Найдено точное статическое решение для поля заряда в равноускоренной НСО, реализуемое в римановом пространстве - времени. Это решение позволяет в принципе отыскивать структуру пространства - времени и находить поля от заряженных проводников произвольной формы.
2. Найдено точное выражение для поля и геометрии пространства - времени вне заряженного металлического шара и точное конечное выражение для энергии поля точечного заряда. Поэтому устраняется основная трудность классической и квантовой электродинамики, приводящая к бесконечной собственной энергии поля точечного заряда.
3. Доказано, что погонная энергия поля вне бесконечного цилиндра и нити является конечной величиной, что резко отличается от классического значения энергии, которая бесконечно велика.
4. Предсказан возможный эффект присутствия электростатического поля внутри проводящей заряженной полости (отсутствие полной экранировки).
Работа является попыткой установления связей между кривизной пространства - времени и классическими полями связанных структур.
Автор выражает искреннюю признательность к.т.н., с.н.с. Меньковой Е.Р. (ВНИИОФИ) за ценные замечания и неоценимую помощь при подготовке этой работы к печати.
Литература
1. Зоммерфельд А. Электродинамика. - M.: ИЛ, 1958.
2. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Наука, 1973.
3. Подосенов С.А. Геометрические свойства неинерциальных систем отсчета в релятивистской механике // В сб.: Дискуссионные вопросы теории относительности и гравитации. - M.: Наука, 1982. С. 95-103.
4. Подосенов С.А. Структура пространства-времени и поля связанных зарядов // Изв. вузов, сер. физ. 1997. N 10. C. 63-74.
5. Подосенов С.А. Пространство, время и классические поля связанных структур. - М.: Компания "Спутник+", 2000 (445 стр.)
6. Desloge E.A. Nonequivalence of uniformly acceleration reference frame and frame at rest in a uniform gravitational field // Am. J. Phys. 1989. V. 57, N 12. P. 1121-1125.
7. Desloge E.A. Relativistic motion of a free Particles in a uniform gravitational field // Int. J. Theor. Phys. 1990. V. 29. N 2. P.193-208.
8. Родичев В.И. Теория тяготения в ортогональном репере. - M.: Наука, 1974. 184 c.
9. Иваницкая О.С. Обобщенные преобразования Лоренца и их применение. - Минск: Наука и техника, 1969.
10. Владимиров Ю.С. Системы отсчета в теории гравитации. - M.: Энергоиздат, 1982.
11. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. - M.: Наука, 1982.
12. Справочник по специальным функциям. Под ред. Абрамовица М. и Стиган И. Пер. с англ. - M.: Наука, 1979.
13. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. т.9. Квантовая механика (II). - М.: МИР, 1967.
14. Тихонов А.Н. и Самарский А.А. Уравнения математической физики. - М.: Наука, 1972.
15. Podosenov S.A., Svekis Y.G., and Sokolov A.A. Transient Radiation of Traveling Waves by Wire Antennas // IEEE Trans. Electromagn. Compat. 1995. V. 37. N 3. P. 367-383.
16. Mikheev O.V., Podosenov S.A., Sakharov K.Y., Svekis Y.G., Sokolov A.A., and Turkin V.A. New Method for Calculating Pulse Radiation from an Antenna with a Reflector // IEEE Trans. Electromagn. Compat. 1997. V. 39. N 1. P.48-54.
17. Podosenov S.A. Comments on “Transient Radiation of Traveling-Wave Wire Antennas” // IEEE Trans. Electromagn. Compat. 2001. V. 43. N 2. P.246-248
18. Mikheev O.V., Podosenov S.A., Sakharov K.Y., Sokolov A.A., and Turkin V.A. Approximate Calculation Methods for Pulse Radiation of a TEM-horn Array// IEEE Trans. Electromagn. Compat. 2001. V. 43. N 1. P. 67-74.
19. Подосенов С.А., Соколов А.А. Излучение и измерение импульсных электромагнитных полей. - М.: Компания "Спутник+", 2000 (250 стр.)
20. Вайнштейн Л.А. Электромагнитные волны. - М.: Радио и связь, 1988.
21. Подосенов С.А., Потапов А.А., Соколов А.А. Импульсная электродинамика широкополосных радиосистем и поля связанных структур. – М.: Издательство «Радиотехника», 2003 (720 стр.)
22. Подосенов С.А. Некоторые возможности в нелинейной классической теории электромагнитного поля связанных зарядов. (Часть 1) // Нелинейный мир, N 1-2, т.1, 2003.
23. Подосенов С.А. Некоторые возможности в нелинейной классической теории электромагнитного поля связанных зарядов. (Часть 2) // Нелинейный мир, вып.1. N 1, т.2, 2004.
Ключевые слова: тензор энергии-импульса, метрика, поля, конгруенции мировых линий, связанные заряды, устранение расходимости полей, тетрады, емкость, индуктивность.
Краткая биографическая справка
Подосенов С.А. родился в 1937 г. в г. Архангельске. Образование: Физический факультет МГУ. Физик – теоретик по квантовой механике и электродинамике. Закончил аспирантуру каф. физики МВТУ им. Баумана, где защитил диссертацию на тему “Релятивистская механика деформируемой среды в тетрадной формулировке”. Ведущий научный сотрудник "Всероссийского научно-исследовательского института оптико-физических измерений". Член ИИЭР (IEEE) (USA) с 1996 г. Действительный член Нью-Йоркской Академии наук с 1997г. Лауреат Премии Правительства Российской Федерации 2002 г. в области науки и техники. Международным Биографическим Центром (Кембридж, Англия) признан "Международным Ученым Года 2002". Автор более 60 научных работ в России и за рубежом, а также 3 монографий: "Пространство, время и классические поля связанных структур" (445 стр.), "Излучение и измерение импульсных электромагнитных полей" (250 стр.), выпущенных в Москве Издательством "Компания Спутник +" (2000 г.) и монографии “Импульсная электродинамика широкополосных радиосистем и поля связанных структур”. – М.: Издательство “Радиотехника”, 2003, (720 стр.) под редакцией д.ф.- м.н. А.А. Потапова.
E-mail: podosenov@mtu-net.ru, podosenov@mail.ru
Homepage: http://www.staspodosenov.narod.ru/
|
|
|