УДК 621.396.67
ПРИМЕНЕНИЕ ТЕОРИИ ЦИФРОВОЙ ФИЛЬТРАЦИИ ПРИ ИССЛЕДОВАНИИ РАДИОСИСТЕМ В ЧАСТОТНО-ВРЕМЕННОЙ И ПРОСТРАСТВЕННОЙ ОБЛАСТЯХ
Ю. Н. Горбунов1, В. А. Гончаров2, Т. М. Волкова3
1 ФГУП «ЦНИРТИ им. академика А.И. Берга», Москва
2
ОАО «Концерн радиостроения «Вега», Москва
3 ФГУП «ВНИИОФИ», Москва
Получена 10 августа 2012 г.
Аннотация. В работе для анализа линейных радиосистем введены конечные разности и разностные уравнения. На основании введенных уравнений построена каноническая схема, по которой цифровые фильтры классифицируются на рекурсивные, нерекурсивные и сложные. По методу множителей Лагранжа прооптимизированы весовые коэффициенты нерекурсивных цифровых фильтров произвольного порядка. Проанализирован коэффициент улучшения передаточной функции режекторного фильтра.
Ключевые слова: разностные уравнения, каноническая схема, радиосистемы, передаточная функция, оптимизация весовых коэффициентов, коэффициент улучшения.
Abstract. In the work the difference equations are entered for the analysis of linear radio systems. Canonical scheme based on the entered of equations is constructed.
Under this scheme digital filters are classified as recursive, non-recursive and complex. According to the method of multipliers Lagrange weights coefficients of nonrecursive digital filters of arbitrary order are optimized. Coefficient of improvement the transfer function of the notch filter is analyzed.
Keywords: difference equations, canonical scheme, radio system, transfer function, optimization of the weight coefficients, coefficient of the improvement.
Теоретические предпосылки и постановка проблемы.
Известно, что характеристика направленности антенной системы с произвольной конфигурацией теоретически находится после несложных преобразований Фурье. Направленность антенной решетки исследуется из соображений квантования сигнала в пространстве, по аналогии с вычислением передаточной функции аналоговых фильтров (как активных, так и пассивных) в частотной области и цифровых фильтров (нерекурсивных и рекурсивных) во временной области. Поэтому проблема расчета и оптимизации радиосистем (многополюсников, антенных решеток) в частотно-пространственно-временной области для современной теории цифровой фильтрации весьма актуальна.
Конечные разности и разностные уравнения.
В теории цифровой фильтрации (см., например [1]) особенности построения
цифровых фильтров (ЦФ) обусловлены дискретным временем. В дискретном времени
такие известные операции как дифференцирование и интегрирование теряют обычный
математический и физический смысл. Рассмотрим пример простейшей системы первого
порядка (см. рис. 1). В этой системе сигнал ![]() представляет
собой сигнал
представляет
собой сигнал ![]() , задержанный на один интервал Т дискретизации. Система описывается уравнением:
, задержанный на один интервал Т дискретизации. Система описывается уравнением:
![]() , (1)
, (1)
откуда
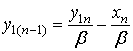 . (2)
. (2)
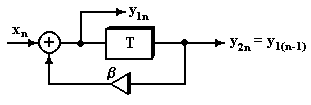
Рис. 1. Рециркулятор – экспоненциальный накопитель
Использовав уравнения (1) и (2), запишем
![]() , (3)
, (3)
где ![]() - оператор первых разностей, определяемый следующим
образом:
- оператор первых разностей, определяемый следующим
образом:
![]() . (4)
. (4)
Уравнение (3), записанное через значения ![]() и первую
разность
и первую
разность ![]() , по форме аналогично дифференциальному уравнению
первого порядка. Более сложные системы описываются разностными уравнениями
более высокого порядка.
, по форме аналогично дифференциальному уравнению
первого порядка. Более сложные системы описываются разностными уравнениями
более высокого порядка.
Для
дискретного сигнала ![]() конечную разность
конечную разность ![]() -го порядка
-го порядка
![]() через конечную разность
через конечную разность ![]() -го порядка
определяют так:
-го порядка
определяют так:
![]() ;
;
![]() ;
;
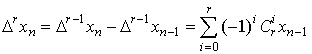 . (5)
. (5)
Здесь ![]() -
число сочетаний из
-
число сочетаний из ![]() по
по ![]() .
.
Из
формулы (5) видно, что для вычисления разности ![]() -го порядка
требует знания
-го порядка
требует знания ![]() значений
значений ![]() .
.
Использовав
введенные обозначения, запишем разностное уравнение ![]() -го
порядка, описывающее линейную дискретную систему с постоянными параметрами:
-го
порядка, описывающее линейную дискретную систему с постоянными параметрами:
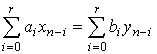 . (6)
. (6)
Данное уравнение составлено по аналогии с дифференциальным уравнением ![]() -го
порядка, описывающим непрерывную линейную систему с постоянными параметрами.
-го
порядка, описывающим непрерывную линейную систему с постоянными параметрами.
Исходное дифференциальное уравнение-прототип имеет вид:
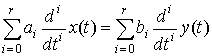 , (7)
, (7)
где ![]() - входной, а
- входной, а ![]() - выходной
сигналы;
- выходной
сигналы; ![]() - постоянные параметры,
- постоянные параметры, ![]() .
.
Классификация цифровых фильтров.
Приняв ![]() , из (6) получим уравнение, определяющее ЦФ:
, из (6) получим уравнение, определяющее ЦФ:
![]()
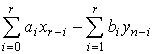 , (8)
, (8)
т. е. в общем случае сигнал на выходе ЦФ есть линейная комбинация отсчетов входного и выходного сигналов.
Часто встречаются различные частные случаи формулы (8).
Если
коэффициенты ![]() равны нулю, то ЦФ называется нерекурсивным (без
обратных связей). Если коэффициенты
равны нулю, то ЦФ называется нерекурсивным (без
обратных связей). Если коэффициенты ![]() равны
нулю, то ЦФ называется рекурсивным (с обратными связями).
равны
нулю, то ЦФ называется рекурсивным (с обратными связями).
Из структурной схемы ЦФ, построенной по уравнению (8) (см. рис. 2), могут быть получены частные структуры нерекурсивного и рекурсивного фильтров.
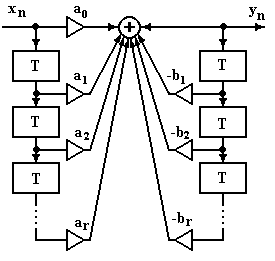
Рис. 2. Каноническая схема цифрового
фильтра r-го порядка
В случае,
если ![]() , имеем простейший цифровой дифференциатор, а если
, имеем простейший цифровой дифференциатор, а если ![]()
![]()
![]()
![]() , то - схему экспоненциального накопителя (см. рис. 1).
, то - схему экспоненциального накопителя (см. рис. 1).
Импульсные и частотные характеристики.
ЦФ по существу является устройством (алгоритмом) преобразования входной последовательности
![]() в выходную
в выходную ![]() . Вид оператора
. Вид оператора ![]() зависит от
свойств конкретной системы. ЦФ достаточно часто описывается импульсной характеристикой
(ИХ)
зависит от
свойств конкретной системы. ЦФ достаточно часто описывается импульсной характеристикой
(ИХ) ![]() , понимаемой как отклик системы в произвольный момент
времени п на импульс единичной амплитуды, воздействующей в момент
времени
, понимаемой как отклик системы в произвольный момент
времени п на импульс единичной амплитуды, воздействующей в момент
времени ![]() (рис 3, а). Связь выхода
(рис 3, а). Связь выхода ![]() со входом
со входом ![]() с
использованием понятия ИХ проиллюстрирована на рис. 3, б.
с
использованием понятия ИХ проиллюстрирована на рис. 3, б.
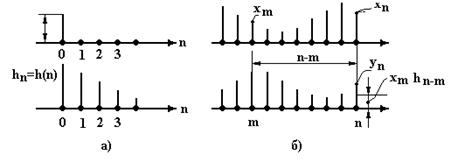
Рис. 3. Связь выхода yn со входом xn с использованием понятия импульсной характеристики hn
В линейном ЦФ вход и выход связаны соотношением типа свертки
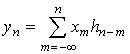 , (9)
, (9)
где ![]() ― отклик ЦФ на единичный импульс, воздействующий
в момент времени
― отклик ЦФ на единичный импульс, воздействующий
в момент времени ![]() (рис 3, б).
(рис 3, б).
Для
физически реализуемых систем реакция не может наступить раньше воздействия, т.
е. ![]() для
для ![]() . Учитывая
это, верхний предел в формуле (9) можно заменить на
. Учитывая
это, верхний предел в формуле (9) можно заменить на ![]() .
.
Пусть на
входе фильтра действует комплексный гармонический сигнал ![]() .
После квантования по времени имеем на входе ЦФ
.
После квантования по времени имеем на входе ЦФ ![]() , а на
выходе
, а на
выходе
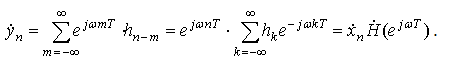 (10)
(10)
Здесь
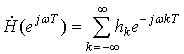 (11)
(11)
частотная характеристика (ЧХ) ЦФ.
Нетрудно заметить, что ЧХ является периодической функцией частоты ![]() ,
причем ее период равен
,
причем ее период равен ![]() .
.
Соотношение между спектрами непрерывных и дискретных сигналов.
Непрерывный сигнал ![]() и его
спектр
и его
спектр ![]() связаны между собой парой преобразования Фурье:
связаны между собой парой преобразования Фурье:
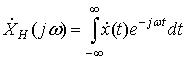 , (12)
, (12)
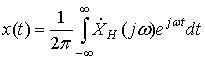 . (13)
. (13)
Аналогичные соотношения для квантованного по времени сигнала имеют вид:
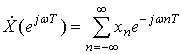 , (14)
, (14)
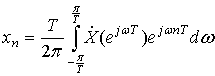 . (15)
. (15)
Для установления связи между спектрами непрерывных и дискретизированных
сигналов достаточно в выражение (13) подставить ![]() и
приравнять его к выражению (15). После несложных преобразований, связанных с
заменой интеграла с бесконечными пределами бесконечной суммой интегралов на
интервалах
и
приравнять его к выражению (15). После несложных преобразований, связанных с
заменой интеграла с бесконечными пределами бесконечной суммой интегралов на
интервалах ![]() и изменением порядка действий, получим
и изменением порядка действий, получим
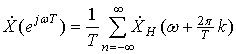 . (16)
. (16)
Таким образом, спектр дискретизированного колебания образуется наложением
спектров непрерывного колебания, смещенных по оси частот на величины ![]() ,
,
![]()
На рис. 4
приведены примеры наложения спектров для случаев ограниченного и
неограниченного в полосе ![]() спектров
непрерывного колебания.
спектров
непрерывного колебания.
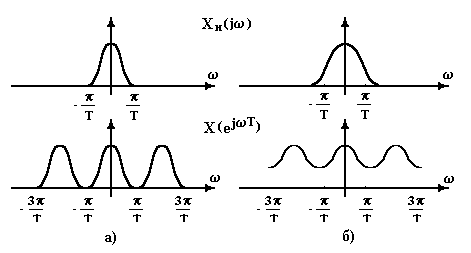
Рис. 4. Примеры наложения спектров непрерывного колебания
Частотные характеристики КИХ-фильтров.
Цифровые фильтры с конечной импульсной характеристикой, или КИХ-фильтры, получили широкое распространение при построении радиотехниеских систем. КИХ-фильтры реализуются, как правило, по нерекурсивной схеме и обладают рядом положительных качеств, обусловленных отсутствием обратных связей.
Обозначим
через ![]() единичный импульс
единичный импульс
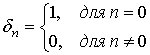 , (17)
, (17)
тогда по определению ИХ из формулы (8) для нерекурсивного фильтра имеем:
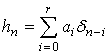 . (18)
. (18)
Использовав (9) и (18), запишем выражение для ЧХ нерекурсивного фильтра:
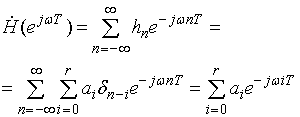 . (19)
. (19)
В общем случае ЧХ – комплексная функция и поэтому может быть выражена через действительную и мнимую части (в декартовой системе)
![]()
![]() (20)
(20)
или через модуль и фазу (в полярной системе)
![]() , (21)
, (21)
причем
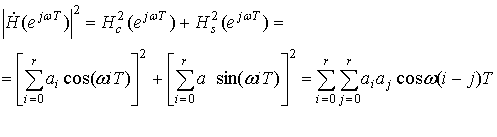 ;
;
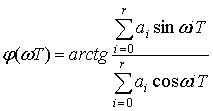 . (22)
. (22)
Зависимость модуля ![]() от частоты
от частоты ![]() называется
амплитудно-частотной характеристикой (АЧХ).
называется
амплитудно-частотной характеристикой (АЧХ).
Зависимость фазы ![]() от частоты
от частоты
![]() называется фазочастотной, характеристикой (ФЧХ).
называется фазочастотной, характеристикой (ФЧХ).
Преобразование Фурье для дискретизированного во времени сигнала, преобразование Лапласа, z-преобразование.
Для определения понятия ДПФ, прежде введем понятие о z-преобра-зовании.
Предположим, что дискретная последовательность ![]() состоит из
состоит из
![]() отсчетов
отсчетов ![]() , тогда ее преобразование Фурье согласно (14)
, тогда ее преобразование Фурье согласно (14)
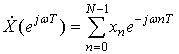 . (23)
. (23)
Путем умножения выражения (23) на ![]() получим
преобразование Лапласа для дискретного сигнала
получим
преобразование Лапласа для дискретного сигнала
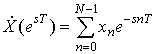 , (24)
, (24)
где ![]() - переменная преобразования Лапласа;
- переменная преобразования Лапласа; ![]() -
вещественная переменная.
-
вещественная переменная.
Введем обозначение ![]() , для
последовательности
, для
последовательности ![]() получим соотношение, определяющее
получим соотношение, определяющее ![]() -
преобразование:
-
преобразование:
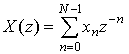 . (25)
. (25)
Таким образом, ![]() -преобразование
с переменной
-преобразование
с переменной ![]() является обобщением преобразования Фурье для
дискретного сигнала, использующего переменную
является обобщением преобразования Фурье для
дискретного сигнала, использующего переменную ![]() .
Соотношение между
.
Соотношение между ![]() - преобразованием и преобразованием (23) такое же, что
и соотношение между преобразованием Лапласа переменной
- преобразованием и преобразованием (23) такое же, что
и соотношение между преобразованием Лапласа переменной ![]() и обычным
преобразованием Фурье с переменной
и обычным
преобразованием Фурье с переменной ![]() .
.
Дискретное преобразование Лапласа (24) и ![]() -
преобразование (25) на комплексных плоскостях
-
преобразование (25) на комплексных плоскостях ![]() и
и ![]() образуют
поверхности. Сечение поверхности преобразования Лапласа плоскостью
образуют
поверхности. Сечение поверхности преобразования Лапласа плоскостью ![]() образует
ЧХ обычной системы. Для дискретной системы ЧХ (23) образуется пересечением
поверхности
образует
ЧХ обычной системы. Для дискретной системы ЧХ (23) образуется пересечением
поверхности ![]() - преобразования с цилиндрической поверхностью
- преобразования с цилиндрической поверхностью ![]() .
.
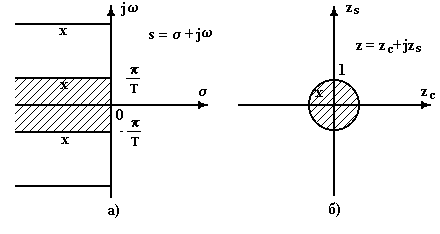
Рис. 5. Комплексные декартовая и полярная плоскости
Учитывая, что ![]() , где
, где ![]() - модуль,
а
- модуль,
а ![]() - фаза комплексной переменной
- фаза комплексной переменной ![]() , можно
сказать, что мнимая ось в комплексной плоскости
, можно
сказать, что мнимая ось в комплексной плоскости ![]() трансформируется
в окружность единичного радиуса на плоскости
трансформируется
в окружность единичного радиуса на плоскости ![]() , а полоса
частот
, а полоса
частот ![]() на плоскости
на плоскости ![]() (рис. 5)
отображается в круг единичного радиуса на плоскости
(рис. 5)
отображается в круг единичного радиуса на плоскости![]() .
.
Определение ДПФ.
Осуществим дискретизацию спектра (23) по частоте, заменив его счетным
множеством точек ![]() , взятых через интервалы
, взятых через интервалы ![]() . В
результате получим последовательность отсчетов:
. В
результате получим последовательность отсчетов:
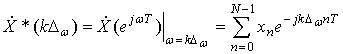 . (26)
. (26)
ДПФ последовательности ![]() обычно
определяют как преобразование (26) для шага дискретизации по частоте
обычно
определяют как преобразование (26) для шага дискретизации по частоте ![]() ,
т.е. период
,
т.е. период ![]() разбивают на
разбивают на ![]() участков
шириной
участков
шириной ![]() .
.
Можно
сказать, что при таком определении число возможных значений спектра ![]() оказывается
равным
оказывается
равным ![]() , т.е.
, т.е. ![]() .
.
Тогда прямое ДПФ можно представить в виде
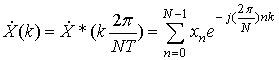 ,
,
![]() , (27)
, (27)
а обратное ДПФ
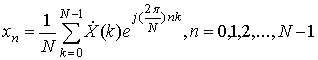 . (28)
. (28)
Использовав геометрическую трактовку ![]() -
преобразования, ДПФ можно определить как оценку
-
преобразования, ДПФ можно определить как оценку ![]() -
преобразования конечной (или периодической) последовательности
-
преобразования конечной (или периодической) последовательности ![]() в
в
![]() точках на
точках на ![]() -плоскости,
равномерно расположенных вдоль единичной окружности под углами
-плоскости,
равномерно расположенных вдоль единичной окружности под углами ![]() .
.
Передаточная функция нерекурсивного режекторного фильтра.
Полагая, что ЦФ
имеет порядок ![]() , воздействуем оператором
, воздействуем оператором ![]() - преобразования
на левую и правую части (8), в результате получим
- преобразования
на левую и правую части (8), в результате получим
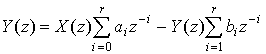 (29)
(29)
Использовав (29), можно получить передаточную функцию цифрового фильтра (ЦФ)
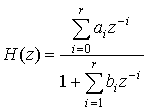 . (30)
. (30)
В нерекурсивном ЦФ все коэффициенты ![]() равны
нулю, поэтому
равны
нулю, поэтому
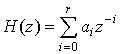 . (31)
. (31)
Подставив в формулу (31) ![]() , можно
получить ЧХ нерекурсивного цифрового фильтра
, можно
получить ЧХ нерекурсивного цифрового фильтра
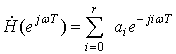 . (32)
. (32)
Если ЦФ является режекторным фильтром (РФ), то сигнал пассивной помехи от
неподвижных местных предметов должен подавляться, поэтому весовые коэффициенты ![]() при
при
![]() должны удовлетворять условию
должны удовлетворять условию 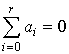 .
.
Этому условию удовлетворяют, например, знакочередующиеся биномиальные
коэффициенты, соответствующие ЦФ в виде ![]() - кратного череспериодного
компенсатора (ЧПК). Действительно, для
- кратного череспериодного
компенсатора (ЧПК). Действительно, для ![]() - кратного ЧПК
- кратного ЧПК
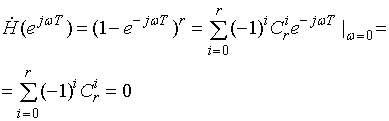 , (33)
, (33)
где ![]() - число сочетаний из
- число сочетаний из ![]() по
по ![]() .
Равенство нулю суммы знакопеременных биномиальных коэффициентов определяются
свойствами треугольника Паскаля.
.
Равенство нулю суммы знакопеременных биномиальных коэффициентов определяются
свойствами треугольника Паскаля.
На плоскости ![]() передаточная функция
передаточная функция ![]() - кратного ЧПК имеет
- кратного ЧПК имеет ![]() - кратного
ноль в точке
- кратного
ноль в точке ![]() , поскольку
, поскольку
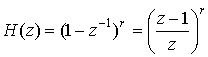 . (34)
. (34)
Таким образом, полученная в ходе анализа канонической схемы и математических преобразований передаточная функция нерекурсивного цифрового фильтра является универсальной. На основе выведенной передаточной функции могут быть реализованы не только аппаратно-алгоритмические комплексы и СВЧ-многополюсники, но и достаточно сложные антенные системы [2-5].
Оптимизация весовых коэффициентов нерекурсивного цифрового фильтра.
Критерии, используемые для определения оптимального набора значений
весовых коэффициентов фильтра, могут быть самыми различными [6]. Довольно часто
используют критерии максимума среднего улучшения. Максимизация среднего
улучшения достигается сведением до минимума знаменателя относительно ![]() при
условии, что числитель
при
условии, что числитель 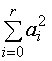 постоянный
(он определяет передачу шума). Используя метод множителей Лагранжа, образуем
величину
постоянный
(он определяет передачу шума). Используя метод множителей Лагранжа, образуем
величину
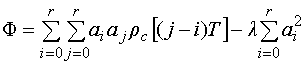 , (35)
, (35)
где ![]() - множитель Лагранжа.
- множитель Лагранжа.
Дифференцирование уравнения (35) относительно ![]() приводит к
следующему условию для экстремума:
приводит к
следующему условию для экстремума:
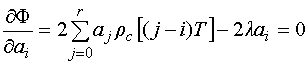 . (36)
. (36)
Здесь ![]()
Уравнение (36) имеет нетривиальное решение для набора ![]() .
Решение задачи оптимизации показывает, что неопределенный множитель Лагранжа
является характеристическим числом корреляционной матрицы помехи
.
Решение задачи оптимизации показывает, что неопределенный множитель Лагранжа
является характеристическим числом корреляционной матрицы помехи ![]() .
Оптимальный набор весовых коэффициентов
.
Оптимальный набор весовых коэффициентов ![]() - это
набор, при котором характеристическое число
- это
набор, при котором характеристическое число ![]() принимает
наименьшее значение, поскольку
принимает
наименьшее значение, поскольку ![]() .
.
При необходимости учета теплового шума вместо матрицы помехи ![]() следует
использовать матрицу смеси «помеха+шум»
следует
использовать матрицу смеси «помеха+шум» ![]() , элементы
которой определяются через элементы матрицы шума
, элементы
которой определяются через элементы матрицы шума ![]() .
.
Оптимизация коэффициентов ![]() при
применении матрицы
при
применении матрицы ![]() приводит к тому, что весовые коэффициенты ЦФ по сравнению
со схемой r -
кратного ЧПК отличаются от биноминальных, а нули ЧХ становятся
комплексно-сопряженными. Однако, если помеха сильно коррелирована и отношение
мощности помехи к мощности шума
приводит к тому, что весовые коэффициенты ЦФ по сравнению
со схемой r -
кратного ЧПК отличаются от биноминальных, а нули ЧХ становятся
комплексно-сопряженными. Однако, если помеха сильно коррелирована и отношение
мощности помехи к мощности шума 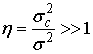 ,
биномиальные весовые коэффициенты
,
биномиальные весовые коэффициенты ![]() ,
соответствующие
,
соответствующие ![]() - кратному ЧПК, удовлетворяют условию оптимальности.
- кратному ЧПК, удовлетворяют условию оптимальности.
Производя оценку на единичном круге, где ![]() , получаем
ЧХ
, получаем
ЧХ ![]() - кратного ЧПК
- кратного ЧПК
![]() . (37)
. (37)
Расположение нулей на ![]() - плоскости
и нормированные к шуму модули ЧХ
- плоскости
и нормированные к шуму модули ЧХ ![]()
![]() -
кратного ЧПК показаны на рис. 6 (а – комплексная плоскость, б – ЧХ).
-
кратного ЧПК показаны на рис. 6 (а – комплексная плоскость, б – ЧХ).
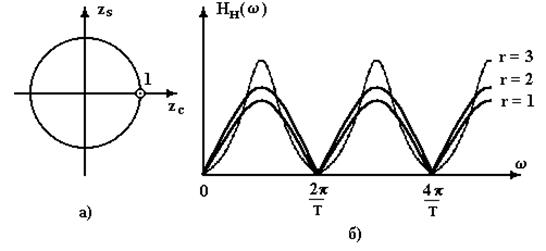
Рис. 6. Положение нулей на комплексной z-плоскости и частотная характеристика r-кратного череспериодного компенсатора пассивных помех
Анализ коэффициента улучшения.
Определим улучшение отношения сигнал/помеха в нерекурсивном ЦФ ![]() -го
порядка, на вход которого поступает аддитивная смесь
-го
порядка, на вход которого поступает аддитивная смесь ![]() гармонического
сигнала
гармонического
сигнала ![]() и помехи
и помехи ![]() . Учитывая,
что выходное напряжение фильтра
. Учитывая,
что выходное напряжение фильтра 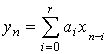 , и
принимая, что помеха
, и
принимая, что помеха ![]() имеет
нулевое среднее, а сигнал и помеха независимы, записываем выражение для
мощности
имеет
нулевое среднее, а сигнал и помеха независимы, записываем выражение для
мощности ![]() на выходе
на выходе
![]() , (38)
, (38)
где ![]() - входная мощность сигнала и мощность помехи, соответственно;
- входная мощность сигнала и мощность помехи, соответственно;
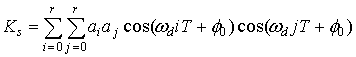 -
коэффициент передачи сигнала цели;
-
коэффициент передачи сигнала цели;
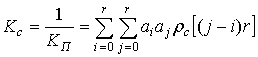
![]() -
коэффициент передачи помех;
-
коэффициент передачи помех;
![]() -
коэффициент подавления;
-
коэффициент подавления;
![]() - функция
корреляции помехи.
- функция
корреляции помехи.
Использовав введенные обозначения, запишем выражения для коэффициента улучшения
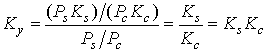 . (39)
. (39)
Переписывая выражение в виде
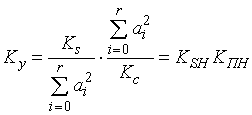 . (40)
. (40)
отмечаем, что коэффициент улучшения ЦФ ![]() -го порядка
выражается через нормированный коэффициент передачи цели
-го порядка
выражается через нормированный коэффициент передачи цели ![]() ,
на которые не влияют помеховые характеристики, и нормированный коэффициент
подавления помехи
,
на которые не влияют помеховые характеристики, и нормированный коэффициент
подавления помехи ![]() , который не зависит от доплеровской частоты
, который не зависит от доплеровской частоты ![]() .
Нормированный коэффициент подавления
.
Нормированный коэффициент подавления ![]() можно
назвать средним улучшением, поскольку средний (по всем доплеровским частотам)
коэффициент улучшения
можно
назвать средним улучшением, поскольку средний (по всем доплеровским частотам)
коэффициент улучшения
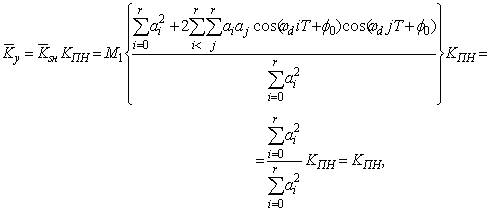 (41)
(41)
т. к. двойная сумма в (41) равна нулю.
Среднее улучшение, как это видно из формулы (41), зависит от амплитудных
весов ![]() , корреляционной функции помехи
, корреляционной функции помехи ![]() и
порядка
и
порядка ![]() ЦФ.
ЦФ.
Основные результаты исследования систем частотно-временной и пространственной селективности.
Научные и практические результаты работы заключаются в следующем. Для анализа линейных дискретных систем, как правило, вводятся специальные разностные уравнения. На основании введенных уравнений представлена классификация цифровых фильтров на рекурсивные и нерекурсивные, а также построена каноническая схема. Исследованы конечно-импульсные и частотные характеристики реализуемых на основе канонической схемы алгоритмов преобразования сигналов. Показано, что разработанный аппарат теории цифровой фильтрации может использоваться при анализе процессов (сигналов) во времени, в частотной области и в пространстве. Оптимизация весовых коэффициентов нерекурсивных цифровых фильтров проведена по методу множителей Лагранжа. После чего с помощью z-преобразований проанализирован коэффициент улучшения передаточной функции нерекурсивного режекторного фильтра.
1. Горбунов Ю. Н. Цифровая обработка радиолокационных сигналов в условиях использования грубого (малоразрядного) квантования: Монография // Федеральное космическое агентство, ФГУП «ЦНИРТИ им. академика А. И. Берга» - М., 2007. – 87 с.
2. Устройства СВЧ и антенны. Проектирование ФАР / Под ред. Д.И. Воскресенского. 3-е изд., доп. и перераб. – М.: Радиотехника, 2003.
3. Амитей Н., Галиндо В., Ву Ч., Теория и анализ фазированных антенных решеток / Пер. с англ. – М.; Мир, 1974.
4. Активные фазированные антенные решетки / Под ред. Д. И. Воскресенского и А. И. Канащенкова.- М.: Радиотехника, 2004.
5. Гостюхин В.Л., Трусов В.Н., Климачев К.Г., Данич Ю.С. Активные фазированные антенные решетки / Под ред. В.Л. Гостюхина. – М.: Радио и связь. 1993.
6. Горбунов Ю. Н. Цифровые системы СДЦ и их оптимизация: Монография // Государственное образовательное учреждение высшего профессионального образования “Московский государственный институт радиотехники, электроники и автоматики (технический университет)”– М., 2008. – 132 с.