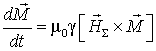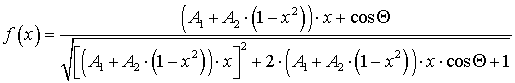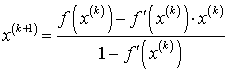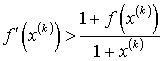АЛГОРИТМ РАСЧЕТА КРИВЫХ ПЕРЕМАГНИЧИВАНИЯ ОДНОДОМЕННОЙ ЧАСТИЦЫ ГЕКСАФЕРРИТА

П. С. Колодин

Национальный исследовательский университет «МЭИ»

Получена 23 июня 2013 г.

Аннотация. Работа посвящена развитию математической модели гексаферритового гиромагнитного материала. Рассмотрена известная задача об определении направления вектора статической намагниченности однодоменной частицы гексаферрита, помещенной во внешнее магнитное поле. При решении задачи учтена возможность существования двух устойчивых положений вектора намагниченности. Предложен способ выбора того или иного положения на основе предыстории состояния вектора намагниченности. Разработан алгоритм расчета кривых перемагничивания и петель магнитного гистерезиса с учетом предыстории состояния намагниченности частицы. Используемый в алгоритме метод позволяет проводить расчет кривых перемагничивания путем изменения напряженности внешнего поля в произвольных пределах при произвольной ориентации частицы. Это существенно упрощает расчет кривых перемагничивания поликристаллических материалов.

Ключевые слова: гексаферрит, однодоменная частица, кривые перемагничивания, петли магнитного гистерезиса.

Abstract. The paper is devoted to the development of the mathematical model of gyromagnetic hexagonal ferrite material. The problem of calculation of static magnetization direction of the single-domain hexaferrite particle in outer magnetic field is revised. The problem solution is taking into account a possibility of existence of two stable states of the magnetization vector. Method of choice one or another state with accounting of the magnetization prehistory is proposed. An algorithm for calculation of the magnetization curves and magnetic hysteresis curves with accounting of the magnetization prehistory is developed. Method, proposed in the algorithm, allows for calculating the magnetization curves by arbitrary variation of the magnetic field with arbitrary orientation of the ferrite particles. Proposed method appreciably simplifies the calculation of the magnetization curves for polycrystalline materials.

Keywords: hexagonal ferrites, single-domain particle, magnetization curves, magnetic hysteresis.

 

Введение

При решении одной из актуальных задач современной радиотехники – освоении миллиметрового и субмиллиметрового диапазонов волн – перед радиоинженерами встают задачи разработки различных функциональных устройств. Поскольку с уменьшением длины волны измерительная аппаратура становится дороже, а физический эксперимент – сложнее, при решении указанных задач вполне рациональным кажется совместное использование как эмпирического подхода, так и компьютерного моделирования.

Моделирование может применяться для решения задач как анализа (например, оптимизации характеристик устройства), так и синтеза (разработки устройства с требуемыми характеристиками). К достоинствам моделирования следует отнести возможность проверки работоспособности устройства еще на стадии проектирования, т.е. до момента изготовления устройства «вживую». Для успешного выполнения этих функций необходимо наличие достаточного количества вычислительных ресурсов и адекватной модели исследуемого устройства.

При создании функциональных устройств на сверхвысоких и крайне высоких частотах (СВЧ и КВЧ) часто применяются гиромагнитные материалы; среди них большое распространение получили материалы на основе гексаферритов. Поэтому одним из условий для разработки моделей и проведения компьютерного моделирования таких устройств является наличие адекватной модели гексаферритового гиромагнитного материала.

Известно [2], что магнитные свойства гексаферритов в диапазонах СВЧ и КВЧ зависят от внешнего постоянного магнитного поля. Одной из отличительных особенностей этой зависимости является гистерезисный характер, который проявляется в неоднозначном (зависящем от предыстории) изменении свойств феррита при его перемагничивании. К настоящему времени для описания кривых намагничивания и петель магнитного гистерезиса ферромагнитных материалов разработано большое количество различных аналитических моделей [5]. Однако в большинстве случаев эти модели не имеют под собой какого-либо физического обоснования, а потому область их применимости ограничена довольно узкими диапазонами изменения напряженности внешнего поля. В связи с этим актуальной кажется задача разработки модели гексаферритового материала, построенной на основе физических представлений о процессах, происходящих в ферритовом теле при его перемагничивании.

В настоящей статье решается задача об определении направления вектора статической намагниченности однодоменной частицы гексаферрита, помещенной во внешнее магнитное поле. На основе полученных результатов формулируются алгоритмы расчета кривых перемагничивания и петель магнитного гистерезиса частицы. Как и в работе [4], предлагаемая здесь методика позволяет рассчитывать петли гистерезиса в «прямой» форме, когда независимой переменной является напряженность внешнего поля. Однако, в отличие от указанной работы, в расчетных формулах, приведенных в данной статье, учтена возможность скачкообразного перехода вектора намагниченности из одного устойчивого состояния в другое при превышении напряженностью внешнего поля так называемого критического значения, а в разработанных алгоритмах расчета кривых перемагничивания автоматически учитывается предыстория состояния намагниченности частицы. Это позволяет рассчитывать кривые перемагничивания при изменении напряженности поля в произвольных пределах, независимо от ориентации частицы. Указанные обстоятельства позволяют существенно упростить расчет кривых перемагничивания и петель гистерезиса поликристаллических материалов, что имеет большое значение для разработки их компьютерных моделей.

 

О кривых перемагничивания

Прежде чем приступить к изложению методики, уделим внимание вопросам терминологии, а именно понятию кривых перемагничивания.

Пусть частица гексаферрита с известными внутренними магнитными свойствами помещена во внешнее однородное магнитное поле. Обозначим вектор напряженности поля . При этом будем полагать, что в пространстве определено условно-положительное направление внешнего магнитного поля, а потому вектор  можно представить в виде

,                                                         (1)

где ,  – единичный вектор (орт) условно-положительного направления внешнего поля.

Через некоторое время после помещения частицы во внешнее поле вектор ее намагниченности займет в пространстве вполне определенное направление. Назовем такое состояние стационарным, а намагниченность частицы в нем – статической намагниченностью .

Тогда под кривыми перемагничивания частицы будем понимать зависимость проекции вектора  на орт  от величины внешнего поля .

 

Физические представления о магнитных свойствах частицы гексаферрита

При решении задачи расчета кривых перемагничивания следует учесть, что частица гексаферрита является анизотропной, т.е. ее магнитные свойства зависят от направления приложения внешнего поля относительно гексагональной оси. Анизотропия проявляется в том, что при произвольной ориентации частицы во внешнем поле направления векторов  и  не совпадают. Между векторами  и  образуется угол  (рис. 1), величина которого зависит от внутренних магнитных свойств частицы, ее ориентации относительно внешнего поля и напряженности поля  (на рисунке  – орт вектора статической намагниченности,  – орт условно-положительного направления гексагональной оси).

 

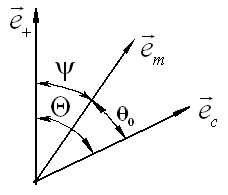
Рис. 1. К проявлению анизотропии

 

Одним из способов учета анизотропии является предположение о существовании внутри частицы магнитного поля, называемого полем анизотропии , которое наряду с внешним полем  воздействует на намагниченность частицы. Для количественного описания такого воздействия принято использовать уравнение Ландау-Лифшица [1], которое можно записать в виде:

,                                                    (2)

 

где  Гн/м – магнитная постоянная,  – гиромагнитное отношение (для магнитно-одноосных гексаферритов обычно полагают  МГц / кА/м),  – суммарное магнитное поле, действующее на намагниченность частицы.

Обычно в поле  к внешнему полю и полю анизотропии добавляют эффективное поле «сил трения» , при помощи которого учитывают потери:

,                                                   (3)

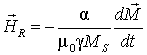,                                                    (4)

 

где  – безразмерный коэффициент (обычно считают ),  – намагниченность насыщения.

Уравнения (2) – (4)  описывают затухающую во времени прецессию вектора намагниченности, вызванную внешним магнитным полем. Если внешнее поле постоянно, то через некоторое время после начала его действия изменениями во времени положения вектора намагниченности можно будет пренебречь:

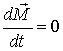.                                                     (5)

 

Это означает, что в стационарном состоянии вектор статической намагниченности  устанавливается параллельно суммарному магнитному полю (3), которое в силу (5) можно записать в виде:

.                                               (6)

Таким образом, для определения направления вектора статической намагниченности  (и вычисления его проекции на орт ) требуется определить направление суммарного магнитного поля (6), которое представляется векторной суммой внешнего магнитного поля и поля анизотропии частицы.

При описании магнитных свойств частицы под полем анизотропии понимают не только кристаллографическую анизотропию, но и анизотропию формы. В квазиклассическом подходе, основанном на уравнении (2), анизотропию формы принято учитывать при помощи размагничивающего поля. Это поле зависит от геометрической формы частицы и ее расположения относительно силовых линий внешнего поля, поэтому в общем случае его расчет очень сложен. Однако для частицы в форме эллипсоида это поле оказывается пропорционально вектору намагниченности (коэффициент пропорциональности является тензором второго ранга). Если одна из осей эллипсоида совпадает с гексагональной осью кристалла, тензор становится диагональным и его компоненты называют размагничивающими факторами. Далее для простоты будем считать, что частица имеет форму эллипсоида вращения, ось симметрии которого совпадает с гексагональной осью кристалла. В этом случае поле анизотропии частицы можно записать в виде [4]:

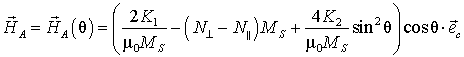,                (7)

 

где  – первая и вторая константы анизотропии,  – размагничивающие факторы в направлении параллельно и перпендикулярно оси симметрии эллипсоида,  – угол отклонения вектора намагниченности от орта .

Для удобства запишем выражение (7) в виде

,                                       (8)

где 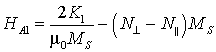,  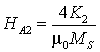– константы поля анизотропии.

 

Таким образом, угол  отклонения вектора статической намагниченности от гексагональной оси определяется направлением вектора суммарного магнитного поля, которое является функцией угла . Если угол  будет известен, то мы будем обладать полными сведениями о направлении вектора статической намагниченности. В этом случае , которому пропорциональна проекция вектора  на орт , можно рассчитать по формуле:

.                              (9)

 

Методика решения задачи

Приступим к решению задачи расчета направления статической намагниченности при заданных напряженности внешнего поля  и ориентации частицы в нем . Внутренние магнитные свойства частицы (константы , ) считаем известными. Начнем с рассмотрения случаев, для которых расчет углов  и  выполнить наиболее просто.

1.     Внешнее магнитное поле отсутствует ().

Благодаря действию поля анизотропии вектор статической намагниченности будет ориентирован вдоль гексагональной оси:

.                                                 (10)

При этом возможно два устойчивых положения вектора намагниченности: параллельно орту  (, ) и противоположно ему (, ). Конкретное положение вектора  определяется направлением поля анизотропии, которое зависит от предыстории изменения внешнего поля и поведения вектора намагниченности.

Если угол  определен, то  из (9) можно определить по формуле:

.                                                  (11)

2.     Внешнее поле направлено вдоль гексагональной оси ().

В этом случае у суммарного поля (6) отсутствуют составляющие, перпендикулярные гексагональной оси. Поэтому, как и в предыдущем случае, вектор статической намагниченности будет ориентирован вдоль гексагональной оси. В таком состоянии справедливо выражение (10), поэтому по абсолютной величине поле анизотропии будет составлять

.                                            (12)

Если напряженность внешнего магнитного поля превосходит первую константу поля анизотропии

,                                                 (13)

вектор статической намагниченности частицы установится по внешнему полю независимо от предыстории. В этом случае расчет интересующих нас величин можно провести по формулам:

,                                     (14)

.                                            (15)

 

Если условие (13) не выполняется, положение вектора статической намагниченности будет определяться направлением поля анизотропии, которое зависит от предыстории изменения внешнего поля и поведения вектора намагниченности. В этом случае для расчета  справедлива формула (11).

3.      В более общем случае (, ) внешнее поле будет стремиться отклонить вектор намагниченности частицы от гексагональной оси, а поле анизотропии – удержать вектор в ее направлении. В итоге вектор намагниченности займет такое положение в пространстве, в котором происходит компенсация моментов сил, действующих со стороны полей  и .

Для определения  запишем скалярное произведение векторов  и :

.                                            (16)

 

Поскольку в стационарном состоянии векторы  и  коллинеарны, орт   можно представить в виде:

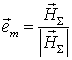.                                                  (17)

Для вычисления произведения (16) введем в плоскости векторов  и  прямоугольную систему координат  (рис. 2).

 

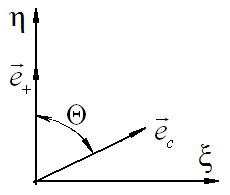
Рис. 2. Вспомогательная система координат

 

В ней векторы  и  можно выразить через орты  осей системы:

,                                     (18)

.                                                    (19)

Тогда в стационарном состоянии вектор суммарного поля (6) можно записать в виде:

.                     (20)

Его абсолютное значение

.  (21)

Тогда выражение (17) можно записать в виде:

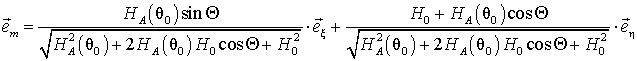.   (22)

Подставляя (22) в скалярное произведение (16) и используя (18), получим:

 

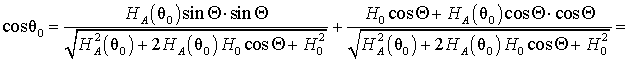
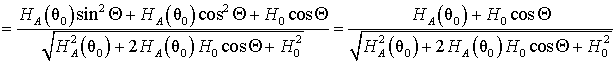.    (23)

 

Если для стационарного состояния поле анизотропии из (8) записать в виде

,                     (24)

уравнение (23) может быть преобразовано в такое:

,                                          (25)

где .

 

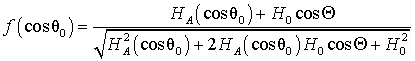Для удобства введем обозначения , ,  и запишем функцию из правой части (25) в виде:

 

.        (26)

Чтобы получить представление о характере функции (26), построим ее графики при различных значениях , ,  (рис. 3, 4).

 

        

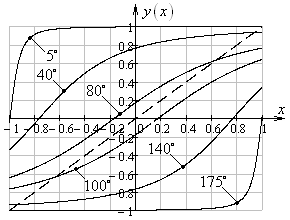
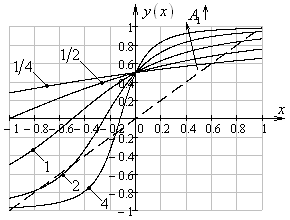
Рис. 3. Графики функции  при , , (слева) и , ,  (справа) (штрихом показан график функции )

 

 

        

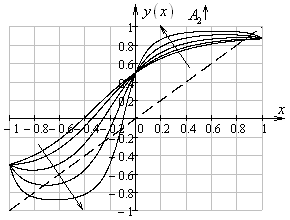
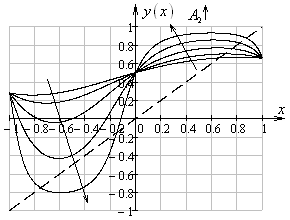
Рис. 4. Графики функции  при , ,  (слева) и , ,  (справа)  (штрихом показан график функции )

 

Как видно из рис. 3, 4, в интервале допустимых значений  графики функций  и  пересекаются от одного до трех раз. Это означает, что при различных параметрах , ,  существует от одного до трех решений уравнения (25), соответствующих возможным положениям вектора статической намагниченности. Однако решение, для которого производная , соответствует неустойчивому положению равновесия, поэтому при расчете петель гистерезиса оно должно исключаться из рассмотрения.

Таким образом, в самом общем случае уравнение (25) имеет два решения  и , соответствующие возможным устойчивым положениям вектора статической намагниченности (далее для краткости будем называть их устойчивыми решениями). При любых допустимых значениях параметров , ,  эти решения имеют разные знаки, что позволяет довольно простым способом учесть гистерезис системы при расчете полевых характеристик. Для этого достаточно при каждом новом значении напряженности внешнего поля из двух решений оставлять то, которое совпадает по знаку с решением, полученным для предыдущего значения . Такой способ позволяет автоматически учесть гистерезис при построении кривых перемагничивания в «прямой» форме, когда независимой переменной является напряженность внешнего поля .

Однако в силу громоздкости выражения (26) аналитическое решение уравнения (25) не представляется возможным. Поэтому при расчете кривых перемагничивания следует воспользоваться численными методами его решения.

 

Численное решение уравнения в задаче об определении направления вектора статической намагниченности

Прежде чем выбрать какой-либо метод численного решения, отметим одну закономерность, которая остается справедливой при любых допустимых значениях параметров , ,  и позволяет сформулировать необходимые условия сходимости последовательности приближений  () к устойчивому решению . На рис. 3, 4 можно видеть, что если для некоторого  значение функции превышает значение аргумента

,                                                        (27)

 

то устойчивое решение  находится справа от , поэтому для приближения к нему следует увеличить аргумент на следующей итерации:

.                                                 (28)

Если же значение функции меньше значения аргумента

,                                                        (29)

 

то устойчивое решение  находится слева от , поэтому для приближения к нему следует уменьшать аргумент на следующей итерации:

.                                                (30)

Указанные закономерности являются необходимым условием сходимости последовательности  к устойчивому решению , поэтому численные методы, используемые для решения уравнения (25), должны формировать последовательности, удовлетворяющие условиям (27) – (30).

К настоящему времени известно большое количество методов решения нелинейных уравнений вида (25) [6]. Среди них можно выделить довольно универсальный метод Ньютона, часто называемый методом касательных. Достоинствами метода Ньютона являются сравнительная простота его реализации (метод является одноточечным, т.е. для вычисления  приближения к решению достаточно знать  приближение и нет необходимости в информации о предыдущих ,  и др. приближениях) и более высокой скоростью сходимости по сравнению с другими одноточечными методами (например, методом деления пополам).

Согласно методу Ньютона, за  приближение к решению  принимается абсцисса точки пересечения функции  и касательной к функции , проведенной в точке  (рис. 5).

 

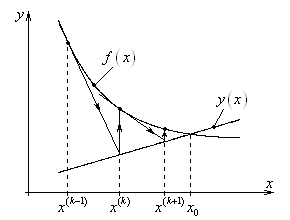
Рис. 5. Геометрическая интерпретация метода Ньютона

 

Для построения алгоритма вычисления  приближения по методу Ньютона запишем уравнение касательной к функции , проведенной в точке с координатами :

.                                     (31)

 

Приравнивая функции  и , получаем выражение для определения  приближения:

.                                          (32)

Итак, для вычисления  приближения по методу Ньютона нужно знать значение функции  и ее производной  в точке . Это требование принято считать недостатком метода, поскольку вычисление производной в каждой точке последовательности  может привести к существенному увеличению объема вычислительных операций.

Для проверки этого опасения найдем производную функции (26). Для этого введем обозначения

,                                    (33)

.                   (34)

 

При таких обозначениях функцию (26) можно представить в виде частного , поэтому ее производная вычисляется по правилу дифференцирования дробей:

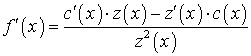.                                     (35)

Производная числителя (33):

.                   (36)

Производная знаменателя (34):

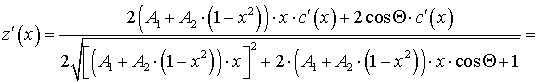
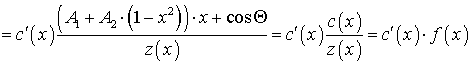.            (37)

Тогда выражение (35) можно преобразовать следующим образом:

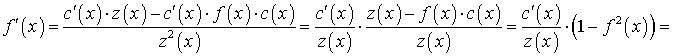
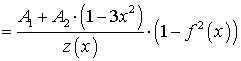.                              (38)

Таким образом, функция  и ее производная  связаны, поэтому, если при расчете производной в точке  использовать результаты расчета функции в той же точке, можно несколько сэкономить на вычислениях. Таким образом, есть основания полагать, что при правильном построении алгоритма численного решения использование метода Ньютона не должно приводить к значительному увеличению объема вычислительных операций по сравнению с методами, для которых вычисление производной не требуется.

Более существенным недостатком метода Ньютона является возможность выхода за пределы интервала , что может привести к непредсказуемым результатам развития итерационного процесса. Рассмотрим подробнее ситуации, когда это может произойти.

1.       Если для текущего приближения  значение функции меньше значения аргумента, то по условию (30) -й элемент формируемой последовательности должен быть меньше -го. В этом случае следует опасаться выхода за нижнюю границу допустимого интервала изменения  величины :

.                                                 (39)

Используя выражение (32), получаем:

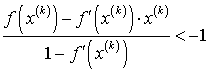.                                            (40)

Считая, что  (в противном случае последовательность, формируемая методом Ньютона, будет либо расходящейся, либо сходящейся к неустойчивому решению), перепишем (40):

.                                  (41)

Тогда

,                                (42)

что равносильно условию для производной функции (26)

.                                                 (43)

2.       Если для текущего приближения  значение функции больше значения аргумента, то по условию (28), -й элемент последовательности должен быть больше -го. В этом случае следует опасаться выхода за верхнюю границу допустимого интервала изменения величины :

.                                                   (44)

Используя выражение (32), запишем

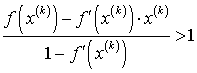.                                             (45)

Считая, что , перепишем это выражение:

.                                    (46)

Тогда

,                                (47)

что равносильно условию для производной функции (26)

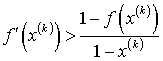.                                                  (48)

Подводя итоги, отметим, что при выполнении условий (29), (43) или (27), (48) получаемое по методу Ньютона приближение  выходит за пределы допустимого интервала . В этих случаях метод Ньютона становится неприменим, поэтому для вычисления -го приближения следует воспользоваться каким-то другим методом.

В качестве такого метода предлагается использовать метод простой итерации. Одним из достоинств метода является его простота реализации: в качестве -го приближения к решению используется значение функции (26) от -го приближения (рис. 6):

 .                                             (49)

 

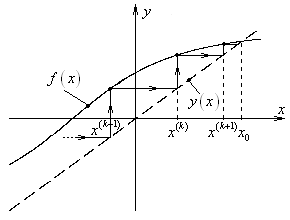
Рис. 6. Геометрическая интерпретация метода простой итерации

 

Следует отметить, что необходимым для сходимости метода является условие , которое не выполняется в окрестности неустойчивого решения уравнения (25). Таким образом, метод простой итерации автоматически расходится в этой окрестности, поэтому его можно использовать для подстраховки и попадания в область сходимости метода Ньютона. Для иллюстрации эффективности такого способа решения на рис. 7 показан пример использования комбинации методов Ньютона и метода простой итерации.

 

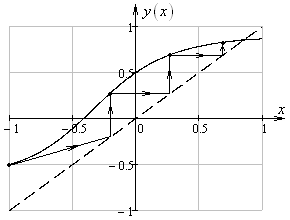
Рис. 7. Графическая иллюстрация решения уравнения (25) при параметрах , , ,  комбинацией методов Ньютона и простой итерации

 

Условием прекращения вычисления элементов последовательности  будем считать примерное равенство значений аргумента и функции на -й итерации:

, .                                               (50)

 

По завершении итерационного процесса решением уравнения (25) будем считать величину :

.                                               (51)

Зная ,  можно рассчитать по формуле (9).

Таким образом, можно сказать, что для общего случая произвольной напряженности внешнего магнитного поля и произвольной ориентации частицы в нем решена задача о направлении вектора статической намагниченности частицы с известными магнитными свойствами. Изложенное решение использовано для разработки компьютерной процедуры «Статика», алгоритм работы которой представлен на рис. 8; на рис. 9 представлен алгоритм работы используемой в ней процедуры «Численное решение».

 

 

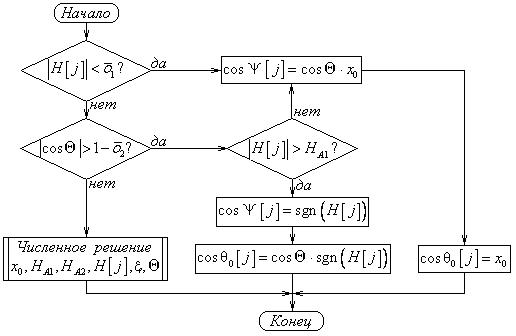
Рис. 8. Блок-схема алгоритма работы процедуры «Статика»

 

 

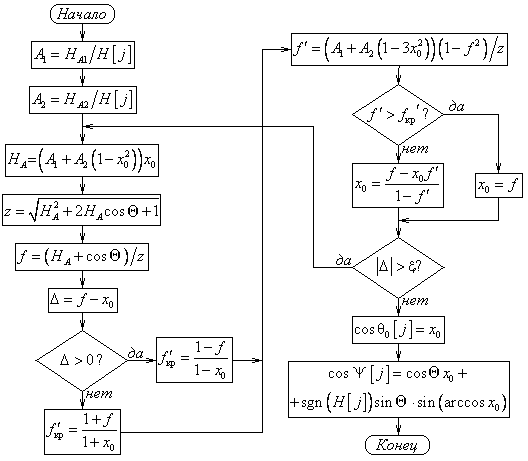
Рис. 9. Блок-схема алгоритма процедуры «Численное решение»

 

Входными параметрами процедуры «Статика» являются константы поля анизотропии , , угол ориентации частицы во внешнем поле , текущее значение напряженности внешнего поля  (подразумевая использование процедуры в теле цикла, организованного для расчета кривых перемагничивания, напряженность внешнего поля обозначена квадратными скобками как элемент массива) и начальное приближение к решению . Установочными параметрами процедуры являются точность решения статической задачи  и малые константы ,  (), используемые для обозначения границ применимости частных случаев, для которых решение задачи возможно без привлечения процедуры «Численное решение». Выходными параметрами процедуры являются значения  и .

 

Расчет кривых перемагничивания и петель магнитного гистерезиса

Итерационный процесс, используемый в процедуре «Численное решение», предполагает наличие некоторого начального приближения , с которого начинается формирование последовательности.

Как указывалось выше, в общем случае существует два устойчивых решения уравнения (25), одно из которых характеризуется острым углом  (), второе – тупым (). При использовании описанных выше численных методов решения уравнения (25) для поиска положительного корня удобно использовать в качестве начального приближения величину , а для поиска отрицательного корня – величину . Даже если уравнение (25) имеет только одно решение, которое не совпадает по знаку с выбранным начальным приближением , комбинация методов Ньютона и последовательных приближений позволяет сформировать последовательность, сходящуюся к этому решению (для примера можно снова обратиться к рис. 7).

Для учета магнитной предыстории системы при расчете кривых перемагничивания и петель гистерезиса будем выбор начального приближения для текущего значения напряженности внешнего поля  проводить на основе знака решения, полученного для предыдущего значения напряженности поля :

.                                            (52)

Если при  намагниченность частицы соответствует верхнему участку петель гистерезиса, то в качестве приближения  будем использовать

,                                          (53)

если нижнему – приближение

.                                          (54)

На рис. 10 приведены схемы алгоритмов расчета верхнего и нижнего участков петель гистерезиса.

 

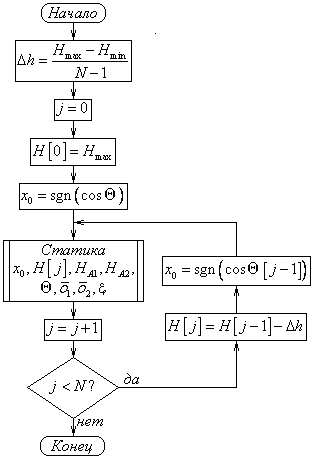
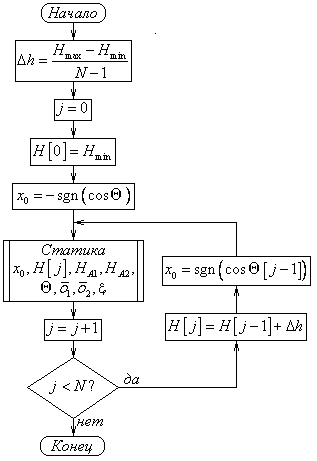
Рис. 10. Блок-схемы алгоритмов расчета верхнего (слева) и нижнего (справа) участков петель гистерезиса

 

Входными параметрами алгоритмов, помимо упоминавшихся ,  и , являются границы диапазона изменения напряженности поля , . Установочным параметром является количество точек на графике . Выходными параметрами являются массивы значений напряженности внешнего поля  и косинусов соответствующих им углов .

В заключение приведем пример расчета кривых перемагничивания и петель гистерезиса при различной ориентации частицы во внешнем поле. Для наглядности и возможности сопоставления результатов с расчетами, проведенными параметрическим способом в работе [3], положим вторую константу поля анизотропии равной нулю (), а по осям координат будем откладывать нормированные величины напряженности поля  и проекции статической намагниченности .

На рис. 11 показан независимый расчет верхнего и нижнего участков петель гистерезиса частицы, гексагональная ось которой ориентирована под углом  к внешнему полю.

 

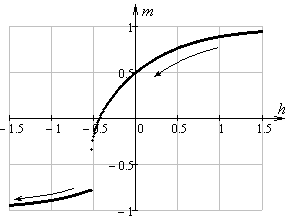
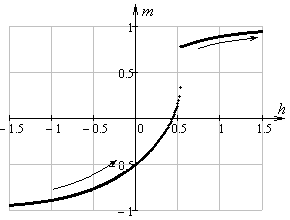
Рис. 11. Графики кривых перемагничивания частицы при ,

 

В первом случае нормированная напряженность поля  уменьшается от значения  до , во втором случае – увеличивается от  до . В обоих случаях в графике функции  наблюдается разрыв, вызванный скачкообразным переходом вектора статической намагниченности из одного устойчивого положения в другое при превышении напряженностью поля критического значения . Значения  различаются для разных направлений изменения внешнего поля (от максимального значения до минимального или наоборот), т.е. зависят от предыстории системы. Если же изменить внешнее поле сначала от  до , а потом в обратную сторону, можно получить график петель гистерезиса частицы (рис. 12):

 

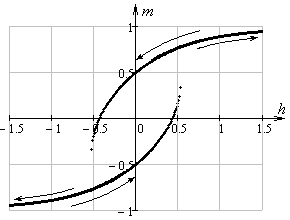
Рис. 12. График петель гистерезиса частицы при ,

 

Как уже отмечалось, разработанная методика позволяет провести расчет кривых перемагничивания при произвольной ориентации частицы во внешнем поле. Для примера на рис. 13 показано семейство петель гистерезиса, построенных для разных значений угла .

 

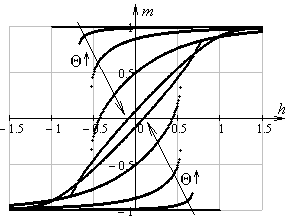
Рис. 13. Пример расчета петель гистерезиса при ,

 

Все эти петли рассчитаны одним и тем же способом при изменении нормированной напряженности внешнего поля сначала от  до , а потом – от  до . Таким образом, изложенная в статье методика позволяет рассчитывать кривые перемагничивания однодоменной частицы гексаферрита при изменении напряженности внешнего поля в произвольных пределах. Это является преимуществом методики перед методикой из [4], при использовании которой напряженность внешнего поля допускалось изменять только в пределах, в которых функция  остается непрерывной. Поскольку, как видно из рис. 13, значение напряженности поля , при котором наблюдается разрыв функции , зависит от ориентации частицы, прежняя методика существенно затрудняла расчет кривых перемагничивания поликристаллических гексаферритов, представляющих собой совокупность большого количества частиц, различным образом ориентированных в пространстве. С использованием изложенной в настоящей статье методики ограничения на изменение напряженности поля могут быть сняты, а расчет кривых перемагничивания поликристаллических гексаферритов – существенно упрощен.

 

Заключение

Итак, в настоящей статье рассмотрена задача об определении направления вектора статической намагниченности однодоменной частицы гексаферрита, помещенной во внешнее магнитное поле. На основе предложенного решения построен алгоритм расчета кривых перемагничивания и петель магнитного гистерезиса частицы при произвольной ее ориентации во внешнем поле.

Практическая ценность полученных результатов заключается не только в возможности их непосредственного использования при исследовании статических полевых характеристик монокристаллических гексаферритов, но и существенном упрощении расчета кривых перемагничивания и петель гистерезиса поликристаллических гексаферритовых материалов, что имеет большое значение для разработки их компьютерных моделей. 

 

Литература

1.     Ландау Л.Д., Лифшиц Е.М. К теории дисперсии магнитной проницаемости ферромагнитных тел, Phys. Zs. Sowjet., 8, 153, 1935.

2.     Kittel C. К теории ферромагнитного резонансного поглощения, Phys. Rev., 73, 1948, 155 – 161; сб. Ферромагнитный резонанс, ИЛ, 1952, с. 46 – 56.

3.     Stoner E.C., Wohlfarth E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Phil. Trans. R. Soc., 240, 1948, 599 – 642.

4.     Pollak B.P., Hanamirow A.E., Korneew I.W. Mono- und polykristalline hexagonale Ferrite als Materialien fuer Resonanzeinrichtungen in der Mikrowellentechnik. Nachrichtentechnik Elektronik, 26, 7, 1976, 245 – 250.

5.     Матюк В.Ф., Осипов А.А. Математические модели кривой намагничивания и петель магнитного гистерезиса. Часть I. Анализ моделей. Неразрушающий контроль и диагностика, 2, 2011, с. 3 – 35.

6.     Амосов А.А., Дубинский Ю.А., Копченова Н.В. – Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. шк., 1994. – 544 с.: ил.