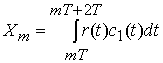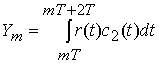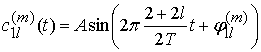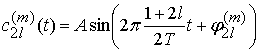УДК 621.391.01
АЛГОРИТМЫ ФОРМИРОВАНИЯ И ПРИЕМА OFDM СИГНАЛОВ НА ОСНОВЕ МАНИПУЛЯЦИИ С МИНИМАЛЬНЫМ СДВИГОМ ЧАСТОТЫ
Л. Е. Назаров ¹, А. С. Зудилин ²
¹Фрязинский филиал Института радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино
²АО
«Информационные спутниковые системы» им. академика М.Ф.Решетнева,
г. Железногорск
Статья поступила в редакцию 4 августа 2016 г.
Аннотация. В статье рассматриваются алгоритмы формирования и приема cигналов с ортогональным частотным мультиплексированием с пониженной внеполосной спектральной плотностью мощности (OFDM-ММС сигналы). Основу формирования данных сигналов составляет фазовый метод - применение манипуляции с непрерывной фазой с минимальным сдвигом частоты (ММС сигналы). Разработанные алгоритмы формирования и приема этих сигналов основаны на использовании решетчатой структуры ММС и производительного алгоритма быстрого спектрального преобразования в базисе Фурье (БПФ). Использование решетчатой структуры при формировании OFDM-ММС сигналов дает возможность реализации оптимального посимвольного приема, являющегося основой алгоритмов итеративного приема класса эффективных помехоустойчивых кодов (турбо-коды, низкоплотностные коды), обеспечивающих достижение практически предельных вероятностных характеристик пропускной способности каналов передачи.
Приведены результаты компьютерного моделирования разработанных алгоритмов. Показано, что максимальное значение первого бокового лепестка спектральной плотности мощности рассматриваемых OFDM-ММС сигналов по отношению к максимальному значению спектральной плотности в рабочей полосе частот достигает -22.2 дБ, что меньше на 9.1 дБ для OFDM сигналов. Падение спектральной плотности мощности достигает -30.4 дБ/октава, что меньше на 12.7 дБ/октава для OFDM сигналов.
Ключевые слова: сигналы, внеполосное излучение, минимальный сдвиг частоты, прием, вероятность ошибки.
Abstract. The orthogonal frequency division multiplexing signals (OFDM) suffer from high sidelobes level. The sidelobes of the OFDM-modulated tones cause the out-of-band power which can induce large interference to the incumbent communication systems. The modulation and decoding algorithms for OFDM signals with sidelobe suppression or out-of-band emission reduction are presented in the article. The proposed method is Minimum Shift Keying in each subcarriers (OFDM-MSK). The developed algorithm for signal modulation is described by means of waveform trellis associated with the trellis of information bit sequence. It is base for iterative decoding of effective block and convolutional codes (turbo-codes, Low-Density Parity Check Codes). The base of modulation and decoding algorithms for OFDM-MSK is Discrete Fourier Transform. The simulation results for developed algorithms are presented. The simulation results show high power spectral efficiency of OFDM-MSK - the largest sidelobe of OFDM-MSK is around 12.7 dB less than OFDM.
Key words: signals, side-lobe spectrum, minimum shift keying, decoding, OFDM-MSK, error performance.
Введение
Сигналы с ортогональным частотным мультиплексированием, известные в литературе как OFDM сигналы (orthogonal frequency division multiplexing), обладают рядом свойств, определяющих перспективность их применения в цифровых системах связи различного назначения [1,2,3]. OFDM сигналы представляют сумму парциальных гармонических сигналов, ортогональных на интервале времени определения. При формировании и приеме этих сигналов используется производительный алгоритм быстрого спектрального преобразования в базисе Фурье (БПФ) [4].
С использованием OFDM сигналов, которые входят в класс широкополосных сигналов, возможна организация надежной передачи информации по нестационарным каналам с многолучевостью, которая обусловливает наличие мультипликативных помех (частотно-селективные замирания сигналов) и явление межсимвольной интерференции, а также по каналам с аддитивными канальными помехами (узкополосные помехи, импульсные помехи) [1,3,5,6]. Положительным свойством рассматриваемых сигналов является возможность адаптивного формирования их спектра с измененяемой шириной полосы, включая формирование оконных спектров и вариацией их расположения в рабочем частотном диапазоне [3].
Эти свойства OFDM-сигналов явились определяющими для их использования в ряде современных цифровых систем связи: IEEE 802.11 (WiFi), IEEE 802.16 (WiMax), DVB-SH (цифровое спутниковое телевещания), 3GPP LTE (мобильная связь 4G).
Недостатком OFDM сигналов является большие значения пик-фактора, что приводит в дополнение к канальным помехам аддитивных интермодуляционных помех на выходе передатчика как нелинейного устройства. Оценивание мощности интермодуляционных помех и исследование их характеристик рассматривались в работах [3,7-14].
Другая проблема при использовании OFDM сигналов обусловлена большими значениями мощности внеполосных излучений [1,3]. Известные алгоритмы цифрового формирования сигналов с пониженной мощностью внеполосного излучения условно можно отнести к трем общим классам: конструктивные методы, амплитудные методы, фазовые методы [1,15].
Один из конструктивных методов формирования основан на использовании дополнительной совокупности парциальных сигналов, выбор которых обусловливает снижение мощности внеполосных излучений результирующих OFDM сигналов [16]. При реализации этого метода решается задача выбора оптимальной совокупности дополнительных парциальных сигналов.
Амплитудные методы снижения мощности внеполосного излучения основаны на использовании огибающих сигналов, отличных от прямоугольной формы. Формирование огибающих производится с использованием взвешивающих окон, ряд которых для OFDM сигналов (трапецеидальное, приподнятый косинус, на основе экспоненциальной функции) рассмотрен в работах [17,18].
В статье рассматриваются алгоритмы формирования и приема OFDM сигналов с пониженной внеполосной мощностью. Основу формирования данных сигналов составляет фазовый метод, суть которого - применение для парциальных сигналов манипуляции с непрерывной фазой с минимальным сдвигом частоты [15].
1. Постановка задачи
OFDM сигналы представляют сумму ![]() парциальных гармонических сигналов,
ортогональных на интервале времени определения
парциальных гармонических сигналов,
ортогональных на интервале времени определения ![]() [1,2,3]
[1,2,3]
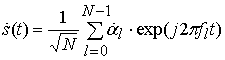 . (1)
. (1)
Значения ![]() определяются используемыми сигнальными “созвездиями”. Ортогональность
составляющих сигналов обеспечивается выбором частот
определяются используемыми сигнальными “созвездиями”. Ортогональность
составляющих сигналов обеспечивается выбором частот ![]() для
двумерных сигналов.
для
двумерных сигналов.
Спектральная плотность мощности данных сигналов определяется суммой спектров парциальных гармонических сигналов с прямоугольной огибающей на интервале определения. В результате вне рабочей частотной полосы OFDM сигналов спектральная плотность мощности убывает достаточно медленно [1].
Эффективное направление снижения мощности внеполосного излучения представляет фазовый метод формирования парциальных гармонических сигналов в составе суммы (1) на основе манипуляции с непрерывной фазой с минимальным сдвигом частоты (ММС сигналы) [1,21].
Спектральная плотность
мощности ММС сигналов с единичной амплитудой задается аналитическим выражением [19]
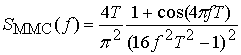 .
.
На рисунке 1 приведена кривая 1 спектральной
мощности в области видеочастоты для ММС сигналов длительностью ![]() сек. При
сек. При ![]() имеем
имеем 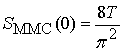 , первое нулевое значение
, первое нулевое значение ![]() достигается при
достигается при ![]() ,
максимальное значение спектральной плотности первого бокового лепестка по
отношению к максимальному значению главного лепестка равно -23.дБ, асимптотическая
зависимость спектральной мощности от частоты
,
максимальное значение спектральной плотности первого бокового лепестка по
отношению к максимальному значению главного лепестка равно -23.дБ, асимптотическая
зависимость спектральной мощности от частоты ![]() имеет
вид
имеет
вид 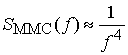 .
.
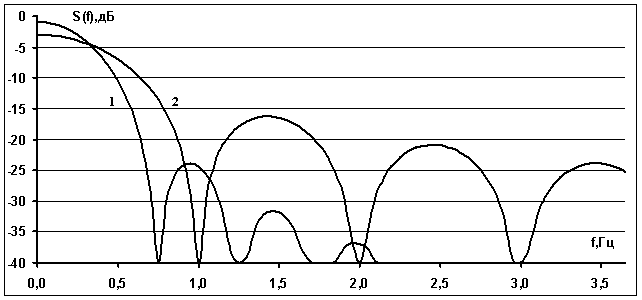
Рис. 1. Кривые спектральных мощностей в области видеочастоты для ММС
сигналов
(кривая 1) и фазоманипулированных сигналов (кривая 2).
Кривая 2 на рисунке 1
соответствует спектральной плотности мощности для фазоманипулированных сигналов
длительностью ![]() сек и с мощностью,
эквивалентной мощности ММС сигналов. В этом случае спектральная плотность
мощности задается выражением
сек и с мощностью,
эквивалентной мощности ММС сигналов. В этом случае спектральная плотность
мощности задается выражением 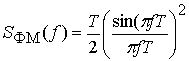 [1]. При
[1]. При ![]() имеем
имеем ![]() ,
первое нулевое значение
,
первое нулевое значение ![]() достигается при
достигается при ![]() , максимальное значение спектральной
плотности первого бокового лепестка по отношению к максимальному значению
главного лепестка равно -13 дБ, асимптотическая зависимость спектральной
мощности от частоты
, максимальное значение спектральной
плотности первого бокового лепестка по отношению к максимальному значению
главного лепестка равно -13 дБ, асимптотическая зависимость спектральной
мощности от частоты ![]() имеет вид
имеет вид 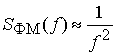 .
.
Таким образом, ММС
сигналы характеризуются большей компактностью и большей скоростью спадания
спектральной плотности при увеличении частоты ![]() по
отношению к фазоманипулированным сигналам [1].
по
отношению к фазоманипулированным сигналам [1].
Известны два метода формирования ММС сигналов [19]: с использованием сигналов с квадратурной модуляцией со сдвигом и их взвешиванием и с использованием решетчатой структуры. Описание этих методов и исследование свойств ММС сигналов даны в работах [1,19,20]. В частности, показана их эквивалентность сигналам с двоичной фазовой манипуляцией относительно вероятностных характеристик при приеме, реализующем правило максимального правдоподобия [1].
В работах [21,22] приведены описания алгоритмов фазового формирования и приема OFDM сигналов с использованием сигналов с квадратурной манипуляцией со сдвигом и их взвешиванием (OFDM-ММС сигналы).
Использование решетчатой структуры при формировании OFDM-ММС сигналов дает возможность реализации оптимального посимвольного приема, являющегося основой алгоритмов итеративного приема класса эффективных помехоустойчивых кодов (турбо-коды, низкоплотностные коды), применение которых обусловливает достижение практически предельных вероятностных характеристик пропускной способности каналов передачи [23].
На рисунке 2 приведен вид решетчатой структуры
сигналов ММС [19]. Решетка содержит два состояния ![]() и
и ![]() , переходы между состояниями определяют
выбор составляющих сигналов
, переходы между состояниями определяют
выбор составляющих сигналов ![]() длительностью
длительностью ![]()
Здесь ![]() - амплитуда сигналов,
- амплитуда сигналов, ![]() - центральная частота,
- центральная частота, ![]() .
.
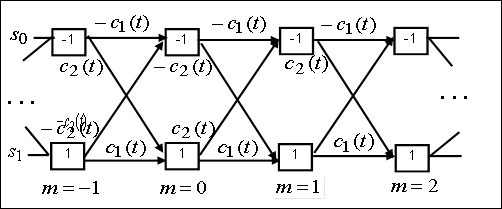
Рис.2. Вид решетчатой структуры сигналов с непрерывной фазой и с минимальным сдвигом частоты.
Путь по решетчатой структуре (последовательный
выбор составляющих сигналов) определяется последовательностью информационных
символов ![]() ,
, ![]() .
Состояние решетки в момент времени
.
Состояние решетки в момент времени ![]() определяется значением
определяется значением
![]() , при
, при ![]() выбирается
нижнее ребро перехода при
выбирается
нижнее ребро перехода при ![]() выбирается верхнее
ребро перехода между состояниями.
выбирается верхнее
ребро перехода между состояниями.
При наличии в канале аддитивного белого
гауссовского шума (АБГШ) ![]() алгоритм приема
символа
алгоритм приема
символа ![]() , реализующий правило максимального
правдоподобия, заключается в вычислении и сравнении величин
, реализующий правило максимального
правдоподобия, заключается в вычислении и сравнении величин ![]() ,
, ![]() [19]
[19]
Здесь ![]() - реализация с выхода канала передачи.
- реализация с выхода канала передачи.
Для четных значений ![]() при
условии
при
условии ![]() принимается решение
принимается решение ![]() , в противном случае
, в противном случае ![]() . Для нечетных значений
. Для нечетных значений ![]() при условии
при условии ![]() принимается
решение
принимается
решение ![]() , в противном случае
, в противном случае ![]() .
.
Суть решаемой в статье проблемы - разработка вычислительных процедур формирования и приема OFDM-ММС сигналов с использованием решетчатой структуры и алгоритма БПФ.
2. Алгоритм формирования OFDM-ММС сигналов
Пусть на длительности ![]() параллельно передается блок из
параллельно передается блок из ![]() информационных битов
информационных битов ![]() ,
, ![]() ,
, ![]() - номер передаваемого блока. Соответствующий
OFDM-ММС сигнал длительностью
- номер передаваемого блока. Соответствующий
OFDM-ММС сигнал длительностью ![]() в цифровом виде можно
сформировать, используя алгоритм БПФ размерностью
в цифровом виде можно
сформировать, используя алгоритм БПФ размерностью ![]() над
дискретной функцией
над
дискретной функцией ![]() ,
, ![]() . Размерность
БПФ определяется соотношением
. Размерность
БПФ определяется соотношением ![]() . Ниже приведено
описание дискретной функции
. Ниже приведено
описание дискретной функции ![]() .
.
Центральная частота
парциальных сигналов ![]() , задаваемых соотношениями (2),
(3), равна
, задаваемых соотношениями (2),
(3), равна ![]() . Эти сигналы, соответствующие передаче
бита
. Эти сигналы, соответствующие передаче
бита ![]() на интервале
на интервале ![]() , имеют
вид
, имеют
вид
Здесь ![]() -
начальные фазы парциальных сигналов.
-
начальные фазы парциальных сигналов.
Относительно начальных
фаз ![]() выполняются условия
выполняются условия ![]() , и
, и![]() ,
, ![]() ,
, ![]() .
Поэтому сигналы
.
Поэтому сигналы ![]() ортогональны на интервале
длительностью
ортогональны на интервале
длительностью ![]() и ортогональны в усиленном
смысле на интервале длительностью
и ортогональны в усиленном
смысле на интервале длительностью ![]() .
.
Если базисные функции
Фурье определены на интервале ![]() , то рассматриваемая
пара сигналов
, то рассматриваемая
пара сигналов ![]() может быть определена путем
задания двух значений дискретной функции
может быть определена путем
задания двух значений дискретной функции ![]() : для
: для ![]() (задание
(задание ![]() ) в
соответствии с решетчатой структурой на рисунке 1 и видом начальных фаз
) в
соответствии с решетчатой структурой на рисунке 1 и видом начальных фаз ![]() имеем
имеем
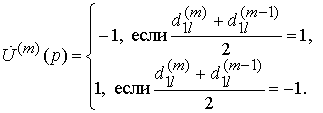 (9)
(9)
Для ![]() (задание
(задание ![]() ) также
имеем
) также
имеем
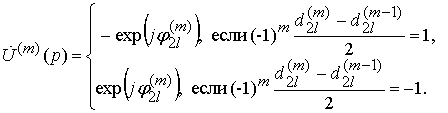 (10)
(10)
Для ![]() при условии
при условии 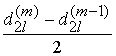 =0
задается значение
=0
задается значение ![]() , для
, для ![]() при
условии
при
условии 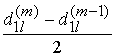 =0 задается значение
=0 задается значение ![]() . Для
. Для ![]() задаются
нулевые значения
задаются
нулевые значения ![]() .
.
Первые ![]() мнимые значения комплексных отсчетов
спектрального преобразования Фурье размерностью
мнимые значения комплексных отсчетов
спектрального преобразования Фурье размерностью ![]() над
дискретной функцией
над
дискретной функцией ![]() определяют значения формируемых
OFDM-ММС сигналов в цифровом виде,
содержащих
определяют значения формируемых
OFDM-ММС сигналов в цифровом виде,
содержащих ![]() отсчетов на временном интервале
отсчетов на временном интервале ![]() .
.
При
применении приведенной процедуры формирования OFDM-ММС сигналов в цифровом виде
с использованием БПФ размерностью ![]() требуется вычисление
требуется вычисление ![]() базовых операций (вычисление комплексных “бабочек”
[4]). При выполнении этой процедуры можно модифицировать алгоритм БПФ с целью
сокращения требуемого числа арифметических операций по отношению к исходному
алгоритму БПФ вследствие значительного множества нулевых значений дискретной
функции
базовых операций (вычисление комплексных “бабочек”
[4]). При выполнении этой процедуры можно модифицировать алгоритм БПФ с целью
сокращения требуемого числа арифметических операций по отношению к исходному
алгоритму БПФ вследствие значительного множества нулевых значений дискретной
функции ![]() и вычисления лишь мнимых компонент первой
половины спектрального множества в результате преобразования Фурье над
и вычисления лишь мнимых компонент первой
половины спектрального множества в результате преобразования Фурье над ![]() .
.
3. Алгоритм приема OFDM-ММС сигналов
Алгоритм приема OFDM-ММС сигналов
на основе правила максимального правдоподобия, требует вычисление соотношений
(5), (6) для каждой пары парциальных сигналов ![]() . При
реализации этого алгоритма приема OFDM-ММС сигналов в цифровом виде можно
использовать алгоритм БПФ, длительность базисных функций Фурье при этом равна
. При
реализации этого алгоритма приема OFDM-ММС сигналов в цифровом виде можно
использовать алгоритм БПФ, длительность базисных функций Фурье при этом равна ![]() . Ниже приведено описание данного алгоритма
приема.
. Ниже приведено описание данного алгоритма
приема.
Входную реализацию ![]() представляем в виде составляющих
реализаций
представляем в виде составляющих
реализаций ![]() длительностью
длительностью ![]() (
(![]() ) с пересечением на интервале
) с пересечением на интервале ![]() . Для принятия решения относительно
переданного символа
. Для принятия решения относительно
переданного символа ![]() осуществляется спектральное
преобразование Фурье (с использованием алгоритма БПФ) размерностью
осуществляется спектральное
преобразование Фурье (с использованием алгоритма БПФ) размерностью ![]() дискретной функции
дискретной функции ![]() в цифровом виде на основе составляющих реализаций
в цифровом виде на основе составляющих реализаций
![]()
![]() , (11)
, (11)
![]() . (12)
. (12)
Размерности базисов Фурье
![]() при формировании и приеме цифровых OFDM-ММС сигналов совпадают. Для
дискретной функции
при формировании и приеме цифровых OFDM-ММС сигналов совпадают. Для
дискретной функции ![]() вычисляется множество
спектральных составляющих
вычисляется множество
спектральных составляющих ![]() ,
, ![]() .
.
Принимается решение ![]() , если
, если ![]() , в
противном случае
, в
противном случае ![]() ,
, ![]() .
Следует отметить, что данное правило приема справедливо для четных и нечетных
значений
.
Следует отметить, что данное правило приема справедливо для четных и нечетных
значений ![]() , это является отличием от приведенной
процедуры приема ММС сигналов на основе вычисления соотношений (5), (6).
, это является отличием от приведенной
процедуры приема ММС сигналов на основе вычисления соотношений (5), (6).
Учитывая,
что анализируемая дискретная функция ![]() имеет лишь ненулевую
мнимую составляющую, возможна модификация алгоритма БПФ с целью уменьшения
объема требуемых вычислительных операций при выполнении приведенной процедуры
приема цифровых OFDM-ММС сигналов.
имеет лишь ненулевую
мнимую составляющую, возможна модификация алгоритма БПФ с целью уменьшения
объема требуемых вычислительных операций при выполнении приведенной процедуры
приема цифровых OFDM-ММС сигналов.
4. Результаты моделирования
На рисунке 3 приведены
примеры спектральных плотностей мощности ![]() для OFDM сигналов (кривая 1) и для OFDM-ММС сигналов (кривая 2),
сформированных с использованием соотношений (7)-(10). В составе OFDM сигналов и OFDM-ММС сигналов 16 парциальных сигналов (передача
информационного блока из 8 битов), размерность БПФ равна 32, длительность
сигналов
для OFDM сигналов (кривая 1) и для OFDM-ММС сигналов (кривая 2),
сформированных с использованием соотношений (7)-(10). В составе OFDM сигналов и OFDM-ММС сигналов 16 парциальных сигналов (передача
информационного блока из 8 битов), размерность БПФ равна 32, длительность
сигналов ![]() сек. По оси абсцисс отложены значения
частоты, нормированные на полосу спектрального анализа.
сек. По оси абсцисс отложены значения
частоты, нормированные на полосу спектрального анализа.
Видно, что для OFDM сигналов максимальное значение первого бокового лепестка вне частотной полосы по отношению к значению спектральной мощности в рабочей частотной полосе (-6.1 дБ) достигает -13.1 дБ. Падение спектральной плотности мощности достигает -17.7 дБ/октава.
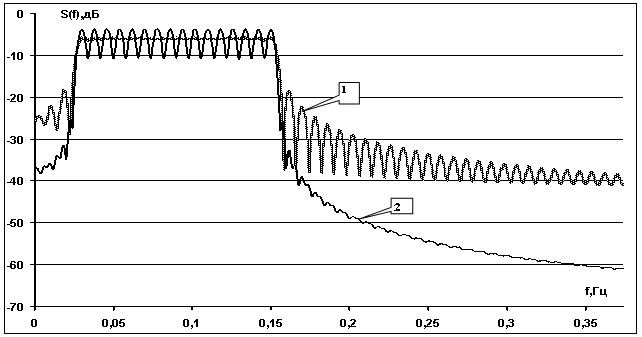
Рис.3. Спектральные плотности
мощности для OFDM сигналов (кривая 1) и для OFDM-ММС сигналов (кривая 2)
(в составе
16 парциальных сигналов (передача блока из 8 битов), длительность сигналов ![]() сек,
сек,
по оси абсцисс отложены значения
частоты, нормированные на полосу спектрального анализа).
Для OFDM-ММС сигналов в рабочей частотной полосе из рисунка 3 (кривая 2) видна гребенчатая структура спектральных плотностей для парциальных сигналов ММС с вариацией амплитуд -10.1…-4.3 дБ, максимальное значение первого бокового лепестка по отношению к максимальному значению спектральной плотности в рабочей частоте (-4.3 дБ) достигает -22.2 дБ. Падение спектральной плотности мощности достигает -30.4 дБ/октава, что меньше на 12.7 дБ/октава для OFDM сигналов.
На рисунке 4 приведена
кривая вероятности ошибки на бит ![]() в зависимости от
отношения сигнал/помеха
в зависимости от
отношения сигнал/помеха ![]() , полученная путем
моделирования разработанного алгоритма приема OFDM-ММС сигналов для АБГШ канала. В составе OFDM-ММС сигналов 16 парциальных сигналов
(передача блоков из 8 битов), длительность сигналов
, полученная путем
моделирования разработанного алгоритма приема OFDM-ММС сигналов для АБГШ канала. В составе OFDM-ММС сигналов 16 парциальных сигналов
(передача блоков из 8 битов), длительность сигналов ![]() сек.
Здесь
сек.
Здесь ![]() - энергия на информационный бит,
- энергия на информационный бит, ![]() - спектральная плотность (односторонняя)
АБГШ. Выше отмечено, что моделируемая вероятностная кривая тождественна
вероятностной кривой для сигналов с двоичной фазовой манипуляцией, для которых
известно соотношение [1]
- спектральная плотность (односторонняя)
АБГШ. Выше отмечено, что моделируемая вероятностная кривая тождественна
вероятностной кривой для сигналов с двоичной фазовой манипуляцией, для которых
известно соотношение [1]
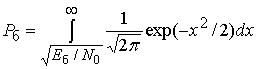 . (13)
. (13)
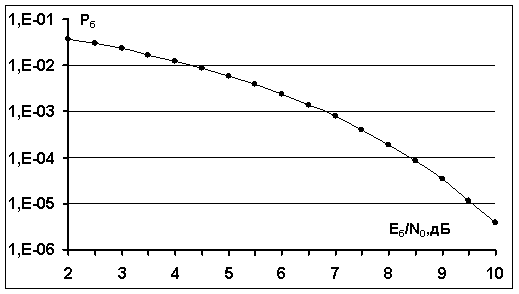
Рис.4. Кривая вероятности ошибки на бит в зависимости от отношения
сигнал/помеха
при приеме OFDM-ММС сигналов для АБГШ
канала (в составе 16 парциальных сигналов).
Из
рис.4 видно, что при 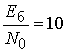 дБ вероятность ошибки равна
дБ вероятность ошибки равна ![]() , что совпадает с теоретическим значением,
вычисленным с использованием соотношения (13).
, что совпадает с теоретическим значением,
вычисленным с использованием соотношения (13).
Заключение
OFDM-ММС сигналы на основе манипуляции с непрерывной фазой с минимальным сдвигом частоты характеризуются пониженной внеполосной спектральной мощностью по отношению к OFDM сигналам. Максимальное значение первого бокового лепестка спектральной плотности мощности OFDM-ММС сигналов по отношению к максимальному значению спектральной плотности в рабочей полосе частот достигает -22.2 дБ, что меньше на 9.1 дБ для OFDM сигналов. Падение спектральной плотности мощности достигает -30.4 дБ/октава, что меньше на 12.7 дБ/октава для OFDM сигналов.
Приведены алгоритмы формирования и приема OFDM-ММС сигналов в цифровом виде, основу которых составляет алгоритм БПФ. Размерность БПФ определяется размером передаваемого параллельно информационного блока.
Разработка модификаций алгоритма БПФ с целью сокращения требуемого числа вычислительных операций при формировании и приеме OFDM-ММС сигналов с учетом свойств анализируемых дискретных функций представляет направление перспективных исследований.
Работа выполнена при поддержке РФФИ (№16-07-00746).
Литература
1. Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.: Эко-Трендз. 2005. 392 c.
2. Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера. 2005. 592 c/
3. Liu H., Li G. OFDM-Based Broadband Wireless Networks. Hoboken: John Wiley & Sons. 2005. 251 p.
4. Ахмед Н., Рао К.Р. Ортогональные преобразования при цифровой обработке сигналов. М.:Связь. 1980. 248 с.
5. Назаров Л.Е., Зудилин А.С. Алгоритмы компенсации сосредоточенных по спектру помех для сигналов с ортогональным частотным мультиплексированием. // Известия высших учебных заведений. Электроника. 2013. №6 (104). Стр. 45-51.
6. Калинин В.И., Радченко Д.Е., Черепенин В.А. Вероятностные характеристики цифрового канала передачи информации на основе непрерывных шумовых сигналов со спектральной модуляцией.// Радиотехника. 2015. №8. Стр. 84-94.
7. Шинаков Ю.С. Интермодуляционные помехи для сигналов OFDM в нелинейных устройствах с амплитудно-фазовой конверсией.// Проектирование и технология электронных средств. 2012. №3. Стр. 19-24.
8. Шинаков Ю.С. Пикфактор сигналов OFDM и нелинейные искажения в радиооборудовании систем беспроводного доступа. // Цифровая обработка сигналов. 2012. №4. Стр.58-65.
9. Шинаков Ю.С. Спектральная плотность мощности помехи нелинейных искажений в устройствах с амплитудно-фазовой конверсией. // Радиотехника и электроника. 2013. Т.58. №10. Стр. 1053-1064.
10. Шинаков Ю.С. Два способа вычисления мощности неискаженного сигнала на выходе нелинейного устройства с амплитудно-фазовой конверсией. // Радиотехника. 2016. №2. Стр. 66-71.
11. Клоков С.С., Шинаков Ю.С. Методы снижения пик-фактора сигнала в системах с технологией OFDM. // Сборник трудов “Технология информационного общества”. X Международная отраслевая научно-техническая конференция. Москва. 2016. С. 131-132.
12. Назаров Л.Е., Зудилин А.С. Оценивание мощности и эффективности интермодуляционных помех при ограничении огибающей OFDM-сигналов.// Радиотехника и электроника. 2015. Т.60. №5. Стр.522-528.
13. Назаров Л.Е., Зудилин А.С. Методики оценивания мощности интермодуляционных помех для сигналов с ортогональным частотным мультиплексированием.// Радиотехника и электроника. 2014. Т.59. №2. Стр.173-178.
14. Назаров Л.Е., Зудилин А.С. Оценка мощности интермодуляционных помех при предельном ограничении огибающей сигналов с ортогональным частотным мультиплексированием.// Журнал радиоэлектроники: электронный журнал.. 2013. №6. URL: http://jre.cplire.ru/jre/jun13/1/text.pdf.
15. Макаров С.Б., Цикин И.А. Передача дискретных сообщений по каналам с ограниченной полосой пропускания. М.: Радио и связь. 1988.
16. Brandes S., Cosovic I., Schnell M. Reduction of Out-of-Band Radiation in OFDM Systems by Insertion of Cancellation Carriers.// IEEE Communications Letters. 2006. V. 10. N 6. P. 420–422.
17. Muller-Weinfurtner S.H. Optimum Nyquist windowing in OFDM receivers.// IEEE Transactions on Communications. 2001. V.49. N3. P. 417-420.
18. Tan P., Beaulieu N.C. Analysis of the effects of Nyquist pulse-shaping on the performance of OFDM systems with carrier frequency offset. // European Transactions on Telecommunications. 2009. N.20. P.9-22.
19. Massey J.L. A generalization of Binary Minimum Shift Keying and Staggered Quadriphase Shift Keying modulation. // The Deep Space Network DSN Progress Report 42-52. Jet Propulsion Laboratory. Pasadena. May and June 1979. P. 26-40.
20. Pasupathy S. Minimum Shift Keying: a spectrally efficient modulation. // IEEE Communications Magazine. 1979. V.17. N4. P.14-22.
21. Mahmoodi S., Saeedi H., Omidi M.J. OFDM-MSK: A Method for Sidelobe Suppression in OFDM Systems. // 20-th Iranian Conference on Electrical Engineering. Tehran. 2012. 15-17 May. P.1474-1477.
22. Yang R.H-H., Chern S-J.,Tseng C-C., Zhan Z-H. OFDM-MSK for Wireless Communications. // Proceedings of International Symposium on Intelligent Signal Processing and Communication Systems. 2005. December 13-16. Hong-Kong. P.269-272.
23. Johnson S.J. Iterative Error Correction: Turbо, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge. University Press. UK. 2010. 356 p.