УДК 621.396.967
ВЛИЯНИЕ СЖАТИЯ ДАННЫХ НА КАЧЕСТВО РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ
И. М. Нестеров1,2
1 Московский физико-технический институт (государственный университет)
2 НПП «САИТ»
Статья поступила в редакцию 13 июля 2016 г.
Аннотация. В работе проведено исследование влияния сжатия данных РСА на качество синтеза радиолокационных изображений. Рассмотрены различные подходы к сжатию с частичными потерями данных, позволяющие достигнуть коэффициента сжатия от 2 до 8 раз для 8-битовых отсчетов квадратур на входе устройства сжатия данных: алгоритмы блочного адаптивного квантования (БАК) в квадратурном формате и в полярном формате, алгоритм векторного квантования (ВК) и сжатие данных на основе вейвлет-преобразования Добеши D4 (ВП D4). Определены статистические свойства отсчетов и количественный критерий качества работы алгоритмов сжатия с частичными потерями данных – отношение сигнал/шум квантования. Описаны созданные модели работы алгоритмов сжатия с различными параметрами, позволившие получить численные значения характеристик работы алгоритмов сжатия и восстановленные после декомпрессии отсчеты, используемые для синтеза радиолокационных изображений. По результатам моделирования даны рекомендации о возможности применения алгоритмов с соответствующими параметрами на практике. Показано, что при коэффициентах сжатия в 4 и более раз рассмотренные алгоритмы ведут себя схожим образом. При коэффициентах сжатия меньше 4 раз алгоритмы ВК, БАК в квадратурном и полярном форматах позволяют получить на 2-5 дБ большее отношение сигнал/шум квантования, чем сжатие данных на основе ВП D4.
Ключевые слова: сжатие данных РСА, БАК, векторное квантование, вейвлет Добеши D4, синтез радиолокационных изображений.
Abstract. In this paper the impact of raw SAR data compression on the quality of synthesis of radar images was researched. Different approaches to the lossy data compression are considered: block adaptive quantization (BAQ), BAQ algorithm in data polar format, Vector Quantization (VQ), Wavelet Transform D4 algorithm (WT D4). These algorithms allow achieving compression ratio from 2 to 8 times for 8-bit inphase and quadrature samples. Statistic properties of raw SAR data were described. The performance measure of SAR data compression (signal quantization noise ratio - SQNR) was introduced. SQNR ratios of above-stated algorithms and decompressed SAR data were obtained by models described in this paper. These decompressed data were used for synthesis SAR image. The algorithms have the same performance, when compression ratio equals 4 or greater. If compression ratio less than 4, BAQ in both formats and VQ have better SQNR performance than WT D4 on 2-5 dB.
Key words: SAR data compression, BAQ, vector quantization, Daubechies wavelet D4, radar images.
Введение
Радиолокаторы с синтезированной апертурой (РСА) являются эффективными средствами получения оперативной и долговременной информации о состоянии и динамике объектов и районов земного шара независимо от метеорологических условий и времени суток [1]. С ростом требований к качеству информации, получаемой РСА, возрастают объемы обрабатываемых информационных потоков. В современных РСА потоки данных с решеток достигают объемов в 4 Гбит/с и более, что затрудняет процессы дальнейшей обработки, хранения и передачи данных на Землю. Поступающая информация содержит статистическую и визуальную избыточность, которые можно устранить, используя алгоритмы сжатия данных РСА. Алгоритмы сжатия без потерь данных устраняют статистическую избыточность и позволяют достичь коэффициентов сжатия данных до 1.4 раз. Алгоритмы сжатия с потерями данных устраняют визуальную избыточность и позволяют достичь коэффициентов сжатия от 2 до 8 раз (для случая, когда в синфазном и квадратурном каналах используются 8-разрядные АЦП) и представляют больший практический интерес [2].
В данной статье рассматривается влияние различных подходов к сжатию данных РСА с частичными потерями на качество синтеза радиолокационных изображений, включая алгоритм на основе вейвлет-преобразования D4. Рядом с количественными критериями сжатия приведены соответствующие им результаты синтеза радиолокационных изображений. В процессе исследования показаны статистические свойства отсчетов сигнала, определены критерии качества работы алгоритмов сжатия, выбраны для рассмотрения различные подходы к сжатию данных, созданы модели работы выбранных алгоритмов сжатия, позволившие получить количественные оценки критериев и проанализировать полученные результаты.
Определение критериев качества алгоритмов сжатия
Для оценки точности восстановления отсчетов исходного сигнала определим критерии качества работы алгоритмов сжатия данных РСА. Рассмотрим статистические свойства отсчетов сигнала на входе устройства сжатия, используемые для минимизации ошибки, появляющейся в процессе компрессии/декомпрессии. Принимаемый сигнал представляет собой суперпозицию откликов элементарных отражателей [3]:
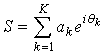 ,
(1)
,
(1)
где ak – амплитуды, θk – фазовые задержки. Амплитуда ak и фаза θk являются статистически независимыми друг от друга и от амплитуд и фаз других элементарных отражателей случайными величинами [4-5]. Из центральной предельной теоремы следует, что распределение значений принимаемого РСА сигнала, представляющего собой сумму независимых случайных величин, стремится к Гауссовому при K→∞. Мгновенные значения синфазной и квадратурной компонент сигнала S имеют нормальное распределение с нулевым средним. Амплитуды сигнала распределены по Рэлею, фазы – равномерно на интервале [-π, π).
Приложению синтеза радиолокационных изображений важно как можно более точно восстановить отсчеты исходного сигнала, подвергнутого компрессии/декомпрессии. Основным критерием качества восстановления сигнала является отношение сигнал/шум квантования [6]:
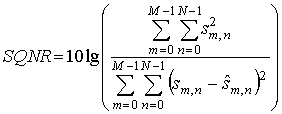 ,
(2)
,
(2)
где ![]() –
исходный отсчет оцифрованного сигнала,
–
исходный отсчет оцифрованного сигнала, ![]() -
восстановленный после сжатия отсчет сигнала.
-
восстановленный после сжатия отсчет сигнала.
Основной характеристикой работы алгоритма является коэффициент сжатия данных, вычисляемый как отношение количества битов на отсчет до и после сжатия.
Подходы к сжатию данных РСА
Для исследования были выбраны различные подходы к сжатию данных РСА: блочное адаптивное квантование (БАК) в тригонометрическом (квадратурном) формате, БАК в полярном формате, векторное квантование (ВК), сжатие на основе вейвлет-преобразования (ВП) D4 (вейвлет Добеши).
Принцип работы алгоритма блочного адаптивного квантования основан на разбиении потока отсчетов сигнала на блоки, для каждого из которых вычисляются пороговые значения квантователя Макса и производится сжатие [7]. Размеры блоков выбирают, исходя из того, чтобы статистика данных в каждом была близка к нормальному распределению, и, в то же время, снимаемая сцена была достаточно однородной. Для алгоритма БАК в тригонометрическом (квадратурном) формате, отсчеты сигнала представлены в виде синфазной и квадратурной компонент. При вычислении пороговых значений выбирают коэффициенты квантователя Макса для нормального распределения и соответствующего коэффициента сжатия [8]. В случае, когда отсчеты представляют собой амплитуду и фазу сигнала (БАК в полярном формате), для амплитуды выбирают коэффициенты Макса соответствующие распределению Рэлея, для фазы – равномерному распределению.
Другим подходом к сжатию является векторное квантование, состоящее из двух этапов. Целью первого этапа является минимизация ошибки квантования потока отсчетов, для этого составляется кодовая книга. Составление кодовой книги представляет собой итеративный процесс, подробно описанный в статье [9]. Кодовая книга требует периодического обновления. На втором этапе работы алгоритма производится квантование, при этом каждому приходящему отсчету ставится в соответствие номер вектора из кодовой книги, для которого ошибка квантования минимальна. Для восстановления данных используется актуальная для данной части потока кодовая книга, при этом каждому пришедшему отсчету-номеру ставится в соответствие вектор в кодовой книге.
Сжатие на основе вейвлет-преобразования Добеши D4 применяется к отсчетам данных, представленных в полярном формате [10]. Вейвлет-преобразование D4 разделяет данные на низкочастотную и высокочастотную составляющие, устраняя одинаковые и линейно растущие компоненты. Преобразование осуществляется путем умножения матрицы преобразования на вектор-столбец отсчетов амплитуд в полярном формате и, далее, выполняется для низкочастотной составляющей до тех пор, пока количество низкочастотных компонент не станет равно двум (меньше количества коэффициентов D4) [11]. Высокочастотные компоненты нормируются на среднеквадратическое отклонение своих абсолютных значений и квантуются. Обратное вейвлет-преобразование для D4 эквивалентно умножению полученных данных на транспонированную матрицу исходного преобразования. Фазовая компонента квантуется равномерно.
Моделирование сжатия данных РСА
Для исследования влияния сжатия данных РСА на качество синтеза радиолокационных изображений были созданы в среде Matlab модели компрессии/декомпрессии данных РСА. При моделировании работы алгоритмов сжатия использовались комплексные отсчеты РСА ERS [12] с 8-битными синфазной и квадратурной компонентами.
В процессе работы модель устройства сжатия данных алгоритмом БАК с квадратурными компонентами разбивает исходный массив комплексных отсчетов на блоки размером 512 (32х16) отсчетов каждой из квадратур. Методом, описанным в статье, производилась оценка СКО квадратурных компонент отсчетов. Этот метод использует взаимно-однозначное соответствие между средним абсолютных значений отсчетов блока данных и СКО отсчетов этого же блока данных. Заранее вычисленные значения СКО хранятся в памяти, адресом которой служит среднее абсолютных значений отсчетов квадратур. Для вычисления СКО нужно только среднее абсолютных значений отсчетов, которое при реализации в железе вычислить проще. Значение СКО амплитуд отсчетов i-го блока данных и коэффициенты Макса для нормального распределения использовались при вычислении пороговых значений для квантования отсчетов (i+1)-го блока данных. СКО i-го блока и сжатые данные (i+1)-го блока данных подавались на схему восстановления сжатых данных, где каждому отсчету ставился в соответствие коэффициент Макса для нормального распределения, умноженный на значение СКО.
Результаты моделирования алгоритма БАК с квадратурным форматом отсчетов (БАК кв.) для сжатия данных до 1, 2, 3, 4-битов на отсчет квадратуры (коэффициенты сжатия 8/1, 8/2, 8/3, 8/4) представлены на рисунке 1.
Изображения, синтезированные по данным, полученным в результате компрессии/декомпрессии алгоритмом БАК с квадратурным представлением отсчетов, представлены на рисунке 2. Также на рисунке 3 представлены изображения, полученные по исходным данным и по восстановленным после сжатия.
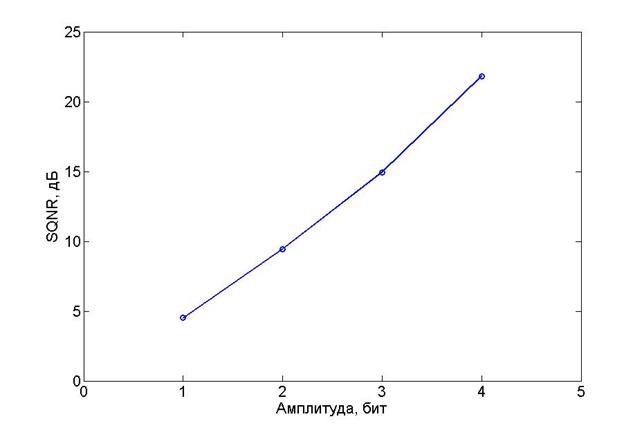
Рисунок 1. SQNR БАК с квадратурным представлением отсчетов.
При сжатии до 4 бит на отсчет (SQNR = 21.8 дБ) квадратуры (коэффициент сжатия равен 2) изображение, синтезированное по восстановленным данным, визуально практически не отличается от изображения, синтезированного по исходным данным. Изображение, синтезированное после сжатия до 3 битов на отсчет (коэффициенты сжатия 8/3), отличается от сжатого до 4 битов на отсчет появлением едва различимых шумов на границах объектов. При сжатии до 2 битов на отсчет (коэффициент сжатия 4) шумы становятся визуально более отчетливыми, но большинство объектов различимы. В результате сжатия до 1 бита на отсчет (коэффициент сжатия 8) на изображении наблюдаются шумы, позволяющие различить лишь контрастные и крупные объекты. Таким образом, данные при отношениях сигнал/шум квантования порядка 14-15 дБ и выше возможно использовать для тех же целей, что и исходное изображение.

Рисунок 2. Синтезированные изображения после восстановления данных БАК.

Рисунок 3. Синтез изображений по данным БАК и по исходным данным.
Для проверки работы алгоритма БАК в полярном формате данных, были вычислены амплитуда и фаза каждого отсчета:
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
где Ai, φi – амплитуда и фаза i-го отсчета, Ii и Qi – исходные отсчеты в квадратурном представлении, round(a) – округленное до ближайшего целого число a, k1 – количество бит в двоичном представлении амплитуды, k2 – количество бит в двоичном представлении фазы, функция arg(a) - вычисляет аргумент комплексного числа ai=Ii+j*Qi на интервале [-π, π).
Для моделирования были выбраны параметры:
k1 = 12, (8 бит – целая часть числа и 4 бита – дробная часть);
k2 = 8, фаза нормируется на π, чтобы значения фазы i-го отсчета были в диапазоне [-1, 1).
СКО амплитуд отсчетов i-го блока использовалось для вычисления пороговых значений квантователя Макса (распределение Рэлея) и сжатия отсчетов амплитуд (i+1)-го блока данных. В качестве пороговых значений для нормированных на π фаз комплексных отсчетов использовались коэффициенты квантователя Макса для равномерного. СКО амплитуд i-го блока данных и сжатые данные амплитуд и фаз отсчетов данных (i+1)-го блока данных подавались на схему восстановления данных. Для восстановления амплитуд отсчетов СКО умножалось на соответствующий отсчету коэффициент Макса для распределения Рэлея. Каждому отсчету фазы ставился в соответствие коэффициент Макса для равномерного распределения.
Результаты моделирования алгоритма БАК с полярным форматом отсчетов (БАК пл.) для сжатия амплитуды сигнала до 1-4 битов и фазы до 2-5 битов представлены на рисунке 4.
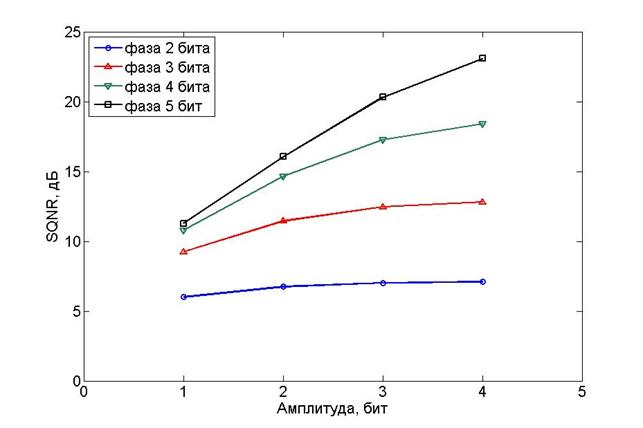
Рисунок 4. SQNR БАК в полярном формате.
Из рисунка 4 видно, что сжатие данных алгоритмом БАК в полярном формате до 2 бит амплитуды и 4 бит фазы (коэффициент сжатия данных 8/3) позволяет достичь отношения сигнал/шум квантования SQNR = 14.6 дБ. Изображение, синтезированное по сжатым с вышеуказанными характеристиками данным, будет визуально практически неотличимо от оригинала. При использовании меньшего количества бит для представления амплитуды и фазы, на синтезируемом изображении будут наблюдаться шумы и визуальные отличия от исходного, аналогичные показанным на рисунке 2 с соответствующими характеристиками.
В созданной модели сжатия данных методом векторного квантования для построения кодовой книги в качестве отсчетов тестовой последовательности использовались амплитуды синфазной и квадратурной компонент. Длина тестовой последовательности N = 65536 отсчетов. Минимальная величина приращения ошибки 10-3.
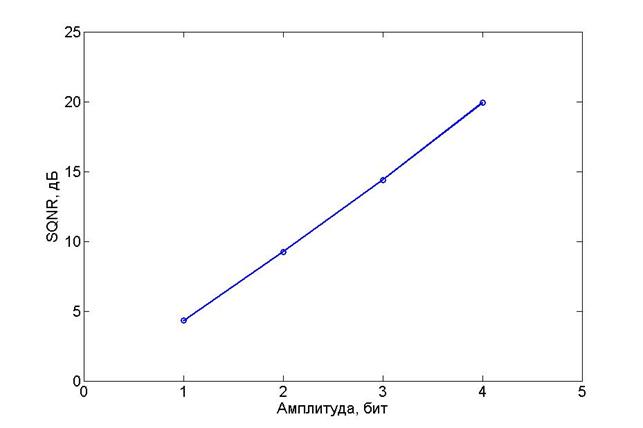
Рисунок 5. SQNR для векторного квантования.
Результаты моделирования алгоритма векторного квантования (ВК) для кодовой книги размером 2, 4, 8, 16 векторов (кодируются соответственно 1, 2, 3, 4 битами) представлены на рисунке 5.
Из рисунка 5 видно, что ВК имеет сравнимые с БАК в квадратурном формате показатели SQNR. Таким образом, изображения, полученные по данным восстановленным после сжатия методом ВК до 3 (SQNR = 14.4 дБ) и до 4 битов (SQNR = 19.9 дБ) на отсчет квадратуры, подходят для использования в тех же задачах, что и исходное изображение. Но в отличие от БАК, ВК имеет более сложную реализацию, требует периодического использования тестовой последовательности для калибровки векторов кодовой книги и помимо передачи номеров векторов в кодовой книге передает и саму кодовую книгу.
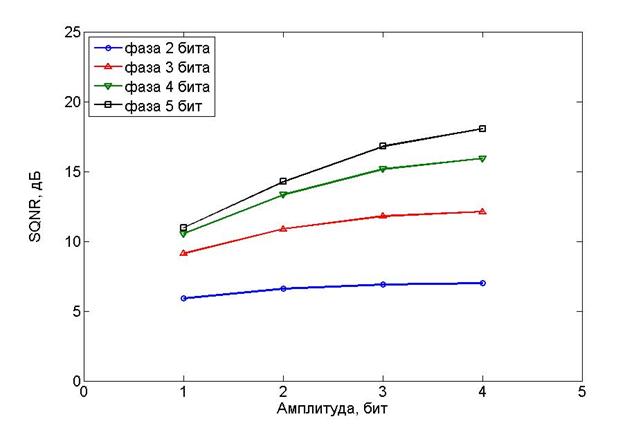
Рисунок 6. SQNR для сжатия на основе ВП D4.
В модели сжатия с использованием вейвлет-преобразования (ВП D4) комплексные данные были приведены к полярному формату тем же алгоритмом, что и для БАК в полярном формате. Сжатию на основе вейвлет-преобразования подвергалась амплитуда сигнала. Размер блока отсчетов амплитуд был выбран равным 2048, т.к. после преобразования D4 остается две низкочастотные компоненты размером 12 бит, остальные компоненты нормируются на СКО и квантуются.
Результаты моделирования для сжатия амплитуды сигнала до 1-4 битов и фазы до 2-5 битов методом вейвлет-преобразования D4 (ВП D4) представлены на рисунке 6.
Из данного рисунка видно, что сжатие данных методом вейвлет-преобразования Добеши D4 имеет сравнимые характеристики SQNR c алгоритмом БАК в полярном формате при коэффициентах сжатия 4 и более (1-2 бита на отсчет амплитуды, 2-3 бита на отсчет фазы). При коэффициентах сжатия меньше 4, сжатие ВП D4 имеет SQNR на 2-5 дБ меньше, чем БАК и векторное квантование. Изображения, синтезированные после сжатия амплитуды до 2 бит и фазы до 5 бит (SQNR = 14.3 дБ) и при больших SQNR, практически неотличимы от исходного. Для увеличения SQNR и более точного восстановления значений амплитуд при сохранении коэффициента сжатия требуются вейвлеты, устраняющие моменты старших порядков, но это усложняет практическую реализацию.
Результаты моделирования сжатия данных ERS для всех рассмотренных алгоритмов представлены в таблице 1.
Таблица 1. Характеристики алгоритмов сжатия данных РСА.
|
Алгоритм сжатия |
Коэффициент сжатия, раз |
SQNR, дБ |
|
БАК квадратурный 1I+1Q |
8 |
4.5 |
|
БАК квадратурный 2I+2Q |
4 |
9.4 |
|
БАК квадратурный 3I+3Q |
8/3 |
14.9 |
|
БАК квадратурный 4I+4Q |
2 |
21.8 |
|
БАК полярный 1А+2Ф |
16/3 |
6.0 |
|
БАК полярный 1А+3Ф |
4 |
9.2 |
|
БАК полярный 1А+4Ф |
16/5 |
10.8 |
|
БАК полярный 1А+5Ф |
8/3 |
11.3 |
|
ВК 1I+1Q |
8 |
4.3 |
|
ВК 2I+2Q |
4 |
9.2 |
|
ВК 3I+3Q |
8/3 |
14.4 |
|
ВК 4I+4Q |
2 |
19.9 |
|
ВП D4 1А+2Ф |
16/3 |
5.9 |
|
ВП D4 1А+3Ф |
4 |
9.1 |
|
ВП D4 1А+4Ф |
16/5 |
10.5 |
|
ВП D4 1А+5Ф |
8/3 |
11.0 |
Использование данных РСА, полученных в результате сжатия/восстановления алгоритмами БАК в квадратурном формате и ВК до 3-4 битов на отсчет квадратуры, позволяет получить изображение визуально практически не отличимое от исходного с отношениями сигнал/шум квантования (SQNR) порядка 14-15 дБ и 19-22 дБ. Аналогичные результаты достигаются при сжатии алгоритмом БАК в полярном формате амплитуды до 2-4 битов на отсчет, фазы до 4-5 битов на отсчет, SQNR свыше 14 дБ. Для алгоритма ВП D4 подобные результаты достигаются для 3-4 бит на отсчет амплитуды и 4-5 бит на отсчет фазы.
Заключение
В данной работе было проведено исследование влияния сжатия данных в РСА космического базирования на приложение синтеза изображений.
В работе определен критерий качества работы алгоритмов сжатия данных, позволяющий оценить точность восстановления данных после сжатия, относительно исходных данных: отношение сигнал/шум квантования (SQNR).
Приведено описание подходов к реализации моделей компрессии/декомпрессии данных РСА на основе алгоритмов блочного адаптивного квантования (БАК) в квадратурном формате, БАК в полярном формате, векторного квантования (ВК), вейвлет-преобразования Добеши D4 (ВП D4), позволивших получить количественные характеристики работы алгоритмов, используемые для дальнейшего анализа.
В статье приведены полученные с помощью моделирования характеристики алгоритмов сжатия, по которым оценена возможность применения различных подходов к сжатию данных в задаче синтеза радиолокационных изображений, показан пример синтеза радиолокационного изображения по данным, подвергшимся компрессии/декомпрессии.
Результаты моделирования с использованием данных РСА ERS показывают, что все рассмотренные алгоритмы, при коэффициентах сжатия в 4 и более раз, имеют сходные характеристики. При этом на синтезированном изображении наблюдаются шумы, отчетливо различимы наиболее яркие и контрастные объекты. Изображение, синтезированное по восстановленным данным при сжатии менее чем в 4 раза, визуально практически не отличается от изображения, синтезированного по исходным данным. При этом, алгоритмы БАК в обоих форматах и ВК позволяют достичь больших на 2-5 дБ отношений сигнал/шум квантования, по сравнению со сжатием методом ВП D4. БАК с квадратурным представлением отсчетов является наиболее простым из рассмотренных алгоритмов с точки зрения практической реализации.
Литература
1. В.С. Верба, Л.Б. Неронский, И.Г. Осипов, В.Э. Турук. Радиолокационные системы землеобзора космического базирования. «Радиотехника», Москва, 2010 – 680 c.
2. И.М. Нестеров. Исследование влияние сжатия данных РСА на синтез радиолокационных изображений. Микроэлектроника и информатика – 2016. 23-я Всероссийская межвузовская научно-техническая конференция студентов и аспирантов: тезисы докладов. – М.: МИЭТ, 2016 – С.137
3. A. El Boustuni, K. Brunham, W. Kinsner. A review of current raw SAR data compression techniques // Electrical and Computer Engineering, 2001. Canadian Conference on, VOL. 2, 2001 – pp.925-930
4. D. Lebedeff, P. Mathieu, M. Barlaud, C. Lambert-Nebout, P. Bellemain. Adaptive vector quantization for raw SAR data // Acoustics, Speech, and Signal Processing, ICASSP-95, vol.4, 1995 – pp. 2511-2514
5. Б.Р. Левин. Теоретические основы радиотехники. М.: Радио и связь, 1989 – С.69-77
6. U. Benz, K. Strodl, A. Moreira. A comparison of several algorithms for SAR raw data compression // IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 33, NO. 5, SEPTEMBER 1995 – pp.1266-1276
7. R. Kwok, W. Johnson. Block Adaptive Quantization of Magellan SAR Data // IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 27, NO. 4, JULY 1989 – pp.375-383
8. J. Max. Quantizing for minimum distortion // Information Theory, IRE Transactions on, VOL. 6, March 1960 – pp.7-12
9. Y. Linde, A. Buzo, R.M. Gray. An algorithm for vector quantizer design // IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. COM-28, NO. 1, JANUARY 1980 – pp.84-95
10. I. Daubechies. “Ten lectures on wavelets“, SIAM, Pennsylvania, Philadelphia, USA 1992.
11. И.М. Нестеров, А. Н. Трунов. Влияние сжатия данных на ошибку определения высоты в радиолокационной интерферометрии РСА космического базирования. // Журнал радиоэлектроники: электронный журнал. 2015. N6. URL: http://jre.cplire.ru/jre/jun15/13/text.pdf
12. Image Focusing with MATLAB [electronics resource]. URL: https://saredu.dlr.de/unit/focussing_matlab.