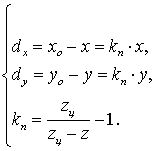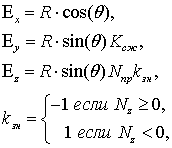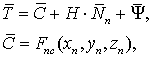УДК 535.31; 001.891.573

Использование оптико-геометрического моделирования для наблюдения космических объектов

 

В. Р. Ахметьянов, И. О. Лутов, М. И. Олейников

Военно-космическая академия имени А.Ф. Можайского

 

Статья поступила в редакцию 14 июня 2016 г.

 

Аннотация. В статье рассматриваются вопросы использования оптико-геометрического моделирования для определения габаритных и отражательных характеристик космических аппаратов, которые после  окончания срока активного существования переходят в разряд космического мусора и требуют непрерывного наблюдения и контроля, в том числе, наземными оптико-электронными средствами. Оптико-геометрическая модель включает в себя геометрическое описание космического аппарата как трехмерного тела, состоящего из функционально - конструктивных элементов (ФКЭ), и оптические характеристики материалов и покрытий ФКЭ.

Для ряда космических аппаратов имеются исходные видовые данные, представляющие собой цифровые фотографические изображения, которые предъявляются разработчиками на этапе монтажных и испытательных работ. Относительные геометрические характеристики космического аппарата могут быть получены из анализа цифрового изображения. С этой целью предлагается использовать компактный алфавит геометрического описания контурной модели конструкции космического аппарата в виде совокупности примитивов, отображаемых на исходное изображение с учетом свойств центрального проецирования объекта наблюдения на картинную плоскость.

Полученные оценки геометрических параметров космического аппарата позволяют осуществить анализ его отражательных характеристик с помощью математической модели численно-аналитического расчета в видимом диапазоне, которая основана на представлении космического аппарата в виде набора геометрических примитивов конического, сферического и плоского типов. В качестве модели отражения поверхности принята модель отражения Ламберта – Фонга. Определение коэффициентов диффузного отражения позволяет получать оценки вектора оптических характеристик элементов конструкции КА посредством обработки результатов наземных фотометрических наблюдений.

Предложенный в статье подход иллюстрируется на примере изображения космического аппарата «Космический телескоп Хаббла», полученного в 2009 году в ходе космического эксперимента «Атлантис» STS-125.

Ключевые слова: космический аппарат, космический мусор, оптико-электронные средства, геометрические характеристики, оптические характеристики материалов и покрытий.

Abstract. In the article the problems of usage of optical-geometrical modeling for definition of the dimensional and reflective characteristics of spacecraft are considered, which one after ending term of fissile existence pass in the category of space debris and require continuous supervising and check, including, ground-level optical-electronic means. The optical-geometrical model includes the geometrical description of spacecraft as three-dimensional body composed from functional - constructive elements (FCE), and optical characteristics of materials and covers FCE.

For a number of spacecraft there are source specific data representing digital photographic images, which one are presented by the developers at a stage of assembly and test operations. The relative geometrical performances of spacecraft can be received from analysis of the digital image. With this purpose it is offered to use the compact alphabet of the geometrical description of the contour pattern of a construction of spacecraft by the way collections of primitives mapped on the source image with allowance for of properties of a central projection of object of supervising on a picture plain.

The received estimations of geometrical arguments of spacecraft allow to realize analysis of his reflective characteristics with the help of a mathematical model of numerically - analytical account in a visible band, which one is based on submission of spacecraft by the way of set of geometrical primitives of conical, spherical and flat types. As the pattern of reflex of a surface the pattern of reflex of a Lambert – Fong is accepted. The definition of diffuse-reflection factors allows receiving estimations of a vector of the optical performances of structural elements of spacecraft by means of processing outcomes of ground-level photometric supervising.

The approach, offered in the article, is illustrated on an example of the image of spacecraft «Hubble Space telescope», received in 2009 during space experiment «Atlantis» STS-125.

Keywords: a spacecraft, space debris, optical-electronic means, geometrical characteristics, optical characteristics of materials and covers.

 

Выводимые на околоземную орбиту космические аппараты (КА) после окончания срока активного существования переходят в разряд космического мусора, требующего непрерывного контроля [1]. Для наблюдения космических аппаратов наземными оптико-электронными средствами (ОЭС) необходимо наличие оптических характеристик, позволяющих осуществлять надежное обнаружение и сопровождение КА, движущихся по орбитальным траекториям. Для ряда КА имеются исходные видовые данные, представляющие собой цифровые фотографические изображения. Эти изображения предъявляются разработчиками КА на этапе монтажных и испытательных работ, проводимых, в том числе, в условиях открытого космоса. Для получения оптических характеристик может быть использована трехмерная оптико-геометрическая модель (ОГМ) КА, определенная в работе [2].

Оптико-геометрическая модель включает в себя геометрическое описание КА как трехмерного тела, состоящего из функционально-конструктивных элементов (ФКЭ), и оптические характеристики материалов и покрытий ФКЭ. Относительные геометрические характеристики КА могут быть получены из анализа его изображения, представляющего собой двумерную проекцию трехмерного тела на картинную плоскость. Для этой цели возможно использование контурных рисунков, построенных с помощью структурированных геометрических моделей анализируемых объектов [3, 4]. Метрическая информация о КА в ряде случаев извлекается из габаритных ограничений на полезную нагрузку, которая выводится на орбиту ракетой-носителем.    Используемые ракеты-носители, как правило, являются адаптированными для КА заданного типа. В этом случае применимы методы калибровки изображений, основанные на совмещении объекта съемки и тест – объекта с калибровочными марками, размещенными в узлах пространственной решетки [5].

Рассмотрим основные свойства изображения, получаемого при центральном проецировании объекта наблюдения на картинную плоскость [4, с. 125-129]. Проецирование трехмерного объекта осуществляется с помощью прямых проецирующих лучей, которые называются проекторами. Они выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. Так как проекция отрезка сама является отрезком, то достаточно спроектировать лишь конечные точки.

При фотографировании объекта картинная плоскость перпендикулярна оптической оси объектива. Для этого случая введем систему декартовых координат в объектном пространстве, связанную с картинной плоскостью следующим образом. Ось абсцисс OX расположена по горизонтали (в плоскости местного горизонта), ось ординат OY расположена по вертикали картинной плоскости. Ось аппликат OZ совпадает с оптической осью объектива, направлена в сторону наблюдателя и вместе с осями OX и OY образует правую систему координат (СК). Центр СК OXYZ расположен в точке пересечения оси OZ и ортогональной плоскости OXY, проходящей через некоторую опорную точку (ОТ) объекта наблюдения. Обозначим аппликату центра проекции как  (), а координаты опорной точки в плоскости OXY как . Тогда для любой точки , принадлежащей проектору, который пересекает плоскость OXY в точке , и имеющей , соблюдаются следующие соотношения [4, с. 134]:

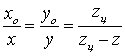.                                                                    (1)

Исходя из (1) смещения проективных координат  относительно координат  определяются как

                                                              (2)

С учетом того, что координаты  являются результатом параллельного проецирования произвольной точки проектора на плоскость OXY, то выражение (2) позволяет осуществлять переход от параллельной проекции трехмерного объекта к центральной проекции в определенной выше системе координат OXYZ. Обозначим координаты точки в картинной плоскости как . Исходя из равного масштаба по координатным осям картинной плоскости, соотношения между координатами  и  определяется следующим образом:

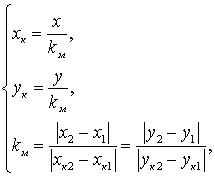                                                    (3)

где  - масштабный коэффициент,

       и  - координаты концевых точек отрезка в объектном пространстве,

       и  - координаты точек проекции отрезка в картинной плоскости.

Для построения трехмерной оптико-геометрической модели КА используются геометрические примитивы. Каждый примитив размещается в строительной системе координат (ССК) с осями, направленными аналогично осям СК OXYZ, и имеет следующие общие параметры:

-      координаты центра (опорной точки) примитива ;

-      углы разворота ССК: вокруг оси OX - , вокруг оси OY - , вокруг оси OZ - ;

-      дополнительное смещение центра примитива: по оси OX - , по оси OY - , по углу вокруг оси OZ - .

Все примитивы по типу формообразующей поверхности разделяются на две группы, образованные плоскими фигурами и поверхностями второго порядка [6]. Основу плоских фигур составляют: прямоугольник, треугольник, круг (сегмент). С помощью прямоугольника и треугольника могут быть построены два объемных примитива, представляющих собой прямые призмы. На основе круга могут быть построены примитивы, называемые обобщенными конусом, сферой, а также пирамида и фигура типа зонтик.

Указанные примитивы [6] позволяют построить в терминах функционально-конструктивных элементов геометрическое описание космического аппарата в целом. Назовем объединенный элемент трехмерного представления - конструкцией КА. Для отображения трехмерной геометрии на картинную плоскость конструкция КА определяется следующей группой параметров , где  - углы разворота строительной системы координат конструкции КА в целом относительно опорной точки, положение которой в проективной системе координат OXYZ задается параметрами: .

Совокупность определенных выше примитивов вместе с объединенным элементом можно трактовать как компактный алфавит геометрического описания контурной модели конструкции КА. Предложенный алфавит обладает свойством информационной полноты геометрического описания конструкции КА, ограниченного погрешностью метрического представления ФКЭ. В то же время, задача оценки группы параметров  относится к классу обратных некорректных задач, характеризующихся наличием, как статистических погрешностей оценок параметров, так и достаточно значимой неопределенностью исходных данных. Именно поэтому в работе [5, с. 87,88] в качестве решения данной задачи предлагаются методы обратной пространственной засечки и построения одиночных объектных моделей методами последовательных приближений.

Из рассмотрения свойств изображения, получаемого при центральном проецировании объекта наблюдения на картинную плоскость, следует, что проекция отрезка сама является отрезком. Поэтому, в качестве маркеров для совмещения объекта съемки и геометрической модели могут выступать концевые точки примитивов, характеризующих положение пространственных осей КА. Для этой цели наиболее подходит параллелепипед, если КА имеет явно выраженные габариты блока служебных систем, как правило, называемого корпусом КА. Другим подходящим примитивом является прямоугольник в случае наличия у КА солнечных батарей. Одна из точек выбранного примитива служит в качестве опорной точки, относительно которой строится как «опорный» примитив, так и остальные элементы геометрического описания контурной модели конструкции КА. Тем самым устраняется пространственный сдвиг контурной модели относительно изображения объекта наблюдения в картинной плоскости и создаются предпосылки для последующего устранения неопределенности в ракурсе и масштабе модели конструкции КА.

Исходя из сказанного, методика совмещения объекта съемки и контурной модели конструкции КА включает следующие этапы [6]:

1)      Выбор опорной точки и геометрического примитива, позволяющего в  наибольшей степени отобразить на картинную плоскость трехмерные характеристики доминирующего ФКЭ конструкции КА.

2)      Последовательное совмещение контурной модели опорного примитива и изображения объекта наблюдения посредством изменения масштабного коэффициента  и параметров ракурса  конструкции КА относительно опорной точки.

3)      Определение параметров  проецирования объекта наблюдения на картинную плоскость и дальнейшее согласование с ним контурной модели опорного примитива с учетом изменения параметров масштаба  и ракурса .

4)       Последовательное задание параметров, описывающих геометрические размеры и ракурсы примитивов наиболее значимых ФКЭ, которые определяются детальностью представления конструкции объекта, и проведение согласования каждого примитива с изображением КА.

 

Рисунок 1 – Изображение КА «Космический телескоп Хаббла»

 

 

Рассмотрим применимость предложенной методики на примере изображения  КА «Космический телескоп Хаббла» («КТХ»). Вид КА «КТХ» с борта космического корабля «Атлантис» STS-125 (2009 г.) [7] показан на рисунке 1. Целью использования предложенной методики будем считать определение геометрических размеров блока служебных систем (корпуса), солнечных батарей КА и экрана бленды. Так как корпус рассматриваемого КА имеет явно выраженную форму цилиндра, то в качестве первоначального примитива для совмещения подходит обобщенный конус, построенный на основе круга. Ниже приводятся аналитические выражения, реализующие алгоритм отображения круга на цифровом изображении с учетом параметров проецирования объекта на картинную плоскость.

Обозначим вектор единичной нормали круга, лежащего в плоскости OXZ, следующим образом:

.                                                               (4)

Результат поворота строительной системы координат примитива и конструкции КА в целом относительно опорной точки может быть описан с помощью трехмерной функции преобразования  в следующем виде:

,                                                       (5)

где  - вектор единичной нормали круга после выполнения преобразования.

Для дальнейшего рассмотрения определим алгебраическое преобразование двухмерного вектора  в следующем виде:

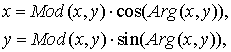
где  - функция взятия модуля вектора ,   - функция определения углового положения вектора  относительно оси OX в направлении против часовой стрелки.

Результатом параллельного проецирования круга на картинную плоскость является, в общем случае, эллипс, задаваемый параметрами:

,

,                                                                (6)

,

где  - модуль проекции вектора единичной нормали  на плоскость OXY,    - угол между большой полуосью эллипса и осью OX,  - коэффициент сжатия эллипса вдоль его малой оси.

С учетом выражения (6) вектор  положения точки круга радиуса  определяется следующим образом:

                                                             (7)

где  - угол, отсчитываемый от большой полуоси эллипса.

Использование выражений (6) и (7) позволяет определить координаты вектора , задающего положение точки круга с учетом ориентации большой полуоси эллипса, в следующем виде:

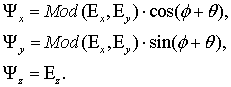                                                   (8)

Положение точки круга в строительной системе координат задается вектором  с помощью следующих соотношений:

                                                                   (9)

где -  вектор положения центра примитива после преобразований, -  высота положения круга по оси OY в исходной ССК примитива,  - функция преобразований поворота и сдвига вектора координат  центра примитива в исходной ССК.

Обозначим как  вектор положения опорной точки конструкции КА. Тогда суммарный вектор, который задает координаты точки примитива в СК OXYZ, приведенной к масштабу картинной плоскости и связанной с центром проекции в объектном пространстве, определяется в следующем виде:

 .                                                           (10)

С учетом выражений (2) и (10) смещение проективных координат относительно суммарного вектора  определяется как:

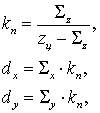                                                                             (11)

где - аппликата центра проекции в СК OXYZ ().

Для отображения точек круга на картинной плоскости зададим угловые положения  вектора , определенного с помощью выражения (7), следующим образом:

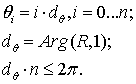                                                                      (12)

Обозначим значения вектора , заданного в соответствии с соотношением (9) для угловых положений , определенных выражениями (12), как . Использование координат вектора  в формулах (10) и (11) позволяет получить смещение проективных координат  для каждого . Тогда смещение координат i – ой точки круга относительно опорной точки конструкции КА на дискретной сетчатке изображения определяется в следующем виде:

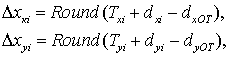                                                    (13)

где  - функция округления вещественной переменной  до ближайшего целого, , - смещение проективных координат относительно опорной точки конструкции КА, задаваемой вектором положения .

Использование выражения (13) позволяет привязать все изменения контурной модели конструкции КА к одной опорной точке, которая остается при этом неподвижной. Для достижения полного согласования контурной модели КА с его изображением используются другие точки геометрических примитивов. При этом точность согласования ограничена пересчитанным к объектному пространству половинным размером элемента разрешения цифрового изображения.

Проиллюстрируем применимость предложенной методики на примере изображения  КА «КТХ» (рисунок 1). Так как корпус рассматриваемого КА имеет форму цилиндра (диаметр 4,3 м), то в качестве объекта для совмещения подходит «кормовая» часть корпуса. В центр торцевой поверхности цилиндра можно поставить опорную точку, положение которой показано на рисунке 2 крестом.

Последовательное совмещение контурной модели опорного цилиндра и изображения объекта наблюдения посредством изменения масштабного коэффициента и параметров ракурса конструкции КА относительно опорной точки приводит к следующим их значениям: , . Определение параметров проецирования объекта наблюдения на картинную плоскость и дальнейшее согласование с ним контурной модели опорного примитива с учетом изменения параметров масштаба и ракурса позволяет получить следующие значения . Положение точки, соответствующей данным координатам в картинной плоскости, показано на рисунке 2 вторым крестом, находящемся на цилиндрической поверхности средней части корпуса. В результате совмещения по параметрам проецирования, показанного на рисунке 3, получается дальнейшее согласование цилиндрических примитивов, описывающих среднюю часть корпуса и бленду. В дальнейшем уточнения параметров проецирования, как правило, не требуется.

 

Рисунок 2 – Опорная точка на изображении КА

Рисунок 3 – Совмещение опорного примитива по масштабу и ракурсу

 

На рисунке 3 также показан результат совмещения изображения и примитивов, соответствующих солнечным батареям и описываемым прямоугольниками с параметрами . Совмещение осуществлялось по геометрическим размерам, ракурсу и положению относительно опорной точки. Одна солнечная батарея состоит из двух фрагментов с размерами . Геометрические параметры экрана бленды определяются в результате согласования двух плоских примитивов: прямоугольника и сегмента круга (рисунок 3). Эквивалентный экрану бленды по площади прямоугольник имеет следующие геометрические параметры . Так как целью использования предложенной методики было определение геометрических размеров корпуса, солнечных батарей КА и экрана бленды, то для описания конструкции объекта оказалось достаточным применение трех примитивов: прямоугольника, сегмента круга и конуса.

Полученные оценки геометрических параметров КА позволяют осуществить анализ его отражательных характеристик. Для решения этой задачи могут быть  использованы результаты фотометрических наблюдений, получаемых наземными оптико-электронными средствами. В настоящее время результаты этих наблюдений преимущественно используются для исследования отражательных характеристик геостационарных КА, а также для оценки технического состояния КА, находящихся на орбитах различных типов [8, 9]. В ряде случаев при исследовании геометрического облика и оптических характеристик элементов конструкции КА отсутствует информация по характеристикам материалов и покрытий элементов конструкции, в том числе и в результате изменения известных оптических характеристик материалов и покрытий под действием факторов космического пространства [10].

В этих условиях возникает необходимость в разработке методического аппарата по определению оптических характеристик элементов конструкции КА сложной формы по результатам наземных фотометрических наблюдений. По своей сути задача определения оптических характеристик КА по результатам фотометрических наблюдений является некорректной и для её решения необходимо применить метод регуляризации Тихонова [11] с использованием априорной информации по наблюдаемому объекту [12]. В рассматриваемом случае это условия наблюдения (углы подсветки и визирования, а также дальность до КА), геометрические размеры элементов конструкции КА и их взаимная ориентация, а также ориентация КА на орбите. Кроме того, необходимо установить ограничения на входные и выходные данные. С этой целью проведём анализ отражённого излучения от КА в видимом диапазоне.

Как известно отражённое солнечное излучение от поверхности большинства материалов и покрытий можно представить в виде суперпозиции двух независимых компонент: диффузно отражённого и зеркально отражённого излучений [13]. Диффузно отражённое излучение распространяется в полусферу, а зеркально отражённое излучение сосредоточено в значительно меньших пространственных углах, что даёт возможность локализовать участки фотометрических наблюдений, в которых присутствует только диффузно отражённое от КА излучение Солнца. Кроме того, проведение сеансов фотометрических наблюдений в видимом диапазоне происходит, когда Солнце опускается за горизонт не менее 20⁰, а зенитный угол наблюдения КА не превышает 60⁰ [14], что позволяет не учитывать при анализе фотометрических наблюдений переотражённое Землёй излучение Солнца.

Анализ конструкции КА позволяет представить его в виде набора из N геометрических примитивов плоского, сферического или конического типов [6], имеющих некоторые коэффициенты диффузного отражения в диапазоне наблюдения ОЭС. Тогда уравнение для расчёта силы отражённого излучения от КА можно представить в виде:

,                                (14)

где  – коэффициент отражения i – го элемента конструкции;

 –

результат расчёта диффузного отражения (при коэффициенте диффузного отражения, равном единице) от элемента конструкции, Wi – область интегрирования, определяемая геометрией элемента конструкции;

 – поток солнечного излучения в диапазоне ;

S – площадь элементарной площадки.

Выражения , обозначаемые ниже как D, рассчитываются с учётом взаимного затенения и экранирования излучения Солнца.

Анализ (14) показывает, что КА является многомерным линейным по отношению к коэффициенту диффузного отражения объектом. Обозначим через , вектор из N уточняемых коэффициентов диффузного отражения , через  - измеренную от объекта силу излучения, а через  невязку, определяемую в пространстве выходных сигналов как разность измеренной и расчётной силы излучения в некоторый момент времени «t_m».

Учитывая (14) и принятые обозначения запишем в векторно-матричной форме [12] следующее соотношение для интервала времени :

                                                           (15)

где  – вектор-столбец отсчётов силы излучения;

M – число отсчётов силы излучения ;

N – число элементов с различными коэффициентами диффузного отражения входящих в состав объекта;

;                               (16)

 –вектор-столбец невязок по M измерениям силы излучения.

Матрица  с элементами представляет собой матрицу наблюдения объекта. Строки данной матрицы определяют последовательность уравнений наблюдений (14) для моментов времени , а столбцы представляют собой N элементов конструкции КА, входящих линейно по параметрам – коэффициентам отражения в модель наблюдения. Иначе элемент  – это характеристика n – го элемента конструкции в m – й момент времени.

Примем, что измерения  не коррелированны. В соответствии с принципом Гаусса-Лежандра для многомерного линейного по параметрам объекта, оценка  вектора  отыскивается при минимизации суммы квадратов невязок:

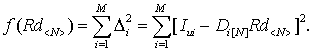                                    (17)

Необходимое условие минимума функции  определяется нормальным уравнением:

 или .                      (18)

Предположим, что матрица  не особая, т.е. . Тогда оценка  вычисляется по формуле:

                                         (19)

Полученный вектор оптических характеристик необходимо подвергнуть проверке, чтобы значения коэффициентов диффузного отражения не были отрицательными или больше единицы. Если значения оценок коэффициентов отражения находятся вне пределов [0…1], необходимо проверить выполнение всех ограничений и условий.

На рисунке 4 представлен алгоритм определения коэффициентов диффузного отражения. Работа данного алгоритма построена следующим образом:

1)   для рассматриваемого сеанса измерений рассчитываются условия подсветки и наблюдения с учётом ориентации КА;

2)   для этих условий формируются матрица наблюдения;

3)   производится пересчёт блеска КА в силу излучения;

4)   на основе D_mn и силы излучения I_m формируется нормальное уравнение;

5)   решением уравнения является вектор диффузных коэффициентов отражения.

 

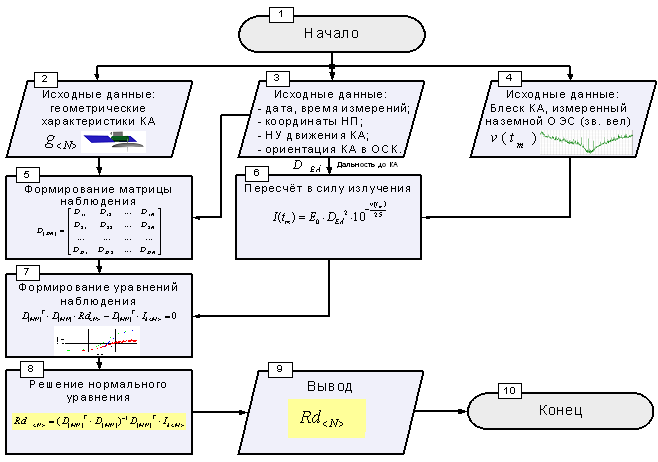
Рисунок 4 - Алгоритм определения коэффициентов диффузного отражения

 

 

Основным условием определения коэффициентов диффузного отражения является неособенность матрицы , которая имеет место при отсутствии линейности между столбцами и строками матрицы наблюдения. Физически это достигается за счёт различия в геометрической форме элементов конструкции КА или за счёт их различной пространственной ориентации в строительной системе координат.

В свою очередь, линейность между строками матрицы , связанными с отсчётами во времени и вектором измерений силы излучения, обусловлена подобием и крутизной изменения фазовых зависимостей каждого элемента конструкции. Это, в первую очередь, определяется условиями подсветки и наблюдения, реализуемыми в конкретном сеансе фотометрических наблюдений. Увеличение числа элементов конструкции также ведёт к появлению линейности между фазовыми зависимостями отдельных элементов конструкции, что существенно влияет на обусловленность матрицы . Возможным выходом из такой ситуации является объединение в один, два и более элементов конструкции, имеющих одинаковые материалы и покрытия.

Ниже приведён расчётный пример определения коэффициентов диффузного отражения в соответствии с приведённой методикой. С учётом определённых выше геометрических характеристик КА осуществлено построение его трёхмерной геометрической модели (рисунок 5).

 

 

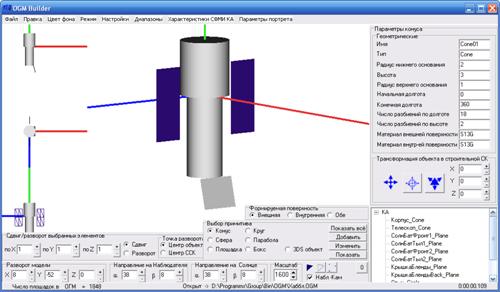
Рисунок 5 – Геометрическая модель КА

 

Анализ трёхмерной модели КА показывает, что в его составе можно выделить три группы элементов конструкции, объединяемых по признаку идентичности материалов и покрытий:

1)    Корпус КА (приборный отсек и бленда) – полированный алюминий;

2)    Панели солнечных элементов – арсенид-галлиевые преобразователи солнечного излучения;

3)    Крышка бленды - покрытие S13G (белая краска).

Такая группировка позволяет при определении диффузных коэффициентов отражения оперировать тремя приведёнными различными по материалу покрытия элементами конструкции КА.

Учитывая, что наклонение орбиты КА составляет 28.471⁰, а высота орбиты 561-566 км, наблюдения такого КА наземными оптическими станциями возможны только при их размещении вблизи экватора. Примером такой оптической станции может выступать астрономическая обсерватория Пико дос Диас в Бразилии. Координаты 22⁰32’06” ю.ш. 45⁰34’58” з.д. На рисунке 6 представлены результаты моделирования характерных условий подсветки и наблюдения КА, реализуемые для указанной оптической станции.

 

 

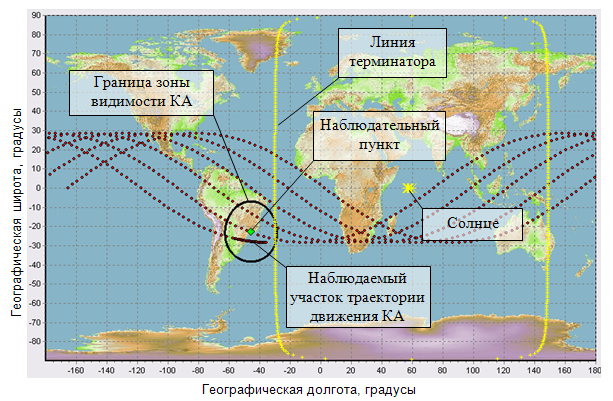
Рисунок 6 – Условия наблюдения КА

 

С учётом текущих условий подсветки и наблюдения КА были проведены расчёты силы излучения данного КА при условии наблюдаемости его в зоне видимости оптической станции. Результаты расчёта силы излучения для диапазона «V» стандартной фотометрической системы Джонсона приведены на рисунке 7.

 

 

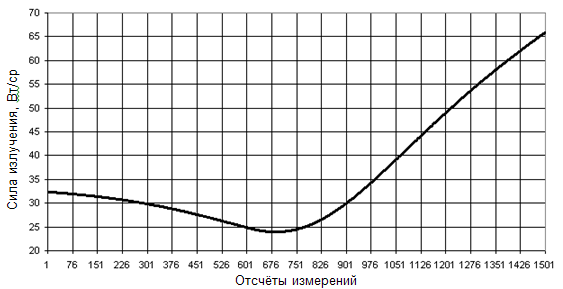
Рисунок 7 – Сила излучения КА

 

В силу отсутствия результатов реальных оптических наблюдений КА, получаемых указанной станцией, результаты расчёта примем за измерения, предварительно подвергнув их зашумлению мультипликативной помехой с относительным среднеквадратическим отклонением 10% (рисунок 8).

Для формирования матрицы наблюдения КА для каждого из определённых выше сгруппированных элементов конструкции проведём расчёт диффузно-отражённого излучения при условиях наблюдения, реализуемых для указанной оптической станции. При этом коэффициент диффузного отражения принимается равным единице. На рисунке 8 представлена полная матрица наблюдения для определённых ранее условий подсветки и наблюдения КА.

Результатом решения системы линейных уравнений, сформированной с учётом матрицы наблюдения, является вектор из трёх компонентов в колонке 3 таблицы 1.

Анализ результатов определения диффузных коэффициентов отражения показывает, что в целом получены достоверные оценки этих коэффициентов, а ошибки определения коэффициентов в первую очередь обусловлены помехами. Результат расчёта силы излучения с учётом определённых выше коэффициентов представлен на рисунке 8.

Представленная методика позволяет получать оценки оптических характеристик элементов конструкции КА посредством обработки результатов наземных фотометрических наблюдений, что особенно актуально при наблюдении КА, находящихся в нештатной ситуации или переходящих в разряд космического мусора.

 

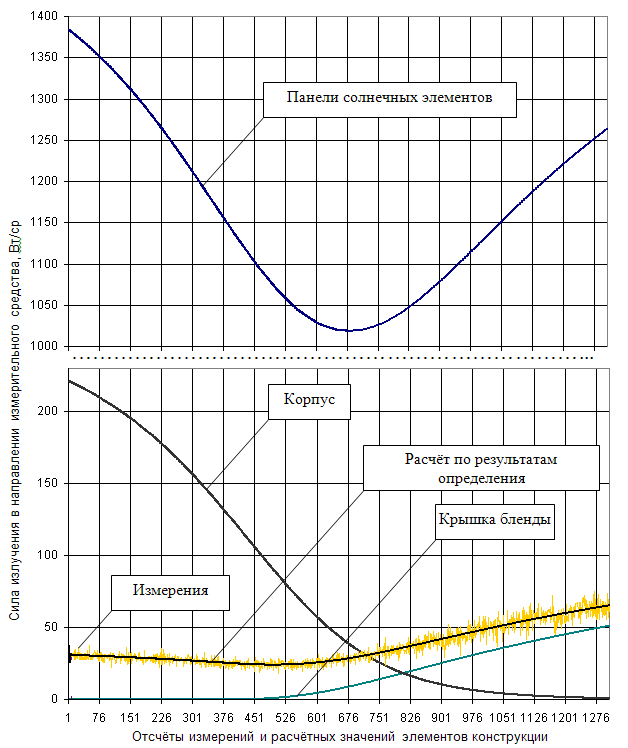
Рисунок 8 – Графическое представление матрицы наблюдения КО

 

Таблица 1 – Результаты определения диффузных коэффициентов отражения

Элемент конструкции	Коэффициенты, используемые при расчёте силы излучения	Коэффициенты, определённые с использованием методики	Ошибка определения, %
1	2	3	4
Корпус	0.0087	0.00825	-5.13468
Панели солнечных элементов	0.021	0.02109	0.4115
Крышка бленды	0.7706	0.75535	-1.98812

 

В заключение отметим, что использование оптико-геометрического моделирования позволяет оценить отражательные характеристики движущихся по орбитальным траекториям космических аппаратов, сведения о которых весьма ограничены. Получаемые оценки отражательных характеристик, в свою очередь, дают возможность осуществлять надежное обнаружение и сопровождение наблюдаемых с помощью оптико-электронных средств как активных, так и выведенных из эксплуатации КА. Таким образом, благодаря разработанной методике предложен подход к решению одной из частных задач в проблеме экологического мониторинга ближнего космоса.

 

Литература

1      Назаренко А.И. Моделирование космического мусора / Серия «Механика, управление и  информатика». - М.: ИКИ РАН, 2013. – 216 с.

2.     Корякин А.В., Лутов И.О. Распознавание космических объектов по разнородной видовой информации.- СПб.: ВИКУ, 2000.- 115 с.

3    Прэтт У. Цифровая обработка изображений: Пер. с англ.- М.: Мир, 1982.- Кн. 2.- 480 с.

4  Сиденко Л.А. Компьютерная графика и геометрическое моделирование: Учебное пособие.- СПб.: Питер, 2009.- 224 с.

5      Дубиновский В.Б. Калибровка снимков.- М.: Недра, 1982.- 224 с.

6       Ахметьянов В.Р., Лутов И.О., Олейников М.И. Метод оптико-геометрического моделирования в задаче определения габаритных и отражательных характеристик космических аппаратов // Журнал радиоэлектроники [электронный журнал], 2015. № 4.
URL: http://jre.cplire.ru/jre/apr15/14/text.pdf

7      Космический телескоп «Хаббла». Международный научный сервер [электронный ресурс]. - htpp://Scientific.ru.

8       Диденко А.В. Исследование фотометрических характеристик геостационарных ИСЗ методами электрофотометрии // Автореферат диссертации. Одесса. 1992.- 15 с.

9      Багров А.В., Выгон В.Г., Рыхлова Л.В., Шаргородский В.Д. Исследование состояния аварийного геостационарного спутника по данным фотометрических наблюдений // Институт астрономии. Околоземная астрономия и проблемы изучения малых небесных тел Солнечной системы. Сборник научных трудов конференции, г. Обнинск, 25-29 октября 1999. М.: 2000.- 372 с.

10  Kissel К.Е. Diagnosis of spacecraft surface properties and dynamic motions by optical photometry // Space Research, 1969, v. 9,  pp. 53-75.

11    Тихонов А.Н. Методы решения некорректных задач – М.: Наука, 1986. – 286 с.

12    Дмитриев А.К., Юсупов Р.М. Идентификация и техническая диагностика: учебн. пособие для вузов. – МО СССР, 1987. – 521 с.

13  Борн М. Основы оптики. Перевод с англ. – 2-е изд. – М.: Наука, 1973. – 720 с.

14    Миронов А.В. Основы астрофотометрии: учебное пособие. – М.: МГУ, 2005. – 194 с.