|
"ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" "JOURNAL OF RADIOELECTRONICS" N 8, 1999 | |
A NEW ANALYTICAL METHOD OF SOLVING 2-D DIFFRACTION PROBLEMS
Michael V. Vesnik,
Institute of Radioengineering and Electronics of Russian
Academy of Sciences
Received August 9, 1999
A new method of solving 2-D diffraction boundary problems for perfectly conducting half-infinite scatterers is presented. The method is based on constructing a universal integral representation of the diffracted wave with use of the theory of conformal transformations. This diffraction wave in integral form being summarized with geometrical optics components of incident and reflected waves represents a solution of Helmholt's equation boundary problem. A rigorous solution for half-infinite scatterers with polygonal envelope is received. The asymptotic of the integral representation is constructed in a compact form, convenient for further applications.
1.Introduction
To the present moment rigorous analytical solutions of diffraction theory boundary problems are received with use of either variables separating method or Wiener - Hopf method with it's modifications and the number of such solutions is not a high one. This paper presents a new method which allows to increase a number of rigorous solutions in 2-D diffraction theory.
2. Statement of the problem
Consider the 2-D perfectly conducting half - infinite body of an arbitrary shape
disposed in (x, y) plane and exited by an incident
wave 
. In terms of
geometrical optics (GO) the incident and reflected waves 
and 
have "light - shadow" boundaries (Fig.
1).
Fig.1. 
and 
regions.
The solution for the diffracted wave u is constructed in the form of an integral representation in the plane of complex variable a:
|
(1) |
the sense of remaining designations will be explained later.
3. Construction of an integral representation and an asymptotic
Assume that y indicates the value of a complex variable and thus the (x, y) plane is a complex one. Using the theory of a complex variable one can find one-to-one conformal transformation of the region w=(u, v) to the region z=(x, y). Here w represents the upper half-plane of the complex plane (u, v) and z represents the exteriority of the scatterer in the complex plane (x, y):
|
(2) |
The inverse to (2) function is:
|
(3) |
and even if the expression (3) does not exist explicitly then fixing z one can uniquely find the corresponding value of w from (2). Therefore we suppose (3) to be known as well.
Consider a case of excitation by plane wave coming from the directing angle 
in the z
region. The expression for the wave in polar coordinates will be:
|
(4) |
but the method presented is suitable for other types of excitation too.
In polar coordinates (2) becomes:
|
(5) |
Here 
, 
are the functions of polar
coordinates. In accordance with (3) the inverse functions 
and 
:
|
(6) |
For the observation point with coordinates 
in z region and coordinates 
in w
region from (5) and (6) we get:
|
(7) |
Let us introduce new complex values a , b
, 
, 
and fix one-to-one relationship between them:
|
(8) |
where 
is the real
value. The curve 
is
shown at Fig.2:
Fig. 2. 
region.
Let us now define a new function 
on the set of complex values a (and at the
same time - on the sets of complex values b , 
or 
):
|
(9) |
Let us designate the earlier introduced regions z and w as 
and 
and regions 
and 
- as 
è 
. Let us
introduce second sheets of complex surface 
, 
, 
and 
to be disposed over the corresponding first
sheets. Now instead of the single (primary) value related to the single sheet we get two
values related to the first or second sheets correspondingly: 
and 
, 
and 
,
, and 
, 
and 
instead of 
, 
, 
and 
.
Now determine that the incident GO field 
exists only in the first sheet and the reflected GO field 
exists only in the second
sheet. Define the relationship between the coordinates of the second sheets with the same
formulas (5), (6) and (8) that the one of the first sheets.
To this point the values without the index "1" or "2": 
, 
, 
and 
were related to the single regions z, w,
and 
which we considered before.
From this point we shall stand that their domain of definition relates to both sheets
"1" and "2".
Let us now perform a reflection of all the points of the region 
from the upper half-plane to
the lower one symmetrically with respect to the horizontal axis. Then, "pasting"
to 
along the horizontal axis
which corresponds to the boundary of the scatterer we compose from them a full plane which
will be named as 
(Fig. 2). The same operation we make with the regions 
and 
thus receiving a new region 
.
Consider now the integral representation (1). The paths of integration in a - plane "1" and "2" are traced in such way that
the corresponding points in the region 
fall to the shadow boundaries of the functions and 
in 
region if 
. In (1) 
from (8) when 
, 
when 
. The direction of
moving along the paths "1" and "2" is shown at Fig. 2.
It may be shown that the integral representation (1) meets wave equation and radiation
condition. It is also continuous fraction by the value 
in region 
. Thus 
is the divergent part of the solution of our boundary problem (sometimes it is being named
as the diffracted wave).
Let us now build a function V:
|
(10) |
Here P is the 
or 
. As the V function is a continuous
fraction on all the region 
including the boundary of the scatterer the function U:
|
(11) |
meets boundary conditions by Dirichle or Newmann correspondingly and thus represents the required solution of our boundary problem. The solution is rigorous for the scatterers with polygonal contour. For other scatterers an additional mathematical investigation of solution accuracy is required.
To receive an asymptotic of integral representation (1) considering 
it is more convenient to use
b coordinate. If the parameter 
is large and varies slowly, i.e. 
, from (8) one can receive
the derivative:
|
(12) |
Then, as 
, from (1)
we get:
|
(13) |
The final expressions will be:
where |
(14) |
The asymptotic for the case of two "light - shadow" boundaries is:
|
(15) |
where 
and 
- are the saddle points of 
function (9) - look [1].
Viewing (15) on can see that it represents a sum of terms connected with the saddle points disposed on GO shadow boundaries of incident and reflected waves. The shadow boundaries diverge from one point on the surface of the scatterer and locate in different sheets.
4. Solution constructing algorithm
So, there is the statement of the problem: 2-D perfectly conducting scatterer of an arbitrary shape exited by the plane (or other) incident wave. The solution of boundary problem is required. In correspondence with the method presented the following algorithm may be offered:
1. The first step should be done is to find the conformal transformation (2) which defines the paths of integration in a region. As soon as it is done one can construct the solution in integral form (1). To find the asymptotic the next steps should be done:
2. Finding the saddle points 
of 
function (9).
3. Finding the 
(12)
and 
(14) in the saddle
points 
.
4. Finding the solution in correspondence with (11).
5. An example of method application for the case of edge diffraction
As an example of method application let us find the known solution for the case of
plane wave (4) scattering by perfectly conducting edge with external angle 
radian. The results of
performing all the steps of our algorithm will be the following:
1. Conformal transformation (1): 
. Inverse function: 
from which for the observation point 
we get: 
and from (8) follows: 
2. Saddle points of the function 
(9): 
, 
.
3. The derivative (12): 
, the function (14):
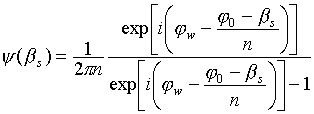
From this one can easily get (15) which fully corresponds with the known solution for the edge [2].
6. Conclusion
In this paper a new analytical method of solving 2-D diffraction problems is presented. The solution for the case of plane wave scattering by half-infinite body is constructed with use of this method. The effectiveness of the method has been illustrated in [3] with receiving a rigorous solution for the case of plane wave scattering by half-infinite plate of finite thickness. It seems to be no limitations preventing to apply the same method for the case of other types of exiting waves and for other types of 2-D scatterers, for instance, multiply connected or of the limited size.
In addition to the generosity of the method presented one can note its essential effectiveness and convenience because if conformal transformation (2) is known then the constructing of analytical formula (15) for asymptotic solution may be done immediately after calculating the derivative (12).
The author wishes to acknowledge Prof. V.A. Kaloshin for useful discussions.
Literature
[1] F. Frank, R. Mises. Differential and integral equations of mathematical physics.
[2] Pauli W. On asymptotic series for functions in the theory of diffraction of light. Physical Review, 54, No. 11, 924-931, 1938.
Author: Vesnik Michael V., e-mail: vesnik@mail.cplire.ru
 |
 |
,
.
,
,
, 
, 
, 
,
.
- at the "lighted" places of 
region and
- at
the "shadowed" places of 
region.
or 
; 
.
,
,