| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2001 |  |
МЕТОД СИНТЕЗА ПЛАВНЫХ СОГЛАСУЮЩИХ ПЕРЕХОДОВ
Д. Н. Панин,
В. В. Зайцев, Г. П. Яровой
Самарский государственный университет
Получена 18 декабря 2001 г.
Описан метод компьютерного синтеза согласующих переходов на отрезках линий с плавно меняющимися волновыми сопротивлениями. Проведен синтез кусочно-линейного перехода. Показано, что синтезированный переход обеспечивает хорошее согласование в широкой полосе частот.
Вопросы согласования волновых сопротивлений участков линий передачи традиционно занимают одно из центральных мест в теории и технике микроволновых систем [1-3]. Считается, что переходы с непрерывным изменением электрофизических параметров (плавные переходы) по сравнению со ступенчатыми переходами при прочих равных условиях обеспечивают наименьшие отражения в широкой полосе частот [3]. При этом из-за отсутствия точных аналитических решений для участка линии с произвольным законом изменения волнового сопротивления расчет согласования проводится либо методом замены плавного перехода ступенчатым с малой величиной ступеньки [4], либо путем использования линий с модельными профилями волнового сопротивления, допускающих аналитическое решение телеграфных уравнений [5]. Решение задач синтеза в рамках первого подхода сопряжено со значительным объемом вычислений, использование второго – проблематично.
В настоящей работе описан компьютерный метод синтеза плавных переходов, основанный на численном интегрировании полученного ранее [6, 7] дифференциального уравнения для коэффициента отражения от неоднородности. На примере синтеза кусочно-линейного перехода продемонстрирована вычислительная эффективность метода.
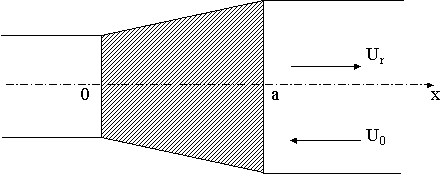
Рассмотрим отрезок неоднородной линии передачи (Рис.
1). На участке ![]() линию характеризуют погонные емкость С(x),
индуктивность L(x) и проводимость G(x), комбинации которых дают
локальные значения волнового сопротивления
линию характеризуют погонные емкость С(x),
индуктивность L(x) и проводимость G(x), комбинации которых дают
локальные значения волнового сопротивления ![]() и фазовой скорости
и фазовой скорости ![]() Соответствующие
величины для однородных выходного и входного участков линии обозначим через Z0
и Za, v0
и va.
Схематическое изображение перехода дано на рис. 1.
Соответствующие
величины для однородных выходного и входного участков линии обозначим через Z0
и Za, v0
и va.
Схематическое изображение перехода дано на рис. 1.
Рис. 1
Рассматриваемый отрезок линии передачи описывается следующей системой телеграфных уравнений :
В
системе уравнений (1) введены следующие обозначения: V(x)=Z0J(x), k=![]() /v0, n(x)=v0/v(x),
/v0, n(x)=v0/v(x),
![]()
Справа по схеме на участок неоднородности падает волна с комплексной амплитудой напряжения U0 . Отношение комплексной амплитуды Ur отраженной волны к U0 определяет коэффициент отражения:
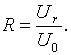
В системе (1) для удобства перейдем к нормированным на U0 переменным:
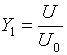 ,
, 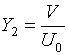 .
.
Тогда система примет следующий вид:
Здесь
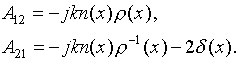
Соответствующие рассматриваемой физической ситуации граничные условия для системы уравнений (2) имеют вид:
При
записи данных равенств использовано понятие коэффициента прохождения T
, как отношения комплексной амплитуды Ut прошедшей
волны к комплексной амплитуде падающей; кроме того введено обозначение ![]()
Граничные условия (3) в предельном случае ![]() позволяют
определить значение коэффициента отражения от резкого перехода между двумя
линиями с волновыми сопротивлениями Za и Z0:
позволяют
определить значение коэффициента отражения от резкого перехода между двумя
линиями с волновыми сопротивлениями Za и Z0:
Это равенство в дальнейшем будет использовано в качестве начального условия при решении уравнения для коэффициента отражения.
Система уравнений (2) совместно с граничными условиями (3) составляет линейную двухточечную граничную задачу. Широко известны следующие математические методы решения задач данного типа: метод пристрелки, метод дифференциальной прогонки, конечно-разностный метод, метод продолжения по параметру и метод инвариантного погружения. В работе [6] в рамках метода дифференциальной прогонки получено дифференциальное уравнение для коэффициента отражения от неоднородности переменной длины L:
Для
расчета коэффициента отражения это нелинейное дифференциальное уравнение с
комплексными коэффициентами должно быть проинтегрировано на отрезке ![]() с начальным
условием (4). Результатом интегрирования является истинное значение
коэффициента отражения
с начальным
условием (4). Результатом интегрирования является истинное значение
коэффициента отражения ![]() .
.
Решение нелинейной задачи Коши (4), (5) не удается получить аналитически. Однако такая формулировка задачи весьма удобна для применения численных методов.
Введем на неоднородном участке линии ![]() равномерную
сетку с шагом
равномерную
сетку с шагом ![]() где N=1- число узловых точек. При этом узел с номером n=0 лежит на левой границе неоднородности, а узел n=N
– на правой, т.е. в плоскости падения волны. Производную в дифференциальном
уравнении (5) аппроксимируем центральной разностью:
где N=1- число узловых точек. При этом узел с номером n=0 лежит на левой границе неоднородности, а узел n=N
– на правой, т.е. в плоскости падения волны. Производную в дифференциальном
уравнении (5) аппроксимируем центральной разностью:
Здесь
индекс n использован
для обозначения значений функции и производной, взятых узле с номером n,
т.е. в точке ![]() С
учетом данной аппроксимации уравнение (5) в n-ом узле
принимает вид
С
учетом данной аппроксимации уравнение (5) в n-ом узле
принимает вид
Здесь
верхний индекс указывает на номер узловой точки, в которой вычисляются значения![]() Кроме того, k аргумент
учитывает зависимость коэффициентов в разностной формуле (7) от частоты.
Кроме того, k аргумент
учитывает зависимость коэффициентов в разностной формуле (7) от частоты.
Формула (7) позволяет проводить вычисления в узлах с
номерами n=2, 3, …, N. Для узла n=1 запишем аналогичное выражение, используя значения
функций в полуцелой точке ![]() :
:
Наконец,
значение ![]() вычисляется
с использованием аппроксимации производной в уравнении (5) правой разностью:
вычисляется
с использованием аппроксимации производной в уравнении (5) правой разностью:
Таким образом, мы получили разностную схему (7)-(9) которая имеет второй порядок точности по шагу дискретизации и, в то же время, требует однократного вычисления правой части уравнения (5). Сопоставимый по точности двухэтапный метод Рунге-Кутты характеризуется меньшим быстродействием по причине двукратного вычисления правой части (5). Быстродействие алгоритма очень важно при решении задачи синтеза.
В общей постановке проблему синтеза плавного перехода можно сформулировать как задачу минимизации целевой функции рассогласования
на заданной сетке частот ![]() в пространстве
параметров
в пространстве
параметров ![]() профиля
волнового сопротивления
профиля
волнового сопротивления ![]() , где
, где ![]() - весовые коэффициенты. Вычисляя
значения
- весовые коэффициенты. Вычисляя
значения ![]() при
помощи разностной схемы (7)-(9), для поиска минимума целевой функции (10) можно
воспользоваться одним из прямых методов оптимизации. Хорошие результаты дает
применение симплексного метода Нелдера-Мида [8].
при
помощи разностной схемы (7)-(9), для поиска минимума целевой функции (10) можно
воспользоваться одним из прямых методов оптимизации. Хорошие результаты дает
применение симплексного метода Нелдера-Мида [8].
В
качестве примера применения изложенного метода проведем синтез
кусочно-линейного перехода, образованного последовательностью двух линейных.
Пространственный профиль волнового сопротивления такого перехода, зависящий от
двух параметров ![]() и
и ![]() , может быть описан выражением
, может быть описан выражением
В
пространстве параметров ![]() оптимальная точка
оптимальная точка ![]() определяется в
соответствии с условием минимума целевой функции (10) – в данном случае функции
двух аргументов:
определяется в
соответствии с условием минимума целевой функции (10) – в данном случае функции
двух аргументов:
В
качестве исходных данных для синтеза перехода между линиями с
![]() возьмем
частотную зависимость коэффициента отражения от параболического перехода с
профилем волнового сопротивления
возьмем
частотную зависимость коэффициента отражения от параболического перехода с
профилем волнового сопротивления
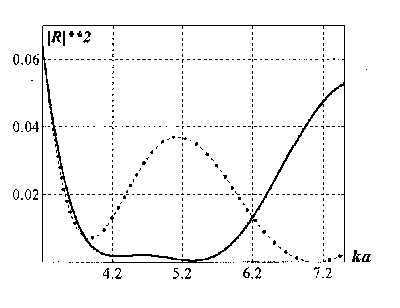
Квадрат модуля коэффициента
отражения от данного перехода для ![]() отмечен на рис. 2 штрихпунктирной линией.
Так как в окрестности частоты
отмечен на рис. 2 штрихпунктирной линией.
Так как в окрестности частоты ![]() наблюдается локальный минимум отражения,
попытаемся оптимизировать кусочно-линейный переход, взяв для целевой функции
(10) сетку частот
наблюдается локальный минимум отражения,
попытаемся оптимизировать кусочно-линейный переход, взяв для целевой функции
(10) сетку частот ![]() . Симплексным методом удается найти, что
. Симплексным методом удается найти, что ![]() при
значениях
при
значениях ![]() .
Время счета на ПК Pentium III-500 порядка 20 секунд.
.
Время счета на ПК Pentium III-500 порядка 20 секунд.
Рис.2
На рис. 2 непрерывной линией показан график частотной зависимости коэффициента отражения по мощности от синтезированного перехода. Как видно из рисунка, оптимизированный кусочно-линейный переход обеспечивает лучшее согласование в широкой полосе частот, чем параболический. При этом из числа плавных переходов он, по-видимому, с наибольшей точностью реализуется технологически.
Литература
-
Микроэлектронные устройства СВЧ / Г.И.Веселов, Е.Н.Егоров, Ю.Н.Алехин и др.; Под ред. Г.И.Веселова. - М.: Высшая школа, 1988.- 280 с.
-
Ильинский А.С., Кравцов В.В., Свешников А.Г. Математические модели электродинамики. - М.: Высшая школа, 1991. - 224 с.
-
Фуско В. СВЧ цепи. Анализ и автоматизированное проектирование. - М.: Радио и связь, 1990. - 288 с.
-
Кац Б.М., Мещанов В.П., Фельдштейн А.Л. Оптимальный синтез устройств с Т-волнами.- М.: радио и связь, 1984. - 288 с.
-
Салий И.Н. Канонические нерегулярные линии передачи и их эквивалентные представления // Лекции по электронике СВЧ и радиофизике: 8-я зимняя школа-семинар инженеров. Книга 4. - Саратов: Изд. СГУ, 1989. С. 73-80.
-
Зайцев В.В., Панин Д.Н., Яровой Г.П. Численный анализ отражений от слоя неоднородной плазмы // Физика волновых процессов и радиотехнические системы. - 2000. - Т.3. - N1. - С.9-12.
-
Жданова О.Н., Зайцев В.В., Панин Д.Н., Яровой Г.П. Численное моделирование отражений акустической волны от движущегося газового слоя // Вестник СамГУ.- 2000. - N2. - С.118-121.
-
Фидлер Дж.К., Найтингейл К. Машинное проектирование электронных схем. - М.: Высшая школа, 1985. - 216 c.
Авторы:
Панин Дмитрий
Николаевич (аспирант), e-mail: persey22@mail.ru,
Зайцев Валерий Васильевич (канд. физ.-мат. наук, доцент),
Яровой Геннадий Петрович (доктор физ.-мат. наук, профессор)
Самарский государственный университет, кафедра радиофизики и компьютерного моделирования радиосистем.
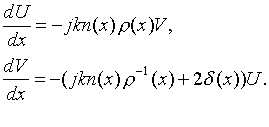 (1)
(1)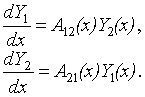 (2)
(2)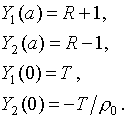 (3)
(3)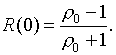
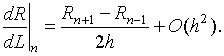 (6)
(6)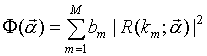 (10)
(10)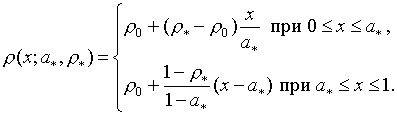 (11)
(11)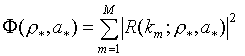 . (12)
. (12)