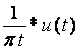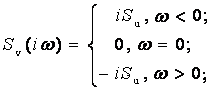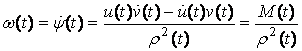АНАЛИЗ СТРУКТУРЫ АТМОСФЕРИКОВ

С ИСПОЛЬЗОВАНИЕМ

АДИАБАТИЧЕСКИХ ИНВАРИАНТОВ

 

 

Ю.А.Краснитский

 

Transport and Telecommunication Institute, Riga, Latvia

Lomonosov str. 1, Riga, LV 1019, Latvia

Ph: (+371)-7100650. Fax: (+371)-7100660. E-mail: alex@chas-daily.com

 

 Получена 8 декабря 2005 г.

 

Исследуется задача обнаружения факта и момента возможного подключения источников дополнительной  энергии к излучателю электромагнитных импульсов, в качестве которого рассматривается канал молниевого разряда. Решение основано на процедуре вычисления адиабатического инварианта для импульса (атмосферика), излучаемого разрядом на стадии обратного удара. Факт и момент возможной подпитки канала определяется по расположению локальных экстремумов адиабатического инварианта на оси времени.

 

Ключевые слова: атмосферик, аналитический сигнал, адиабатический инвариант.

 

1. Введение

 

Согласно одной из гипотез [1], основную роль в формировании атмосферика, излучаемого молниевым разрядом на стадии обратного удара, играет дискретная антенная решетка, образованная локальными неоднородностями канала молнии. Сведения о геометрической и электрофизической структуре этой решетки содержатся в ее импульсной характеристике (ИХ) излучения. Последняя представляет собой операратор, который, воздействуя на ток в основании канала, преобразует его в наблюдаемое поле. ИХ можно восстановить [2] путем решения соответствующей обратной задачи для атмосферика, зарегистрированного на известном расстоянии от разряда.

Результаты исследований обсуждаемой ИХ показывают, что среди узлов решетки должны быть излучающие элементы по меньшей мере двух видов:

а) пассивные, излучение которых вызвано изменением скорости движения основной волны тока, порожденной замыканием вблизи поверхности Земли нисходящего и восходящего лидеров, первоначально формирующих ионизированный канал молнии, и распространяющуюся затем вверх по этому каналу; к ним принадлежат, например, области резких изменений направления канала

Таким образом, возникает задача обнаружения факта и момента возможной подпитки канала со стороны его ветвей. Поступление в канал дополнительной энергии означает, что характер распространения волны тока вдоль него перестает быть адиабатическим.

В работе предложено рассматривать канал молнии как осциллятор с частотой, зависящей от времени, а о нарушении адиабатичности судить по поведению соответствующих инвариантов. Разработана процедура их оценки, которая включает в себя замену исследуемого атмосферика аналитическим сигналом с помощью преобразования Гильберта, нахождение огибающей, фазовой структуры и мгновенной частоты анализируемого сигнала с последующей проверкой, удовлетворяет ли он уравнению осциллятора с переменной частотой. Факт и момент возможной подпитки канала определяется по расположению локальных экстремумов адиабатического инварианта на оси времени.

 

2. Предварительная обработка атмосферика

 

При необходимости учета спектральных компонентов принимаемого сигнала, лежащих за пределами полосы пропускания устройства регистрации, нужно провести предварительную обработку, направленную на устранение влияния приемника на форму атмосферика. С этой целью результат

 

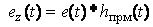                                                                               (1)

 

регистрации электрического поля e(t) атмосферика, искаженный вследствие свертки последнего с импульсной характеристикой приемника h_прм(t), следует подвергнуть обратной фильтрации. Здесь и далее через * обозначена операция свертки. Моделью приемника, как и в [2], может служить каскадное соединение ВЧ и НЧ фильтров Баттерворта соответствующих порядков. Сигнал, приведенный к входу приемника, будет иметь вид

 

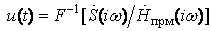,                                                               (2)

 

где 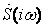 - спектр Фурье принятого атмосферика, 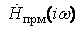- передаточная характеристика приемника.

В некоторых случаях в предварительную обработку целесообразно также включить восстановление индукционной составляющей сигнала посредством процедуры, рассмотренной в [2].

 

3. Представление атмосферика аналитическим сигналом

 

Исследуемый атмосферик можно представить [3] как обобщенный колебательный процесс вида

 

u(t) = r (t) cos y (t) = Re [w(t)] ,                                                        (3)

 

где

 

w(t) = u (t) + i v (t) 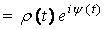,                                                      (4)

 

 - аналитический сигнал, мнимая часть

 

Im [w(t)] = v(t) = 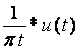= r (t) sin y (t)                                     (5)

 

которого есть преобразование Гильберта [3, 7] от (3).

С вычислительной точки зрения сигнал (5), сопряженный по Гильберту с атмосфериком (3), более удобно находить через спектр последнего

 

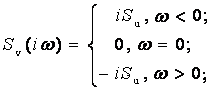                                                                  (6)

 

с помощью обратного преобразования Фурье.

Аналитический сигнал w(t) можно рассматривать как некоторую пространcтвенную траекторию (годограф), описываемую концом вектора (4) при вращении последнего вокруг оси времени t. Выражения (3) и (5) служат параметрическими уравнениями этой траектории. Действительным сигналам u(t) и v(t) соответствуют проекции комплексного сигнала w(t) на взаимно перпендикулярные плоскости.

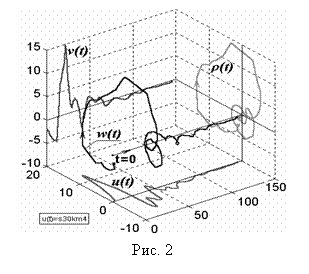Рис. 2 иллюстрирует описанную картину для одного из атмосфериков, принятого на удалении 30 км от молниевого разряда. В левом нижнем углу рисунка указан идентификатор этого сигнала.

Входящие в (3) – (5) функции

 

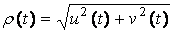,                                                                         (7)

 

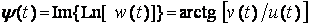                                        (8)

 

описывают соответственно огибающую и полную фазу аналитического сигнала (4), знание которых дает, в частности, возможность отделить мультипликативные компоненты в (3), т.е. факторизовать атмосферик, представляя его в виде u(t) = r (t) c (t), где r (t) - “медленный”, а c (t) = cos y (t) - “быстрый” сомножители.

 

 

Результат такого разложения показан на рис. 3 а - г, где последовательно изображены анализируемый сигнал u(t), его 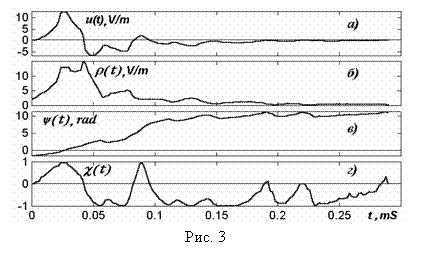огибающая (7), фазовая кривая (8), а также “быстрый” сомножитель c (t).

4. Молниевый разряд как осциллятор с переменной частотой

 

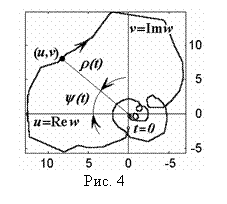
Проекция пространственной траектории, изображенной на рис. 2, на плоскость, перпендикулярную оси t, дает наглядное представление о поведении аналитического сигнала (4) во времени. Она показана в правой части рис. 2, а также - более детально - на рис. 4. Полярные координаты r (t) и y (t) каждой точки (u, v), принадлежащей этой проекции, задаются соотношениями (7) и (8).

Исследуемой кривой можно придать простой механический смысл: она отображает движение шарика единичной массы, закрепленного на конце нити, по горизонтальной поверхности гладкого стола. Нить пропущена в отверстие, расположенное в центре стола. Протягивая нить через это отверстие, можно изменять расстояние r от центра стола до шарика, а, следовательно, и декартовы координаты (u, v) последнего.

Составить уравнение, которое бы точно описывало истинную траекторию перемещения шарика, достаточно сложно. Однако, используя подход, предложенный в [4] и подробно рассмотренный в [5], можно получить дифференциальное уравнение, моделирующее движение шарика по поверхности стола при переменной длине нити и отсутствии трения. Вычисляя вторую производную сигнала u по времени, получим

 

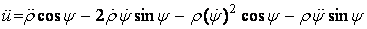.                              (9)

 

Но в процессе перемещения шарика должен сохраняться его момент количества движения

 

,                                                                          (10)

 

где С – некоторая константа, откуда найдем, что

 

                            .                                                                                              (11)

 

Исключив с помощью (11) первую производную фазового угла в (9), получим искомое уравнение

 

,                                                                                       (12)

 

которое описывает колебательный процесс, моделирующий движение шарика.

Частота колебаний, равная

 

                        ,                                                                           (13)

 

зависит от времени. Из последнего выражения следует, что уравнение (12) будет выполняться только в том случае, когда длина нити r (t) подчиняется соотношению

 

                        ,                                                                     (14)

 

которое после замены  переходит в

 

                        .                                                                            (15)

Как известно [5-6], колебания маятника с изменяющейся длиной могут служить классическим примером адиабатического процесса. Адиабатическое поведение параметров осциллятора предполагает, что в масштабе времени, характерном для рассматриваемой колебательной системы, ее параметры изменяются медленно. Это фактически означает, что процессы в системе происходят без структурных изменений и пополнения энергии от внешних источников.

Мерой указанного поведения могут служить адиабатические инварианты, т.е. такие физические величины, которые при медленном изменении параметров системы сохраняются с большой точностью в течение длительного промежутка времени. Так, для осциллятора, удовлетворяющего уравнению (12), точный инвариант определяется [5] как

 

                        ,                                                           (16)

 

где 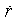 - одно из частных решений уравнения (15). Если же длина нити меняется медленно (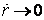) и плавно (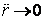), то из (15) следует, что 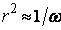. Тогда инвариант (16) принимает вид [5, 6]

 

                        .                                                                       (17)

 

Последнее выражение совпадает с адиабатическим инвариантом I = E /w для случая, когда осциллятор (12) создает колебания с постоянной частотой w. Здесь Е – энергия осциллятора.

Проверим аналитический сигнал (4) на соответствие рассмотренной модели, считая, что с течением времени шарик перемещается вдоль кривой, изображенной на рис. 4 и совпадающей с проекцией пространственной траектории рассматриваемого сигнала на плоскость стола.

С этой целью, используя (7) и (8), вычислим мгновенную частоту

 

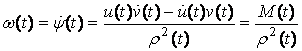,                                                   (18)

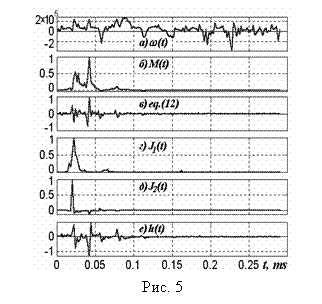
где M(t) – момент количества движения (10), в общем случае переменный во времени. Поведение частоты (18) и момента (10) представлено на рис. 5 а и б соответственно.

Подставляя значения частоты (18) в соотношения (12) – (17), можно выяснить, как ведут себя рассмотренные выше характеристики анализируемого колебательного процесса. Соответствующие кривые показаны на рис. 5 в – д, где последовательно изображены нормированные графики левой части уравнения (12), а также адиабатические инварианты (16) и (17).

 

5. Обсуждение результатов

 

Анализ представленных графиков показывает, что процесс формирования атмосферика не является адиабатическим, о чем свидетельствует “быстрое” поведение момента количества движения (10), отображаемое кривой б на рис. 5, а также инвариантов (16) и (17), изображенных на рис. 5 г и д соответственно. Это говорит о том, что уравнение (12) не вполне адекватно описывает процессы в канале молнии.

Во-первых, оно не учитывает потери энергии в канале при распространении вдоль него волны тока, что в рассмотренной выше механической модели эквивалентно пренебрежению трением шарика о поверхность стола. Во-вторых, импульсный характер графиков на рис. 5 г и д может означать, что резкие изменения в поведении инвариантов (16) и (17) соответствуют ситуациям, когда к осциллятору уже после возникновения колебаний подключаются дополнительные источники энергии.

Применительно к процессам, которые происходят в канале молнии, последнее предположение не противоречит гипотезе о том, что в антенной решетке, эквивалентлентной каналу в электродинамическом смысле, активными элементами служат области, соответствующие началу и концу как главного канала, так и каждой отдельной ветви (рис. 1). Другими словами, источники дополнительной энергии - это электрические заряды, стекающие в главный канал после того, как движущаяся по нему волна тока пройдет точку, из которой начинается соответствующая ветвь. Еще одним подтверждением этому может служить то, что положение локальных экстремумов адиабатических инвариантов (16) и (17) на оси времени соответствует пикам (рис. 5 е) в ИХ h(t) излучения канала разряда. Последняя восстановлена путем обработки атмосферика (рис. 3 а) с помощью процедуры, описанной в [2].

Число и ориентация ветвей в молниевых разрядах могут варьироваться в широких пределах (рис. 1). Кроме того, в процессе нейтрализации заряда отдельного грозового облака обычно возникает несколько (иногда до 20 и более) повторных разрядов. Разряды, наступающие позже, отличаются от произошедших ранее тем, что имеют менее выраженную ветвистость. Это должно отображаться в адиабатических инвариантах уменьшением числа импульсов. Таким образом, по виду функций (16), (17) можно судить о степени активности грозового облака.

Весьма интересным представляется следующее обстоятельство. При сравнении поведения левой части уравнения (12) как функции времени (рис 5 в) и импульсной характеристики h(t) (рис. 5 е) обнаруживается высокая степень их подобия. Это может служить основой для разработки соответствующих алгоритмов анализа электромагнитного поля, а также геометрической и электрофизической структуры таких сложных излучающих систем, какими являются молниевые разряды.

 

Литература

 

1. Krasnitsky Yu.A. Evaluation of lightning current pulse parameters from spherics waveforms. – J. Geophys. Res., 1994, v. 99, No D5, pp. 10.723 – 10.725

2. Краснитский Ю.А. Оценка характеристик канала молниевого разряда по атмосферику. –Тр. 5 Российск. конф. по атмосферному. электричеству. - Владимир: Транзит – НКС, т.2, 2003, с. 285 –290

3. Вайнштейн Л.А, Вакман Д.Е. Разделение частот в теории колебаний и волн. – М.: Наука, 1983, 288 с.

4. Parker L. Adiabatic invariance in simple harmonic motion. – Amer. J. Phys., 1971, v. 39, No 1, pp. 24 - 27

5. Бакай А.С., Степановский Ю.П. Адиабатические инварианты. – Киев, Наукова думка, 1981, 281 с.

6. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. От маятника до турбулентности. – М.: Наука, 1988, 368 с.

7. Hann S.L. Hilbert transform in signal processing. – Artech House, 1996, 442 pp.