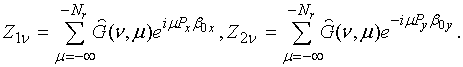| "JOURNAL OF RADIO ELECTRONICS" N 6, 2006 |
NUMERICAL ANALYSIS OF
WAVEGUIDES AND WAVEGUIDE ELEMENTS IN EBG STRUCTURES
S. E. Bankov, M.D. Duplenkova
Institute of Radioengineering and Electronics of RAS
Received December 15, 2006
This paper presents an efficient technique for analysis of waveguides, resonators and waveguide discontinuities in two-dimensional electromagnetic bandgap (EBG) structures. Waveguides and resonators formed by elements removed from EBG array are considered. The technique includes the following key steps. The first step is a solution of problem of electromagnetic (EM) field scattering on a single element of array. Scattered field is presented as a finite series of cylindrical harmonics with coefficients depending on incident field. The second step is an introduction of a compensating source (CS) and excitation of a homogeneous EBG structure by the source. CS produces EM field in the same form of sum of cylindrical harmonics but with fixed coefficients. The last third step is analysis of EM field in waveguide or resonance structure inside EBG array. Elements forming the structure are not removed from array but instead of it CSs with unknown coefficients are placed in the elements. These coefficients are defined under condition that total field produced by the element (scattered field plus field induced by a CS) is equal to zero that is equivalent to removal of the element from array. These conditions formulated for all of removed elements give one a system of linear algebraic equations (SLAE) relatively mentioned coefficients that is simply solved numerically or analytically. Resonator, infinite waveguide, waveguide with lumped discontinuity and waveguide bends are considered in the paper.
Introduction
Photonic bandgap (PBG) or electromagnetic bandgap (EBG) structures are a class of three-dimensional (3-D) periodic objects that prevent the propagation of electromagnetic (EM) waves in a specified frequency range for all angles of propagation and all polarization states [1]. These structures have a lot of applications in frequency selective surfaces and EBG materials [2-4].
A class of EBG structures applications is connected with defects and defect modes in such structures. A typical defect is a removed from periodic array element which provides a cavity in EBG media. Such cavities may be used as resonators for example as high-Q resonators for laser [5]. One may obtain a waveguide in EBG structure removing an infinite series of elements from the structure. Bended waveguides, waveguide junctions [6] and other waveguide elements may be obtained in the same way. An advantage of these elements is absence of radiating loss. Radiation from cavity in EBG structure is impossible because the media surrounding it prevents the propagation of EM waves. Therefore unlike of microwave dielectric waveguides and optical waveguides these elements are extremely compact. For example dielectric waveguide bend should have radius about several wavelengths to avoid radiation loss while EBG waveguide may be bended with zero radius. The situation is typical for microwave metal waveguides. However physical nature of field concentration in EBG structures is different and it may be reached without any metal at all. It is very important for high frequency ranges and for optical range as well because metals at high frequencies have very big dissipative loss. Thus EBG structures give one a unique opportunity to create extremely compact low loss waveguide devices at high frequencies.
Defects in EBG structures were mostly studied with help of numerical techniques. A powerful computational scheme based on a finite-difference time-domain (FDTD) technique with periodic boundary conditions/perfectly matched layers integrated with Prony’s scheme is applied in [7] for EM field analysis in various 3-D and 2-D EBG structures. An advantage of the technique is a possibility to obtain EM field practically for any structure with guaranteed precision. However time required for numerical solution in case of a typical 3-D EBG structure is several decades of minutes when HPC-180 workstation is applied [7].
An approximate concept of effective dielectric constant is also discussed in several articles [8]. As it is shown in [7] this concept models performance of EBG structures only outside the gap region and therefore it does not suite for waveguide elements modeling.
Speaking about numerical techniques one should note that in addition to problem of computing time there is a problem of numerical solution interpretation. Numerical technique usually finds EM field in some region. At the same time a conventional way for waveguide element description is a scattering matrix. The matrix may be simply obtained from EM field if natural modes of infinite waveguide are previously studied. However numerical technique does not suite for such study because it may be applied mostly to finite objects.
Numerical technique based on a direct solution of Maxwell’s equations searches unknown function (EM field) distributed in a whole region of interest. Because of it the larger is this region the longer computing time is required. At the same time techniques based on a Green’s function are well known in electrodynamics. These techniques allow one to reduce a region where unknown function is distributed. For example considering diaphragm in waveguide with help of Moment technique we have deal with unknown function (magnetic current) defined in a small hole in the diaphragm. In this case we should not search EM field in every point inside waveguide structure but it is enough to find magnetic current in a small hole. Evidently such approach is more effective than FDTD technique. However one need to know Green’s function to apply it. The function may be found analytically only for a limited class of structures. Therefore techniques based on a Green’s function are not so general as FDTD or finite elements method.
The focus of this paper is to propose effective analytical-numerical technique based on a EBG structure Green’s function and to apply the technique to EBG waveguide elements analysis. EBG structure sufficiently differs from continuous media and because of it special sources and special Green’s function are introduced in the paper. Proposed technique may be extended to 3-D case however only 2-D version for TE field is presented below.
The first attempt to create such analytical-numerical technique was presented in articles [9,10]. However in these works were considered only 2-D arrays with extremely thin metal cylinders. In this article mentioned above approach will be extended to cylinders with arbitrary electrical dimensions and material parameters.
I. EM field scattering by a single element of 2-D array
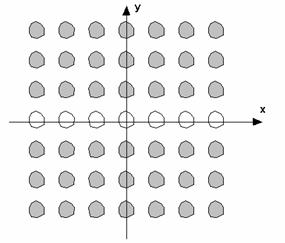
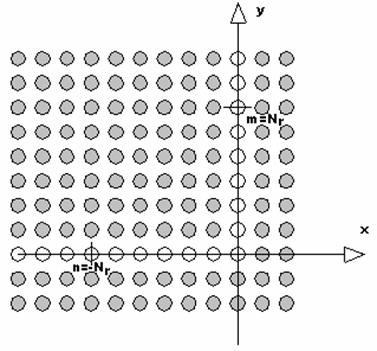
Let us consider a 2-D array of cylinders shown in fig. 1. The cylinder may have an arbitrary cross section. Media inside it may be characterized by a complex dielectric and magnetic constants. Therefore it may be also a metal cylinder.
Fig. 1
The first problem is a field scattering by a single element of the array forming EBG structure (see fig. 2). Let we have an incident TE field characterized by
component. We need to find
component of a scattered field
. We assume that incident field may be written in general case as the following Fourier integral:
,
where
- is a wave number of media surrounding the cylinder. Four terms in formula (1) correspond to waves excited by sources located above, below, left and right relatively the considered cylinder. Functions
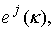
are known one. Field (1) satisfies to Helmgoltz equation.
Fig. 2
A general solution of Helmgoltz equation in cylindrical coordinates is an infinite series of cylindrical harmonics:
where
is a second type Hankel function of the N-th order, coordinates
are shown in fig. 3,
are constants independent on
. Let us call the following function
as a cylindrical harmonic of N-th order. We assume that EM field depends on time as
. Hankel functions are chosen to satisfy radiation conditions at
. Scattered by array element field may be also presented in form (2) for region
, where
is a maximum distance from the coordinate system center to cylinder surface (fig. 3).
Let us suppose that scattered field may be presented with enough tolerance as a finite sum of cylindrical harmonics:
where
are coefficients depending on incident field,
is some fixed number. Functions
depend on properties of the cylinder. Presentation (3) is not absolutely rigorous because of finite value of
. However one may see that for practically interesting EBG structures this number is not above 2-3. It takes place because cylinders forming EBG structure have relatively small electrical dimensions in stop band. The most interesting the lowest stop band appears approximately when period of array P is close to a half of wavelength
in media around array elements. Radius
is evidently smaller than period and therefore
is always smaller than
. The smaller is scattering element the smaller number of cylindrical harmonics should be included in presentation (3). For extremely small cylinders
is equal to zero.
Fig. 3
Tolerance of the expression (3) increases for large radiuses r. Therefore it is enough for below analysis that formula (3) be correct for
because P is the minimum distance between elements in array.
Thus formula (3) restricts a class of EBG structures for which an approach presented below is valid. We suppose that functions
are known i.e. key problem about field scattering by a single element of array was previously solved. We also suppose that functions
may be written in the following way:
where
are known functions,
. We need to note that for circular metal and dielectric cylinders as well as for elliptical metal cylinders analytical solutions in form (2)-(4) are known. For more complicated shapes they should be obtained numerically.
II. Special Green’s function of EBG structure
Now we introduce a special source - CS that produces EM field in the following way:
,
where
are fixed numbers. Field (5) is written in a cylindrical coordinate system which center coincides with a center of some EBG array element. We suppose that every CS existing in EBG structure corresponds to its array element and therefore EM field produced by the element with CS is a sum of scattered field and field induced by the source.
EBG structure shown in fig. 4 contains one CS associated with element characterized by indexes p,q. Two indexes define position of element in the array. The first index corresponds to x coordinate and the second one corresponds to y coordinate.
Fig. 4
Our problem is to find EM field in infinite EBG structure excited by a CS located in p,q-th element. Considering an arbitrary element one may separate total EM field to incident field and secondary field scattered by the element. Let us calculate a field scattered by the array element with indexes n,m. Firstly we should find an incident to this element field. The following expression may be written for incident field:
where
is a distance from k,l-th element to n,m-th element,
is an angle in a coordinate system corresponding to k,l-th element (see fig. 4),
are unknown amplitudes of cylindrical harmonics radiated by k,l-th element. Symbol (n,m) in formula (5) means that term with k=n and l=m should be excluded from summation.
Now we should present incident EM field in form (1). The following presentations are known in theory of cylindrical functions [11]:
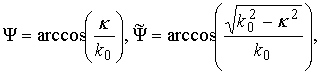
Above expressions allow us to obtain the following formula:
where
- periods of the array along 0x and 0y axis (see fig. 4). Rigorously function
may not be defined for m=n=0 because Hankel function is infinite for zero argument. However incident field does not include an addendum corresponding to n=k, m=l and thus definition of function
in case n=m=0 is not essential for below consideration. In (8) the function is defined as equal to zero.
Then let us introduce the following function
that describes EM field scattered by an element of the array:
Combining formulas (7) and (8) one may obtain new presentation for incident field (7):
Summation in (10) includes all indexes because function
is equal to zero when n-k=m-l=0. Now we may write an expression for amplitudes
characterizing field scattered by n,m-th element with help of formulas (4),(9) and (10):
. (11)
The second proportional to
term is added in (11) to describe amplitudes of cylindrical harmonics produced by a CS in p,q-th element.
Expression (11) is a SLAE that allows one to find unknown amplitudes
. We should note that if these amplitudes are known then EM field in EBG structure is also known because it may be presented as a sum of fields scattered by all elements of EBG array. Let us call a relation that connects amplitudes
with given amplitudes
as a special Green’s function of EBG structure.
A discrete Fourier transform technique may be effectively applied to solution of SLAE (10). Let us present unknown
as the following integral:
where
is an unknown function. Then we substitute formula (12) to expression (11) and apply discrete Fourier transform to obtained equation. Let us consider its parts separately.
Firstly we consider the left part of the equation. One may show that after substitution (12) to (11) and application of discrete Fourier transform it may be written in the following way:
Formula (13) was obtained with help of the following known relation [12]:
where
is a delta function. One may see that only term with n=0 gives a contribution in integral over
because points
,
are out of interval of integration. The same situation is for integral over
.
The right part of the equation consists of two terms. The first one proportional to
may be transformed to a required form with help of new indexes of summation:
which allow one to separate summation over indexes n,m and
. Finally we obtain for the first term the following result:
, (16)
.
The result for the second term of the right part that is proportional to
may be elementary obtained as follows:
Now we can write the final result for equation (11):
Then let us introduce the following vectors and matrixes:
.
Appling expressions (19) we obtain a compact presentation for (18):
One may consider (20) as an equation written relatively unknown vector function
. Solving equation (20) we find the function:
where
is a unit matrix.
Substituting (21) to (12) we find amplitudes of harmonics scattered by an element with arbitrary indexes n and m:
The last expression is a required special Green’s function of EBG structure because it connects a given vector of CS’s amplitudes and vector of amplitudes of waves radiated from elements of EBG array. Plurality of vectors
defines EM field in EBG structure.
III. Resonance cavity in EBG structure
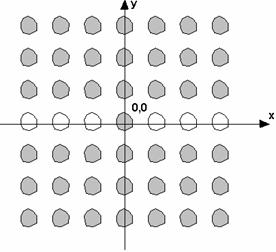
Now we may apply obtained above Green’s function to analysis of some EBG structures with defects. As it was noted above a typical defect is an element removed from EBG array. An advantage of CS is that one may simply model arrays with removed elements with its help.
A resonance cavity is shown in fig. 5.
Fig. 5
Let us imagine at the first step that EBG array has not removed element but instead of it a CS with unknown amplitude vector
is inserted in the really removed element (n=m=0). Let us require for the second step that EM field produced by the element is equal to zero. The last condition plays a role of a boundary condition for removed element. At the third step we may calculate vectors
for all elements in array as well as for removed element with n=m=0 and satisfy above boundary condition:
Substituting (22) to (23) we obtain:
Expression (24) is a system of linear algebraic equations relatively unknown components of vector
. It has non-trivial solution when its determinant is equal to zero:
Equation (25) may be solved numerically relatively frequency. Roots of the equations correspond to natural frequencies of the considering resonance cavity.
V. Infinite waveguide.
Next consider an infinite waveguide in EBG structure (see fig. 6).
Fig. 6
Now elements with indexes
are removed from the array. In accordance with the above scheme we should insert CS’s
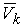
in all removed elements. Let us search our solution in form of a wave traveling along the waveguide:
where
is an unknown propagation constant,
is a vector independent on index n. Boundary condition in this case may be written as follows:
The last formula (27) may be rewritten with help of (22) and (26):
Series in (28) may be reduced to an infinite sum of delta functions (14) that in its turn allows one to calculate integral over variable
. As a result we have the following expression
that is a SLAE relatively components of vector
. Condition for non-trivial solutions of system (29) gives one an equation for propagating constant
:
For a structure without dissipative loss equation (30) may have several roots with imaginary parts equal to zero corresponding to propagating waveguide modes. Let us suppose that a regime when our waveguide has only one propagating mode is possible. Let
is a propagating constant of the mode.
VI. Waveguide with a lumped discontinuity
Now we may consider solution for more complicated structure shown in fig. 7. It is an infinite waveguide formed by an infinite layer of elements removed from array. A discontinuity is one element with indexes n=m=0 inserted in the waveguide. Propagating from left to right waveguide dominant mode excites the structure.
At the first stage we suppose that the waveguide is still regular and all elements with
are removed from array. Instead of element with n=m=0 we insert an additional source with amplitude vector
. In terms of the above approach every removed from array element corresponds to its CS. Therefore if we suppose that all elements in waveguide are removed then it means that they are in array but together with CSs and amplitude vectors of these CSs are selected under the condition (27). Thus speaking about additional source in element with n=m=0 we mean not a corresponding CS but some additional source which we should insert temporary to model an element returned to our array.
Fig. 7
Thus now we have an infinite waveguide excited by the above source. As previously we insert CSs in elements with indexes
. Amplitude vectors of these CSs are
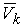
. Boundary conditions now are almost the same as (27) except condition for element with n=0:
where
was defined in (11). As it follows from (31) amplitude vector
is not equal to zero now but it is equal to amplitude vector of additional source. Applying Green’s function and formula (31) we may write the following expression:
We are finding unknown vectors
in form of Fourier integral:
Substituting (33) to (32) and applying discrete Fourier transform we obtain:
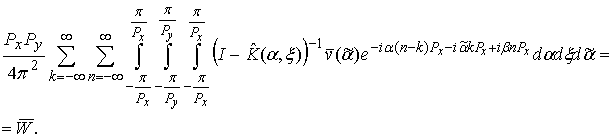
A typical for discrete Fourier transform calculation of infinite sums and integrals over variables
gives us
and
:
Except CSs excited by a source
(see formula (34)) CSs produced by an incident wave are also exist in the waveguide. As it was mentioned above these CSs correspond to a dominant mode with propagating constant
. Therefore we may write these CSs as follows:
Adding (35) to (34) we obtain a complete presentation for CSs in the waveguide:
Now we should take into account that element with k=0 is not really removed from array and therefore CS corresponding to it should be equal to zero (
). Satisfying to this condition we find vector
:
Inverse matrix in (34) may be written as some matrix
divided on a determinant of the original matrix
(see (30)):
One may see that we have in the denominator in (38) a left part of equation (30). Therefore poles of sub-integral function in (38) are equal to propagating constants of waveguide modes. Calculating residues in points
one may obtain amplitudes of dominant waveguide modes which propagate to back and forward directions
and
respectively:
These amplitudes combined with amplitude of incident wave (35) give one a scattering matrix of the considered waveguide discontinuity.
VII. Formulation of problem for waveguide bend
Considered above structures are simple enough to obtain solution in analytical form. When a structure has arbitrary shape a problem corresponding to it may be only reduced to a SLAE which should be solved numerically. Next we consider an algorithm of formulation of SLAE for waveguide bend shown in fig. 8.
Fig. 8
Firstly we introduce new index
which is connected with n and m in the following way:
for
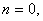
. (40)
One may see that index
corresponds to elements removed from array. In accordance with above approach we should insert CS
to all such elements and then we should satisfy boundary conditions:
Next we express vectors
with help of Green’s function (22):
Expression (42) is an infinite SLAE. Let us reduce the system to a finite one. Two reference planes are shown in fig. 8. These planes correspond to elements with
and
. One may suppose that field in waveguides far enough from waveguide bend may be written as a sum of propagating waveguide natural modes. Let us suppose that only one mode propagates in waveguides that form the bend. In accordance with above assumptions we may write the following relations:
where
are propagating constants of dominant modes in horizontal and vertical vaweguides respectively,
is a known amplitude vector of an incident wave propagating to the bend along horizontal waveguide (see fig. 8),
are unknown amplitude vectors of waves in horizontal and vertical waveguides reflected from the bend. These vectors do not depend on index
. Relations (43) are written for the case when incident wave exists in horizontal waveguide. Another case when the bend is excited from vertical waveguide may be considered analogously.
One may see that relations (43) reduce number of unknown variables from infinity to
. Number of equations in system (42) should be respectively reduced. Now we should not satisfy boundary conditions for all elements forming infinite waveguides. It is enough to do it only for elements with
. Boundary conditions for elements with
will be satisfied automatically due to relation (43). Thus we obtain finally the following finite SLAE:
SLAE (44) should be solved numerically.
VIII. Numerical results
Above technique was applied to waveguide elements formed in array of metal cylinders with circular cross-section. Some numerical results are presented below.
The first result corresponds to a regular waveguide. Investigated array has identical periods along both coordinates - P. Metal cylinders are located in a free space with wave number
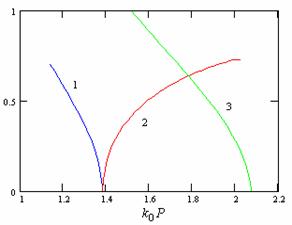
. Plots in fig. 9 demonstrate dependencies of imaginary and real parts of waveguide mode complex propagation constant (curves 1 and 2 respectively) on parameter
which is proportional to frequency. Curve 3 corresponds to imaginary part of propagation constant of regular EBG array mode. All curves are normalized to
.
Fig. 9
All plots are calculated for relation D/P equal to 0.133, where D is a diameter of cylinder. As it is seen from fig. 9 waveguide mode demonstrates properties analogous to properties of a conventional metal waveguide. It has cutoff frequency below which propagating modes in the waveguide are absent. Thus cutoff frequency limits below margin of the waveguide operating frequency range. Upper margin of the range is limited by the upper margin of EBG array stop band.
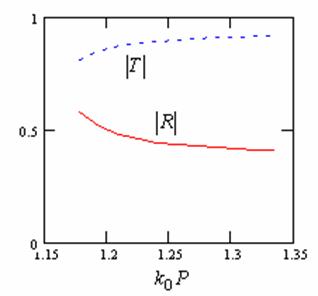
The next results were obtained for waveguide bend and waveguide mitered bend. These results are presented in form of scattering parameters depending on
. Curves in fig. 10 correspond to reflection R and transmission T coefficients of waveguide bend formed by thin wires with D/P=0.0266.
Fig. 10
Fig. 11
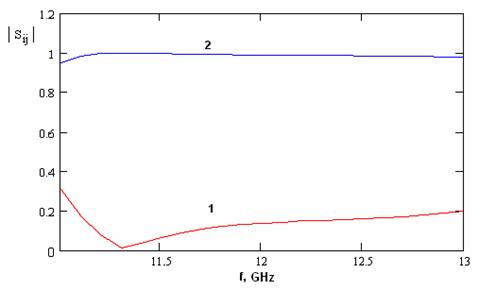
Analogous plots for mitered bend are shown in fig. 11. Mitered bend is the same bend as shown one in fig. 8 but element with indexes m=n=0 is not removed from array. This element may be considered as some mirror that should reduce reflections from the structure. Curves shown in fig. 11 were obtained for array of metal cylinders with radius 1 mm and period 10 mm. Curves 1,2,3 correspond to different radiuses of element in the corner of the bend 0.03, 0.05, 0.1 mm respectively.
Fig. 12
In the same way may be arranged mitered bend in the array of dielectric cylinders. One may see frequency dependencies of S – parameters of such bend in fig. 12. Radius of dielectric cylinders is equal to 1.5 mm and dielectric constant is equal to 10, period of the array is equal to 10 mm. Radius of element in the corner is equal to 1.3 mm. One may conclude that reducing radius of the element it is also possible to match the bend. However range in which it is well matched is not so wide as it is in case of metal cylinders.
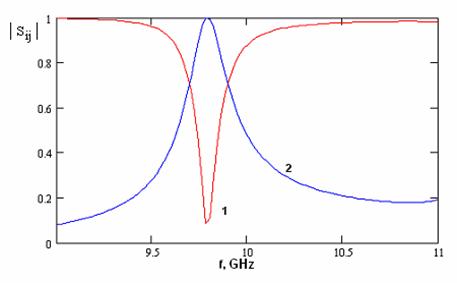
A waveguide resonator with two identical coupling elements is shown in fig. 13. This structure may be considered as a basical part of a microwave filter. S – parameters of the resonator are shown in fig. 14. Presented curves are typical for waveguide resonators with two coupling elements. Coupling element is a cylinder with arbitrary radius. Selecting the radius one may obtain a wide range of loaded Q-factors. Plots shown in fig. 14 correspond to cylinders with radius 1 mm, period of the array is equal to 10 mm. Radius of coupling element is equal to 1.1 mm.
Fig. 13
Fig. 14
As it is seen from fig. 14 curves are not symmetrical relatively resonance frequency. It means that coupling factor between the resonator and output waveguides strongly depends on frequency.
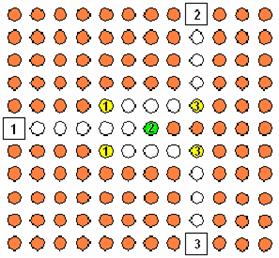
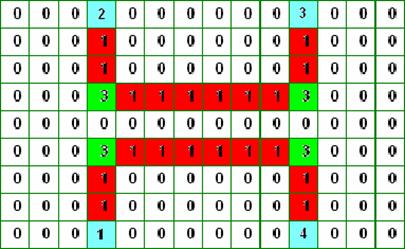
More complicated structure is waveguide T-junction. It is shown in fig. 15. The junction is more complicated than for example conventional waveguide T-junction in E-plane. The junction contains removed from regular array elements (white circles) and elements with radiuses R1-3 different from radius of a regular array element (red circles). The last elements are numbered 1,2,3 (yellow and green circles).
Fig. 15
Radiuses R1-3 were numerically optimized thus to obtain maximum frequency range in which S-matrix element S11 is below 0.1. We note that regular array element radius is 1.5 mm and its period is 10 mm.
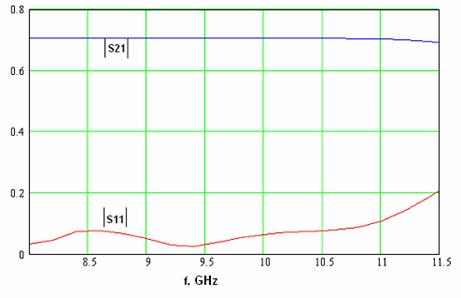
Some results of numerical optimization are shown in fig. 16.
Fig. 16
It is seen from fig. 16 that the junction is well matched in the relative frequency range about 33%. This result may be considered as a well one for waveguide junctions in H-plane.
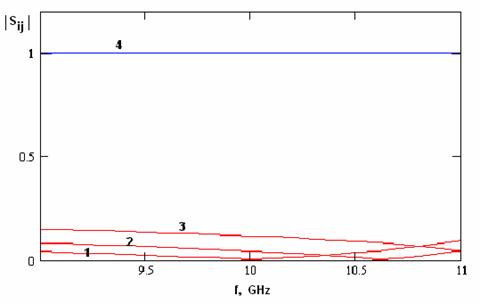
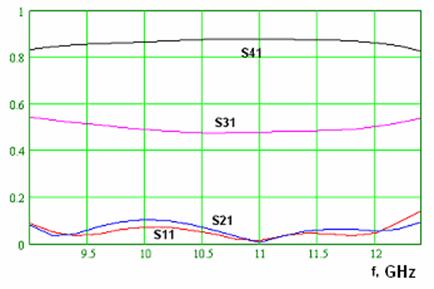
The last of investigated devices is a directional coupler that is shown in fig. 17. The main part of the device is a section of two coupled waveguides. Two coupled waveguides have two dominant modes: odd and even. These modes have different
Fig. 17
propagating constants. Interference of the modes produces transmission of electromagnetic energy from one waveguide to another. For example if port 1 is excited then energy is distributed between ports 3 and 4. In a perfect case ports 1 and 2 should be isolated from each other. However in a real situation S11 and S21 are not zero due to reflections from ends of the coupler.
Numerical analysis allows one to select parameters of the device thus to obtain required coupling level and minimize S11 and S21. Some frequency dependencies of S-parameters are shown in fig. 18. These plots were obtained for cylinders with radius 1.5 mm and array with period 10 mm.
Fig. 18
One may conclude from fig. 18 that the designed coupler has 30% frequency range in which return loss and isolation are better than –20 dB.
SLAE for all structures were solved numerically with help of PC (1700 MHz, 256 MBt). Typical time required for complete solution at ten frequency points is about 5-50 seconds dependently on cylinder diameter. The fastest solution corresponds to thin cylinders that may be described with help of one cylindrical harmonic (see section I).
VIII. CONCLUSION
Thus the proposed technique allows one to obtain analytical solutions for some simple 2-D EBG structures and numerical solutions for complicated structures. EM problems for arrays with defects are reduced to SLAE. Dimension of the system is proportional to a number of elements forming defect. The technique allows one to find parameters of waveguide natural modes and scattering parameters of waveguide discontinuities.
There are no limitations to extend the above approach to a 3-D case. Of course Green’s function and CS will have more complicated form but they may be obtained in the way analogous to the described above one.
A class of structures that may be analyzed with help of the proposed approach is limited by the expression (3). EM field in a region close to cylinder surface may have a complicated structure and one need a lot of cylindrical harmonics to describe it with a high precision. Thus we may suppose that the approach will not be the same effective for arrays with closely located elements as for arrays with relatively small elements. Moreover there are some arrays for which it may not be applied at all. It takes place when circles with radiuses
(see fig. 3) for neighbouring array elements have points of intersection. Such situation for example is possible for closely located cylinders with a rectangular cross section.
We wish to thanks Russian Foundation of Fundamental Researches for support of this work (project
06-08-00608). We also wish to thanks Dr. V.A. Kaloshin for very useful discussion about our results.
REFERENCES
Y. Rahmat-Samii and H. Mosallaei, “Electromagnetic bandgap structures: Classification, characterization and applications,” in Proc. 11th Int. Conf. Antennas and Propagation, Manchester, U.K., Apr. 17-20, 2001, p.p. 560-564.
T.K. Wu, Frequency Selective Surface and Grid Array. New York : Wiley, 1995.
B.A. Munk, Frequency Selective Surfaces: Theory and Design. New York, Wiley, 2000.
J.D. Joannopopoulus, R.D. Meade and J.N. Winn, Photonic Crystals: Molding the Flow of Light. Princeton, NJ: Princeton Univ. Press, 1995.
O. Painter, R.K. Lee, A. Scherer, A. Yariv, J.D. O’Brien, P.D. Dapkus and I. Kim, “Two-dimensional photonic bandgap defect mode laser,” Science, vol. 284, p.p. 1819-1821, June 1999.
A. Mekis, J.C. Chen, I. Kurland, S. Fan, P.R. Villeneuve, and J.D. Joannopopoulus, “High transmission through sharp bends in photonic crystal waveguides,” Phys. Rev. Lett., vol. 77, no. 18, pp. 3787-3790.
H. Mosallaei and Y. Rahmat-Samii, “Periodic bandgap and effective dielectric materials in electromagnetics,” IEEE Trans. Antennas Propagat., vol. 51, 549-563, March, 2003.
S. Datta, C.T. Chan, K.M. Ho and C.M. Soukoulis, “Effective dielectric constant of periodic composite structures,” Phys. Rev. B, Condens. Matter, vol. 48, no. 20, pp. 14936-14943, Nov. 1993.
Bankov S.E. “Waveguide and waveguide components based on sparse photonic crystals”. Journal of Communications Technology and Electronics, Vol. 49, No. 11, 2004, pp. 1208–1217.
Bankov S.E. “Waveguide bends based on sparse two dimensional photonic crystals”. Journal of Communications Technology and Electronics, Vol. 50, No. 1, 2005, pp. 23–30.
Nielsen N., Hadbuch der Theorie der Cylinderfunktionen, Leipzig, 1904.
A. Papoulis. The Fourier Integral and Its Applications. New York: Mc-Graw-Hill, 1962.

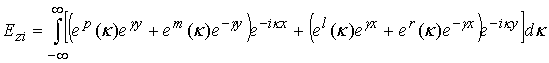 , (1)
, (1)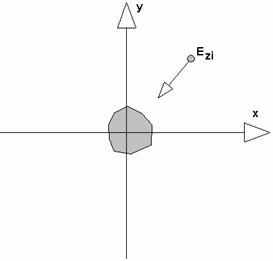
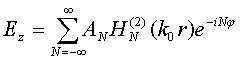 , (2)
, (2)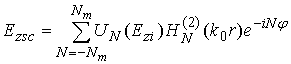 , (3)
, (3)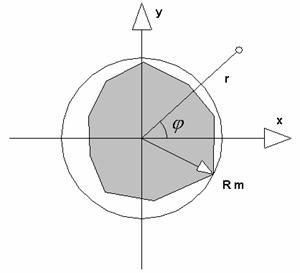
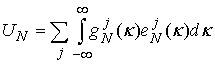 , (4)
, (4)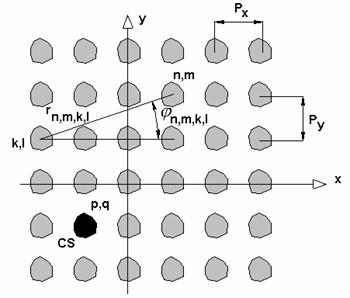
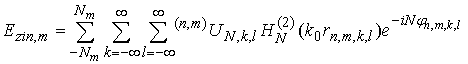 , (5)
, (5)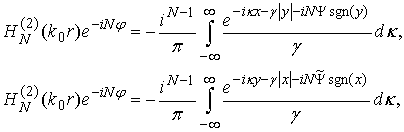 (6)
(6)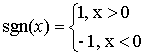
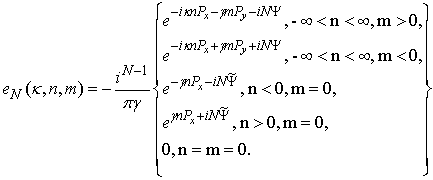
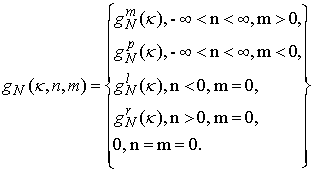
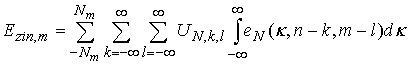 . (10)
. (10)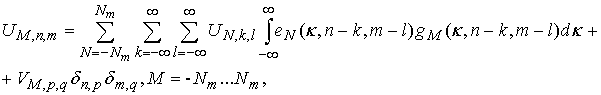 ,
,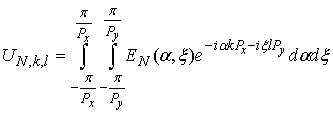 , (12)
, (12)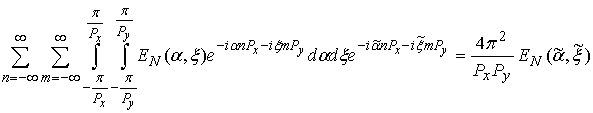
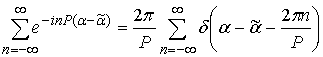 . (14)
. (14)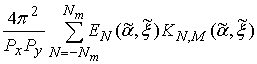 ,
, 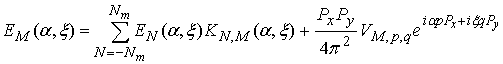 . (18)
. (18)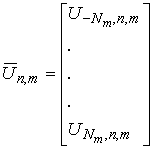 ,
, 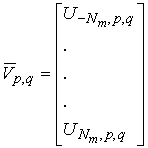 ,
, 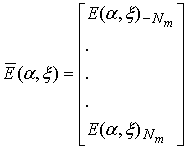 , (19)
, (19)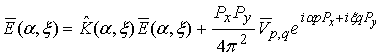 . (20)
. (20)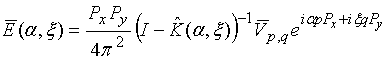 . (21)
. (21)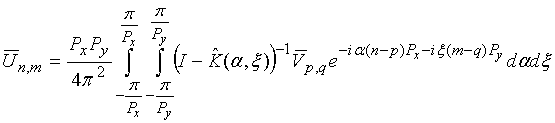 . (22)
. (22)
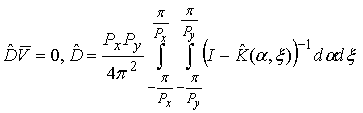
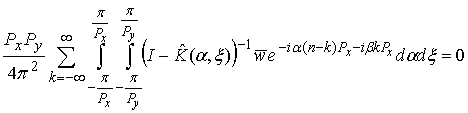 . (28)
. (28)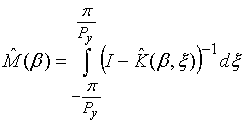
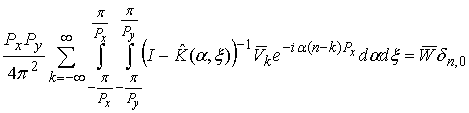 . (32)
. (32)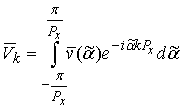 . (33)
. (33)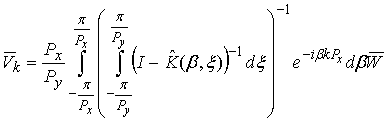 . (34)
. (34)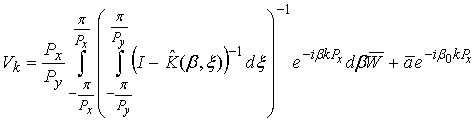
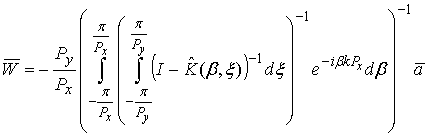
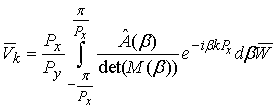 (38)
(38)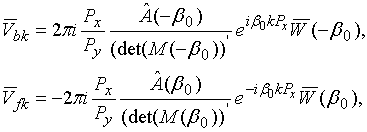 (39)
(39)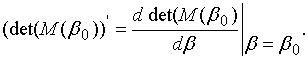
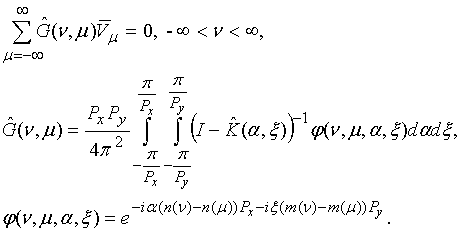 (42)
(42)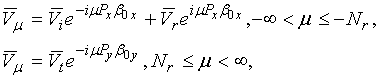 (43)
(43)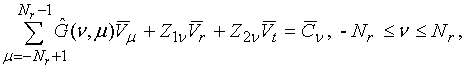 (44)
(44)