"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 12, 2008

оглавление

 

Исследование дисперсионных характеристик однополосковой линии на однослойной диэлектрической подложке
 

В. И. Калиничев, В. А. Калошин, Е. А. Скородумова

Институт радиотехники и электроники им. В.А. Котельникова РАН

Получена 23 декабря 2008 г.

Методом конечных элементов исследованы дисперсионные характеристики замедления и затухания основной и первой высшей моды однополосковой линии на однослойной подложке. Численное решение получено с использованием модели резонатора с расположенной внутри линией и путем прямого нахождения комплексных собственных значений для поперечного сечения. Показано, что результаты обоих методов для основной и первой высшей мод практически совпадают по величине замедления и хорошо согласуются по значениям затухания. Представлены распределения поперечной и продольной компонент электрического поля для основной и первой высшей моды. Проведено сравнение рассчитанных зависимостей затухания основной моды однополосковой и микрополосковой линий от частоты.

Ключевые слова: полосковая линия, численное моделирование в электродинамике.

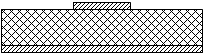
Введение

Однополосковая линия передачи (ОПЛ) была предложена в [1] как альтернатива микрополосковой линии (МПЛ) с целью обеспечения малых потерь на высоких частотах, в частности, в миллиметровом диапазоне волн. Поперечные сечения ОПЛ и МПЛ приведены на рис. 1а и 1б, соответственно.

а) ОПЛ	б) МПЛ
Рис. 1. Поперечные сечения линий

Дисперсионные характеристики замедления и потерь этой линии рассматривались как для основной, так и для высших мод в работах [2-4]. В работе [2] приведены результаты численного исследования дисперсионных свойств и структуры полей мод ОПЛ с однослойной подложкой, а в работе [4] – c двухслойной подложкой. Результаты численного моделирования дисперсионных характеристик ОПЛ методом конечных элементов в [4] сравнивались с решением методом эффективной диэлектрической проницаемости в предположении, что область под металлической полоской эквивалентна удвоенной толщине подложки. Однако результаты были получены только для подложки с большими значениями диэлектрической проницаемости (порядка 10). Потери в [4] были рассчитаны только для одной комбинации диэлектрических проницаемостей слоев и двух значений частоты. В работе [3] ОПЛ анализировалась, главным образом, с точки зрения излучения при возбуждении в ней первой несимметричной моды.

В данной работе представлены результаты численного моделирования дисперсионных характеристик замедления и потерь основной и первой высшей моды ОПЛ на однослойной подложке для различных значений параметров в широкой полосе частот. Исследование проводилось на основе метода конечных элементов путем прямого решения задачи на собственные значения для поперечного сечения и на основе резонаторной модели. Затухание основной моды сравнивалось с затуханием 50-ом МПЛ на аналогичной подложке. Представлены распределения поля электрического поля в резонаторе и его компонент для основной и первой высшей моды ОПЛ.

Резонаторная модель для определения комплексной постоянной распространения

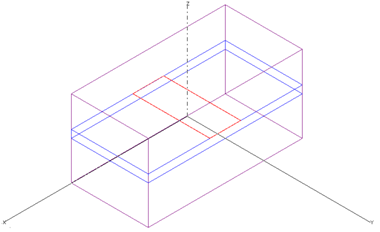
Для определения комплексной постоянной распространения основной (четной) и первой высшей (нечетной) мод ОПЛ в данной работе использовалось прямое решение задачи на собственные значения и резонаторная модель в комбинации с методом конечных элементов. При использовании резонаторной модели исследуемая структура помещалась внутрь замкнутого прямоугольного объема с металлическими  стенками так, что торцы линии располагались на соответствующих металлических стенках (рис.2) и вычислялись собственные частоты резонатора (в отсутствие источника). При наличии тепловых потерь в структуре собственные частоты являются комплексными, и мнимая часть частоты определяет добротность колебаний. Размеры резонатора выбирались из условия, чтобы изменения размеров боковых стенок не вызывали существенного изменения резонансной частоты моды исследуемой линии и потерь.

Рис. 2. Отрезок ОПЛ в резонаторе с металлическими стенками 

На рис. 2 красным цветом обозначен полосковый проводник, а синим – диэлектрическая подложка. Так как данная модель имеет плоскость симметрии, рассчитывалась только одна ее половина с магнитной стенкой в этой плоскости для четных мод и с электрической – для нечетных.

Предположим, что длина резонатора выбрана так, что вдоль оси Y возбуждается основной тип колебаний (один период стоячей волны). Резонансная частота и добротность этого колебания связаны с величиной фазового замедления и постоянной затухания волны на этой частоте следующими формулами:

,                 ,              .

где  – коэффициент фазового замедления волны, L – длина резонатора в мм, f_r – резонансная частота в ГГц, Q – добротность основного типа колебаний, α – затухание в неп/мм. Изменяя длину резонатора в некоторых пределах, можно получить частотные зависимости постоянной распространения и затухания в дискретных частотных точках, которые соответствуют собственным частотам резонатора.

Результаты вычислений

Ниже представлены результаты вычислений с использованием описанной резонаторной модели для двух значений диэлектрической проницаемости подложки.

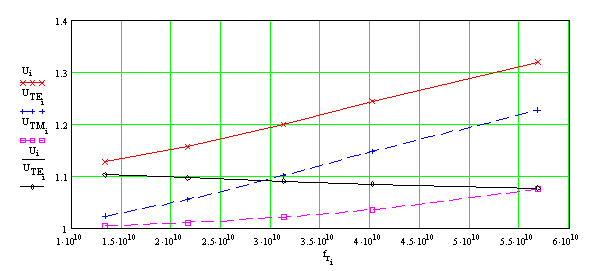
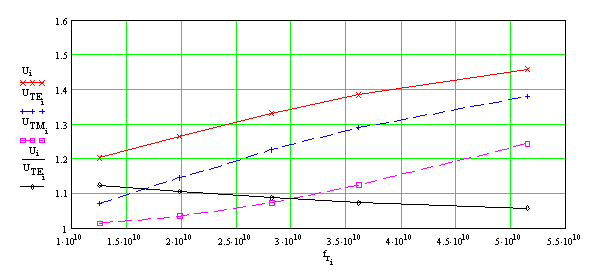
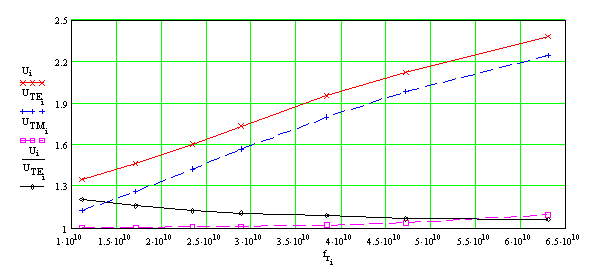
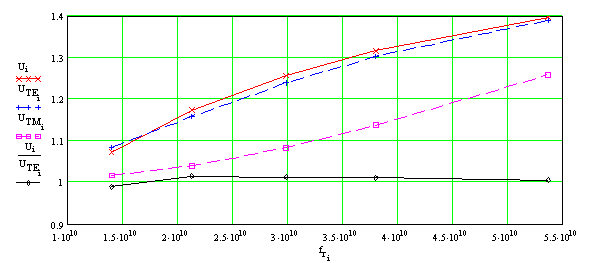
На рис. 3 красным цветом показана дисперсионная зависимость коэффициента замедления (отношения фазовой скорости основной моды ОПЛ к скорости света в свободном пространстве) в диапазоне от 13 до 57 ГГц для подложки с относительной диэлектрической проницаемостью ε = 2.55 (полистирол). Синяя и сиреневая штриховые линии соответствуют аналогичным зависимостям для TE и TM мод подложки. Остальные параметры выбирались следующим образом: толщина подложки h = 1 мм, тангенс угла потерь диэлектрика tgδ = 5х10^-4; ширина проводника w = 4 мм (w/h = 4), толщина металлизации t = 0.017 мм, проводимость σ = 5.8х10⁷ 1/Ом (медь).

Рис. 3. Зависимости коэффициента замедления основной моды ОПЛ (^________), ТЕ (- - - -) и ТМ (- - - - ) мод диэлектрической подложки и коэффициента замедления моды ОПЛ относительно ТЕ моды подложки (^________) от частоты

Отметим, что отношение замедлений основной моды ОПЛ и ТЕ моды подложки n = U/U_TE медленно убывает с ростом частоты и почти во всем рассмотренном диапазоне не превосходит значения n = 1.1.

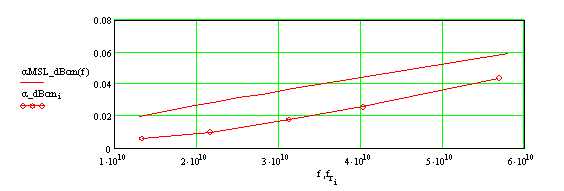
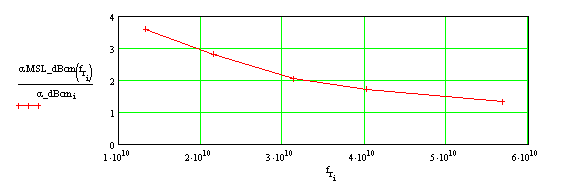
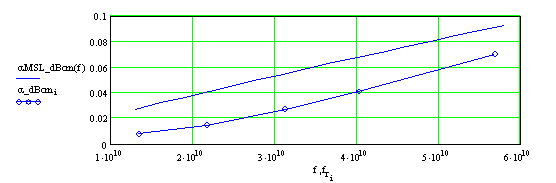
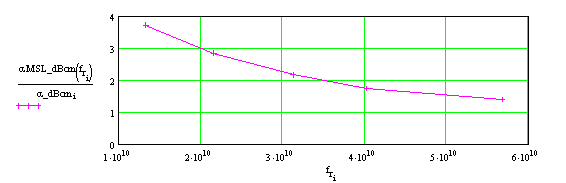
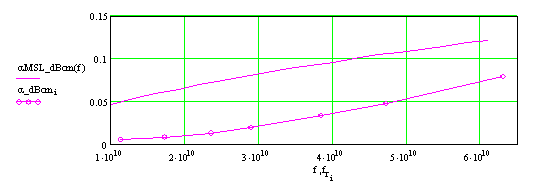
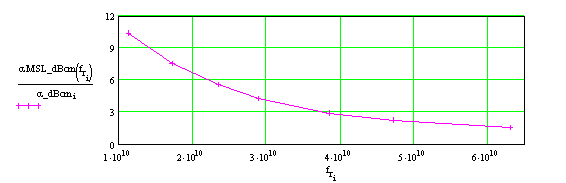
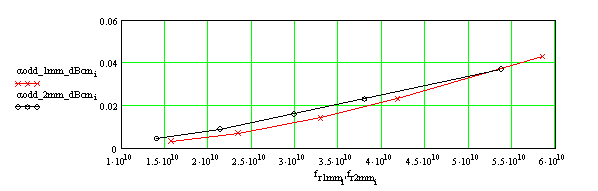
На рис. 4а представлены частотные зависимости затухания для основной моды ОПЛ (точки) и для 50-Ом МПЛ с шириной проводника 2.8 мм на той же подложке (сплошная линия). Последняя зависимость рассчитана с помощью аналитических формул, приведенных в [5]. На рис. 4б показано отношение затухания МПЛ к затуханию ОПЛ. Как видно из рисунка, с ростом частоты эта величина монотонно уменьшается, приближаясь к 1. Необходимо отметить, что при заданной проницаемости ε = 2.55 подложка толщиной 1 мм и проводник шириной 2.8 мм на ней не являются оптимальными по критерию максимальной добротности полуволнового микрополоскового резонатора на основе такой линии. Как отмечено в [6], для выбора оптимальных значений толщины подложки и ширины линии следует учитывать радиационные потери и преобразование в высшие моды подложки на неоднородностях. При таком подходе и выборе оптимальных по критерию максимальной добротности параметров регулярной 50-Ом линии (толщина подложки и ширина полоски при этом уменьшается по сравнению с выбранными нами) затухание из-за конечной проводимости металла и тангенса угла потерь диэлектрика возрастает по сравнению с представленными на рис. 4а величинами. Именно такой выбор параметров МПЛ был использован в [4] при сравнении затухания ОПЛ и МПЛ.

Рис.4а. Затухание в дБ/см для ОПЛ (точки) и для 50-Ом МПЛ (сплошная линия) на подложке с ε = 2.55, tgδ = 5х10^-4 в зависимости от частоты

Рис.4б. Отношение затухания 50-Ом МПЛ к затуханию ОПЛ на подложке с ε = 2.55,
tgδ = 5х10^-4 в зависимости от частоты

На рис. 5 и 6 представлены аналогичные частотные зависимости затухания для других значений тангенса угла потерь материала подложки: tgδ = 10^-3 (рис. 5) и tgδ = 10^-4 (рис. 6). Отметим, что отношение затухания МПЛ к соответствующему затуханию ОПЛ для этих подложек практически такое же, как и на рис. 4б, т.е. не зависит от величины tgδ в исследуемом диапазоне.

Рис. 5а. Затухание в дБ/см для ОПЛ (точки) и для 50-Ом МПЛ (сплошная линия) на подложке с ε = 2.55, tgδ = 10^-3 в зависимости от частоты

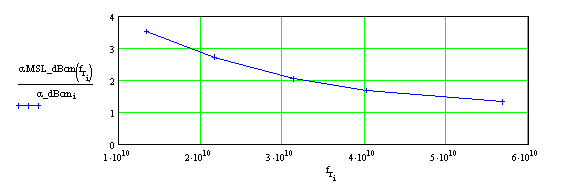
Рис. 5б. Отношение затухания 50-Ом МПЛ к затуханию ОПЛ на подложке с ε = 2.55,
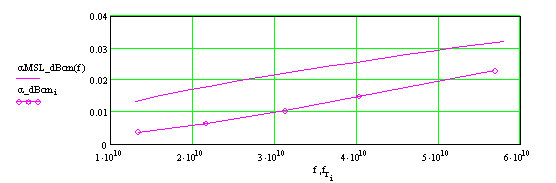
tgδ = 10^-3 в зависимости от частоты

Рис. 6а. Затухание в дБ/см для ОПЛ (точки) и для 50-Ом МПЛ (сплошная линия) на подложке с ε = 2.55, tgδ = 10^-4 в зависимости от частоты

Рис. 6б. Отношение затухания 50-Ом МПЛ к затуханию ОПЛ на подложке с ε = 2.55,
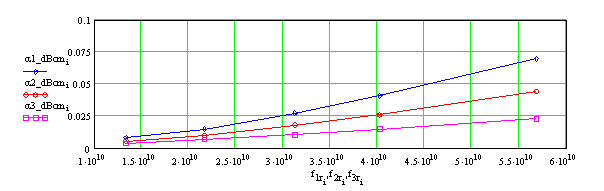
tgδ = 10^-4 в зависимости от частоты

На рис. 7 представлены частотные зависимости затухания основной моды ОПЛ для разных значений tgδ диэлектрической подложки.

Рис. 7. Затухание основной моды ОПЛ в дБ/см в зависимости от частоты для разных значений tgδ материала подложки с проницаемостью ε = 2.55: tgδ =10^-3 (^________),
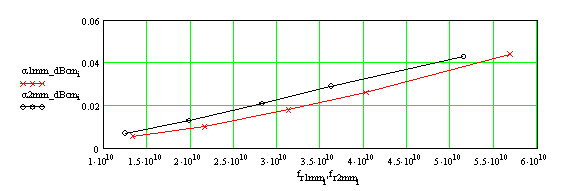
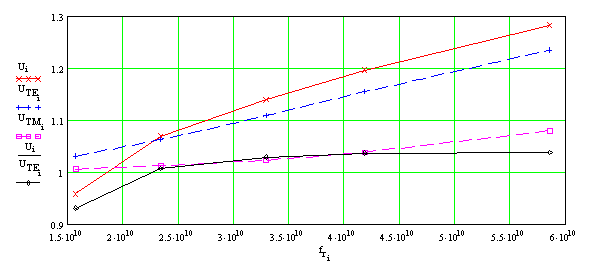
tgδ = 5х10^-4 (^________), tgδ = 10^-4 (^________)

Также были рассчитаны характеристики ОПЛ с той же шириной полоски w = 4 мм на более толстой подложке (толщиной 2 мм, т.е. w/h = 2) с проницаемостью ε = 2.55. Дисперсионные зависимости для этого случая показаны на рис. 8. На рис. 9 приведены сравнения частотных зависимостей затухания основной моды ОПЛ с шириной проводника w = 4 мм на подложках толщиной 1 мм и 2 мм при tgδ = 5х10^-4. Отметим, что хотя значения замедления волн ОПЛ для этих толщин подложки довольно сильно отличаются, разница в величинах погонного затухания для них сравнительно невелика.

Рис. 8.  Коэффициенты замедления основной моды ОПЛ (^________), ТЕ (^_ - - - ) и ТМ (- - - -) мод диэлектрической подложки с относительной проницаемостью ε = 2.55 и толщиной 2 мм и замедление моды ОПЛ относительно ТЕ моды (^_______) в диапазоне частот от 13 до 57 ГГц

Рис. 9. Частотная зависимость затухания основной моды ОПЛ в дБ/см для двух значений толщины подложки с проницаемостью ε = 2.55, tgδ = 5х10^-4: h = 1 мм (^________),
h = 2 мм (^_________)

Аналогичные вычисления были проведены для подложки с относительной диэлектрической проницаемостью ε = 10. На рис. 10 показана дисперсионная зависимость для основной моды ОПЛ в диапазоне частот от 11 до 63 ГГц. Остальные параметры выбирались следующим образом: толщина подложки h = 0.5 мм, тангенс угла потерь диэлектрика tgδ = 10^-4; ширина проводника w = 4 мм (w/h = 8), толщина металлизации t = 0.017 мм, проводимость σ = 5.8х10⁷ 1/Ом (медь).

Рис. 10. Коэффициенты замедления основной моды ОПЛ (^_______), ТЕ (^_ - - ^_) и ТМ (- - - -) мод диэлектрической подложки с относительной проницаемостью ε = 10 и толщиной 0.5 мм и замедления моды ОПЛ относительно ТЕ моды (^________) в диапазоне частот от 11 до 63 ГГц

На рис. 11а представлены частотные зависимости затухания для основной моды ОПЛ (точки) и для 50-Ом МПЛ с шириной проводника 0.48 мм на той же подложке (сплошная линия). Как и для варианта с ε = 2.55, последняя зависимость рассчитана с помощью аналитических формул в [5]. На рис. 11б показано отношение затухания МПЛ к затуханию ОПЛ. Видим, что, как и ранее, с ростом частоты эта величина монотонно уменьшается. Однако в данном случае величина отношения на нижних частотах больше, чем в случае ε = 2.55 (см. рис. 6б).

Рис. 11а. Затухание в дБ/см для ОПЛ (точки) и для 50-Ом МПЛ (сплошная линия) на подложке с ε = 10, tgδ = 10^-4 в зависимости от частоты

 

Рис. 11б. Отношение затухания 50-Ом МПЛ к затуханию ОПЛ на подложке с ε = 10,
tgδ = 10^-4 в зависимости от частоты

 

Первая высшая (нечетная) мода

Вычисления комплексной постоянной распространения были проведены также для первой высшей моды ОПЛ, которая имеет нечетное относительно плоскости симметрии распределение тока на проводнике. Это дает возможность проводить все вычисления для половины структуры с металлической стенкой в плоскости симметрии. Дисперсионные зависимости для двух значений толщины подложки показаны на рис. 12 и 13. Необходимо отметить, что в отличие от основной, для первой высшей моды существует критическая частота, ниже которой ее замедление становится меньше замедления ТЕ-моды подложки. При этом поверхностная волна не направляется проводником и вытекает в подложку. Для подложки толщиной 1 мм эта критическая частота примерно равна 23 ГГц (см. рис. 12), а для подложки толщиной 2 мм – 17 ГГц (см. рис. 13). Кроме того, видно, что во всем диапазоне частот высшая мода очень слабо замедлена относительно ТЕ-моды подложки. На рис. 14 представлены частотные зависимости затухания первой нечетной моды ОПЛ с шириной проводника w = 4 мм на подложках толщиной 1 и 2 мм при значении tgδ = 5х10^-4. Как и для основной четной волны (см. рис. 9), разница в величинах погонного затухания нечетной волны для этих подложек сравнительно невелика.

 

Рис. 12. Коэффициенты замедления первой нечетной моды ОПЛ (^________), ТЕ (^_ - - - ) и ТМ (- - - -) мод диэлектрической подложки с относительной проницаемостью ε = 2.55 и толщиной 1 мм и замедление нечетной моды ОПЛ относительно ТЕ моды (^_______) в диапазоне частот от 16 до 58 ГГц

Рис. 13. Коэффициенты замедления первой нечетной моды ОПЛ (^________), ТЕ (^_ - - - ) и ТМ (- - - -) мод диэлектрической подложки с относительной проницаемостью ε = 2.55 и толщиной 2 мм и замедление нечетной моды ОПЛ относительно ТЕ моды (^_______) в диапазоне частот от 14 до 54 ГГц

 

Рис. 14. Частотная зависимость затухания нечетной моды ОПЛ в дБ/см для двух значений толщины подложки с проницаемостью ε = 2.55, tgδ = 5х10^-4: h = 1 мм (^________),
h = 2 мм (^________)

 

Структура волн ОПЛ

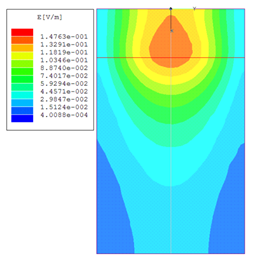
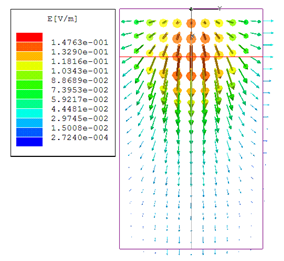
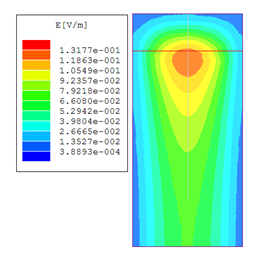
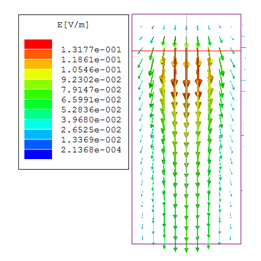
При вычислении дисперсионных характеристик замедления и затухания на основе резонаторной модели важно выбрать и идентифицировать нужный тип колебаний в спектре других существующих типов колебаний резонансного объема, в который помещен отрезок ОПЛ. Так как поле замедленной волны ОПЛ сосредоточено вблизи проводника, соответствующий тип колебаний можно идентифицировать по указанному характерному распределению поля. В качестве иллюстрации на рис. 15 представлен пример рассчитанного распределения амплитуды и вектора электрического поля основного типа колебаний на нижней (свободной) поверхности диэлектрической подложки (ε = 2.55, h = 1 мм) основной моды ОПЛ (на рисунке представлена половина симметричной относительно плоскости YZ структуры). Данное распределение образуется в резонаторе длиной 6 мм на резонансной частоте 21.62 ГГц.

                                                    а                                                                     б                               

Рис. 15. Распределение амплитуды (а) и вектора (б) электрического поля основного типа колебаний в резонаторе на нижней поверхности диэлектрической подложки с ε = 2.55, h = 1 мм

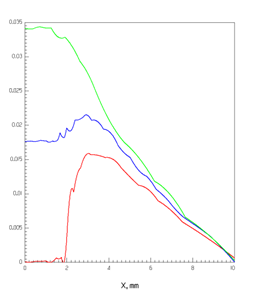
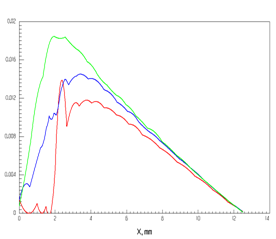
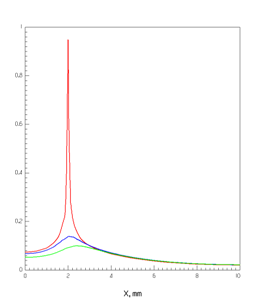
На рис. 16 показаны распределения электрического поля основного колебания вдоль оси Х (перпендикулярно полоске) на верхней и нижней поверхностях диэлектрической подложки, а также в плоскости, проходящей через ее середину. На рис.16а дано распределение в центральной плоскости резонатора XOZ, в которой существуют только поперечные X-  и Z- компоненты электрического поля и отсутствует продольная Y- компонента. На рис. 16б показано распределение продольной Y-компоненты электрического поля на металлических зеркалах резонатора. Распределения построены для половины структуры – от плоскости симметрии до металлической границы резонатора.

                          

                                  а                                                                                          б             

Рис. 16. Распределение поперечной компоненты электрического поля в центральной поперечной плоскости резонатора (а) и продольной компоненты в плоскости зеркал (б) для основной моды на верхней (^_______), средней (^______) и нижней (^______) плоскостях в диэлектрической подложке с ε = 2.55, h = 1 мм

Рис. 16а показывает, что в распределении на верней поверхности подложки наблюдается резкий всплеск напряженности поперечного электрического поля на краю проводника из-за увеличения плотности тока вблизи его края. Внутри подложки и на ее нижней поверхности имеется лишь плавное возрастание поля в окрестности края проводника. На рис. 16б видно, что характер распределения продольной компоненты электрического поля качественно иной. Таким образом, поле основной моды ОПЛ представляет собой суперпозицию двух краевых поверхностных волн [7], что отмечалось и в ранее опубликованных работах.

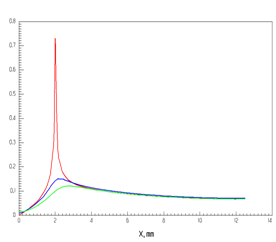
Аналогичные вычисления и построения структуры поля были выполнены также и для первой высшей нечетной волны ОПЛ. На рис. 17 приведен пример распределения амплитуды и вектора электрического поля основного типа колебаний на нижней поверхности диэлектрической подложки (ε = 2.55, h = 1 мм), (показана половина симметричной относительно плоскости YZ структуры). Данное распределение образуется в резонаторе длиной 6 мм на резонансной частоте 23.39 ГГц. Так как на этой частоте замедление нечетной моды очень мало отличается от замедления ТЕ-моды подложки (см. дисперсионные характеристики на рис. 12), распределение моды ОПЛ не локализовано в окрестности проводника. При этом ее поле далеко простирается в подложку, что хорошо видно на рис. 17а и 18а.

                                                          а                                                                б

Рис. 17. Распределение амплитуды (а) и вектора (б) электрического поля высшего нечетного типа колебаний в резонаторе на нижней поверхности диэлектрической подложки
ε = 2.55, h = 1 мм

 

     

                                         а                                                                         б

Рис. 18. Распределение поперечной компоненты электрического поля в центральной поперечной плоскости резонатора (а) и продольной компоненты в плоскости зеркал (б) нечетной моды на верхней (^_______), средней (^______) и нижней (^______) плоскостях в диэлектрической подложке с ε = 2.55, h = 1 мм

 

Сравнение результатов, полученных на основе резонаторной модели и решением задачи на собственные значения

В данной работе дисперсионные характеристики ОПЛ рассчитывались также другим способом, без использования резонаторной модели. При этом комплексная постоянная распространения определялась из решения задачи на собственные значения для поперечного сечения линии.

Сравнение коэффициента фазового замедления и постоянной затухания для основной моды МПЛ, рассчитанных на основе резонаторной модели, с соответствующими результатами, полученными решением задачи на собственные значения, для двух подложек разной толщины представлено в таблицах 1 и 2. Аналогичное сравнение для нечетной моды представлено в таблицах 3 и 4. В столбце частот в скобках указаны соответствующие значения длин резонатора, задаваемые при использовании резонаторной модели. Из таблицы 1 видно, что для подложки h = 1 мм значения замедления основной волны, рассчитанные двумя способами, совпадают во всем рассмотренном диапазоне частот. Значения затухания совпадают на частотах ниже 30 ГГц, а с увеличением частоты значения, рассчитанные прямым методом, постепенно начинают превышать значения, полученные в резонаторной модели. Для подложки толщиной h = 2 мм (табл. 2) значения затухания, рассчитанные двумя способами, совпадают на частотах ниже 20 ГГц, а с увеличением частоты значения, рассчитанные прямым методом, постепенно начинают превышать соответствующие значения в резонаторной модели.

Для нечетной моды (см. таблицы 3, 4) значения замедления, рассчитанные двумя способами, совпадают как для подложки 1 мм, так и для подложки 2 мм. Значения затухания, полученные прямым методом, во всем исследованном диапазоне частот несколько превышают его значения, полученные с использованием резонаторной модели.

Таблица 1. Сравнение коэффициентов замедления и затухания основной модыОПЛ. Толщина подложки h=1 mm.

ε = 2.55, tgδ =5х10^-4, w=4 mm, t=17 um

Частота, ГГц	Резонаторная модель		Собственные значения
	U	α [дБ/см]	U	α [дБ/см]
13.308 (L = 10 mm)	1.127	0.0055	1.127	0.0055
21.617 (L = 6 mm)	1.156	0.01	1.156	0.01
31.252 (L = 4 mm)	1.2	0.018	1.2	0.019
40.207 (L = 3 mm)	1.244	0.026	1.244	0.028
56.809 (L = 2 mm)	1.32	0.044	1.32	0.054

 

Таблица 2. Сравнение коэффициентов замедления и затухания основной модыОПЛ. Толщина подложки h = 2 mm.

ε = 2.55, tgδ = 5х10^-4, w = 4 mm, t = 17 um

Частота, ГГц	Резонаторная модель		Собственные значения
	U	α [дБ/см]	U	α [дБ/см]
12.477 (L = 10 mm)	1.202	0.0068	1.214	0.0068
19.786 (L = 6 mm)	1.264	0.013	1.268	0.013
28.177 (L = 4 mm)	1.331	0.021	1.332	0.024
36.125 (L=3 mm)	1.384	0.029	1.384	0.032
51.491 (L = 2 mm)	1.457	0.043	1.457	0.051

 

Таблица 3. Сравнение коэффициентов замедления и затухания нечетной модыОПЛ. Толщина подложки h = 1 mm.

ε = 2.55, tgδ = 5х10^-4, w = 4 mm, t = 17 um

Частота, ГГц	Резонаторная модель		Собственные значения
	U	α [дБ/см]	U	α [дБ/см]
15.665 (L = 10 mm)	0.958	0.0032	0.958	0.0042
23.386 (L = 6 mm)	1.069	0.0068	1.069	0.0079
32.886 (L = 4 mm)	1.14	0.014	1.14	0.017
41.814 (L = 3 mm)	1.196	0.023	1.196	0.028
58.50 (L= 2 mm)	1.282	0.043	1.282	0.054

 

Таблица 4. Сравнение коэффициентов замедления и затухания нечетной моды ОПЛ. Толщина подложки h = 2 mm.

ε = 2.55, tgδ = 5х10^-4, w = 4 mm, t = 17 um

Частота, ГГц	Резонаторная модель		Собственные значения
	U	α [дБ/см]	U	α [дБ/см]
13.984 (L = 10 mm)	1.073	0.0041	1.072	0.0050
21.280 (L = 6 mm)	1.175	0.0088	1.175	0.0098
29.852 (L = 4 mm)	1.256	0.016	1.256	0.019
37.994 (L = 3 mm)	1.316	0.023	1.316	0.027
53.680 (L = 2 mm)	1.397	0.037	1.397	0.043

 

Заключение

В данной статье представлены результаты численного моделирования замедления и затухания основной и первой высшей моды ОПЛ на симметричной диэлектрической подложке в широком диапазоне частот, включая сантиметровый и миллиметровый. Для моделирования использовалась резонаторная модель и прямое решение задачи на собственные значения для поперечного сечения методом конечных элементов. Сравнение показало, что коэффициенты замедления основной моды, рассчитанные двумя способами, практически совпадают во всем рассмотренном диапазоне от 10 до 60 ГГц. Коэффициенты затухания, практически совпадая в нижней части диапазона, начинают слегка различаться в верхней его части.

Результаты расчета дисперсионной характеристики для первой высшей моды показывают, что она имеет критическую частоту, ниже которой ее замедление становится меньше замедления ТЕ моды диэлектрической подложки, и она становится вытекающей (в подложку). Это подтверждают и рассчитанные распределения электрического поля нечетной моды.

Как показали результаты вычислений, затухание основной моды ОПЛ в отличие от МПЛ растет с ростом частоты нелинейно. В связи с этим затухание в ОПЛ при одинаковых геометрических параметрах на низких частотах (сантиметровый диапазон) меньше, чем в МПЛ в 3-4 раза для подложек с относительно небольшой диэлектрической проницаемостью, и на порядок меньше для подложек диэлектрической проницаемостью порядка 10. На высоких частотах (миллиметровый диапазон, многомодовый режим) величины затухания сближаются.

На низких частотах замедление основной моды ОПЛ меньше, чем на высоких, однако ее замедление относительно ТЕ моды подложки больше (примерно 1.1). Такое малое относительное замедление приводит к большому поперечному размеру поля и, соответственно, сильному излучению в подложку на нерегулярностях, что необходимо учитывать при построении элементов на базе ОПЛ.

Работа выполнена при поддержке РФФИ, проект № 08-07-00327.

Литература

1. В.В. Шевченко, Микрополосковый волновод: Авт. свид. СССР SU № 1626282 А1 // Б.И. 1991. №5. С. 150

2. Темнов В.М. // Известия Высших Учебных Заведений. Радиофизика. 1991. Т.34. № 3. С. 286.

3. Wanchu Hong and Yu-De Lin // IEEE Trans. Antennas and Propagation. 2004. V. 52. No. 7. P. 1783.

4. Шевченко В.В., Грачев Г.Г., Калиничев В.И. // РЭ. 2005. Т. 50. № 2. С. 162.

5. Гупта К. , Гардж Р., Чадха Р. Машинное Проектирование СВЧ Устройств. М.: Радио и связь, 1987. С.43.

6. Gupta K.C., Garg R., Bahl I., Bhartia P. Microstrip Lines and Slot Lines. Boston: Artech House, 1996. P.113.

7. Зайцев С.В. // Известия Высших Учебных Заведений. Радиофизика. 1987. Т.30. № 9. С. 1115.