УДК 621.382;514.8
Сверхрешетки и фигурные числа в модели системы обработки сигналов и восприятия цвета
С. Л. Чернышев 1, Л. С. Чернышев 2
1 МАТИ-Российский государственный технологический университет им. К.Э.Циолковского
2 НПП «Простор»
Статья получена 18 декабря 2013 г.
Аннотация. Фигурные сверхрешетки обладают полезными свойствами для параллельной обработки сигналов в клеточных нелинейных сетях. Рассмотрена модель системы обработки сигналов по типу «искусственной сетчатки», предусматривающая нумерацию сверхрешеток, образующих клеточную нелинейную сеть. Клеточная нелинейная сеть представлена в виде комплекса элементов стохастической матрицы. Исследуются свойства фигурных сверхрешеток в зависимости от их порядковых номеров и положения в матрице.
Ключевые слова: Сверхрешетка Фибоначчи, фигурное число, фигурная сверхрешетка, стохастическая матрица, клеточная нелинейная сеть, искусственная сетчатка.
Abstract: Figurate superlattice possess useful properties for parallel processing of signals in cellular nonlinear networks. The model of the system of pictures processing as artificial retina is examined. The numbering of the superlattice that form cellular nonlinear network as the sets of elements of the matrix, is used. The properties of figured superlattice, depending on their sequence numbers and position in the matrix are investigated.
Key words: Fibonacci superlattice, Figurate number, Figurate superlattice, Stochastic matrices, Cellular nonlinear network, Artificial retina.
1. Введение
Сверхрешетки (СР) передставляют квазипериодические полупровод-никовые структуры, обладающие уникальными электронными свойствами. СР применяют для нелинейного преобразования сигналов, в том числе для параллельной обработки изображений в клеточной нелинейной сети [1-5]. Квазипериодические СР, построенные на основе чисел Фибоначчи, являются характерным примером одномерного квазикристалла, в котором проявляются эффекты квазипериодичности: сильно изрезанный вид спектра электронных состояний и его самоподобие [1,5].
Аналоговая параллельная обработка сигналов, в частности, очистка синусоидального сигнала от гауссовского шума, может осуществляться клеточной нелинейной сетью (КНС), представляющей собой систему нелинейных элементов, расположенных в узлах некоторой решетчатой (или квазирешетчатой) структуры [2,3]. В качестве нелинейных элементов КНС используют разнообразные диодные структуры на основе полупроводниковых квазипериодических сверхрешеток [5].
Фигурные СР, построенные на основе фибоначчиевых СР и фигурных чисел, обладают расширенными возможностями управления их вольтамперными характеристиками [6]. Преимущества фигурных СР для параллельной фильтрации зашумленного аналогового сигнала с помощью клеточной нелинейной сети показаны в [7], где рассмотрены также правила построения фигурных СР на основе фибоначчиевых СР и фигурных чисел.
Фигурные числа и соответствующие им сверхрешетки можно представить в виде элементов бесконечномерных стохастических матриц, возникающих при моделировании процесса измерений с учетом вероятностей ошибок сравнения [8-10]. Фигурные сверхрешетки, построенные на основе фибоначчиевых сверхрешеток и представляющие собой элементы матриц квантовых измерений, характеризуются порядковым номером.
Нумерация сверхрешеток, образующих клеточную нелинейную сеть, используется для моделирования системы обработки сигналов по типу «искусственная сетчатка» [11,12]. Если клеточная нелинейная сеть представляет комплекс, составленный из элементов стохастической матрицы, то при этом одному и тому же номеру, биективно (взаимно однозначно) связанному с определенной точкой наблюдаемого объекта (источника сигнала), могут соответствовать различные сверхрешетки. Известно, что восприятие цвета становится возможным, благодаря различию спектральных характеристик фоторецепторов [13]. Cвойства и различия фигурных сверхрешеток, используемых в модели системы обработки сигналов и восприятия цвета, в том числе Фурье-образы их автокорреляционных функций, исследуются в зависимости от порядковых номеров и положения сверхрешеток в комплексах стохастических матриц.
2. Построение фигурных сверхрешеток
В основе построения фигурных сверхрешеток лежат представления о фибоначчиевых сверхрешетках и фигурных числах. Фибоначчиева сверхрешетка [1,5] — это слоистая структура, состоящая из чередующихся слоев барьеров и ям для электронов проводимости, свойства которой взаимосвязаны с числами Фибоначчи. Слои могут иметь нанометровую толщину и образуют последовательность вида ВАВВА…, где буквой В обозначен барьерный слой, а буквой А — слой потенциальной ямы. Фибоначчиева решетка SN ранга N=1,2,…, начиная с N=3,4,…, в соответствии с определением чисел Фибоначчи строится путем последовательного соединения (конкатенации) SN+2=SN+1+SN решеток двух предыдущих рангов SN+1, и SN. При этом присутствуют два вида базовых структур S1=А и S2=В (табл. 1). Здесь структура SN+1 соответствует величине FN, где FN — число Фибоначчи под номером N=0,1,2,… . Применение фибоначчиевых СР для нелинейного преобразования сигналов рассмотрено в [1,5-7].
Значительное расширение наборов квазипериодических структур, и
соответственно их возможностей для преобразования сигналов, достигается путем
использования фигурных чисел, взаимосвязанных с числами Фибоначчи и
обладающими дополнительными управляемыми параметрами. Фигурное число ![]() задается соотношениями [9,11]:
задается соотношениями [9,11]:
![]()
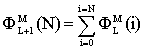 , (1)
, (1)
Здесь L=0,1,2, …; М=0,1,2, … ;
N=0,1,2, … . При этом ![]()
![]() =0;
=0; ![]() =1;
=1; ![]() =М+1 при N>1. Значению параметра L=1 соответствуют фигурные числа на
прямой (евклидово пространство размерности 1); значению L=2 — фигурные числа на плоскости;
значению L=3 — фигурные числа в трехмерном
пространстве (рис.1) и т.д.
=М+1 при N>1. Значению параметра L=1 соответствуют фигурные числа на
прямой (евклидово пространство размерности 1); значению L=2 — фигурные числа на плоскости;
значению L=3 — фигурные числа в трехмерном
пространстве (рис.1) и т.д.
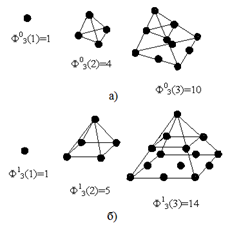
Рис. 1. Фигурные числа в трехмерном пространстве.
Для фигурных чисел на плоскости значение параметра формы М=0 соответствует треугольным числам; М=1 — четырехугольным; М=2 — пятиугольным и т.д. Параметр N определяет эволюцию фигурного числа.
Таблица 1. Символьное представление фибоначчиевых решеток рангов от 1 до 7
|
N |
SN |
|
1 |
A |
|
2 |
B |
|
3 |
B+A=BA |
|
4 |
BA+B=BAB |
|
5 |
BAB+BA=BABBA |
|
6 |
BABBA+BAB=BABBABAB |
|
7 |
BABBABAB +BABBA=BABBABABBABBA |
Для построения
фигурных СР применяется разложение чисел Фибоначчи FN по фигурным числам вида ![]() ,
параметр формы которых М=0 [9].
,
параметр формы которых М=0 [9].
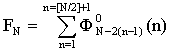 .
(2)
.
(2)
Здесь квадратные скобки означают целую часть числа. Двигаясь слева направо по символьной последовательности SN (табл. 1), ставим в соответствие каждому слагаемому (фигурному числу) в сумме (2), равной FN-1, очередной участок последовательности символов. Для S1=А и S2=B суммы вида (2) для F0 и F1 содержат только по одному слагаемому. Так получаем выражения для исходных элементов последовательности символов
S1=A→F0=![]() ; S2=В→F1=
; S2=В→F1=![]() .
.
Стрелка означает
соответствие решетки SN числу Фибоначчи FN-1.
Аналогично поставим в соответствие фигурным числам ![]() фигурную
решетку
фигурную
решетку ![]() , определяемую последовательностью
символов А и В. Тогда
, определяемую последовательностью
символов А и В. Тогда ![]() и
и ![]() . Из разложения числа Фибоначчи F2, соответствующего структуре S3, получаем символьные представления для
фигурных решеток
. Из разложения числа Фибоначчи F2, соответствующего структуре S3, получаем символьные представления для
фигурных решеток ![]() и
и ![]() .
.
S3=ВA→F2=![]()
Первое в этой сумме
число ![]() =1. В полученном символьном выражении BA
отрезок длиной 1 символ слева равен В. Это и есть символьное
представление фигурной решетки
=1. В полученном символьном выражении BA
отрезок длиной 1 символ слева равен В. Это и есть символьное
представление фигурной решетки ![]() , соответствующей
фигурному числу
, соответствующей
фигурному числу ![]() . Следующему числу
. Следующему числу ![]() =1 соответствует следующий отрезок слева
длиной 1, обозначаемый А. Так получаем символьное представление
=1 соответствует следующий отрезок слева
длиной 1, обозначаемый А. Так получаем символьное представление ![]() =A,
соответствующее фигурной решетке
=A,
соответствующее фигурной решетке ![]() . Продолжая построения,
например, из разложения
. Продолжая построения,
например, из разложения ![]() получаем символьное
представление
получаем символьное
представление ![]() =В (один символ слева).
Аналогично
=В (один символ слева).
Аналогично ![]() =ABBAB (следующие пять
символов слева). Предпоследнее число
=ABBAB (следующие пять
символов слева). Предпоследнее число ![]() =ABBABB (следующие шесть символов
слева). Последнее число
=ABBABB (следующие шесть символов
слева). Последнее число ![]() =A (последний
символ). Получаемые таким способом фигурные СР (табл. 2) при больших номерах N наследуют от фибоначчиевых СР их
свойства. Фигурные решетки вида
=A (последний
символ). Получаемые таким способом фигурные СР (табл. 2) при больших номерах N наследуют от фибоначчиевых СР их
свойства. Фигурные решетки вида ![]() (символьные
последовательности), соответствующие фигурным числам
(символьные
последовательности), соответствующие фигурным числам ![]() при
М>0 получаем из рекуррентного соотношения для фигурных чисел [9]
при
М>0 получаем из рекуррентного соотношения для фигурных чисел [9]
Таблица 2. Символьное
представление фигурных решеток
![]()
|
Решетка |
Параметр N |
|||
|
1 |
2 |
3 |
4 |
|
|
|
B |
AB |
BAB |
ABAB |
|
|
B |
ABB |
ABBABB |
BBABABBABB |
|
|
B |
ABB |
BABAB |
ABABBAB |
|
|
B |
ABBB |
BABABAB |
ABABBABBAB |
Вольтамперные характеристики фигурных СР рассчитывались в [6,7], с учетом следующих характерных параметров: содержание алюминия в барьерном В-слое AlxGa1–xAs составляло X=0,3, что соответствует высоте потенциального барьера 0,37 эВ для электронов проводимости. Толщина барьерного слоя, состоящего из двух монослоев, равна 1,3 нм, а толщина слоя ямы, состоящего из 12 монослоев, — 7,8 нм. Эффективная масса электрона считалась равной 0,08 от массы свободного электрона, а энергия Ферми в крайних n+GaAs-слоях равной 0,069 эВ. К потенциальному профилю барьеров и ям была добавлена контактная разность потенциалов 0,1 эВ между крайними n+GaAs-слоями и средними нелегированными i-AlGaAs-слоями. Температура принята равной 300 К.
3. Фигурные сверхрешетки в виде элементов стохастических матриц
Фигурные числа взаимосвязаны с элементами стохастических матриц [8,9], порождаемых процессом измерения с учетом вероятностей ошибок сравнения. При периодическом контроле состояний влияние вероятностей ошибок сравнения на оценки параметра пуассоновского потока сигналов исследовались в [10]. Фигурным числам, взаимосвязанным с элементами стохастических матриц, можно поставить в соответствие определенные квазипериодические структуры в виде фигурных СР.
Состояния объекта, который может находиться в одном из двух состояний (0 или 1), можно описать следующей матрицей второго порядка М0,1(α,β), где номера строк и столбцов L=0,1; N=0,1:
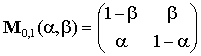 .
.
Рассматриваемая матрица представляет собой матрицу переходов (стохастическую матрицу второго порядка) цепи Маркова с двумя состояниями. Появление данной матрицы можно связать с экспериментом, в котором испускаемая частица может пройти через одну из двух щелей (под номерами 0 и 1) в расположенном перед частицей экране. При неограниченном числе экспериментов с испусканием частицы будем записывать результаты измерения прохождения частицы через щель под номером 0 и через щель под номером 1.
В общем случае возможны ошибки измерения (сравнения): первого рода (прохождение частицы через щель 1 принимаем за прохождение через щель 0) и второго рода (прохождение частицы через щель 0 принимаем за прохождение через щель 1). Эти события характеризуются соответствующими условными вероятностями ошибки первого рода α и ошибки второго рода β. Множество условий проведения данного эксперимента представлены комплексным числом (α,β), а результаты прохождения частицы через щели 0 и 1 отображаются в соответствующих строках матрицы М0,1(α,β). При безошибочном контроле состояний условные вероятности ошибок α и β равны нулю — в результате получаем единичную матрицу.
Предположим теперь, что частица может проходить через неограниченное число щелей, характеризуемых неотрицательным целым числом L=0,1,2,… . Результаты измерения (сравнений) состояний частицы отображаются матрицей бесконечного порядка. Первая строка этой матрицы показывает результаты регистрации прохождения частицы через щель под номером нуль с учетом вероятностей ошибок измерения. Вторая строка — результаты регистрации прохождения частицы через щель под номером единица и т.д. Если вероятности ошибок измерения состояния частицы α и β не зависят от номера щели, результаты определяются следующей матрицей:
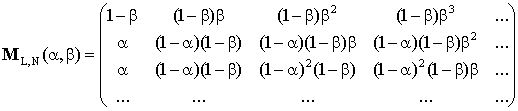 .
.
Таким образом, если исследуемый объект может находиться в бесконечном (счетном) числе состояний (L=0,1,…; N=0,1,…), то приходим к стохастической матрице бесконечного порядка МL,N(α,β),) определенной в [8,9]. Действительно, условие стохастичности выполнено, так как в каждой строке матрицы сумма вероятностей состояний равна единице и все вероятности суть неотрицательные целые числа. Дискретное распределение вероятности в L-й строке матрицы МL,N(α,β) обозначим РL(N;a,b). Независимость вероятностей ошибок от номеров щелей означает, что в данном эксперименте учитывается не расположение щелей, а только их номера, равнозначные априори.
Переход от континуума условий проведения эксперимента, характеризуемых комплексным числом (α,β) к счетному числу, характеризуемому параметром порядка, можно сравнить с квантованием воздействий. В данной матрице в каждой строке, начиная со второй, соответствующей L=1, имеются две моды. Условие квантования воздействий определим равенством вероятностей, соответствующих двум модам распределения РL(N;a,b) в М-й строке (L=М) матрицы при N=0 и N=M (соответствующие этому условию значения вероятностей ошибок обозначим aм и bм):
Рм(0;aм,bм)=Рм(М;aм,bм).
Если aм=bм, то условие равенства вероятностей мод означает, что справедливы следующие соотношения
aм=(1-aм)М+1; bм=(1-bм)М+1.
Это означает, что равные
вероятности ошибок aм и bм
взаимосвязаны с отношением обобщенной золотой пропорции qм, где параметр порядка М — порядок
обобщенной золотой пропорции. Действительно, замена переменных qм=1/(1-aм) и qм=1/(1-bм) преобразует указанные выражения к известному выражению для
отношения qм обобщенной золотой пропорции ![]() [9]. При выполнении условий
квантования матрица
[9]. При выполнении условий
квантования матрица ![]() называется матрицей квантовых
измерений. Каждому элементу матрицы, характеризуемой параметром порядка М, может
быть представлено в соответствие определенное фигурное число. Бесконечномерная
стохастическая матрица квантовых измерений
называется матрицей квантовых
измерений. Каждому элементу матрицы, характеризуемой параметром порядка М, может
быть представлено в соответствие определенное фигурное число. Бесконечномерная
стохастическая матрица квантовых измерений ![]() определяется
соотношением [9]:
определяется
соотношением [9]:
![]() (4)
(4)
где ![]() —
отношение обобщенной золотой пропорции порядка М; K=1, если N<L и К=N-L, если N³L. Изоморфное представление элементов матрицы
—
отношение обобщенной золотой пропорции порядка М; K=1, если N<L и К=N-L, если N³L. Изоморфное представление элементов матрицы ![]() с помощью фигурных чисел имеет следующий вид [9]:
с помощью фигурных чисел имеет следующий вид [9]:
Поставим в соответствие фигурному числу ![]() фигурную сверхрешетку вида
фигурную сверхрешетку вида ![]() . Здесь параметр формы М фигурного числа
представляет собой параметр порядка обобщенной золотой пропорции.
. Здесь параметр формы М фигурного числа
представляет собой параметр порядка обобщенной золотой пропорции.
При этом учитываем рекуррентное соотношение (3), которое для значений переменных N=2, M=KM, L=N преобразуется к следующему виду:
![]() . (6)
. (6)
Заметим, что все фигурные числа вида ![]() согласно выражению (3) соответствуют
решеткам вида А, если N=0 и В, если N>0. Вычисления для фигурных чисел вида
согласно выражению (3) соответствуют
решеткам вида А, если N=0 и В, если N>0. Вычисления для фигурных чисел вида ![]() показывают, что такие числа соответствуют
решеткам, которые образуют символы, начиная со второго и кончая N+2-м символом в последовательности SN+3
(табл. 1). Так, например:
показывают, что такие числа соответствуют
решеткам, которые образуют символы, начиная со второго и кончая N+2-м символом в последовательности SN+3
(табл. 1). Так, например: ![]() соответствует фигурной
решетке
соответствует фигурной
решетке ![]() ;
; ![]() соответствует
фигурной решетке
соответствует
фигурной решетке ![]() ;
; ![]() соответствует
фигурной решетке
соответствует
фигурной решетке ![]() и т. д. Фигурные сверхрешетки
и т. д. Фигурные сверхрешетки ![]() , соответствующие фигурным числам
, соответствующие фигурным числам ![]() в матрицах квантовых измерений могут быть
построены с учетом соотношения (6). Примеры таких сверхрешеток показаны в
табл. 3.
в матрицах квантовых измерений могут быть
построены с учетом соотношения (6). Примеры таких сверхрешеток показаны в
табл. 3.
Таблица 3. Символьное представление фигурных решеток
![]()
|
Решетка |
Параметр N |
|||
|
0 |
1 |
2 |
3 |
|
|
|
А |
AB |
ABВ |
ABBА |
|
|
АА |
ABB |
ABBB |
ABBАB |
|
|
ААА |
ABBВ |
ABBBB |
ABBABВ |
|
|
АААА |
ABBBB |
ABBBBB |
ABBABВB |
Таким образом, фигурные сверхрешетки ![]() образуют последовательности, состоящие из
1+N+KM символов
вида А и В. Первые N+1 символов
представляют символы в последовательности SN+3,
начиная со вто-рого и кончая N+2-м символом. В
конце символьной последовательности, представляющей фигурную сверхрешетку
образуют последовательности, состоящие из
1+N+KM символов
вида А и В. Первые N+1 символов
представляют символы в последовательности SN+3,
начиная со вто-рого и кончая N+2-м символом. В
конце символьной последовательности, представляющей фигурную сверхрешетку ![]() , находятся КМ символов вида В.
, находятся КМ символов вида В.
Вольтамперные характеристики фигурных СР
вида ![]() при М=0 и N>>1
практически не отличаются от аналогичных характеристик фибоначчиевых СР [1,6].
при М=0 и N>>1
практически не отличаются от аналогичных характеристик фибоначчиевых СР [1,6].
4. Модели клеточных нелинейных сетей в виде комплексов матриц
Аналоговая параллельная обработка сигналов, в частности, очистка синусоидального сигнала от гауссовского шума, может осуществляться клеточной нелинейной сетью (КНС), представляющей собой систему нелинейных элементов, расположенных в узлах некоторой решетчатой (или квазирешетчатой) структуры [2,3]. В качестве нелинейных элементов КНС используют традиционные резонансно-туннельные диоды (РТД) и разнообразные диодные структуры на основе полупроводниковых квазипериодических сверхрешеток [5].
Фигурные сверхрешетки вида ![]() , построенные на основе фигурных чисел
, построенные на основе фигурных чисел ![]() , изоморфно связанных с
вероятностями в матрице квантовых измерений на основе соотношения (5), будем
называть нумерованными фигурными сверхрешетками. Номер Z фигурной сверхрешетки
, изоморфно связанных с
вероятностями в матрице квантовых измерений на основе соотношения (5), будем
называть нумерованными фигурными сверхрешетками. Номер Z фигурной сверхрешетки ![]() определим соотношением Z=
определим соотношением Z=![]() . Здесь
N,K,M — неотрицательные целые числа.
Очевидно, что в матрице квантовых измерений одному и тому же порядковому номеру
могут соответствовать различные фигурные сверхрешетки. Каждой фигурной
сверхрешетке вида
. Здесь
N,K,M — неотрицательные целые числа.
Очевидно, что в матрице квантовых измерений одному и тому же порядковому номеру
могут соответствовать различные фигурные сверхрешетки. Каждой фигурной
сверхрешетке вида ![]() соответствует определенный порядковый
номер. Число слоев, равное числу соответствующих символов, представляющих,
например, полупроводниковую сверхрешетку вида
соответствует определенный порядковый
номер. Число слоев, равное числу соответствующих символов, представляющих,
например, полупроводниковую сверхрешетку вида ![]() ,
равно Z+1.
,
равно Z+1.
Построение комплексов в матрице квантовых измерений позволяет классифицировать элементы, характеризуемые порядковыми номерами, размещенные в матрице. Для построения комплексов используются соответствующим образом преобразованные таблицы Юнга. Таблица Юнга — это заполнение, не убывающее по строкам и возрастающее по столбцам. Отражение диаграммы (таблицы) относительно главной диагонали (матрицы квантовых измерений) дает сопряженную диаграмму. Заполнение (нумерацию) сопряженной диаграммы будем называть транспонированным заполнением (нумерацией). Таблицу Юнга в этом случае также будем называть транспонированной.
Косая диаграмма — это диаграмма, полученная вырезанием меньшей диаграммы Юнга из большей, содержащей ее. Косая таблица Юнга — это заполнение клеток косой диаграммы натуральными числами не убывающее по строкам и возрастающее по столбцам [14]. Кроме транспонированной таблицы Юнга введем в рассмотрение также симметричную таблицу, которая получается из таблицы Юнга путем ее зеркального отражения относительно столбца, по которому выравнены строки диаграммы.
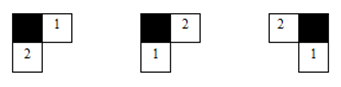
На рис. 2 показана косая диаграмма (таблица) Юнга с тремя ячейками, составленными в две строки (вырезана угловая ячейка), совпадающая с ней сопряженная косая диаграмма с транспонированным заполнением и косая симметричная транспонированная таблица Юнга.
а) б) в)
Рис. 2. а) Косая таблица Юнга; б) косая транспонированная таблица Юнга; в) косая симметричная транспонированная таблица Юнга.
Наряду с косой транспонированной таблицей Юнга и косой симметричной транспонированной таблицей Юнга, с максимальным числом ячеек в строках равным двум (рис. 2б, рис. 2в), будем рассматривать аналогичные таблицы Юнга с максимальным числом элементов в строке, равным 2n, где n — натуральное число. В соответствующих диаграммах Юнга число строк также равно 2n, а число ячеек в строках изменяется согласно арифметической прогрессии с максимальным элементом, равным 2n и минимальным — равным 1. Все такие диаграммы Юнга — косые, причем, вырезаются все диагональные элементы. Обозначения исходных диаграмм Юнга (без вырезания), согласно [19]: (2,1);(4,3,2,1);(6,5,4,3,2,1), … .
Нетрудно убедиться в
том, что косые таблицы Юнга для диаграмм
вида (2n,2n–1,2n–2, …, 2,1) с вырезанными диагональными элементами содержат
2n2 ячеек. Отметим,
что при заданном главном квантовом числе n существует ровно 2n2 квантовых состояний объекта (электрона). В матрице
квантовых измерений первый комплекс размещается так, чтобы заштрихованная центральная
ячейка находится на главной диагонали (L=1, N=1). В этом случае
выполняются условия, при которых крестообразная структура (комплекс) является
унитарной. В комплексе К1 (рис.3) центральная ячейка находится
на главной диагонали матрицы (L=1, N=1). В этом случае верхней (L=0, N=1) и нижней (L=2, N=1) ячейкам под
номером 1, согласно (4) соответствует одно и то же фигурное число 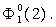 Левой ячейке (L=1,N=0) под номером 2
соответствует фигурное число
Левой ячейке (L=1,N=0) под номером 2
соответствует фигурное число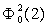 , а правой ячейке (L=1,N=2) под номером 2
соответствует фигурное число
, а правой ячейке (L=1,N=2) под номером 2
соответствует фигурное число 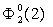 .
.
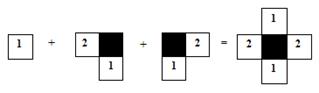
S1 S2л S2п К1
Рис. 3. Построение первого комплекса К1 из ступенчатых структур.
Согласно рассмотренному алгоритму в комплексе под номером n могут быть размещены 2n2 элементов (порядковых номеров). При этом каждый элемент, характеризуемый порядковым номером, может размещаться в одной или двух или трех ячейках комплекса. Показано [12], что размещение элементов, характеризуемых порядковыми номерами, в комплексах позволяет идентифицировать эти элементы (поставить им в соответствие определенный набор значений параметров порядка М) в соответствии с квантовыми числами.
Поскольку каждой ячейке матрицы квантовых измерений соответствует определенное фигурное число согласно (5), следовательно, этим ячейкам соответствуют определенные фигурные решетки. Так, например, в табл. 3 находим фигурные решетки, которые соответствуют указанным ячейкам матрицы квантовых измерений, составляющих комплекс К1:АВ, ААА и АВВ.
Вид комплекса К2 , соответствующего значению главного квантового числа n=2, показан на рис. 4.
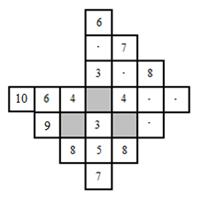
Рис. 4. Комплекс К2 в матрице квантовых измерений.
Положение элементов с порядковыми номерами 1,3,11,29,…,
расположенных подобным образом в комплексах с различными номерами,
соответствующих значению главного квантового числа, характеризуется одинаковым
набором трех других квантовых чисел. Данным порядковым номерам согласно (5) в
матрицах квантовых измерений соответствуют фигурные числа: ![]() ,
, ![]() ,
,
![]() ,
,![]() … ,
которым в свою очередь соответствуют определенные фигурные СР.
… ,
которым в свою очередь соответствуют определенные фигурные СР.
Расчеты, проведенные К.В.Малышевым по методике, изложенной в
[7], показали, что фигурные СР вида ![]() и
и ![]() с порядковыми номерами 19 и 11 в составе обычной клеточной
нелинейной сети, состоящей из 64х64
одинаковых нелинейных элементов в квадратной решеточной структуре, лучше
очищают от шума полутоновое изображение, чем это делают двухбарьерные
гетероструктуры типа резонансно-туннельного диода. У фигурной СР вида
с порядковыми номерами 19 и 11 в составе обычной клеточной
нелинейной сети, состоящей из 64х64
одинаковых нелинейных элементов в квадратной решеточной структуре, лучше
очищают от шума полутоновое изображение, чем это делают двухбарьерные
гетероструктуры типа резонансно-туннельного диода. У фигурной СР вида ![]() =ABBABABBABBA минимальное среднеквадратичное
отклонение преобразованного изображения от эталона почти вдвое меньше, чем у
резонансно-туннельного диода. Это объясняется волнообразным видом вольтамперной
характеристики фигурных СР, приводящим к появлению устойчивых состояний для
точек серого цвета на изображении.
=ABBABABBABBA минимальное среднеквадратичное
отклонение преобразованного изображения от эталона почти вдвое меньше, чем у
резонансно-туннельного диода. Это объясняется волнообразным видом вольтамперной
характеристики фигурных СР, приводящим к появлению устойчивых состояний для
точек серого цвета на изображении.
5. Моделирование системы обработки изображений и восприятия цвета
В основу моделирования системы обработки сигналов может быть положен принцип нумерации фоторецепторов [11,12]. Применение нумерующих функций для построения образов и прообразов (объект наблюдения — элементы системы обработки) обеспечивает взаимно однозначное отображение и соответствует минимальным искажениям информации в процессе ее обработки. Объект наблюдения может быть представлен решеткой (координаты точек-элементов решетки без ограничения общности задаются неотрицательными целыми числами). Элементы модели системы обработки образуют точки-элементы сложной квазирешетчатой структуры (комплекса). При этом каждому рецептору системы обработки ставится в соответствие определенный порядковый номер.
В качестве примера системы обработки сигналов и восприятия цвета рассмотрим сетчатку глаза, содержащую более 130 миллионов рецепторов. На основе исходного множества номеров палочек и колбочек (модели сетчатки) путем применения алгоритмов нумерации устанавливается взаимно однозначно соответствующее данной модели многомерное множество, представляющее объект наблюдения. С другой стороны номера палочек и колбочек могут быть биективно (взаимно однозначно) отображены в координаты другого многомерного множества, представляющего нейронную сеть мозга. Таким образом, посредством нумерации палочек и колбочек может быть организована биекция (взаимно однозначное соответствие) между объектом наблюдения и нейронной структурой мозга.
Определим номера комплексов Кn, для которых число номеров элементов, размещаемых в этих комплексах, равны (с точностью до округления) суммарному числу палочек и колбочек в сетчатке (около 130 млн). Расчеты показывают, что в комплексе К8726 под номером 8726 размещаются 129 983 070 номеров палочек и 7 001 282 номеров колбочек. Колбочки соответствуют номерам от 377 825 676 301 до 377 832 677 582, а палочки номерам от 377 832 677 583 до 377 962 660 652. Для сравнения в комплексе К1871 под номером 1871 размещаются 7 001 282 номеров колбочек. Колбочки соответствуют номерам от 4 362 966 191 до 4 369 967 472.
Предварительный анализ показывает, что объект наблюдения, соответствующий данным номерам рецепторов следует рассматривать в четырехмерном пространстве. При этом значения переменных U,X,Y,Z кортежа (U,X,Y,Z), взаимно однозначно соответствующие порядковым номерам колбочек, размещенных в комплексе К1871, показаны на рис. 5, где к минимальному номеру колбочки 4 362 966 191 нужно прибавить значение, указанное на оси абцисс, умноженное на 100.
Здесь области изменения координат X,Y,Z прообраза, соответствующих, например, положению объекта наблюдения представляют собой множества неотрицательных целых чисел от 0 до 465. Первая координата U прообраза, которая может характеризовать специфическую особенность зрительного восприятия, например, диапазон воспринимаемых частот (длин) волн, изменяется в относительных единицах в пределах от 167 до 95.
В случае трехмерного прообраза только две координаты (вторая и третья) изменяются от минимального значения, равного нулю, до некоторого максимального значения, а первая координата изменяется в определенном диапазоне. Таким образом, трехмерный прообраз по сравнению с четырехмерным прообразом не позволяет представить объект наблюдения в виде точек, координаты которых расположены в области (0-Xmax, 0-Ymax, 0-Zmax).
Возможности цветового зрения обусловлены наличием световоспринимающих рецепторов трех типов, взаимосвязанных с определенным объектом наблюдения (фрагментами этого объекта) [13]. Шкалы измерений цвета — это шкалы наименований, упорядоченные по признаку близости (сходства) цветов. При этом качественно неразличимые цвета (одинаковой цветности) могут отличаться количественно по светлоте (уровню яркости). В колориметрической системе две координаты: цветовой тон (оттенок цвета) и насыщенность (уровень проявления цветового тона) носят качественный характер, а третья координата соответствует количественной характеристике — светлоте (уровню яркости), описываемой аддитивной шкалой отношений [15]. Показано, что нумерующие функции, построенные на основе фигурных чисел, могут служить связующим звеном между шкалами, характеризующими количественные свойства, и шкалами наименований, характеризующими качественные свойства сложных объектов [16]. Эта особенность нумерующих функций проявляется при моделировании механизма восприятия цвета с использованием комплексов рецепторов.
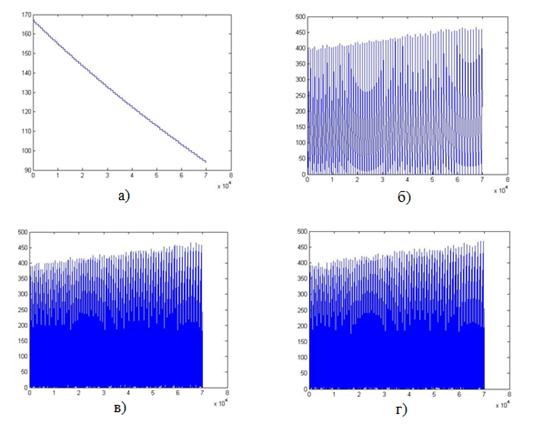
Рис. 5. Изменение координат четырехмерного прообраза в зависимости от номеров рецепторов в комплексе К1871: а) U; б) X; в) Y; г) Z.
Расположение порядковых номеров рецепторов в комплексах приводит к неоднозначности: каждый элемент, характеризуемый порядковым номером, на главной диагонали матрицы отображается в одну или две или три ячейки соответствующего комплекса матрицы. Возникающая неоднозначность проявления порядкового номера позволяет говорить о «цвете» элемента в некоторой особой двух- или трехмерной системе координат.
Отметим, что если для технических систем цветовоспроизведения базовые компоненты образования цвета расположены рядом друг с другом, то рецепторы с одним и тем же порядковым номером (принимающие сигнал из одной точки объекта наблюдения) расположены в различных участках комплекса, представляющего модель сетчатки. Так, элемент с порядковым номером Z=8 на рис. 4 расположен в трех ячейках комплекса удаленных друг от друга. Удаление друг от друга рецепторов с одним и тем же порядковым номером и различными значениями параметра формы в комплексе увеличивается с ростом порядкового номера.
Одному и тому же порядковому номеру в комплексах матриц квантовых
измерений соответствуют фигурные числа, значения параметра формы М у которых
различны. Соответственно возникают фигурные сверхрешетки с различными параметрами
формы. Различия параметров формы моделей рецепторов с одинаковыми порядковыми
номерами могут проявляться в различиях спектральных характеристик
соответствующих фигурных СР. Известно, что различия в пигментации рецепторов
сетчатки служит основой цветового зрения. При этом каждый вид рецепторов
оказывается наиболее чувствительным к определенному спектральному диапазону.
6. Фурье-образы фигурных сверхрешеток
Спектральные характеристики фибоначчиевых и фигурных сверхрешеток с небольшим числом блоков вида А и В исследовались в [18,19]. Показано, что в диапазоне от 2 до 4 ТГц имеются от двух до пяти пиков излучения, сохраняющие свою форму в широком диапазоне напряжений.
При обработке сигналов с использованием
фигурных сверхрешеток, кроме порядкового номера n сверхрешетки вида ![]() необходимо учитывать
также значение параметра формы М. Как показывают расчеты Малышева К.В., выполненные
по методике [7], фигурные сверхрешетки
необходимо учитывать
также значение параметра формы М. Как показывают расчеты Малышева К.В., выполненные
по методике [7], фигурные сверхрешетки ![]() и
и ![]() с порядковыми номерами 19 и 11,
различающиеся значениями параметра формы (М=8 и М=0), в составе клеточной
нелинейной сети по-разному очищают от шума полутоновое изображение. Например,
КНС на основе сверхрешетки
с порядковыми номерами 19 и 11,
различающиеся значениями параметра формы (М=8 и М=0), в составе клеточной
нелинейной сети по-разному очищают от шума полутоновое изображение. Например,
КНС на основе сверхрешетки ![]() лучше убирает
зернистость фона по сравнению со сверхрешеткой
лучше убирает
зернистость фона по сравнению со сверхрешеткой ![]() .
.
Квазипериодическая структура, например, фигурная СР, обладающая дальним порядком, может характеризоваться автокорреляционной функцией, характеризующей степень отображения системы самой на себя при трансляциях. Дифракционная картина определенной структуры вещества представляет собой Фурье образ автокорреляционной функции этой структуры [20]. Известно, что дифракционные методы измерений позволяют судить о спектральных свойствах исследуемых структур.
Рассмотрим фигурные сверхрешетки ![]() , соответствующие фигурным числам
, соответствующие фигурным числам ![]() . На рис. 6 показан вид фигурной СР при n=20, где в последовательности символов (блоков) A и B,
символу A на графике
(рис. 6а) соответствует значение 0, а символу B — значение 1. На этом же
рисунке показаны автокорреляционная функция ρ(n) (рис.
6б), а также Фурье-образ автокорреляционной функции (рис. 6в).
. На рис. 6 показан вид фигурной СР при n=20, где в последовательности символов (блоков) A и B,
символу A на графике
(рис. 6а) соответствует значение 0, а символу B — значение 1. На этом же
рисунке показаны автокорреляционная функция ρ(n) (рис.
6б), а также Фурье-образ автокорреляционной функции (рис. 6в).
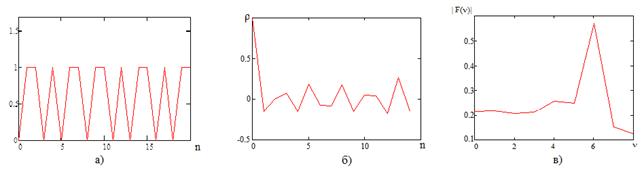
Рис. 6. Характеристики фигурной
сверхрешетки ![]() : а) представление СР для n=20;
: а) представление СР для n=20;
б) автокорреляционная функция СР; в) Фурье-образ (от 0
до π).
Здесь |F(n)| — коэффициенты ряда Фурье. При увеличении порядкового номера фигурной сверхрешетки в большей степени проявляются квазипериодический характер автокорреляционной функции и характерные максимумы Фурье-образа этой функции. На рис. 7 показан вид автокорреляционной функции (рис. 7а), а также Фурье-образ автокорреляционной функции (рис. 7б) фигурной СР при n=1000.
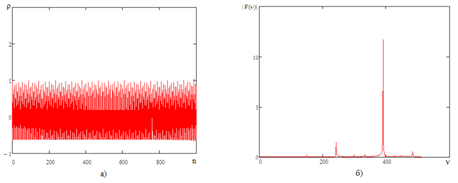
Рис. 7. Характеристики фигурной
сверхрешетки ![]() для n=1000:
для n=1000:
а) автокорреляционная функция СР; г) Фурье-образ (от 0 до π).
Известно, что спектральная чувствительность фоторецепторов сетчатки разного типа различна и определяется спектром поглощения зрительных пигментов. Исследования спектров поглощения рецепторов сетчатки приматов (близкие к свойствам рецепторов человека) позволили выявить особенности поглощения в видимой области. Три вида колбочек обладают следующими максимальными длинами волн поглощения: колбочки первого типа — lmax=447 нм (сине-фиолетовый свет); колбочки второго типа — lmax= 540 нм (зеленый свет) колбочки третьего типа — lmax= 577 нм (желтый свет) [21].
Различия параметров формы моделей рецепторов (фигурных чисел) с одинаковыми порядковыми номерами, составляют от десятков процентов Z (для порядковых номеров СР в пределах 100) до единиц и долей процентов для больших порядковых номеров. Поскольку различия в пигментации рецепторов сетчатки служит основой цветового зрения, важно выяснить, как различия параметров формы фигурных СР могут проявляться в различиях спектральных свойств.
Согласно определению фигурных СР,
взаимосвязанных с элементами матрицы квантовых измерений в конце символьной
последовательности, представляющей фигурную сверхрешетку ![]() , находятся М символов вида В,
которым при изображении структуры поставлено в соответствие 1.
, находятся М символов вида В,
которым при изображении структуры поставлено в соответствие 1.
Расчеты показывают, что параметр формы М>0 фигурной СР ![]() проявляется таким образом, что Фурье-образ автокорреляционной функции
сверхрешетки практически не изменяется по сравнению со сверхрешеткой, у которой
параметр формы равен нулю. Так для фигурных СР с параметрами n=128, M=0, n=128,
M=12, n=128, M=24 изменения
Фурье-образов автокорреляционной функции сверхрешетки находятся в пределах
точности вычислений. С увеличением порядкового номера СР, т.е при Z>>1 влияние параметра формы
фигурной СР на Фурье-образы решетки и ее автокорреляционной функции практически
отсутствует, если отношение M/Z составляет до 20%.
проявляется таким образом, что Фурье-образ автокорреляционной функции
сверхрешетки практически не изменяется по сравнению со сверхрешеткой, у которой
параметр формы равен нулю. Так для фигурных СР с параметрами n=128, M=0, n=128,
M=12, n=128, M=24 изменения
Фурье-образов автокорреляционной функции сверхрешетки находятся в пределах
точности вычислений. С увеличением порядкового номера СР, т.е при Z>>1 влияние параметра формы
фигурной СР на Фурье-образы решетки и ее автокорреляционной функции практически
отсутствует, если отношение M/Z составляет до 20%.
7. Выводы
В рассмотренной модели системы обработки сигналов, основанной на принципе нумерации фоторецепторов, восприятие цвета обусловлено различием параметром формы у двух или трех рецепторов с одинаковыми порядковыми номерами. Определенный порядковый номер обеспечивает биективную (взаимно однозначную) связь рецептора с определенной точкой наблюдаемого объекта, а параметр формы рецептора взаимосвязан с восприятием цвета. Исследование моделей рецепторов в виде фигурных сверхрешеток для больших порядковых номеров рецепторов не выявило влияние параметра формы на Фурье-образы СР и их автокорреляционных функций. В то же время фигурные сверхрешетки с небольшими порядковыми номерами, различающиеся значениями параметра формы, в составе клеточной нелинейной сети по-разному очищают от шума полутоновое изображение, ввиду различий вольтамперных характеристик.
Работа выполнена при финансовой поддержке РФФИ, грант №11-07-00007-а.
Литература
1. Macia E. Aperiodic structures in condensed matter: fundamentals and applications. — CRC Press. New York. 2009. — 443 p.
2. Morfu S. Nonlinear systems for image processing /S.Morfu, P.Marquie, B.Nofiele, D.Ginhac //Advances in Imaging and Electron Physics. — 2008.— V. 152. — P.79-151.
3. Julian P. Simplicial RTD-Based Cellular Nonlinear Networks /P.Julian, R.Dogaru, M.Itoh et al // IEEE Transactions on Circuits and Systems – I: Fundamental Theory and Applications. — 2003. — V. 50. — N4. — P.500-509.
4. Шорохов А.В. Квантовые производные и усиление терагерцового излучения в сверхрешетке/ А.В. Шорохов, К.Н. Алексеев // ЖЭТФ.— 2007.— Т.132.— Вып. 1(7). — С.223.
5. Panchdhyayee P. Current density in generalized Fibonacci Superlattices under a uniform electricfield /P.Panchdhyayee, R.Biswas, A.Khan, P.K.Mahapatra //Journal f Physics: Condensed Matter. — 2008. — V.20.— 275243 (7pp).
6. Малышев К.В., Чернышев С.Л. Вольтамперные характеристики фигурных AlGaAs сверхрешеток //Нано- и микросистемная техника. 2011. — №2. — С.48-54.
7. Малышев К.В, Потапов А.А., Чернышев С.Л. Фигурные сверхрешетки в классической задаче фильтрации шума клеточной нелинейной сетью // Радиотехника и электроника.— 2013.— Т.58.— №4. — С.367-374.
8. Чернышев С.Л., Чернышев Л.С. Квантовый анализ результатов измерений // Измерительная техника. — 2006. — №12. — С.3-8; Chernyshev S. L., Chernyshev L.S. Measurement Techniques.— 2006. — V.49. — N 12. — P.1171.
9. Чернышев С.Л. Моделирование и классификация наноструктур — М.: Книжный дом «ЛИБРОКОМ», 2011. — 216 с.
10. Чернышев С.Л. Исследование потоков событий, наблюдаемых с ошибками // Радиотехника и электроника.— 1996.— Т.41.— №3. — С.340.
11. Чернышев С.Л. Нумерующие функции неотрицательных целочисленных координат L-мерных векторов // Фундаментальная и прикладная математика. — 2009. — Том 15. — №1. — С.147-155.
12. Чернышев С.Л., Чернышев Л.С. Нумерация элементов сетчатки для моделирования зрительных механизмов. Электронный журнал «Исследовано в России» http://zhurnal.ape.relarn.ru/articles/2011/068.pdf.
13. Хьюбел Д. Глаз, мозг, зрение. — М.: Мир, 1990. — 239 с.
14. Фултон У. Таблицы Юнга и их приложения к теории представлений и геометрии/ Пер. с англ. — М.: МЦНМО, 2006. — 328 с.
15. Брянский Л.Н., Дойников А.С., Крупин Б.Н. Метрология. Шкалы,
эталоны, практика. Юбилейная серия научных изданий под. общей ред. М.В.Балаханова. — М.: ВНИИФТРИ, 2004. — 222 с.
16. Исаев Л.К., Чернышев С.Л. Выявление взаимосвязи шкал, характеризующих количественные и качественные свойства сложных объектов на основе нумерации // Метрология, 2012, №12, с.3-12.
17. Биология. Большой энциклопедический словарь/ Гл. ред. М.С.
Гиляров. — 3-е изд. — М.: Большая Российская энциклопедия, 1999. — 864 с.
18. Малышев К.В. Многоцветный терагерцовый лазер на фигурных сверхрешетках // Приборы.— 2012.— №8.— С.43-48.
19. Малышев К.В. Терагерцовая электролюминесценция сверхрешеток Фибоначчи // Физика и техника полупроводников. — 2013. — Том 47. — Вып. 7. — С.939-943.
20. Гратиа Д. Квазикристаллы // УФН, 1988.
21. Жорина Л.В., Змиевской Г.Н. Основы взаимодействия физических полей с биологическими объектами: Воздействие ионизирующего и оптического излучения: Уч. пособие — М.: Изд-во МГТУ им. Н.Э.Баумана, 2006. —240 с.