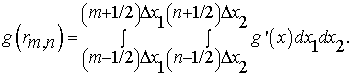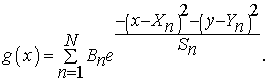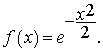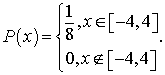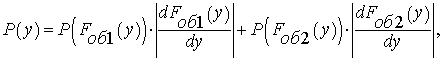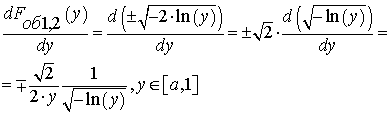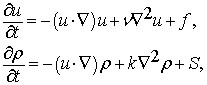ЦИФРОВАЯ
МОДЕЛЬ КАРТИН ВИЗУАЛИЗАЦИИ ПОТОКОВ
А. А. Савин, Д. С.
Харин
Национальный
исследовательский институт «Московский энергетический университет
Статья
получена 19 декабря 2013 г.
Аннотация. В данной статье обобщаются известные из разных источников сведения о картинах визуализации потоков, теоретически получена плотность вероятностей распределения яркости частиц по кадру. На основе известного алгоритма решения уравнений Навье-Стокса, дополненного учетом граничных условий произвольной формы и расчетом траекторий частиц в векторном поле создана нестационарная модель потока.
Ключевые слова: Particle Image Velocimetry, модели нестационарных потоков, моделирование изображений.
Abstract. In this article information about images of flow visualization is generalized from different sources, probability density of the brightness distribution of particles on the frame is theoretically received. The non-stationary model of a flow is created on the basis of known algorithm of the solution Navier-Stokes equations. This model contains the boundary conditions of arbitrary shape and calculation of particle trajectories in the vector field.
Keywords: Particle Image Velocimetry, nonstationary flow modelling, image modelling.
Введение
Наиболее распространенными методами получения полей скоростей в потоках жидкости, газа и полевой плазмы, а, в том числе, жидкостей в организме человека, в настоящее время являются так называемые трассерные методы, суть которых сводится к цифровой видеозаписи траекторий частиц (трассеров), визуализирующих поле скорости, с последующим компьютерным анализом получившихся изображений [1]. Структурная схема метода показана на рисунке 1 [2]:
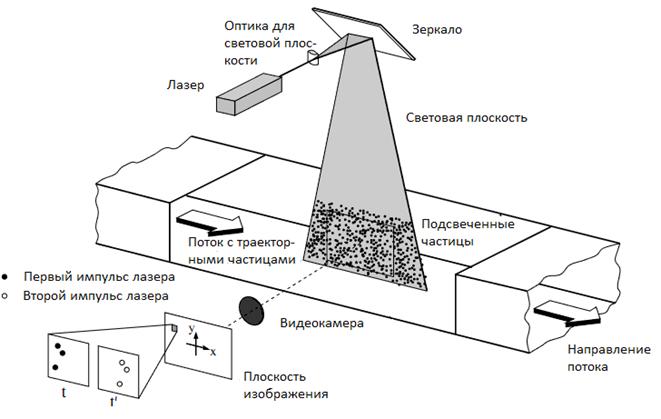
Рисунок 1. Структурная схема метода трассерной визуализации потока
Один из самых широко используемых алгоритмов основан на корреляционном анализе фрагментов изображений [2]. Он получил название Particle Image Velocimetry (PIV). Помимо корреляционной обработки в последнее время большое внимание уделяется алгоритмам отслеживания отдельных частиц. Такие методы носят название Particle Tracking Velocimetry (PTV).
При исследовании алгоритмов анализа для PIV и PTV методов требуется иметь изображения картин визуализации потоков с известным пространственным распределением векторного поля скоростей. Для данных целей необходимо разработать компьютерную модель PIV-изображений и нестационарную модель потока. В данной статье приводится описание такой модели, основанной на общеизвестных наработках и собственных разработках авторов.
Компьютерная модель PIV-изображения
Согласно [3], формирование цифрового изображения состоит из нескольких этапов:
1) искажения реального объекта из-за различий плоскости объекта и плоскости камеры (поворот, увеличение и пр.);
2) сглаживание изображения из-за усреднения по элементам сетки дискретизации;
3) дискретизация;
4) квантование.
Первый пункт мы рассматривать не будем, так как перед началом эксперимента обязательно проводят тщательное выравнивание измерительной аппаратуры. Скажем лишь, что при необходимости, все подобные искажения можно легко описать при помощи аффинных преобразований [4].
Остальные пункты рассмотрим подробнее.
Нашей стартовой точкой является бесконечное непрерывное изображение g(x), которое мы хотим отобразить в матрицу G.
Преобразование в цифровую форму означает, что мы дискретизируем изображение в определенных точках дискретной сетки, rm,n.
Как правило, мы не накапливаем интенсивность освещенности точно в этих точках, а скорее в определенной области вокруг них. В качестве примера возьмем ПЗС-камеру, которая состоит из фотодиодов без каких-либо нечувствительных к свету полос между ними. Далее полагаем, что фотодиоды одинаково чувствительны по всей области. Тогда сигнал в узлах сетки является интегралом по площади отдельных фотодиодов [3]:
Эта операция включает свертку с прямоугольной функцией-ящиком и дискретизацию в узлах сетки. Эти два шага можно отделить. Мы можем выполнить сначала непрерывную свертку, а затем дискретизацию. Таким образом, мы можем обобщить процесс формирования изображений и отделить его от процесса дискретизации.
Процесс формирования изображений приводит к размыванию изображения; мелкие детали теряются. В Фурье-пространстве это ведет к ослаблению высоких волновых чисел. Формируется результирующее яркостное изображение с ограниченной полосой пропускания.
Дискретизация означает, что теряется вся информация, за исключением узлов сетки. Математически этот процесс состоит в умножении непрерывной функции на функцию, которая равна нулю везде, за исключением узлов сетки. Эта операция может выполняться с помощью умножения функции изображения g(x) на сумму δ-функций Дирака, размещенных в узлах сетки rm,n. Тогда дискретизацию можно выразить как:
После преобразования в цифровую форму (формула (2)) пиксели все еще показывают непрерывные уровни яркости. Для использования компьютера мы должны отобразить их в ограниченное число Q дискретных уровней яркости. Этот процесс называется квантованием.
Использовать для компьютерного моделирования формулу (1) не представляется возможным, так как даже если каким-то образом удастся получить функцию g(x) – что возможно для картин визуализации потоков – то вычисление интеграла (1) может занять непозволительно много времени из-за сложности функции. Поэтому при компьютерной реализации процесс сглаживания и дискретизации меняют местами: сначала производится дискретизация (2), а затем выполняется уже дискретная свертка с прямоугольным окном. При достаточном разрешении цифрового изображения это не приводит к существенным отличиям [4].
Итак, для моделирования картин визуализации потоков необходимо знать функцию g(x). Как ясно из введения, картины визуализации потоков представляют собой фотографии частиц, подсвеченных лазерной плоскостью. Обычно считают [5], что частицы имеют форму гауссовой кривой. Обозначим через X массив координат центров частиц по оси x, а через Y – по оси y, через B – массив яркостей частиц и через S – массив размеров частиц. Тогда можно записать:
Основным источником шума на картинах визуализации потоков являются тепловые шумы видеокамер [2]. Моделью данного шума хорошо служит гауссов случайный процесс [4].
Рассмотрим отдельные составляющие, входящие в состав (3).
Сначала рассмотрим яркость. Как известно [1], основная мода лазерного излучения имеет гауссово распределение интенсивности в поперечных направлению распространения плоскостях. Поэтому ее называют гауссовой. Следовательно, световая плоскость с рисунка 1 также имеет гауссово распределение в своем поперечнике. Это означает, что яркость частиц, захваченных этой плоскостью, будет неравномерной. Будем считать, что частица может располагаться в любом месте поперечного сечения плоскости с равной вероятностью.
Итак, изменение амплитуды поля в пучке в любом поперечном сечении описывается гауссовой кривой [1]:
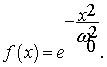 (4)
(4)
где ω0 – минимальный радиус пучка, так называемый радиус в перетяжке. Однако для простоты выкладок удобнее перейти к нормированной форме:
Так как реально размеры пучка ограничены, не имеет смысла рассматривать бесконечные «хвосты» гауссовой кривой. Будем считать, что в световой плоскости сосредоточено четыре среднеквадратичных отклонения. Значение функции (5) на границе обозначим а = f(4).
Как уже говорилось, частица с равной вероятностью может занимать любую точку в пределах световой плоскости:
Общая формула для функциональных преобразований случайных величин для немонотонных преобразующих функций типа (5) [6]:
где 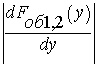 –
якобиан преобразования.
–
якобиан преобразования.
Для начала необходимо найти обратную к f(x) функцию Fоб1,2(y):
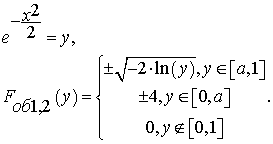 (8)
(8)
Теперь следует заняться поиском Якобиана преобразования. Найдем производную обратной функции:
Подставив (9) и (6) в (7), получим выражение для плотности вероятности распределения яркости частиц в картинах визуализации потоков:
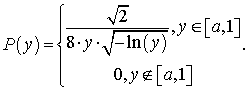 (10)
(10)
Вид плотности распределения показан на рисунке 2:
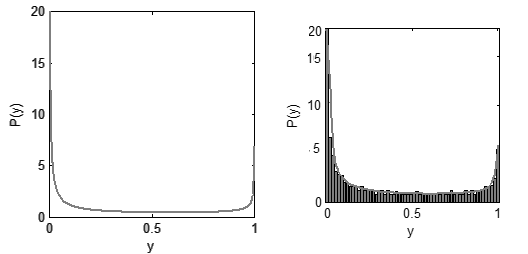
Рисунок 2. Плотность вероятностей (слева) и
гистограмма (справа) распределения яркости на картинах визуализации потоков
Также на рисунке 2 показа гистограмма распределения яркости на смоделированных изображениях, которая подтверждает теоретические выкладки.
Осталось сказать несколько слов о распределении размеров частиц и их координат. Размер частиц в среднем постоянен, имеет лишь небольшие случайные отклонения. В данной работе считалось, что они распределены по нормальному закону. Распределение координат частиц сильно зависит от исследуемого потока. Никаких априорных данных о нем нет. Поэтому приходится задавать случайное распределение по равномерному закону, а затем запускать программу расчета координат частиц в исследуемом векторном поле и ждать, пока поле скоростей промодулирует распределение частиц в потоке.
Нестационарная модель потока
Уравнения Навье-Стокса – система дифференциальных уравнений в частных производных, описывающая движение вязкой Ньютоновской жидкости и газов [7]. Уравнения Навье-Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навье и британского математика Джорджа Стокса.
Запишем данные уравнения в компактной векторной форме [8]:
где u – вектор скорости, t – время, ρ – плотность частиц дыма, ν – вязкость, k – диффузионный параметр и f и S – внешние источники. Второе уравнение в (11) описывает поведение плотности частиц дыма в векторном поле.
Уравнения (11) описывают поведение векторного поля потока во времени. Однако их решение сопровождается значительными вычислительными затратами. Поэтому вместо непосредственного решения данных уравнений предлагается моделировать процессы, описанные в нем [8].
Отметим, что уравнения (11) структурно схожи, однако второе уравнение линейное, поэтому проще начинать разработку методов моделирования с него.
Опишем слагаемые, входящие в уравнения. Первые члены описывают адвекцию векторного поля (движения векторного поля вдоль самого себя) и движение плотности вдоль векторного поля соответственно. Вторые члены описывают потери из-за вязкости потока и диффузии плотности соответственно. Третьи члены описывают внешние источники.
Итак, начнем решение с уравнения для плотности. В методах моделирования есть два больших класса. Методы на регулярной сетке и методы, основанные на изменяющейся сетке. Рассматриваемый в данной статье алгоритм основан на регулярной сетке. В центре каждого элемента сетки содержится значение вектора скорости и плотности. Т.е., на практике мы имеем два массива: массив векторов и массив плотности. В данной работе рассматривается двумерные массивы, однако ничто не мешает расширить данный алгоритм на трехмерный случай.
Вследствие диффузии плотность начинает распространяться по сетке. С одной стороны, значение в ячейке уменьшается за счет ухода в соседние, с другой – увеличивается за счет пополнения из соседних ячеек. Схематично это представлено на рисунке 3:
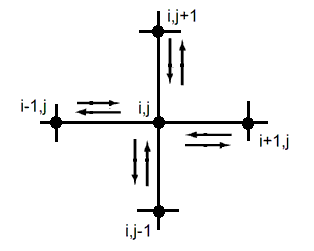
Рисунок 3. Распространение и обмен
плотностью (диффузия)
Следующий шаг – расчет смещения плотности вдоль векторного поля. Как уже упоминалось, значения плотности находится в центре ячейки. Так что остается только подвинуть значение плотности на соответствующий вектор. Однако при таком подходе мы получим нецелые новые координаты, которые мы не можем использовать в качестве индексов массива. Преобразование данных координат в координаты ячейки массива – процесс очень сложный и неоднозначный. Поэтому воспользуемся другим подходом. Пройдем назад во времени и найдем координаты тех частиц, которые на новом шаге попадут точно в центры ячеек массива. Затем интерполируем значение плотности в эти координаты и получим новое значение в текущей ячейке. Это иллюстрируется рисунком 4:
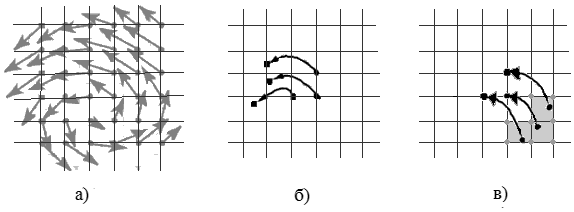
Рисунок 4. Смещение плотности в векторном поле. а) и
б) прямой перенос и нецелые координаты, в) – обратный ход и интерполяция по
ближайшим соседям
После создания алгоритма для движения плотности, его можно применять и для расчета движения векторного поля, так как структурно уравнения очень похожи. Есть только одно изменение. Необходимо учесть сохранение массы и не сжимаемость жидкости. Для этого воспользуемся одним математическим результатом, называемым декомпозицией Ходжа: любое векторное поле представляет собой сумму градиентного поля и поля, сохраняющего массу [8]. Поэтому необходимо вычислить градиент полученного векторного поля и вычесть его для получения итогового поля. Примеры работы алгоритма показаны на рисунке 5:
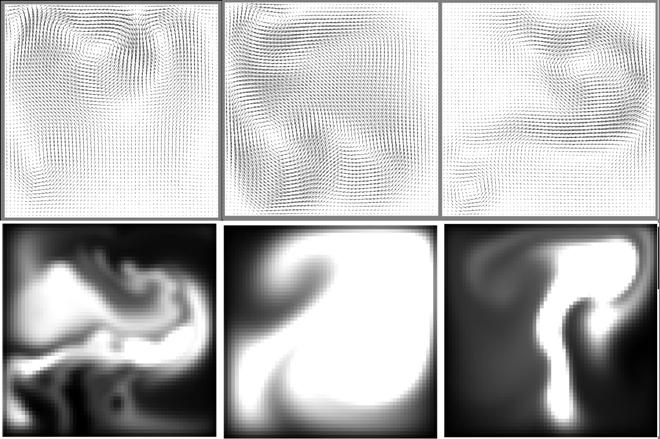
Рисунок 5. Смоделированные векторные поля (сверху) и движение плотности дыма в векторном поле (снизу)
Следующий шаг –
внедрение в алгоритм граничных условий. Будем использовать самые простые
граничные условия – гладкие твердые стены. Это означает, при воздействии на
такой объект по третьему закону Ньютона возникает противодействующая сила такой
же амплитуды. Поэтому для начала необходимо найти все пиксели границы и
построить вектор нормали на них. А в алгоритм добавить нахождение проекции
вектора на вектор границы и построение противоположного направленного вектора.
Данный подход показан на рисунке 6 (справа):
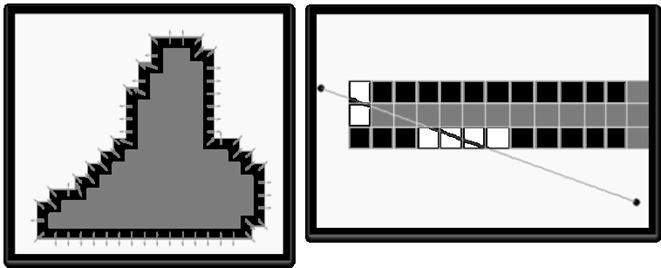
Рисунок 6. Расчет граничных условий (слева, серые пиксели – объект, черные – граница объекта) и расчет движения частиц с учетом граничных условий (справа, серые пиксели – объект, черные – граница объекта, прозрачные – пиксели, которые пересекает частица)
Последний шаг – расчет
движения трассеров в векторном поле. При моделировании движения частицы
задается время между двумя ее положениями. Данное время умножается на вектор
скорости в точки расположения частицы и таким образом получается следующее ее
положение. При таком подходе при больших локальных скоростях либо при больших
временных интервалах между этапами моделирования возникает опасность перехода
частицы на другие линии тока. Чтобы избежать данной проблемы, необходимо
разбивать временной интервал на части (в зависимости от локальных скоростей) и
на каждом подинтервале моделировать движение частицы описанным выше образом
(моделируя плавное движение частицы между двумя ее положениями). Кроме того,
необходимо учесть наличие границ, которые частицы не могут пересекать. Для
этого между двумя итоговыми положениями частиц проводится прямая линия. И если
данная прямая пересекает границы объекта, то траекторию необходимо
соответствующим образом скорректировать.
Заключение
Разработана и реализована компьютерная модель картин визуализации потоков. Данная модель обобщает известные сведения о работе ПЗС-матриц, форме частиц на изображении и выведенной авторами плотности вероятностей распределения яркости частиц по кадру. Кроме того, на основе известного алгоритма моделирования уравнений Навье-Стокса, в который авторы добавили учет граничных условий произвольной формы и расчет траекторий частиц, разработана и реализована нестационарная модель потока. Данные модели можно использовать для исследования работы алгоритмов PIV- и PTV-анализа, а также для получения начальных сведений о векторном поле экспериментального потока.
1. Ринкевичюс Б. С. Лазерная диагностика потоков / Под ред. В. А. Фабриканта. М.: Изд-во МЭИ, 1990.
2. Raffe M, Willert C. E., Wereley S. T., Kompenhans J. Particle Image Velocimetry: A Practical Guide, Second Edition / Berlin Heidelberg New York, Springer 2007.
3. Яне Б. Цифровая обработка изображений. М.: Изд-во Техносфера, 2007.
4. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MatLab. М.: Изд-во Техносфера, 2006.
5. Marxen M., Sullivan P. E., Loewen M. R. Johne. Comparison of Gaussian particle center estimators and the achievable measurement density for particle tracking velocimetry // Experiments in Fluids – Vol. 29 – pp. 145-153, 2000.
6. Баскаков С. И. Радиотехнические цепи и сигналы. М.: Изд-во Высшая школа, 2000.
7. Загузов И. С., Поляков К. А. Математическое моделирование течений вязкой жидкости вблизи твердых поверхностей. Самара: Самарский университет, 1999.
8. Stam J. Stable Fluids. Proceed of SIGGRAPH 99 Conference, Annual Conference Series, August 1999, p. 121-128.