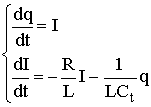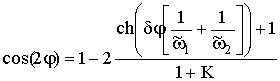УДК 534...537
УСТОЙЧИВОСТЬ ЛИНЕЙНОГО ПАРАМЕТРИЧЕСКОГО ОСЦИЛЛЯТОРА С ДИССИПАЦИЕЙ
А. В. Боловин
МНКП “ВЕСТА”, Днепропетровск,
Украина
Статья получена 7 декабря 2014 г.
Аннотация. В рамках модели Мейснера рассматривается влияние диссипации на параметрическое возбуждение линейной системы. Получены уравнения для переходных кривых и порога затухания параметрических колебаний в линейном осцилляторе. Развитый в настоящей работе подход непосредственно переносится на соответствующие задачи теории распространения волн в пространственно модулированных структурах.
Ключевые слова: параметрический резонанс, модель Мейснера, матрица трансляции, теорема Флоке, устойчивость решений, переходные кривые, порог затухания.
Abstract. Influence of dissipation on the parametric excitation of a linear system is considered in the framework of the Meissner model. Equation transition curves and attenuation threshold were obtained for parametric oscillations in a linear oscillator. Developed in this paper an approach is directly applicable to the corresponding problem in the theory of wave propagation in spatially modulated structures.
Key words: parametric resonance, model Meissner, translation matrix, Floquet theorem, stability of solutions, transition curves, threshold attenuation.
При исследовании систем с периодическими коэффициентами, как правило, опираются на результаты, полученные в рамках двух стандартных моделей параметрического возбуждения: гармонической и кусочно-постоянной. В первом случае говорят об уравнении Матье [1,2], во втором - об анализе модели Мейснера [3-10]. Одним из центральных результатов и того и другого исследования является определение областей неустойчивости и построение переходных кривых соответствующих определенному типу периодических решений. Несмотря на обширную литературу, посвященную вопросам устойчивости, влияние диссипации на поведение параметрически возбуждаемых систем остается исследованным недостаточно.
Целью настоящей работы является получение в аналитическом виде уравнений переходных кривых для анализа в рамках модели Мейснера спектра возникающих в диссипативной системе колебаний.
Простая модель периодической системы, предложенная Мейснером, используется для анализа распространения волн в пространственно - периодических системах [6,7], её квантово-механический аналог - модель Кронига-Пенни (или решетка Дирака) для модельных расчетов в задаче Блоха [8], а в теории колебаний соответствует импульсной накачке параметрической системы [9,10]. Удобство аналитического и численного исследования в рамках модели Мейснера заключается в представлении определяющих решение периодических функций, в виде набора кусочно-постоянных функций, допускающих на отдельных интервалах изменения независимой переменной, аналитическое построение полной системы линейно независимых решений, с последующим сшиванием на границе интервалов.
Дифференциальные уравнения простейшей параметрической системы - контура с периодически изменяющейся емкостью имеют вид:
В рамках модели Мейснера, любое решение системы (1) удовлетворяет обыкновенному дифференциальному уравнению второго порядка
где коэффициент затухания ![]() , а собственная “частота”
, а собственная “частота” ![]() определяется модулированным с периодом
определяется модулированным с периодом ![]() значением емкости
значением емкости
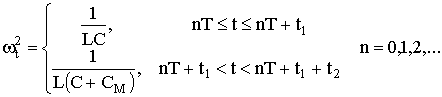 (3)
(3)
Интервалы времени ![]() и
и ![]() , на
которых значение частоты постоянно и равно соответственно
, на
которых значение частоты постоянно и равно соответственно ![]() и
и ![]() , образуют
полный период импульсной накачки
, образуют
полный период импульсной накачки ![]() .
.
В случае отсутствия в
системе диссипации, при ![]() , области
неустойчивости решений уравнения (2) определяются неравенством
, области
неустойчивости решений уравнения (2) определяются неравенством
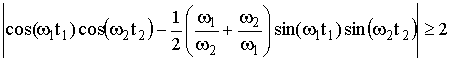 (4)
(4)
Это условие является следствием теоремы Флоке и может быть получено непосредственно из матрицы трансляции, метод построения которой, хорошо известен для модели Мейснера [3]. Случай равенства в выражении (4) соответствует решениям с периодом равным периоду коэффициента, т.е. собственно периодическим и, тем решениям, период которых вдвое больше, так называемым антипериодическим.
Для определения границ областей неустойчивости при наличии диссипации воспользуемся следующей простой схемой. Решение уравнения (2) удовлетворяет системе двух линейных дифференциальных уравнений
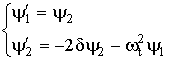 (5)
(5)
или в матричной форме
![]() (6)
(6)
где ![]() – квадратная
– квадратная
![]() - периодическая матрица коэффициентов,
- периодическая матрица коэффициентов, ![]() - вектор-столбец решений с компонентами
- вектор-столбец решений с компонентами ![]() . Для системы (6) теорема Флоке приводит к
матричной задаче на собственные значения
. Для системы (6) теорема Флоке приводит к
матричной задаче на собственные значения
![]() (7)
(7)
где ![]() -
постоянная матрица, называемая матрицей трансляции, а ее собственные числа
-
постоянная матрица, называемая матрицей трансляции, а ее собственные числа ![]() - мультипликаторы (множители Флоке)
уравнения (6). Запишем характеристическое уравнение
- мультипликаторы (множители Флоке)
уравнения (6). Запишем характеристическое уравнение ![]() матричной
задачи (7) в развернутом виде
матричной
задачи (7) в развернутом виде
![]() (8)
(8)
Равенство единице хотя бы одного из мультипликаторов
в уравнении (8) означает наличие периодического решения периода ![]() системы (6). Если имеется мультипликатор
системы (6). Если имеется мультипликатор ![]() , то это означает существование
антипериодического решения (6) периода 2
, то это означает существование
антипериодического решения (6) периода 2![]() , т.е.
решения, для которого
, т.е.
решения, для которого ![]() . Таким образом, равенство
. Таким образом, равенство ![]() определяет следующее из (8) условие
существования стационарных решений
определяет следующее из (8) условие
существования стационарных решений
Детерминант матрицы трансляции определим по формуле Лиувилля-Якоби
![]() , (10)
, (10)
где ![]() - след
оператора
- след
оператора ![]() . Непосредственно из (10) для системы (6)
имеем:
. Непосредственно из (10) для системы (6)
имеем:
Фундаментальная система решений уравнения (2) для двух последовательных интервалов времени, составляющих период накачки T, имеет вид:
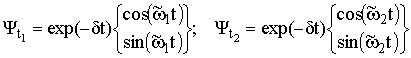 , (12)
, (12)
где ![]() .
. ![]() .
.
Построим фундаментальную матрицу решений для уравнения (2)
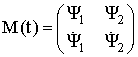 (13)
(13)
Тогда для матрицы Коши уравнения (2) получим
![]() (14)
(14)
Наконец матрица трансляции
![]() , (15)
, (15)
след которой выпишем в развернутом виде
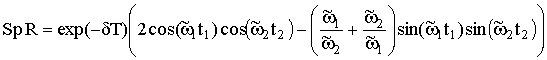 (16)
(16)
Подставим выражения (11) и (16) в уравнение (9) и получим условие существования стационарных решений при наличии диссипации
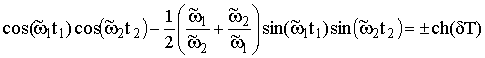 (17)
(17)
Знак плюс в правой части
равенства (17) соответствует периодическим, минус – антипериодическим решениям
уравнения (2). Переходя в (17) к фазовым переменным: ![]() ,
, ![]() , после
элементарные тригонометрические преобразования, получим следующее
характеристическое уравнение:
, после
элементарные тригонометрические преобразования, получим следующее
характеристическое уравнение:
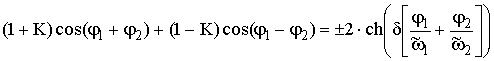 (18)
(18)
где
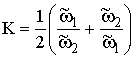 .
.
Выражение (18) является уравнением границ четных (знак плюс) и нечетных (знак минус) областей неустойчивости (рис.1) и определяет периодические и антипериодические решения уравнения (2).
Нечетным областям неустойчивости соответствует условие
![]() , (19)
, (19)
Четным областям отвечает условие
![]() (20)
(20)
В случае, когда фаза колебаний на
каждом интервале модуляции изменяется на одну и ту же величину ![]() , вместо четных областей неустойчивости имеют место почти периодические
решения с убывающей амплитудой (при
, вместо четных областей неустойчивости имеют место почти периодические
решения с убывающей амплитудой (при ![]() ), а характеристическое уравнение для границ нечетных
областей примет вид:
), а характеристическое уравнение для границ нечетных
областей примет вид:
Порог затухания ![]() , возникающий при наличии в системе
диссипации, задает условие развития параметрической неустойчивости в нечетных областях
, возникающий при наличии в системе
диссипации, задает условие развития параметрической неустойчивости в нечетных областях
![]() и, может быть получен из уравнения:
и, может быть получен из уравнения:
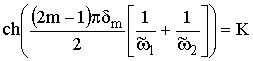 (22)
(22)
Чтобы оценить ширину области неустойчивости, ограничимся двумя членами разложения гармонической функции в правой части выражения (22), решая уравнение относительно фазовой переменной, получим
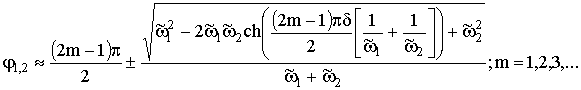 (23)
(23)
Видно, что с ростом
номера зоны и постоянной затухания ширина области неустойчивости ![]() уменьшается. В предельном случае при
уменьшается. В предельном случае при ![]() ширина зоны остается постоянной для всех
нечетных областей:
ширина зоны остается постоянной для всех
нечетных областей:
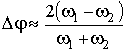 (24)
(24)
На рис.1 в плоскости
фазовых переменных ![]() построены переходные кривые,
ограничивающие первую нечетную область неустойчивости в случае трех различных
коэффициентов затухания:
построены переходные кривые,
ограничивающие первую нечетную область неустойчивости в случае трех различных
коэффициентов затухания: ![]() . Прямая
. Прямая ![]() пересекает переходные кривые в точках,
удовлетворяющих уравнению (21).
пересекает переходные кривые в точках,
удовлетворяющих уравнению (21).
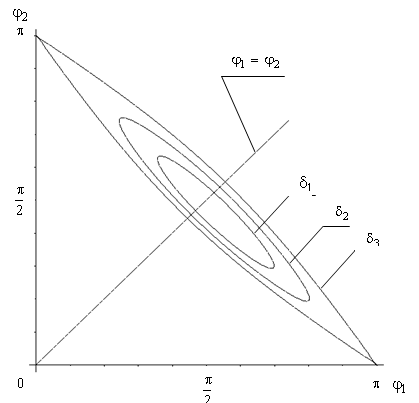
Рис.1. Переходные кривые для трех значений
коэффициента затухания ![]()
В силу существующих динамических аналогий между системами различной физической природы, основанной на формальном сходстве дифференциальных уравнений, описывающих колебательные движения этих систем, выводы, полученные путем исследования исходной системы (1) в рамках выбранной модели модуляции параметра, легко могут быть распространены на динамически аналогичные системы той же или иной природы.
Литература
1. Справочник по специальным функциям. Под. ред. М.Абрамовица и И. Стиган. М.Наука. 1979. 832с.
2. Уиттекер Э.Т., Ватсон Дж.Н. Курс современного анализа, т.2.-М.:Физматгиз, 1964 - 516с.
3. Якубович В.А., Старжинский Г.М. Параметрический резонанс в линейных системах. - М.: Наука, 1987 - 328с.
4. Шмидт Г. Параметрические колебания. - М.: Мир, 1978 - 336с.
5. Займан Дж. Принципы теории твердого тела. - М.: Мир, 1974 - 472с.
6. Ярив А., Юх П. Оптические волны в кристаллах. - М.: Мир, 1987 - 616с.
7. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. - М.: Наука, 1979 - 384с.
8. Займан Дж. Модели беспорядка. Пер. с анг. - М.: Мир, 1982 - 592с.
9. Чечулин С.Л. Параметрические колебания и устойчивость периодического движения. - Л.: Изд-во ЛГУ. 1983 - 220с.
10.Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.М. Основы теории колебаний. - М.: Наука, 1978. - 392с.