Стохастическая интерполяция пеленга в адаптивных антенных решетках с последовательным диаграммо-образованием на базе усечённых (малоэлементных) апертур и робастных статистик сигнала на входе
Ю. Н. Горбунов
Институт радиотехники и электроники им. В.А. Котельникова РАН, Москва, Фрязинский филиал
Московский государственный технический университет радиотехники, электроники и автоматики (МГТУ МИРЭА)
Статья получена 10 декабря 2014 г.
Аннотация. Анализируется построение системы обработки и формирования сигналов РЛС для космических аппаратов, в которых учитываются технические аппаратурные ограничения и ограничения ресурсов цифровой обработки. Заданная эффективность может быть достигнута использованием упрощенных процедур обработки пространственно-временных сигналов с использованием стохастической интерполяции пеленга в адаптивных антенных решетках. Для реализации этого применяется последовательное диаграммо-образование на базе усечённых (малоэлементных) апертур и робастных статистик сигнала на входе грубых («булевых», «бинарно-знаковых») отсчетов сигнала. Это особенно актуально для реализации аппаратуры РЛС в условиях ограничений по аппаратным и вычислительным ресурсам, массо-габаритным ограничениям, ограничениям по разрядности, энергопотенциалу и стоимости. Для достижения преимуществ предлагается нетрадиционный подход, предполагающий в процессе адаптивного формирования результирующей многолучевой (многосегментной) диаграммы направленности фазированной антенной решетки осуществлять поэтапную стохастическую модуляцию положения фазового центра путём активизации малого числа передающих слабонаправленных элементов и использования грубых (малоразрядных) текущих отсчетов входных сигналов.
Ключевые слова: последовательное диаграммо-образование, рандомизация, стохастическая интерполяция, грубые отсчёты, малоразмерные выборки, инструментальная точность.
Abstract. We analyze the construction of a system of radar signal processing and generation for satellites, which takes into account the technical limitations and instrumental resource limitations of digital processing. The desired effectiveness can be obtained by using simplified procedures for processing of spatio-temporal signals using the stochastic interpolation of bearing in adaptive antenna arrays. Sequence beam formation on the basis of truncated (small element) apertures and robust statistics at the input of coarse ("Boolean", "binary-iconic") signal samples is used. This is especially actually for the implementation of radar equipment in conditions of constraints of hardware and computing resources, weight and size restrictions, restrictions on word length, energy potential and cost. To achieve the advantages a non-traditional approach is proposed: to implement a stochastic modulation of phase center position by activation of a small number of transmit elements and to use omnidirectional coarse (low-bit) of the current sample of the input signals.
Keywords: sequence beam formation, randomization, stochastic interpolation, rough readings, small-sized samples, the instrumental precision.
Введение. Построение современных РЛС для предотвращения угрозы столкновения космических аппаратов (КА) с технологическими объектами (ТО) должно учитывать технические аппаратурные ограничения и ограничения ресурсов цифровой обработки. Шумы квантования и округления, стробоскопические и интерференционные эффекты дискретной и цифровой малоразрядной обработки («слепые скорости», «слепые направления»), эффекты наложения окон, нелинейности, боковые лепестки не позволяют напрямую снять ограничения по достижимым пределам потенциальной точности измерения пеленга, т.к. обычным путем эти эффекты не устраняются. Прямой путь приведения в соответствие потенциальной и инструментальной точности приводит к увеличению разрядности АЦП, повышению частот пространственной и временной дискретизации, увеличения размерности окон.
В статье показывается, что заданная эффективность может быть достигнута использованием упрощенных процедур обработки пространственно-временных сигналов с использованием стохастической интерполяции пеленга в адаптивных антенных решетках с последовательным диаграммо-образованием на базе усечённых (малоэлементных) апертур и рандомизации робастных статистик сигнала на входе грубых («булевых», «бинарно-знаковых») отсчетов и т.п.
В работах [1-3] и других российских и зарубежных авторов исследованы вопросы анализа и синтеза адаптивных фазированных антенных решеток (ФАР), однако специальные разделы, относящиеся к повышению инструментальной точности измерения пеленга за счет стохастической интерполяции в антенных решетках с малым числом элементов и грубыми робастными статистиками сигнала в них не исследованы.
Малоразрядной
(малоэлементной) цифровой обработке (ЦО) посвящена работа [4], где сказано, что
разрядность РЛ данных напрямую определяет сложность аппаратуры (фазовращатели
ФВ, умножители, процессоры, нормализаторы задержек, интерфейсы). Это особенно
ощутимо в современных РЛС с ФАР, где система ЦО представляет собой разветвленную
сеть АЦП, ФВ и цифровых сигнальных процессоров (DSP) при числе элементов ФАР достигающим 10![]() - 10
- 10![]() . Таким образом, при прочих условиях,
необходимо учитывать аппаратурные, энергетические, массо-габаритные и ресурсные
(разрядность, частоты квантования, размеры окон ПВ выборок) ограничения, что
особенно важно для современных бортовых авиационных и космических РЛС.
. Таким образом, при прочих условиях,
необходимо учитывать аппаратурные, энергетические, массо-габаритные и ресурсные
(разрядность, частоты квантования, размеры окон ПВ выборок) ограничения, что
особенно важно для современных бортовых авиационных и космических РЛС.
Применительно к измерению пеленга в [4] эти вопросы также не решены.
Постановки задачи. Применительно к рассматриваемой задаче, преследуя цели стохастической интерполяции (СИ) пеленга, расширим номенклатуру неинформативных параметров, подмешиванием на входе квадратурного АЦП случайного напряжения с постоянным законом распределения.
Общий подход к синтезу оптимальных алгоритмов обнаружения сигналов, содержащих случайные неинформативные параметры, сформулируем для наиболее простой задачи оптимального обнаружения гармонического сигнала, когда искусственно вводимые неинформативные параметры случайны, а их законы распределения вероятностей известны. В этих случаях отношение правдоподобия, при каждом конкретном значении параметра рассматривается как условное, а безусловное отношение правдоподобия получается путем усреднения по случайным параметрам. В общем случае, пусть есть вектор неинформативных случайных параметров bТ =(b1,b2,…,bn) и с известной совместной плотностью вероятностей w(b) = w(b1, b2,…, bn).
Дальнейшее обобщение связано с увеличением размерности bТ =(b1,b2,…,bn) с n до n + r с известной совместной плотностью вероятностей w(b) = w(b1, b2,…, b n + r). Особенность решения данной задачи связана с реализацией возможностей использования «грубых статистик» (ГС или rough statistics RS) рандомизированной цифровой обработки RmDP - RS параметров b n + r. Искусственно вводимые неинформативные параметры – это рандомизирующие учитываемые шумовые добавки в квадратурах входных сигналов.
На Рис. 1 ![]() - показана апертура антенны на плоскости
- показана апертура антенны на плоскости ![]() ,
, ![]() - вектор направления прихода
электромагнитного излучения.
- вектор направления прихода
электромагнитного излучения.
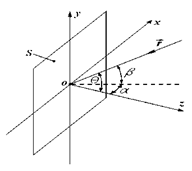
Рис. 1. Взаимосвязь угловых параметров прихода электромагнитной волны с координатами апертуры ФАР
В рассматриваемой задаче
пеленг цели q = q(a, b)
для направления на источник излучения с азимута a и угла места b будем считать постоянным. В плоско-волновом приближении
волна, падающая на апертуру ФАР под углом (пеленгом) ![]() от
оси антенны формирует поле, описываемое пространственными частотами:
от
оси антенны формирует поле, описываемое пространственными частотами:
где ![]() длина
волны,
длина
волны, ![]() - пеленг, являющийся функцией азимута
- пеленг, являющийся функцией азимута ![]() и угла места
и угла места ![]() прихода
электромагнитной волны.
прихода
электромагнитной волны.
Пространственная частота W по аналогии с обычной
(«временной» Ю. Г.) частотой определяется как скорость изменения фазы, в
данном случае по осям x, y. В отличие от обычной обработки сигналов во временной
области, когда мы имели дело с частотой ![]() , здесь
пространственные частоты
, здесь
пространственные частоты ![]() ,
, ![]() является функциями азимута
является функциями азимута ![]() и угла места
и угла места ![]() соответственно.
соответственно.
Поскольку изменением пеленга за время пачки N импульсов, следующих с периодом Т, можно пренебречь, инструментальную погрешность измерения пеленга можно уменьшать за счет рандомизированной обработки [4].
По условиям решения задачи предполагается, что исходная статистика пеленга изначально является грубой «бинарно-знаковой», а при выполнении условий сходимости в методе Монте - Карло эмпирических распределений к теоретическим становится информативной.
Классическая схема рандомизированной обработки предполагает формирование в устройстве обработки случайной величины, либо совокупности случайных величин, параметры распределения которых связаны с оцениваемыми параметрами. При такой обработке за счет «стохастической интерполяции» преобразуемых параметров внутрь «грубого» дискрета (кванта) ЦО: реализуется возможность уменьшения шумов квантования.
Рандомизация (randome - случайный) предполагает искусственное введение случайностей в параметры сигналов и устройств обработки: фазы шкал квантования (измерения), пороги квантования, аддитивные (учитываемые) добавки, весовые коэффициенты ЦФ и др.
Из-за наличия элементов случайности и худших результатов классификации по сравнению с байесовским правилом использовать рандомизированные решающие правила на первый взгляд не имеет смысла. Однако данное правило и подобные ему представляют значительный интерес при переходе к малоразрядной и малоэлементной обработке.
Теоретической основой метода рандомизации является метод Монте-Карло, предполагающего моделирование некоторой случайной величины параметры распределения которой связаны с измеряемой величиной.
Если N достаточно велико, то за счет обработки серии отсчетов представляется возможным уменьшить относительный уровень шумов квантования на выходе процессора цифровой обработки.
Почти всегда имеет место естественная рандомизация за счет собственного шума приемника, однако статистические характеристики входного шума не всегда могут обеспечить гарантированную скорость сходимости измерений.
После того, как случайный механизм создан, обеспечена имитация случайной величины, задача заключается в получении заданного закона ее распределении. Таким образом, указанная задача является типичной для математической статистики. Наиболее распространенной при этом является задача оценки математического ожидания случайной величины. В математическом отношении это эквивалентно вычислению интеграла Лебега по некоторой (конструктивной) вероятностной мере. Вероятностная мера задается естественным образом (естественная рандомизация), однако при этом, как указывалось ранее, не гарантируется сходимость измерений. Гарантия конструктивного задания меры обеспечивается стабильностью характеристик цифрового генератора шума, методы аппаратурной реализации которых в настоящее время хорошо развиты.
Интерполяции пеленга q(a, b)
сводится к косвенному уточнению интерполирующей величины ![]() и связанной с ней вероятностью p=
и связанной с ней вероятностью p=![]() /Δ,
где
/Δ,
где ![]() - ошибка квантования;
- ошибка квантования; ![]() - элемент дискретности, шаг
квантования.
- элемент дискретности, шаг
квантования.
Таким образом, зачастую речь
идет об измерении обобщенного параметра (остатка) ![]() методом
статистических испытаний с использованием грубой статистики
методом
статистических испытаний с использованием грубой статистики ![]() .
.
В многоразрядных
ситуациях «целая» часть измерений является константой, а ее младший разряд
«флюктуирует» также, как и величина ![]() , только на меньшем
интервале (в своей зоне). Случайность является естественной (шум приемника) и
искусственной – шум рандомизации.
, только на меньшем
интервале (в своей зоне). Случайность является естественной (шум приемника) и
искусственной – шум рандомизации.
Решаемой в статье задачей является разработка способа адаптивного диаграммо-образования ФАР в условиях использования бинарно-знаковой статистики входных сигналов и оценка прироста коэффициента направленного действия (коэффициента улучшения) и динамического диапазона ФАР в результате применения рандомизированных алгоритмов.
Формирование грубой
статистики и синтезирование «узких» лучей. Виды естественного приращения стохастичности,
связанного с наличием собственных тепловых шумов приемника, проявляются на
выходе амплитудного (АД) и фазового детектора (ФД) одного элемента ФАР в виде
распределений Релея и Гаусса (нормального) соответственно (см. Рис.
2).
Статистику наблюдений входного сигнала в условиях рандомизации приема назовем
«грубой» (ГС), если она обладает бинарными свойствами, т.е. для единичной ПВ
выборки имеет «грубые» µ = ![]() для АД или µ =
для АД или µ = ![]() для ФД.
для ФД.
В первом случае µ = ![]() - есть результат пороговой обработки,
т.е. сравнения напряжения u(t) c порогом
бинарного квантования, а во втором случае для каждой квадратурной компоненты
входного сигнала u(t)- имеем непараметрическую робастную (бинарно-знаковую) µ =
- есть результат пороговой обработки,
т.е. сравнения напряжения u(t) c порогом
бинарного квантования, а во втором случае для каждой квадратурной компоненты
входного сигнала u(t)- имеем непараметрическую робастную (бинарно-знаковую) µ = ![]() . Непараметрическая статистика µ =
. Непараметрическая статистика µ = ![]() также может быть образована при
сравнении двух отсчетов напряжения u(t), взятых в различные моменты времени на выходе АД. Такую статистику в
зарубежной литературе называют статистикой Манна -Уитни [7].
также может быть образована при
сравнении двух отсчетов напряжения u(t), взятых в различные моменты времени на выходе АД. Такую статистику в
зарубежной литературе называют статистикой Манна -Уитни [7].
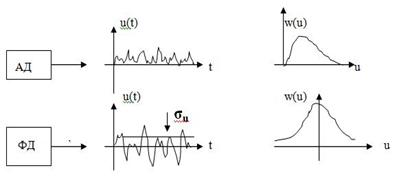
Рис.2. Сигналы на выходе детекторов
Виды естественного приращения
стохастичности, связанного с наличием собственных тепловых шумов приемника,
проявляются на выходе амплитудного (АД) и фазового детектора (ФД) одного
элемента ФАР в виде распределений Релея и Гаусса (нормального) соответственно.
Статистику наблюдений входного сигнала в условиях рандомизации приема мы
назвали ГС, т.к. она обладает бинарными свойствами, т.е. для единичной пространственно-временной
(ПВ) выборки имеет «грубые» µ = ![]() для АД или µ =
для АД или µ = ![]() для ФД, но в дальнейшем сглаживается
(усредняется).
для ФД, но в дальнейшем сглаживается
(усредняется).
В первом случае µ = ![]() - есть результат пороговой обработки,
т.е. сравнения напряжения u(t) c порогом
бинарного квантования, а во втором случае для каждой квадратурной компоненты
входного сигнала u(t)- имеем непараметрическую робастную (бинарно-знаковую) µ =
- есть результат пороговой обработки,
т.е. сравнения напряжения u(t) c порогом
бинарного квантования, а во втором случае для каждой квадратурной компоненты
входного сигнала u(t)- имеем непараметрическую робастную (бинарно-знаковую) µ = ![]() статистику.
статистику.
Применительно к задаче измерения пеленга на Рис. 3 представлена схема формирования квадратурных составляющих сигнала, в которой на квадратурные входы подмешаны шумовые хаотические напряжения x с нулевым средним. Искуственный фазовый джиттер (дрожжание) рандомизирует отсчеты фазы пространственных частот (1) и, таким образом к стохастической интерполяции отсчётов пеленга, который считается постоянным в пределах анализируемой ПВ выборки. Это является эквивалентным стохастической модуляции положения фазового центра на приём – передачу.
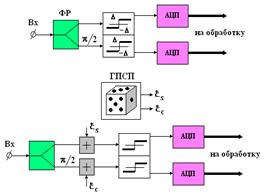
Рис. 3. Схема формирования грубых отсчетов с рандомизацией бинарно - знаковой статистики
Для формирования
статистики грубого квантования пространственных частот (1) можно использовать
малоэлементные апертуры пространственного квантования. Далее в качестве
элементарной ячейки возьмем известную схему «бабочка» алгоритма 2-х точечного
пространственного быстрого преобразования Фурье (БПФ), реализующего на своих
выходах суммарно-разностную обработку. Таких схем нужно взять две: на каждую
угловую координату a
или b - всего 4 элемента («крест»). Для
реализации достаточности измерения пеленга ![]() по
меньшей мере нужно задействовать 3 приемных элементов ФАР, образующих
равносторонний «треугольник». Полученную группу элементов ФАР, состоящую из 4
или 3 элементов, в дальнейшем будем называть сегментом апертуры ФАР.
по
меньшей мере нужно задействовать 3 приемных элементов ФАР, образующих
равносторонний «треугольник». Полученную группу элементов ФАР, состоящую из 4
или 3 элементов, в дальнейшем будем называть сегментом апертуры ФАР.
Данный сегмент, состоящий из 3-4 элементов ФАР, активизируется на «приём – передачу» и имеет 3 или 4 развернутых друг относительно друга пересекающихся по уровню 0.707 «расширенных» луча, соответственно. Положение сегмента на апертуре ФАР задаётся случайным образом, что обусловлено дополнительным требованием иметь взаимную корреляционную функцию зондирующей последовательности в форме тела с круговой симметрией.
Синтезирование «узких» ДН
ФАР осуществляется путем последовательного когерентного суммирования
парциальных лучей в пространстве на передачу, и - путем последовательного
суммирования отсчетов поля ЭМИ во времени на прием. В основе предложения лежит
идея многопозиционной радиолокации [5] и её частного случая многоканальных РЛС:
так называемые MIMO (multiple input- multiple output – «много
входов – много выходов») РЛС «с неразнесёнными антеннами». Снижение мощности
зондирующего сигнала на цели из-за расширения передающего луча компенсируется
увеличением времени наблюдения цели. В задаче цифрового измерения пеленга
полный ресурс обрабатываемых ПВ отсчетов определяется размером выборки равным NxКxМ, где N –
размер временной выборки, К – число сегментов ФАР по оси x, отвечающей за азимут a, а М – число сегментов ФАР по оси y, отвечающей за угол места b, КxМ – размер результирующей пространственной выборки
полномасштабной решетки Рэйли. Прореженная решетка в виде креста Миллса при М =
К имеет размер 2К(М). Для малоэлементной ФАР в виде одного сегмента КxМ =4. В отличие от аналога –
французской РЛС RIAS (1984 г.),
где все элементы передающей решетки излучали одновременно взаимно ортогональные
сигналы, смещенные по частоте и поэтому, как и в обычных ФАР требовалась
большая суммарная пиковая мощность передатчика, в рассматриваемой системе
многочастотный сигнал может быть сформирован последовательно, либо –
использована одна частота, в результате чего резко упрощается аппаратурная
реализация системы системы. Синтезируемая апертура формируется виртуально в
процессоре обработки. В обычной РЛС последовательный обзор заданного сектора
осуществляется узким лучом. В рассматриваемой системе передающие лучи
последовательно накладываются в процессе синтеза апертуры, покрывая общий
сектор. Частотно-временное распределение ресурса при использовании преимуществ
время-импульсной модуляции и СШП радиолокации приводит к необходимости
применения квазинепрерывных шумовых сигналов в качестве несущих хаотических
колебаний, имеющих базу ![]() Аппаратурные упрощения связаны с
уменьшением разрядности промежуточных РЛ данных.
Аппаратурные упрощения связаны с
уменьшением разрядности промежуточных РЛ данных.
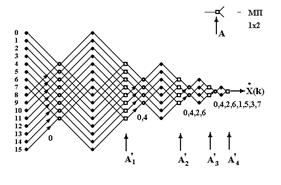
На Рис. 4 показан результирующий граф синтезирования апертуры с помощью алгоритма БПФ 16 «узких» лучей на выходе на основе образованных последовательным образом 16 пространственных отсчетов.
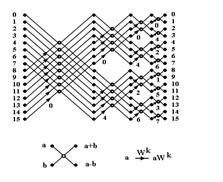
а) б)
Рис. 4. Алгоритм БПФ для реализации параллельного анализа пространственных частот (угловых направлений) и последовательный алгоритм адаптации БПФ в одноцелевой ситуации для пеленгации цели с направления k показан на схеме Рис. 4, где А-коды управления
Схема «бабочка» полусегмента изображена в нижней части Рис. 4 а, а ее возможные положения в пределах отведенной апертуры К (М) =16 на входе и синтезированных К (М) =16 каналов пространственных частот (угловых направлений) на выходе показаны на верхней части этого же рисунка. На Рис. 4 б приведена обобщенная схема мультиплексирования «2х1», приводящая множественность возможного положения лучей к сформированному одному k-му, сокращая число каналов в малоцелевых ситуациях. На схеме показаны 4 ступени формирования синтезированного узкого луча, что приводит к увеличению разрядности на 4 и, соответственно, увеличению динамического диапазона обрабатываемых сигналов на 24 дБ.
Если
предположить, что целая часть малоразрядных ГО составляет 4 разряда, а
флюктуирующая ![]() - 1 бит, то в результате ЦО с
учетом приобретенных разрядов инструментальный динамический диапазон превысит
50 дБ.
- 1 бит, то в результате ЦО с
учетом приобретенных разрядов инструментальный динамический диапазон превысит
50 дБ.
Формирование «бинарно – знаковой» робастной
статистики. Весовые
коэффициенты в цифровых фильтрах БПФ являются бинарными: +1, - 1. Аддитивная смесь ![]() полезного сигнала
полезного сигнала ![]() и
коррелированной по пространству активной помехи
и
коррелированной по пространству активной помехи ![]() по
каждой квадратуре на аналоговых выходах ФАР подвергается бинарно-знаковому
квантованию с помощью идеально симметричного ограничителя, на выходе которого
по каждому
по
каждой квадратуре на аналоговых выходах ФАР подвергается бинарно-знаковому
квантованию с помощью идеально симметричного ограничителя, на выходе которого
по каждому ![]() -му отсчету имеем знаковую статистику
-му отсчету имеем знаковую статистику ![]() , причем
, причем ![]() при
при ![]() и
и ![]() при
при ![]() (
(![]() -
масшт. коэффициент).
-
масшт. коэффициент).
С целью стохастической
линеаризации нелинейной характеристики ограничителя во входную смесь добавим
искусственный шум ![]() , каждая квадратурная компонента
которого распределена по закону
, каждая квадратурная компонента
которого распределена по закону
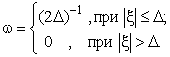 (2)
(2)
В этом случае случайная величина (СВ)
![]()
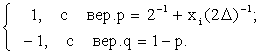 (3)
(3)
Моменты СВ (3):
![]() б)
б) ![]() в)
в)![]() . (4)
. (4)
Из (4 а) следует,
что ![]() , т.е. операция
, т.е. операция ![]() линеаризует
нелинейность
линеаризует
нелинейность ![]() (эффект «стохастической линеаризации»).
(эффект «стохастической линеаризации»).
Условие (4 б)
эквивалентно равенству ![]() , объясняющему эффект
«нормирования мощности» (робастности) за счет амплитудной характеристики
симметричного ограничителя.
, объясняющему эффект
«нормирования мощности» (робастности) за счет амплитудной характеристики
симметричного ограничителя.
Анализ коэффициентов подавления и
улучшения. С целью оценки предельных инструментальных возможностей системы угловую
помеху считаем сильно коррелированной по пространству, причем ее отсчеты 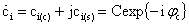 на всей апертуре ФАР постоянны, а
полезный сигнал
на всей апертуре ФАР постоянны, а
полезный сигнал 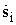 на дискретной шкале отсчетов
на дискретной шкале отсчетов 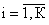 описывается комплексной гармонической
функцией в координатах апертуры ФАР
описывается комплексной гармонической
функцией в координатах апертуры ФАР 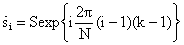 с межэлементным
набегом фазы, согласованным с номером
с межэлементным
набегом фазы, согласованным с номером 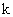 соответствующего
пространственно-частотного (углового) канала процессора ДПФ. Термин
«согласованным с номером k» по существу отражает принцип
«согласованной фильтрации по пространственным
соответствующего
пространственно-частотного (углового) канала процессора ДПФ. Термин
«согласованным с номером k» по существу отражает принцип
«согласованной фильтрации по пространственным 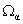 ,
, 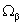 частотам.
частотам.
Для сохранения аналогии обычного спектрального анализа и анализа по пространственным частотам с применением БПФ мы избежали необходимость разложения полей по волновым числам (проекциям волновых векторов).
Для рандомизированной
обработки на выходе ![]() -го канала системы «ограничитель
– ДПФ» мощность смеси «сигнал + помеха» (СП) при независимых сигнале и помехе
как показано в [4] равна:
-го канала системы «ограничитель
– ДПФ» мощность смеси «сигнал + помеха» (СП) при независимых сигнале и помехе
как показано в [4] равна:
![]() (5)
(5)
где
![]() -
мощность нескомпенсированной помехи;
-
мощность нескомпенсированной помехи;
![]() -
выходная мощность полезного сигнала
-
выходная мощность полезного сигнала ![]() -го канала.
-го канала.
Обозначим через ![]() - пороговое отношение сигнал-помеха,
тогда для
- пороговое отношение сигнал-помеха,
тогда для ![]() и произвольных
и произвольных ![]() можно
установить, что требуемое значение амплитуды входного сигнала должно быть не
менее
можно
установить, что требуемое значение амплитуды входного сигнала должно быть не
менее ![]() .
.
Нормированный коэффициент
подавления ПП, при котором обеспечивается единичное усиление шума, ![]() , что говорит о плохом подавлении ПП малой
амплитуды
, что говорит о плохом подавлении ПП малой
амплитуды ![]() и хорошем подавлении ПП большой амплитуды
и хорошем подавлении ПП большой амплитуды
![]() , что характерно для рандомизированной
обработки (см. «узлы» - «пучности» в разделе «введение»).
, что характерно для рандомизированной
обработки (см. «узлы» - «пучности» в разделе «введение»).
Сформулированные условия
стохастической линеаризации гарантируются, если амплитуда принимаемой смеси СП ![]() , поэтому, оценивая предельно достижимое
подавление помехи в формулу для
, поэтому, оценивая предельно достижимое
подавление помехи в формулу для ![]() необходимо подставить
необходимо подставить ![]() :
:
![]() (6)
(6)
где ![]() .
.
Нормированный коэффициент передачи полезного сигнала
![]() (7)
(7)
При ![]() , вследствие ограничения и невозможности
выявления фазовых различий соседних отсчетов эхо-сигнала, наблюдается полная
потеря полезного сигнала. В других случаях потери составляют
, вследствие ограничения и невозможности
выявления фазовых различий соседних отсчетов эхо-сигнала, наблюдается полная
потеря полезного сигнала. В других случаях потери составляют ![]() , дБ, и становятся пренебрежимо малыми при
, дБ, и становятся пренебрежимо малыми при
![]() .
.
Определим коэффициент
улучшения системы обработки через коэффициенты ![]() и
и ![]() , используя известное соотношение
, используя известное соотношение
![]() .
(8)
.
(8)
Подставляя (6), (7) в (8), получаем
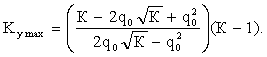
Для заданного значения ![]() при
при ![]() ,
, ![]() .
.
Анализ полученных
значений ![]() показывает, что рандомизация системы
улучшается с ростом
показывает, что рандомизация системы
улучшается с ростом ![]() .
.
Анализ полученных
значений ![]() , проведенный по аналогии с [6]
применительно к пространственным частотам (1) показывает, что рандомизация
системы улучшается с ростом
, проведенный по аналогии с [6]
применительно к пространственным частотам (1) показывает, что рандомизация
системы улучшается с ростом ![]() . Абсолютные значения
. Абсолютные значения ![]() для
для ![]() -
точечных БПФ составляют 33 дБ, 37 дБ, 42 дБ для r = 8, 9 и 10, соответственно.
-
точечных БПФ составляют 33 дБ, 37 дБ, 42 дБ для r = 8, 9 и 10, соответственно.
Для состоятельности
оценок азимута ![]() и угла места
и угла места ![]() прихода электромагнитной волны с пеленга
прихода электромагнитной волны с пеленга ![]() требуется по меньшей мере 2 отсчета
(элемента, точки приема) по каждой координате азимута
требуется по меньшей мере 2 отсчета
(элемента, точки приема) по каждой координате азимута![]() (ось
x) и угла места
(ось
x) и угла места ![]() (ось y). При расстоянии (базе) между точками d = ℓ
(ось y). При расстоянии (базе) между точками d = ℓ![]() стробоскопические
эффекты неоднозначного измерения углов a, b
возникают при ℓ ≥ 1/2 , а максимальные ошибки дискретизации углов
равны π/2, π/3, π/4, π/6 для ℓ = 1/2, 1/
стробоскопические
эффекты неоднозначного измерения углов a, b
возникают при ℓ ≥ 1/2 , а максимальные ошибки дискретизации углов
равны π/2, π/3, π/4, π/6 для ℓ = 1/2, 1/ ![]() ,
, ![]() /2 и 1,
соответственно. Полученные улучшения направленных свойств ФАР
/2 и 1,
соответственно. Полученные улучшения направленных свойств ФАР ![]() позволили получить СКО измерения пеленга
для К = 1024 менее 0,7; 0,38 и 0,2 град., соответственно.
позволили получить СКО измерения пеленга
для К = 1024 менее 0,7; 0,38 и 0,2 град., соответственно.
Последовательное наращивание 2-х координатной апертуры ФАР на гексагональной сетке с использованием 3-х элементного сегмента с общим числом элементов К, соответствующих взаимно-простым числам 3,7,13,19 и 31, показано на Рис. 5.
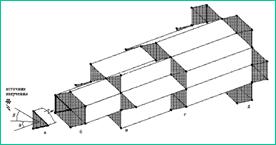
Рис. 5. Эволюция виртуального наращивания эквивалентной апертуры ФАР от 3 (а) до 31 (д) элемента
Для числа элементов К = 31 коэффициент усиления ФАР составил 18 дБ при потерях пороговой чувствительности менее 1,5 дБ.
Таким образом, для построения современной РЛС для защиты КА от угрозы их столкновения с техногенными объектами (ТО: космическим мусором) рекомендуется:
- применять адаптацию приема ПВ сигналов путем организации последовательного диаграммо-образования на базе усечённых (малоэлементных) апертур и робастных статистик сигнала на входе.
- для линеаризации рабочих характеристик обнаружения использовать алгоритмы робастного непараметрического обнаружения ;
- применять рандомизацию («зашумление») грубых отсчетов ПВ сигналов по принципу «удлиняющейся серии» в условиях ограничений размеров ПВ выборок;
- проводить многоканальный (многоэлементный) спектральный анализ обычных и пространственных частот (угловых направлений) с применением отсчетов малой разрядности;
- проводить квантование времени и пространства, в т.ч. с применением стохастических ортогональных базисов – стохастических шкал квантования время-импульсной модуляции (вобуляции) параметров зондирующих последовательностей сигналов для устранения стробоскопических и интерференционных эффектов;
- увеличивать информативность систем обработки ПВ сигналов путем использования стохастических (квазистохастических) шумовых сигналов РЛС.
Заключение. Предложен нетрадиционный подход к повышению инструментальной точности измерения пеленга, предполагающей стохастическую модуляцию положения фазового центра ФАР в процессе адаптивного формирования результирующей многолучевой диаграммы направленности при активизации малого числа слабонаправленных элементов и робастными рандомизированными статистиками сигнала на входе.
Формирование «узкой» диаграммы направленности ФАР, связанное с улучшением отношения «сигнал/помеха+шум» происходит последовательно в процессе рандомизированной обработки грубых «бинарно – знаковых» отсчетов. Данный подход снижает требования к разрядности радиолокационных данных, нормирует уровень выходных шумов, сохраняет линейность обработки и, таким образом, - обеспечивает возможность решения задачи СДЦ и подавления коррелированных по пространству активных помех.
Уровень шумов квантования
пеленга уменьшается как ![]() от размерности
апертуры
от размерности
апертуры ![]() , что подтверждает тезис о том, что рандомизированная
обработка отодвигает пределы достижения потенциальной точности, а шумы
квантования пеленга сглаживаются так же, как и собственные шумы приёмного
тракта.
, что подтверждает тезис о том, что рандомизированная
обработка отодвигает пределы достижения потенциальной точности, а шумы
квантования пеленга сглаживаются так же, как и собственные шумы приёмного
тракта.
Предварительные оценки резервов для решения задачи защиты космических аппаратов (КА) от угрозы их столкновения с техногенными объектами (ТО: космическим мусором) позволяют прогнозировать:
- уменьшение аппаратурных затрат реализации диаграммо-образующих устройств ФАР и аппаратуры поэтапной адаптивной обработки сигналов по обычным и пространственным частотам - не менее, чем в 5-7 раз;
- уменьшение не менее, чем в 10 раз энергопотенциала РЛС за счет активной последовательной «запитки» малого (3-4) элементов при сохранении полномасштабной апертуры гексагональной 331-элементной ФАР с поперечным размером D = 40 см. S – диапазона;
- сокращение время поиска ТО путем применения режимов «наискорейшего спуска» при поперечной модуляции положения фазового центра синтезируемой ААР в 2-3 раза;
- приближение инструментальных характеристик обнаружения, разрешения и оценивания координат ТО к потенциально возможным с энергетическими потерями до 2 дБ.
- сглаживание шумов квантования, линеаризацию нелинейностей, устранение стробоскопических и интерференционных эффектов, повышающих качество обработки сигналов.
В результате проведенных предварительных исследований найдены и оценены резервы повышения эффективности ЦО ПВ сигналов, её основных процедур (обнаружения, оценивания параметров, фильтрации по обычным и пространственным частотам - угловым направлениям в условиях ограничений на ресурсы ЦО (разрядность входных данных, разрядность АЦП, размеры окон ПВ выборок, частоты дискретизации и квантования) путем рандомизации «грубых» отсчётов (ГО) с бинарными свойствами (малоразрядных, бинарно-знаковых, булевых и т. п.)., которые могут быть использованы в разработках РЛС для КА нового поколения.
Литература
1. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию: Пер. с англ. М.: Радио и связь, 1986. – 448 с., ил.
2. R. Klemm. Space-Time Detection Theory // The material in this publication was assembled to support a lecture series under the sponsorship of the sensor and lectronicsTechnology Panel (SET) and the Consultant and Exchange Programmer of RTO presented on 23-24 september 2002 in Moscow, Russia.
3. Воскресенский Д.И. Антенны с обработкой сигнала: Учеб. Пособие для вузов. М.: САЙНС – ПРЕСС, 2002. – 80 с.: ил.
4. Горбунов Ю.Н. Цифровая обработка радиолокационных сигналов в условиях использования грубого (малоразрядного) квантования. Монография. М.: ФКА, ФГУП «ЦНИРТИ им. акад. А. И. Берга», 2008. – 87 с., (http://www.cnirti.ru/pdf/d_260109.doc).
5. Черняк В.С. О новых и старых идеях в радиолокации: МIМО РЛС// Успехи современной радиоэлектроники. 2011. Вып. 2. С. 5 -20.
6. Горбунов Ю. Н. Цифровые системы СДЦ и их оптимизация: Монография // МГТУ МИРЭА.- М., 2008. – 132 с. (http://www.cnirti.ru/pdf/d_260109.doc).
7. Томас. Непараметрические методы обнаружения сигналов.// ТИИЭР. - 1970. - т. 58. - №5. – с. 23 – 31.