УДК 621.391.1:519.86
О модели стохастических динамических систем с квадратичным отклонением не более 9% и ее применении в инвестиционных проектах
А. А. Коршунов
РГУ нефти и газа им. И.М. Губкина
Статья поступила в редакцию 11 декабря 2015 г.
Аннотация. Решается проблема создания адекватной модели динамических систем, описываемых обобщенным стохастическим дифференциальным уравнением Дюпайра, в контексте инвестиционного анализа. Используются методы стохастической теории управления портфелем активов и модель Блэка–Мертона–Шоулза. Найдены характеристики адекватности и построена адекватная адаптивная модель. Достигнуто стабильное квадратичное отклонение модели от реальной динамики актива не более 9%.
Ключевые слова: динамические системы, стохастические дифференциальные уравнения, адекватная адаптивная модель, стохастическая теория управления портфелем активов, модель Блэка–Мертона–Шоулза.
Abstract: The problem of creating an adequate model of the dynamic systems described by the generalized Dupire’s stochastic differential equation in the context of the investment analysis is solved. Methods of the stochastic theory of assets portfolio management and Black–Merton–Sholes’s model are used. Characteristics of adequacy are found and the adequate adaptive model is constructed. The stable square deviation of model from real dynamics of an asset no more than 9% is reached.
Key words: dynamic systems, stochastic differential equations; the adequate adaptive model; stochastic theory of assets portfolio management; Black–Merton–Sholes’s model.
Введение
Методы анализа стохастических дифференциальных уравнений позволяют решать задачи моделирования, фильтрации и управления для широкого класса динамических систем в физике и технике (напр. [1, 2]). Вместе с тем, они позволяют решать [3] и различные экономические задачи. Предлагаемая в статье модель применена для реальной статистики актива – ежедневных и средненедельных цен для всех имеющихся спотовых котировок Dated Brent (агентство Platt (Platt's): http://www.platts.com/) по торгам (с 08.07.1988 по 31.12.2014).
Для моделирования динамики рыночных цен используются самые различные стохастические модели: линейные (модель скользящего среднего MA(q), авторегрессионная модель AR(p), модель авторегрессии и скользящего среднего ARMA(p,q), интегральная модель ARIMA(p,d,q)), нелинейные (ARCH, GARCH, EGARCH, TGARCH, HARCH) и проч. [3. Гл.II]. Однако с точки зрения инвестиционного анализа динамика цен актива является составной частью баланса инвестиционного проекта. Для инвестиционного проекта не менее важной является задача определения минимальных инвестиций для выхода на заданную платежную функцию (достижение желаемых уровней прибыли и рентабельности). Все эти задачи в совокупности изучаются с помощью стохастической теории управления портфелем активов [3–7]. В [7] утверждалось, что статистика цен 1999–2006 гг. адекватно описывается моделью, которая именовалась обобщенной моделью Дюпайра (B.Dupire). В модели Дюпайра [3. Т.1, с.347] динамика цен актива St, описывается стохастическим дифференциальным уравнением
![]()
В модели, предложенной в [5, 7] динамика цен описывалась стохастическим дифференциальным уравнением
![]()
где коэффициенты
постоянны на каждом периоде стабильности (на
которые предварительно разбивается вся статистика цен), но зависят от St, т.е.
случайны: mt ![]() . Таким образом, динамика актива
(нефтяных цен) описывается последовательностью (диффузионных) моделей
Самуэльсона:
. Таким образом, динамика актива
(нефтяных цен) описывается последовательностью (диффузионных) моделей
Самуэльсона: ![]() Решение этого уравнения (с различными m и s на
каждом из периодов):
Решение этого уравнения (с различными m и s на
каждом из периодов): ![]() , где
, где ![]() (wt – винеровский процесс). Это позволяет
использовать все результаты, полученные для модели Блэка–Мертона–Шоулза (BMS-модели) [3, с.345,912;
9; 10], в
частности, формулу Блэка–Шоулза.
(wt – винеровский процесс). Это позволяет
использовать все результаты, полученные для модели Блэка–Мертона–Шоулза (BMS-модели) [3, с.345,912;
9; 10], в
частности, формулу Блэка–Шоулза.
1. Динамика реальных цен
1) Ниже приводятся графики дневных и недельных цен нефтяного рынка 1989–2014 гг. (Рис.1,2).
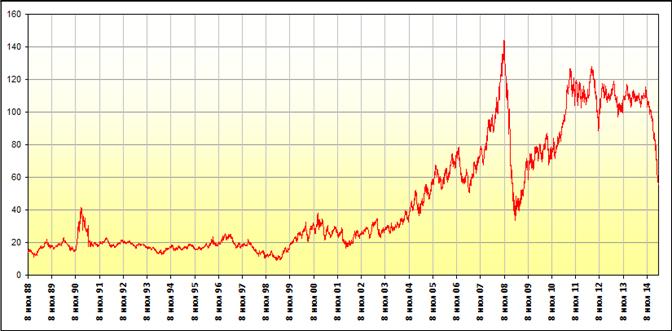
Рис.1. Ежедневная статистика Dated Brent, источник – Platt’s
2) Для построения обобщенной модели Дюпайра необходимо разбить статистику движения цен на периоды стабильности. Мы приведем две методики разбиения, окажется, что они приведут практически к одинаковым результатам (по качеству аппроксимации моделью).
Пусть L = {Lt = ln(Pt): Pt Î P} – упорядоченный набор натуральных логарифмов статистики цен P = {Pt: t Î T = [1; T], T Î N} (N – натуральный ряд), выбранный на временном промежутке T, который требуется разделить на периоды стабильности. Деление проведем рекурсивной процедурой, позволяющей последовательно уточнять множество {X 1, X 2,…, X M} границ периодов.
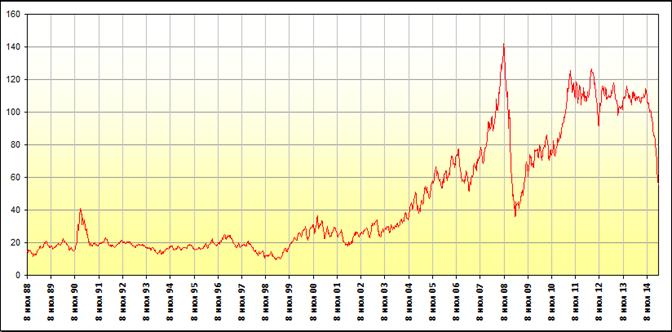
Рис.2. Недельное усреднение ежедневной статистики Dated Brent, источник – Platt’s
2.1) Методика 1. Границы интервалов первоначального разбиения X 1 выбирается интуитивно («на глаз»), далее, посредством уточняющего алгоритма (описан далее), основанного на методах регрессионного анализа, последовательно находятся разбиения X 1, X 2,…, X M, где X M – финальное разбиение. Кратность применения алгоритма определяется критерием стабилизации разбиений.
Положим Xm = {xnm Î T: n Î [1; Nm] Ì N, m Î N} – множество границ интервалов m-го разбиения промежутка T, где Nm – его мощность. Для получения точек m+1-го множества X m+1 из множества X m полагаем N m+1 = N m = =N, x1m+1 = x1m, xN m+1 = xN m для крайних точек и последовательно вычисляем точки xn m+1 при n = 2, ..., N–1. Для получения xnm+1 сначала на смежных интервалах [x1m+1, x2m] и [x2m, x3m] оцениваются коэффициенты прямых l1m+1 и l2m+1 линейной регрессии L по T, и число x2 m+1 полагаем равным целой части абсциссы точки пересечения этих прямых. Затем прямые регрессии lnm+1 и ln+1m+1 строятся последовательно на всех смежных интервалах, смещаясь на 1 вправо; так находим x3 m+1,..., xN–1 m+1.
Этот алгоритм был применен в [8].
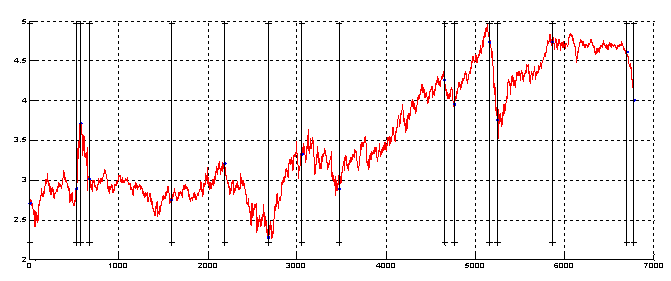
Рис.3. Финальное разбиение ежедневной статистики логарифмов Dated Brent по 1-й методике
|
Datet |
08.07.88 |
20.07.90 |
08.01.97 |
|||||
|
Pt |
15.05 |
18.09 |
41.33 |
20.48 |
15.73 |
24.95 |
9.79 |
27.94 |
|
t |
1 |
523 |
573 |
668 |
1593 |
2184 |
2681 |
3058 |
|
Datet |
||||||||
|
Pt |
18.02 |
71.82 |
52.42 |
113.97 |
43.10 |
115.03 |
101.19 |
54.98 |
|
t |
3475 |
4656 |
4763 |
5158 |
5243 |
5866 |
6699 |
6781 |
Табл.1 Разбиение X M по 1-й методике
Здесь Datet – дата t-го дня котировок.
2.2) Методика
2. Взяв точку t*= 151, k = 1
рассмотрим множество A(t*) = {tk = 1,…, Tk = 301} Ì T (т.е. t* – середина A(t*)).
Построим на A(t*) линейную регрессию L по T : l(t*, t) = b1(t*)×t + b0(t*). Если отклонение s2 = 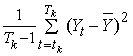 ≤
0.01, где Yt = Lt – l(t*, t), а
≤
0.01, где Yt = Lt – l(t*, t), а ![]() – среднее, то считаем, что пара (b1(t*),
T1) Î B, в противном случае рассматриваем
последовательно сужающиеся множества A(t*,
k) = {tk =t1 + k,…, Tk =T1 – k} до тех пор, пока не получим: s2 (k) ≤ 0.01 или число точек фрагмента A(t*, k)
равно 5 (торговая неделя). Тогда (b1(t*), Tk) Î B. Заметим, Tk = Tk(t*).
– среднее, то считаем, что пара (b1(t*),
T1) Î B, в противном случае рассматриваем
последовательно сужающиеся множества A(t*,
k) = {tk =t1 + k,…, Tk =T1 – k} до тех пор, пока не получим: s2 (k) ≤ 0.01 или число точек фрагмента A(t*, k)
равно 5 (торговая неделя). Тогда (b1(t*), Tk) Î B. Заметим, Tk = Tk(t*).
Далее, последовательно сдвигаясь на 1, рассматриваем середину t* = 152, проделываем ту же процедуру и добавляем к B новую пару (b1(t*), Tk)... И так до t*= T – 150.
Затем множество B анализируется для получения множества границ интервалов стабильности. С этой целью, начиная с t = t*+1, найдём такое t = t', при котором b1(t) меняет знак (в сравнении с предыдущим), и далее новый знак сохраняется при t = t', t' + 1,…, Tk(t') (на длине более половины анализируемого интервала [tk(t'), Tk(t')]). Это t' будем считать первой границей периода стабильности и обозначим через x1. Положив x1 = t', проделываем те же операции при t = t' + 1,... получим x2 и далее множество границ интервалов стабильности X = {xn Î T: n = 1,...,N}.
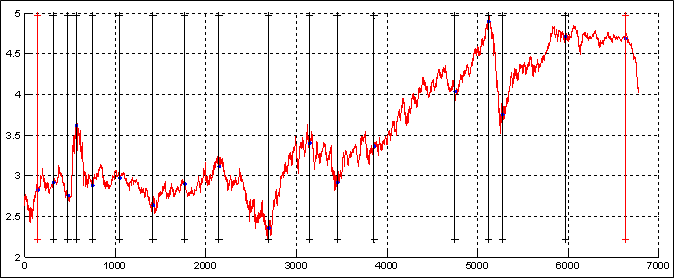
Рис.4. Финальное разбиение ежедневной статистики логарифмов Dated Brent по 2-й методике
|
Datet |
07.02.89 |
02.10.89 |
24.05.90 |
03.10.90 |
17.06.91 |
10.08.92 |
14.01.94 |
06.06.95 |
12.11.96 |
|
Pt |
16.80 |
18.50 |
15.84 |
37.27 |
17.81 |
19.58 |
13.97 |
18.12 |
22.41 |
|
t |
151 |
318 |
483 |
576 |
754 |
1050 |
1418 |
1774 |
2145 |
|
Datet |
04.01.99 |
06.10.00 |
17.12.01 |
17.07.03 |
03.01.07 |
23.06.08 |
22.01.09 |
25.10.11 |
02.06.14 |
|
Pt |
10.54 |
29.89 |
18.54 |
28.82 |
56.73 |
135.06 |
42.70 |
112.13 |
109.09 |
|
t |
2694 |
3147 |
3454 |
3860 |
4751 |
5126 |
5276 |
5972 |
6631 |
Табл.2. Разбиение X по 2-й методике
Разбиения по обеим методикам близки, и модель дает одинаковые по качеству приближения (см. также Рис.4+); в дальнейшем, при проведении расчётов, будем пользоваться разбиением, полученным посредством первой методики.
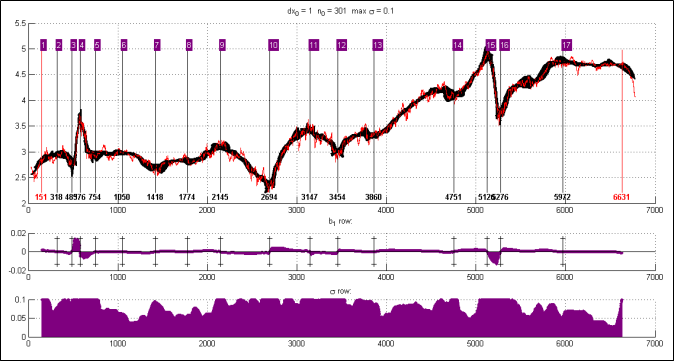
Рис.4+. Детали построения разбиения по 2-й методике: значения b1 и σ
2. Адекватность модели
1) Статистическая проверка адекватности
модели. Если модель
адекватна динамике цен на каждом интервале стабильности, 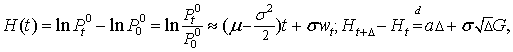
![]()
![]() параметры a, σ2 определяются статистической
оценкой:
параметры a, σ2 определяются статистической
оценкой: 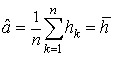 ,
, 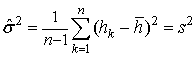 (
(![]() – реальные цены, G и
– реальные цены, G и ![]() –
стандартная гауссов-ская (нормальная) с.в. и гауссовская с параметрами a, σ2 соответственно).
–
стандартная гауссов-ская (нормальная) с.в. и гауссовская с параметрами a, σ2 соответственно).
Проверка гипотезы: hki – гауссовские с параметрами ai, σi2, i – номер стабильного интервала. Для проверки гипотез воспользуемся критерием согласия c2 Пирсона.
В таблице ниже c2 – 0.95-е квантили c2 распределения с ëlog(ni)û –1степенями свободы (ni – длина выборки (hki)k , ë.û – округление до целой части). S2 – значения статистики c2 критерия. (matlab – вычисления, выполненные посредством функционала Matlab Statistics Toolbox™). Жёлтым выделены значения разностей c2 – S2 тех стабильных интервалов, где гипотеза не подтверждается при уровне значимости 0.05 (что не помешает точности приближения).
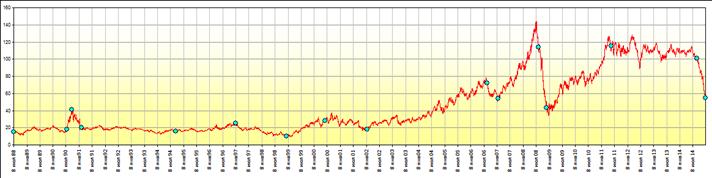
Рис.5. Порядковые номера стабильных интервалов
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
t |
1 |
523 |
573 |
668 |
1593 |
2184 |
2681 |
3058 |
|
c2 |
11.070 |
7.815 |
9.488 |
12.592 |
11.070 |
11.070 |
11.070 |
11.070 |
|
S2 |
27.448 |
11.223 |
13.545 |
37.125 |
16.023 |
28.931 |
7.484 |
10.750 |
|
c2 – S2 |
–16.378 |
–3.409 |
–4.057 |
–24.534 |
–4.952 |
–17.861 |
3.586 |
0.321 |
|
c2 matlab |
5.991 |
5.991 |
3.841 |
5.991 |
7.815 |
5.991 |
9.488 |
9.488 |
|
S2 matlab |
23.837 |
8.575 |
13.343 |
29.969 |
21.135 |
22.148 |
5.775 |
11.187 |
|
c2 – S2 matlab |
–17.846 |
–2.583 |
–9.502 |
–23.978 |
–13.320 |
–16.157 |
3.713 |
–1.700 |
|
I |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
t |
3475 |
4656 |
4763 |
5158 |
5243 |
5866 |
6699 |
|
|
c2 |
12.592 |
9.488 |
11.070 |
7.815 |
11.070 |
12.592 |
7.815 |
|
|
S2 |
20.851 |
1.204 |
9.255 |
3.498 |
30.538 |
17.839 |
3.790 |
|
|
c2 – S2 |
–8.260 |
8.284 |
1.816 |
4.317 |
–19.467 |
–5.247 |
4.025 |
|
|
c2 matlab |
9.488 |
9.488 |
9.488 |
9.488 |
7.815 |
9.488 |
5.991 |
|
|
S2 matlab |
20.649 |
0.924 |
9.585 |
4.725 |
28.937 |
23.245 |
8.160 |
|
|
c2 – S2 matlab |
–11.161 |
8.564 |
–0.097 |
4.763 |
–21.122 |
–13.757 |
–2.169 |
|
Табл.3. Результаты проверки гипотез на каждом стабильном интервале
Проверка незначимости регрессии. Линейная регрессия Y по x:
![]()
где
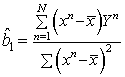 ,
, ![]() ,
,
здесь Y = h, x = (1, 2, … N) (дискретное время).
Статистика Фишера ![]() определяет тест на незначимость регрессии
для h1,…,hN. Критерий проверки значимости: F > fp, где fp – p-квантиль распределения Фишера с параметрами (1, N–2). Полагаем p = 0.95.
определяет тест на незначимость регрессии
для h1,…,hN. Критерий проверки значимости: F > fp, где fp – p-квантиль распределения Фишера с параметрами (1, N–2). Полагаем p = 0.95.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
t |
1 |
523 |
573 |
668 |
1593 |
2184 |
2681 |
3058 |
|
fp |
3.859 |
4.043 |
3.943 |
3.852 |
3.857 |
3.860 |
3.866 |
3.864 |
|
F |
0.030 |
0.125 |
0.002 |
0.001 |
0.329 |
0.000 |
0.913 |
0.709 |
|
fp – F |
3.830 |
3.917 |
3.941 |
3.850 |
3.529 |
3.860 |
2.953 |
3.155 |
|
i |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
t |
3475 |
4656 |
4763 |
5158 |
5243 |
5866 |
6699 |
|
|
fp |
3.849 |
3.932 |
3.865 |
3.956 |
3.856 |
3.853 |
3.960 |
|
|
F |
0.090 |
0.187 |
1.020 |
1.163 |
0.046 |
0.026 |
2.841 |
|
|
fp – F |
3.759 |
3.744 |
2.845 |
2.793 |
3.810 |
3.827 |
1.119 |
|
Табл.4. Результаты проверки гипотез на каждом стабильном интервале
Гипотезы не отвергаются при уровне значимости 0.05 ни на одном из интервалов стабильности.
2) Тренд. Поскольку ![]() и
и ![]() – логарифмически нормально, то Tt = ESt =
– логарифмически нормально, то Tt = ESt = ![]() , если
, если ![]() .
.
Далее приводится статистика по 3-м индикаторам близости тренда модели и реальных цен
– максимальное относительное отклонение (maximum deviation (relative)): maxdr = maxt{|Tt – St|/St};
– среднее (нормированное по длине интервала) квадратичное относительное отклонение (quadratic deviation (relative) average): qdav = ((St(|Tt – St|/St)2)/N)0.5,
– среднее (нормированное) относительное колебание (swing (relative) average): swav = |(St(Tt – St)/St)/N| (которое используется при оценках экономических характеристик [7]).
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
t |
1 |
523 |
573 |
668 |
1593 |
2184 |
2681 |
3058 |
|
maxdr |
0.3902 |
0.2358 |
0.5753 |
0.4508 |
0.3401 |
0.3615 |
0.3886 |
0.3359 |
|
qdav |
0.1423 |
0.0903 |
0.1759 |
0.1355 |
0.1682 |
0.1388 |
0.1430 |
0.1287 |
|
swav |
0.0418 |
0.0004 |
0.1280 |
0.0769 |
0.1302 |
0.0864 |
0.0647 |
0.0470 |
|
i |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
t |
3475 |
4656 |
4763 |
5158 |
5243 |
5866 |
6699 |
|
|
maxdr |
0.3877 |
0.1699 |
0.1987 |
0.2434 |
0.3723 |
0.2734 |
0.1589 |
|
|
qdav |
0.1817 |
0.0869 |
0.0872 |
0.1054 |
0.1661 |
0.0560 |
0.0772 |
|
|
swav |
0.0828 |
0.0402 |
0.0682 |
0.0688 |
0.0711 |
0.0190 |
0.0623 |
|
Табл.5. Показатели близости, вычисленные для трендов на каждом стабильном интервале
Графики трендов (чёрный), реальной ежедневной статистики (красный) и 200-кратных усреднений модельных траектории (зелёный) на трех худших стабильных интервалах приведены ниже (см. также след. стр.).
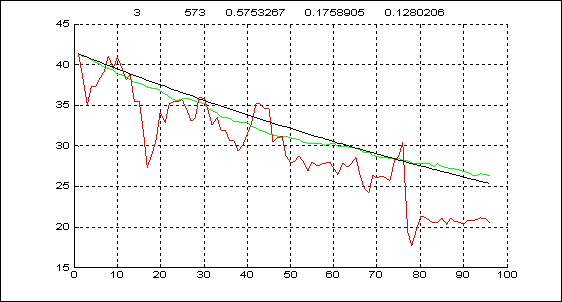
Рис.6. Интервал 3
Столь значительные отклонения не должны ни удивлять, ни смущать. Как мы видели, приращения цен нельзя считать последовательностью одинаково распределенных гауссовских с.в. Но найденная процедура моделирования настолько эффективна, что все равно удается добиться точности приближения по qdav в 9% на любом периоде.
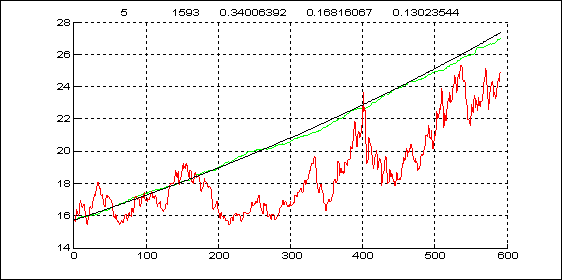
Рис.7. Интервал 5
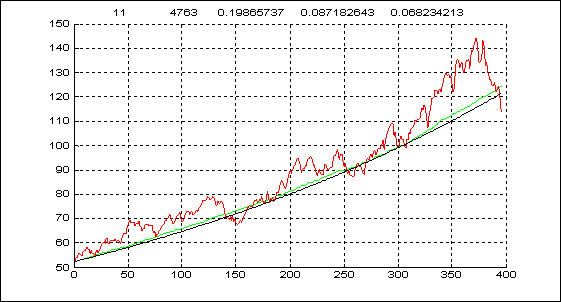
Рис.8. Интервал 11
3. Моделирование динамики цен
На каждом периоде стабильности на последовательно возрастающих (от левого конца) интервалах статистической оценкой по значениям реальных цен (см. разд.2) определяются параметры m, σ2 и a = m – σ2/2. Аппроксимирующая траектория в модели получается специальной процедурой. Интервал, на котором аппроксимирующая траектория стабилизируется (т.е. не меняется при дальнейшем расширении интервала), называется базой. В представленной ниже Табл.6 параметр t – порядковый номер начальной точки периода в реальной статистике цен, T – длина периода, base – длина базы. Остальные параметры уже определены ранее.
Даже в самом худшем случае – на 13-м периоде база составляет 38.5% периода, в абсолютном большинстве случаев – значительно меньше.
Квадратичное отклонение qdav меньше 9% на каждом периоде.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
t |
1 |
523 |
573 |
668 |
1593 |
2184 |
2681 |
3058 |
|
a |
0.000352 |
0.016525 |
–0.007391 |
–0.000285 |
0.000781 |
–0.001882 |
0.002782 |
–0.001052 |
|
σ |
0.020772 |
0.051193 |
0.066978 |
0.016642 |
0.017753 |
0.024617 |
0.026607 |
0.029127 |
|
T |
522 |
50 |
95 |
925 |
591 |
497 |
377 |
417 |
|
base |
120 |
10 |
20 |
160 |
110 |
130 |
50 |
150 |
|
a-base |
0.000182 |
0.022397 |
–0.010074 |
0.000205 |
0.000809 |
–0.002510 |
0.001814 |
–0.001210 |
|
σ-base |
0.027684 |
0.030122 |
0.069259 |
0.020989 |
0.014312 |
0.019272 |
0.037817 |
0.029092 |
|
maxdr |
0.218884 |
0.227111 |
0.285117 |
0.194076 |
0.213831 |
0.203813 |
0.232721 |
0.256795 |
|
qdav |
0.084491 |
0.074467 |
0.085078 |
0.067042 |
0.053371 |
0.086357 |
0.075314 |
0.088807 |
|
swav |
0.018928 |
0.014343 |
0.000801 |
0.010030 |
0.005871 |
0.010497 |
0.000321 |
0.031336 |
|
i |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
t |
3475 |
4656 |
4763 |
5158 |
5243 |
5866 |
6699 |
|
|
a |
0.001171 |
–0.002943 |
0.001966 |
–0.011440 |
0.001576 |
–0.000154 |
–0.007439 |
|
|
σ |
0.020979 |
0.020081 |
0.018153 |
0.036457 |
0.025006 |
0.012925 |
0.016535 |
|
|
T |
1181 |
107 |
395 |
85 |
623 |
833 |
82 |
|
|
base |
320 |
30 |
70 |
30 |
240 |
80 |
20 |
|
|
a-base |
0.000966 |
–0.006588 |
0.003570 |
–0.009434 |
0.002323 |
0.000118 |
–0.003544 |
|
|
σ-base |
0.022078 |
0.021919 |
0.017694 |
0.026812 |
0.034048 |
0.017395 |
0.008472 |
|
|
maxdr |
0.215901 |
0.177373 |
0.219732 |
0.125641 |
0.309599 |
0.270715 |
0.232618 |
|
|
qdav |
0.087864 |
0.074898 |
0.059282 |
0.054756 |
0.087350 |
0.054710 |
0.073868 |
|
|
swav |
0.039446 |
0.020075 |
0.016147 |
0.016950 |
0.023347 |
0.009266 |
0.023634 |
|
Табл.6. Характеристики модели
Графики статистики цен (красный) и модельной ломаной, длины периодов и размеры баз для трех худших периодов (6; 9; 13) и двух лучших (5; 14) приводятся ниже.
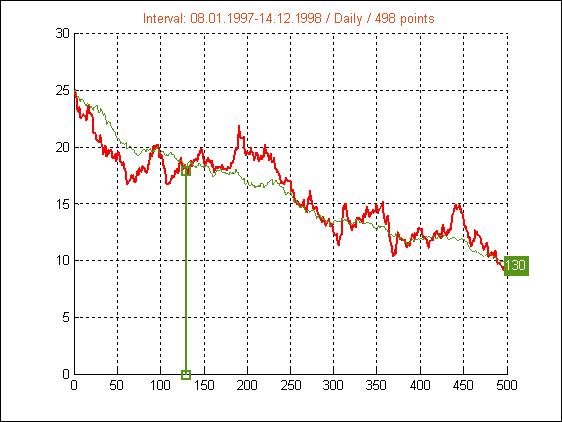
Рис.9. Интервал 6
6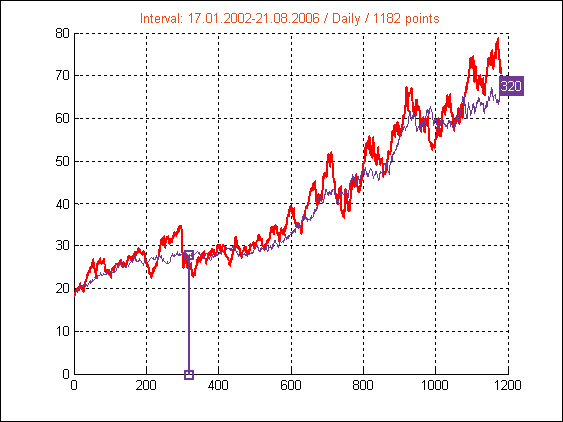
Рис.10. Интервал 9
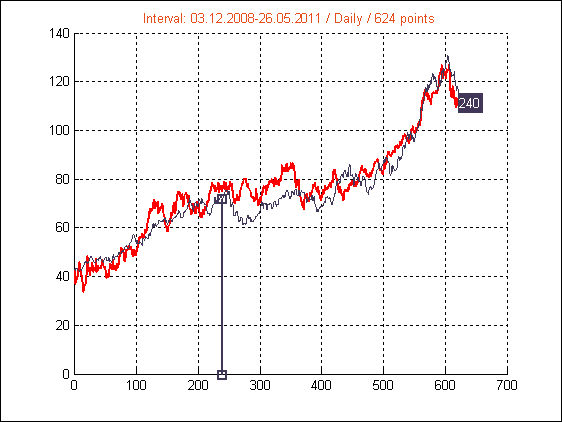
Рис.11. Интервал 13
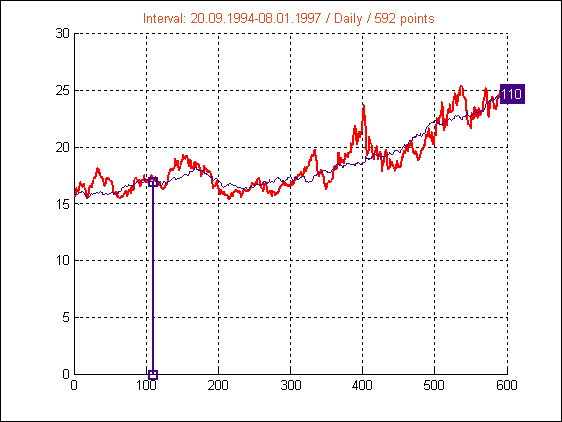
Рис.12. Интервал 5
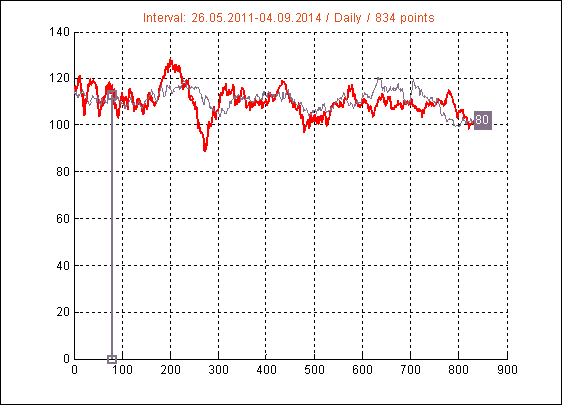
Рис.13. Интервал 14
Изложенный подход позволяет применять для оценки начальных инвестиций глубокие результаты, полученные Ф. Блэком, М. Шоулзом и Р. Мертоном [9, 10].
Литература
1. Дэвис М. Линейное оценивание и стохастическое управление. :Наука. М. 1984
2. Балакришнан А. Теория фильтрации Калмана. :МИР. М. 1988.
3. Ширяев А.Н. Основы стохастической финансовой математики. :Фазис. М. 1998.
4. Лимитовский М.А. Инвестиционные проекты и реальные опционы на развивающихся рынках. :Дело. М. 2004.
5. Жолков С.Ю. Об инвестиционном анализе нефтегазовых проектов, связанном с реальными опционами. Тр. V межд. конф. «Упр. разв. крупномасштабных систем (MLSD’2011)». Т.I. :ИПУ РАН. М. 2011. С.117–119.
6. Жолков С.Ю., Коршунов А.А. Индикаторы стабильности рынка и прогнозирование доходов в инвестиционных нефтегазовых проектах. Тр. V межд. конф. «Упр. разв. крупномасштабных систем (MLSD’2011)». Т.I. :ИПУ РАН. М. 2011. С.119–122
7. Жолков С.Ю., Коршунов А.А. Математическое моделирование динамики цен нефтегазовых рынков в контексте инвестиционного анализа. // Труды РГУ нефти и газа им. И.М.Губкина. N.3. (268). Июль–сент. 2012. С.185–197.
8. Сухарев М.Г., Иткин В.Ю. Статистическое исследование закономерностей газопотребления в центральных областях РФ./ Трубопроводные системы энергетики: математическое и компьютерное моделирование. Новосибирск: Наука. 2014. С.123–129.
9. Black F., Scholes M. The pricing of options and corporate liabilities. //Journal of Political Economy. V.81. N3. 1973.
10. Merton R.S. Theory of rational option pricing. //Bell Journal of Economics and Management Science. N4 (Spring). 1973.