|
|
"ĆÓĐÍŔË ĐŔÄČÎÝËĹĘŇĐÎÍČĘČ" "JOURNAL OF RADIOELECTRONICS" N 1, 1998 |
|
V.A.Cherepenin1, V.P.Shumilin2
1Institute of Radioengineering and
Electronics of Russian Academy of Sciences
2High Energy Density Research Center, Russian Academy of
Sciences, IVTAN
Received December 10, 1998.
INTRODUCTION
Electromagnetic disturbances at explosions of charges of condensed high explosives (HE), apparently, for the first time were found out by A.G.Ivanov in summer of 19381. In the subsequent years these effects were repeatedly investigated in many laboratories of the world2-8, and the frequency range, in which it was possible to find out electromagnetic disturbances, continuously extended toward the high frequencies. According to the results of these experiments, it has appeared, in particular, that at frequencies up to megahertz (fŁ106Hz) these disturbances represent themselves quasi-stationary electromagnetic fields, which quickly decrease depending on distance from a point of explosion (~R-3). At higher frequencies the microwave radiation itself was found out, when the field decreases in inverse proportion to distance (~R-1). We will be interested only in this high-frequency radiation, the presence of which is not explained till now. Concerning low-frequency disturbances see review7.
Purely speaking, the set of the experimental facts, concerning the generation of microwave radiation at explosions of condensed HE, is not big. In 1955 T.Takakura2, working with small charges of lead azide (M=0.1¸0.4 g), has shown, that the radiation is registered on frequencies up to 108Hz (more precisely, up to 90MHz). At f=190MHz and 3.3GHz the radiation was not observed. At frequency 14MHz by direct measurements it was shown, that the field decreases ~R-1. In 1959 B.Koch3 has published results of measurements of radiation at frequency f=24.1MHz from the charge of tolite-hexogene (50/50) with mass M=7.5·102g. From these data it follows, that brightness temperature of radiation at this frequency is ~1015°K. In 1965 W.H.Andersen and C.L.Long4 measured a spectrum of radiation from the charge of tetryl M=20¸103 g in mass over frequency range 4·108¸5·108Hz. It appears to be close to line spectrum. In 1970 V.I.Pechkovskii and G.S.Kalchik8 have registered radiation over frequency range f=7.8·109¸1.12·1010Hz at a distance 300¸350 m apart from a place of explosion M=104g of ammonium nitrate. The experiments were carried out under conditions of brightly expressed channel effect. At last in 1993-1998 A.B.Prishchepenko and co-authors has published a large cycle of work (see, for example,9-11), devoted to creation of electroexplosive sources of wide-band microwave radiation. It is not excluded, that the registered radiation is connected not to presence of radio-technical circuits, but is caused directly by HE. In such case it is possible presumably to assert, that at explosions of HE charges (M=102¸103g) radiation with frequency up to 1.5·1011Hz is registered.
Thus, there is the some of the experimental facts, showing that at explosions of condensed HE charges (as with a shell or without it) of small weight (M=102¸104g) wide-band microwave radiation (f=108¸1011Hz) is registered. The intensity of this radiation much surpasses intensity of thermal radiation.
The present work is devoted to attempt to explain this phenomenon. The essence of the offered mechanism consists in following: during expansion of products of detonation a highly non-equilibrium medium is generated, oscillatory temperature of which can essentially exceed rotational one. Such medium is basically active from the point of view of generation and amplification of microwave radiation. As against laser active media, the frequency of collisions of molecules is about frequency of radiation, therefore the radiation will be wide-band. As an air behind a shock wave is strongly ionized, the radiation can leave the explosion zone boundaries only after the decrease of this ionization because of its expansion and instability of border of detonation products. As presence of a shell as a way of initiation of the charge can accelerate process of destruction of a conducting layer behind a shock wave.
SPHERICAL EXPLOSION IN AIR
For definition and by virtue of obvious advantages of symmetry we shall consider the explosion of a spherical condensed HE charge without a shell in air under normal conditions. We shall also assume, that the initiation comes true in the center of charge.
At the moment of an exit of detonation wave through a surface of charge, a shock wave is formed in air. This wave, gradually reducing the speed, is expanded into environment. The products of detonation during the expansion on the initial stage behave like a piston, which push a shock wave before itself. In later moment of time this piston ever more lags behind a shock wave and finally should stop. Estimations show, that in case of spherical explosion in air under normal conditions the size of area, occupied by the products of detonation, does not surpass approximately ten initial sizes of charge.
Experimental study of the initial stages of condensed spherical HE charges explosions12-14 has shown, that the speed of detonation products is well described by a relationship
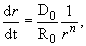 (1)
(1)
where R0 - initial radius of charge, D0 - initial speed of a shock wave, r=R/R0=1¸10, n=const (0<n<1). The quantities of D0 and n are experimentally determined for various HE.
Assuming detonation to be normal, we shall consider, that the substance behind the detonation wave is characterized by Jouguet parameters. Thus, the distribution of state variables over the charge in initial moment of time is extremely non-uniform, though it does not affect the external dimensions of a charge. For further evolution of the detonation products the rather important circumstance is that the substance was exposed to heating up to Jouguet temperature (TH) and is compressed up to density rH.
As estimations show, the moment of non-equilibrium appearance at expansion of detonation products rather poorly depends on the specific law of cooling T(r), the only important factor is that this cooling obeys the power law. Therefore, for many practically important cases it is possible to consider, that this process is an adiabatic one with a constant adiabatic index. At g=5/3
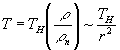 (2)
(2)
The initial speed of a shock wave in air can reach D0 @106 cm/sec, that corresponds to Mach number @30. According to shock adiabat for air15, equilibrium temperature in this case reaches 15 000°K and the electron concentration - ne@1019cm-3. The maximum electron concentration is near to a contact surface which separates the detonation products and heated air behind a shock wave, while the effective thickness of a conducting layer is much less than thickness of an air between a shock wave and a contact surface16. To make an estimation let us accept, that the concentration is equilibrium one. Then from15 it is possible to derive ne as a function of a Mach number, or dependence of critical frequency on r. For D0 @106 cm/sec, n=2/3
![]() 5·1013
5·1013![]() (3)
(3)
where rł1.3, and the frequency is expressed in Hz. One can see, that at r>5 the microwave output of radiation from the zone of explosion is possible. Actually, the process of destruction of a conducting layer behind a shock wave is more complicated. The fact is, that the contact surface appears to be unstable, especially in relation to small-scale disturbances17. This instability is well visible on numerous photos of an initial stage of the condensed spherical HE charges explosion at r>5 (see, for example,14). Thus, the destruction of a conducting layer will occur faster and is non-uniform over the surface of a shock wave.
NON-EQUILIBRIUM IN DETONATION PRODUCTS
Since the temperature is exactly the parameter determining the rates of various relaxation processes , we shall characterize explosion process by time
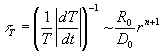 , (4)
, (4)
while the initial charge radius, obviously, is proportional to weight of HE to power 1/3.
Though the characteristic time between collisions of molecules (tcol) at expansion grows proportionally with r4, as translational degrees of freedom, as rotational ones will be in equilibrium, since the initial frequency of collisions is rather high (~1013Hz). The situation with oscillatory degrees of freedom is different. As the resonant exchange of oscillatory quantums between molecules (VV-relaxation) proceeds rather quickly, so Boltzmann’s distribution in energy of oscillatory will not be disturb18. However, characteristic time of energy exchange between oscillatory and translational (and rotational) degrees of freedom (VT- relaxation) grows exponentially with reduction of temperature
![]() (5)
(5)
where A and TVT - constants depending on a type of molecules. Therefore, a time moment inevitably comes, when tVT will exceed tT. At further expansion the oscillatory temperature (TV) already will not decrease. As estimations show, for typical HE it occurs at r=1.5¸2. Both weight and initial HE density influence a moment of oscillatory temperature freezing only as a logarithmic function, while the reduction of TH value (i.e. the use low-calorific HE) can essentially speed up this process.
It is necessary to note also, that in case of strong gas dissociation, an inverse process of recombination is a source of exited molecules, that can in turn increase the time of VT-relaxation more than by a factor of 10019. Generally speaking, it concerns any chemical reaction, because during expansion the endothermic channels of reactions "are blocked", while the remained exothermic channels are sources of exited molecules.
One more important process, which equilibrium state is broken at expansion of detonation products, is ionization. Since the temperature TH is not great, the equilibrium degree of ionization in an initial moment is small (~10-8), that is, the basic process, in difference from20,21, is ionization by heavy particles. In connection with strong temperature dependence of ionization speed (~exp(-I/T), where I- the energy of ionization) the non-equilibrium state is reached rather quickly (r~1) and at further gas expansion the degree of ionization falls down only by recombination processes, that is following the power law. So, for hexogene with initial density r0 =1.66 g/cm3 and M=1gramm the degree of ionization at r=5 will be ~2·10-11, which corresponds to electron concentration ~1010cm-3 (fcr~109Hz). The residual electron concentration grows up with increase of TH and falls down at growth of both M and r0.
![]() (6)
(6)
Thus, the detonation products during the process of expanding represent themselves the medium, in which oscillatory temperature exceed rotational one by an order of magnitude, and the electron concentration is unusually high, despite of strong cooling of gas.
RADIATIONAL INSTABILITY IN DETONATION PRODUCTS
Non-equilibrium of medium is necessary, but not sufficient condition of amplification and generation of electromagnetic radiation. Twiss22 has shown, that for realization of negative absorption over some frequency range it is necessary to comply simultaneously with two conditions:
![]() (7)
(7)
and
![]() (8)
(8)
where F(E) - function of energy (E) distribution, and Qw(E) - effective probability of stimulated radiation.
As over a microwave range of frequencies the energy of quantum of radiation is much less than temperature, so the effect of negative absorption should be described in classical approach. Such consideration was spent for one-dimension oscillators23-26. It has appeared, that the ensemble of harmonic oscillators, as well as in a quantum case, always absorbs energy, and for negative absorption to take place in the monoenergetic oscillators medium they must necessarily be unharmonic ones
![]() (9)
(9)
For unharmonic oscillators with distribution function F(E) the negative absorption will be observed, if
![]() (10)
(10)
across the energy interval
![]() (11)
(11)
where n - frequency of collisions.
Actually the condition (10) is analogous to requirement of population inversion in a quantum case. Usually two types of inversion are distinguished when considering the molecular systems27: oscillatory one, or complete, and oscillatory- rotational, or partial. In our case, the complete inversion is not realized, since the function of distribution in oscillatory degrees of freedom is Boltzmann’s. Therefore, only the partial inversion is possible. The classical analogue of partial inversion can be received by considering vibrating rotator, when function of distribution in oscillatory (EV) and rotational (ER) energies are Boltzmann’s ones:
![]() (12)
(12)
The oscillations of such rotator are non-harmonic ones. In this case
![]() (13)
(13)
at TV>T. As against effects, in which the basic role plays oscillators unharmonism23-26, this effect has a kinetic character and at large frequencies of collisions is realized over a wide range of radiation frequencies. Over the optical range of frequencies this effect was used for creation of lasers28,29.
Thus, in a considered case, the detonation products represent themselves an active medium, capable to amplify and generate the microwave radiation. Certainly, it is necessary, that this amplification exceeds the absorption in plasma of detonation products themselves and conducting layer behind a shock wave.
CONCLUSION
Within the framework of offered model a number of observable effects find its natural explanation, in particular, the absence of high-frequency radiation at explosions of lead azide charges2. The fact is, that the detonation products can represent themselves an active media only if the composition of detonation products is rather rich in molecules with exited oscillatory degrees of freedom, and a great life time. In a case of lead azide (PbN6) there is an obvious contradiction between the low heat of explosive transformation (and, hence, the low temperature TH) and large energy of oscillatory excitation of molecules N2 (@3340°K). For obtaining of wide-band microwave radiation the most optimum for composition are, apparently, the secondary HE such as CaHbNgOd.
The well-known fact of radiation intensity increase at explosions of charges in shells can be explained by acceleration of destruction process of a conducting layer behind a shock wave. An essential moment is also the influence of both a shell and a way of charge initiation on the radiation pattern.
Thus, the considered mechanism of radiation will take effect after some delay from the moment of HE initiation, and this delay time is proportional to weight of HE to power 1/3. In absence of nonlinear effects the average frequency of radiation should decrease during a pulse. The important parameters, influencing the considered mechanism of radiation are: a type of HE and geometry of charge, existence of a shell, the way of initiation, external pressure.
In summary we would like to thank Dr. E.V.Chernykh and Prof. S.L.Ziglin for fruitful discussion of work.
REFERENCES
Authors:
Cherepenin Vladimir Alekseevich, e-mail: cher@mail.cplire.ru
Shumilin Vladimir Pavlovich
|
|
|