| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2 , 2000 |
ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ПОМОЩЬЮ ПРИНАДЛЕЖНОСТНЫХ СПЕКТРОВ
Омский государственный технический университет
Получена 21 февраля 2000 г.
Описана технология представления стационарных случайных сигналов в виде принадлежностных спектров (ПС). Приведены результаты исследований свойств ПС и показана возможность создания на этой базе эмпирических порядковых шкал для распределений вероятности. Рассмотрен алгоритм использования принадлежностной шкалы распределений (ПШР) для решения задач автоматической классификации.
1. Понятие принадлежностного спектра
Понятие "принадлежностный спектр" (ПС) было введено автором в работе
[1] в связи с необходимостью оперативной идентификации стационарных случайных сигналов в условиях реального времени по малым выборкам. Предложенная технология была основана на идее представления распределений вероятности в виде лингвистической переменной (ЛП) "ФОРМА", в качестве терммножеств которой выступают собственные имена распределений вероятности, например, РАВН, НОРМ, ЭКСП и др., используемые в прикладном анализе для компактной характеристики свойств случайных сигналов.Для описания "количественных" отличий указанных терммножеств используется нечеткое обобщение такого известного в статистике, а также в других смежных областях, понятия, как "центр распределения". В теории измерений
[2] например, понятие "центр распределения" определяется путем перечисления имен оценок, которые "в принципе" могут быть использованы для характеристики данного понятия. При анализе результатов наблюдений наиболее часто применяются такие оценки, как "среднее арифметическое", "центр размаха", "медиана", "оценки максимального правдоподобия" и др. Имя оценки косвенно указывает на способ ее вычисления.Общий недостаток известных методов оценивания «центра распределения», по мнению автора, заключается в том, что все виды оценок рассматриваются вне связи друг с другом, представляя собой набор изолированных числовых показателей. Это, в свою очередь, существенно ограничивает возможности выявления скрытых закономерностей в структурах исследуемых данных.
Для устранения данного недостатка предлагается обобщить понятие "центр распределения" и определять его как: нечеткое множество оценок, обладающих свойством лингвистической эквивалентности своих имен и, соответственно, вычисляемых на основании этого свойства.
Формальным представителем введенного понятия выступает нечеткое множество {C} = {y/n}. Оценки {y}, являющиеся элементами нечеткого множества {C}, будем называть нечеткими оценками (НО). Имя нечеткой оценки – такой ее атрибут, который указывает на то, как сформировать данную оценку.
Имя НО образуется перечислением индексов тех исходных значений {x} анализируемой выборки, из которых эта НО вычислена как среднее арифметическое. Индексом называется порядковый номер j исходного значения Xj анализируемой выборки, полученный в результате упорядочения всех исходных значений. Таким образом, имя НО представляет собой совокупность индексов.
Понятие лингвистической эквивалентности (ЛЭ), являющееся критерием принадлежности оценки нечеткому множеству, трактуется как равенство средней суммы совокупности индексов НО индексу медианы, которая является числовым центром любого ограниченного ряда значений и, к тому же, обладает максимально возможной статистической устойчивостью к возможным "засорениям" исходной выборки. Согласно критерию ЛЭ, все НО являются "среднеарифметическими родственниками".
Для пояснения введенных понятий в таблице
1 дана топологическая диаграмма образования некоторых НО из ранжированной по возрастанию выборки объемом N0 = 9. Используемое определение позволяет наряду с традиционными оценками ("центр размаха" – оценка с именем "19", "медиана" – оценка с именем "5", "среднее арифметическое" – оценка с именем "123456789") генерировать большое количество других, ранее неизвестных оценок, структура которых в совокупности (например, взаимное положение НО в ранжированном ряду) отображает особенности рассматриваемого распределения.Звездочки в таблице
1 показывают, какие по порядку значения {x} ранжированной выборки надо взять, чтобы вычислить НО {у} с данным именем. Например, для вычисления НО с именем "267" необходимо взять среднее арифметическое от X2, X6 и X7: Y267 = (X2 + X6 + X7)/3. Обратите внимание на то, что средняя сумма индексов у этой (и всех других) НО равна индексу 5 медианы X5, т.е. ((2+6+7)/3) = 5. Это и есть условие лингвистической эквивалентности НО.|
Имя НО |
Ранжированные исходные данные {x} с индексами |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
19 |
* |
* |
|||||||
|
28 |
* |
* |
|||||||
|
37 |
* |
* |
|||||||
|
46 |
* |
* |
|||||||
|
5 |
* |
||||||||
|
168 |
* |
* |
* |
||||||
|
1478 |
* |
* |
* |
* |
|||||
|
267 |
* |
* |
* |
||||||
|
348 |
* |
* |
* |
||||||
|
2369 |
* |
* |
* |
* |
|||||
|
249 |
* |
* |
* |
||||||
|
123456789 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
Общее число НО зависит от объема выборки. В таблице
2 представлены данные о числе НО для объемов выборки от 2 до 10. Здесь же указано количество независимых и асимметричных НО, являющихся важными подклассами семейства НО.Независимыми называются те НО, которые нельзя получить линейной комбинацией других НО. В таблице
1 независимыми являются все НО, за исключением "среднего арифметического" Y123456789, которое связано с остальными НО соотношением: Y123456789 = (2Y19 + 2Y28 + 2Y37 + 2Y46 + Y5)/9.Оценки с именами от "168" до "249" относятся к подклассу асимметричных НО, т.к. они вычислены из значений {x}, расположенных на разных расстояниях от медианы X
5.|
Нечеткие оценки |
Количество НО при объеме N исходной выборки |
||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Всего |
1 |
3 |
3 |
7 |
7 |
19 |
17 |
51 |
47 |
|
Независимые |
1 |
2 |
2 |
3 |
3 |
6 |
6 |
11 |
? |
|
Асимметричные |
- |
- |
- |
- |
- |
2 |
2 |
6 |
? |
Функция принадлежности
{n} интерпретируется как совокупность порядковых номеров (рангов) сортируемых значений нечетких оценок. Это означает, что для определения характеристик принадлежности, необходимо ранжировать имена НО и зафиксировать отношение системы ИМЯ НО – ПРИНАДЛЕЖНОСТЬ (РАНГ) НО.Наиболее полной и наглядной формой связи имен НО и их степеней принадлежности служит, введенное автором, компактное представление данных в виде принадлежностного спектра [3].
Принадлежностный спектр (ПС) представляет собой квадратную таблицу (матрицу), размер которой зависит от числа используемых НО. Для асимметричных НО (АНО) размер таблицы составит 6´6. Строки таблицы образованы именами НО, а столбцы – порядковыми номерами, которые могут получать эти НО в результате ранжирования. В клетках таблицы, стоящих на пересечении строк и столбцов, ведется статистика того, сколько раз оценка с данным именем принимала данную принадлежность. Дополнительные строки и столбцы в таблице ПС отводятся для отображения вычисленных средних значений, соответственно, имен НО и принадлежностей (средних номеров).В качестве примера в таблицах 3-5 представлены структуры средних ПС для арксинусного (АРКС) и КОШИ распределений, полученных из одиночных выборок объема
N0=400, а также РАВН распределения, полученного усреднением 1000 реализаций объема N0=9.Таблица 3
Средний принадлежностный спектр АРКС
распределения
| 168 | 5 | 5 | 3 | 5 | 4 | 27 | 4.6 | 6 | 0 |
| 1478 | 2 | 5 | 4 | 7 | 27 | 4 | 4.3 | 5 | 0 |
| 267 | 6 | 2 | 6 | 25 | 5 | 5 | 3.7 | 4 | 0 |
| 348 | 6 | 6 | 23 | 4 | 6 | 4 | 3.2 | 3 | 1 |
| 2369 | 6 | 25 | 10 | 3 | 4 | 1 | 2.5 | 2 | 1 |
| 249 |
26 |
6 |
3 |
5 |
3 |
6 |
2.4 |
1 |
1 |
| СР.ИМЯ | 4.8 | 4.1 | 3.9 | 3.2 | 2.8 | 2.1 | |||
| ЛКИ | 6 | 5 | 4 | 3 | 2 | 1 | |||
| ДЛКИ | 0 | 0 | 0 | 1 | 1 | 1 |
Таблица 4
Средний принадлежностный спектр КОШИ
распределения
| 168 | 49 | 0 | 0 | 0 | 0 | 0 | 1.0 | 1 | 1 |
| 1478 | 0 | 49 | 0 | 0 | 0 | 0 | 2.0 | 2 | 1 |
| 267 | 0 | 0 | 49 | 0 | 0 | 0 | 3.0 | 3 | 1 |
| 348 | 0 | 0 | 0 | 49 | 0 | 0 | 4.0 | 4 | 0 |
| 2369 | 0 | 0 | 0 | 0 | 49 | 0 | 5.0 | 5 | 0 |
| 249 |
0 |
0 |
0 |
0 |
0 |
49 |
6.0 |
6 |
0 |
| СР.ИМЯ | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | |||
| ЛКИ | 1 | 2 | 3 | 4 | 5 | 6 | |||
| ДЛКИ | 1 | 1 | 1 | 0 | 0 | 0 |
Таблица 5
Средний принадлежностный спектр РАВН
распределения
| ИМЯ НО |
ПОРЯДКОВЫЕ НОМЕРА НО |
СР.№ | ЛКП | ДЛКП | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 168 | 210 | 123 | 152 | 145 | 165 | 205 | 3.547 | 5 | 0 |
| 1478 | 70 | 239 | 210 | 207 | 167 | 107 | 3.483 | 3 | 1 |
| 267 | 229 | 130 | 146 | 162 | 137 | 196 | 3.436 | 1 | 1 |
| 348 | 186 | 153 | 165 | 156 | 124 | 216 | 3.527 | 4 | 0 |
| 2369 | 118 | 193 | 187 | 200 | 240 | 62 | 3.437 | 2 | 1 |
| 249 |
187 |
162 |
140 |
130 |
167 |
214 |
3.570 |
6 |
0 |
| СР.ИМЯ | 3.49 | 3.54 | 3.44 | 3.45 | 3.61 | 3.46 | |||
| ЛКИ | 4 | 5 | 1 | 2 | 6 | 3 | |||
| ДЛКИ | 0 | 0 | 1 | 1 | 0 | 1 | |||
Обратите внимание, что максимумы принадлежности для вогнутого АРКС распределения группируются вдоль правой диагонали ПС, а для выпуклого КОШИ распределения - вдоль левой диагонали. У РАВН распределения ПС равномерно размыт по всем принадлежностям.
Моделирование на компьютере ПС различных распределений позволило получить результаты, сравнительный анализ которых позволяет сделать следующие выводы.
2. Принадлежностная шкала распределений и ее особенности.
Переход от средних номеров к двоичным лингвистическим кодам (ЛК) (таблица 6) позволяет установить связь между распределениями в логической форме посредством логических операций сложения, умножения, сдвига, инверсии и дополнения (1), а в аналоговой форме – посредством коэффициентов эквивалентности (таблица 7).
|
Значение ЛП |
Разряды вертикального (ДЛКП) и горизонтального (ДЛКИ) лингвистических кодов |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
КОШИ |
1 1 |
1 1 |
1 1 |
0 0 |
0 0 |
0 0 |
|
АРКС |
0 0 |
0 0 |
0 0 |
1 1 |
1 1 |
1 1 |
|
ЛЭКС |
1 1 |
1 1 |
0 0 |
0 0 |
0 1 |
1 0 |
|
ЭКСП |
0 1 |
1 0 |
1 1 |
1 1 |
0 0 |
0 0 |
|
2МОД |
0 0 |
1 0 |
0 1 |
1 0 |
0 1 |
1 1 |
|
КОШИ |
ЛЭКС |
АРКС |
ЭКСП |
РАВН |
2МОД |
|
|
КОШИ |
1 |
4/6 |
0 |
4/6 |
3/6 |
2/6 |
|
ЛЭКС |
4/6 |
1 |
2/6 |
2/6 |
3/6 |
4/6 |
|
АРКС |
0 |
2/6 |
1 |
2/6 |
3/6 |
4/6 |
|
ЭКСП |
4/6 |
2/6 |
2/6 |
1 |
3/6 |
4/6 |
|
РАВН |
3/6 |
3/6 |
3/6 |
3/6 |
0.5 |
3/6 |
|
2МОД |
2/6 |
4/6 |
4/6 |
4/6 |
3/6 |
1 |
Используя матрицу коэффициентов эквивалентности можно построить принадлежностную шкалу распределений (ПШР), полагая, что: а) пара КОШИ
– АРКС задает на числовой оси Х единичный отрезок и б) коэффициенты эквивалентности определяют линейные связи между распределениями. Графическая интерпретация ПШР дана на рис.1.где:
В соответствии с линейной моделью ПШР (рис.1,а): а) идентификация распределений осуществляется по положению максимума функции М(Х) эквивалентности; б) изменение формы распределения эквивалентно сдвигу треугольной функции М(Х) вдоль оси Х; в) произвольное распределение может быть разложено на эталонные компоненты, в качестве которых выступают 2МОД
, АРКС, ЛЭКС, КОШИ и ЭКСП распределения; г) длина связей между распределениями максимальна и равна длине шкалы.Круговая ПШР (рис.1,б) получается путем цилиндрической свертки линейной модели в комплексной плоскости. В этой модели геометрическим местом всех выпуклых, симметричных распределений служит положительное направление оси Х, а всех вогнутых, симметричных – отрицательное направление.
Поскольку РАВН и 2МОД распределения не имеют ни вогнутости, ни выпуклости их точки лежат на мнимой оси. Распределения КОШИ и АРКС, связанные друг с другом в соответствии с (1) прямым дополнением, расположены в точках +1 и –1 пересечения окружности единичного радиуса с действительной осью. Это означает, что угол сдвига между КОШИ и АРКС равен 180°
.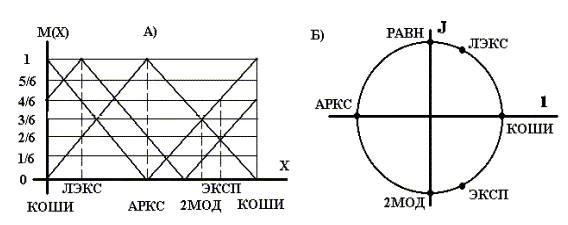
Рис.1. Линейная (а) и круговая (б) модели принадлежностной шкалы распределений
Точки окружности, лежащие в верхней полуплоскости, отображают левоасимметричные односторонние (выпуклые – в первом квадранте, вогнутые – во втором) распределения. Например, выпуклое ЛЭКС распределение, у которого на графике плотности вероятности отсутствует правая ветвь, расположено в первом квадранте. Наоборот, правоасимметричные распределения занимают точки окружности, лежащие в нижней полуплоскости. В частности, выпуклое ЭКСП распределение расположено в четвертом квадранте.Любое симметричное распределение представляет собой сумму проекций асимметричных компонент на действительную ось. Длина вектора симметричного распределения характеризует степень размытости соответствующего ПС. Наименее размытым (наиболее концентрированным) является ПС КОШИ распределения, поэтому длина его вектора формы максимальна и в нормированном виде равна 1. Изменение формы симметричного распределения ведет к увеличению размытости и, соответственно, к уменьшению длины вектора формы.
Рис.2. Векторная модель разделения симметричных выпуклых распределений
Данные особенности круговой ПШР проиллюстрированы рис.2, на котором векторами OC, OL, OG, OS представлено соответственно 4 выпуклых распределения: КОШИ, ЛАПЛ, НОРМ и СИМП. Эти распределения имеют одинаковый двоичный ЛКП, равный 111000, что говорит о совпадении направлений векторов. В то же время разная длина векторов OC, OL, OG, OS говорит о различной степени размытости ПС, что наглядно видно, например, из сравнения таблиц 8 и 9 для ЛАПЛ и СИМП распределений.Таблица 8
Средний принадлежностный спектр ЛАПЛ
распределения
| ИМЯ НО |
ПОРЯДКОВЫЕ НОМЕРА НО |
СР.№ | ЛКП | ДЛКП | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 168 | 40 | 1 | 3 | 3 | 0 | 2 | 1.5 | 1 | 1 |
| 1478 | 2 | 37 | 2 | 3 | 4 | 1 | 2.4 | 2 | 1 |
| 267 | 4 | 7 | 31 | 0 | 3 | 4 | 3.1 | 3 | 1 |
| 348 | 0 | 0 | 10 | 33 | 3 | 3 | 4.0 | 4 | 0 |
| 2369 | 1 | 3 | 3 | 4 | 38 | 0 | 4.5 | 5 | 0 |
| 249 |
2 |
1 |
0 |
6 |
1 |
39 |
5.4 |
6 |
0 |
| СР.ИМЯ | 1.5 | 2.4 | 3.2 | 4.0 | 4.6 | 5.3 | |||
| ЛКИ | 1 | 2 | 3 | 4 | 5 | 6 | |||
| ДЛКИ | 1 | 1 | 1 | 0 | 0 | 0 | |||
Таблица 9
Средний принадлежностный спектр СИМП
распределения
| ИМЯ НО |
ПОРЯДКОВЫЕ НОМЕРА НО |
СР.№ | ЛКП | ДЛКП | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 168 | 37 | 5 | 2 | 2 | 2 | 1 | 1.6 | 1 | 1 |
| 1478 | 3 | 27 | 13 | 3 | 3 | 0 | 2.5 | 2 | 1 |
| 267 | 3 | 12 | 24 | 3 | 4 | 3 | 3.0 | 3 | 1 |
| 348 | 4 | 3 | 4 | 14 | 17 | 7 | 4.2 | 4 | 0 |
| 2369 | 1 | 0 | 3 | 25 | 14 | 6 | 4.4 | 5 | 0 |
| 249 |
1 |
2 |
3 |
2 |
9 |
32 |
5.3 |
6 |
0 |
| СР.ИМЯ | 1.6 | 2.4 | 3.0 | 4.3 | 4.4 | 5.3 | |||
| ЛКИ | 1 | 2 | 3 | 4 | 5 | 6 | |||
| ДЛКИ | 1 | 1 | 1 | 0 | 0 | 0 | |||
Таким образом, технология ПС позволила создать на основе круговой модели (рис.1,б) порядковую ПШР, в которой информативным параметром является угловое положение вектора формы. При этом, если выбрать начальное положение вектора для 2МОД распределения, то получим максимальный диапазон измерений, равный почти 330 угловых градусов в соответствии с данными таблицы 10. В рамках ПШР положение вектора формы исследуемого сигнала определяется интерполяцией, для чего упорядоченные значения реперных точек шкалы записываются в базу эталонов распознающей системы.
Таблица 10
|
Угол вектора |
Оцифрованные отметки (реперные точки) круговой ПШР |
|||||
|
2МОД |
АРКС |
РАВН |
ЛЭКС |
КОШИ |
ЭКСП |
|
|
F |
0 |
90 |
180 |
210 |
270 |
330 |
"Физический смысл" ПШР состоит в том, что она упорядочивает распределения как по фундаментальным топологическим свойствам симметрии-асимметрии, выпуклости-вогнутости, ограниченности-неограниченности, так и по степени сложности: самое простое, 2МОД распределение находится в начальной точке шкалы, самое сложное из симметричных – КОШИ распределение – в конце шкалы. Самое сложное из асимметричных – ЭКСП распределение образует конечную реперную точку ПШР.
Практическое применение ПШР связано с решением двух основных проблем. Во-первых, из-за сильной "размазанности" ПС (в табл.5 максимумы принадлежности явно невыражены), плохо распознается РАВН распределение. Во-вторых, распределение КОШИ маскирует на уровне ЛК ряд других симметричных распределений (ЛАПЛ
, НОРМ, СИМП), затрудняя их надежную идентификацию.Наиболее кардинальный путь решения указанных проблем состоит в переходе от анализа ПС к анализу самой ранжированной функции, из которой как раз и формировался ПС. При этом, в качестве основного идентификационного параметра предлагается использовать коэффициент, характеризующий среднюю крутизну нормированной ранжированной функции на центральном ее участке (табл.11).
|
Имена распределений вероятности |
|||||||||
|
2МОД |
АРКС |
РАВЕН |
СИМП |
РЕЛЕ |
НОРМ |
ЭКСП |
ЛАПЛ |
КОШИ |
|
|
Порядковый номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Параметр крутизны С |
1 |
0.92 |
0.74 |
0.52 |
0.44 |
0.38 |
0.19 |
0.14 |
0.02 |
Пронумеровав имена распределений в порядке убывания значения параметра С, получим порядковую шкалу, во многом похожую на ту, которая следует из анализа ПС (табл.10). Таким образом, логическая согласованность обеих типов шкал подтверждает установленную автором закономерность связи распределений, что позволяет строить на этой основе новую систему приборов – анализаторов распределений.
3. Применение анализатора распределений для автоматической классификации сигналов.
Принцип действия анализатора распределений (АР) заключается в сравнении идентификационных параметров входного сигнала и упорядоченных, в соответствии с табл.11, эталонов. Если принять, что форма распределений является непрерывной величиной, то АР является аналого-цифровым преобразователем, поскольку по шкале отсчет производится в дискретных точках – "оцифрованных" отметках.
В виртуальном цифровом АР исследуемое распределение преобразуется в позиционный 9-ти разрядный код (ПК). Потенциально в этом коде не может быть совпадающих значений разрядов, поэтому сам ПК изменяется от минимального значения, равного 123456789, до максимального – 987654321.
Таким образом, АР
обеспечивает параллельное измерение исследуемого сигнала в полном диапазоне шкалы (от 2МОД до КОШИ) с теоретической разрешающей способностью: Р=9!=362 880 распределений.По сведениям
[4], известные идентификационные технологии, не позволяют достичь подобных результатов.Естественно, что реальная разрешающая способность, определяемая в первую очередь качеством использованных эталонов, будет существенно ниже данной теоретической оценки. Так, например, если суммарная погрешность идентификации имеет порядок 10%, что характерно для большинства известных методов, то реальная разрешающая способность будет составлять всего 4 разряда или Р=4!=24 распределения. Этого, однако, достаточно, чтобы успешно решать многие задачи в области измерений, контроля и диагностики.
В качестве примера приведем алгоритм и результат решения задачи автоматической классификации сигналов
с использованием 9-ти разрядной шкалы распределений типа табл.11. В современных компьютерных системах обработки данных задача классификации, из-за сложности алгоритмов ее реализации, не получила широкого применения, хотя некоторые авторы справедливо указывают на высокую информативность результатов, получаемых при решении этой задачи [5].Пусть исходные данные представлены произвольным набором, состоящим из К-реализаций, имеющих в общем случае разные выборочные объемы. Требуется установить связи между реализациями и отобразить структуру этих связей.
На первом этапе проводится анализ каждой реализации с формированием ПК. Второй этап состоит в совместном анализе полученных ПК с соблюдением следующих принципов:
Результаты работы ИАР (модуль
RecogDos.exe на Web-странице) в режиме классификации 5 квазипериодических сигналов (файлы с именами 00, 32, 36, 80 и 97) сложной формы представлены в табл.12. Вместе с этими сигналами был проанализирован ближайший к ним эталон – реализация случайного сигнала (файл 04), имеющая симметричное треугольное распределение (СИМП). Построенное по данным табл.12, дерево классификации изображено на рис.3. В прямоугольники вписаны значения разрядов, являющихся общими для участков цепи между двумя ветвлениями.Таблица 12
| №п/п | Имя
файла сигнала |
Позиционный код сигнала |
Имя
ближ. эталона |
Кру- тизна |
Откло- нение |
||||||||
| 1 | 00 | 4 | 5 | 3 | 6 | 7 | 2 | 8 | 1 | 9 | SIMP | 56 | 5 |
| 2 | 32 | 4 | 3 | 5 | 6 | 2 | 1 | 7 | 8 | 9 | SIMP | 61 | 10 |
| 3 | 36 | 4 | 5 | 6 | 3 | 7 | 8 | 2 | 9 | 1 | SIMP | 48 | 3 |
| 4 | 80 | 4 | 5 | 3 | 6 | 2 | 7 | 8 | 1 | 9 | SIMP | 58 | 7 |
| 5 | 97 | 4 | 5 | 6 | 3 | 7 | 8 | 2 | 1 | 9 | SIMP | 52 | 1 |
| 6 | 04 | 4 | 5 | 6 | 3 | 7 | 8 | 2 | 1 | 9 | SIMP | 51 | 0 |
Однако, конечные результаты – упорядоченные списки сигналов – оказываются полностью подобными, отличаясь лишь направлением сортировки: от большего значения крутизны ранжированной функции к меньшему (рис.3) или - наоборот (рис.4).
Рис.3. Дерево классификации исследуемых сигналов
Таким образом, на основе предложенной технологии, можно достаточно просто выявлять скрытые закономерности типа упорядоченности в структурах данных любой физической природы. Рассмотренная шкала распределений легко адаптируется – путем проставления соответствующих меток взамен имен распределений - к любой предметной области, в которой исходная информация представляется набором выборочных значений. В медицине, например, можно упорядочить систему диагнозов и затем по шкале проводить мониторинг течения болезни в реальном масштабе времени.Рис.4. "Обратное" дерево классификации исследуемых сигналов
ЛИТЕРАТУРА
Автор:
Кликушин Юрий Николаевич, доцент кафедры
"Информационно-измерительная техника"
Омского государственного технического
университета
Адрес: 644050, Омск-50, пр.Мира, 11, ОмГТУ
Тел. (381-2) 65-37-07