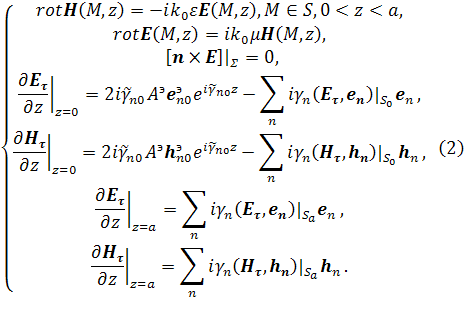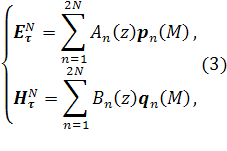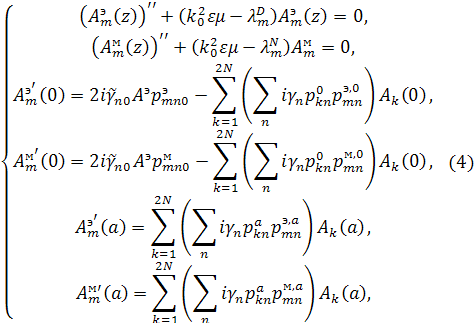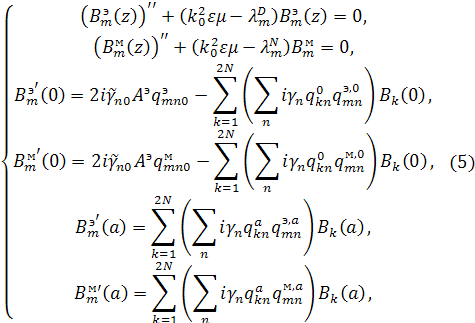УДК 621.372.829
ВЕКТОРНАЯ МОДЕЛЬ ВОЛНОВОДА С ВХОДЯЩИМИ РЕБРАМИ
А. Н. Боголюбов, А. И. Ерохин, И. Е. Могилевский
физический факультет МГУ имени М.В. Ломоносова, кафедра математики
Получена 14 февраля 2012 г.
Аннотация. В работе рассматривается векторная модель бесконечного волновода, имеющего на конечном участке входящие ребра. Приближенное решение ищется неполным методом Галеркина, в котором векторный базис строится с помощью собственных функций сечения. Доказывается существование и единственность приближенного решения, а также его сходимость к точному.
Ключевые слова: волновод, входящие ребра, входящие углы, проекционные методы.
Abstract. Vectorial model of an infinite waveguide with reentrant edges in its finite region is considered in present work. Approximate solution is obtained by incomplited Galerkin’s method in which vectorial basis is constructed with Laplacian eigen functions of cross-section. Existence and uniqueness of the approximate solution and its convergence to the exact solution are proved.
Keywords: waveguide, reentrant edges, reentrant corners, projective methods.
Введение
Волноведущие системы, имеющие входящие ребра, находят широкое применение в различных областях техники [1]. Так, гребенчатый прямоугольный волновод, являющийся примером таких систем, используется в качестве фильтра для пассивного микроволнового устройства или настроечного элемента в нем [2, 3]. С помощью входящих углов в волноводе можно также моделировать наличие дефектов на граничной поверхности системы, например, царапины, а также щупы, возбуждающие волновод.
Для расчета волноведущих систем, имеющих данную геометрическую особенность, в случае скалярной постановки задачи удобно применять комбинацию проекционно-сеточных методов [4]. Для того, чтобы разложить решение краевой задачи, описывающей данную систему, по собственным функциям сечения волновода (неполный метод Галеркина), необходимо численно решать спектральную задачу Дирихле в двумерной области, содержащей входящие углы. Решение спектральной задачи имеет сингулярность в окрестности входящего угла, которую можно выделить аналитически, используя технику, предложенную в [5]. В связи с этим для расчета собственный функций сечения удобно использовать проекционно-сеточный метод, а именно, метод конечных элементов [6], в котором в пространство пробных функций вводится найденная теоретически особенность решения.
Так как скалярная задача дает в основном качественное описание нерегулярного волновода с переменным сечением, то несомненный интерес представляет рассмотрение векторной модели.
В данной работе рассматривается векторная модель бесконечного цилиндрического волновода с входящими ребрами на конечном участке. Для построения приближенного решения векторной задачи, как и в случае скалярной постановки [4], применяется неполный метод Галеркина. Векторный базис, по которому раскладывается приближенное решение, строится с помощью собственных функций сечения и тем самым учитываются особенности, возникающие в окрестности входящих ребер волновода. С помощью техники, предложенной в [7], доказывается существование и единственность приближенного решения, а также его сходимость к точному решению.
Постановка задачи.
Рассмотрим
бесконечный цилиндрический волновод, деформированный так, что сечение его
конечного фрагмента длины ![]() содержит
входящие углы.
содержит
входящие углы.
Пусть ![]() и
и
![]() –
собственные функции и собственные значения спектральной задачи Дирихле для
оператора Лапласа, а
–
собственные функции и собственные значения спектральной задачи Дирихле для
оператора Лапласа, а ![]() и
и
![]() –
спектральной задачи Неймана для сечения регулярной части волновода
–
спектральной задачи Неймана для сечения регулярной части волновода ![]() ,
т.е. круга,
,
т.е. круга, ![]() –
граница круга,
–
граница круга, ![]() –
орт, направленный слева направо вдоль оси
–
орт, направленный слева направо вдоль оси ![]() волновода
(начало
волновода
(начало ![]() лежит
в сечении левого торца нерегулярной части волновода). Введем базисы для
представления векторов, лежащих в плоскости
лежит
в сечении левого торца нерегулярной части волновода). Введем базисы для
представления векторов, лежащих в плоскости ![]() :
:
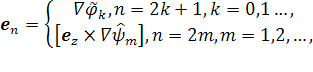
![]()
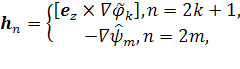
![]()
которые обладают следующими свойствами [7]:
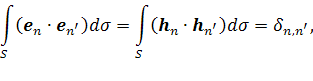
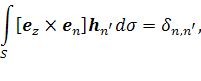
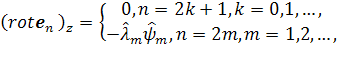
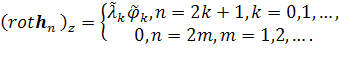
Поперечные составляющие нормальных волн регулярного волновода имеют вид [7]:
![]()
![]()
где ![]() и
и
![]() -
амплитуды нормальных
-
амплитуды нормальных ![]() и
и
![]() волн,
при этом четным значениям
волн,
при этом четным значениям ![]() соответствуют
соответствуют
![]() ,
а нечетным –
,
а нечетным – ![]() волны,
волны,
![]() –
постоянная распространения,
–
постоянная распространения, ![]() –
для нечетных
–
для нечетных ![]() ,
,
![]() –
для четных
–
для четных ![]() .
В дальнейшем, векторы
базиса для волн электрического типа будем обозначать
.
В дальнейшем, векторы
базиса для волн электрического типа будем обозначать ![]() и
и
![]() ,
а для магнитного –
,
а для магнитного – ![]() и
и
![]() .
.
Пусть в рассматриваемом волноводе
распространяется бегущая слева направо ![]() -
ая нормальная волна электрического типа с амплитудой
-
ая нормальная волна электрического типа с амплитудой ![]() :
:
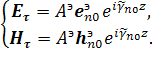
Будем считать, что
сторонние токи отсутствуют, а также что
магнитная проницаемость ![]() .
.
Электромагнитные колебания,
распространяющиеся в волноводе, описываются системой уравнений Максвелла с граничным
условием на поверхности волновода ![]() ,
заключающимся в равенстве нулю касательной составляющей вектора напряженности:
,
заключающимся в равенстве нулю касательной составляющей вектора напряженности:
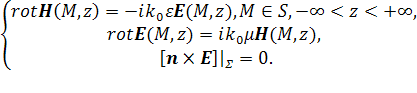
Здесь ![]() – диэлектрическая
проницаемость, причем
– диэлектрическая
проницаемость, причем ![]() ,
,
![]() –
волновое число. На границе регулярной и нерегулярной частей волновода должны выполняться
равенства касательных составляющих векторов напряженностей электрического и
магнитного полей:
–
волновое число. На границе регулярной и нерегулярной частей волновода должны выполняться
равенства касательных составляющих векторов напряженностей электрического и
магнитного полей:
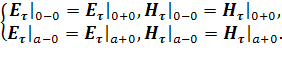
На этой границе
потребуем также непрерывность производных по ![]() от
от ![]() и
и ![]() :
:
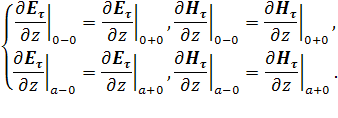
Используя парциальные условия излучения, получим следующую краевую задачу:
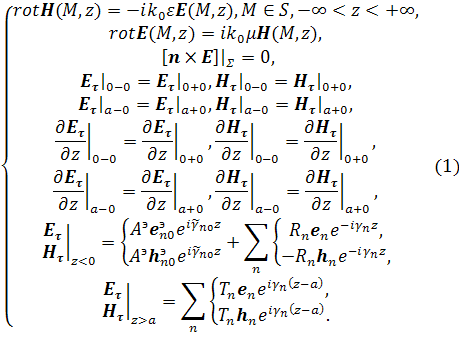
Здесь коэффициенты ![]() обозначают
амплитуды нормальных волн электрического и магнитного типов, отраженных от
нерегулярного участка волновода и прошедших через него соответственно, коэффициенты
обозначают
амплитуды нормальных волн электрического и магнитного типов, отраженных от
нерегулярного участка волновода и прошедших через него соответственно, коэффициенты
![]() обозначим
обозначим
![]() в
случае разложения по базису электрического типа и
в
случае разложения по базису электрического типа и ![]() –
в случае базиса магнитного
типа.
–
в случае базиса магнитного
типа.
Как и в случае скалярной задачи [4],
дифференцируя по ![]() парциальные
условия излучения и учитывая условия сопряжения, сведем задачу (1) к краевой
задаче в ограниченной области:
парциальные
условия излучения и учитывая условия сопряжения, сведем задачу (1) к краевой
задаче в ограниченной области:
Здесь ![]() –
интеграл по сечению
–
интеграл по сечению ![]() соответственно
от скалярного произведения
соответственно
от скалярного произведения ![]() .
.
Построение приближенного решения.
Будем решать задачу (2) неполным методом Галеркина. Запишем приближенное решение в виде
![]()
где базисы ![]() и
и
![]() строятся
аналогично случаю регулярного сечения:
строятся
аналогично случаю регулярного сечения:
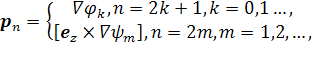
![]()
и
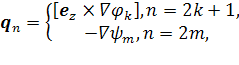
![]()
Здесь ![]() -
собственные функции задачи Дирихле, отвечающие собственным значениям
-
собственные функции задачи Дирихле, отвечающие собственным значениям ![]() ,
и задачи Неймана, отвечающие собственным значениям
,
и задачи Неймана, отвечающие собственным значениям ![]() ,
для сечения
,
для сечения ![]() с
координатой
с
координатой ![]() на
оси
на
оси ![]() нерегулярной
части волновода с входящими углами соответственно.
нерегулярной
части волновода с входящими углами соответственно.
Введем обозначения:
![]()
![]()
Подставляя искомый вид
приближенного решения (3) в уравнения Максвелла из (2) и записывая для них
проекционные соотношения [7], с учетом граничных условий получим следующие краевые
задачи для коэффициентов ![]() и
и ![]() :
:
где использованы обозначения: ![]()
![]()
![]()
![]() ,
а также соотношения для
,
а также соотношения для ![]() и
и
![]() :
:
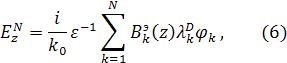
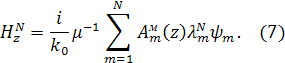
Теоремы существования, единственности и сходимости для приближенного решения.
Введем пространство
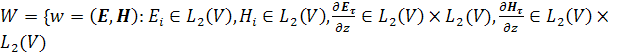 ,
,
где ![]() .
.
Теорема 1. Приближенное
решение ![]() существует
и единственно.
существует
и единственно.
Доказательство.
Помножим первое уравнение задачи (4) на ![]() и
проинтегрируем по
и
проинтегрируем по ![]() от
0 до
от
0 до ![]() :
:
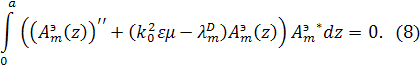
Суммируя
(8) по ![]() от
0 до
от
0 до ![]() и
интегрируя первое слагаемое по частям с учетом граничных условий, получим :
и
интегрируя первое слагаемое по частям с учетом граничных условий, получим :
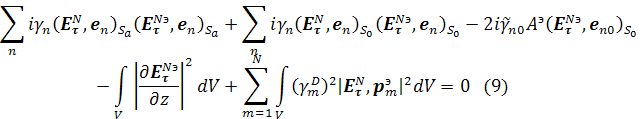
Аналогично из второго уравнения задачи (2) получим:
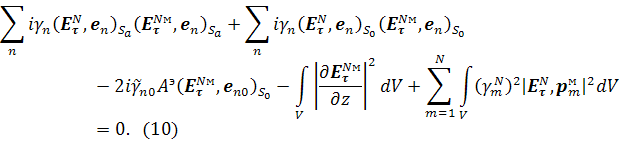
Сложим выражения (9) и (10):
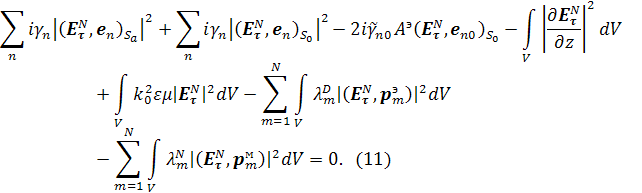
Взяв
от выражения (11) поочередно мнимую и действительную части, получим равномерные
по ![]() оценки:
оценки:
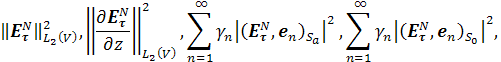
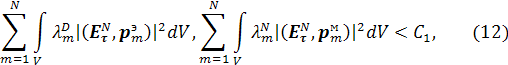
где
![]() не
зависит от
не
зависит от ![]() .
Аналогичным образом из задачи (5) получается равенство:
.
Аналогичным образом из задачи (5) получается равенство:
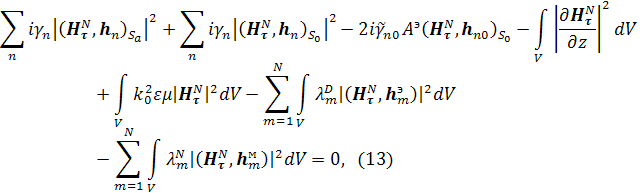
из которого также вытекают следующие оценки:

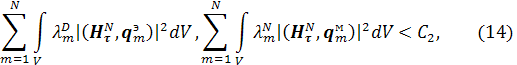
где ![]() –
не зависит от
–
не зависит от ![]() .
Из оценок (12) и (14) следует равномерная по
.
Из оценок (12) и (14) следует равномерная по ![]() ограниченность норм
ограниченность норм
![]() и
и
![]() и
принадлежность
и
принадлежность ![]() пространству
пространству
![]() .
Полагая в (11) и (13)
.
Полагая в (11) и (13) ![]() ,
получим что однородные задачи (4) и (5) имеют только тривиальное решение,
следовательно, построенное приближенное решение единственно. Теорема 1
доказана.
,
получим что однородные задачи (4) и (5) имеют только тривиальное решение,
следовательно, построенное приближенное решение единственно. Теорема 1
доказана.
Можно показать,
что существует обобщенное решение задачи (2). Накладывая на него условия дополнительной
гладкости, рассмотрим обобщенное решение из пространства ![]() .
.
Теорема 2.
Приближенное решение ![]() сходится
к точному решению задачи (2) по норме
сходится
к точному решению задачи (2) по норме ![]() .
.
Доказательство. Обобщенное решение представимо в виде разложения
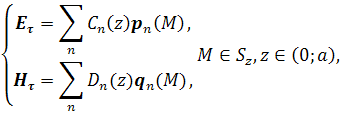
где коэффициенты ![]() и
и
![]() удовлетворяют
краевым задачам (4) и (5), в которых
удовлетворяют
краевым задачам (4) и (5), в которых ![]() нужно
заменить на
нужно
заменить на ![]() .
Введем невязку
.
Введем невязку
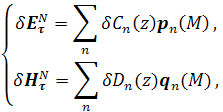
коэффициенты в которой определяются следующим образом:
![]()
![]()
и остаток
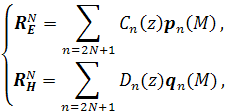
Применяя методику, используемую для доказательства теоремы 1, получим следующие соотношения:
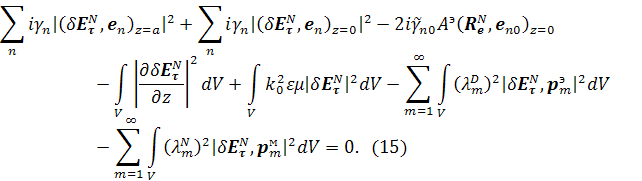
и
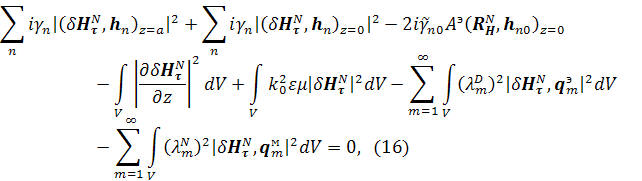
из которых при взятии поочередно
мнимой и действительной частей и устремлении ![]() к
бесконечности следует стремление приближенного решения к точному в пространстве
к
бесконечности следует стремление приближенного решения к точному в пространстве
![]() ,
а также существование пределов:
,
а также существование пределов:
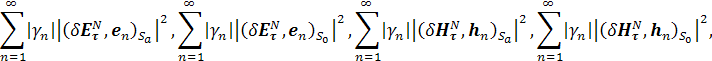
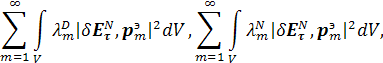
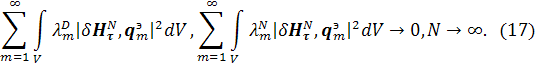
Теорема 2 доказана.
Заключение.
В данной работе рассмотрена
векторная модель волновода с входящими ребрами. Построено приближенное решение
данной математической задачи, для которого доказано существование и
единственность решения в пространстве ![]() . При наложении
дополнительной гладкости на обобщенное решение исходной задачи, доказана сходимость
приближенного решения к точному. Рассмотренный алгоритм построения приближенного
решения удобен для численного расчета задачи и позволяет учитывать особенности
решения, возникающие вследствие наличия входящего угла в поперечном сечении
нерегулярной части волновода.
. При наложении
дополнительной гладкости на обобщенное решение исходной задачи, доказана сходимость
приближенного решения к точному. Рассмотренный алгоритм построения приближенного
решения удобен для численного расчета задачи и позволяет учитывать особенности
решения, возникающие вследствие наличия входящего угла в поперечном сечении
нерегулярной части волновода.
Литература
1. Schiff B., Yosibash Z. Eigenvalues for Waveguides Containing Re-Entrant Corners by a Finite-Element Method with Superelements // IEEE Transactions on Microwave Theory and Techniques. 2000. 48, N 2. 214-220.
2. Mohamed Yahia, Jun W. Tao, Hafedh Benzina and Mohamed N. Abdelkrim. Ridged Waveguide Filter Optimization Using the Neural Networks and a Modified Simplex Method // International Journal of Innovation, Management and Technology. 2010. 1, N 3. 259-263. ISSN: 2010-0248
3. Santiago Cogollos, Stephan Marini, Vicente E. Boria, Pablo Soto, Ana Vidal Hector Esteban, Jose V. Morro, Benito Gimeno. Efficient Modal Analysis of Arbitrarily Shaped Waveguides Composed of Linear, Circular, and Elliptical Arcs Using the BI-RME Method // IEEE Transactions on Microwave Theory and Techniques. 2003. 51, N 12. 2378-2389.
4. Боголюбов А.Н., Ерохин А.И., Могилевский И.Е Математическое моделирование цилиндрического волновода с деформацией боковой поверхности // Вест. Моск. Ун-та. Серия 3. Физика. Астрономия. 2011. №6. С. 127-130.
5. Назаров С.А., Пламеневский Б.А. Эллиптические задачи в областях с кусочно-гладкой границей. М.: Наука, 1991.
6. Сьярле Ф. Метод конечных элементов для эллиптических задач. М.: Мир, 1980.
7. Свешников А.Г., Могилевский И.Е. Математические задачи теории дифракции. - М.: Физический факультет МГУ, 2010.