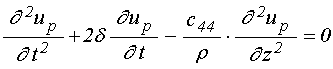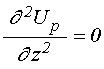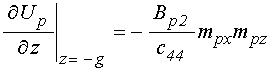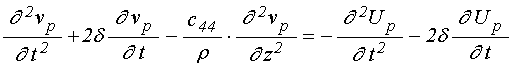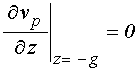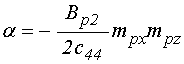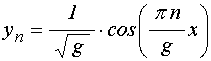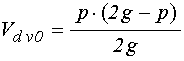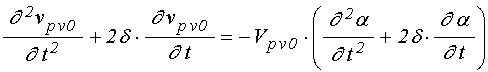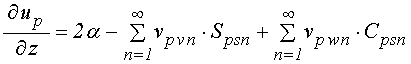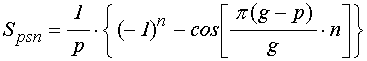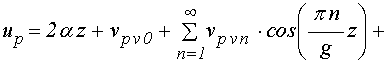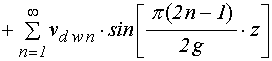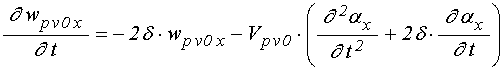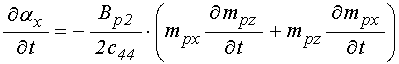УДК 537.874; 537.624
НЕЛИНЕЙНОЕ ВОЗБУЖДЕНИЕ ГИПЕРЗВУКА В ДВУХСЛОЙНОЙ ФЕРРИТОВОЙ СТРУКТУРЕ
В. С. Власов 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет
2 Институт радиотехники и электроники РАН
Получена 19 февраля 2013 г.
Аннотация. Рассмотрена нелинейная задача о возбуждении гиперзвука в нормально намагниченной структуре, состоящей из двух сложенных вместе бесконечно протяженных пластин из упругого магнитодиэлектрика, причем магнитные и магнитоупругие параметры слоев различны, а упругие – одинаковы. Получены уравнения движения и граничные условия для компонент намагниченностей и упругих смещений в слоях в случае произвольных углов прецессии векторов намагниченности. Выполнено численное решение полученной системы методом Рунге-Кутта. Показано, что в нелинейном режиме за счет взаимодействия магнитных резонансов слоев амплитуда возбуждаемого гиперзвука резко возрастает и может превышать амплитуду линейного режима более чем на два порядка.
Ключевые слова: гиперзвук, нелинейные колебания, магнитоупругость.
Abstract. The nonlinear task about hypersound excitation in normal magnetized structure is investigated. This structure consist of two infinite magnetic dielectric plates put together. The magnetic and magnetoelastic parameters of plates are different but elastic parameters are the same. The motion equations and boundary conditions for magnetization and elastic displacement components are found in the case of arbitrary magnetization vector angle. The numeric calculation of equation system is made by Runge-Cutta method. It is shown that in nonlinear regime because of magnetic resonances connection the excited hypersound amplitude increases to a great extent and may to exceed the linear regime amplitude on two orders.
Key words: hypersound, nonlinear vibrations, magnetoelasticity.
Введение
Задача возбуждения ультразвуковых
колебаний с помощью магнитострикционных преобразователей издавна привлекает
внимание исследователей [1-4]. Весьма перспективным является использование
таких преобразователей в магнитной акустоэлектронике, где высокая механическая
добротность ферритовых резонаторов (до ![]() при
использовании железоиттриевого граната (ЖИГ) ) позволяет создать
высокоэффективные устройства обработки информации в диапазоне СВЧ (
при
использовании железоиттриевого граната (ЖИГ) ) позволяет создать
высокоэффективные устройства обработки информации в диапазоне СВЧ (![]() ).
).
Первые экспериментальные работы по возбуждению гиперзвука с помощью магнитоакустических преобразователей на ЖИГ, работающих в условиях ферромагнитного резонанса (ФМР) [5, 6], выявили высокую эффективность возбуждения в сочетании с весьма малым затуханием звуковых импульсов. Однако вскоре было обнаружено [4, 7], что мощность подводимого сигнала не может превышать 1 мВт, что соответствует углу прецессии вектора намагниченности порядка 1 градуса, после чего потери резко увеличиваются из-за параметрического распада однородной прецессии на обменные спиновые волны [8-11].
В работах [12-17] было показано, что параметрический распад можно предотвратить путем выбора геометрии преобразователя в виде нормально намагниченного тонкого диска, низшая частота ФМР которого совпадает с "дном" спектра обменных волн. В результате в экспериментах были достигнуты углы прецессии намагниченности до 10-20 градусов и более [12-16].
Исторически первая теория возбуждения гиперзвука в таких условиях была построена в работах [3, 4]. Однако линейность использованного там приближения не позволила оценить максимально достижимую эффективность возбуждения. Некоторые особенности нелинейного приближения затронуты в работах [18, 19], однако проведенное там рассмотрение, будучи, в основном, качественным, является неполным и не позволяет выявить ограничения и предельные возможности возбуждения гиперзвука.
В работе [20] была построена нелинейная теория и с использованием данных работ [12-16] получена количественная оценка, согласно которой в нелинейном режиме амплитуда возбуждаемого гиперзвука может превосходить таковую в линейном режиме не менее чем в 30 раз.
Проведенное там рассмотрение относится к однородной структуре, магнитные и упругие параметры которой по всему объему сохраняются постоянными, тогда как можно ожидать, что учет неоднородности внесет существенные особенности в свойства возбуждаемых колебаний.
В настоящей работе рассматривается возбуждение гиперзвука в неоднородной структуре, образованной двумя наложенными друг на друга слоями магнитодиэлектрика, имеющими одинаковые упругие, но различные магнитные и магнитоупругие свойства.
1. Геометрия задачи и плотность энергии
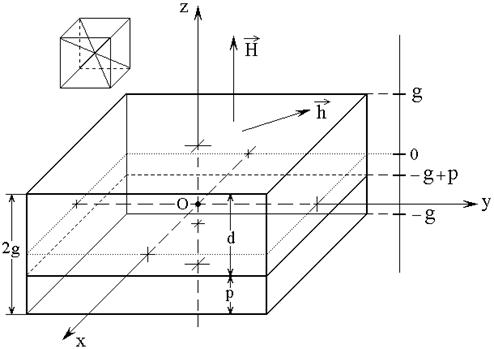
Рис.1. Общая геометрия задачи о двухслойной структуре.
Общая геометрия задачи показана
на рис.1. Двухслойная структура состоит из двух сложенных вместе бесконечно
протяженных пластин из упругого магнитодиэлектрика. Толщина первого слоя равна ![]() , второго равна
, второго равна ![]() ,
полная толщина всей структуры:
,
полная толщина всей структуры: ![]() . Начало координат
выбрано на середине толщины структуры в целом, то есть ее верхняя поверхность
соответствует координате
. Начало координат
выбрано на середине толщины структуры в целом, то есть ее верхняя поверхность
соответствует координате ![]() , нижняя – координате
, нижняя – координате ![]() , а граница раздела между слоями – координате
, а граница раздела между слоями – координате
![]() . Магнитные и магнитоупругие параметры
слоев различны и обозначаются далее индексами
. Магнитные и магнитоупругие параметры
слоев различны и обозначаются далее индексами ![]() и
и ![]() , а упругие – одинаковы и этих индексов не
имеют.
, а упругие – одинаковы и этих индексов не
имеют.
Положим плотность энергии
структуры ![]() в поле
в поле ![]() равной
сумме плотностей магнитной, упругой и магнитоупругой энергий слоев и оставим
только те константы, которые важны для дальнейшего рассмотрения:
равной
сумме плотностей магнитной, упругой и магнитоупругой энергий слоев и оставим
только те константы, которые важны для дальнейшего рассмотрения:
![]()
![]()
![]() , (1)
, (1)
где ![]() –
аналогичные слагаемые с заменой индекса
–
аналогичные слагаемые с заменой индекса ![]() на
индекс
на
индекс ![]() ;
; ![]() –
векторы намагниченности, нормированные на намагниченности насыщения
–
векторы намагниченности, нормированные на намагниченности насыщения ![]() ;
; ![]() –
компоненты тензора деформаций (
–
компоненты тензора деформаций (![]() ), соответствующие
упругим смещениям
), соответствующие
упругим смещениям ![]() ;
; ![]() – константы
кубической магнитной анизотропии;
– константы
кубической магнитной анизотропии; ![]() – константы упругости
(одинаковые в обоих слоях);
– константы упругости
(одинаковые в обоих слоях); ![]() – константы магнитоупругого
взаимодействия.
– константы магнитоупругого
взаимодействия.
2. Основные уравнения и граничные условия
Плотность энергии (1) позволяет записать полные уравнения движения для векторов намагниченности и упругих смещений для каждого из слоев, а также граничные условия, состоящие в отсутствии упругих напряжений на внешних поверхностях структуры в целом в совокупности с равенством напряжений и смещений на границе раздела слоев.
Аналогично [20], будем полагать распределения
намагниченностей ![]() внутри слоев однородными.
внутри слоев однородными.
Уравнения движения для компонент
намагниченности в слое ![]() имеют вид:
имеют вид:
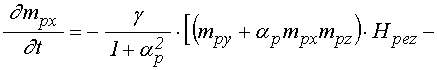
а уравнения для ![]() и
и ![]() получаются
отсюда циклической перестановкой
получаются
отсюда циклической перестановкой ![]() ,
, ![]() ,
, ![]() .
.
Здесь ![]() –
константа затухания, а эффективные поля равны:
–
константа затухания, а эффективные поля равны:
![]() ;
(4)
;
(4)
![]() ;
(5)
;
(5)
где:
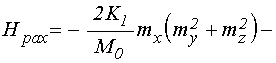
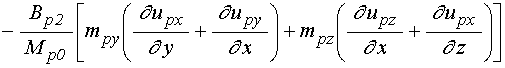 , (6)
, (6)
а ![]() и
и ![]() получаются циклической перестановкой
получаются циклической перестановкой ![]() ,
, ![]() ,
, ![]() .
.
Уравнения движения для компонент
намагниченности в слое ![]() получаются из (2)-(6) заменой
индекса
получаются из (2)-(6) заменой
индекса ![]() на
на ![]() .
.
Относительно упругих смещений, аналогично [20], примем следующие предположения:
упругие смещения,
перпендикулярные плоскости структуры, отсутствуют, то есть ![]() ;
;
упругие смещения в плоскости структуры
![]() и
и ![]() являются
однородными, то есть
являются
однородными, то есть ![]() .
.
Уравнение движения для ![]() - компоненты упругого смещения в слое
- компоненты упругого смещения в слое ![]() имеет вид:
имеет вид:
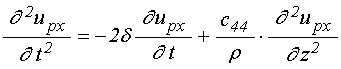 ;
(7)
;
(7)
где ![]() –
параметр затухания,
–
параметр затухания, ![]() – плотность материала, для
обоих слоев одинаковая. Это уравнение – волнового типа, которое при задании
граничных условий по координате
– плотность материала, для
обоих слоев одинаковая. Это уравнение – волнового типа, которое при задании
граничных условий по координате ![]() позволяет свести
координатную зависимость к совокупности собственных функций однородной задачи,
в результате чего главной задачей останется получение развития колебательного
процесса во времени, что и будет реализовано далее.
позволяет свести
координатную зависимость к совокупности собственных функций однородной задачи,
в результате чего главной задачей останется получение развития колебательного
процесса во времени, что и будет реализовано далее.
Уравнение движения для ![]() - компоненты упругого смещения в том же
слое
- компоненты упругого смещения в том же
слое ![]() получается из (7) путем замены индекса
получается из (7) путем замены индекса ![]() на
на ![]() , а
уравнение движения для
, а
уравнение движения для ![]() - компоненты в силу принятых
предположений отсутствует.
- компоненты в силу принятых
предположений отсутствует.
Уравнения движения для тех же компонент
упругих смещений в слое ![]() аналогичны (7) с
заменой индекса
аналогичны (7) с
заменой индекса ![]() на
на ![]() .
.
Граничные условия для
намагниченности в силу ее однородности не нужны, а граничные условия для ![]() - компонент смещений в слоях
- компонент смещений в слоях ![]() и
и ![]() имеют
вид:
имеют
вид:
на нижней поверхности структуры, при ![]() :
:
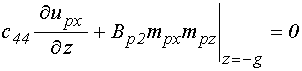 ;
(8)
;
(8)
на границе между слоями, при ![]() :
:
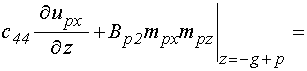
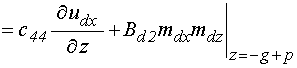 ; (9)
; (9)
![]() ;
(10)
;
(10)
на верхней поверхности структуры, при
![]() :
:
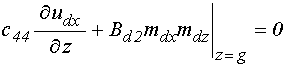 .
(11)
.
(11)
Граничные условия для ![]() - компонент смещений в тех же слоях имеют
вид, аналогичный (8)-(11) с заменой индекса
- компонент смещений в тех же слоях имеют
вид, аналогичный (8)-(11) с заменой индекса ![]() на
на ![]() .
.
Таким образом, полная система содержит: для компонент намагниченности шесть уравнений первого порядка без граничных условий, а для компонент упругих смещений – четыре уравнения второго порядка и восемь граничных условий.
Можно видеть, что уравнения колебаний намагниченности и упругого смещения в каждом из слоев взаимно независимы, а связь между ними осуществляется только через граничные условия (8)-(11). Такое обстоятельство позволяет рассматривать задачу в целом, как граничную задачу для упругости, в которой намагниченности слоев являются параметрами, зависящими только от времени.
С другой стороны, задачи для ![]() и
и ![]() компонент
упругого смещения (уравнение плюс граничные условия) в каждом из слоев взаимно независимы,
то есть достаточно рассмотреть только одну задачу, например, для
компонент
упругого смещения (уравнение плюс граничные условия) в каждом из слоев взаимно независимы,
то есть достаточно рассмотреть только одну задачу, например, для ![]() - компоненты, а решение для
- компоненты, а решение для ![]() - компоненты тогда получится путем замены
индекса
- компоненты тогда получится путем замены
индекса ![]() на
на ![]() . Поэтому
далее будем рассматривать задачу в совокупности для обоих слоев, но только для
. Поэтому
далее будем рассматривать задачу в совокупности для обоих слоев, но только для ![]() - компоненты.
- компоненты.
3. Полная формулировка задачи для упругости
Задача для ![]() - компонент упругого смещения в обоих
слоях имеет вид (индекс
- компонент упругого смещения в обоих
слоях имеет вид (индекс ![]() опускаем):
опускаем):
уравнения:
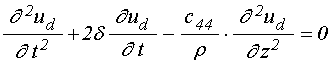 ;
(13)
;
(13)
граничные условия:
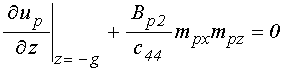 .
(14)
.
(14)
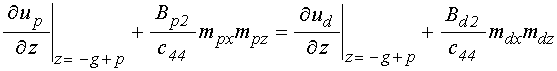 ; (15)
; (15)
![]() ;
(16)
;
(16)
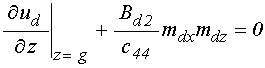 .
(17)
.
(17)
Это – задача для функций ![]() и
и ![]() двух
переменных
двух
переменных ![]() и
и ![]() , для
которых имеются уравнения второго порядка, содержащие производные по обеим переменным,
но не содержащие самих функций (то есть однородные), в совокупности с граничными
условиями для тех же функций и их первых производных по одной из переменных –
, для
которых имеются уравнения второго порядка, содержащие производные по обеим переменным,
но не содержащие самих функций (то есть однородные), в совокупности с граничными
условиями для тех же функций и их первых производных по одной из переменных – ![]() , содержащими в качестве параметров
функции от другой переменной –
, содержащими в качестве параметров
функции от другой переменной – ![]() (то есть неоднородными).
(то есть неоднородными).
Для решения такой задачи, аналогично
случаю одного слоя [20], следуя [21], воспользуемся разделением зависимости полного
решения от координаты ![]() на две части – линейную и
нелинейную.
на две части – линейную и
нелинейную.
4. Разделение задачи для упругости на сумму двух задач
Положим:
![]() ,
(19)
,
(19)
где ![]() и
и ![]() будем полагать линейными функциями
координаты
будем полагать линейными функциями
координаты ![]() при ненулевых граничных условиях, а
при ненулевых граничных условиях, а ![]() и
и ![]() –
нелинейными функциями той же координаты при нулевых граничных условиях.
–
нелинейными функциями той же координаты при нулевых граничных условиях.
Подставляя (18)-(19) в (12)-(17), разделяем единую задачу (12)-(17) на две отдельные задачи.
ЗАДАЧА № 1 – для ![]() и
и ![]() :
:
уравнения:
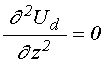 ;
(21)
;
(21)
граничные условия:
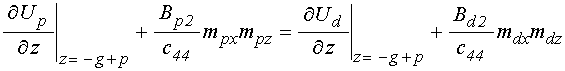 ;
(23)
;
(23)
![]() ;
(24)
;
(24)
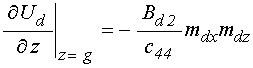 .
(25)
.
(25)
ЗАДАЧА № 2 – для ![]() и
и ![]() :
:
уравнения:
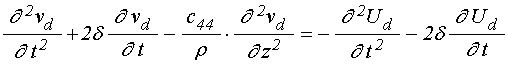 ;
(27)
;
(27)
граничные условия:
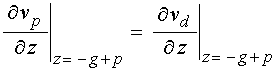 ;
(29)
;
(29)
![]() ;
(30)
;
(30)
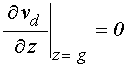 .
(31)
.
(31)
Задача №1 функций ![]() не содержит, поэтому может быть решена
независимо. Полученные в результате ее решения функции
не содержит, поэтому может быть решена
независимо. Полученные в результате ее решения функции ![]() должны
быть подставлены далее в задачу №2. Полное решение всей задачи в целом определяется
формулами (18)-(19). Рассмотрим эти задачи последовательно.
должны
быть подставлены далее в задачу №2. Полное решение всей задачи в целом определяется
формулами (18)-(19). Рассмотрим эти задачи последовательно.
5. Задача № 1 – для ![]() и
и ![]()
Интегрируя уравнения (20)-(21) два раза и подставляя полученные решения в граничные условия (22)-(25), получаем для определения четырех постоянных интегрирования систему из четырех уравнений, в которой только три являются независимыми.
Полагая не зависящую от ![]() часть функции
часть функции ![]() равной
нулю, получаем решение задачи (20)-(25) в виде:
равной
нулю, получаем решение задачи (20)-(25) в виде:
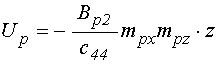 ;
(32)
;
(32)
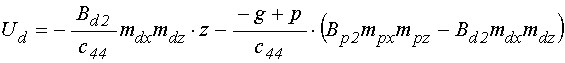 .
(33)
.
(33)
Как видим, оба эти выражения
линейно зависят от координаты ![]() , а при
, а при ![]() совпадают друг с другом.
совпадают друг с другом.
Введем обозначения:
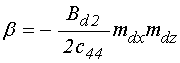 ;
(35)
;
(35)
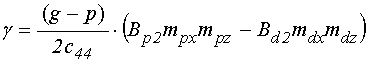 .
(36)
.
(36)
При этом получаем:
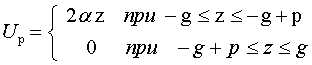 ;
(37)
;
(37)
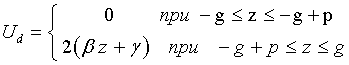 .
(38)
.
(38)
Итак, задача №1 решена, то есть
можно перейти к задаче №2 (26)-(31). Однако, поскольку эта задача является
неоднородной (правая часть уравнений (26)-(27) нулю не равна), то ее решение
может быть представлено только в виде суммы ряда по собственным функциям координатной
части соответствующей однородной задачи с нулевыми граничными условиями для
структуры в целом [20, 21]. Соответственно функции ![]() и
и ![]() , содержащиеся в правых частях уравнений (26)-(27),
также должны быть представлены в виде разложения в ряд по тем же собственным
функциям.
, содержащиеся в правых частях уравнений (26)-(27),
также должны быть представлены в виде разложения в ряд по тем же собственным
функциям.
6. Собственные функции координатной части однородной задачи для структуры в целом
Рассмотрим координатную часть
однородной задачи для структуры в целом. Согласно общей геометрии задачи
(рис.1), начало координат находится в центре структуры, а ее полная длина равна
![]() , то есть координаты начала и конца структуры
равны:
, то есть координаты начала и конца структуры
равны: ![]() ,
, ![]() . Поставленная
так задача имеет две системы ортогональных собственных функций:
. Поставленная
так задача имеет две системы ортогональных собственных функций:
четные собственные функции:
нечетные собственные функции:
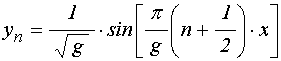 .
(40)
.
(40)
где ![]() -
любое целое число.
-
любое целое число.
7. Разложение функции ![]() в ряд по собственным функциям однородной задачи
в ряд по собственным функциям однородной задачи
Рассмотрим разложение функции ![]() в ряд по собственным функциям (39)-(40).
Полная функция
в ряд по собственным функциям (39)-(40).
Полная функция ![]() представляет собой ломаную
кривую, состоящую из двух линейных отрезков. Согласно общим правилам разложения
в ряд Фурье [22], такую функцию сначала надо представить в виде суммы двух частичных
функций, каждая из которых представляет собой один линейный отрезок, по обе
стороны от которого эта частичная функция равна нулю. Далее каждую частичную
функцию надо представить в виде суммы четной и нечетной частей, после чего
разложение производится отдельно для каждой из таких частей в ряды по четным и
нечетным собственным функциям. Исходная функция
представляет собой ломаную
кривую, состоящую из двух линейных отрезков. Согласно общим правилам разложения
в ряд Фурье [22], такую функцию сначала надо представить в виде суммы двух частичных
функций, каждая из которых представляет собой один линейный отрезок, по обе
стороны от которого эта частичная функция равна нулю. Далее каждую частичную
функцию надо представить в виде суммы четной и нечетной частей, после чего
разложение производится отдельно для каждой из таких частей в ряды по четным и
нечетным собственным функциям. Исходная функция ![]() будет
равна сумме всех этих рядов. Следуя такой процедуре, получаем разложение
функции
будет
равна сумме всех этих рядов. Следуя такой процедуре, получаем разложение
функции ![]() в виде:
в виде:
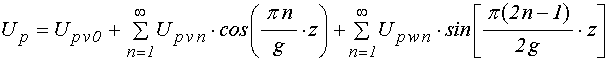 ,
(41)
,
(41)
где:
![]() ;
(42)
;
(42)
![]() ;
(43)
;
(43)
![]() ;
(44)
;
(44)
причем:
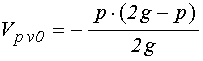 ;
(45)
;
(45)
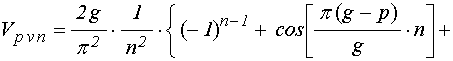
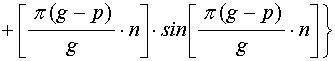 ;
(46)
;
(46)
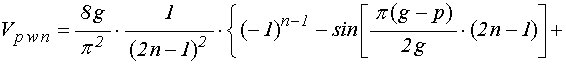
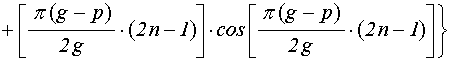 ,
(47)
,
(47)
Аналогично получаем разложение
функции ![]() :
:
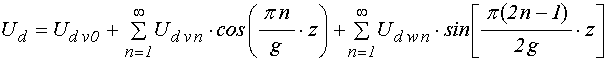 , (48)
, (48)
где:
![]() ;
(49)
;
(49)
![]() ;
(50)
;
(50)
![]() .
(51)
.
(51)
причем:
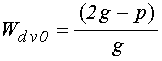 ;
(53)
;
(53)
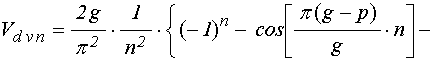
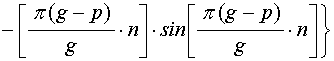 ; (54)
; (54)
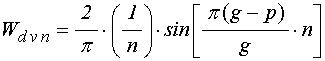 ;
(55)
;
(55)
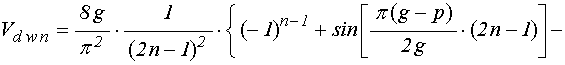
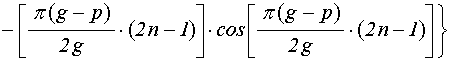 ;
(56)
;
(56)
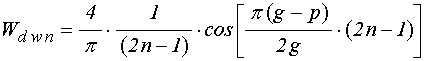 .
(57)
.
(57)
8. Задача № 2 – для ![]() и
и ![]() :
:
Рассмотрим теперь задачу №2 вида
(26)-(31), решение которой будем искать в виде разложения по собственным
функциям однородной задачи (39)-(40), для слоя ![]() имеющего
вид:
имеющего
вид:
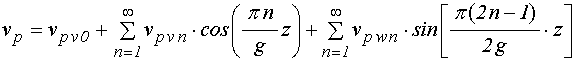 ; (58)
; (58)
где ![]() ,
, ![]() ,
, ![]() –
зависящие только от времени функции, подлежащие определению. Вид решения для
слоя
–
зависящие только от времени функции, подлежащие определению. Вид решения для
слоя ![]() аналогичен с заменой индекса
аналогичен с заменой индекса ![]() на
на ![]() .
.
Представление решения в таком виде обеспечивает выполнение граничных условий (28)-(31) автоматически.
Подставляя функции ![]() и
и ![]() в (26),
получаем уравнение, левая часть которого кроме свободного члена содержит
зависящие от
в (26),
получаем уравнение, левая часть которого кроме свободного члена содержит
зависящие от ![]() синусы и косинусы, происходящие из собственных
функций, тогда как правая его часть равна нулю. Такое уравнение может быть
удовлетворено только в том случае, если свободные члены, а также коэффициенты
при синусах и косинусах равны нулю. Аналогичное уравнение получается и для слоя
синусы и косинусы, происходящие из собственных
функций, тогда как правая его часть равна нулю. Такое уравнение может быть
удовлетворено только в том случае, если свободные члены, а также коэффициенты
при синусах и косинусах равны нулю. Аналогичное уравнение получается и для слоя
![]() .
.
В результате для коэффициентов
разложения функций ![]() и
и ![]() получаем
следующие уравнения:
получаем
следующие уравнения:
для слоя ![]() :
:
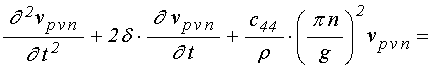
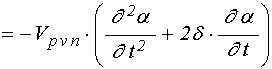 ; (60)
; (60)
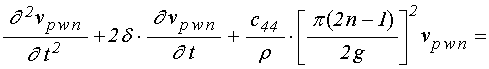
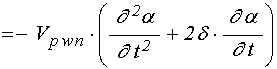 ; (61)
; (61)
для слоя ![]() :
:
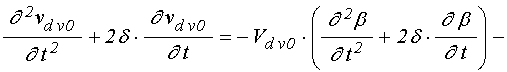
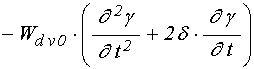 ;
(62)
;
(62)
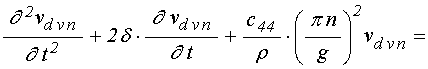
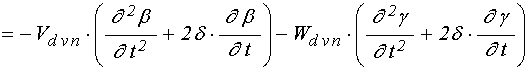 ;
(63)
;
(63)
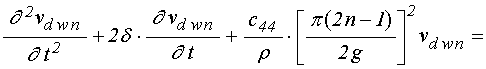
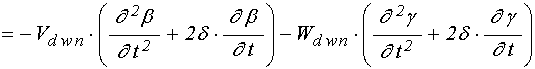 .
(64)
.
(64)
Таким образом, задача №2 решена.
При этом полная система уравнений исходной задачи включает в себя уравнения для
компонент векторов намагниченности ![]() вида (2) в
совокупности с уравнениями для функций
вида (2) в
совокупности с уравнениями для функций ![]() (59)-(64).
Однако полученная так система не позволяет в чистом виде найти искомые
зависимости намагниченностей и смещений от времени, так как входящие в
уравнения для намагниченностей эффективные поля (3)-(6), а также производные по
времени от функций
(59)-(64).
Однако полученная так система не позволяет в чистом виде найти искомые
зависимости намагниченностей и смещений от времени, так как входящие в
уравнения для намагниченностей эффективные поля (3)-(6), а также производные по
времени от функций ![]() ,
, ![]() ,
, ![]() (34)-(36), в свою очередь содержащие те
же поля, содержат на данном этапе не определенные координатные производные от
смещений
(34)-(36), в свою очередь содержащие те
же поля, содержат на данном этапе не определенные координатные производные от
смещений ![]() . Для устранения неопределенности, аналогично
работе [20], используем усредненные по координате
. Для устранения неопределенности, аналогично
работе [20], используем усредненные по координате ![]() значения
этих производных, с условием сохранения их зависимости от времени, то есть возьмем
производные в виде:
значения
этих производных, с условием сохранения их зависимости от времени, то есть возьмем
производные в виде:
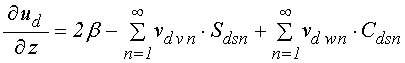 ,
(66)
,
(66)
где:
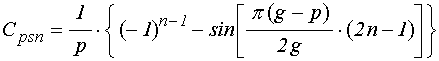 ;
(68)
;
(68)
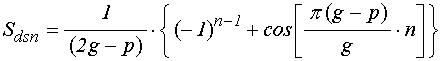 ;
(69)
;
(69)
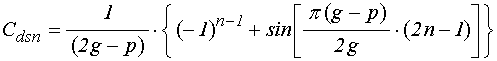 .
(70)
.
(70)
9. Вид решения полной задачи для упругости
Таким образом, решение полной задачи для упругости (18)-(19) принимает вид:
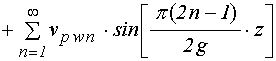 ; (71)
; (71)
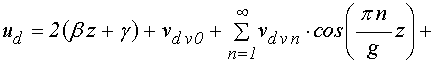
Полученные формулы содержат
зависимость от координаты ![]() , что позволяет найти
упругие смещения в любой точке слоев
, что позволяет найти
упругие смещения в любой точке слоев ![]() или
или ![]() соответственно. Чтобы найти смещения на
внешних поверхностях структуры надо в формуле (71) положить
соответственно. Чтобы найти смещения на
внешних поверхностях структуры надо в формуле (71) положить ![]() , а в формуле (72)
, а в формуле (72) ![]() .
.
Напомним, что приведенные здесь
выражения получены для ![]() - компоненты упругого смещения.
Для получения
- компоненты упругого смещения.
Для получения ![]() - компоненты смещения в этих
выражениях надо использовать составляющие, соответствующие координате
- компоненты смещения в этих
выражениях надо использовать составляющие, соответствующие координате ![]() .
.
10. Приведение полной задачи к виду, удобному для численного решения
Итак, полная система уравнений
для зависящих от времени намагниченностей и смещений содержит шесть уравнений
первого порядка для компонент намагниченности ![]() вида
(2) и
вида
(2) и ![]() уравнений второго порядка (59)-(64) для
функций смещений
уравнений второго порядка (59)-(64) для
функций смещений ![]() .
.
Используя стандартную процедуру
сведения одного уравнения второго порядка к двум уравнениям первого порядка [23,
24], из этих последних уравнений получаем ![]() уравнений
первого порядка. Таким образом, полная система уравнений первого порядка для
намагниченностей и упругих смещений, пригодная для численного решения, будет содержать
уравнений
первого порядка. Таким образом, полная система уравнений первого порядка для
намагниченностей и упругих смещений, пригодная для численного решения, будет содержать
![]() уравнений, где
уравнений, где ![]() –
число членов ряда разложения по собственным функциям однородной задачи.
–
число членов ряда разложения по собственным функциям однородной задачи.
Запишем теперь полную систему уравнений,
предназначенную для численного решения. Поскольку большинство полученных
выражений для слоя ![]() совпадает с подобными выражениями
для слоя
совпадает с подобными выражениями
для слоя ![]() при условии замены индекса
при условии замены индекса ![]() на индекс
на индекс ![]() , то
подробно запишем лишь уравнения для слоя
, то
подробно запишем лишь уравнения для слоя ![]() , а для
слоя
, а для
слоя ![]() укажем лишь отличия.
укажем лишь отличия.
Кроме особо оговоренных случаев
ограничимся выражениями для ![]() - компонент переменных,
учитывая, что подобные выражения для
- компонент переменных,
учитывая, что подобные выражения для ![]() и
и ![]() - компонент получаются циклической
перестановкой индексов
- компонент получаются циклической
перестановкой индексов ![]() ,
, ![]() ,
, ![]() .
.
Итак, получаем полную систему уравнений для численного решения в виде:
уравнения для компонент намагниченности, аналогичные (2):
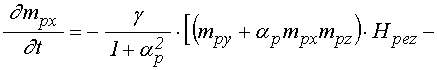
уравнения для функций ![]() :
:
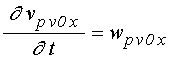 ;
(74)
;
(74)
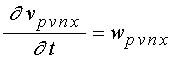 ;
(75)
;
(75)
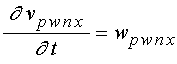 ;
(76)
;
(76)
уравнения для функций ![]() в слое
в слое ![]() :
:
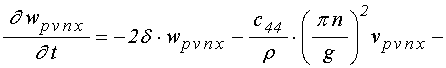
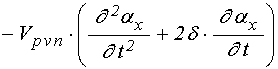 ; (78)
; (78)
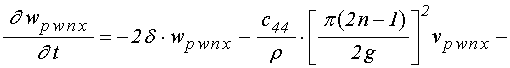
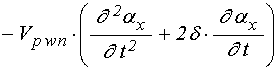 ; (79)
; (79)
уравнения для функций ![]() в слое
в слое ![]() :
:
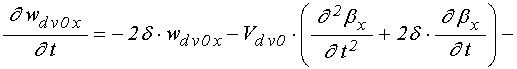
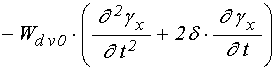 ;
(80)
;
(80)
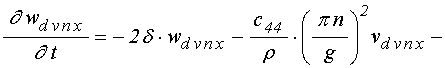
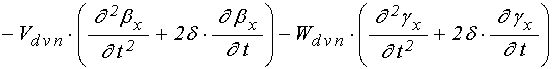 ;
;
(81)
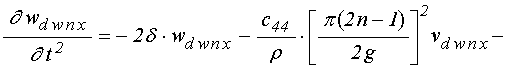
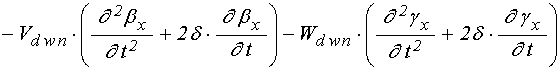 .
(82)
.
(82)
Входящие в уравнения для намагниченностей (73) эффективные поля определяются выражениями (3)-(6).
Входящие в эффективные поля
(3)-(6) первые производные от смещений по координате ![]() в
слоях
в
слоях ![]() и
и ![]() определяются
выражениями (65)-(66).
определяются
выражениями (65)-(66).
Функции ![]() ,
,
![]() ,
, ![]() и
коэффициенты
и
коэффициенты ![]() ,
, ![]() а
также
а
также ![]() ,
, ![]() определяются
выражениями (34)-(36), (67)-(70), (52)-(57).
определяются
выражениями (34)-(36), (67)-(70), (52)-(57).
Входящие в уравнения для смещений
(77)-(82) производные от функций ![]() ,
, ![]() ,
, ![]() имеют
вид:
имеют
вид:
первые и вторые производные от ![]() ,
, ![]() в
слое
в
слое ![]() :
:
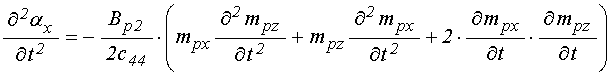 ; (84)
; (84)
первые и вторые производные от ![]() ,
, ![]() ,
, ![]() ,
, ![]() в
слое
в
слое ![]() :
:
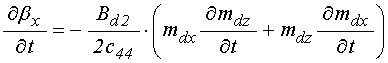 ;
(85)
;
(85)
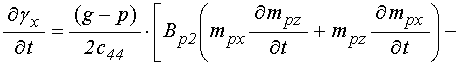
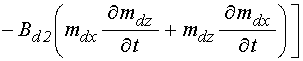 . (86)
. (86)
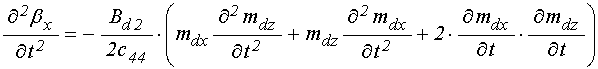 ; (87)
; (87)
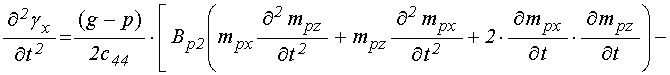
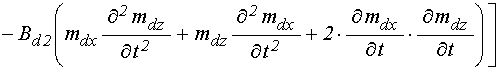 . (88)
. (88)
Входящие в выражения для
производных от функций ![]() ,
, ![]() ,
, ![]() (83)-(88) вторые производные по времени
от компонент намагниченностей, с учетом циклической замены координат, имеют
вид:
(83)-(88) вторые производные по времени
от компонент намагниченностей, с учетом циклической замены координат, имеют
вид:
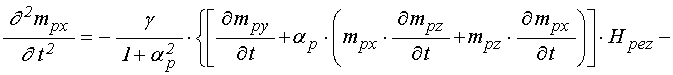
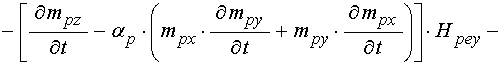
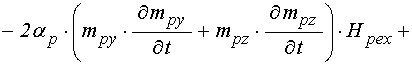
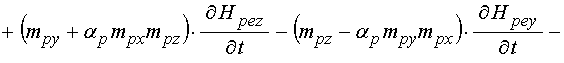
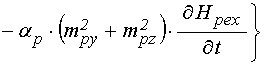 ; (89)
; (89)
Входящие в выражения для вторых производных от компонент намагниченности по времени (89) производные от эффективных полей имеют вид:
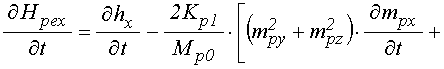
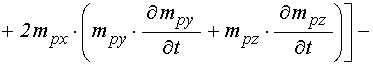
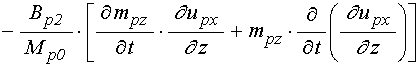 ;
(90)
;
(90)
аналогичное выражение для ![]() , получается из (90) циклической перестановкой
индексов
, получается из (90) циклической перестановкой
индексов ![]() ,
, ![]() ,
, ![]() , а выражение для
, а выражение для ![]() имеет
вид:
имеет
вид:
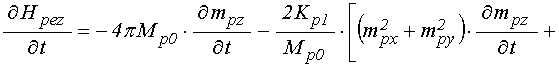
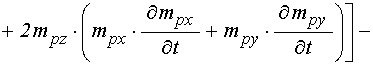
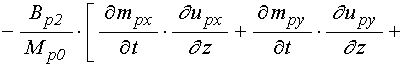
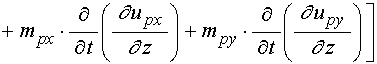 . (91)
. (91)
Входящие в выражения для производных от эффективных полей (90)-(91) смешанные производные от смещений по координате и времени имеют вид:
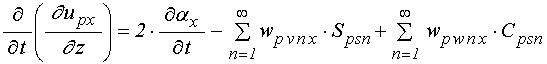 ; (92)
; (92)
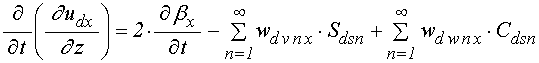 ; (93)
; (93)
Получаемые в результате решения системы уравнений (73)-(82) с учетом (83)-(93) компоненты и составляющие функций смещений позволяют найти полные функции смещений в обоих слоях с помощью выражений (71)-(72).
11. Схема реализации численного расчета
Как показано выше, полная система
(73)-(82) содержит ![]() уравнений первого порядка, где
уравнений первого порядка, где ![]() – число членов ряда.
– число членов ряда.
Контрольный расчет разложения
функций ![]() показал, что при одном члене ряда (
показал, что при одном члене ряда (![]() ) точность получаемого приближения
составляет около 15-20%, а для точности не хуже 5% требуется уже пять членов
ряда (
) точность получаемого приближения
составляет около 15-20%, а для точности не хуже 5% требуется уже пять членов
ряда (![]() ).
).
Однако при столь большом числе
членов ряда расчет, не давая серьезных качественных преимуществ, становится
крайне громоздким (система содержит 94 уравнения), поэтому для упрощения задачи
ограничимся далее одним членом ряда, то есть будем полагать ![]() . При этом получаем шесть уравнений
первого порядка для компонент намагниченностей и 24 уравнения первого порядка для
компонент упругих смещений, то есть всего 30 уравнений первого порядка.
. При этом получаем шесть уравнений
первого порядка для компонент намагниченностей и 24 уравнения первого порядка для
компонент упругих смещений, то есть всего 30 уравнений первого порядка.
В настоящей работе именно такая система была решена численно методом Рунге-Кутта четвертого порядка [25], результатом чего явилось получение развития во времени возбуждаемых переменным полем колебаний намагниченности и смещения.
Ввиду сложности задачи кратко остановимся на некоторых моментах ее решения.
12. Последовательность численных вычислений на одном шаге по времени
Единичный шаг по времени состоит
из двух этапов, соответствующих каждому из слоев ![]() и
и ![]() . Будем считать, что на каждом шаге
полагаются известными начальные значения компонент намагниченностей
. Будем считать, что на каждом шаге
полагаются известными начальные значения компонент намагниченностей ![]() и упругих смещений
и упругих смещений ![]() в обоих слоях и приведем возможную схему
последовательных вычислений для слоя
в обоих слоях и приведем возможную схему
последовательных вычислений для слоя ![]() внутри отдельного шага
по времени:
внутри отдельного шага
по времени:
1) вынуждающие поля ![]() ;
;
2) производные от вынуждающих
полей ![]() ;
;
3) первые производные от смещений
по координате ![]() ;
;
4) эффективные поля ![]() ;
;
5) первые производные от
намагниченностей по времени ![]() ;
;
6) первые производные от функций ![]() по времени
по времени ![]() ;
;
7) смешанные производные от
смещений по координате и времени ![]() ;
;
8) первые производные от
эффективных полей по времени ![]() ;
;
9) вторые производные от
намагниченностей по времени ![]() ;
;
10) первые производные от функций
![]() по времени
по времени ![]() ;
;
11) вторые производные от функций
![]() по времени
по времени ![]() ;
;
12) числовые коэффициенты ![]() ;
;
13) первые производные от функций
![]() по времени
по времени ![]() ;
;
14) полные функции ![]() .
.
Далее следует аналогичная
последовательность вычислений для слоя ![]() с заменой
в пунктах 10 и 11 функций
с заменой
в пунктах 10 и 11 функций ![]() на функции
на функции ![]() ,
, ![]() , а
также в пункте 12 дополнительного вычисления коэффициентов
, а
также в пункте 12 дополнительного вычисления коэффициентов ![]() . В результате получается совокупность
первых производных по времени от компонент намагниченностей
. В результате получается совокупность
первых производных по времени от компонент намагниченностей ![]() и функций
и функций ![]() ,
, ![]() (пункты 5, 6, 13), составляющих полную
систему уравнений для данного шага численного решения. Полученные производные
позволяют найти новые значения намагниченностей
(пункты 5, 6, 13), составляющих полную
систему уравнений для данного шага численного решения. Полученные производные
позволяют найти новые значения намагниченностей ![]() и
упругих смещений
и
упругих смещений ![]() , которые затем передаются на следующий
шаг.
, которые затем передаются на следующий
шаг.
Применение такой схемы последовательных вычислений позволяет найти развитие колебаний намагниченности и упругих смещений во времени, что и дает решение поставленной задачи.
Отметим некоторые особенности численного решения.
13. Нормировка намагниченности
При выполнении математических действий в пределах каждого шага по времени, получаемое на конце шага значение намагниченности, как правило, несколько отличается от значения, вводимого в начале шага, что обусловлено приближенным характером численного интегрирования.
При последовательном прохождении нескольких шагов подобная ошибка накапливается, что приводит к постепенному увеличению значения намагниченности.
Так, при величине шага порядка 0,01 от периода переменного поля, после прохождения 100-200 периодов колебаний, ошибка может составлять до 10-20% от начальной величины намагниченности, а при дальнейшем развитии колебаний может привести к бесконечно большому ее росту, что противоречит физическому смыслу задачи.
Для предотвращения такой ошибки в конце каждого шага по времени длина нормированного вектора намагниченности приводится к единице, для чего координатные компоненты намагниченности умножаются на поправочный коэффициент, обратный полученному в конце шага модулю вектора намагниченности.
14. Немагнитный слой
Для рассмотрения слоя, являющегося немагнитным, в условиях данной задачи нельзя устанавливать намагниченность этого слоя равной нулю, так как возникает расходимость уже при расчете нормированной намагниченности, а также во многих последующих выражениях.
В численном расчете для предотвращения расходимости достаточно положить намагниченность такого слоя равной крайне малой величине, например, на четыре-пять порядков меньше намагниченности магнитного слоя.
В линейном режиме при этом амплитуда колебаний намагниченности такого «немагнитного» слоя будет на те же четыре пять порядков меньше амплитуды колебаний намагниченности магнитного слоя.
Однако в сильно нелинейном режиме это соотношение значительно ухудшится и составит не более одного-двух порядков, что в ряде задач нельзя считать достаточно корректным.
Для устранения такого обстоятельства следует на этапе приведения длины вектора намагниченности к начальному значению коэффициент приведения заведомо положить равным величине, на четыре-пять порядков меньшей единицы (положить этот коэффициент равным нулю нельзя из-за той же расходимости).
Проверочным критерием того, что слой действительно является немагнитным, может явиться нулевая или крайне малая амплитуда магнитных колебаний в этом слое (по крайней мере на четыре-пять порядков меньшая амплитуды колебаний в магнитном слое).
При описанной нормировке коэффициента приведения такая проверка дает положительный результат в том числе в режиме столь сильной нелинейности, когда нормированная поперечная компонента переменной намагниченности в магнитном слое приближается к единице.
15. Пример численного расчета для случая двух магнитных слоев с различными параметрами
Применим теперь описанный математический аппарат к задаче о возбуждении гиперзвука. Будем решать систему уравнений (73)-(82), с учетом выражений (83)-(93), численно методом Рунге-Кутта четвертого порядка [25].
Рассмотрим развитие колебаний во времени при различных частотах магнитных резонансов отдельных слоев.
Будем использовать параметры материала слоев близкие к параметрам ЖИГ:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() . Кубическую
анизотропию учитывать не будем:
. Кубическую
анизотропию учитывать не будем: ![]() . Для лучшего
разрешения кривых на рисунках, параметры затухания магнитных и упругой
подсистем выберем равными
. Для лучшего
разрешения кривых на рисунках, параметры затухания магнитных и упругой
подсистем выберем равными ![]() ;
; ![]() ,
, ![]() (что
несколько превышает типичные для ЖИГ значения
(что
несколько превышает типичные для ЖИГ значения ![]() и
и ![]() ). При таких значениях параметров
затухания времена установления стационарной амплитуды для всех видов колебаний
составляют около
). При таких значениях параметров
затухания времена установления стационарной амплитуды для всех видов колебаний
составляют около ![]() .
.
Положим частоту возбуждения ![]() . Для первой упругой моды этой частоте
соответствует толщина структуры:
. Для первой упругой моды этой частоте
соответствует толщина структуры: ![]() . Толщины слоев в этих
пределах могут быть заданы произвольно, поэтому положим их равными:
. Толщины слоев в этих
пределах могут быть заданы произвольно, поэтому положим их равными: ![]() ,
, ![]() (то
есть толщина слоя
(то
есть толщина слоя ![]() составляет
составляет ![]() , а толщина слоя
, а толщина слоя ![]() -
-
![]() от толщины структуры в целом).
от толщины структуры в целом).
Постоянное поле положим равным ![]() . Амплитуду переменного поля
. Амплитуду переменного поля ![]() в линейном режиме зададим равной
в линейном режиме зададим равной ![]() , а в нелинейном –
, а в нелинейном – ![]() .
Поляризацию переменного поля в плоскости структуры зададим круговой:
.
Поляризацию переменного поля в плоскости структуры зададим круговой:
![]() ;
(94)
;
(94)
![]() .
(95)
.
(95)
При принятых условиях частота
упругого резонанса структуры в целом, а также частота линейного магнитного
резонанса в слое ![]() получаются равными частоте
возбуждения
получаются равными частоте
возбуждения ![]() , а частота линейного магнитного резонанса
в слое
, а частота линейного магнитного резонанса
в слое ![]() при этом будет несколько меньшей и
составит
при этом будет несколько меньшей и
составит ![]() .
.
Полученные зависимости от времени
для компонент намагниченности ![]() и смещения
и смещения ![]() на внешних поверхностях структуры в
случаях линейного и нелинейного режимов показаны на рис.2.
на внешних поверхностях структуры в
случаях линейного и нелинейного режимов показаны на рис.2.
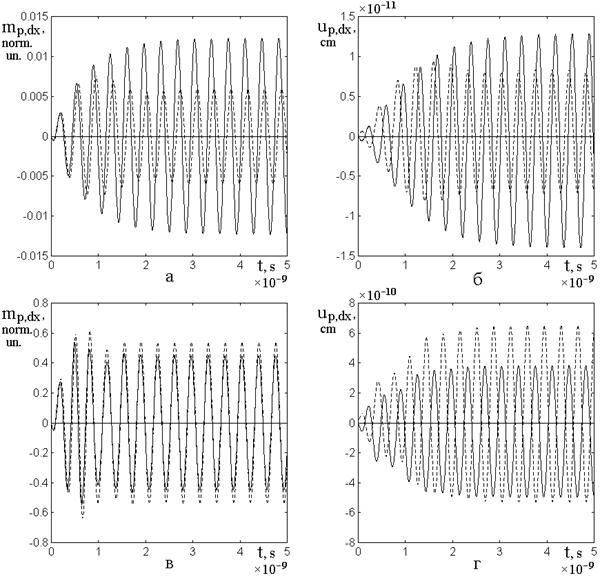
Рис.2. Развитие колебаний
намагниченности ![]() и смещения
и смещения ![]() во времени для слоев
во времени для слоев ![]() (сплошные линии) и
(сплошные линии) и ![]() (пунктирные линии)
(пунктирные линии)
в линейном (а, б) и нелинейном (в, г) режимах.
Из рисунка видно следующее.
На рис.2а, 2б (линейный режим) в
слое ![]() развитие как магнитных, так и упругих колебаний
происходит путем плавного нарастания без биений, тогда как в слое
развитие как магнитных, так и упругих колебаний
происходит путем плавного нарастания без биений, тогда как в слое ![]() оба вида колебаний нарастают с небольшими
биениями.
оба вида колебаний нарастают с небольшими
биениями.
Амплитуда как магнитных, так и
упругих колебаний в стационарном режиме в слое ![]() меньше,
чем в слое
меньше,
чем в слое ![]() приблизительно в два раза.
приблизительно в два раза.
Фаза магнитных колебаний в слое ![]() опережает фазу в слое
опережает фазу в слое ![]() на угол порядка
на угол порядка ![]() градусов,
фаза упругих колебаний в слое
градусов,
фаза упругих колебаний в слое ![]() отстает от фазы в слое
отстает от фазы в слое
![]() на примерно ту же величину.
на примерно ту же величину.
На рис.2в, 2г (нелинейный режим) развитие магнитных колебаний в обоих слоях происходит с биениями, тогда как при развитии упругих колебаний биения отсутствуют.
Амплитуда как магнитных, так и
упругих колебаний в стационарном режиме в слое ![]() заметно
превышает амплитуду тех и других колебаний в слое
заметно
превышает амплитуду тех и других колебаний в слое ![]() . Такое
превышение для магнитных колебаний составляет 1,2 раза, а для упругих – 1,5
раза.
. Такое
превышение для магнитных колебаний составляет 1,2 раза, а для упругих – 1,5
раза.
Фазы магнитных колебаний в обоих
слоях совпадают, фазы упругих колебаний в слоях ![]() и
и ![]() отличаются на 180 градусов, то есть
противоположные поверхности структуры колеблются в противофазе.
отличаются на 180 градусов, то есть
противоположные поверхности структуры колеблются в противофазе.
Из сравнения линейного и нелинейного режимов видно следующее:
амплитуда магнитных колебаний в
нелинейном режиме превышает амплитуду тех же колебаний в линейном режиме в слое
![]() в 38 раз, а в слое
в 38 раз, а в слое ![]() - в 110 раз;
- в 110 раз;
амплитуда упругих колебаний в
нелинейном режиме превышает амплитуду тех же колебаний в линейном режиме в слое
![]() в 33 раза, а в слое
в 33 раза, а в слое ![]() - в 71 раз.
- в 71 раз.
Физическая природа наблюдаемых
явлений состоит в том, что в линейном режиме магнитные резонансные
характеристики в обоих слоях имеют достаточно узкий симметричный
колоколообразный вид и между собой не перекрываются. При этом резонансная частота
в слое ![]() равна частоте возбуждения, в результате
чего биения отсутствуют и стационарная амплитуда принимает максимальное
допустимое параметром затухания значение. Для слоя же
равна частоте возбуждения, в результате
чего биения отсутствуют и стационарная амплитуда принимает максимальное
допустимое параметром затухания значение. Для слоя же ![]() частота
возбуждения выше резонансной, что и вызывает биения и не позволяет амплитуде
развиться до максимума. Амплитуды упругих колебаний в обоих слоях
пропорциональны амплитуде магнитных, поэтому в слое
частота
возбуждения выше резонансной, что и вызывает биения и не позволяет амплитуде
развиться до максимума. Амплитуды упругих колебаний в обоих слоях
пропорциональны амплитуде магнитных, поэтому в слое ![]() амплитуда
упругих колебаний меньше, чем в слое
амплитуда
упругих колебаний меньше, чем в слое ![]() .
.
В нелинейном режиме магнитные
резонансные характеристики в обоих слоях значительно расширяются и становятся
резко несимметричными, принимая вид широких треугольников, вершины которых
сильно отклонены в сторону высоких частот. Такое их поведение обусловлено
традиционным расстроечным механизмом ограничения нелинейных колебаний [26, 27].
При достаточной нелинейности наклоненная вершина резонансной кривой слоя ![]() достигает частоты возбуждения, в
результате чего амплитуда магнитных колебаний в этом слое резко возрастает,
приводя к значительному росту амплитуды упругих колебаний. Такой рост магнитных
колебаний в слое
достигает частоты возбуждения, в
результате чего амплитуда магнитных колебаний в этом слое резко возрастает,
приводя к значительному росту амплитуды упругих колебаний. Такой рост магнитных
колебаний в слое ![]() и обусловливает наблюдаемое
превышение амплитуды как магнитных, так и упругих колебаний этого слоя над такими
же колебаниями слоя
и обусловливает наблюдаемое
превышение амплитуды как магнитных, так и упругих колебаний этого слоя над такими
же колебаниями слоя ![]() .
.
Относительный сдвиг фазы линейных
магнитных колебаний в слоях ![]() и
и ![]() вызван различием их резонансных частот и
соответствует известному сдвигу фазы вынужденных колебаний при возбуждении вне
резонанса [26, 27]. Относительный сдвига фазы упругих колебаний в этом случае,
надо полагать, вызван суперпозицией магнитных колебаний различных слоев при
учете единства упругой колебательной системы. В нелинейном режиме все три
системы, упругая и обе магнитных, возбуждаются в резонансных условиях, поэтому
фазы магнитных колебаний в обоих слоях совпадают, а фазы упругих колебаний на
противоположных поверхностях структуры являются противоположными, что
аналогично противофазному характеру первой моды колебаний концов струны со
свободными концами [21].
вызван различием их резонансных частот и
соответствует известному сдвигу фазы вынужденных колебаний при возбуждении вне
резонанса [26, 27]. Относительный сдвига фазы упругих колебаний в этом случае,
надо полагать, вызван суперпозицией магнитных колебаний различных слоев при
учете единства упругой колебательной системы. В нелинейном режиме все три
системы, упругая и обе магнитных, возбуждаются в резонансных условиях, поэтому
фазы магнитных колебаний в обоих слоях совпадают, а фазы упругих колебаний на
противоположных поверхностях структуры являются противоположными, что
аналогично противофазному характеру первой моды колебаний концов струны со
свободными концами [21].
Можно отметить также некоторую
наблюдаемую на рис.2г несимметричность колебаний смещения. Так для слоя ![]() общая синусоида развертки колебаний во
времени сдвинута вниз по рисунку на
общая синусоида развертки колебаний во
времени сдвинута вниз по рисунку на ![]() , а синусоида развертки
колебаний для слоя
, а синусоида развертки
колебаний для слоя ![]() – сдвинута вверх на примерно
такую же величину. Такая несимметричность означает, что в нелинейном режиме
средняя во времени толщина структуры в целом несколько изменяется, а именно –
увеличивается приблизительно на
– сдвинута вверх на примерно
такую же величину. Такая несимметричность означает, что в нелинейном режиме
средняя во времени толщина структуры в целом несколько изменяется, а именно –
увеличивается приблизительно на ![]() от своей первоначальной
величины.
от своей первоначальной
величины.
Причиной несимметричности, по-видимому, является несимметричность граничных условий на различных поверхностях каждого слоя в отдельности: внутренние поверхности слоев контактируют друг с другом, тогда как внешние – свободны. Дополнительную неэквивалентность граничных условий для обоих слоев создает различие их намагниченностей, что особенно сильно проявляется в нелинейном режиме.
Заключение
Основные результаты работы сводятся к следующему.
Рассмотрена нелинейная задача о возбуждении гиперзвука в нормально намагниченной двухслойной структуре, состоящей из двух сложенных вместе бесконечно протяженных пластин из упругого магнитодиэлектрика, причем магнитные и магнитоупругие параметры слоев различны, а упругие – одинаковы.
Получены уравнения движения и граничные условия для компонент намагниченностей и упругих смещений в слоях в случае произвольных углов прецессии векторов намагниченности.
Показано, что в результате разложения по собственным модам упругих колебаний структуры в целом, задача сводится к системе бесконечного числа дифференциальных уравнений второго порядка относительно упругих мод.
В частном случае возбуждения только первой упругой моды полная задача упрощается до системы из тридцати нелинейных дифференциальных уравнений первого порядка (шесть уравнений для компонент намагниченностей слоев и двадцать четыре уравнения для компонент упругих смещений).
Такая упрощенная система уравнений решена численно методом Рунге-Кутта четвертого порядка. Рассмотрено развитие колебаний во времени, происходящее в результате включения переменного поля.
Показано, что при возбуждении на частоте упругого резонанса, если частота магнитного резонанса одного из слоев в линейном режиме совпадает с частотой возбуждения, а в другом – ниже этой частоты, то амплитуда упругих колебаний выше в том слое, частота магнитных колебаний которого совпадает с частотой возбуждения.
В сильно нелинейном режиме амплитуда упругих колебаний в другом слое резко возрастает, превышая амплитуду упругих колебаний в первом слое, в результате чего общая амплитуда возбуждаемого гиперзвука значительно увеличивается.
Наблюдаемая особенность нелинейного режима объяснена асимметричным наклоном резонансной кривой магнитных колебаний второго слоя, обусловленным нелинейной расстройкой.
Показано, что при увеличении амплитуды возбуждения на два порядка амплитуда упругих колебаний в сильно нелинейном режиме превышает амплитуду тех же колебаний в линейном режиме от 30 до 70 раз.
Работа поддержана РФФИ (гранты №10-02-01327-а, №12-02-01035-а).
Литература
1. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.
2. Голямина И.П. Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М., Наука, 1967.
3. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.
4. Ле-Кроу Р., Комсток Р. В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.
5. Bommel H.E., Dransfeld K. // Phys. Rev. Lett. 1959. V.3. № 2. P.83.
6. Spencer E.G., Denton R.T., Chambers R.P. // Phys. Rev. 1962. V.125. № 6. P.1950.
7. Eggers F.G., Strauss W. // J. Appl. Phys. 1963. V.34. № 4. Pt.2. P.1180.
8. Ферриты в нелинейных сверхвысокочастотных устройствах: Сб. статей: Пер. с англ. под ред. А.Г. Гуревича. М.: ИЛ. 1961.
9. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209. (Перевод в [8]. С.163.).
10. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
11. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.
12. A.G. Temiryazev, M.P. Tikhomirova, P.E. Zilberman. // J. Appl. Phys. 1994. V.76. №12. P.5586.
13. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ, 1995. Т.108. №1. С.281.
14. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
15. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
16. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
17. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. № 8. С.831.
18. Власов В.С. // Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. М.: МГУ. 2007.
19. Карпачев С.Н., Власов В.С., Котов Л.Н. // Вестник МГУ. Сер.3. 2006. № 6. С.60.
20. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
21. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука. 1972.
22. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. М.: Наука. 1964.
23. Степанов В.В. Курс дифференциальных уравнений. М.,Л.: ОГИЗ. Гос. изд. техн.-теор. лит. 1945.
24. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука. 1965.
25. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
26. Стрелков С.П. Введение в теорию колебаний. М.: Наука. 1964.
27. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.