УДК 621.396.67
Синтез апланатической линзы с двумерным градиентом показателя преломления
А. С. Венецкий, В. А. Калошин
Институт радиотехники и электроники им. В.А. Котельникова РАН
Получена 14 февраля 2013 г.
Аннотация. В приближении геометрической оптики рассмотрена двумерная задача синтеза среды с двумерным градиентом показателя преломления, преобразующей поле точечного источника в плоский фронт с выполнением условия синусов Аббе. Для нахождения закона распределения показателя преломления использован метод заданных лучевых траекторий. Задача сведена к дифференциальному уравнению в частных производных первого порядка относительно коэффициента преломления среды, которое решено методом характеристик. Приведено несколько вариантов реализации среды в зависимости от выбора распределения коэффициента преломления вдоль оси. Исследованы аберрации эйконала на границе синтезированной среды при смещении источника из фокуса. Проведено сравнение c характеристиками линзы Микаэляна.
Ключевые слова: геометрическая оптика, неоднородные среды, линзы, синтез.
Abstract: Two-dimensional problem of synthesis of media with two-dimensional gradient of a refraction index, transforming a field from a point source to a flat front with of Abbe sine condition satisfaction is considered in a geometrical optics approach. The method of the given ray trajectories to find a refraction index distribution is used. The problem is reduced to a partial differential equation of the first order for the refraction index which is solved by the method of characteristics. Some realizations of media depending on a choice of the index of refraction distribution along the axis are given. The eikonal aberrations in the synthesized medium boundary for the source shifted from the focus are investigated. A comparison with Mikaelian lens characteristics is carried out.
Key words: geometrical optics, inhomogeneous media, lenses, synthesis.
Среда с одномерным градиентом коэффициента преломления и прямолинейными границами не позволяют обеспечить преобразование падающего волнового фронта в заданный волновой фронт с заданным законом отображения. Задача синтеза линзы с одномерным градиентом коэффициента преломления и криволинейными границами по падающему и выходящему волновым фронтам и заданному закону отображения рассмотрена в работах [1-3]. Ниже, в приближении геометрической оптики рассмотрена задача синтеза среды с прямолинейными границами и двумерным градиентом, преобразующая поле точечного источника в плоский фронт с выполнением условия апланатизма (условия синусов Аббе). Такой закон отображения обеспечивает отсутствие аберраций, пропорциональных первой степени величины поперечного смещения источника из фокуса линзы.
Рассмотрим задачу синтеза неоднородной среды, осуществляющей преобразование поля точечного источника, расположенного в начале декартовой системы координат Z,X (точка О на рис. 1) в плоскую волну на границе среды Z=1 с законом отображения:
![]() (1)
(1)
где Х0 – координата точки выхода луча на границе среды Z=1, a - угол наклона луча в точке О, f – постоянный коэффициент.
Соотношение (1) – известное условие синусов Аббе для апланатических телескопических систем [4,5]. Среда с одномерным градиентом показателя преломления в декартовой системе координат (линза Микаэляна) этому условию не удовлетворяет [5].
Будем синтезировать среду с коэффициентом преломления n, зависящим от двух координат (x, z). Используем для этого метод нахождения показателя преломления неоднородной среды по заданным траекториям лучей [6].
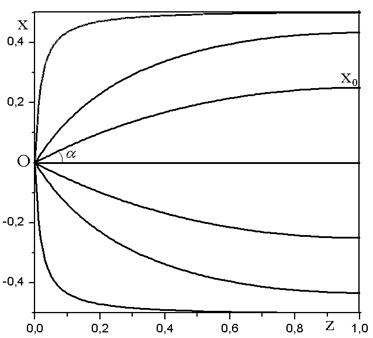
Рис. 1 Траектории лучей в среде с двумерным градиентом
Зададим однопараметрическое семейство кривых, ![]() ,
удовлетворяющих условиям фокусировки и синусов Аббе
,
удовлетворяющих условиям фокусировки и синусов Аббе
![]()
![]() ,
,
![]()
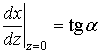 (2)
(2)
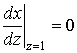
![]()
Этим условиям удовлетворяет бесконечное множество семейств кривых, а каждому семейству – бесконечное множество решений для коэффициента преломления n(z,x). Будем искать частное решение задачи. Нетрудно показать, что приведенным выше условиям удовлетворяет семейство лучей:
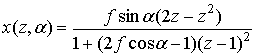 (3)
(3)
Траектории семейства лучей, описываемых формулой (3) для f =0.5 показаны на рис.1. При данном значении f и –p/2 <a < p/2 размеры среды по обеим координатам равны. При этом любой точке с координатами z,x при 0<z£1, f<x<f соответствует единственная кривая из семейства (3), проходящая через эту точку, а значение параметра a этой кривой определяется формулами:
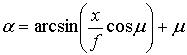 ,
, 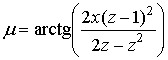 , (4)
, (4)
Будем искать закон распределения коэффициента преломления n(z,x), реализующий данные траектории лучей. Для траектории произвольного луча в двумерной неоднородной среде справедливо уравнение Эйлера:
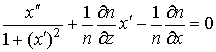 (5)
(5)
которое, если
ввести новую функцию ![]() , можно записать в виде:
, можно записать в виде:
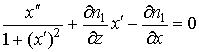 (6)
(6)
Для лучей семейства (3) справедливо
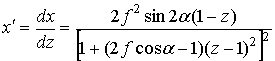 (7)
(7)
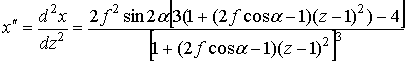 (8)
(8)
Так как лучи семейства (3) плотно покрывают область 0<z£1, –f<x< f , то подставляя параметр a ,выраженный через z,x в (4), в (7), (8) и, затем, в уравнение (6), получим дифференциальное уравнение относительно n1(z,x) во всей искомой области:
![]() (9)
(9)
где 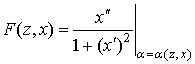 ,
, ![]() .
.
Из теории линейных дифференциальных уравнений в частных производных первого порядка известно (см., например, [7]), что интеграл такого уравнения может быть получен из интегралов системы обыкновенных дифференциальных уравнений, построенных из коэффициентов исходного уравнения – так называемых характеристических уравнений, которые для уравнения (9) имеют вид:
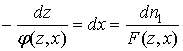 (10)
(10)
Необходимо отметить, что эта задача имеет бесконечно много решений.
Для получения единственного решения будем задавать величину n(z,x) на оси z:
n(z,0)= n0(z) (11)
В этом случае значение n(z0,x0) в произвольной точке Р среды с координатами z0,x0 , удовлетворяющими условиям 0<z0£1, –f<x0<f, находится последовательным интегрированием уравнений (10). Интегрируя первое уравнение системы (10), находим характеристическую кривую z=y(x) на отрезке [0, x0], проходящую через точку Р(z0,x0 ). После чего интегрируем второе уравнение системы (10), в котором переменные разделяются, и получаем решение в виде:
![]()
Возвращаясь к исходной функции показателя преломления, получаем:
![]() (12)
(12)
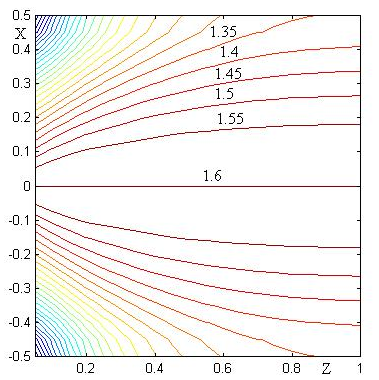
Рис. 2 Линии уровня n(z,x) при n0(z)=1.6
На рисунках 2-4 приведены линии уровня n(z,x) при f=0.5 для трех распределений n0(z), рассчитанные по формуле (12).
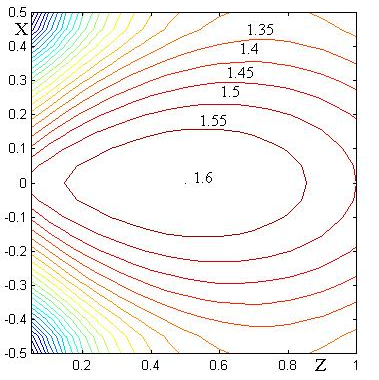
Рис. 3 Линии уровня n(z,x) при n0(z)=1.5+0.4z–0.4z2
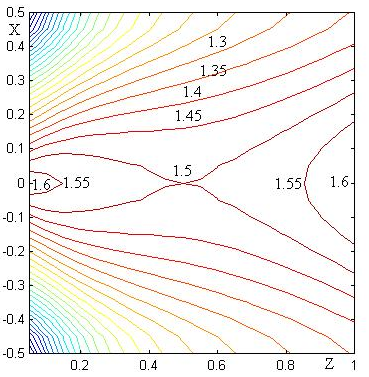
Рис. 4 Линии уровня n(z,x) при n0(z)=1.6–0.4z+0.4z2
Проведем исследование сканирующих свойств синтезированной линзы для частного случая распределения показателя преломления вдоль оси n0(z)=1.6 (рис.2). Для этого рассмотрим возбуждение линзы источником, смещенным из фокуса ортогонально оси z. На рис.5 приведены графики распределения эйконала на границе среды Z=1 после вычета постоянной и линейной составляющих, рассчитанные методом геометрической оптики для трех величин смещения источника, соответствующих трем величинам угла наклона выходного фронта - 3 градуса (кривая 1), 7.7 градусов (кривая 2) и 10.5 градусов (кривая 3). График зависимости величины аберрации (амплитуды колебаний величины эйконала) от угла наклона выходного фронта приведен на рис. 6 (кривая 1).
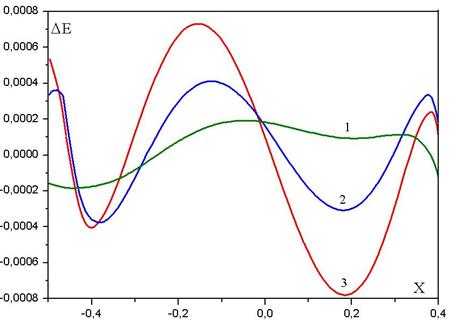
Рис. 5 Аберрации эйконала.
Для сравнения кривой 2 на рис.6 показана аналогичная зависимость для линзы Микаэляна с теми же размерами и коэффициентом преломления на оси (n0=1.6). Ввиду апланатических свойств линзы с двумерным градиентом у кривой 1 , как и следовало ожидать, в окрестности начала координат отсутствует линейная часть. Синтезированная среда позволяет в несколько раз уменьшить аберрации по сравнению с линзой Микаэляна.
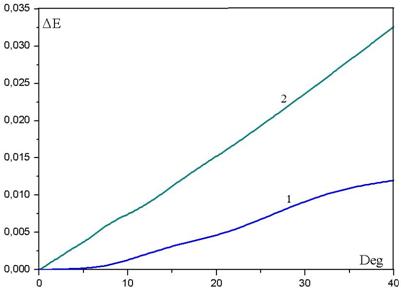
Рис. 6. Зависимость аберрации от угла наклона выходного фронта.
Попытки дальнейшего уменьшения аберраций за счет смещения источника вдоль оси z в данной работе не привели к каким либо существенным результатам. Это говорит о том, что в рамках аберраций третьего порядка, наряду с отсутствием комы, у синтезированной линзы отсутствует кривизна поля.
Работа выполнена при поддержке РФФИ, проект № 12-08-12003-офи_м.
1. Венецкий А.С., Калошин В.А. Синтез градиентной линзовой антенны с осевой симметрией и заданной формой одной из преломляющих поверхностей, ДАН, 1994, т.335, №1, с. 39-41.
2. Венецкий А.С., Калошин В.А. Синтез градиентной линзовой антенны с осевой симметрией и криволинейной формой преломляющих поверхностей, Радиотехника и электроника, 1997, т.42, №12, с.1452-1458.
3. Венецкий А.С., Калошин В.А. Синтез неоднородной диэлектрической линзы с осевой симметрией, Письма в ЖТФ, 2006, т.32, №7, с.74-79.
4. Борн М., Вольф Э. Основы оптики, М., «Наука», 1970 г.
5. Зелкин Е.Г., Петрова Р.А. Линзовые антенны, М., «Советское радио», 1974 г.
6. Микаэлян А.Л. Оптические методы в информатике, М., «Наука», 1990 г.
7. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений, «Наука», Москва, 1970 г.