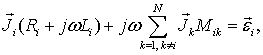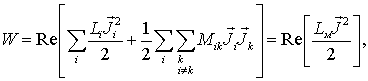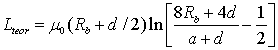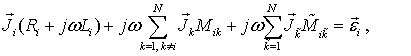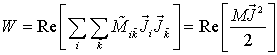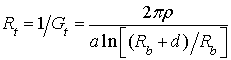УДК 537.8+621.396
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ ПЛОСКИХ (ПЕЧАТНЫХ) КОЛЕЦ ПРИ РАЗЛИЧНЫХ СПОСОБАХ ВОЗБУЖДЕНИЯ
А. В. Савельев, Н. П. Чубинский
Московский физико-технический институт (государственный университет)
Статья получена 29 января 2015 г.
Аннотация. Предложены алгоритмы расчёта индуктивностей, взаимных индуктивностей и сопротивлений плоских колец при произвольной ширине проводника. Они основаны на определении трёхмерных распределений плотности тока в сечении колец. Вычисленные распределения плотности тока неравномерны и радикально изменяются в зависимости от способа их возбуждения. Используя найденные распределения токов, определены величины индуктивностей, взаимных индуктивностей и сопротивлений колец. Они существенно отличаются от результатов стандартных расчётов. Относительные поправки наших результатов возрастают с ростом частоты и относительной ширины проводника и могут превышать 400%. Представленные расчёты позволили корректно определить индуктивности и взаимные индуктивности печатных колец с широким проводником (ширина близка к его радиусу) во всём диапазоне частот применимости квазистатического приближения. Полученные результаты для колец с узким проводником хорошо согласуются с известными асимптотическими расчётами.
Ключевые слова: плоское кольцо, индуктивность, взаимная индуктивность, распределение плотности тока.
Abstract. The calculation algorithms for inductances, mutual inductances and resistances of the flat rings with arbitrary conductor width are proposed. They are based on definition of three-dimensional distributions of the current density on section of a ring. Calculated distributions of the current density are non-uniformly and considerably changes depending on a way of its excitation. Using the found distributions of current values of the ring’s inductance, mutual inductance and resistance are determined. They essentially differ from results of standard calculations. Relative corrections of our results are increasing with growth of frequency and relative width of a conductor and can exceed 400 %. The submitted calculations have allowed to determine correctly inductance and mutual inductance of printed rings with a wide conductor (the width is close to its radius) in all the frequency range of the quasistatic approximation. Our results for rings with a narrow conductor are converged well to known asymptotic calculations.
Key words: flat ring, inductance, mutual inductance, distribution of the current density.
1. Введение
Существующие асимптотические приближения для расчёта собственных и взаимных индуктивностей плоских (печатных) колец удовлетворительно работают только для колец, ширина проводника которых существенно меньше их радиуса. Целью работы является создание алгоритмов расчёта указанных параметров для колец с произвольно широким проводником в частотном диапазоне квазистатического приближения. Они основаны на разбиении сечения кольца на элементарные контуры и определении распределений тока в них.
Величины индуктивности и активного сопротивления произвольного
кольца на высоких частотах отличаются от их значений при низкой частоте (явление
скин-эффекта). Оно усиливается с ростом частоты тока, поэтому при расчете
индуктивности и активного сопротивления различают случаи низкой частоты,
высокой частоты и предельный случай весьма высокой частоты [1]. В данном случае
индуктивность и сопротивление кольца являются сосредоточенными
радиотехническими элементами, то есть размеры кольца должны быть много меньше
длины волны электромагнитного поля. Первое аналитическое определение
индуктивности кольца с круглым проводником при равномерном распределении
плотности тока по его сечению дано Рэлеем [2], а для случая сильного
скин-эффекта – получено Фоком [3]. Асимптотические решения для разнообразных
форм контуров и проводников даны в [1,4] только для двух крайних случаев:
равномерного распределения плотности тока в проводнике (низкочастотное
приближение) и для сильного скин-эффекта (высокочастотное приближение). Решение
Фока хорошо работает только для колец с достаточно тонким проводником, то есть
когда радиус кльца ![]() значительно больше радиуса
проводника
значительно больше радиуса
проводника ![]()
![]() .
.
В работе [5] разработан алгоритм и проведены
вычисления индуктивностей и сопротивлений колец с толстым проводником ![]() в широком частотном диапазоне применимости
квазистатического приближения. Было обнаружено влияние способа возбуждения на
величину индуктивности. Первый способ реализуется при возбуждении кольца
переменным магнитным полем с индукцией
в широком частотном диапазоне применимости
квазистатического приближения. Было обнаружено влияние способа возбуждения на
величину индуктивности. Первый способ реализуется при возбуждении кольца
переменным магнитным полем с индукцией ![]() ,
второй – является стандартным и соответствует возбуждению кольца источником
сторонней э.д.с. (Рис. 1а,б). Для колец с тонким проводником оба способа дают
одинаковые значения искомых параметров на низких частотах, которые совпадают с
результатами классических расчетов.
,
второй – является стандартным и соответствует возбуждению кольца источником
сторонней э.д.с. (Рис. 1а,б). Для колец с тонким проводником оба способа дают
одинаковые значения искомых параметров на низких частотах, которые совпадают с
результатами классических расчетов.
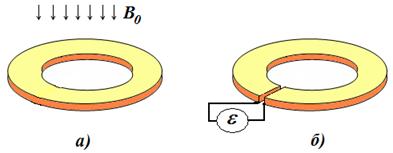
Рис. 1. Два способа возбуждения кольца при определении индуктивности
С ростом толщины проводника кольца ![]() и увеличением частоты значения
индуктивностей ведут себя существенно различным образом: для первого способа – в
сторону увеличения, а для второго – в сторону уменьшения по отношению к
значениям, получаемых из [1-4].
и увеличением частоты значения
индуктивностей ведут себя существенно различным образом: для первого способа – в
сторону увеличения, а для второго – в сторону уменьшения по отношению к
значениям, получаемых из [1-4].
В настоящее
время большой интерес представляют плоские (печатные) кольца, ширина проводника
которых ![]() соизмерима с их радиусом
соизмерима с их радиусом ![]() . Такие элементы слабо исследованы, хотя
находят широкое применение в радиоаппаратуре СВЧ диапазона и при создании
искусственных сред с эффективной магнитной проницаемостью менее единицы [6].
. Такие элементы слабо исследованы, хотя
находят широкое применение в радиоаппаратуре СВЧ диапазона и при создании
искусственных сред с эффективной магнитной проницаемостью менее единицы [6].
2. Цель работы и алгоритм решения задачи
Работа посвящена изучению влияния геометрии плоских колец при различных уровнях скин-эффекта на их индуктивность, а так же вычислению взаимной индуктивности колец с широким прводником во всём частотном диапазоне квазистатического приближения:
где ![]() – длина волны,
– длина волны, ![]() – внешний радиус кольца.
– внешний радиус кольца.
2.1 Рассмотрим вначале проводящее кольцо
прямоугольного сечения, возбуждаемое внешним магнитным полем с индукцией ![]()
![]() с частотой
с частотой ![]() (Рис. 1а). Геометрия сечения кольца дана
на Рис. 2. В данной задаче толщина
(Рис. 1а). Геометрия сечения кольца дана
на Рис. 2. В данной задаче толщина ![]() и внешний радиус
кольца
и внешний радиус
кольца ![]()
![]() фиксированы и равны
фиксированы и равны ![]() 36 мкм и
36 мкм и ![]() 1152
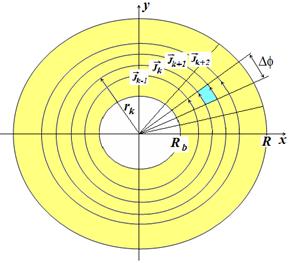
мкм, соответственно. При моделировании варьировался внутренний радиус кольца Rb. В некоторых случаях мы будем приводить
геометрические размеры, нормированные к толщине кольца а.
1152
мкм, соответственно. При моделировании варьировался внутренний радиус кольца Rb. В некоторых случаях мы будем приводить
геометрические размеры, нормированные к толщине кольца а.
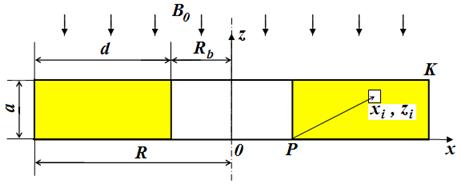
Рис. 2. Геометрия задачи
Для расчета распределения плотности тока в сечении кольца (в квазистатическом приближении) при разных уровнях скин-эффекта оно разбивается на множество соосных элементарных контуров (колец квадратного сечения), внутри которых распределение токов можно считать равномерным.
Вначале использовалось неравномерное разбиение, которое было использованно в [5], где сечение элементарных контуров уменьшалось в направлении к границам сечения кольца в области с наибольшей неоднородностью распределения плотности тока. Однако в данной задаче от этой идеи было решено отказаться, так как в распределениях токов наблюдались заметные перепады в местах соприкосновения элементов различных размеров. Поэтому было использовано равномерное разбиение до 11 слоев.
Пронумеровав элементы разбиения, запишем систему линейных уравнений, описывающих распределения токов в квазистатическом приближении [5]:
где ![]() – комплексная амплитуда тока в
– комплексная амплитуда тока в ![]() -ом контуре,
-ом контуре, ![]() – его
импеданс (
– его
импеданс (![]() – индуктивность и
– индуктивность и ![]() –
активное сопротивление),
–
активное сопротивление), 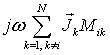 – сумма э.д.с.,
вносимых в
– сумма э.д.с.,
вносимых в ![]() -тый контур из всех остальных контуров,
-тый контур из всех остальных контуров, ![]() – взаимные индуктивности,
– взаимные индуктивности, ![]() – комплексная амплитуда э.д.с. в
– комплексная амплитуда э.д.с. в ![]() -ом элементе, возбуждаемая внешним
магнитным полем с индукцией
-ом элементе, возбуждаемая внешним
магнитным полем с индукцией ![]() :
:
![]() – активное сопротивление
– активное сопротивление ![]() -того контура,
-того контура, ![]() –
удельное сопротивление проводника,
–
удельное сопротивление проводника,
площадь сечения элементарного контура, а ![]()
![]() определяет мелость разбиения сечения
проводника. Классические алгоритмы расчета собственных и взаимных
индуктивностей приведены в [1].
определяет мелость разбиения сечения
проводника. Классические алгоритмы расчета собственных и взаимных
индуктивностей приведены в [1].
2.2 Соотношение (3) использовалось в [5]
для толстых колец с проводником круглого сечения при определении их
индуктивности. Учитывая, что при разбиении сечения проводника элементарные круговые
контуры с равномерным распределением токов по их сечениям имеют гальваническую
связь, а э.д.с. в контурах сечения различны (пропорциональны квадрату
расстояния от оси кольца), была сделана следующая оговорка: элементарные
контуры считались изолированными друг от друга. Проанализируем данный вопрос
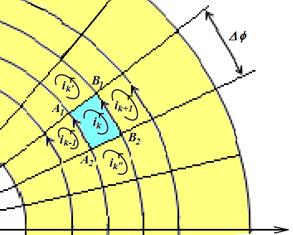
более подробно. На Рис. 3а приведена система кольцевых токов в элементарных
контурах одного слоя, а на Рис.3б – крупным планом дана часть, включающая
выделенную ячейку ![]() с углом
с углом ![]() .
В прилегающих к ней ячейках в секторе
.
В прилегающих к ней ячейках в секторе ![]() показаны
контурные токи, связанные с азимутальными токами соотношениями:
показаны
контурные токи, связанные с азимутальными токами соотношениями: ![]()
![]() Радиальные
составляющие токов равны нулю –
Радиальные
составляющие токов равны нулю – ![]() , так как контурные токи равны во всех ячейках, находящихся на
одинаковом расстоянии от центра кольца. Это значит, что радиальные компоненты
токов отсутствуют, а выражения (2) и (3) остаются справедливыми, как и в случае
изолированных элементарных контуров.
, так как контурные токи равны во всех ячейках, находящихся на
одинаковом расстоянии от центра кольца. Это значит, что радиальные компоненты
токов отсутствуют, а выражения (2) и (3) остаются справедливыми, как и в случае
изолированных элементарных контуров.
|
|
|
|
а) |
б) |
Рис. 3. Распределение токов в кольце с широким проводником:
а) – система кольцевых токов в элементарных контурах,
б) – картина контурных токов в элементарной ячейки А1В1В2А2
2.3
Решение системы уравнений (2) определяет распределение плотности тока в сечении
кольца. На основе этих данных можно определить индуктивность кольца ![]() , используя выражения для реактивной
энергии системы токов в элементах разбиения [7]:
, используя выражения для реактивной
энергии системы токов в элементах разбиения [7]:
где ![]() – полный ток через сечение
кольца.
– полный ток через сечение
кольца.
Вычислим эквивалентное сопротивление системы ![]() , используя соотношение (6):
, используя соотношение (6):
Далее, полученные результаты для индуктивности кольца с прямоугольным сечением сравнивались с результатами, вычисленными на основе существующих алгоритмов [1]:
2.4 Для расчета взаимной индуктивности двух
одинаковых плоских колец, имеющих параллельные оси и находящихся во внешнем
магнитом поле использован уже описанный алгоритм. Геометрия задачи дана на рис.
4, когда оси колец лежат в одной плоскости. Разобьем каждое из колец на
множество круговых элементов квадратного сечения аналогично тому, как это было
сделано выше. Распределение плотности тока в каждом из взаимодействующих колец
перестанет быть симметричным по толщине проводника. Исключение составляет
только случай расположения колец в одной плоскости, когда токи распределены
симметрично отноительно плоскости ![]() . Придадим элементам
разбиения согласованную нумерацию по
. Придадим элементам
разбиения согласованную нумерацию по ![]() следующим образом.
Пусть некоторый номер
следующим образом.
Пусть некоторый номер ![]() относится к элементу нижнего
кольца на Рис. 4. Тогда номер
относится к элементу нижнего
кольца на Рис. 4. Тогда номер ![]() верхнего кольца должен
относиться к зеркальному относительно горизонтальной плоскости
верхнего кольца должен
относиться к зеркальному относительно горизонтальной плоскости ![]() элементу верхнего кольца и в силу
симметрии токи в элементах с одинаковыми номерами будут совпадать. Запишем
систему уравнений, описывающую распределения токов в данной системе.
элементу верхнего кольца и в силу
симметрии токи в элементах с одинаковыми номерами будут совпадать. Запишем
систему уравнений, описывающую распределения токов в данной системе.
где первые 2 слагаемых тождественны аналогичным слагаемым в уравнении
(2), а третье определяется взаимными индуктивностями ![]() между
между
![]() -м элементом первого кольца и
-м элементом первого кольца и ![]() -м элементом второго кольца. Правила
нахождения
-м элементом второго кольца. Правила
нахождения ![]() подробно изложены в [1].
подробно изложены в [1].
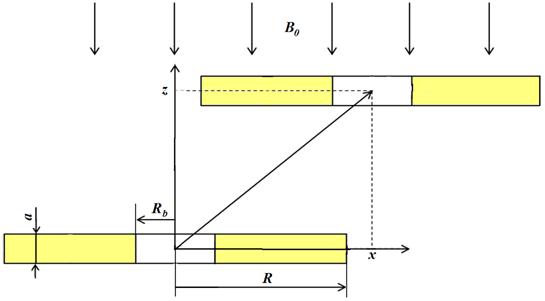
Рис. 4. Определение взаимной индуктивности плоских колец с широким проводником
Решив систему уравнений (8), найдем распределение
токов в сечениях колец, и далее, с помощью соотношения (9) для энергии
взаимодействия колец, определим взаимную индукцию колец ![]() :
:
3. Результаты расчёта индуктивности и сопротивления кольца при возбуждении внешним магнитным полем
Для определения индуктивности и сопротивления кольца необходимо найти распределение комплексного вектора плотности тока в его сечении. Выполнение условий квазистатического приближения (1) даёт ограничение на максимальную частоту в численном эксперименте:
Для частоты, удовлетворяющей (10), поперечные размеры сечения элементов
разбиения должен быть по крайней мере в два раза меньше толщины скин-слоя. При
оценках толщины скин-слоя в медном проводе использована формула для проводящего
полупространства – ![]() [м]. При выбранном радиусе
кольца квазистатическое приближение ограничено частотой
[м]. При выбранном радиусе
кольца квазистатическое приближение ограничено частотой ![]()
![]() .
.
3.1 Распределение токов в сечении
проводника – трехмерная поверхность. Для количественного анализа этого
распределения необходимо определить некоторое число срезов распределения в
плоскостях ![]() и
и ![]() . Более
наглядно и компактно представить срез данной поверхности, дающий возможность
одновременно определять степень неоднородности распределения плотности тока по обеим
осям, является срез по диагонали сечения кольца
. Более
наглядно и компактно представить срез данной поверхности, дающий возможность
одновременно определять степень неоднородности распределения плотности тока по обеим
осям, является срез по диагонали сечения кольца ![]() на
Рис. 2. Данную диагональ можно спроектировать на ось
на
Рис. 2. Данную диагональ можно спроектировать на ось ![]() ,
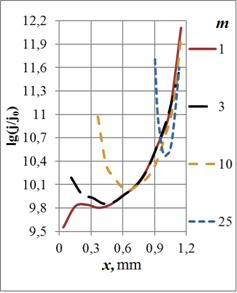
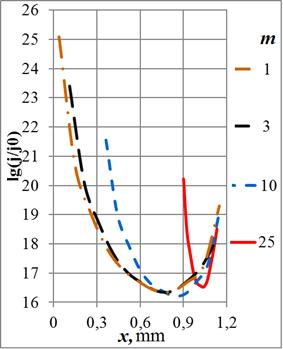
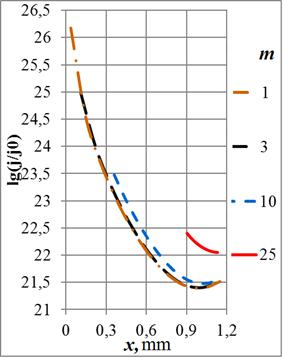
что использовано ниже. На Рис. 5 даны распределения тока в сечении кольца
толщиной
,
что использовано ниже. На Рис. 5 даны распределения тока в сечении кольца
толщиной ![]() 36 мкм для ряда частот в зависимости от
размеров отверстия
36 мкм для ряда частот в зависимости от
размеров отверстия ![]() . Справа указано отношение внутреннего
радиуса к толщине кольца
. Справа указано отношение внутреннего
радиуса к толщине кольца ![]() , (
, (![]() – единичная плотность тока).
– единичная плотность тока).
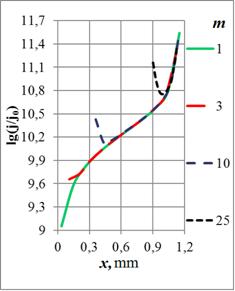
Функция ![]() имеет два экстремума
при небольшой относительной ширине проводника и высоких частотах. Максимум
максиморум всегда находится на внешней кромке кольца, а максимум – у внутренней
кромки. При уменьшении внутреннего радиуса
имеет два экстремума
при небольшой относительной ширине проводника и высоких частотах. Максимум
максиморум всегда находится на внешней кромке кольца, а максимум – у внутренней
кромки. При уменьшении внутреннего радиуса ![]() увеличивается
перепад между значениями плотности тока на внешней и внутренней границах
кольца, причем при значительном уменьшении радиуса отверстия (
увеличивается
перепад между значениями плотности тока на внешней и внутренней границах
кольца, причем при значительном уменьшении радиуса отверстия (![]() 36 мкм) возникает перегиб функции
плотности тока, а минимум плотности тока смещается к внутренней границе кольца.
36 мкм) возникает перегиб функции
плотности тока, а минимум плотности тока смещается к внутренней границе кольца.
|
а) |
б) |
|
в) |
г) |
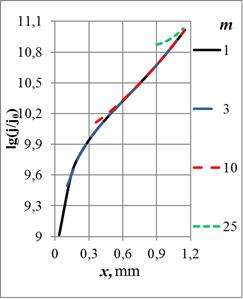
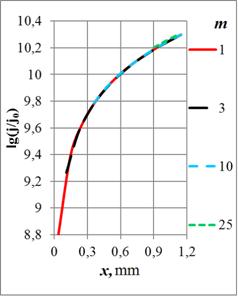
Рис. 5. Зависимости плотности тока в сечении кольца от радиуса отверстия на частотах: а) – 108 Гц, б) – 107 Гц, в) – 106 Гц и г) – 105 Гц
В Таблице 1 даны характерные размеры неоднородности
распределения плотности тока (изменение амплитуды в ![]() раз) у
внутренней
раз) у
внутренней ![]() и внешней
и внешней ![]() границ кольца. В нижней строке приведены
значения толщины скин-слоя для тех же частот. Характерные размеры
неоднородностей в распределениях плотности тока у внешней кромки кольца
существенно больше, чем у внутренней, оба параметра значительно отличаются от толщины
скин-слоя. Поведение распределений при уменьшении внутреннего радиуса и
увеличением частоты обусловлено в основном увеличением наводимой внешним полем э.д.с
в элементах разбиения в направлении к внешней кромке кольца.
границ кольца. В нижней строке приведены
значения толщины скин-слоя для тех же частот. Характерные размеры
неоднородностей в распределениях плотности тока у внешней кромки кольца
существенно больше, чем у внутренней, оба параметра значительно отличаются от толщины
скин-слоя. Поведение распределений при уменьшении внутреннего радиуса и
увеличением частоты обусловлено в основном увеличением наводимой внешним полем э.д.с
в элементах разбиения в направлении к внешней кромке кольца.
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,900 |
0,0154 |
– |
– |
– |
0,0384 |
0,0534 |
– |
– |
|
0,720 |
0,0282 |
– |
– |
– |
0,0554 |
0,0623 |
– |
– |
|
0,612 |
0,0348 |
– |
– |
– |
0,0742 |
0,0764 |
– |
– |
|
0,540 |
0,0394 |
– |
– |
– |
0,0865 |
0,0868 |
– |
– |
|
0,360 |
0,0562 |
– |
– |
– |
0,1000 |
0,1032 |
0,3075 |
– |
|
0,252 |
0,0721 |
– |
– |
– |
0,1200 |
0,1199 |
0,3138 |
– |
|
0,180 |
0,1052 |
– |
– |
– |
0,1327 |
0,1316 |
0,3187 |
– |
|
0,108 |
– |
– |
– |
– |
0,1431 |
0,1440 |
0,3240 |
– |
|
0,036 |
– |
– |
– |
– |
0,1381 |
0,1422 |
0,3144 |
– |
|
|
0,0067 |
0,0211 |
0,0666 |
0,2105 |
0,0067 |
0,0211 |
0,0666 |
0,2105 |
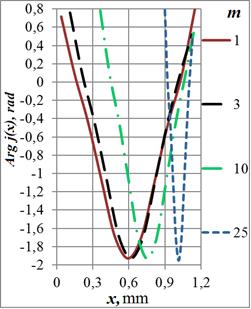
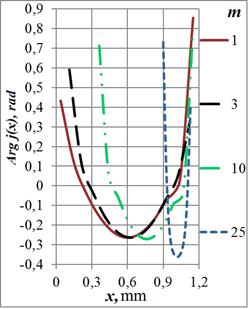
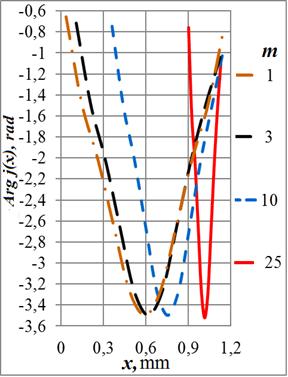
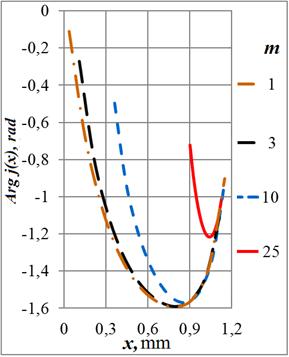
На графиках Рис. 6 приведены распределения фаз плотностей тока для ряда
частот в зависимости от размеров отверстия. Для получения абсолютного набега
фазы по отношению к фазе внешнего поля ![]() к
приведенным результатам следует добавить (
к
приведенным результатам следует добавить (![]() ).
Несколько неожиданный результат заключается в том, что на частотах выше 100 МГц
(область квазистатики!) диапазон изменения фазы по ширине проводника приближается
к
).
Несколько неожиданный результат заключается в том, что на частотах выше 100 МГц
(область квазистатики!) диапазон изменения фазы по ширине проводника приближается
к ![]() . Зависимость имеет глубокий провал
приблизительно в середине проводника. Размах изменений уменьшается как при
уменьшении частоты, так и ширины проводника.
. Зависимость имеет глубокий провал
приблизительно в середине проводника. Размах изменений уменьшается как при
уменьшении частоты, так и ширины проводника.
|
а) |
б) |
|
в) |
г) |
Рис. 6. Зависимости фазы плотности тока в сечении кольца от радиуса отверстия на частотах: а) – 108 Гц, б) – 107 Гц, в) – 106 Гц и г) – 105 Гц
3.2 На основании найденных распределений
плотности тока были определены зависимости индуктивности ![]() и сопротивления кольца
и сопротивления кольца ![]() от частоты и его геометрии и
проведено сравнение их с теоретическим расчетом по формуле (7). В Таблице 2
представлены рассчитанные значения индуктивностей и сопротивлений кольца в зависимости от размеров отверстия при различных
частотах, а так же низкочастотные величины индуктивности
от частоты и его геометрии и
проведено сравнение их с теоретическим расчетом по формуле (7). В Таблице 2
представлены рассчитанные значения индуктивностей и сопротивлений кольца в зависимости от размеров отверстия при различных
частотах, а так же низкочастотные величины индуктивности ![]() (7)
и сопротивления кольца
(7)
и сопротивления кольца ![]() .(11) при постоянном токе:
.(11) при постоянном токе:
Таблица 2 (![]() , толщина
, толщина ![]() 36мкм)
36мкм)
|
мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
мОм |
мОм 108 Гц |
мОм 107Гц |
мОм 106 Гц |
мОм 105 Гц |
|
1,116 |
6,179 |
5,880 |
5,768 |
5,760 |
5,759 |
96,24 |
181,8 |
98,39 |
96,26 |
96,24 |
|
1,008 |
4,575 |
4,753 |
4,521 |
4,255 |
4,242 |
22,88 |
76,63 |
30,47 |
,23,20 |
23,01 |
|
0,9 |
3,674 |
4,252 |
4,016 |
3,555 |
3,493 |
12,38 |
53,43 |
20,44 |
13,14 |
12,63 |
|
0,792 |
3,026 |
3,945 |
3,711 |
3,152 |
3,009 |
8,154 |
43,21 |
16,24 |
9,429 |
8,541 |
|
0,684 |
2,514 |
3,735 |
3,504 |
2,901 |
2,665 |
5,861 |
37,57 |
13,99 |
7,641 |
6,399 |
|
0,576 |
2,089 |
3,584 |
3,356 |
2,736 |
2,411 |
4,408 |
34,09 |
12,62 |
6,649 |
5,117 |
|
0,468 |
1,728 |
3,475 |
3,249 |
2,622 |
2,221 |
3,392 |
31,82 |
11,73 |
6,048 |
4,296 |
|
0,36 |
1,414 |
3,396 |
3,172 |
2,543 |
2,082 |
2,627 |
30,31 |
11,14 |
5,665 |
3,757 |
|
0,252 |
1,140 |
3,342 |
3,118 |
2,489 |
1,985 |
2,010 |
29,32 |
10,76 |
5,417 |
3,407 |
|
0,144 |
0,898 |
3,308 |
3,085 |
2,455 |
1,924 |
1,469 |
28,73 |
10,52 |
5,266 |
3,200 |
|
0,036 |
0,685 |
3,294 |
3,070 |
2,438 |
1,897 |
0,882 |
28,48 |
10,42 |
5,194 |
3,110 |
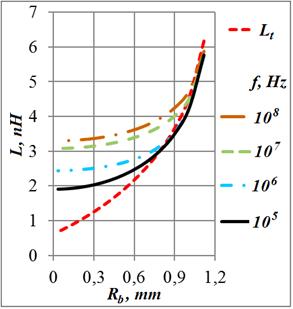
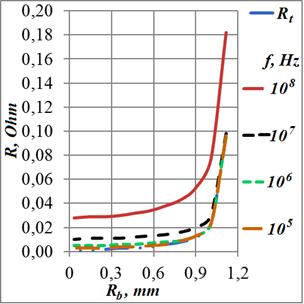
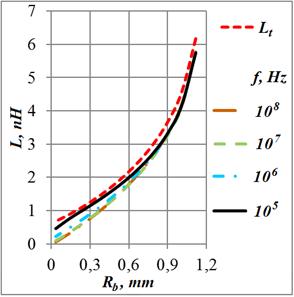
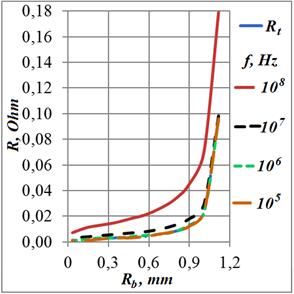
На графиках Рис. 7а,б приведены эти зависимости. В пределах выбранного диапазона частот от 100 кГц до 100 МГц при толщине кольца 36 мкм мы наблюдаем области от очень слабого до сильного скин-эффекта.
|
а) |
б) |
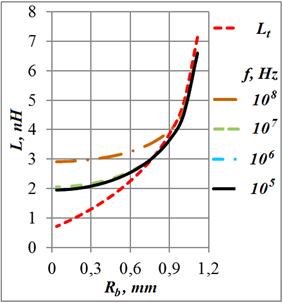
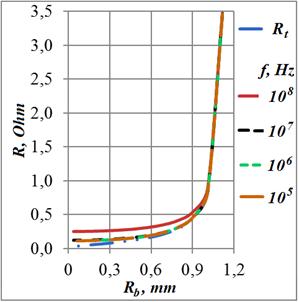
Рис.
7. Индуктивность и сопротивление кольца в зависимости от величины внутреннего
радиуса для ряда частот при ![]() 36 мкм
36 мкм
Известное асимптотическое приближение (7) для индуктивности не очень
широкого проводника (Рис. 7а) ![]() 0,3 (
0,3 (![]() 0,7) хорошо согласуется с нашими расчётами
на частотах до 1 МГц. При увеличении относительной ширины проводника вплоть до
0,97 расхождение увеличивается, причём индуктивность всегда выше
значений согласно (7) в 2,8 раза на низкой и более чем в 4,8 раз – на высокой
частоте (Таблица 2). Аналогичные закономерности относятся и к сопротивленям
колец для относительно узкого проводника –
0,7) хорошо согласуется с нашими расчётами
на частотах до 1 МГц. При увеличении относительной ширины проводника вплоть до
0,97 расхождение увеличивается, причём индуктивность всегда выше
значений согласно (7) в 2,8 раза на низкой и более чем в 4,8 раз – на высокой
частоте (Таблица 2). Аналогичные закономерности относятся и к сопротивленям
колец для относительно узкого проводника – ![]() 0,22
(Рис. 7б). При увеличении относительной ширины проводника вплоть до 0,97 найденные
сопротивления больше величин согласно (11) в 3,5 раза на низкой и более чем
в 32 раза – на высокой частоте (Таблица 2). Рост сопротвления обусловлен все
большей неравномерностью распределения тока с увеличением частоты.
0,22
(Рис. 7б). При увеличении относительной ширины проводника вплоть до 0,97 найденные
сопротивления больше величин согласно (11) в 3,5 раза на низкой и более чем
в 32 раза – на высокой частоте (Таблица 2). Рост сопротвления обусловлен все
большей неравномерностью распределения тока с увеличением частоты.
Были проведены аналогичные расчёты для двух других
толщин колец, при которых скин-эффект в том же частотном диапазоне проявляется
слабо (![]() 9 мкм) и где скин-эффектом можно
принебречь (
9 мкм) и где скин-эффектом можно
принебречь (![]() 1 мкм). Опуская результаты расчёта
комплексных распределений плотности тока, приведем их только для индуктивности
и сопротивления (Таблицы 3 и 4). Соответствующий графический материал иллюстрируют
Рис. 8а,б и Рис. 9а,б.
1 мкм). Опуская результаты расчёта
комплексных распределений плотности тока, приведем их только для индуктивности
и сопротивления (Таблицы 3 и 4). Соответствующий графический материал иллюстрируют
Рис. 8а,б и Рис. 9а,б.
Таблица 3 (![]() , толщина
, толщина ![]() 9 мкм)
9 мкм)
|
мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
мОм |
мОм 108 Гц |
мОм 107Гц |
мОм 106 Гц |
мОм 105 Гц |
|
1,116 |
6,849 |
6,586 |
6,480 |
6,477 |
6,477 |
384,9 |
431,0 |
385,6 |
384,9 |
384,9 |
|
1,008 |
4,796 |
5,015 |
4,565 |
4,465 |
4,463 |
91,52 |
139,1 |
96,53 |
92,09 |
92,04 |
|
0,9 |
3,801 |
4,418 |
3,910 |
3,634 |
3,628 |
49,51 |
91,10 |
58,72 |
50,65 |
50,49 |
|
0,792 |
3,112 |
4,066 |
3,559 |
3,123 |
3,108 |
32,62 |
71,57 |
44,82 |
34,42 |
34,12 |
|
0,684 |
2,577 |
3,831 |
3,333 |
2,771 |
2,743 |
23,44 |
61,23 |
37,77 |
26,00 |
25,53 |
|
0,576 |
2,138 |
3,664 |
3,175 |
2,518 |
2,476 |
17,63 |
55,02 |
33,63 |
21,03 |
20,37 |
|
0,468 |
1,766 |
3,543 |
3,062 |
2,335 |
2,276 |
13,57 |
51,02 |
30,99 |
17,89 |
17,06 |
|
0,36 |
1,446 |
3,457 |
2,980 |
2,204 |
2,130 |
10,51 |
48,38 |
2,92 |
15,86 |
14,87 |
|
0,252 |
1,165 |
3,397 |
2,923 |
2,113 |
2,028 |
8,041 |
46,66 |
28,11 |
14,55 |
13,46 |
|
0,144 |
0,919 |
3,360 |
2,888 |
2,056 |
1,964 |
5,877 |
45,64 |
27,41 |
13,78 |
12,62 |
|
0,036 |
0,702 |
3,344 |
2,871 |
2,030 |
1,936 |
3,526 |
45,19 |
27,09 |
13,4 |
12,25 |
|
а) |
б) |
Рис. 8. Индуктивность
и сопротивление кольца в зависимости от величины внутреннего радиуса для ряда
частот при ![]() 9 мкм
9 мкм
Таблица 4 (![]() ,толщина
,толщина![]() 1 мкм)
1 мкм)
|
мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
мОм |
мОм 108 Гц |
мОм 107Гц |
мОм 106 Гц |
мОм 105 Гц |
|
1,116 |
7,128 |
6,607 |
6,601 |
6,601 |
6,601 |
3465 |
3473 |
3465 |
3464 |
3464 |
|
1,008 |
4,869 |
4,617 |
4,487 |
4,485 |
4,485 |
823,7 |
876,0 |
829,0 |
828,0 |
828,0 |
|
0,9 |
3,841 |
3,963 |
3,647 |
3,639 |
3,639 |
445,6 |
535,0 |
456,0 |
454,0 |
454,0 |
|
0,792 |
3,139 |
3,608 |
3,135 |
3,115 |
3,115 |
293,6 |
409,0 |
310,0 |
307,0 |
307,0 |
|
0,684 |
2,597 |
3,378 |
2,784 |
2,749 |
2,749 |
211,0 |
345,0 |
235,0 |
230,0 |
230,0 |
|
0,576 |
2,153 |
3,218 |
2,534 |
2,481 |
2,480 |
158,7 |
307,0 |
191,0 |
183,0 |
183,0 |
|
0,468 |
1,778 |
3,103 |
2,354 |
2,281 |
2,280 |
122,1 |
282,0 |
163,0 |
154,0 |
153,0 |
|
0,36 |
1,455 |
3,020 |
2,225 |
2,135 |
2,134 |
94,56 |
267,0 |
145,0 |
134,0 |
134,0 |
|
0,252 |
1,173 |
2,962 |
2,136 |
2,032 |
2,031 |
72,37 |
256,0 |
133,0 |
121,0 |
121,0 |
|
0,144 |
0,926 |
2,926 |
2,081 |
1,968 |
1,967 |
52,89 |
250,0 |
126,0 |
114,0 |
113,0 |
|
0,036 |
0,708 |
2,909 |
2,055 |
1,940 |
1,938 |
31,742 |
247,0 |
123,0 |
110,0 |
110,0 |
|
а) |
б) |
Рис. 9. Индуктивность
и сопротивление кольца в зависимости от величины внутреннего радиуса для ряда
частот при ![]() 1 мкм
1 мкм
Анализ графиков показывает качественное совпадение результатов с
приведёнными ранее закономерностями. Во всех случаях прооводников с узким
проводником (![]() ) в области отсутствия скин-эффекта
найденные значения индуктивностей на 3…7% ниже стандартных. Это отчасти может
быть связано с систематической ошибкой общепринятых алгоритмов. Для
индуктивностей колец с очень широким проводником (
) в области отсутствия скин-эффекта
найденные значения индуктивностей на 3…7% ниже стандартных. Это отчасти может
быть связано с систематической ошибкой общепринятых алгоритмов. Для
индуктивностей колец с очень широким проводником (![]() )
найденные значения выше стандартных в 2,5…4,8 раза больще стандартых в
диапазоне частот от 100 кГц до 100 МГц. При уменьшении толщины расхождение со
стандартными расчётами немного уменьшается, а для сопротивлений – уменьшается
существенно.
)
найденные значения выше стандартных в 2,5…4,8 раза больще стандартых в
диапазоне частот от 100 кГц до 100 МГц. При уменьшении толщины расхождение со
стандартными расчётами немного уменьшается, а для сопротивлений – уменьшается
существенно.
4. Результаты расчёта индуктивности и сопротивления кольца при возбуждении от источника э.д.с. (классический случай)
Рассмотрим теперь
классический случай возбуждения проводящего кольца прямоугольного сечения
источником единичной э.д.с. ![]() В (Рис. 1б) с
частотой
В (Рис. 1б) с
частотой ![]() , тех же размеров и геометрии как и ранее.
При проведении вычислении в системе уравнений (2) набор э.д.с., возбуждаемых
внешним магнитным полем в элементах разбиения, заменен фиксированной единичной э.д.с.
внешнего источника.
, тех же размеров и геометрии как и ранее.
При проведении вычислении в системе уравнений (2) набор э.д.с., возбуждаемых
внешним магнитным полем в элементах разбиения, заменен фиксированной единичной э.д.с.
внешнего источника.
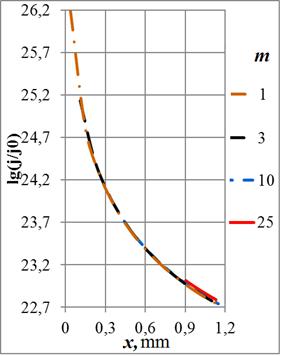
4.1 Проведены вычисления распределения
плотности тока, аналогичные пункту 3.1, индуктивности и сопротивлений плоских
колец, аналогичные пункту 3.2. Срезы распределения плотностей тока вдоль
проекции диагонали сечения ![]() представлены на
графиках Рис. 10 а,б,в,г при толщине кольца
представлены на
графиках Рис. 10 а,б,в,г при толщине кольца ![]() 36 мкм.
Справа указаны отношения внутреннего радиуса к толщине кольца
36 мкм.
Справа указаны отношения внутреннего радиуса к толщине кольца ![]() , (
, (![]() – единичная
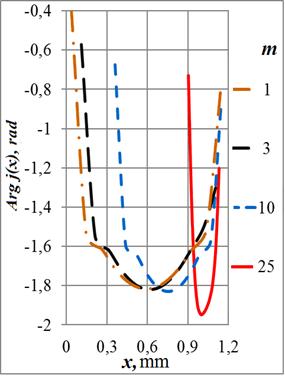
плотность тока). Соответствующие распределения фаз плотности тока даны на Рис.
11а,б,в,г.
– единичная
плотность тока). Соответствующие распределения фаз плотности тока даны на Рис.
11а,б,в,г.
|
а) |
б) |
|
в) |
г) |
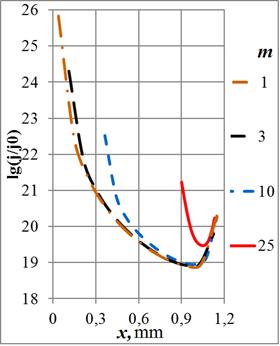
Рис. 10. Зависимости плотности тока в сечении кольца от радиуса отверстия на частотах: а) – 108 Гц, б) – 107 Гц, в) – 106 Гц и г) – 105 Гц
|
а) |
б) |
|
в) |
г) |
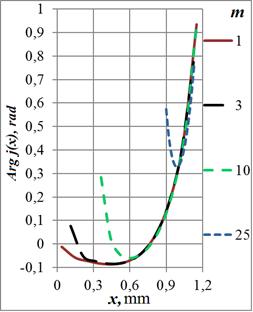
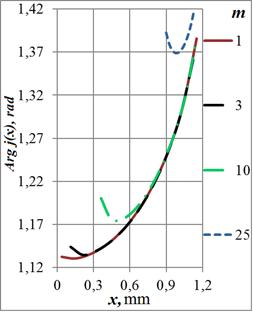
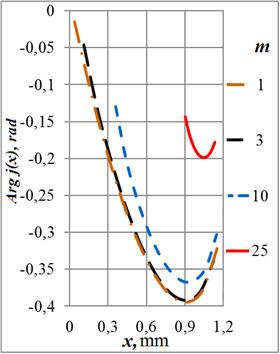
Рис. 11. Зависимости фазы плотности тока в сечении кольца от радиуса отверстия на частотах: а) – 108 Гц, б) – 107 Гц, в) – 106 Гц и г) – 105 Гц
Функция ![]() имеет два экстремума
при небольшой относительной ширине проводника и высоких частотах. Максимум
максиморум всегда находится на внутренней кромке кольца, а максимум – у внешней
кромки (при возбуждении колец магнитным полем было наоборот). При уменьшении
внутреннего радиуса
имеет два экстремума
при небольшой относительной ширине проводника и высоких частотах. Максимум
максиморум всегда находится на внутренней кромке кольца, а максимум – у внешней
кромки (при возбуждении колец магнитным полем было наоборот). При уменьшении
внутреннего радиуса ![]() увеличивается перепад между
значениями плотности тока на внешней и внутренней границах кольца, а минимум
плотности тока смещается к внешней границе кольца. Величины перепадов в
распределениях тока существенно больше, чем в случае возбуждения кольца от источника
магнитного поля (на частоте 100 МГц – более чем на три порядка). Поведение фаз
плотности тока качественно совпадает с результатами расчёта для случая
возбуждения кольца магнитным полем.
увеличивается перепад между
значениями плотности тока на внешней и внутренней границах кольца, а минимум
плотности тока смещается к внешней границе кольца. Величины перепадов в
распределениях тока существенно больше, чем в случае возбуждения кольца от источника
магнитного поля (на частоте 100 МГц – более чем на три порядка). Поведение фаз
плотности тока качественно совпадает с результатами расчёта для случая
возбуждения кольца магнитным полем.
В
Таблице 5 даны характерные размеры неоднородности распределения плотности тока
(изменение амплитуды в ![]() раз) у внутренней
раз) у внутренней ![]() и внешней
и внешней ![]() границ кольца. В нижней строке приведены
значения толщины скин-слоя для тех же частот. При этом характерные размеры
краевого эффекта значительно отличаются от оценочных значений, полученных для
полупространства (нижняя строка Таблицы). В данном случае перегиба в
распределении токов не наблюдается.
границ кольца. В нижней строке приведены
значения толщины скин-слоя для тех же частот. При этом характерные размеры
краевого эффекта значительно отличаются от оценочных значений, полученных для
полупространства (нижняя строка Таблицы). В данном случае перегиба в
распределении токов не наблюдается.
Таблица 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,900 |
14,2 |
45,8 |
– |
– |
41,4 |
71,2 |
– |
– |
|
0,720 |
25,5 |
44,8 |
– |
– |
56,6 |
66,3 |
– |
– |
|
0,612 |
30,8 |
42,6 |
– |
– |
78,7 |
82,9 |
– |
– |
|
0,540 |
34,3 |
43,4 |
262,1 |
– |
94,0 |
96,2 |
– |
– |
|
0,360 |
44,5 |
49,8 |
204,6 |
– |
102,4 |
108,0 |
– |
– |
|
0,252 |
49,3 |
53,3 |
175,0 |
412,4 |
128,1 |
129,1 |
– |
– |
|
0,180 |
52,2 |
55,4 |
149,0 |
297,8 |
145,7 |
145,2 |
– |
– |
|
0,108 |
54,8 |
56,9 |
111,4 |
176,4 |
160,4 |
146,2 |
– |
– |
|
0,036 |
58,6 |
59,1 |
76,0 |
85,7 |
140,4 |
148,0 |
– |
– |
|
|
6,7 |
21,1 |
66,6 |
210,5 |
6,7 |
21,1 |
66,6 |
210,5 |
Поведение распределения токов при фиксированной э.д.с. возбуждения и уменьшении внутреннего радиуса кольца обусловлено главным образом тем, что импеданс каждого элемента разбиения быстро уменьшается вблизи края отверстия, где плотность тока достигает абсолютного максимума.
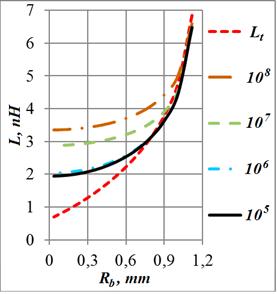
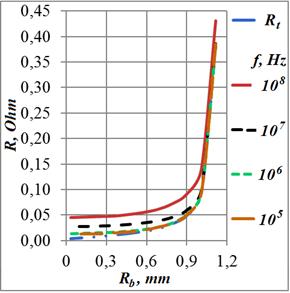
4.2 На основании полученных распределений
плотности тока были определены зависимости индуктивности ![]() и сопротивления кольца
и сопротивления кольца ![]() от частоты и его геометрии. В Таблице
6 и на графиках Рис. 12 представлены рассчитанные значения индуктивностей и
сопротивлений кольца, а так же низкочастотные величины индуктивности
от частоты и его геометрии. В Таблице
6 и на графиках Рис. 12 представлены рассчитанные значения индуктивностей и
сопротивлений кольца, а так же низкочастотные величины индуктивности ![]() (7)
и сопротbвления кольца
(7)
и сопротbвления кольца ![]() .(11) при постоянном токе.
.(11) при постоянном токе.
Были проведены аналогичные расчёты для двух других
толщин колец, при которых скин-эффект в том же частотном диапазоне проявляется
слабо (![]() 9 мкм) и где скин-эффектом можно принебречь
(
9 мкм) и где скин-эффектом можно принебречь
(![]() 1 мкм). Опуская результаты расчёта
комплексных распределений плотности тока, приведем их только для индуктивности
и сопротивления (Таблицы 7 и 8).
1 мкм). Опуская результаты расчёта
комплексных распределений плотности тока, приведем их только для индуктивности
и сопротивления (Таблицы 7 и 8).
Таблица 6 (![]() , толщина
, толщина ![]() 36мкм)
36мкм)
|
Rb, мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
мОм |
мОм 108 Гц |
мОм 107Гц |
мОм 106 Гц |
мОм 105 Гц |
|
1,116 |
6,179 |
5,759 |
5,747 |
5,749 |
5,749 |
96,24 |
179,1 |
98,16 |
96,22 |
96,20 |
|
1,008 |
4,575 |
4,196 |
4,127 |
4,159 |
4,163 |
22,88 |
70,30 |
28,52 |
22,98 |
22,87 |
|
0,9 |
3,674 |
3,322 |
3,264 |
3,305 |
3,328 |
12,38 |
44,85 |
17,55 |
12,60 |
12,38 |
|
0,792 |
3,026 |
2,675 |
2,632 |
2,688 |
2,745 |
8,154 |
32,95 |
12,67 |
8,494 |
8,156 |
|
0,684 |
2,514 |
2,148 |
2,119 |
2,190 |
2,290 |
5,861 |
25,94 |
9,867 |
6,305 |
5,865 |
|
0,576 |
2,089 |
1,697 |
1,680 |
1,765 |
1,912 |
4,408 |
21,25 |
8,021 |
4,933 |
4,415 |
|
0,468 |
1,728 |
1,300 |
1,294 |
1,393 |
1,586 |
3,392 |
17,83 |
6,688 |
3,975 |
3,402 |
|
0,36 |
1,414 |
0,944 |
0,947 |
1,060 |
1,294 |
2,627 |
15,15 |
5,648 |
3,241 |
2,640 |
|
0,252 |
1,140 |
0,621 |
0,633 |
0,760 |
1,025 |
2,010 |
12,84 |
4,764 |
2,626 |
2,026 |
|
0,144 |
0,898 |
0,326 |
0,346 |
0,485 |
0,762 |
1,469 |
10,55 |
3,896 |
2,040 |
1,487 |
|
0,036 |
0,685 |
0,064 |
0,089 |
0,218 |
0,457 |
0,882 |
6,791 |
2,574 |
1,280 |
0,896 |
|
а) |
б) |
Рис. 12. Индуктивность и сопротивление кольца при возбуждения его источником э.д.с. в зависимости от радиуса отверстия для ряда частот
Таблица 7 (![]() , толщина
, толщина ![]() 9 мкм)
9 мкм)
|
Rb, мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
мОм |
мОм 108 Гц |
мОм 107Гц |
мОм 106 Гц |
мОм 105 Гц |
|
1,116 |
6,849 |
6,475 |
6,458 |
6,458 |
6,458 |
384,9 |
428,2 |
385,4 |
384,8 |
384,8 |
|
1,008 |
4,796 |
4,457 |
4,347 |
4,364 |
4,364 |
91,52 |
129,9 |
94,24 |
91,53 |
91,49 |
|
0,9 |
3,801 |
3,486 |
3,381 |
3,437 |
3,439 |
49,51 |
78,06 |
53,64 |
49,55 |
49,49 |
|
0,792 |
3,112 |
2,795 |
2,712 |
2,814 |
2,819 |
32,61 |
55,73 |
37,43 |
32,71 |
32,61 |
|
0,684 |
2,577 |
2,243 |
2,185 |
2,333 |
2,345 |
23,44 |
43,14 |
28,51 |
23,59 |
23,44 |
|
0,576 |
2,138 |
1,776 |
1,741 |
1,935 |
1,956 |
17,63 |
34,97 |
22,75 |
17,83 |
17,63 |
|
0,468 |
1,766 |
1,367 |
1,354 |
1,590 |
1,622 |
13,57 |
29,15 |
18,63 |
13,83 |
13,57 |
|
0,36 |
1,446 |
1,001 |
1,009 |
1,281 |
1,325 |
10,51 |
24,70 |
15,42 |
10,82 |
10,51 |
|
0,252 |
1,165 |
0,670 |
0,696 |
0,996 |
1,052 |
8,041 |
20,94 |
12,69 |
8,400 |
8,043 |
|
0,144 |
0,919 |
0,367 |
0,411 |
0,721 |
0,787 |
5,877 |
17,39 |
10,05 |
6,254 |
5,880 |
|
0,036 |
0,702 |
0,090 |
0,147 |
0,413 |
0,477 |
3,526 |
12,25 |
6,425 |
3,833 |
3,529 |
Таблица 8 (![]() , толщина
, толщина ![]() 1 мкм)
1 мкм)
|
Rb, мм |
нГн |
нГн 108 Гц |
нГн 107Гц |
нГн 106 Гц |
нГн 105 Гц |
Ом |
Ом 108 Гц |
Ом 107Гц |
Ом 106 Гц |
Ом 105 Гц |
|
1,116 |
7,128 |
6,577 |
6,576 |
6,576 |
6,576 |
3,465 |
3,471 |
3,463 |
3,463 |
3,463 |
|
1,008 |
4,869 |
4,368 |
4,382 |
4,382 |
4,382 |
0,8237 |
0,853 |
0,824 |
0,823 |
0,823 |
|
0,9 |
3,841 |
3,393 |
3,444 |
3,447 |
3,447 |
0,4456 |
0,487 |
0,446 |
0,445 |
0,445 |
|
0,792 |
3,139 |
2,722 |
2,817 |
2,824 |
2,824 |
0,2936 |
0,340 |
0,295 |
0,293 |
0,293 |
|
0,684 |
2,597 |
2,192 |
2,333 |
2,348 |
2,348 |
0,2110 |
0,259 |
0,213 |
0,211 |
0,211 |
|
0,576 |
2,153 |
1,747 |
1,932 |
1,957 |
1,958 |
0,1587 |
0,207 |
0,161 |
0,159 |
0,159 |
|
0,468 |
1,778 |
1,358 |
1,584 |
1,623 |
1,623 |
0,1221 |
0,169 |
0,125 |
0,122 |
0,122 |
|
0,36 |
1,455 |
1,011 |
1,272 |
1,326 |
1,327 |
0,0946 |
0,140 |
0,098 |
0,095 |
0,095 |
|
0,252 |
1,173 |
0,696 |
0,985 |
1,053 |
1,054 |
0,0724 |
0,115 |
0,076 |
0,072 |
0,072 |
|
0,144 |
0,926 |
0,409 |
0,708 |
0,787 |
0,788 |
0,0529 |
0,091 |
0,057 |
0,053 |
0,053 |
|
0,036 |
0,708 |
0,143 |
0,401 |
0,477 |
0,478 |
0,0317 |
0,059 |
0,035 |
0,032 |
0,032 |
Соответствующий графический материал показан на Рис. 13а,б и Рис. 14а,б.
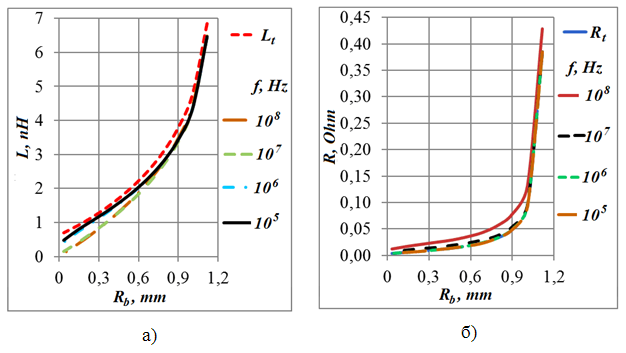
Рис. 13. Индуктивность и сопротивление кольца в зависимости
от величины внутреннего радиуса
для ряда частот для случая возбуждения от
источника э.д.с. при a=9 мкм
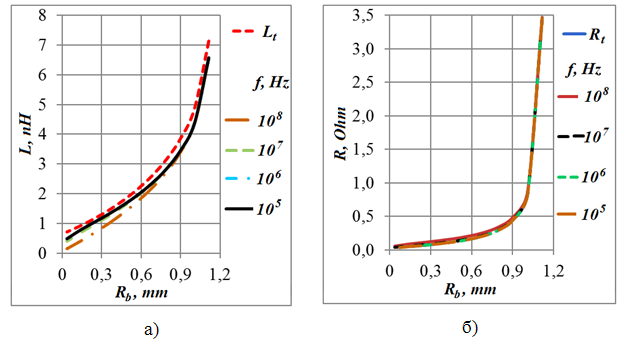
Рис.
14. Индуктивность и сопротивление кольца в зависимости
от величины внутреннего радиуса
для ряда частот для случая возбуждения от
источника э.д.с. при ![]() 1 мкм
1 мкм
Анализ графиков показывает, что распределение
токов в сечении проводника кольца принципиально отличается от аналогичных
распределений при возбуждении кольца внешним магнитным полем. Поэтому и
найденные величины индуктивностей с ростом частоты и ширины проводника имеют
обратную закономерность. Для колец с широким проводником (![]() ) при всех толщинах в частотном диапазоне
ниже 1 МГц наблюдается уменьшение индуктивностей приблизительно в 1,5 раза. С
ростом частоты происходит уменьшение индуктивностей для тонкого кольца (
) при всех толщинах в частотном диапазоне
ниже 1 МГц наблюдается уменьшение индуктивностей приблизительно в 1,5 раза. С
ростом частоты происходит уменьшение индуктивностей для тонкого кольца (![]() 1 мкм) в 5 раз, а для наиболее толстого (
1 мкм) в 5 раз, а для наиболее толстого (![]() 36 мкм) – в 11 раз по сравнению со
стандартными расчётами. Во всех случаях происходит рост сопротивлений колец с
увеличением частоты, причём для кольца с наиболее широким проводником в 2 раза
(
36 мкм) – в 11 раз по сравнению со
стандартными расчётами. Во всех случаях происходит рост сопротивлений колец с
увеличением частоты, причём для кольца с наиболее широким проводником в 2 раза
(![]() 1 мкм) и в 8,5 раз (
1 мкм) и в 8,5 раз (![]() 36мкм) на частоте 100 МГц.
36мкм) на частоте 100 МГц.
5. Результаты расчёта взаимной индуктивности одинаковых плоских колец с широким проводником, лежащих в параллельных плоскостях (при возбуждении внешним магнитным полем)
Алгоритм расчёта взаимной индуктивности одинаковых плоских колец с широким проводником, лежащих в параллельных плоскостях (Рис. 4), при возбуждении внешним магнитным полем дан в п. 2.4 определяется соотношениями (8) и (9).
Результаты расчёта взаимной индуктивности ![]() одинаковых плоских колец при слабом
скин-эффекте в зависимости от расстояния по вертикали
одинаковых плоских колец при слабом
скин-эффекте в зависимости от расстояния по вертикали ![]() приведены
на графиках Рис. 15, а в зависимости от расстояния по горизонтали
приведены
на графиках Рис. 15, а в зависимости от расстояния по горизонтали ![]()
![]() – на
графиках Рис. 16 для разных значений внутреннего радиуса плоского кольца (
– на
графиках Рис. 16 для разных значений внутреннего радиуса плоского кольца (![]() ).
).
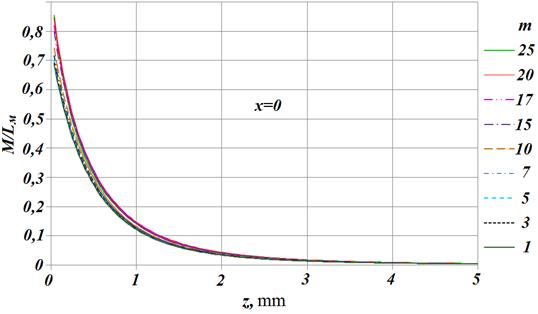
Рис. 15. Зависимости взаимной индуктивности колец от расстояния
по вертикали для разных значений ![]() =1…25
=1…25
Графики Рис. 15 и
Рис. 16 показывают, что взаимная индуктивность слабо зависит от размеров внутреннего
радиуса, причём при увеличении внутреннего радиуса абсолютная величина
взаимной индуктивности ![]() возрастает. Взаимная
индуктивность копланарных колец очень быстро спадает с увеличением расстояния
(на расстояниях равных диаметру кольца взаимная индуктивность составляет не
более 5% от индуктивности кольца. При определенных ненулевых значениях
возрастает. Взаимная
индуктивность копланарных колец очень быстро спадает с увеличением расстояния
(на расстояниях равных диаметру кольца взаимная индуктивность составляет не
более 5% от индуктивности кольца. При определенных ненулевых значениях ![]() и
и ![]() взаимная
индуктивность меняет знак.
взаимная
индуктивность меняет знак.
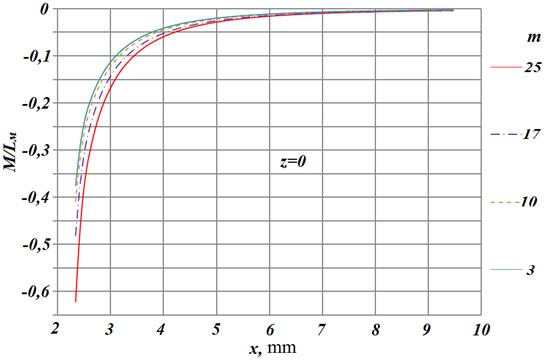
Рис. 16. Зависимости взаимной индуктивности колец от расстояния
по горизонтали для разных значений ![]() =3,
10, 17 и 25
=3,
10, 17 и 25
6. Выводы
1. Алгоритм расчёта индуктивностей при
произвольной степени скин-эффекта, разработанный в [5] для колец с круглым
проводником, модифицирован для плоских (печатных) колец с произвольно широким
проводником. Причём ширина их сечения ![]() может
быть не просто сравнима с внутренним радиусом
может
быть не просто сравнима с внутренним радиусом ![]() , но и
значительно больше него (
, но и
значительно больше него (![]() ).
).
2. Показано, что распределение
плотности тока по ширине кольца существенно зависит от способа его возбуждения:
от сторонней э.д.с. (классический случай) или от внешнего магнитного поля. Эти
различия сглаживаются по мере уменьшения ширины проводника. Перепад распределения
плотности может превышать 2…3 порядка и становятся всё более асимметричными по
мере увеличения ширины сечения и с ростом частоты. В первом случае максимум
распределения находится на кромке отверстия, а во втором – на внешней кромке
кольца. Распределения фаз при сильном скин-эффекте (область квазистатики!)
имеет глубокий провал приблизительно в середине проводника, близкий к ![]() . Размах изменений фазы уменьшается как
при уменьшении частоты, так и ширины проводника.
. Размах изменений фазы уменьшается как
при уменьшении частоты, так и ширины проводника.
3. Большая неоднородность и асимметрия
распределения тока в сечении кольца приводит к существенным погрешностям в
определении его индуктивности и сопротивления по классическим алгоритмам. Расхождение
увеличивается с ростом частоты и относительной ширины проводника кольца и может
превышать 1000% вниз – при классическом способе возбуждения кольца и 450% вверх
– при возбуждении его внешним магнитным полем. При уменьшении частоты и
уменьшении относительной ширины кольца значения индуктивности и сопротивления
асимптотически сходятся к результатам классических расчётов. Это говорит о том,
что классические формулы для расчёта индуктивностей печатных колец неприменимы
для вычисления индуктивности и сопротивления плоских колец с относительной
шириной проводника ![]() при возбуждении внешним магнитным
полем. При возбуждении от внешней э.д.с. классические формулы дают
удовлетворительный результат даже для колец с весьма широким проводником (
при возбуждении внешним магнитным
полем. При возбуждении от внешней э.д.с. классические формулы дают
удовлетворительный результат даже для колец с весьма широким проводником (![]() ), толщина которого не превышает половины
толщины скин-слоя на данной частоте.
), толщина которого не превышает половины
толщины скин-слоя на данной частоте.
4. Разработанные алгоритмы расчета индуктивностей, сопротивлений и взаимных индуктивностей плоских колец могут быть применены и для расчета указанных параметров колец с различной геометрией сечения.
Литература
1. П.Л. Калантаров, Л.А. Цейтлин. Расчет индуктивностей: Справочная книга. – Л.: Энергоатомиздат. Ленингр. отд., 1986. – 488 с.
2. Rayleigh, S.D.W.. Proceedings of Royal Society, 32, p. 104 (1881); 86, p. 562 (1912).
3. В. А. Фок. Журнал Русского Физико-Химического общества, часть физическая, 62, № 3 (1930).
4. Цейтлин Л.А. Индуктивности проводов и контуров. – Л.: Госэнергоиздат, 1950 – 228 с.
5. А.В. Савельев, Н.П. Чубинский. Расчёт индуктивности колец при произвольной степени скин-эффекта. // Журнал радиоэлектроники: электронный журнал. 2014. N1. URL: http://jre.cplire.ru/iso/jan14/1/text.pdf
6. Shelby R. A., Smith D. R. and Schulz S. Experimental Verification of Negative Index of Refraction. –Science. – 2001. – V. 292. – P. 77-79
7. В.В. Никольский, Т.И. Никольская. Электродинамика и распространение радиоволн: Учеб. Пособие для вузов – М.: Наука. Гл. ред. физ-мат. лит.,1989 – 544 с.