|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2003 |
|
ОЦЕНКА ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ НЕПРЕРЫВНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ ОБРАБОТКИ ШИРОКОПОЛОСНОГО ЧАСТОТНОМОДУЛИРОВАННОГО СИГНАЛА
Поршнев С. В.
Нижнетагильский государственный педагогический институт
Получена 12 января 2003 г.
Приведены результаты исследования возможности применения непрерывного вейвлет-преобразования в задаче определения закона изменения частоты ЧМ модулированного сигнала.
Задача обработки широкополосного ЧМ сигнала (точнее, определения закона изменения частоты по известной зависимости мгновенных значений сигнала от времени) возникает при измерении параметров движения снарядов (ПДС) в стволах артиллерийских систем на внутрибаллистическом этапе выстрела радиолокационными методами [1]. В [2] построены различные алгоритмы обработки радиолокационных сигналов (РС), получаемых в задаче измерения ПДС в стволе: метод временных интервалов; метод граничной частоты; метод мгновенного спектра; метод аналитического сигнала; и на основе анализа результатов обработки моделей РС даны оценки их точностных характеристик.
Однако за рамками монографии [2] осталось активно развиваемое в настоящее время направление цифровой обработки сигналов - вейвлет-преоб-разование (Wavelet) [3], которое в ряде случаев оказывается эффективным при анализе сигналов с изменяющимися частотно-временными характеристиками [4,5]. Данное обстоятельство определяет актуальность темы исследования: оценить возможность применения вейвлет-анализа в задачах обработки широкополосных ЧМ сигналов.
Отметим, что проведенный нами анализ научной литературы на русском языке показывает, что несмотря на определенные успехи достигнутые при решении ряда задач из различных областей науки и техники, число публикаций по данной проблеме относительно невелико (см., например, [4-14]), а терминология, используемая в данной области обработки сигналов, пока не является устоявшейся. Поэтому представляется целесообразным предварить обсуждение основной проблемы статьи кратким изложением необходимых сведений из теории вейвлет-преобразования, а также способов представления получаемых результатов.
Понятие вейвлет (wavelet в дословном переводе - маленькая волна) был введен в научный оборот Гроссманом (A. Grossman) и Морле (J. Morle) в середине 80-х гг. в связи с необходимостью анализа свойств сейсмических и акустических сигналов [3], являющихся по своей природе нестационарными. В настоящее время цифровой анализ сигналов, основанный на вейвлет-преобразовании, начинает применяться в задачах распознавания образов и сжатия видеоизображений, самой различной природы (снимки минералов, спутниковые изображения облаков или поверхностей планет, галактик, снимки различных турбулентных процессов и т.д.); при обработке и синтезе различных сигналов, например, речевых, виброакустических, сейсмосигналов; для изучения свойств турбулентных полей и т.д.
2.1. Непрерывное вейвлет-преобразование
Рассмотрим пространство ![]() функций, определенных на всей действительной
оси
функций, определенных на всей действительной
оси ![]() и имеющих
конечную энергию
и имеющих
конечную энергию
и
пространство ![]() ,
квадратично интегрируемых функций на интервале [0,2p].
,
квадратично интегрируемых функций на интервале [0,2p].
Отметим, что функциональные пространства ![]() и
и ![]() существенно различны, в
частности, функция не принадлежит пространству
существенно различны, в
частности, функция не принадлежит пространству ![]()
![]() , как не удовлетворяющая условию (1).
Следовательно, набор синусоидальных волн
, как не удовлетворяющая условию (1).
Следовательно, набор синусоидальных волн ![]() не может быть базисом функционального пространства
не может быть базисом функционального пространства
![]() .
.
Базисные функции («волны») пространства ![]() должны стремиться к нулю
при
должны стремиться к нулю
при ![]() . Для
построения базиса пространства
. Для
построения базиса пространства ![]() наиболее подходящими оказались
солитоноподобные функции
- вейвлеты.
Аналогично методу, использовавшемуся при построении базиса пространства
наиболее подходящими оказались
солитоноподобные функции
- вейвлеты.
Аналогично методу, использовавшемуся при построении базиса пространства ![]() , который был полностью
сформирован с помощью одной базисной функции
, который был полностью
сформирован с помощью одной базисной функции ![]() , базис пространства
, базис пространства ![]() также конструируется с помощью
одного вейвлета
также конструируется с помощью
одного вейвлета ![]() . При этом спектр данного вейвлета может иметь одну
частоту или набор частот.
. При этом спектр данного вейвлета может иметь одну
частоту или набор частот.
Для построения базиса пространства ![]() вводят систему сдвигов
вводят систему сдвигов ![]() , которые для простоты
будем считать целыми, и аналог синусоидальной частоты, которые для
определенности будем считать кратными степени числа 2:
, которые для простоты
будем считать целыми, и аналог синусоидальной частоты, которые для
определенности будем считать кратными степени числа 2: ![]() , здесь
j,
k
- целые числа
(
, здесь
j,
k
- целые числа
(![]() ). Выполняя
масштабные преобразования, можно описать все частоты и покрыть всю временную
ось, используя один базисный вейвлет.
). Выполняя
масштабные преобразования, можно описать все частоты и покрыть всю временную
ось, используя один базисный вейвлет.
Найдем связь между нормами функций ![]() и
и ![]() . По определению нормы функции находим
. По определению нормы функции находим
![]() ,
,
т. е.
![]() .
.
Следовательно, если вейвлет ![]() имеет единичную норму, то все
вейвлеты семейства
имеет единичную норму, то все
вейвлеты семейства ![]() вида
вида
также
нормированы на единицу, т.е. ![]() .
.
Вейвлет ![]() называется ортогональным, если
определенное соотношением (2) семейство представляет собой ортонормированный
базис функционального пространства
называется ортогональным, если
определенное соотношением (2) семейство представляет собой ортонормированный
базис функционального пространства ![]() , т.е.
, т.е.
и каждая функция ![]() может
быть представлена в виде ряда
может
быть представлена в виде ряда
Можно
показать, что при соответствующем выборе функций ![]() ряд будет сходится равномерно в
ряд будет сходится равномерно в ![]() , следовательно,
, следовательно,
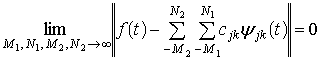 .
.
Отметим, что доказательство многих положений теории вейвлетов (полноту и ортогональность базиса, сходимостью рядов и др.) удалось получить именно для дискретного частотно-временного пространства, образованного целыми сдвигами и растяжениями по степеням двойки [3,10]. Данные положения имеют особую важность в задачах, где необходимо проведение разложения сигнала с использованием минимального числа независимых коэффициентов вейвлет-преобразования и иметь точную формулу обратного преобразования (например, при сжатии информации или в задачах численного моделирования).
Аналогично описанному выше подходу осуществляется
построение базиса пространства ![]() , состоящего из непрерывных вейвлетов. Здесь
значения коэффициента масштабного преобразования и параметра сдвига являются
произвольными действительными числами:
, состоящего из непрерывных вейвлетов. Здесь
значения коэффициента масштабного преобразования и параметра сдвига являются
произвольными действительными числами:
где ![]() ,
, ![]() .
.
Непрерывное вейвлет-преобразование, используя (5), можно записать следующим образом:
Далее, проводя аналогию с преобразованием Фурье,
коэффициенты ![]() разложения
(4) функции
разложения
(4) функции ![]() в
ряд по вейвлетам определяют через интегральное вейвлет-преобразование:
в
ряд по вейвлетам определяют через интегральное вейвлет-преобразование:
Для обозначения коэффициентов вейвлет-преобразования в
научной литературе используются более компактные обозначения: ![]() ,
, ![]() или
или ![]() .
.
Таким образом, любая функция ![]() может быть получена суперпозицией
масштабных преобразований и сдвигов выбранного базисного вейвлета
может быть получена суперпозицией
масштабных преобразований и сдвигов выбранного базисного вейвлета ![]() , т.е. представлена
набором «вейвлетных волн», амплитуды которых зависят номера волны
(соответственно, частоты или масштаба) и от параметра сдвига (времени).
, т.е. представлена
набором «вейвлетных волн», амплитуды которых зависят номера волны
(соответственно, частоты или масштаба) и от параметра сдвига (времени).
Простейшим примером ортогонального вейвлета является вейвлет Хаара (Haar), определяемый соотношением
Подставив (8) в (3), легко убедиться в том, что любые
две функции ![]() ,
, ![]() , полученные из
Haar-вейлета
с помощью масштабных преобразований
, полученные из
Haar-вейлета
с помощью масштабных преобразований ![]() ,
, ![]() и сдвигов
и сдвигов ![]() ,
, ![]() , ортогональны и имеют единичную норму. Отметим,
что вейвлет Хаара хорошо локализован во временной области и плохо в частотной
области, т.к. меандр имеет широкий спектр частот.
, ортогональны и имеют единичную норму. Отметим,
что вейвлет Хаара хорошо локализован во временной области и плохо в частотной
области, т.к. меандр имеет широкий спектр частот.
Известны и другие виды ортогональных вейвлетов, исторически первым из которых был предложен И. Добеши [6]. Вейвлет Добеши, реализуемый итерационными формулами, хорошо локализован и во временной и в частотной областях. Однако он также не свободен от недостатков, в частности, вейвлет Добеши оказывается несимметричным.
2.2. Пространственно-временная локализация
Рассмотрим механизм частотно-временной локализации
вейвлет-преобразования. Будем считать, что нетривиальная оконная функция ![]() и функция
и функция ![]() принадлежат
принадлежат ![]() . Тогда центр
. Тогда центр ![]() функции
функции ![]()
радиус
![]() функции
функции
![]()
при
этом ширина оконной функции есть ![]() , средняя частота окна
, средняя частота окна
![]()
радиус
окна в частотной области ![]()
Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() - определенные
по формулам (9)-(12) центры и радиусы вейвлета
- определенные
по формулам (9)-(12) центры и радиусы вейвлета ![]() во временной и
частотной областях, соответственно. Найдем
во временной и
частотной областях, соответственно. Найдем ![]() - радиус
временного окна вейвлет-преобразования, задаваемого базисным вейвлетом
- радиус
временного окна вейвлет-преобразования, задаваемого базисным вейвлетом ![]() , считая что вейвлет
нормирован на единицу. Подставив выражение для базисного вейвлета
, считая что вейвлет
нормирован на единицу. Подставив выражение для базисного вейвлета ![]() в (9)
в (9)
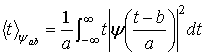 ,
,
и
выполнив очевидную замену переменных ![]() , получаем
, получаем
где
Далее, подставив выражение для базисного вейвлета ![]() в (10) и повторив замену
переменных, получим
в (10) и повторив замену
переменных, получим
где
Таким образом, интегральное преобразование вида
где
![]() - функция окна,
- функция окна,
![]() - переменная, определяющая положение окна на временной
оси, ограничено временным окном
- переменная, определяющая положение окна на временной
оси, ограничено временным окном
Будем считать, что энергия спектра основного вейвлета ![]() сосредоточена в области
сосредоточена в области
где
Для произвольного базисного вейвлета ![]() , по аналогии с (18),
можно записать
, по аналогии с (18),
можно записать
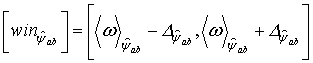 ,
,
где
![]() ,
, ![]() вычисляются,
соответственно, по формулам (20), (21) с заменой функции
вычисляются,
соответственно, по формулам (20), (21) с заменой функции ![]() на функцию
на функцию ![]() . Следовательно, для понимания
механизма действия вейвлет-преобразования остается получить соотношение между
. Следовательно, для понимания
механизма действия вейвлет-преобразования остается получить соотношение между ![]() и
и ![]() ,
, ![]() и
и ![]() . Для этого сначала найдем связь между
спектрами
. Для этого сначала найдем связь между
спектрами ![]() и
и ![]() :
:
Подставляя (22) в (20), (21) получим
Из (23), (24) очевидно, что спектр базисного вейвлета ![]() локализован в области
локализован в области
Таким образом, частотная локализация происходит около
центра окна, расположенного в точке ![]() , ширина окна равна
, ширина окна равна ![]() . Отметим, что отношение центральной
частоты к ширине окна
. Отметим, что отношение центральной
частоты к ширине окна
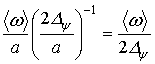 ,
,
не
зависит от значения центральной частоты вейвлета, а частотно-временное окно ![]() , имеющее площадь
, имеющее площадь ![]() , сужается при высокой
центральной частоте и расширяется при низкой.
, сужается при высокой
центральной частоте и расширяется при низкой.
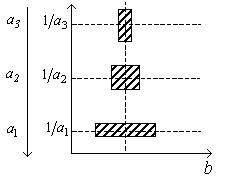
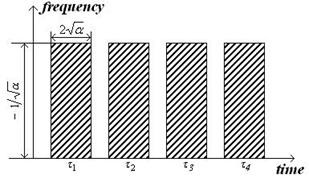
Рис. 1а. Частотно-временная локализация с использованием вейвлетов
Рис. 1б.
Частотно-временная локализация с использованием оконного преобразования Фурье
[15] с оконной функцией вида 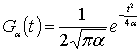
Иллюстрация частотно-временного преобразования с использованием вейвлетов в плоскости время-частота представлена на рис. 1а. Для сравнения на рис. 1б представлена иллюстрация частотно-временного преобразования при использовании оконного преобразования Фурье.
Необходимо отметить, что в научной литературе на сегодняшний день отсутствует общепринятое определение термина «вейвлет». (Одно из наиболее простых определений вейвлета приведено в [10].) Для практического использования вейвлет-анализа важнее знать необходимые свойства, при наличии которых функция может быть отнесена к вейвлетам:
1. Локальность (вейвлет должен быть локализован во времени и в пространстве).
2. Нулевое среднее:
![]() =0.
=0.
(При выполнении условия
![]()
вейвлет называется вейвлетом m-го порядка. Вейвлеты данного типа позволяют исключить из рассмотрения наиболее регулярные, полиномиальные составляющие сигнала и проводить анализ мелкомасштабных флуктуаций высокого порядка.)
3. Ограниченность:
![]() .
.
(Оценка хорошей локализации и ограниченности может быть записана в виде
![]()
или
![]() ,
,
где ![]() - центральная частота спектра вейвлета. Здесь
число n должно быть возможно большим.)
- центральная частота спектра вейвлета. Здесь
число n должно быть возможно большим.)
4. Автомодельность базиса: вейвлеты данного
семейства ![]() , будучи
полученными посредством масштабных преобразований и сдвигов, имеют такое же
число осцилляций, как и базовый вейвлет
, будучи
полученными посредством масштабных преобразований и сдвигов, имеют такое же
число осцилляций, как и базовый вейвлет ![]() .
.
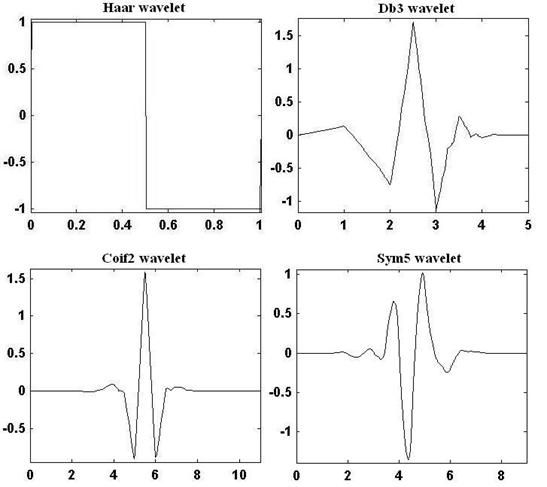
Рассмотрим в качестве примеров некоторые используемые на практике базисные вейвлеты (рис. 2). Из рис. 2 видно, что каждый вейвлет имеет характерные особенности во временном и частотном пространстве, поэтому иногда с помощью разных вейвлетов можно полнее выявить и подчеркнуть те или иные свойства сигнала. При этом надо также учитывать, что вейвлет-коэффициенты содержат информацию не только о сигнале, но и о вейвлете. Если производная вейвлета также является вейвлет-функцией, то мы имеем возможность получить вейвлет более высокого порядка, который имеет больше нулевых моментов, нежели исходный, и позволяет извлечь информацию об особенностях более высокого порядка, содержащихся в сигнале. Отметим, что общепринятых правил и рекомендаций для выбора типа вейвлета в конкретной задаче в настоящее время не существует.
Рис. 2. Примеры базисных вейвлет-функций
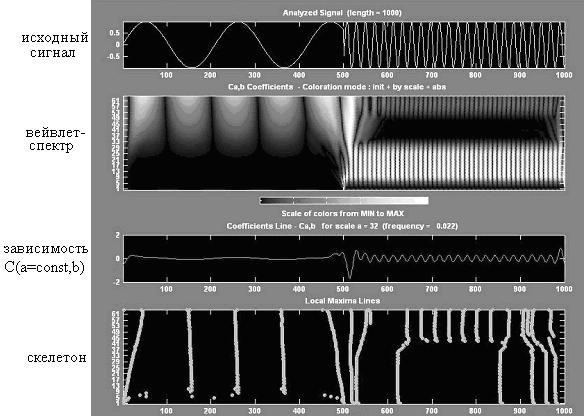
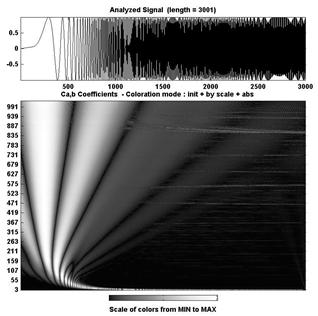
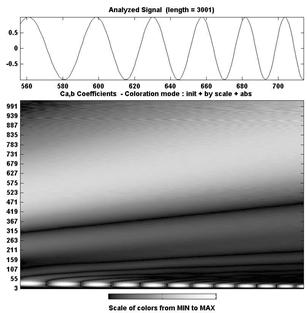
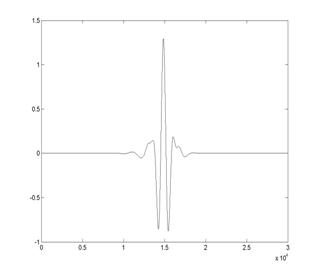
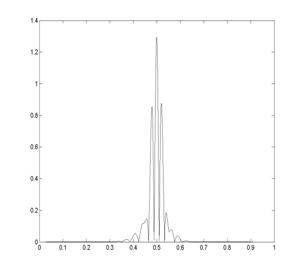
Рис. 3. Примеры представления вейвлет-спектров модельного сигнала
2.4. Способы представления результатов вейвлет-преобразования и энергетические характеристики сигнала
Вейвлет-спектр W(a,b) представляет собой некоторую поверхность в трехмерном пространстве, способы визуализации которой могут быть различны. Обычно для анализа частотно-временного состава исследуемого сигнала используют:
1) карту проекций изоуровней или изолиний функции W(a,b) на плоскость (a,b), позволяющих проанализировать изменение интенсивности амплитуд вейвлет-преобразования на различных частотных масштабах и во времени;
2) карты линий локальных экстремумов данных поверхностей, называемых скелетонами (sceleton), четко выявляющих структуру сигнала;
3) зависимости коэффициентов вейвлет преобразования для выбранного масштаба преобразования от времени.
Примеры исходного сигнала и представления результатов его вейвлет преобразования представлены на рис. 3.
Наличие коэффициентов вейвлет-преобразования позволяет также исследовать энергетические характеристики сигнала. Анализ энергетических характеристик сигнала основан на теореме, являющейся аналогом теоремы Парсеваля для преобразования Фурье [10]:
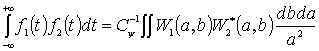 , (25)
, (25)
где
![]() ,
, ![]() - коэффициенты вейвлет-преобразования функций
f1(t),
f2(t),
соответственно.
- коэффициенты вейвлет-преобразования функций
f1(t),
f2(t),
соответственно.
Следствием существования аналога равенства Парсеваля является возможность записать полную энергию сигнала Ef в пространстве действительных функций через амплитуды вейвлет-преобразования:
Из (26) видно, что величину Ew(a,b)=W2(a,b), характеризующую энергетические уровни исследуемого сигнала f(t) в пространстве (a,b), можно рассматривать как локальную плотность энергии.
Локальная плотность энергии Ed в точке b = t0 («локальный энергетический спектр»), позволяющая проанализировать временную динамику передачи энергии сигнала по масштабам, имеет вид
Величину
описывающую распределение энергии сигнала по масштабам называют дисперсией вейвлет-преобразования (wavelet variance) или также скалограммой (scalogram).
Можно показать, выразив дисперсию
вейвлет-преобразования
Ew(a) через спектр энергии сигнала в пространстве Фурье
EF(w)=![]() , что дисперсия
вейвлет-преобразования (28) есть сглаженный спектр мощности сигнала
EF:
, что дисперсия
вейвлет-преобразования (28) есть сглаженный спектр мощности сигнала
EF:
Так как анализируемая функция имеет конечную энергию, а используемый вейвлет - нулевое среднее значение, дисперсия вейвлет-преобразования EW(a) должна стремиться к нулю на левом и правом концах шкалы масштабов. Следовательно, по теореме Ролля, данная функция на указанном интервале имеет по крайней мере один максимум. Положение данных максимумов дисперсии вейвлет-преобразования, аналогично максимумам спектра Фурье EF(w), связывается с частотами и соответствующими характерными составляющими исследуемого сигнала, обеспечивающими основной вклад в его энергию. Отметим, что данный вывод справедлив для периодических, однако, результаты его экспериментальной проверки, проведенной с использованием различных вейвлетов и различными типами сигналов, показали, что он с достаточной точностью выполняется и для непериодических сигналов [16].
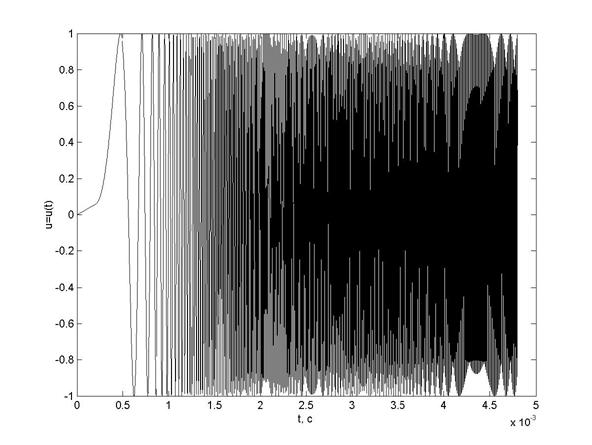
Рис. 4а. Зависимость мгновенных значений модели РС от времени
3. ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ
НЕПРЕРЫВНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ
ОБРАБОТКИ ШИРОКОПОЛОСНОГО ЧМ СИГНАЛА
В работе [3] автором было предложено для оценки работоспособности алгоритмов обработки радиолокационных сигналов (РС), получаемых в задаче измерения параметров движения снаряда (ПДС) внутри канала ствола во время выстрела, и оценки их точности использовать модели РС, законы изменения фазы и частоты которых от времени известны. Используем данный подход для
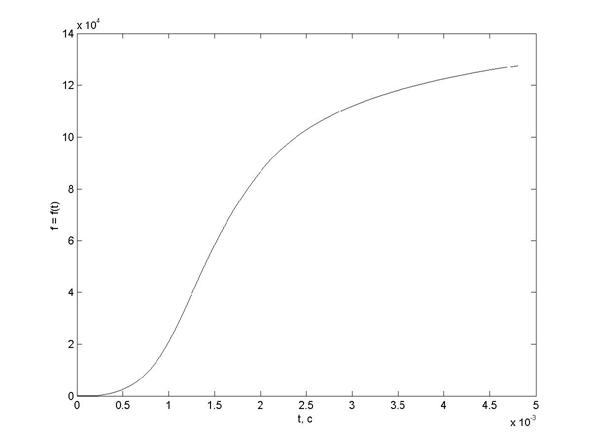
Рис. 4б. Закон ЧМ модели радиолокационного сигнала
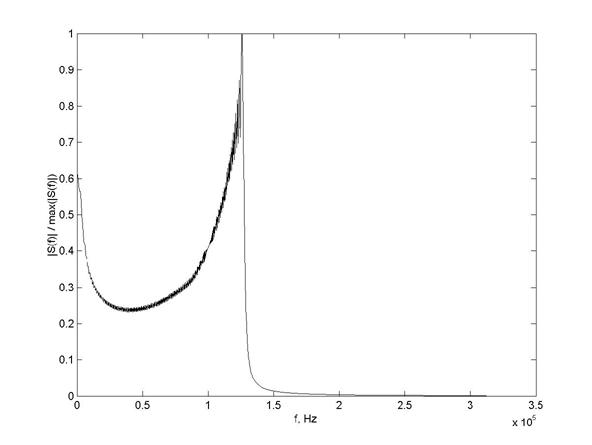
Рис. 4в. Нормированный энергетический спектр модели РС
оценки применимости вейвлет-анализа в задаче обработки РС на примере модели радиолокационного сигнала, получаемого в задаче измерения ПДС бронебойно-подкалиберного снаряда в стволе во время выстрела. Зависимость мгновенных значений модели РС от времени, вычисленная в N = 3000 точках, закон ЧМ сигнала и его спектр представлены на рис. 4а-4в, соответственно. Из рис. 4а-4в видно, что рассматриваемый РС является ЧМ сигналом со сложным монотонно возрастающим законом ЧМ, частота которого изменяется в диапазоне [0;130] кГц за время 4.8 мс.
Предваряя анализ результатов обработки модели РС, получаемого в задаче измерения ПДС в стволе во время выстрела, методом вейвлет-преобразования, особо отметим принципиальное отличие рассматриваемой задачи от известных примеров использования вейвлет-анализа [17], в которых абсолютном большинстве случаев вейвлет-коэффициенты использовались скорее для качественного нежели количественного анализа частотно-временных характеристик сигналов. В рассматриваемой задаче, напротив, необходим не качественный, но количественный анализ, позволяющий с максимально возможной точностью определить закон ЧМ.
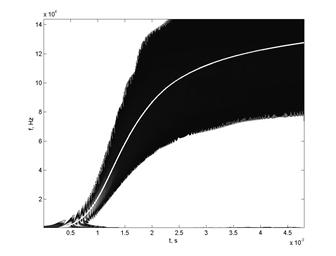
Рис. 5а. Вейвлет-спектр модели РС
Рис. 5б. Фрагмент вейвлет-спектра модели
Рис. 6а. Вейвлет-функция базисного
вейвлета Койфлета 5-го порядка
Рис. 6б. Спектр базисного
вейвлета Койфлета 5-го порядка
Рассмотрим типичные результаты, получаемые при обработке модельного РС методом вейвлет-преобразования (рис. 5). Здесь в качестве базового вейвлета был использован вейвлет Койфлета 5-го порядка, вейвлет-функция и спектр которого представлены на рис. 6. Коэффициенты непрерывного вейвлет-преобразования вычислялись с помощью пирамидального алгоритма Маллата [18]. Масштабные множители a вейвлет-преобразования изменялись в диапазоне [3; 1025] с шагом равным единице, что соответствует диапазону частот [419.7; 1.435×105] Гц. Из вейвлет-спектра, представленного на рис. 5, хорошо видно, что с течением времени частота исследуемого сигнала увеличивается. Это проявляется в том, что белые полосы, соответствующие экстремумам РС, смещаются в высокочастотную область (область малых значений масштабных коэффициентов).
Как видно из рис. 5б, на котором представлен фрагмент вейвлет-спектра модели РС, в области высоких частот хорошо различимы чередования темных, соответствующих точкам перехода сигнала через ноль, и светлых полос, соответствующих экстремумам сигнала. Оценка мгновенной частоты по непрерывному вейвлет-спектру может быть получена как обратная величина удвоенного временного интервала между двумя последовательными экстремумами. В данном подходе, являющимся по своей сути методом, основанном на измерении периода сигнала, априори предполагается, что частота сигнала на рассматриваемом временном интервале остается постоянной. Данное предположение для ЧМ сигналов с произвольным законом изменения частоты, вообще говоря, не справедливо, поэтому возможность использования периодомерного способа оценки мгновенной частоты для конкретного ЧМ сигнала требует отдельного исследования. Методика такого исследования описана в [2] на примере РС, получаемых в задаче измерения ПДС в стволе артиллерийской системы во время выстрела, там же получены оценки соответствующих погрешностей и показано, что алгоритм обработки сигнала, базирующий на периодомерном способе измерения частоты, обладает наихудшими точностными характеристиками из всех известных алгоритмов обработки РС. Отметим также, что по вейвлет-спектру невозможно получить оценку закона изменения частоты до момента достижения сигналом первого максимума (как и при использовании фурье-анализа, в котором для оценки частоты сигнала на данном временном интервале необходимо иметь по крайней мере один период сигнала).
Рассматриваемый РС является ЧМ сигналом со сложным монотонно возрастающим законом изменения частоты, поэтому с течением времени энергия сигнала будет определяться энергией гармоник, находящихся в высокочастотной области. Наиболее эффективно указанное свойство сигнала можно продемонстрировать, используя оконное преобразование Фурье, называемым в [15] «мгновенным спектром». Результатом применения оконного преобразования Фурье является набор мгновенных спектров S(w,ti)
где ti - центр временного окна, Dt - ширина окна, карта линий уровней, которых представлена на рис. 7.
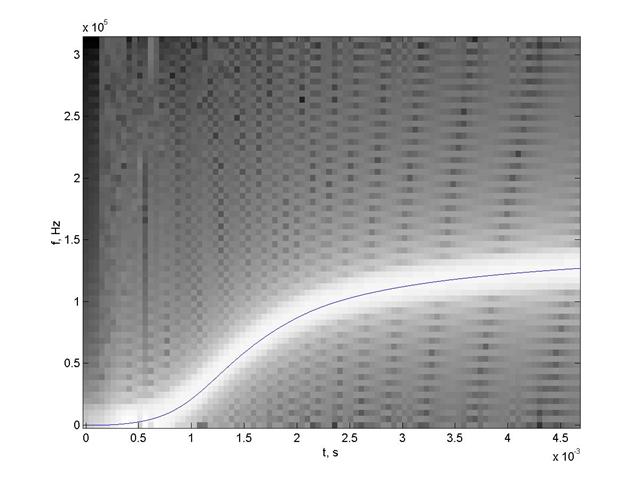
Рис. 7. Карта линий уровня мгновенных спектров модели РС в плоскости «время-частота» (сплошная линия закон ЧМ модели РС)
Из рис. 7 видно, что эволюция во времени значений частоты, соответствующей максимальному значению мгновенного спектра, происходит в соответствии с законом ЧМ рассматриваемого сигнала. Более подробное алгоритм обработки РС, получаемых в задаче измерения параметров движения снаряда в стволе во время выстрела, основанный на оконном преобразовании Фурье, и оценки его точностных характеристик при использовании различных методов спектрального оценивания представлены в [2].
Проводя аналогию с оконным преобразованием Фурье, естественно предположить, что локальная плотность энергии Ed (а,t0) (27) («локальный энергетический спектр»), характеризующая временную динамику передачи энергии сигнала по масштабам [4], в момент времени t0 принимает максимальное значение в точке а = am, соответствующей значению мгновенной частоты сигнала в момент времени t0
где Fc - частота базисного вейвлета.
Отметим, что для получения
значений частоты вейвлет-преобразования в Гц необходимо умножить безразмерную
частоту ![]() на частоту дискретизации
на частоту дискретизации ![]() анализируемого сигнала:
анализируемого сигнала:
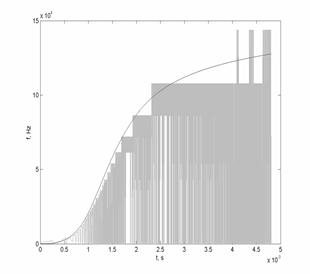
Зависимость мгновенной частоты сигнала от времени, определенная как набор частот, соответствующих максимумам локальных энергетических спектров Ed (а,ti), i = 1,2,…,N, представлена на рис. 8.
8а. Результаты обработки модели РС
при использовании непрерывного
вейвлет-преобразования
(гладкая кривая - закон ЧМ модели РС)
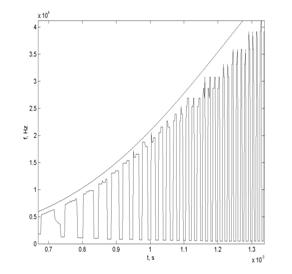
8б. Результаты обработки модели РС
при использовании непрерывного
вейвлет-преобразования (фрагмент)
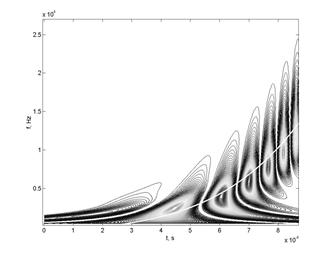
9а. Карта эквипотенциалей функции W 2 (a,b)
в плоскости «время - частота»
(сплошная линия - истинный закон изменения частоты сигнала)
9б. Карта эквипотенциалей функции W 2 (a,b) в плоскости
«время- частота» (сплошная линия - истинный
закон изменения частоты сигнала) (фрагмент)
Полученный результат выглядит достаточно неожиданным: оказывается, что, во-первых, существуют моменты времени, в которые локальные энергетические спектры имеют максимумы на частотах, существенно отличающихся от истинной мгновенной частоты сигнала. Во-вторых, как видно из рис. 8б, значения частоты, получаемые при анализе дисперсии коэффициентов вейвлет-спектра, всегда оказываются смешенными относительно истинных значений мгновенной частоты сигнала.
Для качественного объяснения полученного результата рассмотрим карту эквипотенциалей дисперсии вейвлет-коэффициентов W 2 (a,b) в плоскости «время-частота» (рис. 9). Сравнение вейвлет-спектра, представленного на рис. 5, и карты эквипотенциалей функции W 2 (a,b), позволяет сделать вывод о том, что последняя более наглядно отображает частотно-временные особенности исследуемого ЧМ сигнала. Как видно из рис. 9, поверхность, задаваемая набором значений W 2 (a,b), состоит из ряда пиков, отделенных друг от друга глубокими впадинами. Существование данных впадин является причиной обнаруженных «провалов» на графике зависимости закона изменения частоты сигнала от времени (рис. 8).
Сравнение зависимости мгновенных значений исходного сигнала от времени (рис. 4а) и карты эквипотенциалей функции W 2 (a,b) позволяет сделать вывод о совпадении моментов времени, соответствующих экстремумам исходного сигнала, и координат пиков функции W 2 (a,b). Обнаруженное свойство дисперсии вейвлет-коэффициентов позволяет использовать для нахождения закона изменения частоты следующий алгоритм:
1. Определить моменты времени ti, соответствующие экстремумам исходного сигнала.
2. Вычислить вейвлет-коэффициенты W 2 (a,b).
3. Для каждого момента времени ti, определить соответствующие значения коэффициентов bi.
4. Для каждого значения коэффициента bi, найти значения ai, в которых функция W 2 (ai,bi) достигает максимального значения.
5. Вычислить, используя набор значений ai, по формуле (32) соответствующие значения частоты Fi.
6. Для нахождения значений мгновенной частоты сигнала в промежуточных точках провести интерполяцию данных таблицы, содержащей значения ti, Fi.
1. Проведено исследование возможности использования непрерывного вейвлет-преобразования для обработки широкополосных ЧМ сигналов, в частности, радиолокационных сигналов, получаемых в задаче измерения параметров движения артиллерийских снарядов в стволе во время выстрела.
2. Показано, что представление результатов вейвлет-преобразования ЧМ сигнала в виде карты эквипотенциалей дисперсии вейвлет-коэффициентов W 2 (a,b) (локального энергетического спектра) оказывается более информативным, чем вейвлет-спектр сигнала.
3. Выявлены принципиальные отличия свойств вейвлет-коэффициентов и мгновенных спектров сигнала, получаемых с помощью оконного преобразования Фурье.
4. Показано, что дисперсия вейвлет-коэффициентов задает в пространстве поверхность, состоящую из набора пиков, отделенных друг от друга впадинами, при этом координаты максимумов на временной оси совпадают с моментами времени, соответствующими экстремумам сигнала.
5. Построен алгоритм обработки широкополосных ЧМ сигналов, основанный на свойстве локального энергетического спектра вейвлет-преобразования.
6. Показана эффективность подхода, основанного на анализе результатов вейвлет-анализа сигнала с известными частотно-временными, который можно использовать при оценке возможности использования вейвлет-преобразования для оценки частотно-временных характеристик нестационарных сигналов и интерпретации получаемых результатов.
1. Поршнев С.В. Радиолокационные методы измерений кинематических характеристик снаряда на начальном этапе выстрела// Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 1999. № 9. C. 43–78.
2. Поршнев С.В. Радиолокационные методы измерений экспериментальной баллистики. Екатеринбург: УрО РАН, 1999.
3. Grossman A., Morlet J. SIAM Journal Mathematics Analysis. 1984. Vol. 15. P. 723.
4. Астафьева Н. М. Вейвлет-анализ: основы теории и примеры применения// Успехи физических наук. 1996. Т. 166. № 1. С. 1145-1170.
5. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование// Успехи физических наук. 2000. Т. 171. № 5.
6. Добеши И. Десять лекций по вейвлетам. М.: Регулярная и хаотическая динамика, 2001.
7. Новиков И.Я., Стечкин С.Б. Основы теории всплесков// Успехи математических наук. 1998. № 6. С. 53-128.
8. Дьяконов В., Абраменкова И. Обработка сигналов и изображений. Специальный справочник. Спб.: Питер, 2002.
9. Дьяконов В.П. Вейвлеты. От теории к практике.М.: Солон-Р, 2002.
10. Чуи К. Введение в вейвлеты. М.: Мир, 2001.
11. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразований. СПб: ВУС, 1999.
12. Переберин А.В. О систематизации вейвлет-преобразований// Вычислительные методы и программирование. 2001. Т. 2.
13. Поликар Р. Введение в вейвлет-преобразование. СПб.: АВТЭКС, 2001.
14. Кравченко В.Ф., Рвачев В.А. «Wavelet»-системы и их применение в обработке сигналов// Зарубежная радиоэлектроника. 1996. № 4. С. 3-20.
15. Макс Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х тт. Т. 2. М.: Мир, 1983.
16. Wavelet and Their Applications (Ed. R. Coifman) (Boston: Jones and Barlett Publ., 1992)
17. M. Misiti, Y. Misiti, G. Oppenheim, J.-Ml Poggi, Wavelet Toolbox User’s Guide, The MathWorks Inc, 2001.
18. Mallat S. A theory for multiresolution signal decomposion: the wavelet representation// IEEE Pattern Analog and Machine Intell. Vol. 11. № 7. PP. 674-693.
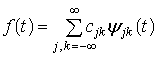 .
(4)
.
(4)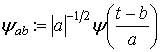 ,
(5)
,
(5)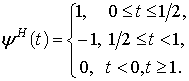 (8)
(8)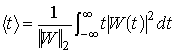 ,
(9)
,
(9)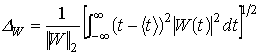 ,
(10)
,
(10)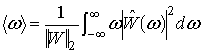 ,
(11)
,
(11)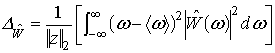 .
(12)
.
(12)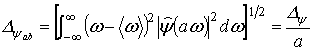 . (24)
. (24)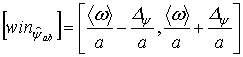 .
(25)
.
(25)
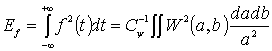
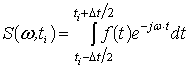 ,
(30)
,
(30) 
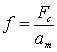 , (31)
, (31)