|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2003 |
|
Математическое обоснование параметров
зондирующих сигналов для реализации
бистатической локации в низкочастотной томографии
*Стародубцев П. А., e-mail: pavel@jas.ru
**Стародубцев Е. П.e-mail: pavel@jas.ru
*Тихоокеанский военно-морской институт им. С.О. Макарова
**Дальневосточный Государственный технический университет
Получена 20 января 2003 г.
В работе приводится оригинальный научно-математический анализ и новые теоретические предложения по применению тональных и сложных сигналов в низкочастотной томографии для реконструкции образов морских неоднородностей. Для реализации принципов бистатической локации и низкочастотной томографии в различных ситуациях, получения объективной информации о морском объекте обосновано применение фазоманипулированной псевдослучайной М - последовательности, которая обладает большой устойчивостью к нестабильности каналов распространения (особенно мелководных), высокой помехоустойчивостью и возможностью обработки в приемных элементах томографических систем.
Результаты проведенных многочисленных исследований показывают, что для задач классической акустической томографии разрешающая способность является одной из важнейших характеристик системы обнаружения [1-4].
Из-за нестационарности и неоднородности морской среды, как волновода, наибольший интерес для акустической томографии представляют:
- разрешающая способность сигнала по времени приема (многолучевость распространения);
- разрешающая способность по сдвигу несущей частоты (доплеровские деформации спектра);
- разрешающая способность по углу прихода акустической волны ( вариации структуры акустического поля).
Эти положения, в большей степени, присущи высокочастотной акустической томографии, для которой лучевое распространение сигнала является определяющим при формировании срезовой структуры томографических образов обнаруженных объектов.
Хотя условия распространения в водной среде низкочастотных сигналов другие чем высокочастотных, сам процесс формирования томографического образа в низкочастотной томографии, основанной на параметрическом взаимодействии нескольких акустических волн, в некотором приближении такой же, как в высокочастотной, и производится по конкретным значениям одного параметра.
За основной информационный параметр разового фронтального «среза» пространственно-временного амплитудно-фазового поля морского объекта принимаются фазовые изменения спектра несущей просветного сигнала. Такие «срезы», из-за большого объема пространственного положения различных составляющих поля объекта, получаются, при одном и том же низкочастотном сигнале, с некоторыми временными задержками. Для их интегрирования на горизонтальных и вертикальных приемных элементах системы наблюдения, математического обоснования оптимальных параметров сигналов, необходимо иметь общий подход и качественный показатель, объективно оценивающий их различимость, например, разрешающая способность по временному положению [5].
Поэтому дальнейшие теоретические рассуждения, для простоты понимания, будут схожи с элементами лучевой теории распространения акустических сигналов и высокочастотной бистатической локации водного пространства, с аннотациями их применимости для низкочастотной акустической томографии.
Количественно разрешающая способность по некоторому параметру h сигнала характеризуется минимальной разностью dh = h1 - h2 двух разрешаемых по этому параметру сигналов, имеющих одинаковые прочие величины. Чтобы два сигнала v1(t) = v(t,h1) и v2(t) = v(t,h2), c различными параметрами (или совокупностью параметров) h1 и h2 , были различимы в устройстве обработки сигналов необходимо, чтобы они как можно больше отличались друг от друга по своим параметрам. Оценим это различие интегральной мерой - средним квадратом их разности [1-5]:
Очевидно, что
где: Е1 и Е2 - энергии сигналов;
R12 - функция их взаимной корреляции.
Поскольку сигналы различаются только параметром h, который считается неэнергетическим (т.е. его изменение не влияет на энергию), то энергии сигналов одинаковы, а функцию их взаимной корреляции R12 является автокорреляционной функцией
зависящей от разности параметров, Dh = h1-h2.
Для обеспечения высокого разрешения сигналов по параметру h необходимо выбрать эти сигналы так, чтобы их автокорреляционная функция была максимально компактна. Другими словами, уменьшалась при возможно меньшем изменении этого параметра.
Реально, с учетом резонансных свойств акустических систем (особенно в области низких частот), не представляется возможным генерировать сигналы по полосе шире, чем описываемые представлением Гильберта[6]:
где:![]() ;
; ![]() - комплексные
амплитуды сигналов, а
- комплексные
амплитуды сигналов, а ![]() ;
;![]() - комплексно-сопряженные функции. Поэтому:
- комплексно-сопряженные функции. Поэтому:
Легко убедиться, что подинтегральные выражения являются комплексно сопряженными функциями. Поэтому их сумма является действительной функцией и равна:
Пусть сигналы для любой пары мод различаются смещением, как по времени на величину t, из-за дисперсии скорости звука, так и по частоте на величину F, из-за доплеровских деформаций, т.е.
![]() ;
;
Тогда их разрешающую способность по «t» и «F» будет характеризовать интеграл
А выражение 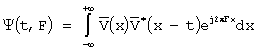 может
трактоваться как совместная корреляционная функция модуляции. И по существу является
обобщением автокорреляционной функции комплексной огибающей (амплитуды) сигнала
двух переменных t и F[6].
может
трактоваться как совместная корреляционная функция модуляции. И по существу является
обобщением автокорреляционной функции комплексной огибающей (амплитуды) сигнала
двух переменных t и F[6].
Например, при F = 0
имеем обычную автокорреляционную функцию комплексной огибающей сигнала. Из изложенного следует, что совместная корреляционная функция модуляции характеризует разрешающую способность системы обнаружения по временному сдвигу и смещению частоты. Выражение (9) из временной формы записи легко может быть преобразовано к частотному виду [4-6]:
где ![]() - частотный
спектр комплексной амплитуды сигнала
- частотный
спектр комплексной амплитуды сигнала ![]() .
.
Тогда имеем
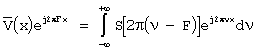
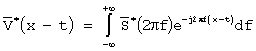 ,
,
а выражение (9) будет иметь вид
Так как
внутренний интеграл представляет собой дельта функцию 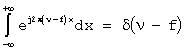 , то используя ее
фильтрующие свойства, получаем частотную форму записи функции (9)
, то используя ее
фильтрующие свойства, получаем частотную форму записи функции (9)
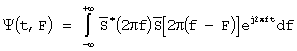 .
.
Из теории
оптимальной фильтрации известно, что ![]() c точностью до постоянного множителя
представляет собой передаточную функцию оптимального фильтра для сигнала
c точностью до постоянного множителя
представляет собой передаточную функцию оптимального фильтра для сигнала ![]() , где s[2p(f-F)]- спектр сигнала, сдвинутого по
частоте на F, а произведение - спектр отклика оптимального фильтра на сдвинутый
по частоте сигнал.
, где s[2p(f-F)]- спектр сигнала, сдвинутого по
частоте на F, а произведение - спектр отклика оптимального фильтра на сдвинутый
по частоте сигнал.
Поэтому, совместная корреляционная функция, будучи преобразованием Фурье, от этого произведения, и является указанным откликом. Эта функция в литературе имеет название время - частотной функции рассогласования [7].
Обычно используется нормированная совместная корреляционная функция модуляции
где 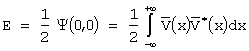 - энергия
сигнала.
- энергия
сигнала.
Физически, эта функция показывает относительную величину отклика оптимального фильтра на сигнал, сдвинутый по времени на t и по частоте на F относительно сигнала, оптимального этому фильтру. Иными словами, она характеризует степень различия откликов фильтра на два указанных выше сигнала и тем самым количественно описывает разрешающую способность по времени и частоте. Поэтому, анализируя совместную корреляционную функцию модуляции (функцию рассогласования) различных сигналов, можно подобрать подходящие сигналы для решения конкретных задач обнаружения и тем самым оптимизировать приемно-излучающий комплекс.
При использовании тонального сигнала (в случае прямоугольного импульса длительностью t1) его комплексная амплитуда может быть определена как
Соответственно
энергия сигнала E=0,5V![]() .
.
Искомая функция y0(t, F)равна:
y0(t, F)=0 при |t|>t1 ;
В частности
при F=0 получаем автокорреляционную функцию огибающей ![]() при -t1<t<t1 и
при -t1<t<t1 и ![]() при t=0. Таким образом, сечение этой
функции вертикальной плоскостью F=0 является треугольным, а сечение t=0 и
t=const имеют вид функции
при t=0. Таким образом, сечение этой
функции вертикальной плоскостью F=0 является треугольным, а сечение t=0 и
t=const имеют вид функции ![]() с шириной центрального максимума по оси
частот
с шириной центрального максимума по оси
частот ![]() и
последующим уширением по мере увеличения t.
и
последующим уширением по мере увеличения t.
Нормированная функция рассогласования дает исчерпывающую характеристику разрешающей способности по времени и частоте, но ее анализ обычно затруднен вследствие трех мерности. С целью упрощения, вместо всей функции анализируют ее область корреляции, которая объединяет все значения переменных t и F для которых выполняется условие 0,5 £ Y0(t,F) £ 1.
Согласно классического критерия разрешения Рэлея два сигнала, сдвинутые относительно опорного по времени на t и по частоте на F, которые соответствуют на плоскости переменных t, F точкам, лежащим в пределах этой области, разрешить невозможно. Поэтому область высокой корреляции, в литературе, называют диаграммой неопределенности. Чем она меньше, тем выше разрешение сигнала по времени и частоте. Эту область можно определить как проекцию на плоскости t, F сечения нормированной совместной корреляционной функции модуляции горизонтальной плоскости Y0(t,F)=0,5. Диаграмма неопределенности для тонального сигнала представляет собой фигуру, подобную усеченному овалу, с шириной по оси времени, равной длительности t1 импульса, по оси частот -1, 2/t1 и площадью порядка единицы. Ширина области высокой корреляции по времени и частоте является количественной мерой разрешающей способности сигнала по этим параметрам: dt=t1, dE=1,2/t1.
Из полученных характеристик следует вывод, что увеличение длительности излучения тонального сигнала ухудшает разрешающую способность по времени. Приводит к невозможности разрешения разовых фронтальных срезов пространственно-временного, амплитудно-фазового поля обнаруживаемого объекта и потери объективности при проведении классификации, улучшает разрешение по частоте. Кроме того, при анализе необходимо учитывать характерное время нестационарности среды и время существования объемной локальной неоднородности, вызванное прохождением объекта (или время нахождения цели в канале распространения звука). Исходя из изложенного, следует признать данный класс сигналов малоподходящим для локации водного пространства. С точки зрения диагностики среды использование тональных сигналов представляет собой наихудший вариант, поскольку для него, при любых соотношениях параметров зондирующего сигнала, база равна Dft1»1.
При использовании режима излучения непрерывного тонального сигнала, в точке приема суммируются сигналы, прошедшие по всем путям, в том числе и через области пространства “не затронутые” локальной неоднородностью, вызванной присутствием объекта. В данном случае эти сигналы выступают в качестве помехи, маскируя наряду с классической помехой полезные изменения отклика.
В случае значительной протяженности трасс потребуется и значительный энергетический потенциал источника. Так как, для тонального непрерывного и для импульсного сигналов, невозможно улучшение отношения сигнал/помеха методами временной компрессии, то лучше использовать сложные сигналы.
Практические возможности генерирования сложных сигналов ограничены двумя основными случаями. Это использование либо частотно-модулированных импульсов с большой девиацией, либо фазоманипулированных сигналов, т.е. импульсов с многократными скачками фазы несущей [8], например, линейно частотно модулированных (ЛЧМ).
Применение сигналов с внутриимпульсной частотной модуляцией вполне возможно. Первичные исследования с ними в направлении диагностики среды проводились в [6-8] и дали обнадеживающие результаты, но их использование сомнительно с точки зрения наличия оказийных источников сигналов этого типа, хотя сами сигналы широко используются в современных средствах наблюдения. При обработке сигналов данного класса, огибающая отклика на выходе оптимального фильтра, представляющего собой дисперсионную линию задержки и осуществляющего временную компрессию спектральных компонент сигнала, наряду с основным выбросом имеет достаточно интенсивные боковые (дополнительные) пики, которые могут маскировать соседние, более слабые сигналы от совокупности мод и тем самым ухудшать разрешающую способность системы по времени. Необходимо отметить, что несущая частота таких сигналов составляет несколько кГц, что говорит о невозможности их применения в низкочастотной акустической томографии.
Для разрешения сигналов и локальных неоднородностей необходимо, чтобы область высокой корреляции была единственной. Это требование принципиально невыполнимо в случае периодического или квазипериодического сигналов. Поэтому приходится ограничиваться требованием: различные области высокой корреляции были достаточно удалены друг от друга.
Для получения высокой разрешающей способности необходимо использовать такие формы сигналов, время - частотная функция рассогласования которых удовлетворяет двум требованиям [9]:
- она близка к единице только в небольшой, максимально компактной, окрестности точки t=F=0;
- во всех других областях плоскости t, F модуль этой функции значительно меньше единицы.
К сожалению, невозможно добиться одновременного сосредоточения области высокой корреляции в неограниченно малой окрестности начала координат и равенства нулю совместной корреляционной функции во всех других областях плоскости t, F. Причина в том, что эта функция удовлетворяет условию
описывающая принцип неопределенности. Согласно принципа неопределенности всякое сужение центральной области высокой корреляции с неизбежностью ведет к увеличению значений совместной корреляционной функции в других областях и может вызвать появление новых областей высокой корреляции, что является причиной неоднозначности измерений.
Указанным выше требованиям в наибольшей степени удовлетворяет совместная корреляционная функция шумового сигнала. При этом ширина главного максимума этой функции имеет порядок 1/Df, а по частоте - 1/t1. Общая протяженность функции по осям:
времени - 2t1
частоте - 2Df,
где Df - ширина спектра, а t1 - длительность сигнала.
В случае Dft1>>1, при постоянстве значений квадрата модуля функции в указанном участке плоскости t, F из принципа неопределенности (14) следует
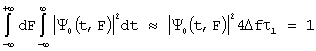
откуда ![]() , для зоны вне
области главного максимума. В действительности же указанная функция не
постоянна, а колеблется около нулевого значения. Поэтому боковые максимумы этой
функции, по крайней мере, в два раза выше проведенной оценки и для шумового
сигнала в качестве основы может быть взято соотношение
, для зоны вне
области главного максимума. В действительности же указанная функция не
постоянна, а колеблется около нулевого значения. Поэтому боковые максимумы этой
функции, по крайней мере, в два раза выше проведенной оценки и для шумового
сигнала в качестве основы может быть взято соотношение
из которого следует, что по мере увеличения базы шумового сигнала превышение главного максимума над боковыми может быть очень большим. Однако применение шумовых сигналов связано с большими техническими трудностями при осуществлении оптимальной фильтрации, но обеспечивает оптимальность подсветки водного пространства при параметрическом взаимодействии низкочастотных акустических сигналов.
В связи с этим, рассмотрим основные характеристики еще одного вида сигналов, манипулированных по фазе псевдослучайными кодами и обладающими, по меньшей мере, двумя свойствами:
- каждый из сигналов данного множества легко отличим от своей сдвинутой по времени копии;
- каждый из сигналов данного множества легко отличим от любого другого (возможно, сдвинутого по времени) сигнала этого множества.
Этот вид сигналов достаточно подробно рассмотрен в существующей литературе, но его применимость в бистатической локации и томографии нигде не обоснована.
Оба свойства определяют разрешающую способность системы и в процессе отбора сигналов, обладающих наилучшей структурой в этом смысле особое внимание специалистов было привлечено к псевдослучайным и родственным им последовательностям, изучение которых ведется уже свыше 25 лет.
В большинстве работ по периодическим последовательностям термины бинарные псевдослучайные последовательности максимальной длины, генерируемые линейными сдвиговыми регистрами, и М-последовательности используются как синонимы [10]. Такое внимание обусловлено целым рядом уникальных свойств, которыми они обладают и прежде всего их превосходными периодическими автокорреляционными свойствами.
В литературе наибольшее внимание уделяется двоичным последовательностям максимальной длины, порождаемым линейными сдвиговыми регистрами (М-последовательностям). В полном соответствии с названием эти последовательности представляют собой последовательности максимально возможного периода (равного N = 2n - 1), генерируемые n-каскадным двоичным сдвиговым регистром с линейной обратной связью. Наиболее важная особенность М-последовательности состоит в том, что ее автокорреляционная функция равна N при отсутствии сдвига, или -1 для всех остальных значений сдвига (1£l<N), т.е. оптимальна в классе возможных автокорреляционных функций двоичных последовательностей периода N=2n-1. Оптимальность здесь понимается в смысле минимальности пикового значения боковых лепестков в функции автокорреляции.
Основные свойства двоичных последовательностей можно получить из рассмотрения механизма их генерации.
Пусть h(x)=h0xn+h1xn-1+...+hn-1x+hn - двоичный полином степени n. Здесь h0=hn=1, а другие hi принимают значения 0 или 1. Говорят, что двоичная последовательность {uj} порождается полиномом h(x), если при всех j
Здесь ![]() - знак операции
сложения по модулю 2 (т.е. логическая операция “Исключающее Или”). Производя в
(17) замену индекса j на j+n и учитывая, что n0=1, получим
- знак операции
сложения по модулю 2 (т.е. логическая операция “Исключающее Или”). Производя в
(17) замену индекса j на j+n и учитывая, что n0=1, получим
Отсюда следует, что последовательность {uj} можно получить с помощью n-каскадного сдвигового регистра с линейной цепью обратной связи, к которой подключены отводы от каскадов с теми номерами 0< i £n, для которых hi=1. Поскольку hn=1, отвод от n-го каскада используется всегда.
Любой сдвиговый регистр может генерировать множество различных последовательностей, в том числе и тривиальную нулевую. Поскольку последняя интереса не представляет, то ее специальными мерами исключают из механизма генерации сдвиговым регистром - нулевое состояние является запрещенным. В связи с этим, период последовательности максимальной длины не превосходит величины 2n-1, где n - число разрядов регистра или, что эквивалентно, степень порождающего полинома h(x).
В отношении самого полинома h(x) и М-последовательностей им порождаемых следует сделать несколько замечаний, описывающих их основные свойства.
Во-первых,
период истинной М-последовательности в точности равен N=2n-1 и
получить ее можно лишь в единственном случае, если порождающий полином ![]() примитивен,
т.е. неприводим и первичен на поле Галуа.
примитивен,
т.е. неприводим и первичен на поле Галуа.
При выполнении этого условия появляется возможность для генерирования детерминированного процесса, значения которого в точности известны наперед, и обладающего в то же время статистическими свойствами идеального процесса бросания симметричной монеты. Причем достаточно несложное устройство в принципе позволяет сформировать последовательность, которая будет идти века без повторения. Например, при n=100 период повторения последовательности, генерируемой с тактовой частотой 10 Мгц, в миллионы раз превышает возраст Вселенной.
Подобные свойства обусловили широкое использование М-последовательностей в криптографии, при линейном шифровании сообщений, кодировании речи, обнаружении ошибок и стимулировали их углубленное изучение, поскольку подбор и численная проверка результатов в свете сделанной оценки представляется абсолютно бесперспективным делом.
Во-вторых, существует в точности N различных последовательностей, порождаемых полиномом h (x). Все они являются N различными сдвигами М-последовательности {u} и имеют вид {u}, {Tu}, {T2u}.
В-третьих, для произвольных i и j 0 £ i, j < N, существует единичное K, 0 £ K £ N, отличное от i и j и такое, что
Последовательность периода N является М-последовательностью тогда и только тогда, когда она обладает свойством (19), которое обычно называют свойством сдвига и сложения.
В-четвертых,
если М-последовательность {u} как двоичный N-фактор, то вес Хэмминга этого
вектора (число входящих в него единиц) в точности равен ![]() .
.
В-пятых, если окно ширины n перемещается вдоль М-последовательности, то каждый из 2n -1 ненулевых двоичных наборов из n чисел будет виден точно один раз. Это свойство окна следует из примитивности полинома h(x). Чтобы избежать затруднений на концах последовательности, ее следует записать в виде замкнутой окружности.
Последние два свойства фактически означают, что в каждом цикле генерации М-последовательности (N периодов тактовой частоты) половину всех единиц составляют “одиночные”, четвертую часть - двойные (то есть две следующие подряд), восьмую часть - тройные и т.д. То же самое относится и к последовательно идущим нулям, за исключением, разумеется, пропущенного при состоянии “все разряды регистра - ноль”. Это свидетельствует о том, что вероятность появления начала и конца единичного состояния не зависит от результата последнего переброса и, следовательно, вероятность завершения цепочки последовательно возникших единиц или нулей для каждого переброса составляет одну вторую.
В шестых, если последовательность полного цикла (N периодов тактовой частоты) сравнить с этой же последовательностью по сдвинутой на любое число тактов n (где n¹0 и не кратно N), то число несовпадений будет превышать число совпадений на единицу [11]. Иными словами автокорреляционная функция М-последовательности при нулевой задержке равняется N, а во всех остальных точках: -1. Иногда говорят о нормированной автокорреляционной функции:
В этом случае
r(0)=1,
r(i)=-1/N 1 £ i £ 2n-2
и существует доказательство, что в смысле минимизации величины r(i) эта функция является возможной наилучшей автокорреляционной функцией любой двоичной последовательности длины 2n -1.
Следует отметить, что в большинстве практических приложений алфавит двоичной последовательности сдвигового регистра, т.е. ноль и единица, замещается на бинарную последовательность бинарных импульсов с амплитудами ±1, от чего свойства М-последовательностей не изменяются, за исключением некоторых численных оценок.
До сих пор рассматривались свойства модулирующей функции, между тем и выбор типа модуляции имеет существенное значение. Как уже указывалось, практические возможности генерирования сложных сигналов, по существу, ограничены двумя основными случаями:
- частотно-модулированные импульсы с большой девиацией;
- фазоманипулированные сигналы.
Первые кратко уже рассматривались, а последние представляют собой непрерывную последовательность прямоугольных радиоимпульсов, образованную в результате многократных скачков фазы несущей. Хотя возможно осуществить скачкообразные изменения фазы на любую величину в пределах от нуля до 2p, практическое применение нашли главным образом такие сигналы, у которых каждый скачок равен p. Это объясняется тем, что два импульса, имеющие одинаковую мощность и отличающиеся только фазой на p, обладают максимально возможной степенью различия.
Функция их взаимной корреляции при отсутствии временного сдвига равна -1. Именно поэтому, использование таких сигналов при передаче дискретных сообщений обеспечивает наибольшую помехоустойчивость [8]. Последнее весьма существенно, поскольку оптимизирует энергетический потенциал источника сигнала.
Во-вторых, сигналы такого рода сравнительно просто формировать, коммутируя “полярность” в нужные моменты времени, хотя получение любой другой дискретности по фазе не вызывает особых схемотехнических проблем.
Особенностью фазоманипулированного сигнала является то, что он состоит из прямоугольных импульсов фиксированной длительности (дискретов) и моменты скачков фазы кратны этой длительности, ввиду детерминированности тактового интервала у модулирующей М-последовательности.
Может показаться, что такое положение дел неоправданно сужает класс рассматриваемого сигнала, поскольку скачки фазы можно расположить произвольно. В действительности это ограничение несущественно, так как увеличивая число дискретов N всегда можно выбрать интервал дискрета достаточно малым.
Рассмотрим возможности использования фазоманипулированного бинарной М-последовательностью {di} гармонического сигнала в низкочастотном методе гидролокации на просвет.
Аналитически данный вид сигнала может быть представлен в виде
где q(t)- функция, описывающая закон манипуляции фазы с дискретностью p в моменты времени t=it0.
Изменение начальной фазы в моменты времени t=it0 составляет q(it0) = qi = arccos di = p, что соответствует di=-1. В остальные дискретные моменты времени t = it0 начальная фаза не меняется, поскольку для них di=+1 и q(it0) = qi = arccos di = 0; t0 - длительность одного дискрета.
Полученный в результате фазоманипулированный сигнал [7,10] имеет период T=Nt0=(2n-1)t0 и комплексную амплитуду
где 1(f) - единичная функция.
Нормированная корреляционная функция комплексной амплитуды этого сигнала при временном сдвиге tkt0+e, где k- целое неотрицательное число, 0<e<t0, имеет вид
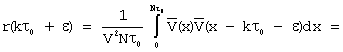
Поскольку
рассматриваемый сигнал является непрерывным и периодическим, то корреляционная
функция вычисляется путем интегрирования по времени на интервале длительности
периода T = Nt0 cигнала.
Используя свойство М-последовательностей,![]() предыдущее выражение может быть
приведено к виду
предыдущее выражение может быть
приведено к виду
r(e)=1-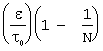 , при 0£e<t0
, при 0£e<t0
r(kt0+e)=-![]() , при 1£k<N-2
, при 1£k<N-2
или, что - то же
r(t)=1-(1+![]() )|t|/t0 ,при |t|<t0
)|t|/t0 ,при |t|<t0
r(t)=-![]() при t0£t£(N-1)t0.
при t0£t£(N-1)t0.
Кроме того, поскольку сигнал периодический, то его корреляционная функция имеет тот же период:
r(t+rNt0)=r(t), где r - любое целое число.
Таким образом,
корреляционная функция имеет за период T=Ne0
один максимум шириной порядка t0,
в течение большей части периода длительностью (1-![]() )T ее абсолютная величина в N раз
меньше максимума. Поскольку N можно выбрать сколь угодно большим, то корреляционная
функция таких сигналов может быть получена весьма близкой к идеальной.
)T ее абсолютная величина в N раз
меньше максимума. Поскольку N можно выбрать сколь угодно большим, то корреляционная
функция таких сигналов может быть получена весьма близкой к идеальной.
Дополнительные
максимумы нормированной совместной корреляционной функции модуляции Y0(t,F) на плоскости t, F имеют
высоту порядка ![]() , т.е. могут быть достаточно малыми.
, т.е. могут быть достаточно малыми.
Для оценки потенциальных возможностей использования фазоманипулированных сигналов в интересах обнаружения и уточнения технических требований к аппаратуре излучения, приема и обработки просветных сигналов необходимо определитьcя со спектральными характеристиками М-последовательностей.
Прежде всего следует отметить, что рассматриваемый сигнал является периодическим, с периодом T=Nt0, и поэтому имеет дискретный спектр [10]. Модуляционный сигнал в бинарном представлении относится к классу последовательности прямоугольных импульсов со случайным периодом, кратным детерминированному тактовому интервалу t0. Поэтому наиболее целесообразным путем расчета энергетического спектра является определение его по автокорреляционной функции, которая ввиду периодического характера последовательности, также является периодической.
Амплитуда k-ой гармоники автокорреляционной функции последовательности может быть представлена [11]
а постоянная составляющая этой функции
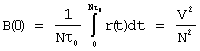 .
.
Вследствие этого постоянная составляющая двоичной псевдослучайной последовательности
а амплитуда ее k-ой гармоники
Если рассмотреть периодическую последовательность, период которой имеет ту же длительность, что и период двоичной М-последовательности, но включающей один прямоугольный импульс той же амплитуды, и длительностью t0, равной детерминированному тактовому интервалу, как и у псевдослучайной последовательности, то тогда имеем:
- для постоянной составляющей
- для амплитуды k-ой гармоники
Из по парного сопоставления четырех последних выражений (25 - 28) следует, что кодирование прямоугольных импульсов по закону бинарной М-последовательности не изменяет постоянной составляющей, что объясняется специфической структурой этой последовательности, но увеличивает в (N+1)1/2=2n/2 раз амплитуды всех гармонических составляющих сигнала (функциональная зависимость от частоты огибающей спектра с точностью до постоянного множителя сохраняется).
Таким образом, фазовая манипуляция М-последовательностью несущей с частотой f0 сводится к сдвигу спектра модулирующей функции из области низких частот в область с центральной частотой f0.
Видим что, спектральные характеристики сигнала полностью определяются модулирующей М-последовательностью, огибающая спектральной плотности мощности которой может быть описана следующей функциональной зависимостью
где: s2 - дисперсия процесса.
Фактически имеем линейчатый спектр, но это проявляется только в случае анализа за время, много большее периода последовательности T=Nt0.
Степень неравномерности спектральной плотности можно оценить путем разложения в ряд частотно зависимого члена выражения (29)
Так, в полосе частот равной 26% от тактовой частоты сдвигающего регистра, неравномерность спектра составляет -1дБ, а первый ноль спектра размещается на частоте, равной тактовой, как и у обычного прямоугольного импульса.
В заключение рассмотрения свойств и параметров фазоманипулированных псевдослучайными последовательностями сигналов можно отметить, что ширина их спектра равна ширине спектра элементарных импульсов длительности t0 (дискретов), из которых составлены эти сигналы, т.е. Df@1/t0. Поэтому база сигнала, характеризующая его информативность, определяющая размеры диаграммы неопределенности и численно равная произведению ширины спектра Df на длительность периода T = Nt0, определяется как B = DfT = N = 2n - 1 и обычно много больше единицы. Системы, использующие такой сигнал позволяют получать высокую разрешающую способность как по пространственным структурам (времени), так и по радиальной скорости перемещения неоднородностей (частоте).
Указанные
характеристики достигаются при сравнительно больших значениях N (порядка
тысячи). Это требует выбора n (разрядность регистра) порядка десяти. Следует
обратить так же внимание на энергетический аспект. Применение систем со
сложным сигналом, по сравнению с простейшей, применяемой в настоящее время,
импульсной системой позволяет увеличить энергию сигнала в N раз. При этом
энергетическая дальность действия возрастет в ![]() раз (или
раз (или ![]() для сонаров), что при N
= 1023 дает рост этого параметра ~32 раза (или 5,66 раз).
для сонаров), что при N
= 1023 дает рост этого параметра ~32 раза (или 5,66 раз).
Для реализации принципов бистатической локации в различных тактических ситуациях и получения объективной информации об морском объекте любой физической природы на широкомасштабных морских акваториях (по изменению фазы спектра сигналов) применение фазоманипулированной псевдослучайной М -последовательности наиболее оптимально. Это объясняется большой устойчивостью данных сигналов к нестабильности каналов распространения (особенно мелководных), высокой помехоустойчивостью и возможностью их обработки в приемных элементах томографических систем. Дополнительно, необходимо отметить, что в низкочастотной волне, соизмеримой с размерами объекта, наиболее информативными для обнаружения объекта являются фазовые изменения спектра просветного сигнала, как наиболее помехоустойчивые в условиях дальнего распространения сигналов в морской среде.
ЛИТЕРАТУРА
1. Зверев В.А, Калачев А.И. Модуляция звука звуком при пересечении акустических волн //Акуст. журн. - 2000. - № 2. -Т.16. - С. 245 - 251.
2. Баскаков С.И. Радио-технические цепи и сигналы// - М.: Высшая школа, 1988. - С. 11 -38.
3. Мироненко М.В. Результаты теоретических и экспериментальных исследований пространственной амплитудно-фазовой структуры поля низкочастотной подсветки среды: // Сб. статей. - Владивосток, ТОВМИ. - Вып.2. 1985. - С. 26-31.
4. Мироненко М.В., Стародубцев П.А. Проблемы разработки метода низкочастотной томографии морской среды и нетрадиционные пути их решения // Сб. статей. - Владивосток, ТОВМИ. - Вып.21. - С. 117-128.
5. Мироненко М.В., Минаев Д.Д. Закономерности параметрического взаимодействия волн различной физической природы в морской среде и их реализации в разработках систем дальней звукоподводной связи // Сб. статей. - Владивосток, ТОВМИ. - Вып. 3. - С. 82 – 87.
6. Пауэрс Дж., Лондри Дж., Уэйд Г. Восстановление изображений по фазовым и амплитудным голограммам: Акустическая голография: Пер. с англ. / Под ред. В.Г. Прохорова. – Л.: Судостроение, 1975. - С.132 -145.
7. Пестряков В.Б. Фазовые радиотехнические системы// - М.: Сов. Радио, 1958. - С. 308 -352.
8. Харкевич А.А. Влияние вида модуляции. Борьба с помехами. – М.: Радиосвязь, 1965. - С. 50 - 60.
9. Тихонов В.И. Различие сигналов со случайными амплитудой и фазой. Оптимальный прием сигналов. – М.: Радиосвязь, 1963. - С. 123 -140.
10. Мироненко М.В., Короченцев В.И., Сургаев И.Н. Способ приема упругой волны в морской среде (варианты): Патент на изобретение РФ № 2158029 от 20.11.2000.
11. Шостак С.В., Мироненко М.В., Сургаев И.Н. Амплитудно-фазовая модуляция акустических волн при их взаимодействии в морской среде // Сб. статей. - Владивосток, ТОВМИ. - Вып.22.2001. - С. 82-88.
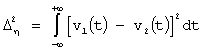 . (1)
. (1)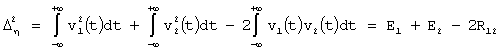 ,
(2)
,
(2)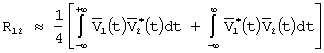 . (5)
. (5)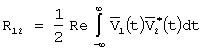 .
(6)
.
(6)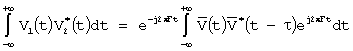 .
(8)
.
(8)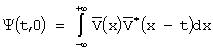 (9)
(9)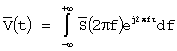 ,
(10)
,
(10)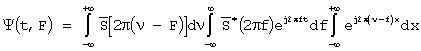 . (11)
. (11)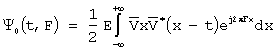 ,
(12)
,
(12)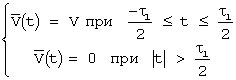 (13)
(13)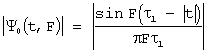 при -
при -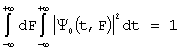 ,
(15)
,
(15)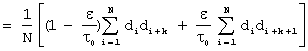 (23)
(23)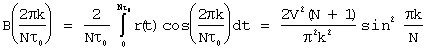 , (24)
, (24)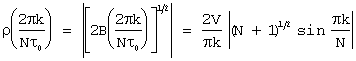 . (26)
. (26)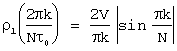 .
(28)
.
(28)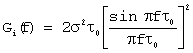 ,
(29)
,
(29)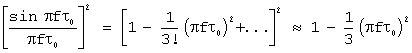 .
(30)
.
(30)