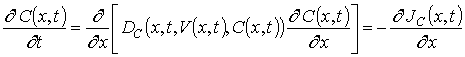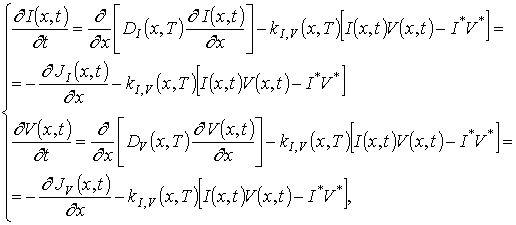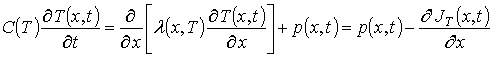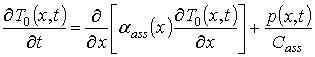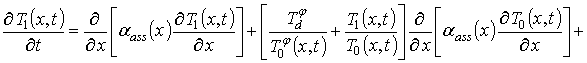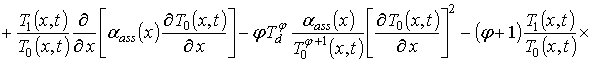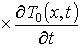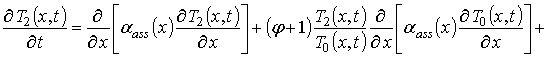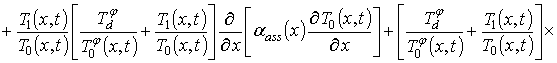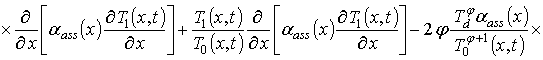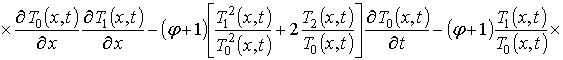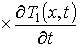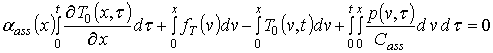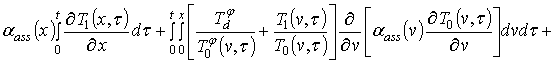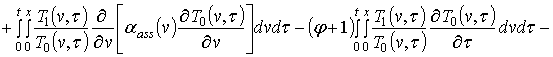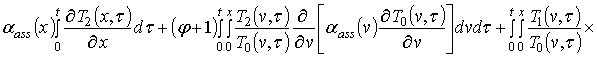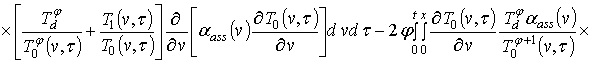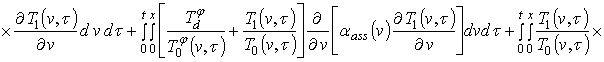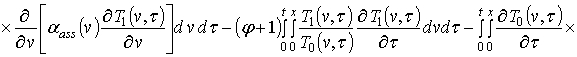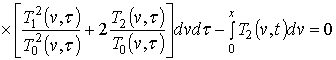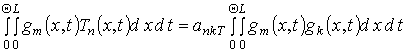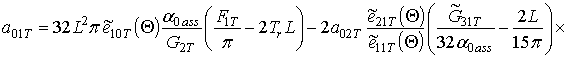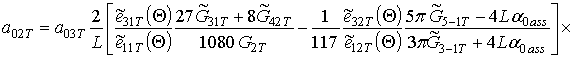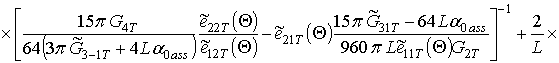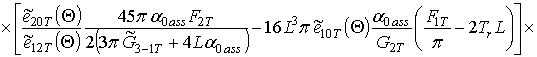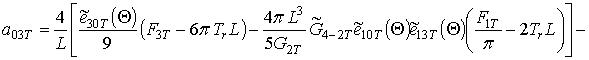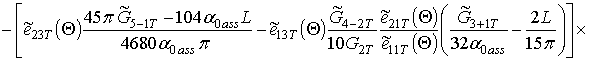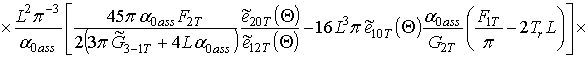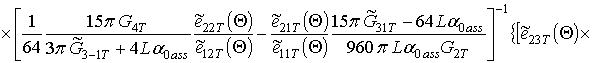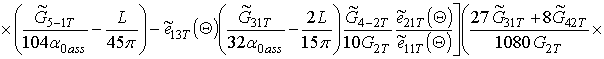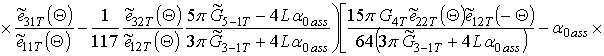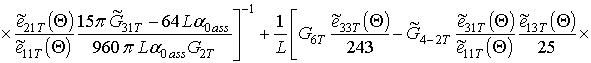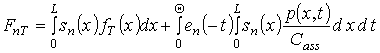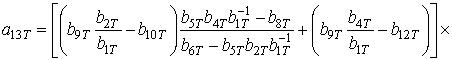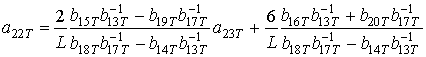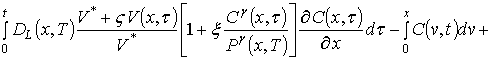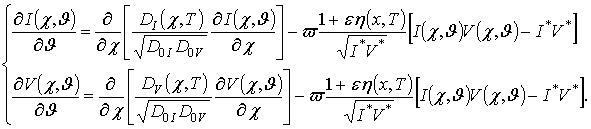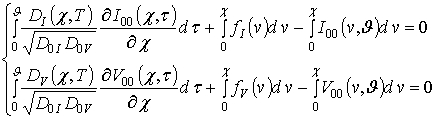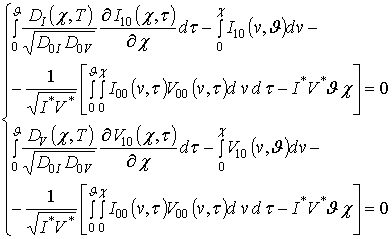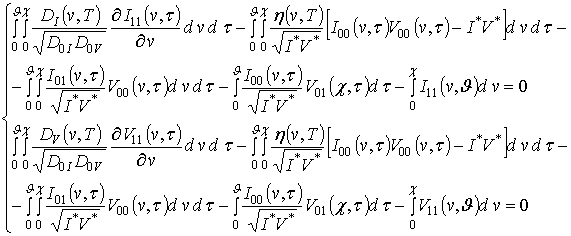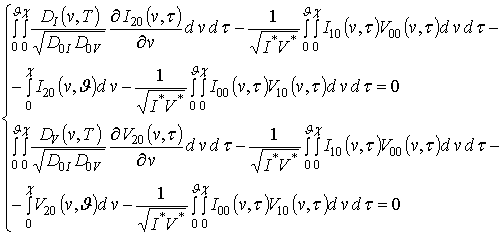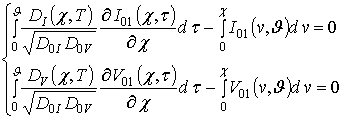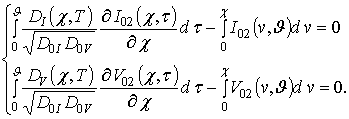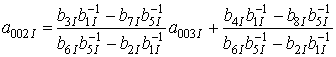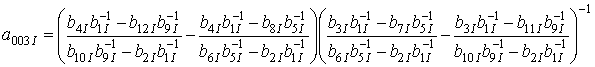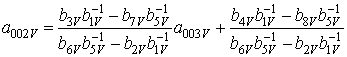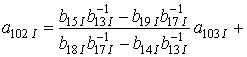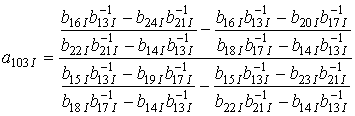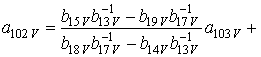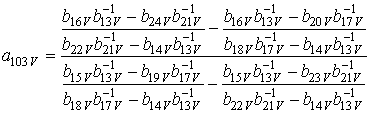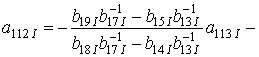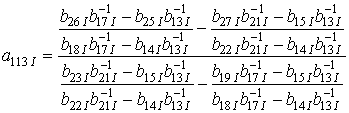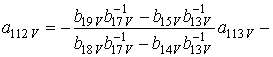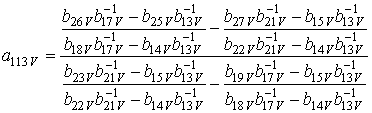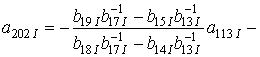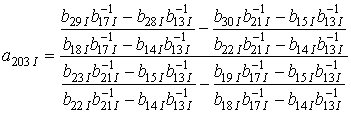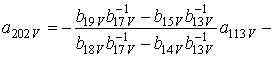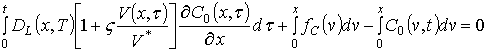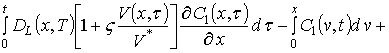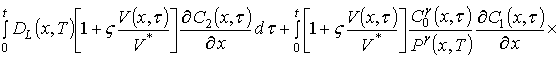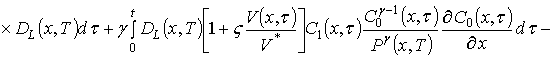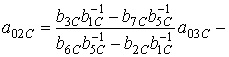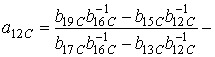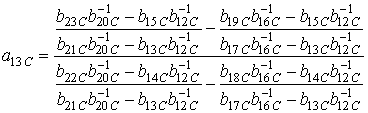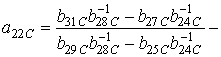"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 1, 2008

оглавление

Распределение примеси в многослойной структуре при формировании транзисторных структур

Е.Л. Панкратов

Институт физики микроструктур РАН, Нижний Новгород

Получена 9 января 2008 г.

 

В настоящей работе проведен анализ динамики перераспределения примеси в многослойной структуре в процессе формирования транзисторных структур. Предложен способ увеличения резкости диффузионных и имплантационных p-n-переходов, входящих в состав транзисторной структуры, а также увеличения равномерности распределения примеси в обогащенной ею области. Проведена оптимизация длительности отжига, позволяющая одновременно увеличить и равномерность распределения примеси в обогащенной ею области, резкость p-n-переходов.

 

Введение

В последние годы происходит интенсивное увеличение быстродействия устройств полупроводниковой электроники, а также – увеличение плотности элементов интегральных схем. Одним из направлений повышения быстродействия полупроводниковых устройств является уменьшение емкостей электронно-дырочных переходов [1,2]. Большой интерес для увеличения надежности полупроводниковых устройств представляет увеличение однородности распределения примеси в легированных областях [1-3]. Актуальной задачей также является повышение точности теоретического описания технологических процессов, что приводит к повышению их предсказуемости и, как следствие, позволяет повышать воспроизводимость характеристик твердотельных устройств.

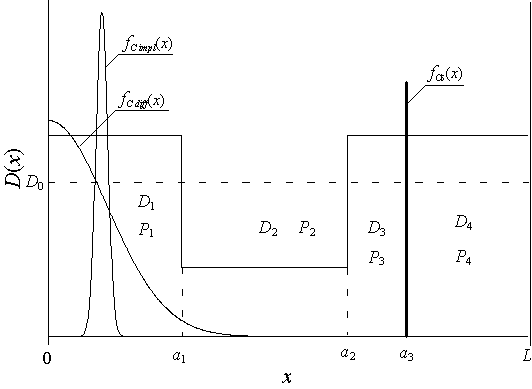
Для получения p-n-переходов используются различные технологические методы [1-5]. Один из основных - внедрение примеси в исходную пластину или эпитаксиальный слой (ЭС) путем ее диффузии, имплантации или в процессе эпитаксиального роста. В настоящей работе рассматривается многослойная структура (МС), состоящая из трех ЭС с толщинами соответственно a₁ (0£x£a₁), a₂-a₁ (a₁£x£a₂) и a₃-a₂ (a₂£x£a₃), коэффициентами диффузии D₁, D₂ и D₃ и пределами растворимости P₁, P₂ и P₃ (см. рис. 1). Рассмотренные слои сформированы на подложке толщиной L-a₃ (a₃£x£L) с коэффициентом диффузии D₄, пределом растворимости P₄ и заданным типом проводимости (p или n) (см. рис. 1). В первом ЭС формируется введенное с помощью диффузии или имплантации распределение примеси, позволяющее создать в ЭС необходимый тип проводимости (n или p). Между третьим ЭС и подложкой сформирован тонкий слой примеси заданного типа проводимости, позволяющий после отжига сформировать p-n-переход в окрестности границы раздела между вторым и третьим ЭС. Будем считать, что остальные ЭС выращивались при достаточно низкой температуре, соответствующей слабому расплыванию данного слоя примеси. В принятый за начало отсчета момент времени (t=0) начинается отжиг соответственно примеси (при диффузионном легировании) или радиационных дефектов (после окончания имплантации ионов) длительностью Q. В случае диффузионного легирования отжиг приводит увеличению глубины залегания p-n-перехода до требуемого значения. В случае имплантации примеси с одной стороны отжиг приводит к уменьшению количества радиационных дефектов и активизации имплантированной примеси, с другой стороны - к уширению исходного распределения примеси и, как следствие, к отклонению характеристик формируемых диодных и транзисторных структур от запланированных при их проектировании значений.

Целью данной работы является поиск условий, при которых распределение концентрации внедряемой примеси будет наиболее равномерным в первом и третьем ЭС, а во втором ЭС внедряемая примесь будет практически отсутствовать. Сопутствующей целью является развитие математического аппарата для данных задач.

Рис. 1. МС, содержащая три ЭС (xÎ[0,a₁], xÎ[a₁,a₂], xÎ[a₂,a₃]) и подложку (x₄Î[a,L]). На данном рисунке также приведены начальные распределения имплантированной в первый ЭС примеси и примеси, введенной в данный ЭС диффузионно, а также начальное распределение примеси, сформированное между третьим ЭС и подложкой.

 

Методика анализа

Динамика перераспределения примеси в приведённой на рис. 1 МС описывалась вторым законом Фика в следующей форме [1-3,5]

,         (1)

где  – пространственно-временное распределение примеси;  – концентрация вакансий;  – пространственно-временное распределение потока примеси;  – коэффициент диффузии примеси, величина которого зависит от динамических свойств примеси в материалах слоев МС, скорости прогрева и охлаждения МС, а также от пространственно-временного распределения образовавшихся в процессе имплантации радиационных дефектов и концентрации примеси. Такие зависимости могут быть аппроксимированы соответствующими функциями [6,7] и [3]

            (2)

где  – коэффициент диффузии примеси до начала имплантации при низком уровне легирования;  – равновесная концентрация вакансий;  – предел растворимости примеси; определяемый свойствами материала параметр  может принимать целые значения в интервале  [3]. В случае диффузионного легирования вторым слагаемым второго множителя правой части соотношения (2) можно пренебречь по сравнению с первым (т.е. можно считать, что параметр  пренебрежимо мал), т.к. радиационное повреждение материала отсутствует. Далее рассмотрим предельный случай, когда количество различных комплексов (например, дефектов) мало по сравнению количеством точечных дефектов. Пространственно-временное распределение точечных дефектов в данном случае может быть определено с помощью следующей системы уравнений [8]

                                                                       (3)

где I(x,t) - пространственно-временное распределение междоузельных атомов;  - равновесное распределение междоузельных атомов;  и  – коэффициенты диффузии точечных дефектов;  – параметр рекомбинации дефектов;  и  - пространственно-временные распределения потоков соответственно вакансий и междоузельных атомов.

Пространственно-временное распределение температуры может быть описано с помощью уравнения теплопроводности

,                                     (4)

где  – теплоемкость материала;  – температура Дебая [9] (в наиболее интересующем нас случае является сопоставимой по величине с температурой Дебая или превышает ее, что позволяет считать: );  – коэффициент теплопроводности; температурная зависимость коэффициента теплопроводности в искомой области температур может быть аппроксимирована следующим образом:  (см., например, [9]);  – коэффициент температуропроводности; p(x,t) – объемная плотность мощности.

Уравнения (1), (3) и (4) необходимо дополнить граничными и начальными условиями, которые могут быть представлены в следующем виде

; ; ;

; ; ; .

На первом этапе проведем оценку температурного поля. В общем случае решения уравнения (4) неизвестно. Определим его приближенно в виде следующего степенного ряда по

.

Подстановка данного ряда в (4) позволяет получить систему уравнений для функций  в следующем виде
 

…     …     …

Поставим в соответствие данной системе параболических уравнений систему следующих интегро-дифференциальных уравнений

                (5)

…     …     …

Определим решение уравнений системы (5) с помощью метода Бубнова-Галёркина (см., например, [10]). В рамках данного метода искомые функции  представляются в виде суммы N линейно независимых функций некоторого полного базиса

.

Неизвестные коэффициенты  определяются по аналогии с коэффициентами ряда Фурье, т.е. из условия

,              (6)

где  - длительность отжига.

Далее в качестве базиса функций  рассмотрим базис, определяющий распределение температуры при усредненном коэффициенте температуропроводности, т.е.

,                             (7)

где , ,  – совпадающая с комнатной равновесная температура. Соотношение (6) с учетом соотношения (7) позволяет получить для исходного приближения температуры
 

,

,

,

где

;

;;

;

 

. Из-за быстрой сходимости ряда (7) по n при типичных длительностях и температурах отжига обычно достаточно ограничиться первыми тремя (из зависящих от n) членами рассматриваемого ряда.

Известно (см., например, [11]), что поправочные функции к исходному приближению температуры имеют немонотонную зависимость от времени. Для упрощения анализа для оценки поправочных функций  рассмотрим следующий базис немонотонных во времени функций, близких по форме к полученным ранее

.                                                   (8)

В данном случае соотношения (6) и (8) с учетом первого и второго уравнений системы (5) позволяют получить:
 

,  ,

,  ;

.

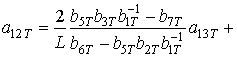
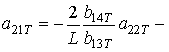
Коэффициенты  определяются с помощью соотношения (6). Однако полученные для данных коэффициентов выражения приводиться не будут из-за их громоздкости.

Для проведения качественного анализа и некоторых количественных оценок часто достаточно второго приближения по методу осреднения и параметру, по которому проводится разложение в степенной ряд (см., например, [11]). По этой причине при оценке температурного поля, а также концентраций примеси и радиационных дефектов ограничимся соответствующими вторыми приближениями.

Используя оценку пространственно-временного распределения формирующегося в МС температурного поля проведем анализ динамики перераспределения радиационных дефектов и примеси в рассматриваемой структуре. Далее поставим в соответствие уравнению (1) следующее интегро-дифференциальное уравнение

.                                           (9)

В случае диффузионной разгонки примеси можно считать, что . Анализ имплантации примеси приводит к необходимости учитывать радиационные дефекты, описываемые уравнениями (3). Для упрощения анализа динамики перераспределения точечных радиационных дефектов введем следующие безразмерные переменные ; , а также безразмерные параметры  и , где  ; . После такой замены уравнения (3) принимают вид:
 

Далее будем искать решение последней системы уравнений в виде следующих рядов

; .

Далее запишем систему интегро-дифференциальных уравнений для функций  и  в следующей форме
 

 

 

 

 

 

                                  (10)
 

 

Для определения пространственно-временного распределения точечных дефектов воспользуемся методом Бубнова-Галеркина. Для определения исходных приближений концентрации радиационных дефектов воспользуемся базисом функций, используемым для представления функций  и  в виде ряда Фурье при усредненных значениях коэффициентов диффузии радиационных дефектов  и , а также нулевом значении параметра рекомбинации . Такой ряд Фурье может имеет вид: , где ; ; ; ; . Далее будем искать решение первой пары уравнений системы (10) в следующей форме:

.

Коэффициенты  определяются стандартным способом (см., например, [10]). В окончательной форме эти коэффициенты имеют вид
 

;  

;

.

Коэффициенты  определяются с помощью соотношения, аналогичного соотношению (6). Однако полученные для данных коэффициентов выражения здесь и далее приводиться не будут из-за их громоздкости.

Поправочные функции к исходным распределениям радиационных дефектов будем искать в форме, аналогичной форме решения поправочных функций к исходному распределению температурного поля, т.е.

.

В данном случае можно получить упрощающий анализ динамики перераспределения радиационных дефектов результат: . Расчет коэффициентов ,  и  позволяет получить следующие соотношения
 

;

;

;

;

;

;

;

;

;

;

;

; .

Для оценки пространственно-временного распределения концентрации примеси воспользуемся изложенной выше процедурой. На первом этапе будем искать решение уравнения (1) в виде следующего степенного ряда

.

Далее запишем систему интегро-дифференциальных уравнений для функций  следующего вида
 

                  (11)

.

Для определения исходного приближения концентрации примеси воспользуемся базисом функций, описывающим решение первого уравнения системы (11) при усредненном коэффициенте диффузии , т.е.

.

и искать решение рассматриваемого уравнения при переменном коэффициенте диффузии  в следующей форме

.

Коэффициенты  находятся с помощью стандартной (см., например, [10]) и могут быть представлены в следующей форме

;

; .

Коэффициенты  определяются с помощью соотношения, аналогичного соотношению (6). Однако полученные для данных коэффициентов выражения здесь и далее приводиться не будут из-за их громоздкости.

Для оценки второй и третьей поправки к исходному приближению концентрации примеси воспользуемся следующим базисом

.

Искомые коэффициенты определяются стандартным способом и в окончательной форме соотношения для них имеют вид

;

;

;

;.
 

Далее проведем анализ динамики перераспределения примеси в МС. Полученные аналитические соотношения позволяют провести наглядное исследование динамики перераспределения примеси в процессе отжига дефектов. Использование численных методов позволяет уточнить полученные результаты. По этой причине в дополнение к аналитическим использовались также и численные методы решения уравнений (1), (3) и (4).

 

Результаты анализа

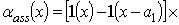
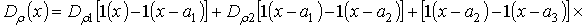
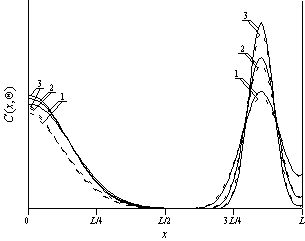
Проведем анализ динамики перераспределения примеси в МС в приближении малой ширины переходной области между слоями. В таком приближении пространственные зависимости коэффициентов диффузии и теплопроводности без учета нелинейных и радиационных эффектов могут быть аппроксимированы следующими функциями:  ;  ; r =I,V,L. Пространственные распределения примеси в фиксированные моменты времени, соответствующие диффузионному легированию и ионной имплантации приведены на рис. 2. Из данных рисунков следует, что  граница раздела между  слоями МС позволяет  увеличить

 

Рис. 2а. Расчетные пространственные распределения примеси при диффузионном легировании после отжига длительностью . Кривые 1-3 соответствуют распределению примеси в ДС при ;  для различных значений отношения  (,  и ). Границы раздела между слоями имеет координату ; ; . Сплошные кривые – аналитический расчет. Пунктирные кривые – численный расчет.

 

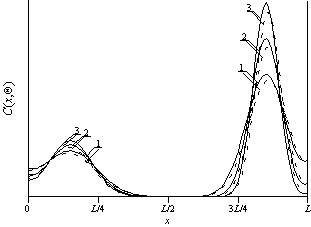
Рис. 2б. Расчетные пространственные распределения примеси при диффузионном легировании после отжига длительностью . Кривые 1-3 соответствуют распределению примеси в ДС при ;  для различных значений отношения  (,  и ). Границы раздела между слоями имеет координату ; ; . Сплошные кривые – аналитический расчет. Пунктирные кривые – численный расчет.

 

резкость p-n-переходов в ее окрестности (и, как следствие, уменьшить диффузионную составляющую емкости p-n-переходов), а также увеличить равномерность распределения примеси в обогащенной ею области (и, как следствие, позволяет снизить локальные разогревы в процессе работы p-n-перехода или уменьшить глубину его залегания при фиксированном допуске на величину разогрева).

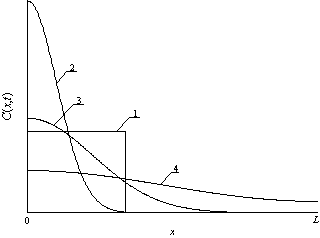
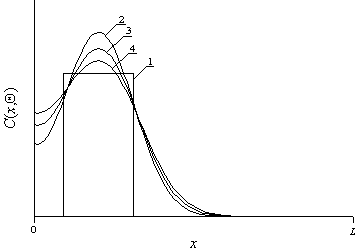
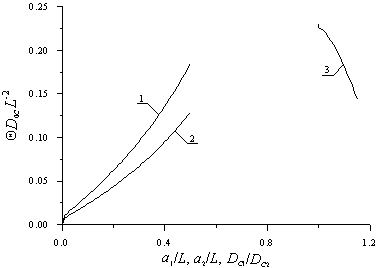
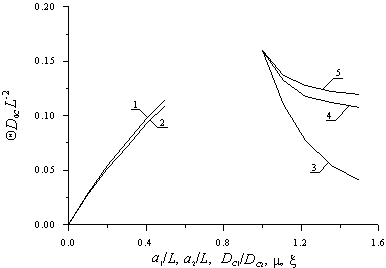
С увеличением длительности отжига увеличивается равномерность распределения примеси с одновременным уменьшением резкости p-n-перехода. Для одновременного проявления обоих этих эффектов необходим выбор компромиссной длительности отжига. Следует заметить, что выбор длительности отжига в случае ионной имплантации представляет интерес, когда происходит быстрый отжиг радиационных дефектов по сравнению с компромиссной длительности отжига (быстрая рекомбинация радиационных дефектов, быстрая активизация примеси). Для определения такой длительности воспользуемся введенным в [11] критерием. В рамках данного критерия распределение примеси C(x,t) аппроксимируется скачкообразной функцией заданной ширины (см., например, рис. 3). Далее длительность отжига выбирается таким образом, что бы минимизировать среднеквадратичное отклонение аппроксимирующей функции от аппроксимируемой (таким образом, его можно считать также оптимальным). Зависимости времен отжига от различных параметров приведены на рис. 4. Из анализа рисунков 4 следует, что оптимальное время отжига в случае диффузионного легирования превышает аналогичное время в случае ионной имплантации, что является физически понятным.

 

Рис. 3а. Пространственные распределения примеси в МС при диффузионном легировании. Кривая 1 – требуемое идеализированное распределение примеси. Кривые 2-4 –реальные распределения примеси в различные моменты времени (увеличение номера кривой соответствует увеличению длительности отжига).

 

Рис.3б. Пространственные распределение имплантированной в МС примеси. Кривая 1 - требуемое идеализированное распределение примеси. Кривые 2-4 – реальные распределения примеси в различные моменты времени (увеличение номера кривой соответствует увеличению длительности отжига).

 

Рис.4а. Зависимость безразмерного оптимального времени отжига при диффузионном легировании МС примеси, полученного из условия минимума среднеквадратического отклонения, от различных параметров МС. Кривые 1 и 2 – зависимости оптимального времени отжига от  и  при  и . Кривая 3 – зависимость времени отжига от  при ,  и .

 

Рис.4б. Зависимость безразмерного оптимального времени отжига имплантированной в МС примеси, полученного из условия минимума среднеквадратического отклонения, от различных параметров МС. Кривая 1 и 2 – зависимости времени отжига от  и  при попарном равенстве коэффициентов диффузии. Кривые 3-5 – зависимости времени отжига соответственно от ,  и  при попарных равенствах друг другу остальных коэффициентов диффузии и ,  и .

 

Заключение

В данной работе предложен способ увеличения резкости диффузионных и имплантационных p-n-переходов, входящих в состав транзисторной структуры, а также увеличения равномерности распределения примеси в обогащенной примесью области. Выполненный анализ показал, что обе цели могут быть одновременно достигнуты путем формирования p-n-переходов в многослойных структурах при подобранным специальным образом соотношении в свойствах слоев. На основе введенного ранее критерия проведена количественная оценка оптимальной длительности отжига, при котором достигается компромисс между увеличением равномерности распределения концентрации примеси в требуемой области структуры и увеличением резкости p-n-перехода. Также проведено исследование влияния ряда параметров на величину компромиссного времени отжига.

Литература:

 

[1] В.Г. Гусев, Ю.М. Гусев. Электроника. М.: Высшая школа, 1991. 622с.

[2] A.B.Grebene. Bipolar and MOS analogous integrated circuit design. New York,John Wyley and Sons, 1983,894 p.

[3] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[4] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян // ФТП. 2002. Т.36. № 5. С. 611-617.

[5] T. Ahlgren, J. Likonen, J. Slotte, J. Räisänen, M. Rajatore, J. Keinonen // Phys. Rev B. 1997. V.56, №8. P. 4597-4603.

[6] Е.И.Зорин, П.В.Павлов, Д.И.Тетельбаум. Ионное легирование полупроводников. М.: Энергия. 1975.130 с.

[7] H. Ryssel, I. Ruge. Ion implantation. B.G. Teubner, Stuttgart. 1978. 360 с.

[8] P.M. Fahey, P.B. Griffin, J.D. Plummer // Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.

[9] К.В. Шалимова. Физика полупроводников. М.: Энергоатомиздат, 1985. 391 с.

[10] М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Интегральные уравнения. М.: Наука, 1976. 215 с.

[11] E.L. Pankratov // Phys. Rev. B. 2005. V.72, №7. P. 075201-075208.