ФРАКТАЛЫ, СКЕЙЛИНГ И ДРОБНЫЕ ОПЕРАТОРЫ В РАДИОТЕХНИКЕ И ЭЛЕКТРОНИКЕ:
СОВРЕМЕННОЕ СОСТОЯНИЕ И РАЗВИТИЕ
А.А. Потапов
ИРЭ им. В.А. Котельникова РАН
Получена
25 января 2010 г.
Аннотация. Кратко систематизированы основные результаты теоретических и экспериментальных исследований, проводимых автором и коллективом под его руководством в Институте радиотехники и электроники им. В.А. Котельникова РАН, начиная с 80-х гг. XX в., которые привели к становлению и развитию нового фундаментального научного направления "Фрактальная радиофизика и фрактальная радиоэлектроника: Проектирование фрактальных радиосистем". Показано, что фракталы, дробные операторы и скейлинг являются важным инструментом исследования, хорошо приспособленным и к запросам практики, и к абстрактным конструкциям современной математики.
Ключевые слова: фракталы, дробные операторы, обработка изображений, антенны, наноструктуры.
При изучении наук примеры не менее поучительны, чем правила.
И. Ньютон
Научная красота – это обретение неочевидной истины.
Ф. Хатчесон
Введение
Стационарные режимы и периодические движения долгое время считались единственно возможными состояниями. Однако открытия второй половины XX века кардинально изменили наше представление о характере динамических процессов. В настоящее время явно ощущается недостаточность традиционных физических моделей. Другими словами, полное описание процессов современной обработки сигналов и полей невозможно с помощью формул классической математики, полученных на основе представления сигналов в пространстве целочисленной меры и гладких функций.
Сегодня совершенно очевидно, что применение в радиофизике, радиотехнике, радиолокации, электронике и в современных информационных технологиях идей масштабной инвариантности – “скейлинга” и разделов современного функционального анализа, которые связаны с теорией множеств, теорией дробной размерности, общей топологией, геометрической теорией меры и теорией динамических систем, открывают большие потенциальные возможности и новые перспективы в обработке многомерных сигналов и в родственных научных и технических областях. В конце двадцатого века в связи с созданием Б. Мандельбротом общей концепции фракталов [1] возникла мысль о применении их в области радиофизики и радиолокации.
Начиная с 80-х гг. XX в., в работах автора и научного коллектива под его руководством активно и последовательно ищутся новые радиофизические подходы, так или иначе связанные с применением теории фракталов, детерминированного хаоса, скейлинговых эффектов и дробных операторов. Наличие в уравнениях дробной производной современными исследователями интерпретируется как отражение особого свойства процесса/системы – память или немарковость (эредитарность).
Одна из целей работы – представить кратко историю и логику развития пионерских работ в ИРЭ им. В.А. Котельникова РАН (Москва) – по фракталам и КГТУ (КАИ) им. А.Н. Туполева (Казань) – по дробным операторам, чтобы расставить все по своим местам и исключить неоднократное “изобретение велосипеда”. По сути дела, речь идет о новом фундаментальном направлении в радиофизике и радиоэлектронике – применение теории фракталов, теории детерминированного хаоса, теории дробной меры и скейлинговых инвариантов в задачах повышения информативности радиосистем и устройств различного назначения.
Исходя из теории фракталов и дробных операторов, автор поставил задачу найти возможные формы их применения в радиофизике, радиоэлектронике, теории управления и т.д. За 30 - летний период работы автора в ИРЭ им. В.А. Котельникова РАН (с 3.09.1979 г.) удалось разработать ряд “нелинейных” глав фрактальной радиофизики и фрактальной радиоэлектроники [2 - 16]. Одновременно, эти результаты открывают новые выходы этих направлений в классическую радиофизику, современную нелинейную физику колебаний и волн, а также в радиоэлектронику и показывают перспективы современных теоретических и практических применений. Обобщение результатов, изложенных в авторских работах, позволяют охватить и возникающие новые проблемы [17 - 31].
В своем изложении автор придерживается разумного компромисса между строгим и интуитивным изложениями материала. Основное внимание было уделено принципам, а не деталям, которые подробно рассмотрены в [2 – 13, 16]. Для понимания достаточно владеть основными понятиями общей теории множеств, теории размерности и теории дробных операторов. Для тех, кто не имеет соответствующей математической подготовки, изложение, вероятно, будет не слишком понятным.
Цель работы – достаточно подробное, но и вместе с тем, и компактное, изложение на избранных примерах «фрактальной техники вычислений» и «фрактального языка» для множества современных физических и прикладных задач с дальнейшим выходом на проектирование фрактальных радиосистем различного назначения (что уже с 2008 г. делается автором с коллегами из Казани). Данная работа базируется исключительно на исследованиях автора, его учеников и коллег.
1. Эволюция фрактального подхода к решению радиофизических и радиотехнических задач (1979 – 2009 гг.)
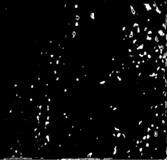
Основные принципы данного направления разрабатываются автором в ИРЭ им. В.А. Котельникова РАН, как отмечено выше, начиная с 80-х гг. XX в., и вначале касались вопросов фильтрации сверхслабых радиосигналов и изображений при существенно негауссовских помехах [8, 14 - 16]. В наших работах (в отличие от зарубежных) с самого начала была заложена идея фрактальной цифровой обработки малоконтрастных изображений, в том числе и фракталов на фрактальном фоне.
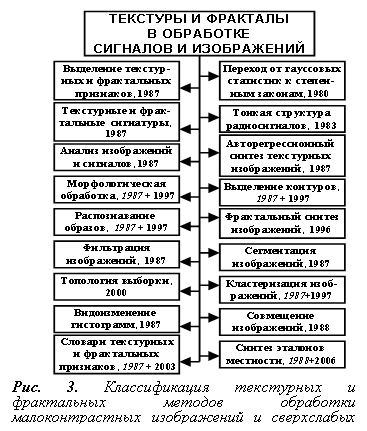
Затем стало абсолютно ясным, что такой «фрактальный» подход пригоден и для других задач. На рис. 1 схематически показаны основные направления исследований в ИРЭ РАН и приведены сведения о начале развертывания соответствующих работ. Условно в этих исследованиях можно проследить три этапа [2 – 14, 16, 17].
На первом этапе акцент был сделан на экспериментальной проверке фрактальности различных природных и искусственных образований, что позволило применить к ним понятия дробной размерности и масштабной инвариантности, и начать разработки методов фрактальной фильтрации объектов в различных интенсивных негауссовских помехах и шумах.
Второй этап был целиком посвящен усовершенствованию созданных оригинальных алгоритмов фрактальной цифровой обработки сигналов и изображений (аэрофотосъемка (АФС) и радиолокационные изображения - РЛИ), фрактальным методам обнаружения, распознавания, повышения контрастности, т.е. фрактальной обобщенной фильтрации.
Третий этап характеризуется переходом к проектированию фрактальной элементной базы и некоторых фрактальных узлов, а в перспективе фрактальных радиосистем в целом.
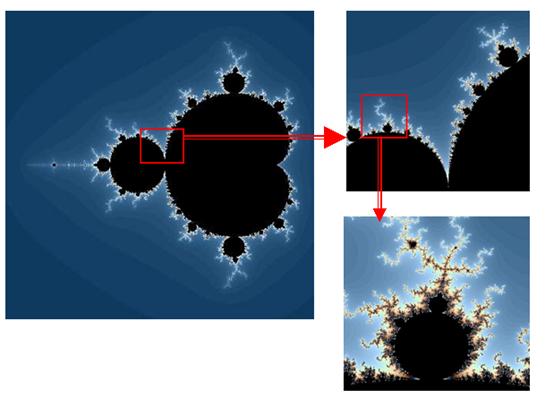
Фракталы относятся к множествам с крайне нерегулярной разветвленной или изрезанной структурой. Разработанная автором классификация фракталов была в декабре 2005 г. в США одобрена Б. Мандельбротом [4] и приведена на рис. 2, где описаны их свойства при условии, что D0 – топологическая размерность пространства, в котором рассматривается фрактал с дробной размерностью D.
|
|
|
|
Рис. 1. Развитие новых методов исследований в радиофизике и радиотехнике. |
Рис. 2. Классификация и морфология фрактальных множеств, разработанная автором. |
Большое значение приобретает глубокая аналогия между современными задачами радиофизики и радиоэлектроники и современной флуктуационной теорией фазовых переходов и критических явлений. Как известно, в основе современной ренормгрупповой теории фазовых переходов лежит подход, базирующийся на гипотезе скейлинга, или масштабной инвариантности. Аналогичный подход удалось разработать автору для решения радиофизических и радиотехнических задач.
2. Краткий исторический обзор по теории дробного интегродифференцирования
Дробный математический анализ имеет давнюю историю и чрезвычайно богатое содержание. Прежде чем перейти к рассмотрению современных идей, рассмотрим эскизно развитие теории дробных операторов. Их физико-химическое моделирование рассмотрено далее. Вопрос, поднятый Лейбницем о дробной производной, является постоянной темой в последние более чем 300 лет. Современное состояние дробного исчисления характеризуется большим потоком публикаций, созданием журналов и ежегодным проведением международных конференций (см. например, [13, 30]).
Интерес к дробному математическому анализу возник почти одновременно с появлением классического анализа (Г. Лейбниц в письмах к Г. Лопиталю в 1695 г. при рассмотрении дифференциалов и производных порядка ½ высказал пророческие слова: “…Из этого парадокса со временем будут выведены полезные следствия”). Вероятно, самое раннее более или менее систематическое исследование этого вопроса относится к XIX в. и принадлежит Н. Абелю (1823), Ж. Лиувиллю (1832), Б. Риману (1847 г.) и Х. Хольмгрену (1864 г.), хотя ранее вклад внесли Л. Эйлер (1730 г.) и Ж. Лагранж (1772 г.).
Именно в своем цикле работ Ж. Лиувилль (1832 - 1835 гг.), применяя разложение функций в степенные ряды, определял “q”-ю производную путем почленного дифференцирования. Он же, в частности, дал первые практические приложения созданной им теории к решению задач математической физики. Затем Б. Риман (1847 г.) предложил иное решение на основе определенного интеграла, пригодное к степенным рядам с нецелыми показателями. Данная работа, выполненная Б. Риманом в студенческие годы, была опубликована лишь в 1876 г. (спустя 10 лет после его смерти). Конструкции Лиувилля и Римана являются основными формами дробного интегрирования. Развивая идею Лиувилля, А. Грюнвальд (1867 г.) ввел понятие дробной производной как предела разностных отношений.
Параллельно с теоретическими начинаниями разрабатывались приложения дробного анализа к решению различных задач. Одним из первых таких приложений явилось открытие Н. Абеля (1823 г.), показавшего, что решение задачи о таутохроне может быть получено путем интегрального преобразования, которое записывается как производная полуцелого порядка. Существует историческое заблуждение, что Абель решил задачу только при значении индекса, равном ½. На самом деле, Абель рассмотрел решение в общем случае, и его работы сыграли огромную роль в развитии идей дробного интегродифференцирования. Заслугой Хольмгрена является рассмотрение дробного дифференцирования как операции, обратной интегрированию, и приложение данных понятий к решению обыкновенных дифференциальных уравнений.
Следует особо отметить цикл работ чл.-корр. Петербургской Академии наук (1884 г.) А.В. Летникова (1837 - 1888 г.г.) [13], который за время своей 20-летней научной деятельности разработал полную теорию дифференцирования с произвольным показателем (в настоящее время его работы преданы почти полному забвению). Работы А.В. Летникова остались почти неизвестными за рубежом. В рассматриваемый период в России за работами А.В. Летникова последовали работы Н.Я. Сонина и П.А. Некрасова. С именами этих русских ученых также связано распространение формулы Коши для аналитических функций в комплексной плоскости на нецелые значения индекса интегродифференцирования.
Признавая важность работ упомянутых выше ученых, необходимо, однако отметить, что дробное исчисление стало строгой математической теорией, только начиная с работ А.В. Летникова.
В конце XIX в. вышла содержательная работа Ж. Адамара (1892 г.), в которой на основе разложения в ряд Тейлора было рассмотрено дробное дифференцирование аналитической в круге функции по радиусу, которое носит название подхода Адамара.
В первой половине XX в. заметный вклад, как в теорию, так и в практику дробного анализа внесли Г. Харди, Г. Вейль, М. Рисс, П. Монтель, А. Маршо, Д. Литтлвуд, Я. Тамаркин, Э. Пост, С.Л. Соболев, А. Зигмунд, Б. Надь, А. Эрдейи, Х. Кобер, Ж. Коссар, и ряд других ученых. В 1915 г. Г. Харди и М. Рисс использовали дробное интегрирование для суммирования расходящихся рядов. В 1917 г. Г. Вейль определил дробное интегрирование для периодических функций в виде свертки с некоторой специальной функцией. Аналог неравенства С.Н. Бернштейна для дробных производных алгебраических многочленов на конечном отрезке дал в 1918 г. П. Монтель. В работе А. Маршо (1927 г.) была введена новая форма дробного дифференцирования, которая применима в случае функций с “плохим” поведением на бесконечности. Были введены в обиход дробные производные Маршо. В работах М. Рисса (1936, 1938, 1949 г.г.) были получены операторы типа потенциала (потенциалы Рисса), позволившие определить дробное интегрирование функций многих переменных. Для некоторых интегральных операторов и интегральных уравнений очень полезными оказались дробные интегралы Эрдейи и Кобера (1940 г.) и т.д.
Специально для радиофизиков и радиоинженеров отметим тот факт, что операционное исчисление, разработанное О. Хевисайдом (1892, 1893, 1920 гг.), оказалось важным этапом в применении обобщенных производных. Именно О. Хевисайд (1920 г.) применил дробное дифференцирование в теории линий передач. После этого другие теоретики признали преимущества такого подхода и стали развивать его в соответствии с принятыми математическими концепциями (Н. Винер, Дж. Карсон (1926 г.)). Обширная хронологическая библиография по дробному анализу приведена в [13].
Автор привел имена выдающихся ученых, внесших большой вклад на основных этапах развития дробного исчисления. Дальнейшее рассмотрение его развития не входит в нашу задачу и может составить тему для специальной книги, аналогичной [13]. Аппарат дробных производных и интегралов используется в физике, механике, химии, гидрологии, теории гравитации и др. Приложения данного математического аппарата слишком многочисленны, чтобы все их перечислять. Настало время применить его к задачам фрактальной радиофизики и фрактальной радиолокации [2, 3, 13].
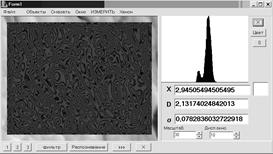
3. Текстурная и фрактальная обработка изображений и фрактальное обнаружение сверхслабых сигналов в интенсивных негауссовских помехах и шумах
В монографиях [2 – 4, 8 - 13] вся математическая и физическая теория фракталов приведена автором в достаточно стройную логическую систему.
 ванных
текстур на основе авторегрессионных моделей был проведен автором в ИРЭ им.
В.А. Котельникова РАН в середине 80-х гг. XX в.
совместно с Воронежским университетом [2 –
4, 14 - 16].
ванных
текстур на основе авторегрессионных моделей был проведен автором в ИРЭ им.
В.А. Котельникова РАН в середине 80-х гг. XX в.
совместно с Воронежским университетом [2 –
4, 14 - 16].
Многолетние натурные эксперименты проводились автором совместно с ЦКБ «Алмаз» и другими ведущими промышленными организациями. При этом была поставлена и решена задача расчета текстурных признаков с учетом дрейфа сигнатур при изменении времени года. Были также оптимизированы оценки влияния размера окон на точность определения текстурных признаков для изображений различных типов земных покровов. Продолжительное время работы автора в области исследования РЛИ земных покровов на ММВ с использованием текстурной информации фактически были единственными в России и не потеряли актуальность, по отзывам специалистов, и в настоящее время [16].
Анализ полученных данных
позволил доказать очень важную особенность: одномерные области существования
текстурных признаков РЛИ в диапазоне ММВ (множество R) почти полностью
вкладываются в соответствующие области признаков АФС (множество А): R![]() А. Таким образом,
области признаков РЛИ как бы сжимаются по сравнению с областями признаков АФС.
Это происходит, из-за сглаживания в РЛИ тонкой структуры текстур
исследуемых покровов, характерной для АФС. Следовательно, со значительной
степенью достоверности множество R можно прогнозировать по множеству A.
А. Таким образом,
области признаков РЛИ как бы сжимаются по сравнению с областями признаков АФС.
Это происходит, из-за сглаживания в РЛИ тонкой структуры текстур
исследуемых покровов, характерной для АФС. Следовательно, со значительной
степенью достоверности множество R можно прогнозировать по множеству A.
На основе полученных
результатов нами были впервые предложены и реализованы следующие нетрадиционные
и достаточно эффективные методы обнаружения сигналов при малых отношениях
сигнал/фон ![]() : дисперсионный
метод, метод обнаружения с помощью линейно моделированных эталонов и метод с
прямым использованием ансамбля текстурных признаков [14 -
16].
: дисперсионный
метод, метод обнаружения с помощью линейно моделированных эталонов и метод с
прямым использованием ансамбля текстурных признаков [14 -
16].
Анализ полученных экспериментально обширных баз данных (более чем 30 категорий земных покровов [14 - 16] в совокупности с визуальным исследованием степени сложности изолиний амплитуд рассеянного излучения, зафиксированного на АФС и РЛИ, и привел автора к идеям введения ансамблей принципиально новых признаков, основанных на скейлинговых показателях и характеристиках дробной размерности, т.е. к фрактальным сигнатурам.
4. Отказ от гауссовских статистик в экспериментах. Тонкая структура отраженных импульсных сигналов и новый класс признаков
Как хорошо известно, на ранних и более поздних этапах экспериментальных работ по рассеянию электромагнитных волн исследователи столкнулись с вопросами применимости гауссовских моделей. Вскоре начались многочисленные искусственные попытки создания моделей рассеяния с целью повышения хвостов вероятностных распределений амплитуд отраженных сигналов.
Продолжительное и
плодотворное участие автора в многомасштабных экспериментальных работах (1979 -
1990 гг.) совместно с ведущими организациями СССР, привели его к необходимости
принципиального отказа от гауссовских статистик в случае достаточно
высокого разрешения радиолокаторов (см. рис. 3). Все исследования проводились
автором на длинах волн λ = 2,2 и
8,6 мм (активное излучение) и λ
= 3,5 мм (пассивное излучение) [14, 15]. Именно в физических
экспериментах на длине волны 2,2 мм автором была показана в 1979 – 1980 гг.
неприменимость гауссовских статистик для почти всего диапазона углов падения ![]() электромагнитного
излучения.
электромагнитного
излучения.
Экспериментальные исследования периода 1979-1990 гг.
позволили автору помимо решения традиционных задач рассеяния установить общие
закономерности формирования
тонкой структуры модулированного сигнала в диапазоне ММВ и предложить
принципиально новый класс признаков, основанных на тонкой структуре
модулированных сигналов, рассеянных статистически неровной поверхностью [14]. К характеристикам тонкой структуры отраженных радиолокационных
сигналов автор предложил отнести: внутриимпульсные флуктуации, их статистику,
корреляционные и спектральные зависимости и среднее уширение импульса, определяемое величиной, обратной полосе когерентности ![]() .
.
На первом этапе проводили дискретизацию увеличенных огибающих отраженных импульсов на необходимое число отчетов. Полученные данные являлись исходным материалом для определения усредненных огибающих импульсных сигналов, отраженных различными земными покровами. На втором этапе обработки были рассмотрены репрезентативные выборки внутриимпульсных амплитудных флуктуации, полученные путем вычитания дискретов средних импульсов из отсчетов мгновенных огибающих. Ввиду того, что рассматриваемые реализации огибающих относятся к периодически нестационарным случайным процессам, необходимо было провести исследования на стационарность внутриимпульсных амплитудных флуктуации. Контроль стационарности проводился методами непараметрической статистики.
Стационарность процессов оценивалась с помощью рангового критерия Вилкоксона. Асимптотическая эффективность этого критерия по сравнению с критерием Стьюдента равна 3/π. Кроме того, данный критерий применим к выборкам малого объема. Выяснилось, что для всех типов земных покровов соблюдается стационарность внутриимпульсных и внутрипериодных флуктуации по среднему и по форме распределения с доверительной вероятностью Рд =0,95. Показано, что функции распределения внутриимпульсных амплитудных флуктуаций р(n) отраженных импульсов в диапазоне ММВ для исследуемых типов земных покровов принадлежат преимущественно одному классу распределений (но не гауссовскому и с увеличенными хвостами!).
Таким образом, многолетние радиофизические эксперименты, в которых активно участвовал автор, дают весьма убедительные доводы в пользу негауссовских статистик. Также более 15 лет назад (см. ниже) автором было показано, что негауссовские функции распределения с тяжелыми хвостами (степенные/устойчивые) естественно возникают (!) при фрактальной обработке одномерных и многомерных сигналов в радиочастотном и оптическом диапазонах с учетом скейлинговых соотношений.
5. Фрактальные сигнатуры и их применение в обработке сигналов
Впервые предложенные и разрабатываемые автором с учениками (к.ф.-м.н. В.А. Герман и др.) цифровые фрактальные методы позволяют частично преодолевать априорную неопределенность в радиолокационных задачах с помощью информации о геометрии (топологии) выборки - одномерной или многомерной [2 – 4, 8 – 11, 13, 16]. При этом большое значение приобретают топологические особенности индивидуальной выборки, а не усредненные реализации, имеющие зачастую совершенно другой характер. Весьма плодотворным оказалось введение автором в практику измерений понятий фрактальных сигнатур и фрактальных кепстров. Всегда в методах фрактальной обработки необходим учет скейлинговых эффектов реальных радиосигналов и электромагнитных полей.
Введение дробной меры и скейлинговых инвариантов вызывает необходимость работы преимущественно со степенными распределениями. Их называют еще фрактальными распределениями, распределениями с «тяжелыми хвостами» или паретианами. Распределения с «тяжелыми хвостами» входят в класс устойчивых распределений. Данные распределения являются следствием обратных связей, усиливающих события. Отметим, что для распределений с «тяжелыми хвостами» выборочные средние неустойчивы и малоинформативны из-за неприменимости закона больших чисел. Степенные законы распределения представляют собой одну из отличительных черт сложности. Простые системы обычно имеют экспоненциальное и гауссовское распределения. Природа степенных законов распределения связана с сильной взаимозависимостью событий (эффект не «домино», а «цепной реакции»). Отметим, что устойчивый паретиан является отличительной чертой многих сложных открытых систем, обменивающихся с окружающей средой веществом, энергией и информацией с перераспределением энтропии.
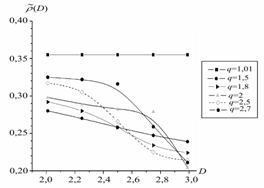
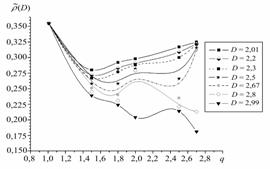
Кратко рассмотрим избранные примеры по экспериментальным вероятностным распределениям мгновенной фрактальной размерности радиофизических процессов. На рис. 4а приведен общий вид распределений фрактальных размерностей D.
Фрактальная
цифровая обработка реализаций двумерных сигналов в шумах показала (см. рис. 4б),
что при отношении сигнал/шум ![]() = +10 дБ мы точно измеряем статистику
сигнала. С уменьшением значения
= +10 дБ мы точно измеряем статистику
сигнала. С уменьшением значения ![]() в сторону отрицательных значений
(например,
в сторону отрицательных значений
(например, ![]() =
-3 дБ) происходит смещение максимума (моды) итогового фрактального
распределения в сторону значений фрактальной размерности шума или помехи. При
этом всегда (!) в окрестности значения фрактальной размерности D
полезной составляющей присутствует «тяжелый хвост» фрактального распределения (паретиана),
достигающий стабильной величины, порядка 10 - 20 % (рис. 4в - сверхмалые
отношения сигнал/помеха).
=
-3 дБ) происходит смещение максимума (моды) итогового фрактального
распределения в сторону значений фрактальной размерности шума или помехи. При
этом всегда (!) в окрестности значения фрактальной размерности D
полезной составляющей присутствует «тяжелый хвост» фрактального распределения (паретиана),
достигающий стабильной величины, порядка 10 - 20 % (рис. 4в - сверхмалые
отношения сигнал/помеха).
|
|
|
|
(а) (б) |
|
|
(в) |
|
Рис. 4. Общий вид (а) распределений D для фрактальных сцен;
примеры (б) с ![]() дБ (1),
дБ (1), ![]() =10 дБ (2),
=10 дБ (2), ![]() =3 дБ (3),
=3 дБ (3), ![]() = - 3дБ (4);
= - 3дБ (4);
распределения D для сцен с гауссовскими помехами (в): 1 и 3 – сцена А, 2 и 4 – сцена Б,
1 и 2 - ![]() = - 10 дБ, 3 и 4 -
= - 10 дБ, 3 и 4 - ![]() = - 20 дБ.
= - 20 дБ.
Предложенные фрактальные методы существенно дополняют текстурные и позволяет более надежно производить операцию кластеризации. Интересно отметить, что после цифровой фрактальной обработки изображений поверхности, кроме устойчивого разделения по типам земных покровов, отмечаются невидимые (скрытые) до этой обработки особенности (как, например, данные кластеризации дистанционного зондирования различных земных покровов [2 – 4, 8]. Это позволяет говорить о применении созданных методов фрактального распознавания для идентификации участков изображения, «невидимых» при классических методах кластеризации по полю яркостей.
Экспериментально также доказана возможность эффективной кластеризации однородных протяженных связных областей с помощью фрактальной фильтрации. В качестве примера на рис. 5 приведены результаты фрактального анализа рентгеновских томограмм, предоставленных из Института прикладной физики НАН Беларуси [4, 8].
|
|
|
|
(а) (б) |
|
|
Рис. 5. Фрактальная фильтрация томограмм нижней (а) и верхней (б) частей головы. |
|
Фрактальной обработке
подвергались изображения нижней части головы человека, включающие большое число
контрастных деталей, и изображения верхней части головы с малоконтрастным
изображением срезов мозга. Исходное томографическое изображение показано слева
на рис. 5. Реконструкции томограмм проводились при различных значениях
выделенной по паретиану фрактальной размерности D, а именно D(1), D(2)![]() D(1) и D(3)
D(1) и D(3)![]() D(2)
D(2)![]() D(1). Отчетливо видны
разнообразные кластеры, незаметные ранее на исходном снимке.
D(1). Отчетливо видны
разнообразные кластеры, незаметные ранее на исходном снимке.
Возможности
применения фрактального анализа в медицинской диагностике кожных заболеваний
иллюстрируется данными рис. 6, полученными в 2007 г. На рис. 6 приведены
результаты фрактальной цифровой обработки фотографий пациенток с диагнозом
“жирная себорея”, на фоне которой развивается угревая сыпь. В результате
обработки серии снимков было отмечено, что оценка фрактальной размерности ![]() (по измеренным
фрактальным сигнатурам) имеет индивидуальный характер для каждого пациента,
независимо от участка изображения, по которому производился анализ. В настоящий
момент широко развиваются с рядом организаций фрактальная обработка медицинских
изображений.
(по измеренным
фрактальным сигнатурам) имеет индивидуальный характер для каждого пациента,
независимо от участка изображения, по которому производился анализ. В настоящий
момент широко развиваются с рядом организаций фрактальная обработка медицинских
изображений.
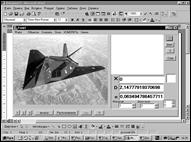
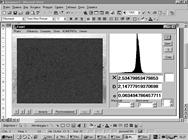
На
рис. 7а представлено изображение самолета F 117,
подвергнутое затем зашумлению аддитивным гауссовым шумом (рис. 7б). В
данном случае, отношение сигнал/шум ![]() = -3 дБ. Видно, что вся полезная информация
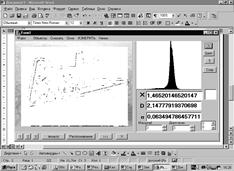
скрыта шумовым фоном. Результаты фрактальной непараметрической фильтрации
такого изображения приведены на рис. 7в,г. Выбор оптимального
режима фильтрации контуров или объектов производится оператором по
автоматически построенному пространственному распределению мгновенных
фрактальных размерностей
= -3 дБ. Видно, что вся полезная информация
скрыта шумовым фоном. Результаты фрактальной непараметрической фильтрации
такого изображения приведены на рис. 7в,г. Выбор оптимального
режима фильтрации контуров или объектов производится оператором по
автоматически построенному пространственному распределению мгновенных
фрактальных размерностей ![]() сцены, которое отображается на экране
компьютера справа.
сцены, которое отображается на экране
компьютера справа.
Созданные
в ИРЭ им. В.А. Котельникова РАН при непосредственным участием и под руководством
автора эффективные методы измерения фрактальных характеристик (фрактальных
сигнатур) и обработки изображений могут широко использоваться и уже частично
применяются в различных физико-технических, астрономических, биологических,
медицинских, томогафических и т.п. исследованиях. В частности, с помощью
синтезированных фрактальных алгоритмов удается выделить номера автомобилей,
оптические изображения которых получены в условиях очень сильных помех (пыль,
дым, туман).
|
(а) |
(б) |
|
||
|
(г) |
(д) |
(е) |
||
Рис. 6. Фото
пациентки (а), фрактальный портрет (б), фрактальная сигнатура (в), сечения поля
фрактальных размерностей (г - е).
|
(а) |
(б) |
|
(в) |
(г) |
|
Рис. 7. Цифровая фрактальная обработка изображения (а) самолетa F 117: (б) -
изображение самолета F 117 в гауссовских шумах при |
|
6. Основы методов построения фрактальных сигналов и
фрактальные методы передачи информации
Выделение темы синтеза разнообразных фрактальных сигналов и методов фрактальной модуляции в отдельную часть имеет важное методологическое значение. Дело в том, что нарастающий в последнее десятилетие интерес к применению теории фракталов в радиофизике и радиоэлектронике вызывает в последние годы появление ряда статей и докладов, авторы которых не учитывают или не знают (? !) прежние работы автора, выполненные им в ИРЭ им. В.А. Котельникова РАН еще более двух десятилетий назад.
Кратко
остановимся на этом историческом аспекте. Первое упоминание о создании и
работе макета (ЦКБ «Алмаз» и ИРЭ им. В.А. Котельникова РАН) радиолокационной
станции (РЛС) в диапазоне ММВ со сложным квазинепрерывным стохастическим
сигналом на длине волны 8,6 мм сверхбольшой базы ![]() и стохастическим квадратичным
детектированием было опубликовано нами еще в 1988 г. (ссылки в [2,
3, 14]). Для уменьшения времени обзора применялся параллельный анализ 20
элементов дистанции с помощью многоканальной цифровой обработки. В РЛС были
предусмотрены квадратурные каналы. Работа комплекса на одну приемно–передающую
антенну на ММВ была обусловлена оригинальным применением в трактах приема и
передачи фазируемых и тактируемых параметрических делителей частоты или
параметронов в данном диапазоне волн [14]. Тактовая частота составляла
величину 10 МГц.
и стохастическим квадратичным
детектированием было опубликовано нами еще в 1988 г. (ссылки в [2,
3, 14]). Для уменьшения времени обзора применялся параллельный анализ 20
элементов дистанции с помощью многоканальной цифровой обработки. В РЛС были
предусмотрены квадратурные каналы. Работа комплекса на одну приемно–передающую
антенну на ММВ была обусловлена оригинальным применением в трактах приема и
передачи фазируемых и тактируемых параметрических делителей частоты или
параметронов в данном диапазоне волн [14]. Тактовая частота составляла
величину 10 МГц.
При
выделении сигнала ММВ, рассеянного разнообразными земными покровами, нами уже в 1988 г.
проводились операции выделения участков частотного и временного скейлинга,
которые и предполагают наличие фрактальных свойств принятой выборки.
Затем был всесторонне исследован двухчастотный режим работы
приема-передатчика для реализации фрактальной обработки на двух частотных
интервалах. Второй действующий комплекс макета РЛС использовал метод
двухчастотного зондирования на ММВ с разносом частот около 850 МГц. База
сложного фазоманипулированного сигнала (ФМ) при этом была увеличена до значения
![]() [2,
3, 14].
[2,
3, 14].
В развитие данного направления тогда же проводились работы по проектированию принципиально нового в то время радиофизического комплекса [2, 3, 14] с применением несинусоидальных волн на основе теории секвентного анализа. В этом случае энергия сложных сигналов будет распределена в полосе частот до десятков гигагерц. Кроме того, сложные несинусоидальные сигналы позволяют добиваться эффектов, недостижимых при использовании традиционных синусоидальных несущих. В секвентном анализе применяют частотно-независимые антенны: биконические, плоские спиральные и логарифмически-периодические антенны. В настоящее время, к таким антеннам, бесспорно, добавлен широкий класс фрактальных антенн разных конфигураций и фрактальных антенных решеток. Автор совместно с представителями ЦКБ «Алмаз», по сути, в начале 90–х гг. XX в. и предпринимал первые попытки разработки и проектирования [2 – 4, 14] таких необычных (для того времени) фрактальных антенных структур (конкретно, был изготовлен действующий макет фрактальной щелевой решетки в диапазоне ММВ). При совмещении указанного радиолокационного комплекса с радиометром был реализован пассивно-активный метод зондирования с использованием квазинепрерывного шумоподобного ФМ сигнала в качестве сигнала подсветки [14]. При этом, в частности, решались задачи обнаружения слабоотражающих биологических объектов (стаи птиц в воздухе, человек на фоне сильных помех от земных покровов, подвижные объекты и т.д.).
Разрабатываемые автором фрактальные методы объединены им под общим названием фрактальных методов передачи информации. Декларируемый здесь подход позволяет перейти к конкретным структурным схемам фрактальных модуляторов и фрактальных демодуляторов сигналов. Рассмотрим кратко принципы фрактальной модуляции, когда любые модулируемые параметры высокочастотного сигнала формируют по фрактальному закону с заданным скейлингом. Можно использовать классические фрактальные функции и множества (канторово и т.п.) на основе i - ой и k - рекурсии. Применяя фрактальные законы изменения параметров гармонического колебания и электромагнитной волны, получаем фрактальные: амплитудную (ФАМ), частотную (ФЧМ), фазовую (ФФМ) и поляризационную (ФПМ) виды модуляции. Также осуществляется двойная модуляция с поднесущей. Для дискретных систем передачи информации можно реализовать фрактальные: амплитудно-импульсную (ФАИМ), широтно-импульсную (ФШИМ), частотно-импульсную (ФЧИМ), фазо-импульсную (ФФИМ), импульсно-кодовую (ФИКМ) виды модуляции. Для радиоканалов вторая ступень модуляции может быть и традиционной (АМ, ЧМ, ФМ, поляризационная).
Аналогично
автором был введен новый класс фрактальных шумоподобных сигналов – когда
в качестве переносчика информации используется случайный процесс с
распределением мгновенных амплитуд по закону «устойчивого паретиана», т.е. мы
применяем фрактальное распределение с тяжелыми хвостами. Существует возможность
синтеза фрактальных шумоподобных составных сигналов. Можно так же
использовать известное стохастическое кодирование информации, в котором
необходимо выделить участки скейлинга. В этом случае мы просто синтезировали новый
тип фрактальных простых или шумоподобных сигналов. Автором также предложены
новые классы сигналов, основанные на текущей оценке показателя Херста Н, названные
им «Н – сигналы» [4, 11]. Показатель Херста в зависимости от
своего значения относительно величины ![]() характеризует или персистентность (
характеризует или персистентность (![]() ) или антиперсистентность
(0 <
) или антиперсистентность
(0 <![]() )
текущей выборки. В первом случае, когда
)
текущей выборки. В первом случае, когда ![]() , мы наблюдаем процесс, сохраняющий тенденцию
роста или уменьшения мгновенных амплитуд в выборке, т.е. процесс с памятью.
Во втором случае, когда 0 <
, мы наблюдаем процесс, сохраняющий тенденцию
роста или уменьшения мгновенных амплитуд в выборке, т.е. процесс с памятью.
Во втором случае, когда 0 <![]() , рост амплитуд огибающей сигнала в
“прошлом” означает уменьшение в “будущем”, и наоборот, т.е. процесс, более
подверженный переменам, который часто обозначают как “возврат к среднему”.
Необходимое значение параметра Н или его функциональную
временную/частотную зависимость необходимо предварительно «вкладывать» в
зондирующий радиолокационный сигнал. При этом затрудняется обнаружение такого
сигнала и измерение его параметров с целью создания преднамеренных помех. Очень
интересным и чрезвычайно перспективным является применение операторов
дробного интегродифференцирования в синтезе новых классов простых и сложных сигналов.
Насколько известно автору, эти факты никогда не рассматривались в литературе.
, рост амплитуд огибающей сигнала в
“прошлом” означает уменьшение в “будущем”, и наоборот, т.е. процесс, более
подверженный переменам, который часто обозначают как “возврат к среднему”.
Необходимое значение параметра Н или его функциональную
временную/частотную зависимость необходимо предварительно «вкладывать» в
зондирующий радиолокационный сигнал. При этом затрудняется обнаружение такого
сигнала и измерение его параметров с целью создания преднамеренных помех. Очень
интересным и чрезвычайно перспективным является применение операторов
дробного интегродифференцирования в синтезе новых классов простых и сложных сигналов.
Насколько известно автору, эти факты никогда не рассматривались в литературе.
Совершенно ясно, что оценка текущего значения параметра Н легко может быть введена сегодня в теорию и практику классической обработки радиолокационной информации на фоне помех, не требуя существенных изменений схем действующих радиосистем. Представляет также интерес вывести правила использования дополнительной информации о параметре Н выборки из соображений оптимальности. При этом учет значений показателя Херста Н повлияет на структуры оптимального или согласованного фильтров.
Из всего сказанного следует несомненный авторский приоритет с 80 гг. XX в. по основам методов построения фрактальных сигналов и фрактальных методов передачи информации.
7. Фрактальная электродинамика и фрактальные “интеллектуальные” материалы
7.1. Анализ и синтез фрактальных антенн
Антенные устройства и частотно-избирательные поверхности (ЧИП) являются неотъемлемой частью радиосистемы. Опыт анализа и синтеза фрактальных антенн доказывает их широкополосность и многодиапазонность [2 – 4, 9, 10, 13]. Поэтому такие фрактальные антенны чрезвычайно эффективны при разработке многочастотных радиолокационных и телекоммуникационных систем. На основе алгоритмов численного решения гиперсингулярных интегральных уравнений нами был проведен анализ электродинамических свойств разнообразных фрактальных антенн (монополи и диполи с применением классической кривой Серпинского и дерева Кейли различного порядка итераций) [2 – 4, 9, 10, 13]. Анализ проведен для фрактальных антенн с изменяющимся углом раствора (рис. 8).
|
(а) (б) |
|
(в) |
|
(г) |
|
|
|
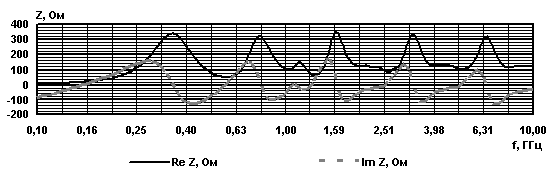
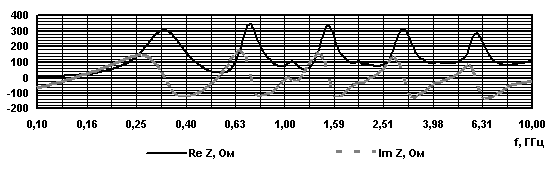
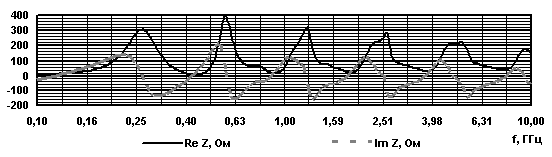
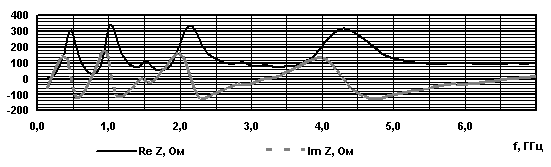
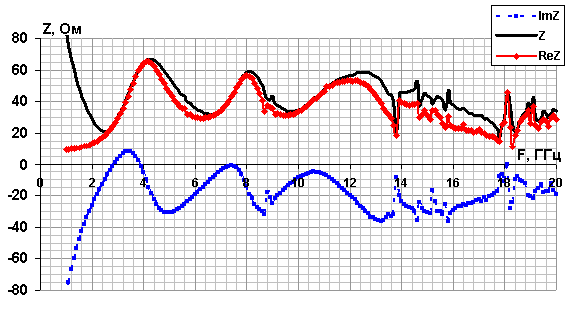
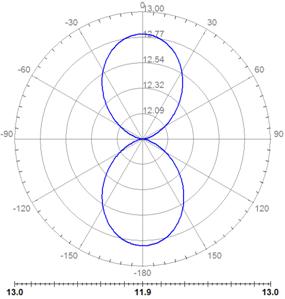
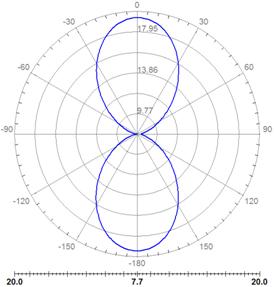
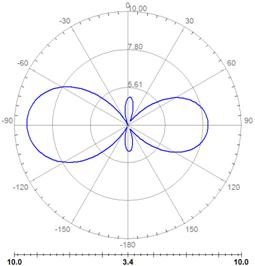
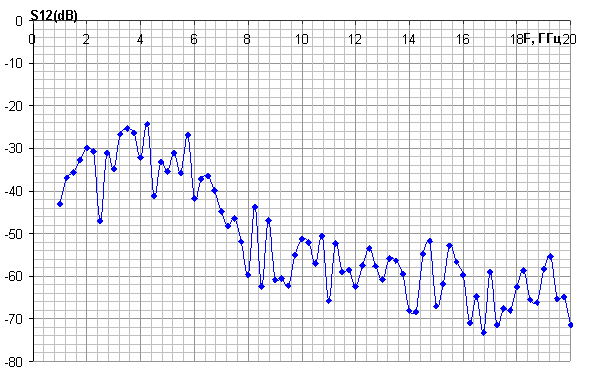
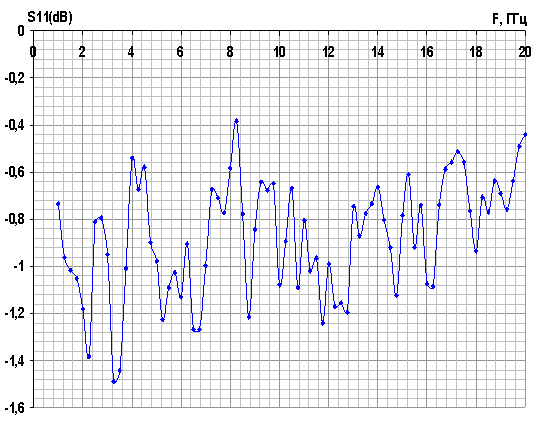
Рис. 8. Импеданс фрактальных антенн - монополей при |
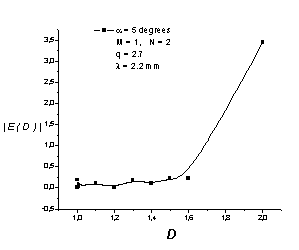
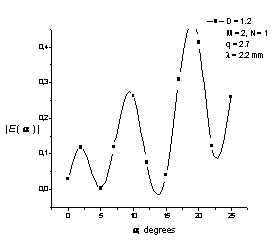
Были
вычислены входные импедансы фрактальных антенн ![]() в диапазоне частот 0,1 – 10,0 ГГц и
определены все резонансные частоты исследуемых фрактальных антенн (или
фрактальных ЧИП). Впервые проводился расчет структуры электромагнитных полей в
ближней зоне рассматриваемых фрактальных антенн.
в диапазоне частот 0,1 – 10,0 ГГц и
определены все резонансные частоты исследуемых фрактальных антенн (или
фрактальных ЧИП). Впервые проводился расчет структуры электромагнитных полей в
ближней зоне рассматриваемых фрактальных антенн.
Работа фрактальных антенн достигнута через геометрию проводников, а не через накопление отдельных компонентов или элементов (как в классических антеннах), что, в последнем случае, увеличивает сложность и потенциальные точки отказа. Фрактальные антенны также позволяют создать многополосные варианты, уменьшенный размер, и оптимальную или «шикарную» технологию антенн. Несомненным достоинством фрактальных антенн (монополей и диполей) является тот факт, что они могут иметь меньшие резонансные частоты по сравнению с классическими (или евклидовыми) антеннами тех же размеров. Врожденные широкополосные качества фрактальных антенн идеальны для интеллектуальных приложений и защиты информации.
В отличие от традиционных методов, когда синтезируются гладкие диаграммы направленности антенны, в основе теории фрактального синтеза заложена идея реализации характеристик излучения с повторяющейся структурой на произвольных масштабах. Это дает возможность создавать новые режимы во фрактальной электродинамике [2, 3, 13], а также получать принципиально новые свойства. В частности, размещение фрактальных элементов на корпусе объекта может существенно исказить сигнатуру или радиолокационный портрет данного объекта [(а)].
Области применения фрактальных антенн: современные телекоммуникации, шумовая радиолокация, нелинейная радиолокация, системы поиска, локализации и трассировки мобильных объектов, пеленгация в сложных городских условиях, определение местоположения несанкционированных источников радиоизлучения при борьбе с террористами, оперативная связь в войсках, маркеры на различных предметах, космическая связь, современный физический эксперимент и т.п. Число зарубежных исследований по разработке различных конструкций фрактальных антенн в настоящее время стремительно растет (см. гл. 11 «Фрактальные антенны и методы их проектирования» монографии [3]).
Автором с учениками (Е.Н. Матвеев, В.А. Потапов и др.) предложено большое количество видов фрактальных антенн, а также рассчитаны их параметры. Их краткое обсуждение по данным [3, 9, 13, 32 - 39] приведено ниже в пп. 7.2 и 7.3, а также в п. 7.6.
7.2. Фрактальные антенны на основе дерева Кейли
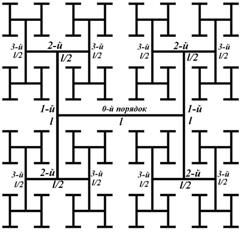
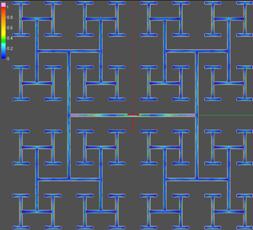
Фрактальная антенна представляет собой ряд отрезков проводников разной длины. С каждой новой итерацией к антенне наращиваются отрезки определенной длины, так что для каждой нечетной итерации длина остается прежней, а с каждой четной итерацией – длина уменьшается в 2 раза (рис. 9). Распределение тока в антенне «Дерево Кейли» 6-го порядка приведено на рис. 10. Распределение токов по апертуре фрактальной антенны (рис. 10) наглядно демонстрирует, как с каждой следующей резонансной частотой в формировании параметров антенны начинают играть роль новые участки апертуры.
Компьютерное моделирование было проведено в диапазоне частот 1 - 6 ГГц. Получены зависимость импеданса (рис. 11) и КСВ от частоты, а также сечения диаграммы направленности антенны.
7.3. Фрактальные кольцевые монополи
Исследование фрактальных кольцевых структур, впервые предложенных авторами, проводилось средствами САПР Antsoft HFSS, в которой благодаря удобному интерфейсу проектирования легко можно создать кольцевые структуры, учитывая свойства симметрии и подобия.
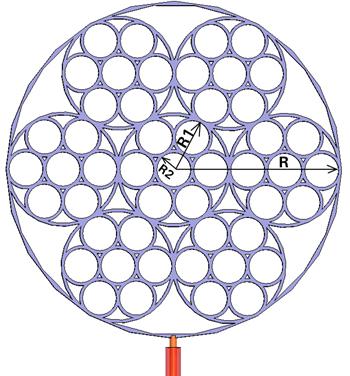
1. В качестве базового элемента фрактальной антенной структуры первой итерации А1 было взято кольцо радиуса 11 мм, толщиной 0,4 мм по оси 0х и 0,2 мм по радиусу. Алгоритм построения структуры фрактальной апертуры, представленной на рис. 12, выглядит следующим образом.
|
|
|
|
Рис. 9. Построение “Дерева Кейли” 6го порядка. |
Рис.10. Распределение токов по фрактальной антенне “Дерево Кейли” на частоте
|

Рис. 11. Зависимость импеданса антенны “Дерево Кейли” от частоты.
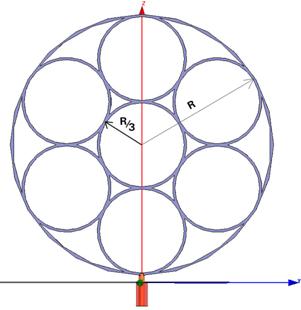
Рис.12. Модель монопольной антенны А1.
Внутри базового элемента нулевой итерации размещены 7 колец с радиусом в три раза меньше исходного элемента. Остальные параметры (ширина и толщина кольца базового элемента) оставлены без изменений. Центры 6 маленьких окружностей расположены на расстоянии R*2/3, в вершинах шестиугольника. Центр 7-й окружности совпадает с центром основной антенны. Назовем это построение первым циклом итерации алгоритма построения, а антенну кратко обозначим аббревиатурой А1.
Запитана антенна от коаксиального провода радиуса 0,25 мм, выполненного из идеально-проводящего материала. Апертура антенны расположена на высоте 0,7 мм от идеально проводящей плоскости, играющей роль земли, и приведена на рис. 12. Зависимость коэффициента отражения от частоты для представленной антенны показана на рис. 13. Частотная зависимость коэффициента отражения антенны показана на рис. 14.
|
|
|
|
Рис.13. Частотная зависимость коэффициента отражения фрактальной апертуры А1. |
|
|
|
|
|
|
Рис. 14. Частотная зависимость импеданса Z для монопольной антенны А1. |
|
|
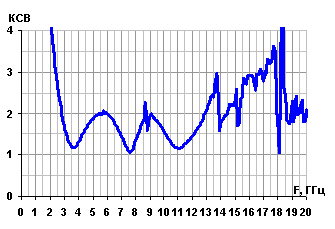
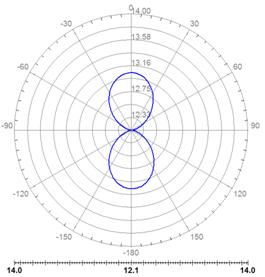
Результаты моделирования диаграммы направленности (ДН) антенны на некоторых частотах представлены на рис. 15. Достаточно хорошие результаты расчета КСВ (меньше 2), представленные на рис.16, также говорят о наличии повторяемости электродинамических параметров антенны А1 на разных частотах.
|
|
|
|
Рис. 15,а |
Рис. 15,б |
|
|
Рис. 16. Зависимость КСВ антенны А1 от частоты. |
|
Рис. 15,в Рис. 15. ДН антенны на сетке частот. |
Ширина полос пропускания фрактальной монопольной антенны А1 представлена в табл. 1. Из полученных результатов видно, что выбранная структура антенны действительно проявляет широкополосные и диапазонные свойства. Во второй колонке табл. 1 отображено процентное соотношение диапазона излучения антенны, в пределах которого значение ее КСВ менее 2, к частоте излучения.
Полоса пропускания на резонансных частотах антенны А1. Таблица 1.
|
Частота, ГГц |
|
|
3,90 |
100 |
|
7,5 |
66 |
|
11,1 |
72 |
2. Для построения кольцевого монополя второй итерации А2 использовался тот же алгоритм, что и для модели А1 – рис. 17.
|
В радиус каждой окружности вставлено шесть окружностей втрое меньшего радиуса, центры которых расположены в вершинах шестиугольника на расстоянии R*2/3 от первоначального радиуса. Седьмая окружность расположена в центре базовой окружности. Таким образом, полученная модель предложенной фрактальной антенны выглядит как на рис. 17. Запитка антенны выполнена так же, как и в предыдущих случаях, коаксиальной линией диаметра 0,5 мм. Толщина антенны, 0,4 мм, ширина колец 0,2 мм. Радиус внешней окружности R = 11 мм, R1 = R / 3, R2 = R / 9.
|
|
|
Рис. 17. Схема монопольной антенны А2. |
Результаты компьютерного моделирования коэффициента отражения представлены на рис. 18 и позволяют сделать вывод, что в обеих итерациях антенны прослеживается повторяемость полос пропускания антенны через равные промежутки частот.
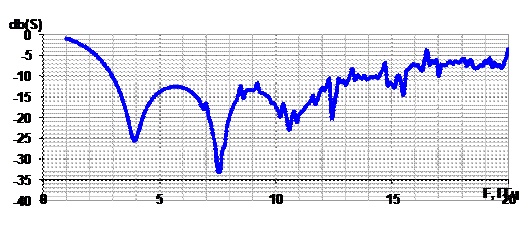
Рис. 18. Зависимость коэффициента отражения фрактальной антенны А2 от частоты.
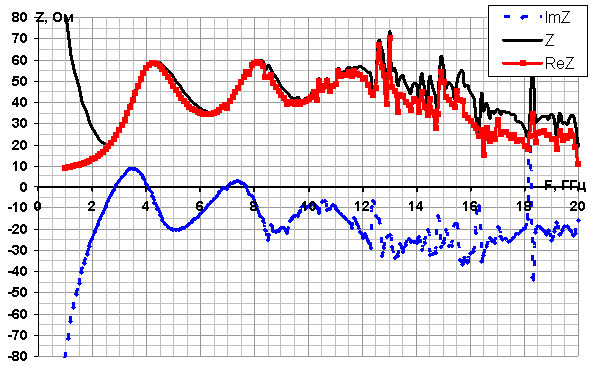
Исхода из рассчитанных значений коэффициента отражения и значений импеданса можно сделать предварительный вывод о том, что антенна должна обладать хорошими пропускающими свойствами на частотах вблизи 4,0 ГГц, 7,6 ГГц и 10,6 ГГц, а также 12,4 ГГц. График зависимости импеданса от частоты представлен на рис. 19.
|
|
|
Рис.19. Зависимость импеданса антенны А2 от частоты в диапазоне 0,1 - 20 ГГц. |
Как видно из графика зависимости импеданса, анализируемая антенна А2 имеет резонансы на частотах 2,9ГГц (4,1); 7,1 ГГц (7,7). Для этих частоты были смоделированы диаграммы направленности, которые представлены на рис. 20.
|
(а) |
(б) |
|
(в)
|
(г) |
|
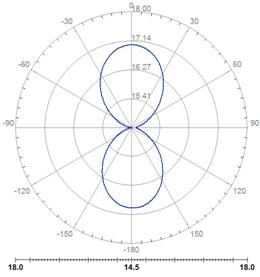
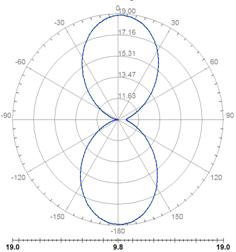
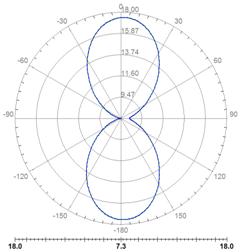
Рис. 20. Диаграмма направленности фрактальной антенны А2 на частотах: а) 2,9 ГГц; б) 4,1 ГГц; в) 7,1 ГГц; г) 7,7 ГГц. |
|
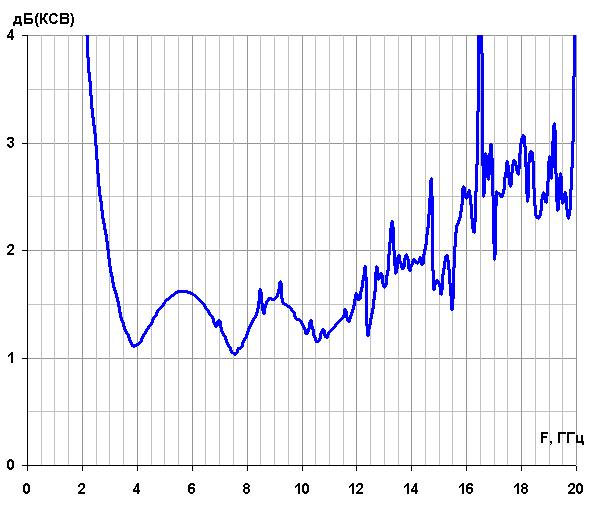
Зависимость КСВ антенны А2 от частоты представлена на рис. 21.
Рис. 21. Зависимость КСВ от частоты для фрактальной антенны А2.
Значения КСВ для выбранных выше частот приведены в табл. 2. В средней колонке табл. 2 показано соотношение предыдущей и текущей частоты излучения. В последней колонке показано значение КСВ антенны на резонансной частоте. Как видно, частоты находятся достаточно близко друг к другу (соотношение fn/fn-1 < 2); а значения КСВ менее 2 позволяют сделать вывод о хорошей согласованности структуры антенны А2.
Кроме того, в табл. 3 представлено соотношение диапазона излучающих частот к резонансной частоте. Как видно из результатов на некоторых частотах этот диапазон соответствует значениям более 50%. На основании этого можно предположить наличие широкополосных свойств фрактальной антенны на основе предложенных кольцевых структур.
Зависимость значений КСВ от частоты для антенны А2. Таблица 2.
|
Частота, ГГц |
fn/fn-1 |
КСВ |
|
2,9 |
- |
2,05 |
|
4,1 |
1,41 |
1,15 |
|
7,1 |
1,73 |
1,24 |
|
7,7 |
1,08 |
1,09 |
Ширина полосы пропускания на резонансных частотах антенны А2. Таблица 3.
|
Частота, ГГц |
|
|
4,1 |
87 |
|
7,7 |
52 |
Отметим, что в зарубежной литературе встречаются различные виды кольцевых структур, алгоритмической основой которых также является внедрение в базовую структуру окружностей с меньшим радиусом. Отличием в нашем случае является способ упаковки элементов каждой итерации и соотношение размеров предыдущей и последующей итерации в виде 1 к 3.
Уникальной особенностью фрактальных антенн является теоретически бесконечное уплотнение ограниченной области пространства геометрий антенны, и как результат - дополнительные резонансные частоты в диапазоне длин волн, часто значительно превышающих геометрические размеры фрактальной структуры. На сегодняшний день не существует строгой электродинамической теории, объясняющей и предсказывающей достаточно уникальные свойства структур, построенных на основе фрактальных множеств. Но все попытки использовать геометрические фракталы в реальных задачах радиофизики подразумевают под собой ограничение числа итераций построения фрактала, что, по сути, означает использование предфрактала. Под предфракталом следует понимать структуру с конечным порядком итерации или множество, имеющее свойство самоподобия в конечных масштабах (см. рис. 2).
7.4. Метод дробного интегро-дифференцирования в классической электродинамике
В [13, 31] представлен один из первых способов
введения дробного интегро-дифференцирования в основные уравнения
электродинамики материальных сред[1].
Как хорошо известно, центральное место в современном дробном исчислении
занимают интегро-дифференциальные операторы Римана-Лиувилля и Капуто [2,
3,
13]. Оператор дробного интегро-дифференцирования Римана-Лиувилля порядка
![]() с началом в
точке s удобно представить в следующем виде:
с началом в
точке s удобно представить в следующем виде:
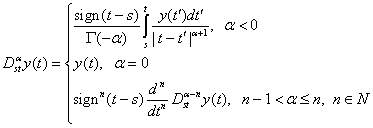 , (1)
, (1)
где ![]() – гамма-функция Эйлера.
– гамма-функция Эйлера.
Оператор Капуто (регуляризованная дробная производная) определяется с помощью равенства
![]() . (2)
. (2)
Связь между операторами Римана-Лиувилля и Капуто дается соотношением
![]() (3)
(3)
Если выполняется равенство ![]() , то операторы Римана-Лиувилля и
Капуто тождественны
, то операторы Римана-Лиувилля и
Капуто тождественны ![]() .
При целочисленном значении параметра
.
При целочисленном значении параметра ![]() эти операторы также совпадают между собой
и совпадают с обычными производными целого порядка.
эти операторы также совпадают между собой
и совпадают с обычными производными целого порядка.
В [13, 31] получена система уравнений Максвелла в дробных производных:
![]() ,
, ![]() , (4)
, (4)
![]() ,
, ![]() . (5)
. (5)
Векторный потенциал ![]() вводится стандартно
вводится стандартно
![]() . (6)
. (6)
Подставляя (6) в первое уравнение (4), получим
![]() . (7)
. (7)
Так как ротор от градиента любой скалярной функции равен нулю, то в (7) выражение в скобках равно градиенту этой функции. Стало быть
![]() , (8)
, (8)
где ![]() – скалярный потенциал.
– скалярный потенциал.
Несложно убедиться, что выражению (8) отвечают следующие соотношения калибровочной инвариантности
![]() ,
, ![]() , (9)
, (9)
где f – произвольная скалярная функция.
После подстановки (6) и (8) в уравнения (5) находим
![]() , (10)
, (10)
![]() . (11)
. (11)
Далее, не ограничивая общности, примем калибровку
![]() . (12)
. (12)
С использованием (12) из (10) и (11) получаются следующие уравнения для векторного и скалярного потенциалов:
![]() , (13)
, (13)
![]() , (14)
, (14)
где ![]() – скорость света в вакууме.
– скорость света в вакууме.
Уравнения (13) и (14) представляют собой уравнения с
изменяющимся типом: при ![]() – гиперболический тип; при
– гиперболический тип; при ![]() – параболический тип.
Такие уравнения в литературе называют диффузионно-волновыми уравнениями. Их
решение можно получить методом функции Грина. В отсутствие зарядов и токов из (13)
и (14) получаются однородные уравнения с частной производной дробного порядка.
В отличие от классического случая – решения Даламбера, решениями этих уравнений
уже не могут быть произвольные функции. С физической точки зрения это означает,
что протекающая по определенным правилам пространственно-временная эволюция
заряженных частиц будет накладывать ограничения на характер порождаемого
электромагнитного поля.
– параболический тип.
Такие уравнения в литературе называют диффузионно-волновыми уравнениями. Их
решение можно получить методом функции Грина. В отсутствие зарядов и токов из (13)
и (14) получаются однородные уравнения с частной производной дробного порядка.
В отличие от классического случая – решения Даламбера, решениями этих уравнений
уже не могут быть произвольные функции. С физической точки зрения это означает,
что протекающая по определенным правилам пространственно-временная эволюция
заряженных частиц будет накладывать ограничения на характер порождаемого
электромагнитного поля.
Проанализируем свойства свободного электромагнитного
поля в диэлектрике с постоянными ![]() и
и ![]() , исходя из диффузионно-волнового
уравнения. Для этого запишем одномерное уравнение дробного порядка
, исходя из диффузионно-волнового
уравнения. Для этого запишем одномерное уравнение дробного порядка
![]() , (15)
, (15)
где под функцией ![]() понимается A или
понимается A или ![]() . Уравнение (15) – линейное,
и его частное решение представимо в виде
. Уравнение (15) – линейное,
и его частное решение представимо в виде
![]() , (16)
, (16)
где z(t) – неизвестная функция, ![]() – комплексная амплитуда, k
– компонента волнового вектора в направлении x. Подставляя
(16) в (15), получаем уравнение
– комплексная амплитуда, k
– компонента волнового вектора в направлении x. Подставляя
(16) в (15), получаем уравнение
![]() , (17)
, (17)
где ![]() – безразмерная частота. Решение уравнения
(10.128) ищется обычным способом в виде степенного ряда [27, 155]. Частным решением
уравнения (17) является функция:
– безразмерная частота. Решение уравнения
(10.128) ищется обычным способом в виде степенного ряда [27, 155]. Частным решением
уравнения (17) является функция:
![]() ,
, ![]() , (18)
, (18)
где ![]() – функция Миттага-Леффлера.
– функция Миттага-Леффлера.
Из (16) и (18) находим
![]() . (19)
. (19)
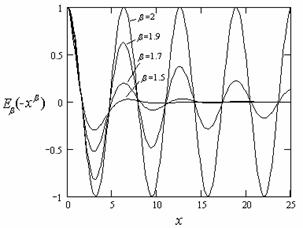
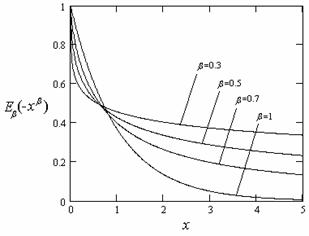
На рис. 22 в качестве примера показаны графики функции
![]() . Если в (19) параметр
. Если в (19) параметр ![]() находится в интервале от 1/2 до 1, то по
переменной t будем иметь периодическую функцию с частотой
находится в интервале от 1/2 до 1, то по
переменной t будем иметь периодическую функцию с частотой ![]() (рис. 22,а).
Если параметр
(рис. 22,а).
Если параметр ![]() находится
в интервале от 0 до 1/2, то функция становиться монотонно убывающей (рис. 22,б).
Параметры
находится
в интервале от 0 до 1/2, то функция становиться монотонно убывающей (рис. 22,б).
Параметры ![]() и
и ![]() ответственны за
скорость убывания.
ответственны за
скорость убывания.
|
(а) |
(б) |
|
Рис. 22. Графики функции Миттага-Леффлера при различных
значениях параметра |
|
Для наглядной интерпретации решения (19) выделим из
него предельные случаи. При ![]() (гиперболический случай), пользуясь тем
что
(гиперболический случай), пользуясь тем
что
![]() , (20)
, (20)
для решения уравнения (15) запишем
![]() .
(21)
.
(21)
Решение вида (21) определяет плоскую монохроматическую волну, являющуюся периодической функцией обеих переменных x и t.
При ![]() (параболический случай) имеем
(параболический случай) имеем
![]() , (22)
, (22)
![]() .
(23)
.
(23)
Решение (23) является периодическим лишь по переменной x. Его также можно понимать как плоскую волну, но с убывающей со временем амплитудой. При этом время, за которое амплитуда поля уменьшается в е раз, будет равно
![]() , (24)
, (24)
где ![]() .
.
Таким
образом, в нашем случае дробное интегродифференцирование и, соответственно,
феноменологический параметр ![]() , учитывают влияние фрактальных свойств движения
зарядов в диссипативной среде на создаваемое электромагнитное поле. При
уменьшении
, учитывают влияние фрактальных свойств движения
зарядов в диссипативной среде на создаваемое электромагнитное поле. При
уменьшении ![]() происходит
затухание электромагнитных волн, причем при медленном диффузионном блуждании (
происходит
затухание электромагнитных волн, причем при медленном диффузионном блуждании (![]() ) затухание имеет
степенную асимптотику
) затухание имеет
степенную асимптотику ![]() , свойственную для многих фрактальных
систем [2, 3, 13].
, свойственную для многих фрактальных
систем [2, 3, 13].
Отметим, что попытка записать волновые уравнения для
электромагнитных полей через дробные производные предпринималась и ранее.
Однако предположение о принадлежности функций ![]() и
и ![]() к классу Липшица-Гельдера не дает
оснований для замены простых производных на дробные производные Римана-Лиувилля
в исходных уравнениях Максвелла. Остальные детали и следствия подробно изложены
в работах [13, 31].
к классу Липшица-Гельдера не дает
оснований для замены простых производных на дробные производные Римана-Лиувилля
в исходных уравнениях Максвелла. Остальные детали и следствия подробно изложены
в работах [13, 31].
7.5. Фрактальные радиопоглощающие материалы и покрытия.
Фрактальные фотонные и магнонные кристаллы
Современные и перспективные радиопоглощающие покрытия и материалы должны обеспечивать поглощение широкого спектра электромагнитного излучения при произвольных углах зондирования и поляризации падающего излучения. С этой точки зрения наиболее перспективный путь – применение фрактальных искусственных композитов и метаматериалов, которые можно отнести к «интеллектуальным» или «умным» [2 – 4, 9 – 11, 13, 25, 27]. Помимо прямого назначения, они могут иметь разнообразное функциональное назначение.
Расчет коэффициентов отражения и пропускания таких материалов можно производить по методикам, изложенным в монографиях [2, 3]. Затем решается обратная задача, т.е. определяются эффективные диэлектрические и магнитные проницаемости фрактальной многослойной среды, которые могут быть и тензорами в случае анизотропных материалов. При этом необходимо использовать многократное обращение к прямой задаче.
Применение рекурсивного процесса позволяет, в принципе, создавать самоподобную иерархическую структуру, вплоть до отдельных проводящих дорожек в микросхеме и в наноструктурах. При этом необходимо учитывать и научиться рассчитывать взаимное и коллективное влияние всех электромагнитных полей со всеми компонентами микросхемы: проводящие дорожки, полупроводник, диэлектрик и т.д.
Фрактальные фотонные и магнонные кристаллы обладают целым рядом преимуществ перед своими классическими аналогами и являются принципиально новыми средами для передачи информации. Традиционные материалы с фотонными запрещенными зонами (ФЗЗ) используют брэгговское рассеяние, чтобы создать запрещенные зоны. Естественным следствием брэгговского механизма рассеяния является то, что толщина и поперечные размеры фотонных кристаллов должны составлять несколько длин волн.
Частотно-избирательные поверхности (ЧИП) селективно отражает электромагнитную волну заданной частоты. Они функционируют по принципу собственного резонанса ряда взаимодействующих металлических элементов, расположенных периодически. Системы ФЗЗ и ЧИП работают обычно в одном единственном частотном диапазоне с подходящей длиной волны, затухающей в объеме периодически расположенных базовых функциональный блоков.
Применение планарных проводящих фракталов дает возможность создавать сложные отражающие и пропускающие зоны в широком диапазоне частот. В этом случае фрактальная структура может быть сверхволновой. При конструировании фрактальных фотонных и магнонных кристаллов удобны детерминированные геометрические фракталы, которые имеют легко прогнозируемые характеристики и могут быть достаточно просто сгенерированы. Именно они и применяются чаще всего во фрактальных антеннах и аналогичных устройствах. Анализ результатов численного моделирования [3, 9 – 11, 13] показал, что электромагнитная волна возбуждает токи в металлических проводниках фрактала, амплитуда которых достигает максимума в диапазоне сильно отражающих частот. Фаза тока по отношению к фазе падающей волны всякий раз испытывает прыжок на величину π, когда рабочая частота переходит через точки, определяемые максимальными коэффициентами отражения, указывая на резонансное поведение.
Фрактал N-го порядка
должен теоретически иметь N
собственных резонансов. Каждый резонанс определяется током возбуждения в
проводящих линиях определенного порядка итераций, который течет по направлению
к структурам более высокого порядка. Всегда желательно, чтобы коэффициент отражения/прохождения
фрактальной структуры можно было регулировать с помощью внешней «ручки
управления». Каждый сегмент линии в фрактале соединен друг с другом. Вторичным
источником может быть внешний электрический ток, который подводится к
центру линии первого уровня с определенной фазой. Модулирование коэффициента
пропускания определяется разностью фаз (или временной задержкой ![]() принимаемого сигнала
относительно основного падающего пучка) между падающей волной и подпитывающим
током.
принимаемого сигнала
относительно основного падающего пучка) между падающей волной и подпитывающим
током.
В этом случае мы можем говорить о моделировании интеллектуальных покрытий с целенаправленным управлением их характеристиками рассеяния или полем прошедшей волны в широкой полосе частот. При наложении двух идентичных фрактальных образцов, когда один повернут на 900 относительно другого, можно получить инвариантную относительно вращения структуру. Таким образом, такая «активная» фрактальная структура может моделировать полное отражение, не зависящее от угла падения и типа поляризации, что обычно является характерной особенностью 3D фотонных кристаллов.
Следует отметить, что размеры
традиционного 3D фотонного кристалла должны составлять, по
крайней мере, несколько длин волн, прежде чем он сможет полностью проявлять
свои ФЗЗ свойства. Таким образом, для волны с частотой 1 ГГц толщина структуры
должны быть порядка 1 метра. С другой стороны, плоские фрактальные
структуры таковы, что их полоса пропускания ![]() f/f0, определяемая закона подобия, (
f/f0, определяемая закона подобия, (![]() f/f0
f/f0 ![]() полоса запрещенной
зоны/середина запрещенной зоны и
полоса запрещенной
зоны/середина запрещенной зоны и ![]() f/f0 ~ 5% для одной фрактальной пластины) может быть значительно
увеличена с помощью наложения друг на друга одинаковых фракталов. Увеличение
толщины фрактальных пластин приводит к возрастанию крутизны границ полос
пропускания. Полосы ослабления также могут быть увеличены с помощью более
широких металлических проводников фрактальных пластин.
f/f0 ~ 5% для одной фрактальной пластины) может быть значительно
увеличена с помощью наложения друг на друга одинаковых фракталов. Увеличение
толщины фрактальных пластин приводит к возрастанию крутизны границ полос
пропускания. Полосы ослабления также могут быть увеличены с помощью более
широких металлических проводников фрактальных пластин.
Эмпирическая формула для резонансных длин волн фрактальной структуры N-го порядка имеет вид:
![]() , (25)
, (25)
где ![]() = (
= (![]() +1)/2,
+1)/2, ![]() - параметры,
определяемые из эксперимента,
- параметры,
определяемые из эксперимента, ![]() - максимальная длина линии i-й
итерации.
- максимальная длина линии i-й
итерации.
Прямым следствие уравнения (25) является то, что резонансные длины волн могут быть намного больше, чем размеры образца. Это происходит потому, что низкочастотный резонанс определяется самой длинной металлической линией во фрактале, а такая линия просто намного длиннее, чем линейные размеры самого фрактала. Это придает фракталу его “сверхволновые” свойства, т.е. фрактальная пластина может эффективно отражать электромагнитные волны с длинами, намного большими, чем поперечные размеры. Сверхволновые свойства означают, что фрактальная пластина может действовать как компактный отражатель. Для таких микро- и нанотехнологий автором с учениками разработаны алгоритмы и программы, позволяющие рассчитывать различные конфигурации фрактальных структур рассматриваемых кристаллов.
Для управляемых интеллектуальных покрытий также можно использовать принцип реконфигурируемых фрактальных антенных решеток с электронной коммутацией подрешеток, подробно изложенный в монографиях [2, 3]. Многополосный режим функционирования, перекрытие обширного спектрального диапазона и полосы пропускания, соответствующие длинам волн, которые значительно больше размеров образцов, делают фрактальные пластины чрезвычайно интересной и полезной в практических приложениях частотно-избирательной средой.
7.6. Фрактальные частотно – избирательные поверхности и объемы
На основе исходных предпосылок из пп. 7.1 – 7.3 и 7.5 - 7.6 данной статьи рассмотрим приоритетные в России результаты по моделированию фрактальных частотно - избирательных структур. Приведенные далее результаты опираются на работы [38, 39]; расчеты выполнены совместно с аспирантом Е.Н. Матвеевым.
Были исследованы электродинамические свойства некоторых типов фрактальных частотно-избирательных поверхностей на основе «Дерева Кейли» (рис. 9) в САПР Antsoft HFSS. Для моделирования двух пластин с выбранной фрактальной геометрией “Дерево Кейли” 6-го порядка, мы развернули их относительно друг друга на 90º, как показано на рис. 23. Расстояние между пластинами составляло 3 мм. Фрактальная структура облучалась плоской волной с вектором E, параллельным оси 0Х.
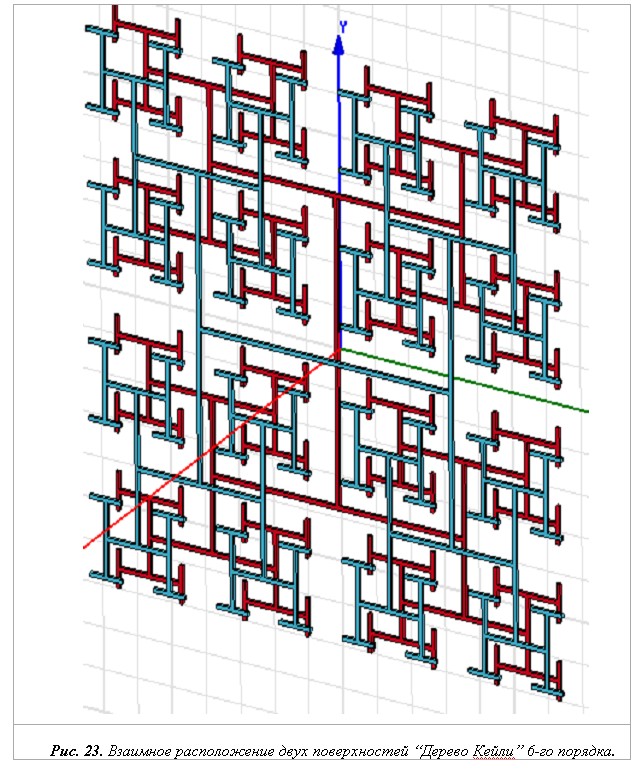
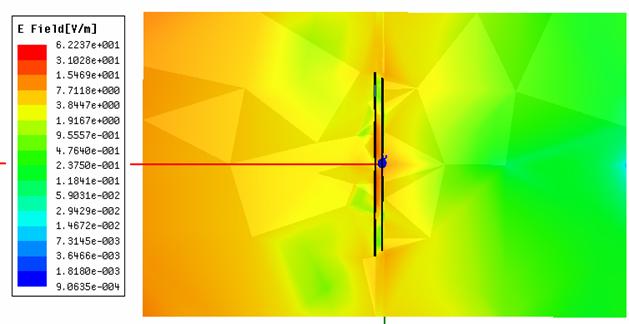
Распределения поля до и после исследуемой фрактальной поверхности на частоте 1 ГГц представлены на рис. 24.
|
|
|
Рис. 24. Распределение поля в плоскости z0y на частоте 1 ГГц. |
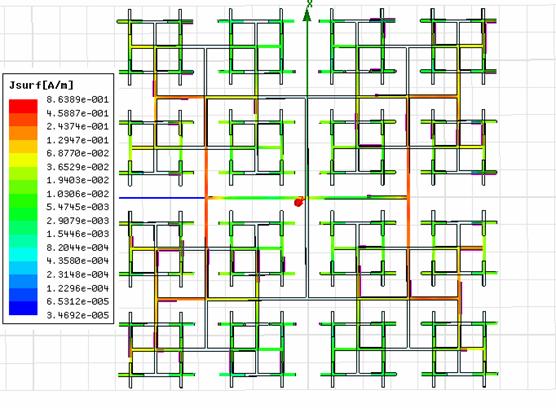
Распределение токов по поверхности двух фрактальных структур показывает наличие токов в элементах наибольшей длины (рис. 25)
|
|
|
Рис. 25. Распределение тока по поверхности фрактальных структур на частоте 1ГГц. |
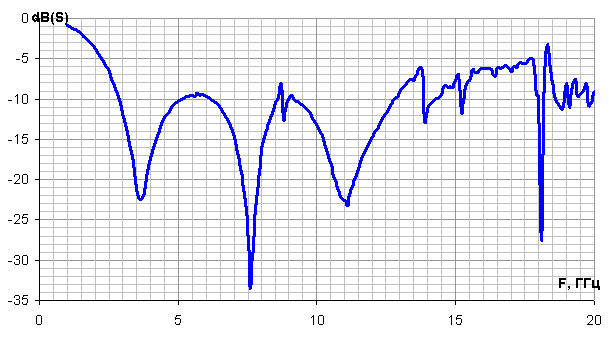
В результате расчетов коэффициента пропускания и отражения были получены частотные характеристики, представленные на рис. 26.
|
(а) |
|
(б) |
|
Рис. 26. Зависимость коэффициента пропускания (а) и коэффициента отражения (б) двухслойной фрактальной структуры “Дерево Кейли” 6-го порядка от частоты. |
По сравнению с классическими частотно-избирательными структурами, где присутствует в основном один диапазон пропускания и отражения электромагнитных волн, в двухслойной фрактальной пластине на основе “Дерева Кейли” 6-го порядка мы наблюдаем наличие нескольких самоподобных окон пропускания и отражения [2 – 4, 9, 10, 13, 25, 27, 39]. Данные окна, аналогично фрактальной пластине, обладают свойством самоподобия или скейлинга. Каждый элементарный участок “Дерева Кейли” вносит свой вклад в общую картину распространения и отражения электромагнитных волн.
Таким образом, данные численных экспериментов позволяют сделать вывод о многодиапазонности частотно-селективных поверхностей, синтезированных на основе фрактальных множеств. Кроме того, такие фрактальные структуры можно использовать как радиолокационные экраны, искажающие радиопортреты исследуемых объектов [2 – 4].
8. Скейлинг шероховатого слоя и фрактальные сигнатуры в задачах оценки
микрорельефа обработанных поверхностей
В связи с интенсивным развитием методов обработки методов обработки концентрированными потоками энергии – КПЭ (лазерной, плазменной, электроэрозионной), а также нанотехнологий (химическая сборка, золь – гель процессы, парофазное осаждение металлов, атомно–слоевая эпитаксия), возникают значительные трудности в описании и оценке шероховатости профильным методом [40]. В этих случаях форма элементов шероховатости, их распределение на площади обработки сильно отличается (рис. 27) от традиционного представления о них, сформированного в рамках процесса обработки резанием, как о периодическом чередовании «выступов» и «впадин», описываемых в рамках Евклидовой геометрии.
|
Название |
Элементы рельефа |
Название |
Элементы рельефа |
|
Грибообразный |
|
Лунки |
|
|
Т - образный |
|
Глобулы |
|
|
Пики |
|
Висперы (глобульно – висперный) |
|
|
Сплэты |
|
Гребни |
|
|
Ботироидальные |
|
Муар |
|
Рис. 27. Виды элементов рельефа микроповерхностей.
Следовательно, проблемы формирования качества поверхности, и в частности, такой важнейшей его характеристики как шероховатость, приобретают в настоящее время особую актуальность в связи с созданием новых технологий обработки материалов. Эти проблемы отчетливо проявляются в области нанотехнологий, для которых топология шероховатостей рассматривается не как вторичная характеристика, являющаяся “откликом” структуры поверхностного слоя на воздействие того или иного физического процесса (как в обработке резанием, например), а как свойство самой структуры, тем более, что размеры таких слоев сопоставимы с длиной свободного пробега в них электронов.
Автором с учениками было доказано [2, 3, 9, 10, 40] существование на уровне микрорельефа таких обработанных поверхностей фрактальных кластеров с распределением неровностей по степенным законам с тяжелыми хвостами (в качестве примера - рис. 28).
|
(а)
|
(б)
|
|
(в)
|
|
Рис. 28. Фрактальный анализ поверхности образца: а) 2D - изображение образца, обработанного алмазным точением с последующим оксидированием; б) фрактальная сигнатура образца; в) поле и гистограмма локальных фрактальных размерностей (обратить внимание на тяжелый хвост распределения (!)).
Наличие фрактальности в таких различных средах можно контролировать, в частности, по изменению скин–эффекта и импеданса. Именно пространственная/временная эволюция тока позволяет электромагнитному полю «прощупать» фрактальные характеристики (фрактальные сигнатуры) исследуемой физической среды. Скейлинговые модели шероховатого слоя поверхности твердого тела можно представить в виде эквивалентных электрических схем, имеющих вид, например, канторовой пыли и т.д. [2 – 4, 9 – 11, 13, 25].
Таким образом, автор в 2008 г. предложил для широкого обсуждения еще одну новую концепцию, а именно, “Скейлинг шероховатого фрактального слоя и нанотехнологии”.
9. Фрактальные импедансы и моделирование дробных операторов. Первый
фрактальный конденсатор
На практике довольно часто, как отмечено выше, сумма случайных величин сходится не к гауссовским, а к устойчивым или «Леви – Парето» распределениям с тяжелыми хвостами. У таких распределений функция распределений является «широкой». Это приводит к тому, что некоторые моменты такого распределения формально будут бесконечными. Моделирование распределенных по Леви - Парето случайных величин приводит к процессам аномальной диффузии, описываемой дробными производными по пространственным и/или временным переменным [2, 3, 13]. По сути дела, уравнения с дробными производными учитывают эффекты памяти и нелокальности и описывают немарковские процессы с памятью.
Физическое моделирование дробных интегральных и
дифференциальных операторов позволяет на основе микро- и нанотехнологий
создавать радиоэлементы на пассивных элементах, моделирующие фрактальные
импедансы ![]() с
частотным скейлингом
с
частотным скейлингом
![]() , (26)
, (26)
где ![]() – угловая частота, Аa = const;
– угловая частота, Аa = const;
![]() – порядок
операции дробного интегро-дифференцирования, которую можно реализовать,
используя данный фрактальный импеданс вместо емкости в схеме классического
интегратора или дифференциатора; 0 <
– порядок
операции дробного интегро-дифференцирования, которую можно реализовать,
используя данный фрактальный импеданс вместо емкости в схеме классического
интегратора или дифференциатора; 0 < ![]() < 1;
< 1; ![]() – модуль или амплитудно-частотная
характеристика;
– модуль или амплитудно-частотная
характеристика; ![]() - фазочастотная характеристика,
представляющая собой постоянную величину при фиксированном показателе степени
- фазочастотная характеристика,
представляющая собой постоянную величину при фиксированном показателе степени ![]() .
.
Еще до выдвижения концепции фрактальных радиосистем, автору представлялось заманчивой идеей первым смоделировать фрактальный импеданс в виде “фрактального конденсатора”.
Для этого нами была создана модель импеданса ![]() в виде бесконечной
цепной (непрерывной) дроби. В случае конечной стадии построения эквивалентной
электрической схемы для RC -
цепочек, когда используем n-ую подходящую дробь к данной непрерывной дроби, можно
регулировать диапазоны частот, в которых будет наблюдаться степенная
зависимость импеданса вида
в виде бесконечной
цепной (непрерывной) дроби. В случае конечной стадии построения эквивалентной
электрической схемы для RC -
цепочек, когда используем n-ую подходящую дробь к данной непрерывной дроби, можно
регулировать диапазоны частот, в которых будет наблюдаться степенная
зависимость импеданса вида ![]() . В этом случае мы впервые реализуем на
практике в аналоговом и цифровом виде нелинейный «фрактальный конденсатор»
[2, 26], чем был чрезвычайно заинтересован Б. Мандельброт.
. В этом случае мы впервые реализуем на
практике в аналоговом и цифровом виде нелинейный «фрактальный конденсатор»
[2, 26], чем был чрезвычайно заинтересован Б. Мандельброт.
Элементы, реализующие зависимость вида (26), в литературе еще называют “элементы с постоянной фазой”, “фрактансы” или “фракторы”. В работах автора впервые введено (и получило полное признание у специалистов) для таких элементов (в том числе и фрактальных ЧИП, и миниатюрных фрактальных антенн) обобщенное название “фрактальные элементы” или “фрактальные импедансы”, которое более точно отражает их физический смысл [2 – 4, 9 – 11, 13, 16, 19, 22, 25 – 27, 38, 39][2].
К данному направлению следует также отнести целый массив задач моделирования микроэлектронных фрактальных импедансов для фрактальных радиоэлементов низкочастотных и высокочастотных диапазонов длин волн, которые проводятся автором в Казани.
Физически операторы дробного интегрирования играют роль своеобразных «фильтров», выделяющих только те составляющие, которые локализованы на фрактальных (дробных) множествах исследуемого процесса. Отметим, что в последнее время в научном мире интенсивно обсуждаются фрактальные объекты и процессы, имеющие отрицательные и комплексные дробные степени [9 – 11, 13, 19, 23, 24, 26].
10. Основные методы конструирования фрактальных импедансов и их
перспективные области применения
Большие возможности при конструировании фрактальных импедансов в микроминиатюрном исполнении предоставляют RC-элементы с распределенными параметрами (RC-ЭРП). Их методы создания и основные области применения рассмотрены в [11, 13, 26]. Перспективы применения RC-ЭРП необходимо в первую очередь связывать с теми свойствами и возможностями, которые нельзя получить на основе RC-элементов с сосредоточенными параметрами (RC-ЭСП). Возможно их применение и в том случае, когда решения на основе традиционной элементной базы по своим эксплуатационным характеристикам (занимаемой площади, надежности, возможности регулировки и др.) существенно уступают решениям, полученным при использовании RC-ЭРП.
Естественно, что невозможно рассмотреть все области применения RC-ЭРП для создания радиоэлектронных устройств, в научных исследованиях, в системах контроля и др. Проведем сравнительный анализ преимуществ замены RC-ЭСП на RC-ЭРП лишь в тех научно-технических областях, где, на наш взгляд, необходимость такой замены достаточно очевидна и может дать наибольший эффект.
1. Анализ отечественной и зарубежной литературы показывает, что число работ, посвященных применению дифференциальных уравнений дробного порядка для описания разнообразных процессов и объектов лавинообразно растет во времени. Увеличивается и число работ, посвященных разработке аналоговых устройств дробного интегродифференцирования (ДИД), при помощи которых в режиме реального времени можно выполнять интегрирование дифференциальных уравнений дробного порядка, производить обработку сигналов, создавать системы управления объектами и процессами фрактальной природы и т.п. Более подробно – см. [11, 26].
Интеграторы и дифференциаторы дробного порядка можно
построить по таким же схемам, как и традиционные интеграторы и дифференциаторы
целого порядка на операционных усилителях (ОУ), но конденсатор в них заменяют
двухполюсником с фрактальным импедансом ![]() и частотным скейлингом,
удовлетворяющим уравнению (26). Как известно, передаточные функции таких
интеграторов и дифференциаторов представляют собой отношения импеданса элемента
с постоянной фазой (ЭПФ) к величине сопротивления R резистора
с сосредоточенными параметрами, включаемого на входе интегратора или в цепи
обратной связи ОУ дифференциатора.
и частотным скейлингом,
удовлетворяющим уравнению (26). Как известно, передаточные функции таких
интеграторов и дифференциаторов представляют собой отношения импеданса элемента
с постоянной фазой (ЭПФ) к величине сопротивления R резистора
с сосредоточенными параметрами, включаемого на входе интегратора или в цепи
обратной связи ОУ дифференциатора.
Тогда с учетом (26) для них можно записать следующие выражения:
![]() , (27)
, (27)
![]() . (28)
. (28)
Для случая, когда ![]() = 1, уравнение (27) соответствует
передаточной функции интегратора целого порядка, а уравнение (28) –
дифференциатора целого порядка. Для
= 1, уравнение (27) соответствует
передаточной функции интегратора целого порядка, а уравнение (28) –
дифференциатора целого порядка. Для ![]() = 0 схемы превращаются в масштабирующие
усилители. При 0 <
= 0 схемы превращаются в масштабирующие
усилители. При 0 < ![]() <
1 выражения (27) и (28) будут представлять передаточные функции интегратора и
дифференциатора дробного порядка соответственно.
<
1 выражения (27) и (28) будут представлять передаточные функции интегратора и
дифференциатора дробного порядка соответственно.
В отличие от традиционного подхода, при котором ЭПФ
представляет цепь на ЭСП, более эффективно задачу реализации ЭПФ произвольного
порядка можно решить с помощью разработанных методов анализа и синтеза RC-ЭРП
[11, 26]. Постоянство фазо-частотной характеристики (ФЧХ) входного
сопротивления, отличного от 45° (a = ½)
в широком диапазоне частот можно получить, синтезируя определенные законы
изменения ширины или удельных параметров слоев одномерно неоднородных (ОН) RC-ЭРП.
Эту же задачу можно решить формированием RC-ЭРП из нескольких одномерно
однородных (ОО) R1-C1-R-C2-R2 ЭРП, дальнейшим синтезированием ЭПФ с заданным
значением ![]() и
изменений схем включения и параметров их слоев.
и
изменений схем включения и параметров их слоев.
ЭПФ можно получить и на основе фрактальных двумерно однородных (ДО) RC-ЭРП с топологией резистивного слоя или контактных площадок в виде одного из регулярных геометрических фракталов (стержни Кантора, ковер Серпинского, снежинка Коха и т.д.).
2. Имеющийся опыт формирования моделей фрактальных процессов и объектов, описываемых дифференциальными уравнениями дробного порядка, на основе цепей из RC-ЭСП свидетельствует о том, что структура модели (виды и количество элементов, схема соединения и т.п.) должна однозначно отражать скрытые от наблюдателя физические закономерности, происходящие в исследуемом объекте. В результате, в отличие от синтеза ЭПФ, синтез аналоговых моделей на RC-ЭРП должен проводиться с учетом предполагаемых физических механизмов образования материалов (композитов, пластмасс, цементов и т.п.) или особенностей конструкции исследуемого объекта и характера протекающих в нем электрохимических процессов (электролитических конденсаторов, аккумуляторов, элементов интегральных микросхем и т.п.) [11, 26].
Преимущества моделей фрактальных процессов и объектов на основе RC-ЭРП, на наш взгляд, заключаются в следующем. Во-первых, RC-ЭРП представляет среду с распределенными параметрами, которая в большей степени отражает характер реальных физических объектов и процессов. Во-вторых, многослойные RC-ЭРП, например, можно использовать для моделирования процессов в слоистых средах (поглощающие и маскирующие покрытия, многослойные покрытия на поверхностях деталей, многослойные структуры биологических тканей, многослойные элементы интегральных схем и т.п.). В третьих, в отличие от моделей на RC-ЭСП, в которых для моделирования используется только два типа элементов (R и C), в многослойных RC-ЭРП появляется возможность использовать гораздо большее число различных элементов с распределенными параметрами [11, 26].
Использование для моделирования сложных фрактальных объектов многослойного “виртуального обобщенного” LRCG-ЭРП, анализ и синтез которого можно выполнять с помощью предлагаемого метода конечных распределенных элементов [11, 26], позволяет создать универсальную среду моделирования, пригодную для идентификации параметров достаточно сложных динамических систем дробного порядка.
3. Описание фрактальных процессов и объектов дифференциальными уравнениями дробного порядка привело к появлению контроллеров, адекватно реагирующих на реакции этих систем. В многочисленных работах в этом направлении можно найти теоретические и экспериментальные доказательства того, что применение регуляторов дробного порядка для управления динамическими процессами дробного порядка гораздо эффективнее, чем применение регуляторов целого порядка [11, 13, 26].
Примером практической реализации этого
подхода в построении систем управления является реализация идеи ПИД (PIlDm) - регулятора
дробного порядка (здесь обозначение образуется первыми буквами названий блоков,
входящих в регулятор: П (P) - пропорциональный; И (I)
– интегрирующий; Д (D) – дифференцирующий, ![]() – порядок интегратора,
– порядок интегратора, ![]() – порядок дифференциатора) в
виде так называемого CRONE-контроллера (Commande Robuste d’Ordre Non Entrier controller).
– порядок дифференциатора) в
виде так называемого CRONE-контроллера (Commande Robuste d’Ordre Non Entrier controller).
Однако аппаратная реализация таких PIlDm-регуляторов ориентирована на цифровые технологии. Очевидно, что для регулирования медленных процессов такой подход вполне оправдан. Но если скорости протекания процессов достаточно велики или процессы связаны с обработкой сигналов с частотами в сотни мегагерц, то недорогие аналоговые ПИД-регуляторы дробного порядка могут быть хорошей альтернативой дорогим высокоскоростным сигнальным процессорам.
Общим недостатком рассмотренных устройств является невозможность установления порядка ДИД в соответствии с требованиями к системе управления. Такая возможность появляется, если в качестве фрактального элемента использовать параметрические RC-ЭРП, удельное сопротивление материала резистивного слоя которого чувствительно к управляющему полю [11, 26].
4. Как известно, решение дифференциальных уравнений в режиме реального времени наиболее быстро осуществляют аналоговые вычислительные машины (АВМ). Однако, для решения ряда задач, связанных с управлением быстродвижущимися объектами, оптимизацией и моделированием систем управления, созданием комплексных тренажеров и др., возможности отдельно взятых АВМ и ЦВМ оказываются уже недостаточными. Поэтому наблюдается интерес к созданию гибридных вычислительных машин (ГВМ).
Введение в состав операционных блоков аналоговой части ГВМ интеграторов и дифференциаторов произвольного дробного порядка на основе RC-ЭРП, а также блоков аналогового вычисления специальных функций на их основе, позволило бы повысить быстродействие, обеспечить гибкость в выборе методов решения и конкурентоспособность на рынке специализированных ЭВМ.
5. Большинство процессов, протекающих в технических и природных системах, являются пространственно-временными скалярными или векторными полями самой различной природы. Измерение и контроль состояния таких систем играют основную роль в информационном обеспечении процессов управления техническими системами и сложными процессами современных производств.
Выбирая электрофизические и физико-химические параметры измерительной среды, можно добиться ее избирательной чувствительности к тем или иным измеряемым полям. Так, применяя в качестве компонентов, входящих в измерительную среду, термо-, фото-, тензо-, магниторезистивные, полупроводниковые и другие материалы, можно формировать прямую или косвенную чувствительность среды к теплофизическим, гидро- и газодинамическим, световым, силовым, электромагнитным и другим полям самой различной физической природы.
6. Перечень задач, которые можно решать, используя возможности RC-ЭРП, не ограничивается рассмотренными выше. Например, при анализе шумов полупроводниковых приборов с целью прогнозирования их надежности выполняется дробное дифференцирование при помощи лестничной RC-цепи, которую, очевидно, можно заменить на RC-ЭРП. Существует аппаратная реализация восстановления истинного сигнала на входе датчика путем дробного дифференцирования выходного сигнала, где дифференциатор строится на основе двухполюсных фрактальных RC-ЭРП. Рассматривается также возможность повышения эффективности криптографической защиты информации за счет использования устройств или алгоритмов, реализующих фрактальные функции.
Область применения дробного исчисления, а, следовательно, поле возможного применения RC-ЭРП все время расширяется [2 – 4, 9 - 11, 13, 25 – 27, 30]: сейсмический анализ, динамика двигательных нейронов глазодвигательных систем, упругое демпфирование, 1/f шумы, генераторы гармонических колебаний дробного порядка, дистанционное зондирование, новые фрактальные частотно-избирательные среды передачи информации и т.д.
11. Динамические фрактальные модели распространения и рассеяния волн
случайно-неоднородными средами
11.1. Динамические системы и волновые процессы
Радиолокационный сигнал, рассеянный земными покровами, обычно моделируется как случайный шумовой процесс. Однако прогресс в теории динамических систем (ДС) позволяет рассмотреть более детально эту проблему с других позиций. Под ДС подразумевают объект или процесс, для которого однозначно определено состояние или совокупность некоторых величин в заданный момент времени и задан детерминированный оператор эволюции. Притягивающее множество в фазовом пространстве ДС, характеризующееся режимом установившихся непериодических колебаний, называется странным аттрактором. Странный аттрактор имеет дробную фрактальную размерность D.
Теория случайных процессов опирается на эмпирический метод, позволяющий справиться с недостаточной информацией о физических источниках, ответственных за создание изучаемого явления, но эта теория ничего не говорит о причинах случайности. В соответствии с теорией ДС достаточно очень малого числа степеней свободы для создания детерминированного хаоса. Идея применения таких моделей для описания радиолокационного отклика очень привлекательна и способствует более глубокому пониманию природы рассматриваемого явления [2 – 4, 9 - 11, 13].
Ранее задачи дифракции волн на статистически неровной поверхности были преимущественно ориентированы на неровности одного масштаба. Затем было осознано, что многомасштабные поверхности дают более адекватные результаты. Сейчас можно уверенно утверждать, что физическое содержание теории дифракции, включающей многомасштабные поверхности, становится более четким при фрактальном подходе и выделении фрактальной размерности или фрактальной сигнатуры D как параметра. Более того, учет фрактальности, по нашим расчетам, значительно сближает теоретические и экспериментальные характеристики индикатрис рассеяния земных покровов в СВЧ – диапазоне. Этот факт всегда интерпретировался практиками (и продолжает интерпретироваться) как, в основном, результат чисто инструментальных погрешностей (!).
В последнее время возрос также интерес к исследованию
рассеяния волн неровными поверхностями, имеющими негауссовскую статистику.
Часто приводятся доводы, что пространственный коэффициент корреляции
рассеивающей поверхности ![]() не может быть экспоненциальным из-за
недифференцируемости соответствующего стохастического процесса. Иногда в этом
случае применяют регуляризирующую функцию в окрестности нуля. Более глубокое
физическое обоснование применимости недифференцируемых функций для
описания процессов рассеяния волн появилось лишь при внесении теории фракталов,
теории дробной меры, операторов дробного интегродифференцирования и скейлинговых
соотношений в данные задачи.
не может быть экспоненциальным из-за
недифференцируемости соответствующего стохастического процесса. Иногда в этом
случае применяют регуляризирующую функцию в окрестности нуля. Более глубокое
физическое обоснование применимости недифференцируемых функций для
описания процессов рассеяния волн появилось лишь при внесении теории фракталов,
теории дробной меры, операторов дробного интегродифференцирования и скейлинговых
соотношений в данные задачи.
Отметим, что гауссовская модель является параболической
вблизи угла падения ![]() ,
в то время как экспоненциальная модель – линейной. Фрактальная
поверхность предполагает наличие неровностей всех масштабов относительно
длины рассеиваемой волны. Особенности рассеяния волн фрактальной поверхностью
обусловлены ее недифференцируемостью. Поэтому фрактальный фронт волны,
являясь недифференцируемым, не имеет нормали. Тем самым исключаются понятия «лучевая
траектория» и «эффекты геометрической оптики». Однако хорды,
соединяющие значения характерных высот неровностей на определенных расстояниях
по горизонтали, все-таки имеют конечный среднеквадратичный наклон. В этом
случае вводят «топотезу» фрактальной хаотической поверхности; она равна
длине, на которой наклоны поверхности близки к единичным [2,
3].
,
в то время как экспоненциальная модель – линейной. Фрактальная
поверхность предполагает наличие неровностей всех масштабов относительно
длины рассеиваемой волны. Особенности рассеяния волн фрактальной поверхностью
обусловлены ее недифференцируемостью. Поэтому фрактальный фронт волны,
являясь недифференцируемым, не имеет нормали. Тем самым исключаются понятия «лучевая
траектория» и «эффекты геометрической оптики». Однако хорды,
соединяющие значения характерных высот неровностей на определенных расстояниях
по горизонтали, все-таки имеют конечный среднеквадратичный наклон. В этом
случае вводят «топотезу» фрактальной хаотической поверхности; она равна
длине, на которой наклоны поверхности близки к единичным [2,
3].
11.2. Фрактальные флуктуации миллиметровых волн в тропосфере
При проведении автором совместно с представителями ЦКБ
“Алмаз” натурных экспериментов были исследована и фрактальность флуктуаций сверхширокополосных
и простых сигналов на ММВ и СМВ в турбулентной тропосфере (в начале 80-х гг. XX в.
это было экзотикой) при стробировании дистанции по дальности [14,
23, 24].
Средняя скорость ветра при проведении натурных экспериментов равнялась 3![]() 0,5 м/c.
Простейшая обработка показала, что в летнее время (температура воздуха 200
– 250) на приземной трассе протяженностью около 150 м на высоте 10 м и длине волны излучения
0,5 м/c.
Простейшая обработка показала, что в летнее время (температура воздуха 200
– 250) на приземной трассе протяженностью около 150 м на высоте 10 м и длине волны излучения ![]() =8,6 мм для амплитудных
флуктуаций фрактальная размерность D
=8,6 мм для амплитудных
флуктуаций фрактальная размерность D![]() 1,63.
1,63.
В этом случае параметр Херста (коразмерность)
равен H![]() 0,37. В случае радиолокационного зондирования
фрактальная размерность повышалась до D
0,37. В случае радиолокационного зондирования
фрактальная размерность повышалась до D![]() 1,72
(H
1,72
(H![]() 0,28). При моросящем дожде фрактальная размерность
амплитудных флуктуаций уменьшалась до значений порядка D
0,28). При моросящем дожде фрактальная размерность
амплитудных флуктуаций уменьшалась до значений порядка D![]() 1,59
(H
1,59
(H![]() 0,41). Величина среднеквадратичного отклонения во всех
случаях не превышала значения 0,02. В экспериментах никогда не наблюдалась процессы
с D = 1,5. Таким образом, в процессе наших натурных
экспериментов наблюдались исключительно антиперсистентные процессы.
Необходимо отметить, что метод Херста – это исключительно устойчивый метод [1 –
4, 9 -
11, 13]. В его основе нет изначального предположения о гауссовских
распределениях. Для одномерного сигнала фрактальная размерность
0,41). Величина среднеквадратичного отклонения во всех
случаях не превышала значения 0,02. В экспериментах никогда не наблюдалась процессы
с D = 1,5. Таким образом, в процессе наших натурных
экспериментов наблюдались исключительно антиперсистентные процессы.
Необходимо отметить, что метод Херста – это исключительно устойчивый метод [1 –
4, 9 -
11, 13]. В его основе нет изначального предположения о гауссовских
распределениях. Для одномерного сигнала фрактальная размерность ![]() , характеризующая его
структурные свойства, при условии
, характеризующая его
структурные свойства, при условии ![]() связана следующим соотношением с
показателем Херста H = D – 1. Значение H = 0,5 соответствует
классическому броуновскому движению, являющимся марковским процессом.
связана следующим соотношением с
показателем Херста H = D – 1. Значение H = 0,5 соответствует
классическому броуновскому движению, являющимся марковским процессом.
В моделях случайного каскада, позволяющих
демонстрировать перемежаемость и получать скейлинговые законы, при
использовании преобразований Лежандра, часто возникают отрицательные
фрактальные размерности. В рамках процедуры ренормализации по Крамеру,
это просто означает, что коразмерность H больше трех, и вероятность ![]() встретить соответствующий скейлинг
стремится к нулю быстрее, чем
встретить соответствующий скейлинг
стремится к нулю быстрее, чем ![]() [24]. Отрицательную фрактальную
размерность D можно понимать как параметр, управляющий
скоростью разрежения последовательности множеств, сходящихся к пустому множеству.
[24]. Отрицательную фрактальную
размерность D можно понимать как параметр, управляющий
скоростью разрежения последовательности множеств, сходящихся к пустому множеству.
11.3. Странные аттракторы и фракталы в моделях рассеяния волн
растительным покровом
Автором с учениками было доказано экспериментально наличие странного аттрактора, управляющего радиолокационным рассеянием ММВ от растительности, гипотеза о чем была высказана нами еще в 1997 г. В качестве исходных экспериментальных данных используются результаты из [14], полученные на волне 2,2 мм при круговой поляризации излучения весной 1980 г. Исследуемая поверхность имела следующие биометрические характеристики: травяной покров с двумя характерными высотами 0,4 и 1,0 м; густота растительности около 500 стеблей/м2; среднее сечение стебля 0,04 см2, удельная биомасса 700 г/м2, степень покрытия поверхности примерно 20%.
При реконструкции данного
аттрактора по упорядоченным измерениям одной переменной необходимо построить
пространство вложения размерности ![]() , чтобы описать все возможные топологические
особенности аттрактора. Величина
, чтобы описать все возможные топологические
особенности аттрактора. Величина ![]() определяет число дифференциальных
уравнений 1-го порядка, необходимых для описания физического поведения
исследуемой ДС. Здесь
определяет число дифференциальных
уравнений 1-го порядка, необходимых для описания физического поведения
исследуемой ДС. Здесь ![]() -
операция выделения целой части D, а D - истинная фрактальная размерность аттрактора.
-
операция выделения целой части D, а D - истинная фрактальная размерность аттрактора.
Корреляционный интеграл C(r) является
нормированным на ![]() числом
пар точек, расстояние между которыми меньше r,
где r - размер ячейки разбиения фазового
пространства. Наклон линейного участка в логарифмических координатах
числом
пар точек, расстояние между которыми меньше r,
где r - размер ячейки разбиения фазового
пространства. Наклон линейного участка в логарифмических координатах ![]() определяет искомое
значение размерности D странного аттрактора.
определяет искомое
значение размерности D странного аттрактора.
На рис. 29 показаны экспериментальные зависимости C(r) от r для гауссовского шума и радиолокационных отражений от растительности без шума при угле падения волны 500. Одновременно на тех же диаграммах показаны вычисленные фрактальные размерности D в зависимости от значения размерности вложения m. Наиболее точную оценку D получаем при изломе зависимости D(m). Непосредственно для процесса отражения радиоволн растительностью размерность вложения m = 7. Когда уровень шума превосходит уровень полезного сигнала, процесс насыщения прекращается.
Значение фрактальной
размерности странного аттрактора по данным рис. 29 равно ![]() 2,8. Корреляционный интеграл C(r) можно также
использовать как средство разделения детерминированного хаоса и внешнего белого
шума. Для гауссовского шума (рис. 29) нет тенденции к насыщению. Поэтому ему
соответствует аттрактор бесконечной размерности. Это различие широко
используется при обработке временных реализаций неизвестной природы. Основным
ограничением в экспериментах при идентификации хаоса на фоне аддитивного шума
является отношение сигнал/шум. Минимальное отношение сигнал/шум оказалось
равным 10 дБ. Дальнейшее увеличение интенсивности шума вызывает расползание
аттрактора.
2,8. Корреляционный интеграл C(r) можно также
использовать как средство разделения детерминированного хаоса и внешнего белого
шума. Для гауссовского шума (рис. 29) нет тенденции к насыщению. Поэтому ему
соответствует аттрактор бесконечной размерности. Это различие широко
используется при обработке временных реализаций неизвестной природы. Основным
ограничением в экспериментах при идентификации хаоса на фоне аддитивного шума
является отношение сигнал/шум. Минимальное отношение сигнал/шум оказалось
равным 10 дБ. Дальнейшее увеличение интенсивности шума вызывает расползание
аттрактора.

В итоге были получены следующие значения: ![]() ;
; ![]() ;
; ![]() бит/c;
бит/c; ![]() 1,7 с при времени корреляции интенсивности
отраженного сигнала
1,7 с при времени корреляции интенсивности
отраженного сигнала ![]() 210
мс и скорости ветра 3 м/с. Следовательно, если текущие условия измеряются с
точностью до 1 бита, то вся предсказательная мощность во времени потеряется
примерно за 1,7 с. При этом интервал предсказания
210
мс и скорости ветра 3 м/с. Следовательно, если текущие условия измеряются с
точностью до 1 бита, то вся предсказательная мощность во времени потеряется
примерно за 1,7 с. При этом интервал предсказания ![]() интенсивности радиолокационного
сигнала превышает время корреляции примерно в 8 раз (!).
интенсивности радиолокационного
сигнала превышает время корреляции примерно в 8 раз (!).
Полученные результаты показывают, что для корректного
описания процесса рассеяния радиоволн требуется не более 5 независимых переменных.
На рис. 30 приведены зависимости D (фрактальные сигнатуры -
слева) и корреляционных интегралов (справа) исследуемых экспериментально
радиолокационных процессов рассеяния ММВ с ![]() = 2,2 мм березовым (1) и еловым (2
и 3) участками леса с
= 2,2 мм березовым (1) и еловым (2
и 3) участками леса с ![]() 2,6.
2,6.
|
Рис. 30. Зависимости D - слева и C(r) – справа для рассеяния ММВ лесом D |
Рис. 31. Показатель Херста H для флуктуаций ММВ, отраженных еловым участком леса. |
Расчеты показателя Херста (рис. 31) говорят, что в двух случаях из трех процесс рассеяния ММВ лесными массивами соответствует персистентному процессу c H > 0,5, т.е. процессу с памятью. Значения Н и их вариации важны при синтезе адаптивных фрактальных обнаружителей радиосигналов.
Предложенная автором динамическая фрактальная модель рассеяния электромагнитных волн земными покровами принципиально отличается от существующих классических моделей. Она имеет конечное число степеней свободы, описывает процессы негауссовского рассеяния, впервые вводит в рассмотрение интервал предсказания интенсивности принятого радиолокационного сигнала и его фрактальные характеристики (сигнатуры).
11.4. Рассеяние волн стохастической фрактальной поверхностью
В этой части исследований автором и аспирантом А.В. Лактюнькиным была применена частотно - ограниченная функция Вейерштрасса [1 – 4, 6 – 11, 13, 21], на которую налагается, естественно, меньше ограничений, чем на класс недифференцируемых функций. Данная модификация функции Вейерштрасса обладает как свойством самоподобия, так и все-таки конечным числом производных в пространственном диапазоне. Это позволяет выполнить аналитические и численные расчеты. Модифицированная двумерная диапазонно-ограниченная функция Вейерштрасса записывается в виде:
![]() , (29)
, (29)
Здесь ![]() - константа,
обеспечивающая единичную нормировку;
- константа,
обеспечивающая единичную нормировку; ![]() - параметр пространственно-частотного
масштабирования; 2 < D <
3; K – основное пространственное волновое число; N
и M – число гармоник;
- параметр пространственно-частотного
масштабирования; 2 < D <
3; K – основное пространственное волновое число; N
и M – число гармоник; ![]() - произвольная фаза, распределенная
равномерно в интервале [-π, π]. Функция (29) анизотропная в двух
направлениях, если M и
N не
очень велики. Поверхность на ее основе имеет достаточно много масштабов, а
шероховатость может изменяться в зависимости от рассматриваемого масштаба.
Усредненный коэффициент пространственной автокорреляции двумерной фрактальной поверхности
равен
- произвольная фаза, распределенная
равномерно в интервале [-π, π]. Функция (29) анизотропная в двух
направлениях, если M и
N не
очень велики. Поверхность на ее основе имеет достаточно много масштабов, а
шероховатость может изменяться в зависимости от рассматриваемого масштаба.
Усредненный коэффициент пространственной автокорреляции двумерной фрактальной поверхности
равен
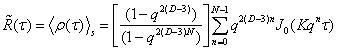 , (30)
, (30)
где ![]() - функция Бесселя первого рода нулевого
порядка.
- функция Бесселя первого рода нулевого
порядка.
Таким образом, из соотношений (29) и (30) мы можем
установить связь между усредненным интервалом корреляции ![]() и фрактальной размерностью D,
а также значением q. На рис. 32 показаны зависимости
и фрактальной размерностью D,
а также значением q. На рис. 32 показаны зависимости ![]() от значений q
и D соответственно
[21].
от значений q
и D соответственно
[21].
|
(а) |
(б) |
|
|
|
Рис.
32. Интервал корреляции |
|||
С увеличением D величина ![]() уменьшается более быстро для тех
же самых изменений q. Из данных рис. 32 видно, что величина
уменьшается более быстро для тех
же самых изменений q. Из данных рис. 32 видно, что величина ![]() монотонно спадает с
возрастанием значения D. Величина неровностей фрактальной поверхности в
основном управляется фрактальным параметром D.
монотонно спадает с
возрастанием значения D. Величина неровностей фрактальной поверхности в
основном управляется фрактальным параметром D.
Характерные примеры из
обширной базы данных трехмерных индикатрис рассеяния и их сечений,
рассчитанные в начале 2006 г. для длин волн ![]() мм,
мм, ![]() мм и
мм и ![]() см при разных значениях фрактальной размерности
D и изменяющейся геометрии рассеяния, показаны
на рис. 33, где
см при разных значениях фрактальной размерности
D и изменяющейся геометрии рассеяния, показаны
на рис. 33, где ![]() -
угол падения [21].
-
угол падения [21].
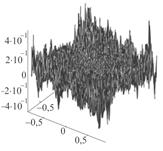
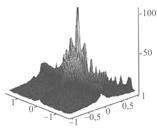
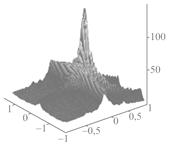
(а) (б)
(в)
Рис. 33. Фрактальная поверхность и индикатриса рассеяния g(θ2, θ3)
при θ1 = 10°:
а – фрактальная поверхность D = 2,2; N = M = 20; q = 2,7; б – g(θ2, θ3) для λ = 2,2 мм;
в – g(θ2, θ3) для λ = 8,6 мм.
На основе функции Вейерштрасса для одномерной фрактальной
рассеивающей поверхности были также рассчитаны зависимости модуля поля
рассеяния ![]() от
фрактальной размерности поверхности D и от угла
падения (рис. 34 и рис. 35 соответственно). Чем больше фрактальная размерность,
тем выше абсолютное значение поля рассеяния. Данное явление можно объяснить
увеличивающимся вкладом вторичного рассеяния на мелких неровностях по сравнению
с менее шероховатой поверхностью. При изменении угла падения поле рассеяния
меняется спонтанно, что объясняется хаотической структурой рассеивающей поверхности.
от
фрактальной размерности поверхности D и от угла
падения (рис. 34 и рис. 35 соответственно). Чем больше фрактальная размерность,
тем выше абсолютное значение поля рассеяния. Данное явление можно объяснить
увеличивающимся вкладом вторичного рассеяния на мелких неровностях по сравнению
с менее шероховатой поверхностью. При изменении угла падения поле рассеяния
меняется спонтанно, что объясняется хаотической структурой рассеивающей поверхности.
|
Рис. 34. Зависимость модуля поля рассеяния от фрактальной размерности для падающей
длины волны |
Рис. 35. Зависимость модуля поля рассеяния от угла падения. |
Дальнейшие исследования рассеяния волн
на фракталах будут продолжены нами в рамках расчета частотных функций
когерентности ![]() и
полосы когерентности Δfk в
виде:
и
полосы когерентности Δfk в
виде:
![]() =
=![]() , (31)
, (31)
в случае фрактального радиолокационного канала
зондирования [2, 3, 9,
10, 13 – 15, 41]. Для этого автором в [14, 41] были ранее
введены и рассчитаны обобщенные корреляторы полей обратного рассеяния ![]() .
.
Эффекты частотной корреляции модулированных волн,
рассеянных шероховатой поверхностью, особенно важны при оценках ширины спектра
зондирующих сложных сигналов, разноса частот в многочастотных радиосистемах и
полосы частот в случае передачи широкополосных сигналов, частотного усреднения
интенсивности волнового поля, искажений формы зондирующих сигналов, высоты
полета летательного аппарата и океанографических характеристик, фазы волны (так
называемая, фазовая проблема) и т.п. Частотная полоса когерентности ![]() , определяющая меру
коррелированности волн на двух различных частотах в любой момент времени.
Величина, обратная
, определяющая меру
коррелированности волн на двух различных частотах в любой момент времени.
Величина, обратная ![]() ,
представляет собой уширение импульса, обусловленное рассеяние на протяженной
шероховатой поверхности. Концепция полосы когерентности лежит в основе
правильности выбора ширины спектра зондирующих простых или сложных сигналов или
разноса частот в многочастотных системах радиолокационного зондирования и в
каналах связи с рассеянием.
,
представляет собой уширение импульса, обусловленное рассеяние на протяженной
шероховатой поверхности. Концепция полосы когерентности лежит в основе
правильности выбора ширины спектра зондирующих простых или сложных сигналов или
разноса частот в многочастотных системах радиолокационного зондирования и в
каналах связи с рассеянием.
11.5. Фрактальные характеристики радиотеплового излучения атмосферы
Миллиметровые волны активно взаимодействуют с газами
земной атмосферы, особенно с кислородом и водяным паром, а также с
гидрометеорными образованиями, к которым относятся дожди, облака, снегопады и
т.п. В результате этого взаимодействия ММВ сильно поглощаются и рассеиваются в
тропосфере. Ниже впервые рассмотрены фрактальные характеристики
реального процесса радиотеплового излучения на длине волны 8,2 мм[3].
Интенсивность радиотеплового излучения тропосферы, характеризуемая как
радиояркостная температура ![]() , измерялась радиометрическим методом на
длине волны
, измерялась радиометрическим методом на
длине волны ![]() = 8,2 мм.
= 8,2 мм.
На основе экспериментальных данных были восстановлены
фазовые портреты для каждой полученной серии и построены автокорреляционные
функции ![]() исследуемых
серий. Эмпирические распределения вероятностей значений радиотеплой
температуры, построенные на различных сериях (№№ 1 … 5) экспериментальных данных,
слабо различаются между собой.
исследуемых
серий. Эмпирические распределения вероятностей значений радиотеплой
температуры, построенные на различных сериях (№№ 1 … 5) экспериментальных данных,
слабо различаются между собой.
Анализ статистических характеристик радиотеплового излучения производился с помощью диаграммы Пирсона (рис. 36). Оказалось, что статистические характеристики серий № 1 и № 2 группируются в области законов распределений, близких к гауссовскому, с другой стороны, серии №№ 3 - 5 находятся в области степенных законов с тяжелыми хвостами. Таким образом, данный факт говорит о целесообразности использования именно фрактальной обработки [2 - 4]. Далее измерялись фрактальная размерность D и показатель Херста H - табл. 4.
Фрактальная обработка позволила установить, что в трех случаях (серии №№ 1 – 4) наблюдался антиперсистентный процесс; еще в одном случае наблюдался процесс, близкий к классическому броуновскому движению, являющимся марковским процессом (серия № 5).
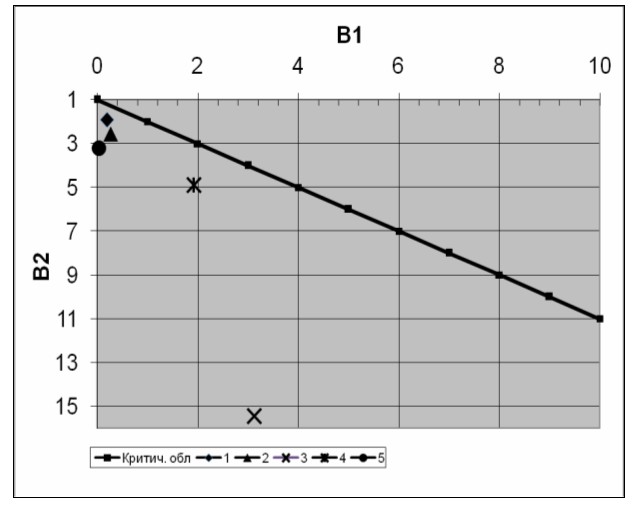
Рис. 36. Диаграмма Пирсона для серий радиотепловых измерений: серия 1 - чистая
тропосфера, 2 - кучево – дождевая облачность, 3 - слоисто – кучевые облака.
Фрактальные характеристики радиотеплового излучения. Таблица 4.
|
Номер серии |
Фрактальная размерность |
Показатель Херста H |
|
1 |
1,7746 |
0,2254 |
|
2 |
1,6509 |
0,3491 |
|
3 |
1,7172 |
0,2828 |
|
4 |
1,5190 |
0,4810 |
|
5 |
1,4943 |
0,5057 |
Таким образом, мы впервые ввели в научный обиход фрактальные характеристики радиотеплового излучения тропосферы в диапазоне ММВ. Дальнейшие исследования проводятся с целью определения фрактальных характеристик стохастического флуктуационного процесса, выделенного после удаления тренда из экспериментальных зависимостей. Этот метод предложен ранее автором при анализе эволюции отраженных импульсов ММВ, которые разделялись на две части: с гауссовской и негауссовской статистикой [14].
12. Авторская концепция фрактальных радиоэлементов и
фрактальных радиосистем
12.1. Фрактальный непараметрический обнаружитель радиолокационных
сигналов
Создание первого эталонного словаря фрактальных признаков классов целей и постоянное усовершенствование алгоритмического обеспечения явились основными этапами при разработке в ИРЭ им. В.А. Котельникова РАН первого в мире фрактального непараметрического обнаружителя радиосигналов (ФНОРС) в виде спецпроцессора – рис. 37 [3, 4, 8 – 11, 13, 16, 22, 25, 27] - (автор и к.ф.-м.н. В.А. Герман).
В схеме на рис. 37 приняты следующие обозначения: УВЧ – усилитель высокой частоты; СМ – смеситель; Г – гетеродин; ПФ – полосовой фильтр; УПЧ – усилитель промежуточной частоты; КД – квадратурный детектор (перенос спектра на нулевую частоту); Re, Im – действительная и мнимая квадратуры; АЦП – аналого – цифровой преобразователь; ЦП – центральный процессор; ОЗУ – оперативное запоминающее устройство; УВВ – устройство ввода/вывода (монитор, клавиатура, манипулятор «мышь», принтер, сетевой адаптер); НЖМД – устройство накопления на жестких магнитных дисках; ОС – операционная система; ПО – программное обеспечение.
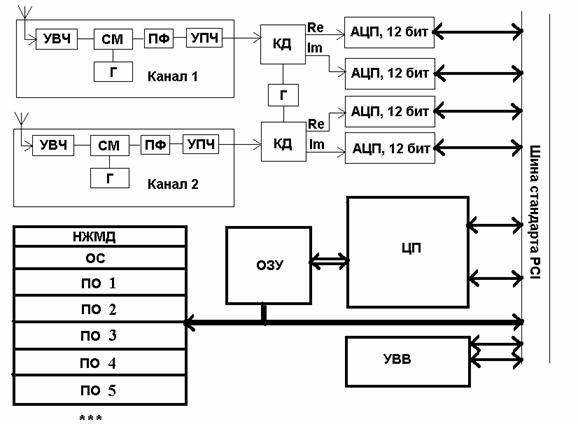
Рис. 37. Структурная схема фрактального непараметрического обнаружителя
радиолокационных сигналов (ФНОРС)
В НЖМД ФНОРС хранятся следующее программное
обеспечение (ПО): а) «ПО 1» - вычисление мгновенных значений фрактальной
размерности ![]() ; б)
«ПО 2» - вычисление полной сигнатуры
; б)
«ПО 2» - вычисление полной сигнатуры ![]() , обрабатываемого массива данных; в)
«ПО 3» - вычисление в реальном времени реализаций наблюдаемых данных в разных
временных масштабах, прореживание, интерполяция (сгущение); г) «ПО 4»
отбор данных по значениям их дробной меры; д) «ПО 5» - восстановление
полезного сигнала из входной смеси с помощью многомасштабного фрактального
анализа.
, обрабатываемого массива данных; в)
«ПО 3» - вычисление в реальном времени реализаций наблюдаемых данных в разных
временных масштабах, прореживание, интерполяция (сгущение); г) «ПО 4»
отбор данных по значениям их дробной меры; д) «ПО 5» - восстановление
полезного сигнала из входной смеси с помощью многомасштабного фрактального
анализа.
В соответствии с решаемыми задачами, ПО ФНОРС может быть в дальнейшем расширено. Подробное описание работы ФНОРС, результаты фрактальной обработки реальных радиосигналов и характеристики обнаружения подробно рассмотрены в [3, 4, 8 – 11, 13, 16, 22, 25, 27].
12.2. Наноструктуры и фракталы
На основе нанофазных материалов также можно создать [3, 4, 8 – 11, 13, 16, 22, 25, 27, 42, 43] планарные и объемные микро- и наноструктуры, моделирующие рассмотренные выше «фрактальные» радиоэлементы и радиоустройства микроэлектроники, т.е. речь идет о построении элементной базы нового поколения на основе фрактальных эффектов и свойств (см. рис. 1). В частности, элементарное обобщение канторова множества на физическом уровне позволяет перейти к так называемым канторовым блокам в планарной технологии молекулярных наноструктур.
Для рассматриваемых задач автором предложены и используются в настоящее время следующие основные пути: a)-миниатюрные фрактальные антенны, b)-фрактальные структуры в фотонных и магнонных кристаллах, с)-физическое моделирование фрактальных импедансов и дробных операторов, d)-перколяционный синтез наноструктурированных композитов и т.п.
Теория перколяции - теория, описывающая возникновение бесконечных связных структур или кластеров, состоящих из отдельных элементов. Представляя среду в виде решетки, можно сформулировать два типа задач. Можно выборочно случайным образом красить (открывать) узлы решетки, считая долю окрашенных узлов основным независимым параметром и полагая два окрашенных узла принадлежащими одному кластеру, если их можно соединить непрерывной цепочкой соседних окрашенных узлов. Такие вопросы, как среднее число узлов в кластере, распределение кластеров по размерам, появление бесконечного кластера и доля входящих в него окрашенных узлов, составляют содержание задачи узлов.
Можно также выборочно красить (открывать) связи между соседними узлами и считать, что одному кластеру принадлежат узлы, соединенные цепочками открытых связей. Тогда те же самые вопросы о среднем числе узлов в кластере и т.д. составляют содержание задачи связей. Когда все узлы (или все связи) закрыты, решетка является моделью изолятора. Когда они все открыты и по проводящим связям через открытые узлы протекает ток, то решетка моделирует металл. При каком-то критическом значении произойдет перколяционный переход, являющийся геометрическим аналогом перехода металл-изолятор. Теория перколяции важна именно в окрестности перехода. Вдали от перехода достаточно аппроксимации эффективной среды. Перколяционный переход аналогичен фазовому переходу второго рода.
Применение рекурсивного процесса в принципе позволяет создавать самоподобную иерархическую структуру (см.выше п.7.5). При этом необходим учет взаимного и коллективного влияния электромагнитных полей с компонентами устройств.
В настоящее время заметное внимание специалистов уделяется моделированию фрактальных объектов комплексной динамики различными диссипативными системами. Наиболее естественный путь моделирования – это использование сценария Фейгенбаума перехода к хаосу через удвоение периода. В контексте нашей работы, множества Жюлиа, Фату и Мандельброта (рис. 38) – интересные объекты для физической разработки новых форм и видов фрактальных антенн и других фрактальных наноструктур и метаматериалов на их основе [3, 4, 8 – 11, 13, 16, 22, 25, 27, 42, 43]. Здесь можно говорить и о “модных” в настоящее время “фрактальных лабиринтах”. Такие фрактальные конструкции выполнимы при существующем уровне развития нанотехнологий.
|
(а)
|
|
(б) |
|
Рис. 38. Множество Мандельброта zn+1
= впервые представил Б. Мандельброт в черно-белом цвете; б) цветовое. |
12.3. Методы фрактального анализа наноструктурированных
композитных материалов
В современной науке и технике одним из важнейших направлений является создание наноструктурированных материалов, исследование их свойств и разработка на их основе новых технологий, устройств и электронных приборов. Материалы со специальными физико-механическими и химическими свойствами, технология их изготовления и обработки являются основой создания новой наукоемкой продукции. Ценность разработкам и исследованиям в области новых материалов придает тот факт, что некоторые из разработанных технологий являются так называемыми прорывными, генеративными, то есть, порождающими принципиально новые научно-технические направления, либо дающими основу для техники новых поколений. Изложение данного п. 12.3 ведется по работам [25, 42, 44 - 46].
С помощью таких материалов можно создавать объемные среды и планарные наноструктуры с уникальными физическими характеристиками. Эти структуры могут быть объемными, планарными (пленочными), а также могут состоять из наночастиц и отдельных молекул, распределённых в структурах и матрицах различных типов, обладать уникальными характеристиками, связанными с пониженной физической размерностью объектов: нульмерной, одномерной, двумерной, а также иметь дробную размерность, связанную с фрактальными свойствами наноструктур.
Наноструктурированные материалы представляют собой вещества с внутренней структурой, имеющей характерные размеры нанометрового масштаба. Структурированные композитные нанофазные материалы имеют специфические особенности и свойства, отличные от веществ, находящихся в обычных фазах, например, могут иметь другие механические и электрофизические характеристики в различных частотных диапазонах в том числе в микроволновом и оптическом диапазонах. Основой наномасштабной структуры могут быть как наночастицы различной природы, так и молекулярные кластеры, обладающие типичной для молекул абсолютной идентичностью свойств. Разработка наноструктурированных материалов связана с технологией формирования наночастиц.
В рамках феноменологического подхода наночастицы рассматриваются как специфические псевдомолекулы, отличающиеся от истинных молекулярных соединений непостоянством состава. Таким образом, наночастицы представляют собой новый объект, занимающий место между молекулярными кластерными соединениями, с одной стороны, и традиционными ультрадисперсными порошковыми материалами, с другой.
Металлическая наночастица - это находящийся в среде из легких атомов объект сфероидальной формы, состоящий из 10 - 103 атомов, имеющий диаметр 1 - 10 нм и соотношение между количествами поверхностных частиц и частиц в объеме, равное и более единицы (Nпов > Nоб ≥ 1). Многочисленные методы получения наночастиц можно сгруппировать вокруг двух основных путей их образования- из атомов металлов в результате нуклеации или из компактного металла путем диспергирования.
Для наночастиц доля поверхностных атомов Nпов соизмерима (или даже больше) с числом атомов в объеме частицы Nоб. Простое выражение дает долю поверхностных атомов от общего числа атомов п в сферической частице: S = 4/n1/3. Энергия взаимодействия наночастиц такова, что они способны эффективно взаимодействовать с любыми химическими соединениями, включая инертные газы. Глубина взаимодействия со средой определяется двумя основными факторами: размером частиц (соответственно долей поверхностной энергии в общей энергии частицы) и природой металла.
Объединение наночастиц в объеме и на плоскости довольно сильно различается: трехмерная диффузия приводит к образованию компактных объемных вторичных частиц, в то время как на плоской поверхности объединение наночастиц носит ярко выраженный фрактальный характер с образованием дендритных структур различной размерности. Движущей силой агломерации наночастиц является стремление минимизировать поверхностную энергию. Как правило, имеются “кинетические” препятствия слиянию наночастиц в компактный материал. Обычно таким препятствием является тончайший моноатомный слой из легких атомов, и сближение взаимодействующих наночастиц заканчивается на равновесном расстоянии 3,5 - 4 Å. В результате образуются так называемые вторичные частицы, являющиеся той или иной формой объединения наночастиц. Вторичные частицы могут достигать значительных размеров. При этом многие свойства индивидуальных наночастиц сохраняются.
Основные отличия электронного строения наночастиц от строения соответствующих компактных металлов состоят в дискретности электронных уровней энергии наночастицы и статистическом характере их распределения. От кластерных молекул наночастицы отличаются тем, что у них отсутствует энергетическая щель (HOMO-LUMO separation).
Нанофазные материалы представляют собой вещества с внутренней структурой, имеющей характерные размеры нанометрового масштаба. Структурированные композитные нанофазные материалы имеют специфические особенности и свойства, отличные от веществ, находящихся в обычных фазах, например, могут иметь другие механические и электрофизические характеристики в различных частотных диапазонах в том числе в микроволновом и оптическом диапазонах. Основой наномасштабной структуры могут быть как наночастицы различной природы, так и молекулярные кластеры, обладающие абсолютной идентичностью.
Металлические кластеры необходимого состава можно внедрять в матрицы простейших органических полимеров таких как полиэтилен, полипропилен, полифениленоксид, полиэтиленгликоль и др. Полимерные матрицы- полиэтилен и тефлон известны как высокотехнологичные материалы, обладающие достаточно высокой химической устойчивостью в агрессивных средах. Предварительные исследования показали, что технология синтеза позволяет варьировать содержание металла в матрице в пределах 1 – 50 % веса; верхняя граница содержания металла, как правило, совпадает с максимальной плотностью заполнения естественных вакансий в данной полимерной матрице.
Структурированные материалы на полимерной основе широко применяются при разработке новых конструкционных материалов. Поэтому в целях получения материалов с заданными механическими, электрическими и теплофизическими свойствами разрабатываются композиции, состоящие из полимерного связующего, наполнителей и других добавок. Композиционные материалы, в отличие от растворов и пластифицированных полимеров, не являются смесями на молекулярном уровне. Размеры включений всегда значительно превышают размеры молекул. В матричной смеси полимер образует непрерывную среду (матрицу), в которой дискретно распределены не контактирующие между собой включения, причем две фазы смеси не равноправны. Форма частиц наполнителя может быть различной: сферы, цилиндры (волокна), пластинки и т. д.
Как известно, большинство металлических наночастиц термодинамически нестабильно. Для их стабилизации можно использовать следующие полимеры: полиэтилен, полипропилен, политетрафлюороэтилен, полифениленоксид, полиэтиленгликоль и другие. Эти полимеры имеют сравнительно высокую термическую и окислительную устойчивость, уникальные реологические свойства и высокую диэлектрическую прочность. Также важно, что эти полимеры- достаточно технологичны и химически инертны.
При технологии синтеза используются два основных метода включения наночастиц в полимерные матрицы для получения наноструктурированных материалов. В первом методе наночастицы металлов формировались в полимерной матрице in situ в результате высокой скорости термораспада металлсодержащего композита. В качестве композитных металлсодержащих соединений могут быть использованы карбонилы, ацетаты, формиаты и др.. Второй метод включает использование жидкости в сверхкритическом состоянии, например диоксида углерода. С помощью вышеупомянутых технологий синтеза были получены образцы наноструктурированных полимеров в виде порошка, пластин, и пленок, которые содержали магнитные наночастицы в количестве вплоть до 50 масс. %. Эксперименты по кинетике показали, что рост наночастиц происходит одновременно во многих полостях по всему объему полимера; а размеры и число наночастиц являются специфическими для каждой полимерной матрицы.
В настоящее время разработка и исследование композиционных наноматериалов имеет приоритетное направление, поскольку такие материалы обладают уникальным набором химических, физических, физико-механических и эксплутационных свойств: повышенной тепло- и электропроводностью, высокой магнитной восприимчивостью, низкой поверхностной адгезией, способностью экранировать излучение. Применение таких композиционных материалов в микроволновой аппаратуре в качестве распределенных нелинейных элементов позволит разработать целый ряд новых устройств для преобразования электромагнитных сигналов, элементы пассивной и активной стелс-технологии и др.
В работе [45] осуществлен синтез и проведены комплексные исследования композиционных наноматериалов, в которых в качестве матрицы стабилизатора наночастиц использован полиэтилен высокого давления (ПЭВД). В качестве наполнителей были использованы наночастицы, содержащие висмут (Bi), железо (Fe), сульфид кадмия (CdS), кобальт (Co), медь (Cu), молибден (Mo), оксид церия (CeO2). Образцы были синтезированы методом термического разложения металлсодержащих соединений (прекурсоров) в раствор-расплаве полиэтилен-масло при температуре 270-300°С. Структуру и распределение по размерам металлсодержащих наночастиц стабилизированных в объеме матрицы полиэтилена можно определить при исследовании наноматериалов методом просвечивающей электронной микроскопии (ТЕМ). В частности показано, что разработанная технология позволяет получать средний размер наночастиц наполнителя в диапазоне 3 – 100 нм. Эти различия непосредственно проявляются в электрофизических свойствах материалов.
Практический интерес представляют, в первую очередь, концентрационные зависимости электрофизических характеристик полимерных композиционных материалов на основе ПЭВД, содержащего наночастицы различного состава. Наиболее полно эти зависимости исследованы для композитов на основе железосодержащих наночастиц. В технологии термического разложения пентакарбонила железа (ПКЖ) в раствор-расплаве полиэтилена состав синтезируются так называемые «core-shell» наночастицы – наночастицы, состоящие из металлического ядра α-железа и оболочки из оксидов железа II и III в различных массовых соотношениях. Строение наночастиц определяется особенностями технологического процесса.
На основе исследования электропроводности наполненного полимерного нанокомпозита в зависимости от процентного содержания наночастиц металла продемонстрировано изменение механизма проводимости. Показано, что изменение диэлектрической проницаемости коррелирует с изменением плотности образцов в зависимости от концентрации наночастиц металла. Исследования сверхвысокочастотных свойств проводились в волноводном тракте на различных частотах. Измерения показали увеличение поглощающей способности наноструктурированного материала с увеличением плотности наночастиц металла в полимерной матрице. Показано, что такие материалы могут быть использованы в устройствах, эффективно экранирующих электромагнитное излучение в широком частотном диапазоне.
На рис. 39 и 40 представлены зависимости диэлектрической проницаемости и тангенса угла потерь на частоте 1 ГГц.
Известно, что конденсированное состояние вещества может существовать не только в форме плотной сплошной среды, но и в виде сильно разрыхленных пористых структур. Такого рода структуры образуются, как правило, в результате конденсации в сложных неравновесных условиях, например при слипании движущихся по определенному закону твердых частиц или в результате взаимодействия дислокаций при пластической деформации металлов. Подобного рода структуры получили название фрактальных агрегатов. Они в большинстве своем являются неупорядоченными, сложными для исследования, и их макроскопические свойства практически не изучены.
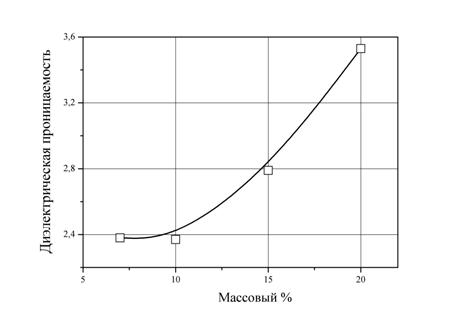
Рис. 39. Концентрационная зависимость диэлектрической проницаемости композита
ПЭВД – Fe - наночастицы на частоте 1 ГГц.
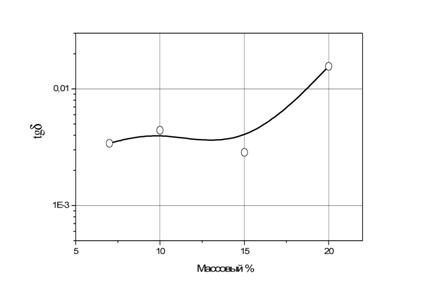
Рис. 40. Концентрационная зависимость тангенса угла потерь композита
ПЭВД – наночастицы Fe на частоте1 ГГц.
Интуитивно геометрические модели различных природных объектов традиционно строились на основе сравнительно простых геометрических фигур: прямых, окружностей, сфер, многогранников. Однако очевидно, что этот классический набор, вполне достаточный для описания структуры плотных кристаллических и аморфных твердых тел, недостаточен при рассмотрении структурированных материалов. Поэтому в последние 30 лет для описания сложных объектов и систем самых различных размеров все чаще используются новые геометрические представления [2, 4].
Фрактальный агрегат каждого вещества формируется при определенных физических условиях, которые до конца не поняты. Тем не менее, то, что уже известно, дает возможность использовать законы образования фрактальных агрегатов для создания и анализа материалов с необычными физическими свойствами. Так, можно создавать материалы, способные поглощать электромагнитное излучение в достаточно широком диапазоне длин волн, новые красители, жидкокристаллические системы, наноструктуры, твердые вещества с пористостью до 99 % .
Как известно, основным компонентам наноструктурированных наполненных полимеров– матрице, наночастицам и агрегатам частиц присущи фрактальные свойства [2, 3, 46]. Наночастицы из-за их высокой реакционной способности чувствительны к примесям, агломерируют друг с другом при воздействии на систему. Повышение устойчивости наночастиц достигается применением стабилизаторов, в качестве которых используются низкомолекулярные органические соединения и синтетические полимеры.
Исследование свойств сильно неоднородных, неупорядоченных и некристаллических аморфных материалов обусловлено, по крайней мере, двумя причинами. Необходимость более глубокого понимания физических процессов, происходящих в средах с высокой степенью неоднородности связана с широким и все возрастающим применением этих материалов в микроэлектронике и других областях, например, проблема получения диэлектриков с низкой диэлектрической проницаемостью. Это достигается путем применения высокопористых диэлектриков. Второй причиной, вызывающий интерес к исследованию подобных материалов, является как необычность физических процессов, протекающих в них, так и недостаточность качественного понимания и количественного описания в отличие от классической физики кристаллических твердых тел. Многие представления традиционной физики твердого тела нельзя непосредственно применять для описания неупорядоченных и аморфных материалов, поскольку последние не обладают трансляционной симметрией.
Успехи качественного понимания процессов переноса в случайно неоднородных средах: от движения электрона в случайном потенциале до исследования макроскопических характеристик: диффузии, проводимости, просачивание- связаны с теорией перколяции и интенсивно развиваемыми в последнее время фрактальными представлениями [2 – 4, 8 - 14]. Теория перколяции (см. п. 12.2) адекватно описывает системы с геометрическим фазовым переходом по связности. Согласно современным представлениям перколяционные кластеры на пороге протекания являются случайными статистическими фракталами, т.е. заполняют евклидово пространство самоподобным образом.
Идеи фрактальной геометрии получили чрезвычайно широкое распространение. Фрактальная структура оказалась присуща многим физическим явлениям [2 - 14]. В свою очередь, дробные фрактальные размерности отражают симметрию фрактальных структур относительно масштабных преобразований и в силу своей универсальности могут служить характеристиками изучаемых систем. Согласно сложившейся точке зрения фракталы разделяют на два класса: регулярные и случайные. Примерами первых могут служить разнообразные ковры Серпинского. Как отмечалось выше, перколяционные кластеры на пороге протекания относят к статистическим фракталам. Аналогичную структуру представляют собой наноструктурированные композитные материалы (рис. 41).
В настоящее время структурные свойства материала описываются на основе рассмотрения его как открытой нелинейной системы. Свойства материала определяются процессами структурообразования при обмене энергией и веществом с внешней средой. При определенном характере взаимодействия могут формироваться устойчивые регулярные и стохастические самоподобные (фрактальные) структуры на разных масштабных уровнях.
Использование методов фрактального анализа и принципов мультифрактального формализма дает возможность ввести фрактальную параметризацию, характеризовать структурные особенности, отражающие топологию тонкой внутренней структуры рассматриваемых материалов, описать их свойства в понятиях меры и размерности, а также предсказывать физические эффекты, связанные с количественными изменениями фрактальных параметров среды (рис. 42).
|
(а) |
(б) (в) |
|
|
|
Рис. 41. Фрактальная структура композитных наноматериалов: а) ТЕМ-микрофотография наноматериала и компьютерная модель структуры до (б) и после (в)
перколяционного перехода.
Фрактальная сигнатура D (усл. ед.)
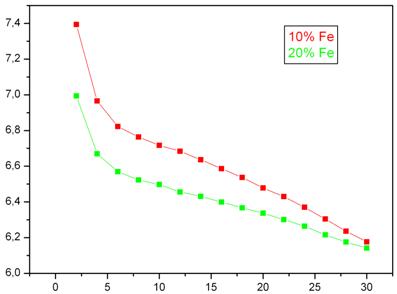
Масштаб измерительного окна
Рис. 42. Фрактальная параметризация композитных наноматериалов.
В последние годы во многих странах мира ведут интенсивные работы по уменьшению радиолокационной заметности объектов с помощью перспективных радиопоглощающих материалов, имеющих предельно малые коэффициенты отражения (стелс-технология) [4]. По мнению военных специалистов эти разработки могут в принципе изменить характер военных действий, что потребует пересмотра военной стратегии.
Использование наноструктурированных металлополимеров на основе Co, Fe, Ni и других металлов в качестве радиопоглощающих материалов нового поколения с расширенными функциональными и потребительскими возможностями, в том числе, с повышенным радиопоглощением в широком частотном диапазоне позволит, как отмечалось автором ранее, обеспечить экологическую защиту биообъектов, а также обеспечит решение задач помехозащищенности и формирования адаптивных характеристик радиоэлектронной аппаратуры.
Технологический опыт показывает, что можно совместить в одном материале наночастицы градиентных радиопоглощающих материалов, интерференционных, рассеивающих, керамических и ферритовых. Таким образом, покрытие может сочетать в себе свойства нескольких известных типов композиционных радиопоглощающих материалов, совмещенных на наноуровне.
В магнитных полимерных композита наночастицы ферромагнитного материла являются ферромагнитными монодоменами, изолированными в матрице немагнитного полимерного материала. Такие пленки с высоким содержанием наночастиц открывают новые перспективы для создания магнитных систем с высокой плотностью записи и хранения информации. Оценки показывают, что в пленке с наночастицами размером около 5 нм, находящимися в среднем на расстоянии ~5 нм друг от друга, потенциальная плотность записи информации может достигать 1013 бит/кв. дюйм.
Разработка различных нанофазных композитных структур с металлическими наночастицами, обладающими легкостью изменения функциональных свойств позволит разработать новые и модернизировать достаточно широкий круг радиоэлектронных устройств: аттенюаторы, эквивалентные нагрузки, фильтры мод и гармоник радиосигнала. Использование специфических особенностей нанофазных материалов позволит создавать “умные” адаптационные материалы с заранее заданными свойствами, которые могут меняться под воздействием параметров внешней среды и в частности внешнего электромагнитного поля, а также целенаправленно меняться под управляющим воздействием. На основе таких материалов также можно создавать распределенные радиоэлектронные устройства нового поколения [3, 4, 8 – 11, 13, 16, 22, 25, 27, 42, 43, 47, 48].
12.4. Фрактальные элементы (устройства) и фрактальные радиосистемы
Основываясь на полученных результатах, мы можем смело говорить о проектировании не только фрактальных элементов (устройств), но и непосредственно (рис. 43) фрактальных радиосистем [3, 4, 8 – 11, 13, 16, 22, 25, 27, 38, 39, 42, 43, 47, 48]. Такие фрактальные радиосистемы структурно включают в себя (начиная с входа) фрактальные антенны и цифровые фрактальные обнаружители, основаны на фрактальных методах обработки информации, а в перспективе могут использовать фрактальные методы модуляции и демодуляции радиосигналов. При таком «фрактальном» подходе естественно сосредоточить внимание на описании, а также обработке радиофизических сигналов (полей), исключительно в пространстве дробной меры с применением гипотезы скейлинга и распределений с «тяжелыми хвостами» или устойчивых распределений.
Предложенные автором фрактальные радиосистемы и фрактальные радиоэлементы (рис. 43) открывают новые возможности в современной радиоэлектронике и могут иметь в будущем самые широкие перспективы практического применения.
Конечно, все многочисленные аспекты предложенных автором новых методов построения (анализа и синтеза) радиосистем и радиоэлементов («фрактальных» в широком смысле) просто невозможно досконально рассмотреть в данной работе.
Главная цель – познакомить читателя с принципиально новыми, а именно, фрактальными и скейлинговыми, методами анализа и синтеза и их применениями в науке и технике.
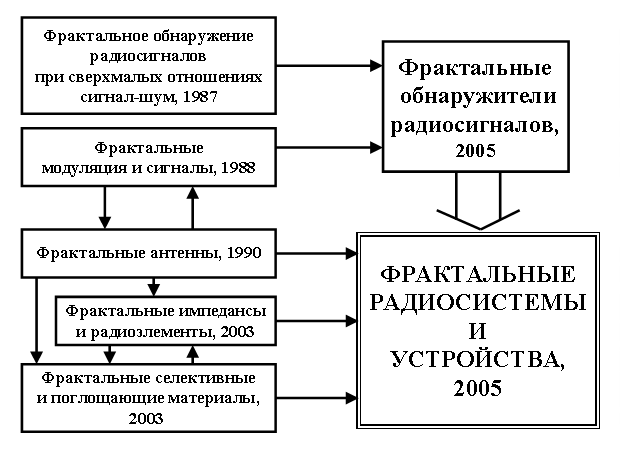
Рис. 43. Авторская концепция фрактальных радиосистем и устройств
Заключение
Результативность радиофизических исследований может быть значительно повышена благодаря учету фрактальности волновых явлений, развивающихся на всех этапах излучения, рассеяния и распространения волн в различных средах. Кардинальные шаги, заключающиеся в переводе принятых радиосистемой сигналов целочисленной меры в пространство дробной меры и привлечение затем скейлинговых соотношений, позволяют привнести в традиционные области классической науки совершенно новые идеи и методы, и получать на их основе достаточно неожиданные для практики, но физически обоснованные результаты.
Стремительному развитию фракталов и дробных операторов способствует и само существование чрезвычайно широкого круга физических и технических проблем (и не только!), адекватно описываемых этими теориями. Возможности здесь очень велики. Конкретное использование в радиофизике и радиоэлектронике понятия “фрактал” не только оправдано, но и необходимо. При этом требуются принципиальные изменения общих устоявшихся представлений в работе ученых, инженеров и обучении студентов и аспирантов. Только тогда дробные операторы, фракталы и скейлинг прочно войдут в обиход физика, математика и инженера. Можно выразить надежду, что новая генерация специалистов возьмет барьеры “фрактального” видения мира и тем самым обеспечит нарастающие успехи российской науки и промышленности в технологической гонке различных стран.
Перефразируя известное высказывание Х. Хармута, автор утверждает, что теперь мы освобождаемся от психологических оков гипотезы, которая отводила особую роль гладким непрерывным функциям и целочисленным мерам. Поиск возможных применений фрактальных методов и дробных операторов нельзя начинать с попытки разрешить известные проблемы, так как тот, кто привык мыслить в терминах гладких функций и целочисленных мер, никогда не выйдет из сферы задач, которые имеют простое решение. (Для любознательных читателей автор ставит вопрос: “Что такое фрактальная индуктивность, фрактальный трансформатор, фрактальный дроссель?” Торопитесь с ответом…).
В книге [49] в подразделе “Локационные системы” (раздел "Информационные технологии и вычислительные системы", стр. 41) включены некоторые авторские результаты фундаментальных исследований в виде следующего текста: “Создан эталонный словарь фрактальных признаков оптических и радиоизображений, необходимый для реализации принципиально новых фрактальных методов обработки радиолокационной информации и синтеза высокоинформативных устройств обнаружения и распознавания слабых сигналов на фоне интенсивных негауссовских помех. Установлено, что для эффективного решения задач радиолокации и проектирования фрактальных обнаружителей многомерных радиосигналов существенное значение имеют дробная размерность, фрактальные сигнатуры и кепстры, а также текстурные сигнатуры фона местности. (ИРЭ РАН)”.
В общем и целом современная системотехника достаточно хорошо подготовлена к введению отдельных фрактальных подсистем и узлов в классические радиосистемы, которые зачастую не требует сложной переделки, а достаточно лишь параллельных каналов обработки информации. Автор берет на себя смелость утверждать, что достаточно кратко представленный им в данной работе подход характеризует новый этап развития радиофизики и радиоэлектроники.
Фрактальный подход к классическим задачам радиофизики, радиотехники, радиолокации и электроники дал возможность прийти к самостоятельным и весьма плодотворным для многочисленных приложений концепциям. В результате чтения лекций по разработанным автором «фрактальным» технологиям и докладам по проекту МНТЦ в 2000 г. и 2005 г. в США (Вашингтон, Нью-Йорк, Хантсвилл, Атланта, Франклин) в декабре 2005 г. американскими специалистами в официальном письме на имя директора ИРЭ им. В.А. Котельникова РАН академика Ю.В. Гуляева было отмечено [4], что «…Семинары были крайне интересны и подтвердили высокую научную квалификацию доктора А. Потапова. Радиолокационные технологии, представленные доктором А. Потаповым, основаны на теории фракталов и являются новыми. Важность этих исследований для международного сообщества специалистов и ученых неоспорима». Тогда же состоялась научная встреча А.А. Потапова с основателем фрактальной геометрии Б. Мандельбротом.

Рис. 44. Встреча А.А. Потапова с Б. Мандельбротом у него дома (США, 16 декабря 2005 г.).
Методы, аналогичные излагаемым в настоящей работе, могут быть применены при рассмотрении волновых и колебательных процессов в оптике, акустике и механике. Следует отметить, что за 30-летний период работы автора в ИРЭ им. В.А. Котельникова РАН, по данному направлению выпущено в свет 12 монографий и опубликовано более 350 научных работ; с 2003 г. выходит специальный журнал “Нелинейный мир” (см., авторский сайт: http://www.potapov-fractal.com). Обобщение результатов, изложенных в них, позволяют охватить и всевозможные возникающие новые проблемы.
Исходя из вышесказанного, можно объективно говорить о становлении московской школы фрактальных методов с центром в ИРЭ им. В.А. Котельникова РАН.
Список литературы
1. Mandelbrot B.B. Les Objects Fractals: Forme, Hasard et Dimension.- Paris: Flammarion, 1975, 1984, 1989, 1995; Mandelbrot B.B. Fractals: Forme, Chance and Dimension.- San - Francisco: Freeman, 1977.- 365 p.; Mandelbrot B.B. The Fractals Geometry of Nature.– N. Y.: Freeman, 1982.- 468 p. (Рус. пер.: Мандельброт Б. Фрактальная геометрия природы: Пер. с англ. – М.: Институт компьютерных исследований, 2002. – 656 с.); Mandelbrot B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk.– N. Y.: Springer-Verlag, 1997.- 551 p.; Mandelbrot B.B. Fractales, Hasard et Finance (1959–1997).– Paris: Flammarion, 1997.- 246 p. (Рус. пер.: Мандельброт Б. Фракталы, случай и финансы / Пер. с фр. В.В. Шуликовской.- М.: Эдиториал УРСС, 2004 г.- 256 с.); Mandelbrot B.B. Multifractals and 1/f Noise: Wild Self – Affinity in Physics. – N. Y.: Springer-Verlag, 1999.- 442 p.; Mandelbrot B.B. Gaussian Self – Affinity and Fractals: Globality, the Earth, 1/f, and R/S.– N. Y.: Springer-Verlag, 2002.- 654 p.; Mandelbrot B.B., M.L. Frame. Fractals, Graphics, and Mathematics Education.– N. Y.: Springer-Verlag, 2002; Mandelbrot B.B. Fractals and Chaos: The Mandelbrot Set and Beyond.– N. Y.: Springer-Verlag, 2004.- 308 p.; Mandelbrot B.B., Hudson R.L. The (mis) Behavior of Markets.– N. Y.: Basic Books, 2004.- 328 p. (Рус. пер.: Мандельброт Б., Хадсон Р.Л. (Не)послушные рынки: фрактальная революция в финансах.- М.: Вильямс, 2006.- 400 с.).
2. Потапов А.А. Фракталы в радиофизике и радиолокации. – М.: Логос, 2002.–664 c.
3. Потапов А.А. Фракталы в радиофизике и радиолокации: Топология выборки.–2-е изд., перераб. и доп. – М.: Университетская книга, 2005. – 848 c.
4. Потапов А.А. Фракталы и хаос как основа новых прорывных технологий в современных радиосистемах // Дополнение к книге: Кроновер Р. “Фракталы и хаос в динамических системах”: Пер. с англ. – М.: Техносфера, 2006.- С. 374 – 479.
5. Подосенов С.А., Потапов А.А., Соколов А.А. Импульсная электродинамика широкополосных радиосистем и поля связанных структур / Под ред. А.А. Потапова.- М.: Радиотехника, 2003.- 720 с.
6. Бункин Б.В., Реутов А.П., Потапов А.А. и др. Вопросы перспективной радиолокации (Коллективная монография).- М.: Радиотехника, 2003.- 512 с.
7. Быстров Р.П., Потапов А.А., Соколов А.В. Миллиметровая радиолокация с фрактальной обработкой.– М.: Радиотехника, 2005.- 368 с.
8. Потапов А.А., Гуляев Ю.В., Никитов С.А., Пахомов А.А., Герман В.А. Новейшие методы обработки изображений / Под ред. А.А. Потапова.– М.: Физматлит, 2008. – 496 c. (Грант РФФИ № 07 – 07 - 07005).
9. Потапов А.А. Фрактальные модели и методы на основе скейлинга в фундаментальных и прикладных проблемах современной физики // Сб. науч. тр. “Необратимые процессы в природе и технике” / Под ред. В.С. Горелика и А.Н. Морозова. - М.: МГТУ им. Н.Э. Баумана, 2008. Вып. II. С. 5 – 107.
10. Потапов А.А. Фрактальные методы исследования флуктуаций сигналов и динамических систем в пространстве дробной размерности // Глава в книге “Флуктуации и шумы в сложных системах живой и неживой природы” / Под ред. Р.М. Юльметьева, А.В. Мокшина, С.А. Демина, М.Х. Салахова.- Казань: Министерство образования и науки Республики Татарстан, 2008.- С. 257 – 310.
11. Потапов А.А., Гильмутдинов А.Х., Ушаков П.А. Фрактальные элементы и радиосистемы: Физические аспекты / Под ред. А.А. Потапова (Библиотека журнала «Нелинейный мир»: Научная серия «Фракталы. Хаос. Вероятность»).- М.: Радиотехника, 2009. - 200 с.
12. Антипов О.И., Неганов В.А., Потапов А.А. Детерминированный хаос и фракталы в дискретно-нелинейных системах / Под ред и с предисловием акад. Ю.В. Гуляева и чл.-корр. РАН С.А. Никитова.- М.: Радиотехника, 2009.- 235 с.
13. Потапов А.А., Черных В.А. Дробное исчисление А.В. Летникова, теория фракталов и скейлинг / Под ред. А.А. Потапова.– М.: Физматлит, 2009.- 820 с.
14. Потапов А.А. Спецтема // Автореферат диссертации … к. т. н.- М.: МФТИ, 1989.- 28 с.; Потапов А.А. Синтез изображений земных покровов в оптическом и миллиметровом диапазонах волн // Дис. ... докт. физ.-мат. наук. М.: ИРЭ РАН, 1994.-436 с.
15. Потапов А.А. Радиофизические эффекты при взаимодействии электромагнитного излучения миллиметрового диапазона волн с окружающей средой // Зарубежная радиоэлектроника. 1992. № 8. С. 36 - 76; № 9. С. 4 - 28; № 11. С. 23 - 48; 1993. № 3. С. 36-48; № 7-9. С. 32-49; 1994. № 7/8. С.11-30; 1995. № 1. С. 27-36 (журн. вариант монографии).
16. Potapov A.A. The Textures, Fractal, Scaling Effects and Fractional Operators as a Basis of New Methods of Information Processing and Fractal Radio Systems Designing // Proc. SPIE. 2009. V. 7374. P. 73740E-1 - 73740E-14 (http://spie.org/x648.html?product_id=829032).
17. Потапов А.А., Рехвиашвили С.Ш., Гаев Д.С. Фрактальная модель фотолюминесценции диэлектрической частицы // Нелинейный мир. 2007. Т. 5. № 10-11. С. 716 – 721.
18. Першин С.М., Адикс Т.Г., Лукьянченко В.А., Нигматуллин Р.Р., Потапов А.А. Наблюдение спектральной компоненты льдоподобных комплексов в ОН полосе воды при температуре от 13о до 99о С // Нелинейный мир. 2009. Т. 7, № 2. С. 79 – 90.
19. Нигматуллин Р.Р., Потапов А.А. Фракталы, дробные операторы и дробная кинетика в диэлектрической спектроскопии и волновых процессах // Физика волновых процессов и радиотехнические системы. 2007. Т. 10, № 3. С. 30 – 49.
20. Нигматуллин Р.Р., Потапов А.А. Неинвазивные методы выделения и ”прочтения” значимых информационных составляющих акустических шумов произвольной природы // Физика волновых процессов и радиотехнические системы. 2009. Т. 12, № 3.
21. Потапов А.А., Лактюнькин А.В. Теория рассеяния волн фрактальной анизотропной поверхностью // Нелинейный мир. 2008. Т. 6. № 1. С. 3 – 36.
22. Потапов А.А. О применении показателя Херста H в адаптивной фрактальной обработке информации и синтезе новых классов фрактальных «Н – сигналов» // Обозрение прикладной и промышленной математики. 2008. Т. 15, № 6. С. 1121 – 1123.
23. Потапов А.А. О фрактальных флуктуациях СВЧ - радиоволн в поглощающей среде и об отрицательной фрактальной размерности // Обозрение прикладной и промышленной математики. 2008. Т. 15, № 6. С. 1123 – 1124.
24. Потапов А.А. Стохастичность и фрактальность флуктуационной структуры электромагнитных волн СВЧ-, КВЧ- и ГВЧ-диапазонов, распространяющихся в тропосфере, метеорологических образованиях, пылевых бурях и взрывах // Нелинейный мир. 2008. Т. 6. № 2. С. 69 – 109.
25. Potapov A.A. On Fractal Theory in Radio Engineering, Micro- and Nanoelectronics // Problems of Non-Linear Analysis in Engineering Systems. 2008. V. 14, № 1(29). P. 165 – 177.
26. Потапов А.А., Гильмутдинов А.Х., Ушаков П.А. Системные принципы и элементная база фрактальной радиоэлектроники. Ч. I. Этапы становления и состояние // Радиотехника и электроника. 2008. Т. 53. № 9. С. 1033 – 1080; Ч. II. Методы синтеза, модели и перспективы применения // Радиотехника и электроника. 2008. Т. 53. № 11. С. 1347 – 1394.
27. Потапов А.А. Фракталы, скейлинг и дробные операторы как основа новых методов обработки информации и конструирования фрактальных радиосистем // Технология и конструирование в электронной аппаратуре. 2008. № 5(77). С. 3 – 19.
28. Подосенов С.А., Потапов А.А., Менькова Е.Р. Новый аналитический метод расчета электромагнитных полей от бегущих волн тока // Нелинейный мир. 2007. Т. 5. № 12. С. 725 – 738.
29. Подосенов С.А., J. Foukzon, Потапов А.А. Задача Белла и исследование электрон-ных сгустков в линейных коллайдерах // Нелинейный мир. 2009. Т. 7, № 8, C. 612 – 621; Foukzon J., Podosenov S.A., Potapov A.A. Relativistic Length Expansion in General Accelerated System Revisited // http://arxiv.org/abs/0910.2298v1 or http://eprintweb.org/S/article/physics/0910.2298
30. Нигматуллин Р.Р., Потапов А.А. Дробные операторы и их приложения (итоги Международного симпозиума “Дробная производная и ее приложения”) // Нелинейный мир. 2009. Т. 7, № 2. С. 154 – 155; Ерофеев В.И., Потапов А.А. Международный научный коллоквиум "Механика обобщенных континуумов: сто лет после Коссера" // Нелинейный мир. 2009. Т. 7, № 8.
31. Боголюбов А.Н., Потапов А.А., Рехвиашвили С. Ш. Способ введения дробного интегро-дифференцирования в классической электродинамике // Вестник Моск. ун-та. Физика. Астрономия. 2009. № 4. С. 9 – 12.
32. Potapov A.A., Matveev E.N., Potapov V.A., Laktyunkin A.V. Mathematical and Physics Modelling of Fractal Antennas and fractal frequency Selective Surfaces and Volumes for the Fractal Radio Systems // Proc. the Second European Conference on Antennas and Propagation EuCAP 2007 (11 - 16 November 2007, The EICC, Edinburgh, UK).- Edinburgh: The Institution of Engineering and Technology & EurAAP AISBL, 2007. ThPA.031. pdf. 6 pp. (http://www.eucap2007.org/programme1.htm).
33. Потапов А.А., Матвеев Е.Н. Фрактальные антенны: свойства, результаты расчетов, применение // Сб. докладов XIV Междунар. НТК “Радиолокация, навигация, связь” (Воронеж, 15 – 17 апреля 2008 г.).- Воронеж: НПФ “Саквоее”, 2008. Т. III. С. 1964 – 1970.
34. Potapov A.A., Matveev E.N. Modeling and Computation of Fractal Antennas: Circle Monopole, the Life-Flower Antenna // Book of Abstracts 2nd Int. Conf. (CHAOS’ 2009) on Chaotic Modeling, Simulation and Applications (01 - 05 June 2009, Chania, Crete, Greece).- Chania: National and Kapodistrian University, 2009. P. 61. (http://www.chaos2009.net/programabstracts.html).
35. Matveev E.N., Potapov A.A. Computational Modeling of New Kinds of Fractal Antennas and Fractal Frequency-Selective Structures Based on them // Proc. PIERS 2009 in Moscow “Progress in Electromagnetics Research Symp” (18 - 21 August, 2009, Moscow, Russia).- Cambridge, MA: Electromagnetics Academy, 2009. P. 1933 – 1936. (http://piers.mit.edu/piersproceedings/piers2k9MoscowProc.php?searchname=potapov).
36. Matveev E.N., Potapov A.A. Fractal Antennas for the New Class of Radio Systems: Keily Tree and Circular Monopole // Proc. Int. Radar Symp. (IRS - 2009)” (09 - 11 September, 2009, Hamburg, Germany) / Ed. H. Rohling.- Hamburg: Technical University Hamburg-Harburg and German Institute of Navigation (TUHH and DGON), 2009. P. 465 – 468.
37. Матвеев Е.Н., Потапов А.А. Численное моделирование антенн с фрактальной геометрией // Нелинейный мир. 2009. Т. 7, № 9. С. 689 – 693.
38. Потапов А.А., Потапов В.А. Фрактальные антенны: анализ, синтез и новые применения в радиофизике и радиоэлектронике // Тр. Четвертого междунар. междисциплинарного симпозиума "Фракталы и прикладная синергетика - ФИПС-05" (Москва, 14 - 17 ноября 2005 г.).- М.: Изд. Интерконтакт – Наука, ИМЕТ РАН. 2005. С. 113 – 114; Potapov A.A., Potapov V.A. Scales Continuum and Fractional Processes in Complicated Dynamical Systems // Proc. Int. Conf. “Intellectual Systems of Decision Making and the Problems of Computational Intelligence (ISDMCI’ 2009)” (18 – 22 May 2009, Yevpatoria, Crimea, Ukraine).- Kherson: KNTU, 2009. V. 2. P. 175 – 177.
39. Potapov A.A. Modern Classes of Fractal Antennas and Fractal Frequency Selective Surfaces and Volumes // Abstracts Int. Seminar “Days on Diffraction - 2006” (Russia, St. Petersburg, 30 May– 2 June 2006).- St. Petersburg: SPbU, 2006. P. 84 – 85.
40. Потапов А.А., Булавкин В.В., Герман В.А., Вячеславова О.Ф. Исследование микрорельефа обработанных поверхностей с помощью методов фрактальных сигнатур // ЖТФ. 2005. Т. 75, № 5. С. 28 – 45.
41. Потапов А.А. К теории функционалов стохастических полей обратного рассеяния // Радиотехника и электроника. 2007. Т. 52, № 3. С. 261 – 310.
42. Потапов А.А. Фрактальные антенны, импедансы и радиопоглощающие покрытия – “умные” материалы // Материалы Первой междунар. научн. конф. "Наноструктурные материалы - 2008: Беларусь – Россия – Украина (НАНО - 2008)" (Минск, 22 – 25 апреля 2008 г.).- Минск: Белорус. наука, 2008. С. 532; Потапов А.А. Фракталы, скейлинг, дробные операторы – применение в нанотехнологиях? // Сб. материалов Первой ежегодной НТК Нанотехнологического общества России “Развитие нанотехнологического проекта в России: состояние и перспективы” (Россия, Москва, 9 октября 2009 г.).- М.: НИЯУ-МИФИ, 2009. 5 стр. (http://ntsr.info/nor/bulletin/seminars/index.php?ID=1601).
43. Потапов А.А. Фракталы и дробные операторы как основа новых технологий обработки информации и синтеза фрактальных радиосистем // Сб. научно-практической конф. “Ориентированные фундаментальные исследования – от современной науки к технике будущего” в рамках 10-й юбилейной специализированной выставки с международным участием “Изделия и технологии двойного назначения. Диверсификация ОПК” (Россия, Москва, ВВЦ, пав. № 69, 10 - 13 ноября 2009 г.). / Под ред. член-корр. РАН Б.В. Гусева.- М.: Эксподизайн-Холдинг, 2009. 5 стр. (Гл. 8. - http://www.expo-design.info/_templates/vwp.php?mmid=1929&wpid=2036&lang=R).
44. Колесов В.В., Фионов А.С., Потапов А.А. Методы фрактального анализа наноструктурированных композитных материалов // Материалы международной науч. конф. “Интеллектуальные системы принятия решений и проблемы вычислительного интеллекта (ISDMCI’ 2009)” (Евпатория, 18 - 22 мая 2009 г.).- Херсон: ХНТУ, 2009. Т. 2. С. 325 – 331.
45. Фионов А.С., Юрков Г.Ю., Потапов А.А., Колесов В.В., Таратанов Н.А. Перспективные наноструктурированные полимерные композиционные материалы для физических исследований их методами фрактального анализа // Нелинейный мир. 2008. Т. 6, № 1. С. 37 - 41.
46. Фионов А.С., Потапов А.А., Колесов В.В., Герман В.А., Горшенев В.Н. Эффекты скейлинга и дробной размерности в полимерных композитах на основе ПВХ пластизолей // Труды Четвертой Всероссийской конф. “Необратимые процессы в природе и технике” (29 - 31 января 2007 г.).- М.: МГТУ им. Н.Э. Баумана, Физический институт им. П.Н. Лебедева РАН, 2007. Часть I. С. 44 – 47; Потапов А.А., Фионов А.С., Колесов В.В., Юрков Г.Ю., Таратанов Н.А. Исследование структуры неупорядоченных наноматериалов методами фрактального анализа // Материалы Первой междунар. научн. конф. "Наноструктурные материалы - 2008: Беларусь – Россия – Украина (НАНО - 2008)" (Минск, 22 – 25 апреля 2008 г.).- Минск: Белорус. наука, 2008. С. 550.
47. Потапов А.А. Применение теории фракталов, эффектов скейлинга и дробных операторов в обработке сигналов и текстурных изображений при интенсивных негауссовских помехах // Доклады XII научной школы-семинара им. академика Л.М. Бреховских “Акустика океана”, совмещенной с XXI сессией Российского Акустического Общества (Москва, 02 - 05 июня 2009 г.).- М.: ГЕОС, 2009. С. 398 – 402; Потапов А.А. Современное состояние радиофизических применений фракталов, дробных операторов и скейлинга // Сб. докл. III Всероссийской НТК “Радиолокация и радиосвязь” (Москва, 26 – 30 октября 2009 г.).- М.: ИРЭ им. В.А. Котельникова РАН, 2009. С. 842 – 876. (http://jre.cplire.ru/jre/3conference/pdffiles/ts002.pdf).
48. Potapov А.А. Fractal Radio Physics and Radio Electronics. The Design of Fractal Radio Systems // Proc. Int. Conf. “Mode Conversion, Coherent Structures and Turbulence” (MSS-09), devoted to Prof. S.S. Moiseev’s memory regards to his 80-th year birthday (Russia, Moscow, Space Research Institute of RAS, November 23 – 25, 2009). - M.: URSS Publishing House, 2009. P. 18 – 23. (http://www.iki.rssi.ru/conf/mss09/index.htm).
49. Отчетный доклад Президиума Российской Академии наук. Научные достижения Российской академии наук в 2007 г.- М.: Наука, 2008. - 204 с.
[1]
Параграф подготовлен по материалам статьи [31], соавторы д.ф.-м.н. С. Ш.
Рехвиашвили (Нальчик, Кабардино-Балкарский гос. университет) и д.ф.-м.н. А.Н.
Боголюбов (физфак МГУ). Первый вариант статьи был подготовлен С.Ш. Рехвиашвили
и А. А. Потаповым в июне 2007 г.
[2]
Интересно отметить, что наш пионерский метод реализации фрактального
конденсатора на основе радиофизического моделирования дробных операторов очень
заинтересовал многих исследователей в мире. Почти на всех зарубежных и
отечественных конференциях по фракталам, дробным операторам и близкой тематике
с 2006 г. автору задают вопросы по данному направлению и просят рассказать все
более подробно о фрактальном конденсаторе. В свое время мы не придавали слишком
большого значения этому рядовому, с нашей точки зрения, физическому и
компьютерному эксперименту (но, как видим, заблуждались…).
[3] Экспериментальные данные представлены д.ф.-м.н. Е.В. Сухониным. Результаты фрактальной обработки (В.А. Герман и А.А. Потапов) были доложены на “Progress in Electromagnetics Research Symp. (PIERS 2009)”, 18 - 21 August, 2009, Moscow, Russia и опубликованы в “Proc. PIERS” (Cambridge, MA: Electromagnetics Academy), 2009, pp. 1813-1817.
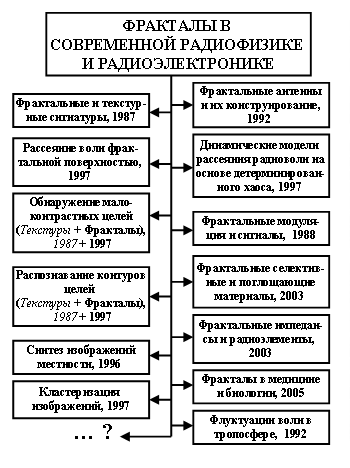
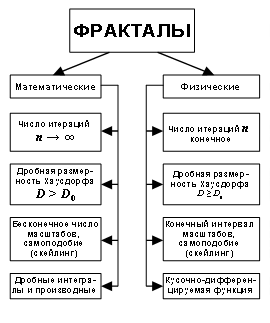
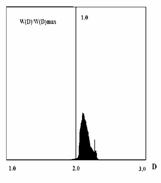
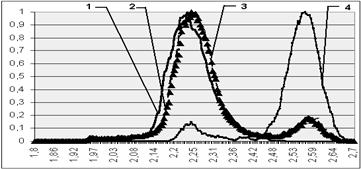
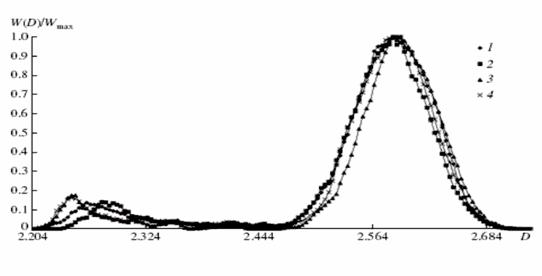
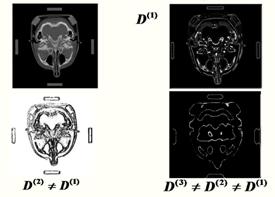
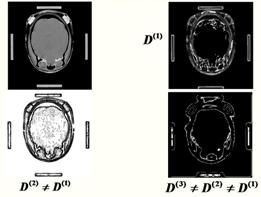
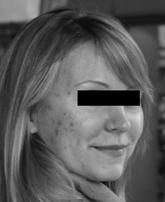

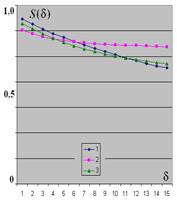 (в)
(в)