УДК 621.396.67
СОГЛАСОВАНИЕ РЕШЕТКИ ПЛАНАРНЫХ ДИЭЛЕКТРИЧЕСКИХ ВОЛНОВОДОВ
С. Е. Банков 1, А. В. Клементьева 2
1 ИРЭ им. В.А. Котельникова РАН, 2 НИУ МЭИ
Получена 18 января 2013 г.
Аннотация. Решается задача согласования решетки планарных диэлектрических волноводов в широком секторе сканирования. Рассматриваются бесконечные решетки планарных диэлектрических волноводов. Решетка возбуждается плоскими волнами свободного пространства, падающими на ее поверхность под произвольным углом падения. Рассматривается численное решение граничной задачи, полученное с помощью периодических граничных условий методом конечных элементов. Обсуждаются вопросы, связанные с построением адекватной модели для численного анализа. Рассматривается приближенное решение методом эффективной диэлектрической проницаемости. Приводятся результаты сопоставления строгого и приближенного решений. Рассматриваются возможности улучшения согласования решетки в диапазонах углов сканирования и частот.
Ключевые слова: интегральные антенны миллиметрового диапазона, линзы с принудительным преломлением, планарный диэлектрический волновод, плоский волновод.
Abstract. The problem of matching of array of planar dielectric waveguides with free space in a wide range of angles is solved. Infinite array of planar dielectric waveguides is considered. Array is excited by free space plane waves that incident on an array surface under the arbitrary angle of incidence. Numerical solution of boundary problem obtained with help of periodical boundary conditions and finite elements method is considered. Specific features of numerical model are discussed. Approximate solution for array of planar dielectric waveguides is considered. Comparison of results obtained with help of numerical and approximate solutions is presented. A way to improve the array matching with free space is proposed.
Keywords: integral millimeter wave antennas, planar dielectric waveguide, parallel plate waveguide, array of planar waveguides.
1. Постановка задачи
Техническое освоение коротковолновой части миллиметрового и субмиллиметрового диапазонов (КЧ ММД и СММД) делает актуальной задачу поиска новых технологий построения экономичных СВЧ устройств указанных диапазонов. К их числу относятся антенны и антенные решетки. Достижение высокой технологичности в СВЧ технике традиционно связывают с использованием технологии печатных схем [1], которые обладают высокой повторяемостью, низкой стоимостью и т.д.
В технике дециметрового и сантиметрового диапазонов активно используются печатные антенны. Они могут выполнять функцию одиночного излучателя или объединяться в систему – антенную решетку (АР). Традиционно печатные АР содержат две важные части: излучающая решетка и схема ее возбуждения. В относительно низкочастотных диапазонах схемы возбуждения выполняются на основе печатных линий передачи: микрополосковых, полосковых, копланарных и т.д. С повышением частоты такие технические решения становятся неэффективными [2] вследствие роста тепловых потерь в указанных линиях передачи. Поэтому при переходе в ММД их заменили волноводы разных видов: металлические, диэлектрические, щелевые.
Дальнейшее продвижение в КЧ ММД может быть связано с отказом от волноводного способа построения схемы возбуждения АР и переходом к квазиоптическому способу возбуждения АР.
В последнее время появился ряд технических решений в данной области, в которых схемы возбуждения печатных АР строятся на основе таких квазиоптических элементов, как зеркала и линзы. Здесь можно отметить многолучевую щелевую АР, которая возбуждается двухзеркальной оптической системой Кассегрена [3]. Схематично она показана на рис. 1.
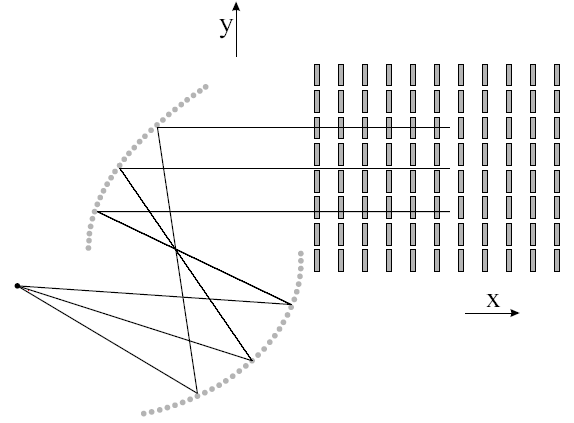
Рис. 1. Планарная зеркальная антенна
В работе [4] рассматриваются ленточные АР, которые возбуждаются линзовыми схемами. Роль планарной линзы выполняет область диэлектрической подложки, в которой на ее поверхностях размещаются ленточные периодические решетки (см. Рис. 2).
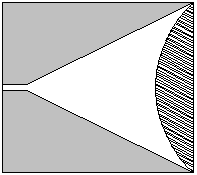
Рис. 2. Возбудитель ленточной решетки на основе планарной линзы
В указанных работах показано, что подложка с ленточными решетками может рассматриваться как среда с принудительным преломлением [5], которая позволяет проектировать широкоугольные линзовые системы. В работе [6] рассматривается двухслойное планарное зеркало, которое используется для построения схемы возбуждения щелевой решетки на основе ПВ.
Отметим, что в перечисленных работах рассматриваются планарные остронаправленные антенны, построенные по схеме, в которой амплитудно – фазовое распределение поля по одной координате формируется квазиоптическим возбудителем на основе линзы или зеркала, а по другой координате решеткой бегущей волны. Основным достоинством таких антенн является их технологичность, поскольку они могут быть выполнены в виде единой печатной схемы. Вместе с тем, антенны с последовательным возбуждением, к которым относятся решетки бегущей волны, имеют ряд известных недостатков [7]. Среди них следует отметить ограниченную полосу рабочих частот, обусловленную эффектом частотного сканирования.
Указанный недостаток может быть устранен в антенне на основе линзы, показанной на рис. 3. Она представляет собой решетку планарных диэлектрических волноводов (ПДВ) или диэлектрических пластин.
В каждом ПДВ сформирована планарная линза, осуществляющая заданный тип преобразования фазового фронта волны. Все вместе планарные линзы образуют одну трехмерную линзу, которая преобразует сферическую волну, создаваемую облучателем, в плоскую волну на выходе линзы. Синтез линз на основе ПДВ представляет собой самостоятельную проблему, которая в данной работе не рассматривается. Для нас важно отметить, что согласование линзы данного типа сводится к задаче согласования решетки диэлектрических пластин. Отметим также, что в силу электродинамических свойств ПДВ линзы на их основе работают на волнах, поляризованных параллельно плоскости пластин, которые также принято называть Н – волнами [8].
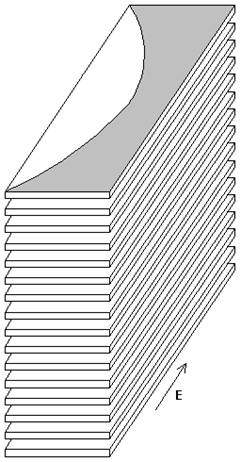
Рис. 3. Линзовая антенна на основе планарных линз для Н – волн
Известно, что ПДВ является двухмодовой линией передачи, в которой существуют две волны, не имеющие критических частот. Эти волны отличаются плоскостью поляризации. Одна из них является Е – волной, а другая Н – волной. По ряду причин для создания планарных линз на ПДВ удобнее оказываются Н – волны.
Отметим, что интерес к антеннам, аналогичным антенне, представленной на рис. 3, обусловлен следующими факторами. Они представляют собой совокупность технологичных планарных структур, каждая из которых выполняется в виде печатной схемы. С другой стороны, они не имеют ограничений на полосу рабочих частот, характерных для решеток с последовательным возбуждением. Следует также отметить, что в линзовых антеннах достаточно просто реализуется многолучевой режим, в котором может осуществляться в некотором секторе углов обзор пространства. Кроме того, облучатель линзы также может быть выполнен в виде набора печатных схем, которые не ухудшат технологичность всего устройства в целом.
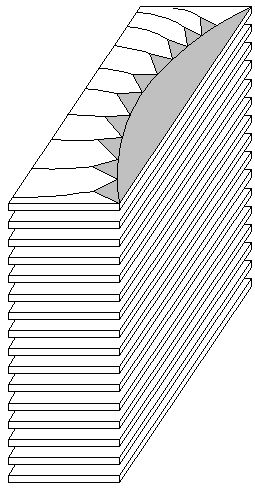
Рис. 4. Облучатель линзовой антенны
Пример выполнения облучателя показан на рис. 4. Отметим, что для его функционирования задача согласования со свободным пространством также является актуальной и она также сводится к задаче согласования решетки диэлектрических пластин.
2. Ограничения на параметры структуры, методы анализа
Рассмотрим задачу согласования со свободным
пространством решетки ПДВ. Будем решать эту задачу в приближении бесконечной
решетки полубесконечных волноводов. Эта структура показана на рис. 5. Она
возбуждается плоской волной свободного пространства, падающей на ее границу при
![]() . Направление распространения волны
характеризуем углами в сферической системе координат
. Направление распространения волны
характеризуем углами в сферической системе координат ![]() .
Углы отсчитываются обычным образом: угол
.
Углы отсчитываются обычным образом: угол ![]() от оси
0z, а угол
от оси
0z, а угол ![]() от оси 0х.
от оси 0х.
Будем рассматривать структуры с периодом ![]() , меньшим половины длины волны
, меньшим половины длины волны ![]() в свободном пространстве. Это ограничение
обеспечивает отсутствие в пространственном спектре решетки распространяющихся в
области
в свободном пространстве. Это ограничение
обеспечивает отсутствие в пространственном спектре решетки распространяющихся в
области ![]() волн высших типов при любых углах
волн высших типов при любых углах ![]() . Отметим, что требование отсутствия таких
волн является естественным для нормального функционирования линзы.
. Отметим, что требование отсутствия таких
волн является естественным для нормального функционирования линзы.
Следует отметить, что хорошее согласование
рассматриваемой структуры в широком диапазоне углов ![]() будет
крайне затруднительно, особенно при высокой диэлектрической проницаемости ПДВ.
Достижение малых коэффициентов отражения потребует использования дополнительных
согласующих элементов, о которых мы еще будем говорить ниже.
будет
крайне затруднительно, особенно при высокой диэлектрической проницаемости ПДВ.
Достижение малых коэффициентов отражения потребует использования дополнительных
согласующих элементов, о которых мы еще будем говорить ниже.
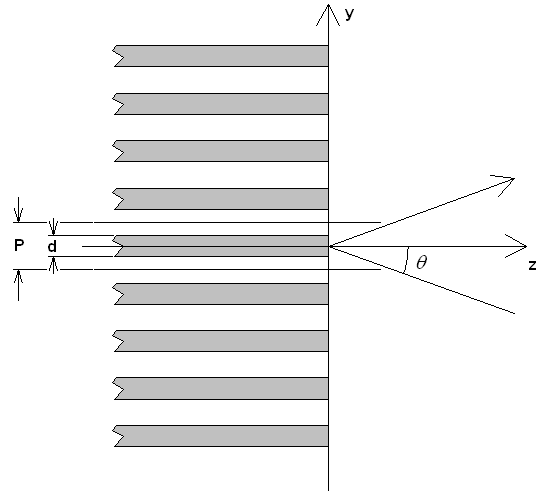
Рис. 5. Решетка диэлектрических пластин
Тем не менее, прежде чем переходить к исследованию более сложных структур, полезным оказывается построение эффективной модели простого сочленения решетки ПДВ со свободным пространством. Данная модель будет далее использована для анализа решетки с согласующим слоем.
Для построения модели решетки будем использовать два подхода. Один из них основан на строгом численном решении электродинамической задачи методом конечных элементов, который реализован в системе HFSS [9]. Другой подход приближенный. Его можно назвать методом эффективной диэлектрической проницаемости (ЭДП). В рамках этого метода исследуются собственные волны периодической структуры из диэлектрических пластин. Далее данная структура рассматривается как эквивалентная однородная среда с эффективной диэлектрической проницаемостью и характеристическим сопротивлением, которые находятся из анализа собственных волн. На последнем этапе решается задача о дифракции плоской волны на границе полубесконечной эквивалентной среды, из которой находится искомый коэффициент отражения. Структура в виде полубесконечной эквивалентной среды рассматривается как модель исследуемой решетки.
Мы будем сравнивать коэффициенты отражения, полученные двумя разными подходами. Сравнение позволит нам сделать вывод о пределах применимости метода ЭДП. Забегая вперед, отметим, что приближенный метод ЭДП показал весьма высокую точность во всем исследованном диапазоне диэлектрических проницаемостей. Поэтому далее на его основе строится модель решетки с согласующим слоем. Она также проверяется путем сравнения со строгим решением и используется для поиска оптимальных параметров структуры.
3. Модель для численного решения
Рассмотрим далее особенности численной модели, которая использовалась для расчетов в системе HFSS.
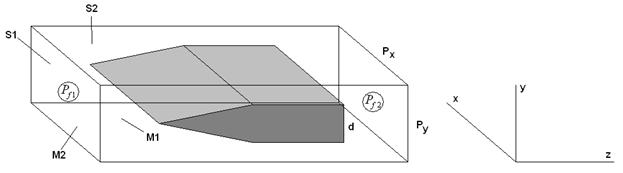
Рис. 6. Модель для расчета в HFSS
Она показана на
рис. 6. Параллелепипед на рис. 6 ограничивает область пространства, в которой
ищется электромагнитное поле. Переход от бесконечной структуры к конечной
модели возможен благодаря использованию периодических граничных условий [9].
Эти условия устанавливаются в парах плоскостей ![]() и
и ![]() . Поля в этих плоскостях связаны фазовыми
множителями, которые определяются углами
. Поля в этих плоскостях связаны фазовыми
множителями, которые определяются углами ![]() . В HFSS пара плоскостей, на которых устанавливаются
периодические граничные условия, условно делится на плоскость master и плоскость slave. Фаза на
плоскости master равна нулю, а на плоскости slave она задается углами
. В HFSS пара плоскостей, на которых устанавливаются
периодические граничные условия, условно делится на плоскость master и плоскость slave. Фаза на
плоскости master равна нулю, а на плоскости slave она задается углами ![]() .
.
Отметим, что структура в виде канала с прямоугольным сечением, на поверхностях которого установлены периодические граничные условия, носит название канала Флоке. Канал Флоке – это волновод специального вида, позволяющий моделировать бесконечные периодические структуры. Таким образом, мы видим из рис. 6, что анализ бесконечной решетки сводится нами к анализу диэлектрической неоднородности, расположенной внутри канала Флоке.
Установка
периодических граничных условий при ![]() может вызвать
возражения, так как периодичность вдоль оси 0х отсутствует. Вдоль нее структура
однородна. Однородность структуры не препятствует корректному использованию
периодических граничных условий [9]. При этом период
может вызвать
возражения, так как периодичность вдоль оси 0х отсутствует. Вдоль нее структура
однородна. Однородность структуры не препятствует корректному использованию
периодических граничных условий [9]. При этом период ![]() может
выбираться произвольно. Целесообразно сделать его меньшим половины длины волны,
чтобы исключить влияние высших типов волн. Строго говоря, они вообще не должны
возбуждаться. Однако в ходе численного анализа из-за неидеального разбиения
пространства на ячейки они могут возникнуть и исказить общую картину. Период
может
выбираться произвольно. Целесообразно сделать его меньшим половины длины волны,
чтобы исключить влияние высших типов волн. Строго говоря, они вообще не должны
возбуждаться. Однако в ходе численного анализа из-за неидеального разбиения
пространства на ячейки они могут возникнуть и исказить общую картину. Период ![]() равен реальному периоду решетки
равен реальному периоду решетки ![]() .
.
На гранях параллелепипеда параллельных плоскости ХOY устанавливаются граничные условия типа порт Флоке, которые позволяют осуществлять возбуждение структуры собственными волнами канала Флоке, свойства которых идентичны свойствам плоских волн свободного пространства.
Диэлектрическая
неоднородность внутри канала Флоке имеет вид пластины. С одной стороны при ![]() пластина имеет резкий обрыв также, как в
реальной решетке. С другой стороны она имеет клиновидный переход. Справа и
слева от неоднородности располагаются отрезки регулярного канала Флоке. Наличие
таких отрезков необходимо для корректной установки портов Флоке, которые могут
быть введены только в поперечном сечении регулярного канала Флоке. По этой
причине невозможно продлить диэлектрическую пластину до пересечения с портом
Флоке.
пластина имеет резкий обрыв также, как в
реальной решетке. С другой стороны она имеет клиновидный переход. Справа и
слева от неоднородности располагаются отрезки регулярного канала Флоке. Наличие
таких отрезков необходимо для корректной установки портов Флоке, которые могут
быть введены только в поперечном сечении регулярного канала Флоке. По этой
причине невозможно продлить диэлектрическую пластину до пересечения с портом
Флоке.
Клиновидный переход обеспечивает плавную трансформацию волн регулярного канала Флоке в волны канала, частично заполненного диэлектриком. Длина клина выбирается таким образом, чтобы коэффициент отражения от него был много меньше коэффициента отражения от обрыва диэлектрической пластины. При выполнении этого условия общий коэффициент отражения от диэлектрической неоднородности можно считать равным коэффициенту отражения от обрыва пластины, который равен коэффициенту отражения от решетки на рис. 5. На практике сделать коэффициент отражения от клина пренебрежимо малым весьма затруднительно, так как это требует существенного увеличения его длины. При этом резко возрастают затраты компьютерных ресурсов, необходимых для получения численного решения с гарантированной точностью. Поэтому влияние отражения от клина учитывалось при обработке результатов расчетов с помощью специальной методики, о которой речь пойдет ниже.
Следует отметить, что канал Флоке является двухмодовым волноводом. Наличие двух основных распространяющихся в нем волн, не имеющих критических частот, соответствует двум Т – волнам свободного пространства с ортогональными плоскостями поляризации. Одна из них имеет вектор электрического поля, преимущественно ориентированный вдоль оси 0х, а другая вдоль оси 0у. Как отмечено выше, с практической точки зрения больший интерес представляет волна, поляризованная в плоскости ХОZ.
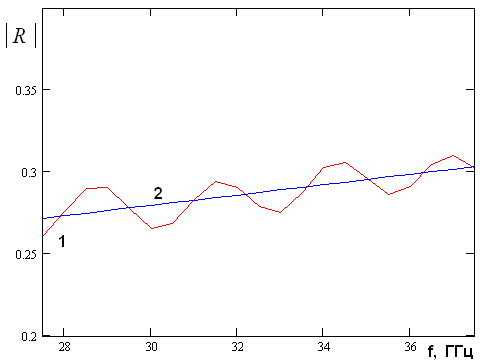
Рис. 7. Частотная зависимость модуля коэффициента
отражения при ![]() , d=1.25,
Р=4,
, d=1.25,
Р=4, ![]() ,
, ![]()
Численные расчеты
проводились для волн, падающих в двух главных плоскостях, соответствующих ![]() и
и ![]() . На
рис. 7 показана частотная зависимость модуля коэффициента отражения от модели,
изображенной на рис. 6. Она получена для
. На
рис. 7 показана частотная зависимость модуля коэффициента отражения от модели,
изображенной на рис. 6. Она получена для ![]() , d=1.25, Р=4,
, d=1.25, Р=4, ![]() ,
, ![]() . Все размеры здесь и далее приводятся в
миллиметрах. Отметим, что рассматриваемая нами структура с точки зрения цепей
СВЧ является недиссипативным четырехполюсником. Известно, что в таком
четырехполюснике коэффициенты отражения на разных его входах равны по модулю
[10]. Поэтому далее мы можем при описании коэффициентов отражения избегать
применения стандартных двойных индексов и использовать более удобное
обозначение
. Все размеры здесь и далее приводятся в
миллиметрах. Отметим, что рассматриваемая нами структура с точки зрения цепей
СВЧ является недиссипативным четырехполюсником. Известно, что в таком
четырехполюснике коэффициенты отражения на разных его входах равны по модулю
[10]. Поэтому далее мы можем при описании коэффициентов отражения избегать
применения стандартных двойных индексов и использовать более удобное
обозначение ![]() .
.
Кривая 1 на рис. 7 получена непосредственно из численного решения электродинамической задачи. Видно, что кривая 1 имеет некоторый средний уровень, на который накладываются колебания. Средний уровень задается волной отраженной от обрыва пластины, а небольшие по амплитуде колебания порождаются ее интерференцией с волной отраженной от клина. Усреднение по частоте дает нам медленно меняющуюся кривую 2, которую можно рассматривать в качестве частотной зависимости модуля коэффициента отражения от обрыва пластины. Описанная выше методика обработки численных данных применялась ко всем исследованным структурам для определения интересующего нас параметра.
4. Приближенная модель
Рассмотрим далее модель, полученную в рамках метода ЭДП. Кратко опишем вывод дисперсионного уравнения, из которого находятся постоянные распространения собственных волн решетки диэлектрических пластин. Период анализируемой структуры показан на рис. 8.
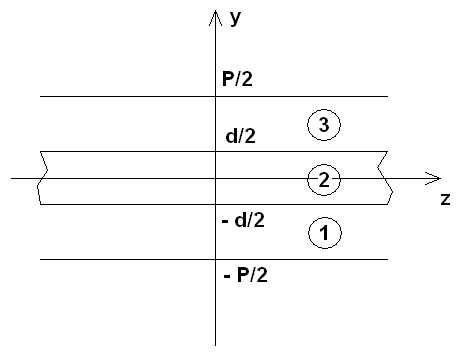
Рис. 8. Период решетки диэлектрических пластин
Предполагаем, что
пластина бесконечна в плоскости XOZ. Поскольку
структура изотропна в данной плоскости, то мы без потери общности можем
рассматривать волны, распространяющиеся вдоль оси 0z.
При этом их поля не зависят от координаты ![]() , то
есть решаемая задача двумерная. В двумерной структуре поля разделяются на Е и Н
– волны. Как отмечалось выше, нас интересуют Н – волны, имеющие компоненты
, то
есть решаемая задача двумерная. В двумерной структуре поля разделяются на Е и Н
– волны. Как отмечалось выше, нас интересуют Н – волны, имеющие компоненты ![]() . Компоненту электрического поля
. Компоненту электрического поля ![]() ищем в следующем виде:
ищем в следующем виде:
![]() ,
,
![]() ,
(1)
,
(1)
![]() ,
,
![]() ,
, ![]() ,
,
где ![]() -
неизвестные постоянные, индексы 1,2,3 соответствуют полям в разных областях
(см. рис. 8),
-
неизвестные постоянные, индексы 1,2,3 соответствуют полям в разных областях
(см. рис. 8), ![]() - неизвестная постоянная
распространения волны,
- неизвестная постоянная
распространения волны, ![]() - волновое число свободного
пространства,
- волновое число свободного
пространства, ![]() - относительная диэлектрическая
проницаемость пластины. Множитель
- относительная диэлектрическая
проницаемость пластины. Множитель ![]() , описывающий
зависимость поля от координаты z в выражениях (1)
опущен. Компоненты магнитного поля могут быть получены из (1) с помощью
уравнений Максвелла.
, описывающий
зависимость поля от координаты z в выражениях (1)
опущен. Компоненты магнитного поля могут быть получены из (1) с помощью
уравнений Максвелла.
Поля должны
удовлетворять граничным условиям при ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
(2)
,
(2)
![]() ,
,
![]() , (3)
, (3)
![]() .
.
Граничные условия
непрерывности тангенциальных компонент поля (2) установлены на поверхностях
пластины. Условия (3) установлены на границах периода структуры. Они описывают
квазипериодичность поля в решетке, которая заключается в том, что поля в
соседних периодах равны друг другу с точностью до фазового множителя ![]() , где
, где ![]() -
постоянная задающая фазовый сдвиг между полями в соседних периодах.
-
постоянная задающая фазовый сдвиг между полями в соседних периодах.
Постоянная ![]() связана с углами
связана с углами ![]() из
задачи о падении на границу периодической структуры плоской волны:
из
задачи о падении на границу периодической структуры плоской волны:
![]() . (4)
. (4)
Таким образом, на
этапе исследования собственных волн решетки пластин мы считаем параметр ![]() заданной величиной.
заданной величиной.
Дальнейшее решение
граничной задачи связано с подстановкой выражений для полей в граничные условия
(2) и (3). Данная операция приводит нас к системе линейных алгебраических
уравнений относительно коэффициентов ![]() . Мы имеем шесть
неизвестных и шесть уравнений. Далее воспользуемся условием существования
нетривиальных решений системы, приравняв ее определитель нулю. Условие
равенства определителя нулю дает нам искомое уравнение относительно постоянной
распространения
. Мы имеем шесть
неизвестных и шесть уравнений. Далее воспользуемся условием существования
нетривиальных решений системы, приравняв ее определитель нулю. Условие
равенства определителя нулю дает нам искомое уравнение относительно постоянной
распространения ![]() . Уравнения такого типа получили
название дисперсионных уравнений. Для них возможно только численное решение.
. Уравнения такого типа получили
название дисперсионных уравнений. Для них возможно только численное решение.
Приводить в явном виде громоздкое
дисперсионное уравнение мы не будем, а рассмотрим некоторые результаты его
решения. На рис. 9 приведена зависимость коэффициента замедления ![]() собственных волн решетки от угла
собственных волн решетки от угла ![]() . Кривые 1 и 2 получены при
. Кривые 1 и 2 получены при ![]() ,
, ![]() ,
, ![]() ,
, ![]() =30
ГГц. Они соответствуют разным корням дисперсионного уравнения. Кривая 1
описывает основную волну, а кривая 2 волну высшего типа. Угол
=30
ГГц. Они соответствуют разным корням дисперсионного уравнения. Кривая 1
описывает основную волну, а кривая 2 волну высшего типа. Угол ![]() вводится соотношением (4) при
вводится соотношением (4) при ![]() . Он задает параметр
. Он задает параметр ![]() .
.
Коэффициент замедления
основной волны слабо зависит от угла ![]() . Такое поведение
данного параметра соответствует слабой связи волн в соседних пластинах.
Известно, что волны в слое диэлектрика являются поверхностными волнами, поле
которых экспоненциально затухает при удалении от слоя. Поэтому, удаляя пластины
на достаточное расстояние, можно свести взаимодействие поверхностных волн к нулю.
. Такое поведение
данного параметра соответствует слабой связи волн в соседних пластинах.
Известно, что волны в слое диэлектрика являются поверхностными волнами, поле
которых экспоненциально затухает при удалении от слоя. Поэтому, удаляя пластины
на достаточное расстояние, можно свести взаимодействие поверхностных волн к нулю.
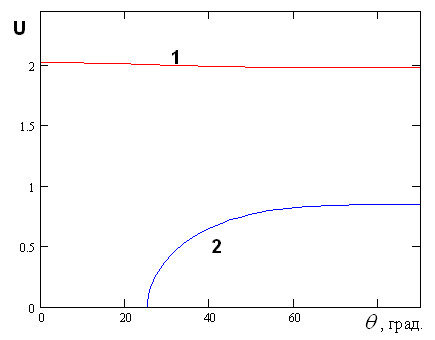
Рис. 9. Зависимость коэффициента замедления от угла ![]() при
при ![]()
Очевидно, что уменьшение периода должно увеличивать связь между волнами в пластинах. При этом зависимость коэффициента замедления от угла станет более ярко выраженной.
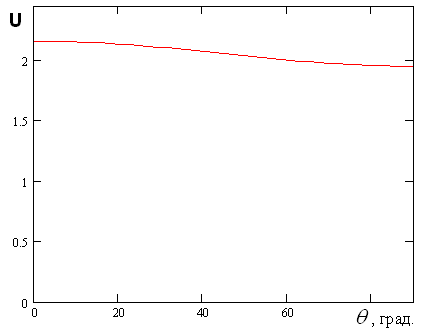
Рис. 10. Зависимость коэффициента замедления от угла ![]() при
при ![]()
Подтверждением
приведенных выше соображений служит кривая на рис. 10, которая получена при тех
же параметрах, что и рис. 9, за исключением того, что теперь ![]() .
.
Можно отметить, что
с уменьшением периода параметр ![]() действительно сильнее
меняется при изменении угла
действительно сильнее
меняется при изменении угла ![]() . Интересно также то,
что теперь распространяющихся высших типов волн в структуре нет.
. Интересно также то,
что теперь распространяющихся высших типов волн в структуре нет.
В дальнейшем нас
будет интересовать основная волна периодической структуры. Используя найденную
из решения дисперсионного уравнения постоянную распространения основной волны,
введем характеристическое сопротивление эквивалентной анизотропной среды ![]() .
.
Определим параметр ![]() через отношение тангенциальных к
плоскости XOY компонент электрического и магнитного
полей:
через отношение тангенциальных к
плоскости XOY компонент электрического и магнитного
полей:
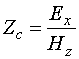 . (5)
. (5)
При этом мы будем рассматривать произвольное направление распространение волны в плоскости XOZ. В этом случае с помощью соотношений для компонент поля магнитных волн в декартовой системе координат [11] получаем следующее выражение:
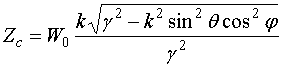 , (6)
, (6)
![]() -
волновое сопротивление свободного пространства.
-
волновое сопротивление свободного пространства.
Аналогично вводим
характеристическое сопротивление магнитной волны в свободном пространстве ![]() :
:
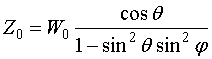 . (7)
. (7)
Коэффициент отражения волны свободного пространства от поверхности эквивалентной среды находим как коэффициент отражения от сочленения двух линий передачи с разными характеристическими сопротивлениями [10]:
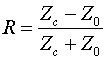 . (8)
. (8)
Нетрудно увидеть, что модель, описанная выше, не учитывает многих физических эффектов. К их числу относится преобразование магнитных волн в электрические волны. Также она не учитывает возбуждение на границе решетки полубесконечных пластин волн высших типов. Тем не менее, ниже будет показано, что эти эффекты имеют второй порядок малости по сравнению с основным эффектом взаимодействия волн одинакового типа. Доказательством этого утверждения могут служить сопоставление результатов, полученных по формуле (8) и путем численного решения граничной задачи.
5. Сопоставление результатов для решетки диэлектрических пластин
На рис. 11 показана
зависимость модуля коэффициента отражения от угла ![]() .
.
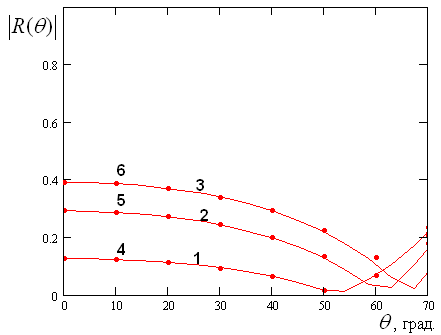
Рис. 11. Зависимость модуля
коэффициента отражения от угла ![]() при
при ![]()
Кривые 1,2, 3 и точки 4,5,6
получены при ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ГГц.
ГГц.
Кривые 1 – 3 получены по
формуле (8), а точки 4 – 6 с помощью HFSS. Видно, что результаты строго решения и приближенной модели весьма
хорошо совпадают вплоть до угла ![]() . Важно, что хорошее
совпадение наблюдается, в том числе и для пластин с достаточно большой
проницаемостью, равной десяти.
. Важно, что хорошее
совпадение наблюдается, в том числе и для пластин с достаточно большой
проницаемостью, равной десяти.
Аналогичная картина имеет
место при ![]() . Кривые зависимости модуля коэффициента отражения от угла
. Кривые зависимости модуля коэффициента отражения от угла ![]() в указанной плоскости приведены на рис.
12. Обозначения кривых и точек на рис. 12 такие же, как на рис. 11.
в указанной плоскости приведены на рис.
12. Обозначения кривых и точек на рис. 12 такие же, как на рис. 11.
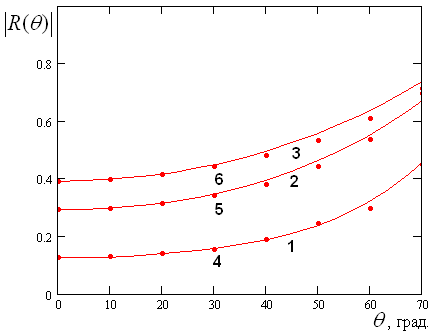
Рис. 12. Зависимость модуля коэффициента отражения от угла ![]() при
при ![]()
Кривые на рис.
11,12 показывают также, что добиться хорошего согласования рассматриваемой
решетки в широком секторе углов весьма непросто, начиная с ![]() . Коэффициент отражения в плоскости
. Коэффициент отражения в плоскости ![]() меньше, чем в плоскости
меньше, чем в плоскости ![]() за счет эффекта аналогичного эффекту
Брюстера [11], который наблюдается при дифракции волны, поляризованной в
плоскости падения на границе раздела двух сред. Нетрудно увидеть, что Н – волна
при
за счет эффекта аналогичного эффекту
Брюстера [11], который наблюдается при дифракции волны, поляризованной в
плоскости падения на границе раздела двух сред. Нетрудно увидеть, что Н – волна
при ![]() , также поляризована в плоскости падения,
то есть в плоскости XOZ. Ее коэффициент отражения
уменьшается при увеличении угла
, также поляризована в плоскости падения,
то есть в плоскости XOZ. Ее коэффициент отражения
уменьшается при увеличении угла ![]() . При некотором угле
. При некотором угле ![]() , который можно по аналогии с упомянутым
выше случаем называть углом Брюстера, он обращается в нуль. Однако в нашем
случае значение угла Брюстера отличается от полученного в работе [11].
Выражение для него при
, который можно по аналогии с упомянутым
выше случаем называть углом Брюстера, он обращается в нуль. Однако в нашем
случае значение угла Брюстера отличается от полученного в работе [11].
Выражение для него при ![]() имеет следующий вид:
имеет следующий вид:
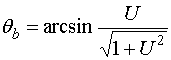 . (9)
. (9)
При других
значениях угла ![]() точка, в которой коэффициент
отражения равен нулю, может быть найдена только численно, поскольку замедление
точка, в которой коэффициент
отражения равен нулю, может быть найдена только численно, поскольку замедление ![]() является функцией угла
является функцией угла ![]() .
.
В
плоскости ![]() решетка согласована хуже, чем при
решетка согласована хуже, чем при ![]() и коэффициент отражения растет с ростом
параметра
и коэффициент отражения растет с ростом
параметра ![]() . Поэтому мы можем сделать вывод о том,
что достижение приемлемого уровня коэффициента отражения требует применения
дополнительных средст, улучшающих согласование решетки. Пусть максимальное
значение коэффициента отражения
. Поэтому мы можем сделать вывод о том,
что достижение приемлемого уровня коэффициента отражения требует применения
дополнительных средст, улучшающих согласование решетки. Пусть максимальное
значение коэффициента отражения ![]() лежит в диапазоне 0.2
– 0.3.
лежит в диапазоне 0.2
– 0.3.
6. Решетка с согласующим слоем
Улучшение
согласования решетки диэлектрических пластин может быть достигнуто разными
способами. Мы рассмотрим один из них. Решетка с улучшенным согласованием
показана на рис. 13. Она содержит согласующий слой, в котором диэлектрические
пластины имею меньшую толщину ![]() . Толщина согласующего
слоя
. Толщина согласующего
слоя ![]() и толщина пластин
и толщина пластин ![]() выбираются
из условия минимизации коэффициента отражения.
выбираются
из условия минимизации коэффициента отражения.
Расчет решетки с
согласующим слоем в рамках приближенной модели сводится к расчету структуры,
показанной на рис. 14. Она представляет собой сочленение трех линий передачи с
разными характеристическими сопротивлениями и разными постоянными
распространения. Линия передачи с сопротивлением ![]() описывает
решетку пластин толщиной
описывает
решетку пластин толщиной ![]() . Линия с
сопротивлением
. Линия с
сопротивлением ![]() соответствует согласующему слою
и линия с сопротивлением
соответствует согласующему слою
и линия с сопротивлением ![]() описывает свободное
пространство.
описывает свободное
пространство.
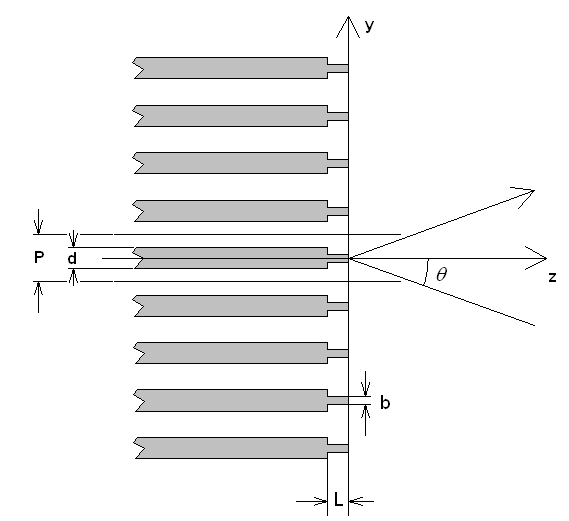
Рис. 13. Решетка с улучшенным согласованием
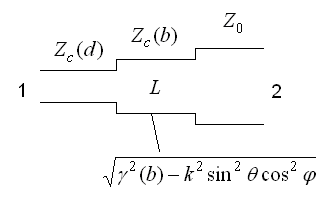
Рис. 14. Схема для расчета решетки с согласующим слоем
Постоянная
распространения волны в согласующем слое, описывающая изменение фазы поля вдоль
оси 0z ![]() в
согласующем слое описывается следующим выражением:
в
согласующем слое описывается следующим выражением:
![]() , (10)
, (10)
где ![]() -
постоянная распространения, полученная из решения двумерной задачи (см.
рис. 8)
для пластин толщиной
-
постоянная распространения, полученная из решения двумерной задачи (см.
рис. 8)
для пластин толщиной ![]() . Отметим, что отличие постоянной
распространения
. Отметим, что отличие постоянной
распространения ![]() от решения двумерной задачи
обусловлено тем, что в двумерной структуре волна бежит вдоль оси 0z и ее поле от координаты
от решения двумерной задачи
обусловлено тем, что в двумерной структуре волна бежит вдоль оси 0z и ее поле от координаты ![]() не
зависит. При падении плоской волны на решетку поле вдоль оси 0х меняется.
Поэтому меняется и его поведение вдоль оси 0z. Эти
изменения приводят к отличию
не
зависит. При падении плоской волны на решетку поле вдоль оси 0х меняется.
Поэтому меняется и его поведение вдоль оси 0z. Эти
изменения приводят к отличию ![]() от
от ![]() . При
. При ![]() , когда
волна падает по нормали, обе постоянные распространения совпадают. При этом поле
в решетке не меняется вдоль оси 0х также как в двумерной структуре.
, когда
волна падает по нормали, обе постоянные распространения совпадают. При этом поле
в решетке не меняется вдоль оси 0х также как в двумерной структуре.
Входное сопротивление на входе 2 можно определить по известной формуле [10]:
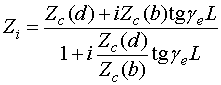 . (11)
. (11)
Далее находим
коэффициент отражения ![]() :
:
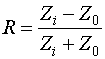 . (12)
. (12)
Коэффициент отражения находился также из численного решения. Модель для численных расчетов модифицировалась, как показано на рис. 15 с учетом введенных изменений в структуру.
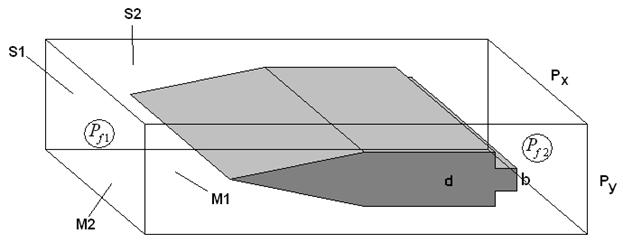
Рис. 15. Модель для численного исследования решетки с согласующим слоем
На рис. 16 и 17
показаны зависимости коэффициента отражения от угла ![]() в
плоскостях
в
плоскостях ![]() и
и ![]() соответственно.
соответственно.
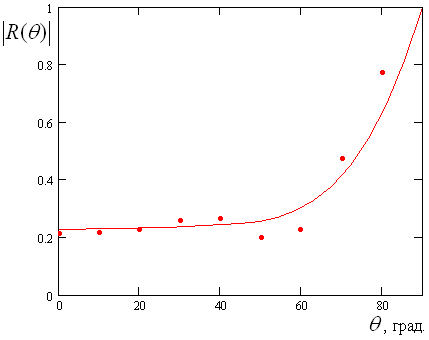
Рис. 16. Модуль коэффициента отражения при ![]()
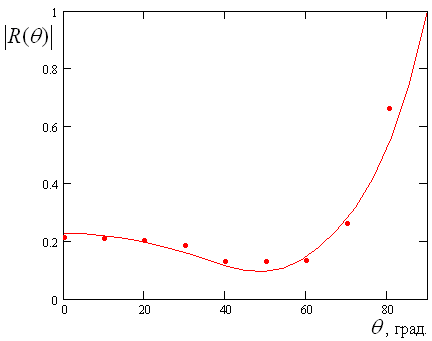
Рис. 17. Модуль коэффициента отражения при ![]()
Точки получены путем
численного решения граничной задачи, а сплошные кривые из приближенной модели
(12). Расчеты проводились для следующих параметров: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
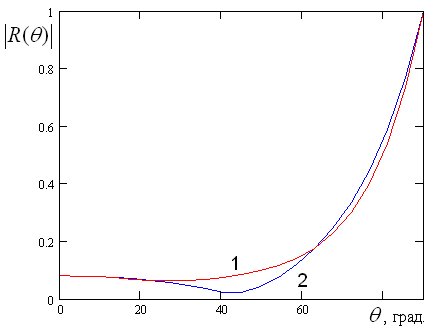
Рис. 18. Зависимость модуля коэффициента отражения при ![]()
Видно, что результаты
расчетов, полученных разными методами, достаточно близки, что подтверждает
возможность использования приближенной модели для оптимизации решетки с
согласующим слоем. На рис. 18 и 19 показаны зависимости модуля коэффициента
отражения от угла ![]() . Кривые 1,2 на рис. 18 получены
при следующих параметрах:
. Кривые 1,2 на рис. 18 получены
при следующих параметрах: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ГГц. Кривые 1,2 на рис. 19 получены для
ГГц. Кривые 1,2 на рис. 19 получены для ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ГГц.
Кривые 1 и 2 на рис. 18 и 19 соответствует
ГГц.
Кривые 1 и 2 на рис. 18 и 19 соответствует ![]() и
и ![]() .
.
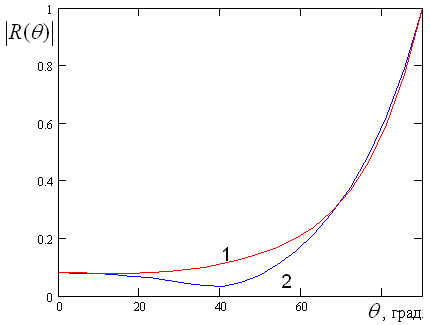
Рис. 19. Зависимость модуля коэффициента отражения при ![]()
Видно, что с
помощью согласующего слоя можно получить максимальный коэффициент отражения ![]() на уровне 0.2 в диапазоне углов
на уровне 0.2 в диапазоне углов ![]() меньших
меньших ![]() для
для ![]() и
и ![]() для
для ![]() .
.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 12-08-12003/12 офи_м.
1. Нефедов Е.И., Фиалковский А.Т. Полосковые линии передачи. М.: Наука, 1980.
2. Банков С.Е. Щелевые интегральные схемы миллиметрового диапазона // Радиотехника и электроника. 2006, Т. 51, №9, С. 1066-1086.
3. M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, Vol.6, pp. 537-539, Dec. 2007.
4. Bankov S.E., Douplenkova M.D., Kalinichev V.I., Kozin V.N., Levchenko I.V., Kuranov U.V., Rodionova E.V., Vasjukov V.D. 60 GHz Sensors Based on Dielectric Slotted Waveguide // 22nd European Microwave Conf. Proc. of Workshop “Commercial Applications of Microwave and Millimeter Waves”, 1992, p.p. 41-46.
5. Корнблит С. СВЧ оптика. Оптические принципы в приложении к конструированию СВЧ антенн. М.: Связь. 1980.
6. Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.
7. Уолтер К. Антенны бегущей волны. М.: Энергия, 1970.
8. Взятышев В.Ф. Диэлектрические волноводы. М.: Сов. Радио. 1970.
9. Банков С.Е., Курушин А.А. Расчет антенн и СВЧ структур с помощью HFSS Ansoft v. 10 // М.: ООО «Оркада». 2009. 250 С.
10. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. школа. 1988.
11. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.