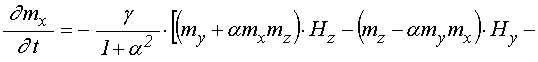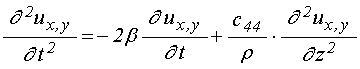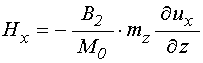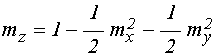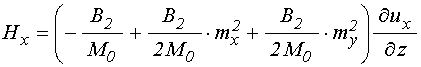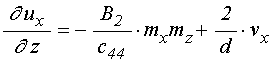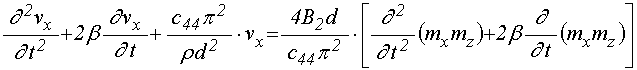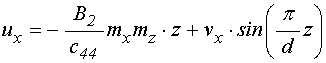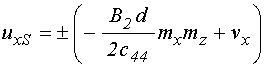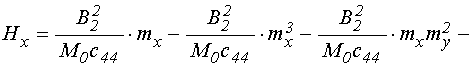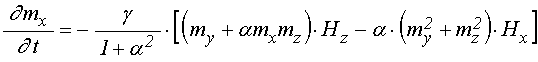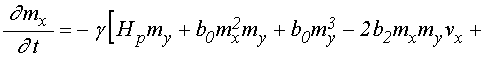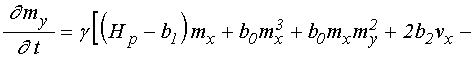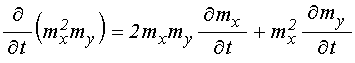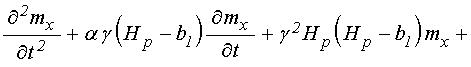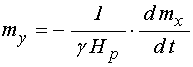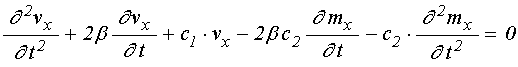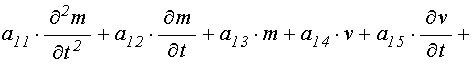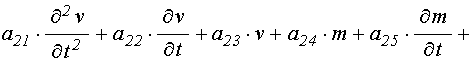УДК 537.874; 537.624
АНАЛИЗ НЕЛИНЕЙНОГО ВОЗБУЖДЕНИЯ ГИПЕРЗВУКОВЫХ КОЛЕБАНИЙ МАГНИТОСТРИКЦИОННОГО ПРЕОБРАЗОВАТЕЛЯ НА ОСНОВЕ МОДЕЛИ СВЯЗАННЫХ ОСЦИЛЛЯТОРОВ В КВАДРАТИЧНОМ ПРИБЛИЖЕНИИ
В. С. Власов1, А. П. Иванов1, В. Г. Шавров2, В. И. Щеглов2
1Сыктывкарский государственный университет
2Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья получена 14 января 2014 г.
Аннотация. В применении к анализу работы магнитострикционного преобразователя СВЧ диапазона рассмотрено возбуждение гиперзвука переменным магнитным полем в геометрии нормально намагниченной ферритовой пластины. В рамках квадратичного приближения получена система двух связанных уравнений второго порядка для намагниченности и упругого смещения, включающая нелинейные составляющие третьего порядка, эквивалентная модельной системе из двух связанных осцилляторов. Путем рассмотрения развития колебаний во времени и анализа амплитудно-частотных характеристик выявлены пределы применимости и точность квадратичного приближения вплоть до углов прецессии намагниченности, достигающих 40 градусов. Показано, что использование квадратичного приближения приводит к сокращению времени машинного счета на два порядка.
Ключевые слова: гиперзвук, нелинейные колебания, магнитоупругость.
Abstract. In connection to microwave magnetostriction transducer the hypersound vibrations excitation in geometry of normal magnetized ferrite plate is investigated. In quadratic approximation it is obtained the system of two connected second order equations for magnetization and elastic displacement maintained nonlinear three order components which equivalent to model system of two connected oscillators. By the analysis of vibrations time development and amplitude-frequency characteristics it is found that the quadratic approximation is applicable to magnetization angle precession as 40 degree. It is shown that quadratic approximation leads to decrease of computer calculation time on two order value.
Key words: hypersound, nonlinear vibrations, magnetoelasticity.
Введение
Возбуждение гиперзвуковых колебаний в диапазоне СВЧ является весьма актуальной задачей для общей физики [1], технической акустики [2,3] и аналоговой обработки информации [4-9]. Весьма перспективными здесь являются ферритовые магнитострикционные преобразователи, работающие в условиях ферромагнитного резонанса (ФМР) [10,11] на частотах до десятков ГГц. Традиционными материалами для таких преобразователей являются железоиттриевый и тербиевый ферриты-гранаты (ЖИГ и ТбФГ), имеющие рекордно низкие потери и высокое значение константы магнитоупругого взаимодействия [11].
Помехой на пути повышения мощности возбуждаемого гиперзвука в таких преобразователях является рост потерь за счет параметрического возбуждения обменных спиновых волн [12-14], которого однако можно избежать путем выбора геометрии преобразователя в виде нормально намагниченного тонкого диска [15-19]. В работе [20] показано, что при этом амплитуда гиперзвука может превышать таковую в линейном режиме более чем в 30 раз, что открывает путь для создания магнитоакустических преобразователей высокой мощности.
Расчет свойств работы таких преобразователей в условиях ФМР требует привлечения весьма сложного аналитического аппарата, успешно реализуемого только ценой ряда упрощающих предположений. В простейшем варианте задача сводится к системе семи нелинейных дифференциальных уравнений первого порядка, разрешимой только численными методами [20]. Условия практики однако требуют создания достаточно простого расчетного аппарата, позволяющего оценить возможности и рассчитать основные параметры преобразователя без привлечения сложных аналитических и численных методов.
В работе [21] предложен аппарат, позволяющий свести задачу о возбуждении гиперзвука магнитострикционным преобразователем в условиях ФМР к упрощенной модели возбуждения двух связанных осцилляторов – магнитного и упругого. Предложена линеаризованная система, содержащая два уравнения второго порядка, коэффициенты которых определяются параметрами материала и геометрией преобразователя, а также показана возможность ее аналитического решения для случая свободных колебаний. На основе численного решения выявлены два режима вынужденных колебаний, соответствующие спаду и нарастанию амплитуды во времени. Найдены аналитические критерии, определяющие критическое значение константы связи и частоту резонансных колебаний. Показано, что точка перехода, соответствующая бесконечному росту амплитуды колебаний модельной системы, для случая железоиттриевого граната эквивалентна точке переориентации вектора намагниченности.
Однако рассмотрение, выполненное в работе [21], проведено путем линеаризации полной системы связанных магнитоупругих уравнений [20], что исключает явления нелинейного характера и не позволяет рассматривать возможные пути повышения амплитуды возбуждаемых колебаний. Наряду с этим линеаризация препятствует определению максимального уровня нелинейного ограничения колебаний [22,23], исследованию импульсного и комбинационного возбуждения гиперзвука [24,25], а также других явлений, в том числе прецессии намагниченности второго порядка [26-32].
В настоящей работе, в продолжение [21], предпринята попытка расширения возможностей модели связанных осцилляторов, путем введения квадратичного приближения с целью упрощения системы связанных магнитоупругих уравнений. Получена система двух уравнений второго порядка, позволяющая описать некоторые из перечисленных выше нелинейных явлений с высокой точностью.
1. Геометрия задачи и основные уравнения
Геометрия задачи, совпадающая с
принятой в [20,21], показана на рис.1. В ее основе лежит плоскопараллельная
пластина толщины ![]() , обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую
кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью
пластины.
, обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую
кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью
пластины.
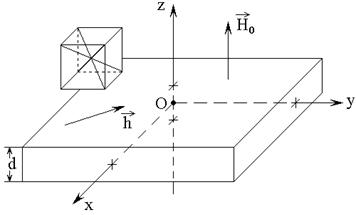
Рис.1. Геометрия задачи. Слева – схема кристаллографической ячейки.
Внешнее постоянное магнитное поле
![]() приложено перпендикулярно плоскости пластины,
переменное магнитное поле
приложено перпендикулярно плоскости пластины,
переменное магнитное поле ![]() действует в плоскости
пластины. Задача решается в декартовой системе координат
действует в плоскости
пластины. Задача решается в декартовой системе координат ![]() , плоскость
, плоскость ![]() которой
совпадает с плоскостью пластины, а оси
которой
совпадает с плоскостью пластины, а оси ![]() ,
, ![]() и
и ![]() параллельны
ребрам куба кристаллографической ячейки. Центр системы координат
параллельны
ребрам куба кристаллографической ячейки. Центр системы координат ![]() находится в центре пластины, так что ее
плоскости соответствуют координатам
находится в центре пластины, так что ее
плоскости соответствуют координатам ![]() .
.
Основная система уравнений движения для нормированных компонент намагниченности имеет вид [20,21]:
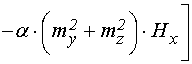 , (1)
, (1)
где уравнения для ![]() ,
, ![]() получаются
циклической перестановкой
получаются
циклической перестановкой ![]() ,
, ![]() ,
, ![]() .
.
Уравнения для компонент упругого
смещения ![]() имеют вид:
имеют вид:
граничные условия:
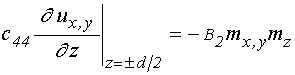 .
(3)
.
(3)
Полные эффективные поля имеют вид [20]:
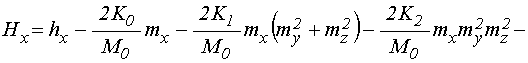
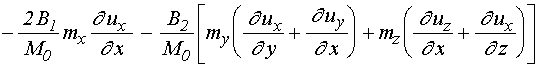 ;
(4)
;
(4)
Выражение для ![]() получается
циклической перестановкой
получается
циклической перестановкой ![]() ,
,![]() ,
, ![]() .
.
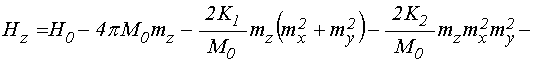
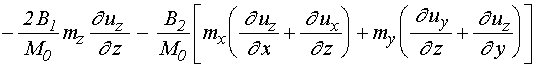 .
(5)
.
(5)
Таким образом, здесь имеются три уравнения первого порядка (1) для компонент намагниченности и два уравнения второго порядка (2) для компонент упругого смещения, что эквивалентно системе из семи уравнений первого порядка. Анализ развития колебаний в такой системе методом фазового пространства [22,23,33] требует нахождения координат особых точек, что сводится к решению линейного алгебраического уравнения седьмой степени. Сложность решения такой задачи стимулирует поиск возможностей уменьшения общего числа уравнений, одна из которых реализована в работе [21] путем линеаризации, исключающей нелинейность. Настоящая работа является развитием работы [21] путем введения квадратичного приближения, позволяющего учесть нелинейные свойства рассматриваемой системы.
2. Основные предположения и укороченные эффективные поля
Аналогично [21], полагаем
следующее: анизотропия отсутствует: ![]() ,
, ![]() ,
, ![]() ; продольные
упругие волны отсутствуют:
; продольные
упругие волны отсутствуют: ![]() ; упругие смещения вдоль
оси
; упругие смещения вдоль
оси ![]() отсутствуют:
отсутствуют: ![]() ; упругие
волны распространяются только вдоль оси
; упругие
волны распространяются только вдоль оси ![]() :
: ![]() ;
; ![]() ; внешние
переменные поля отсутствуют:
; внешние
переменные поля отсутствуют: ![]() ,
, ![]() .
.
Заметим, что предположение ![]() не является безупречно корректным, однако
в ряде случаев, будучи примененным на первом этапе, позволяет существенно
сократить требуемый объем вычислений [34,35].
не является безупречно корректным, однако
в ряде случаев, будучи примененным на первом этапе, позволяет существенно
сократить требуемый объем вычислений [34,35].
Для упрощения дальнейшей записи введем для постоянного поля обозначение с учетом размагничивания:
то есть:
![]() .
(7)
.
(7)
При этом эффективные поля (4)-(5) принимают вид:
![]() ;
(9)
;
(9)
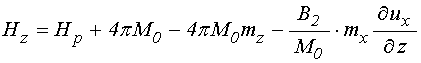 .
(10)
.
(10)
3. Квадратичное приближение
Условие сохранения длины вектора намагниченности требует выполнения соотношения [37]:
![]() ,
(11)
,
(11)
откуда:
![]() ,
(12)
,
(12)
а также:
![]() .
(13)
.
(13)
Рассмотрим задачу в квадратичном
приближении, то есть положим ![]() и разложим выражение (13)
в ряд Тейлора в окрестности единицы с точностью до второй степени по
и разложим выражение (13)
в ряд Тейлора в окрестности единицы с точностью до второй степени по ![]() и
и ![]() :
:
4. Эффективные поля в квадратичном приближении
Подставляя (14) в (8)-(10) и оставляя члены не выше второй степени по намагниченности, получаем эффективные поля в виде:
![]() ;
(16)
;
(16)
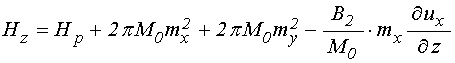 .
(17)
.
(17)
В эти выражения входит
производная от упругого смещения по координате ![]() . Согласно
работе [20] (формула (62)), эта производная имеет вид:
. Согласно
работе [20] (формула (62)), эта производная имеет вид:
где ![]() – функция,
удовлетворяющая уравнению (формула (53)):
– функция,
удовлетворяющая уравнению (формула (53)):
Это уравнение в совокупности с уравнениями для намагниченности типа (1) составляет полную систему, описывающую магнитоупругие колебания в данной геометрии.
Поскольку функция ![]() представляет собой решение краевой задачи
с однородными (нулевыми) граничными условиями для координатных производных,
редуцированное к случаю первой упругой моды [20], для удобства терминологии далее
будем называть ее «редуцированной функцией упругого смещения» или просто «редуцированным
упругим смещением». При этом полная
представляет собой решение краевой задачи
с однородными (нулевыми) граничными условиями для координатных производных,
редуцированное к случаю первой упругой моды [20], для удобства терминологии далее
будем называть ее «редуцированной функцией упругого смещения» или просто «редуцированным
упругим смещением». При этом полная ![]() -компонента упругого
смещения имеет вид (формула (51) в [20]):
-компонента упругого
смещения имеет вид (формула (51) в [20]):
и на поверхностях пластины при ![]() равна:
равна:
С учетом квадратичного приближения (14) производная (18) принимает вид:
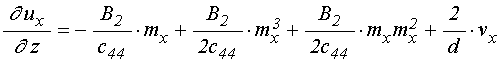 ;
(22)
;
(22)
Подставляя (22) в (15)-(17), получаем поля в виде:
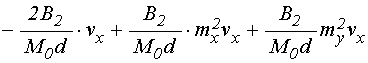 ;
(23)
;
(23)
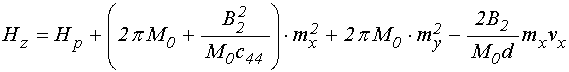 .
(25)
.
(25)
Введем вспомогательные обозначения:
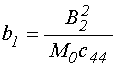 ;
(27)
;
(27)
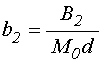 .
(28)
.
(28)
С этими обозначениями поля (23)-(25) принимают вид:
![]() ;
(30)
;
(30)
![]() .
(31)
.
(31)
5. Уравнения для намагниченности первого порядка
С учетом (30) уравнения типа (1) для ![]() и
и ![]() принимают
вид:
принимают
вид:
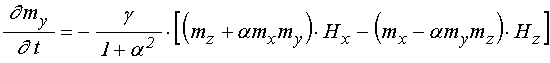 .
(33)
.
(33)
Уравнение для ![]() не рассматриваем, так как его правая
часть мала (для полной корректности это требует проверки, которую пока
проделывать не будем).
не рассматриваем, так как его правая
часть мала (для полной корректности это требует проверки, которую пока
проделывать не будем).
Положим, что затухание мало, то
есть ![]() . При этом
. При этом ![]() и
слагаемыми вида
и
слагаемыми вида![]() будем пренебрегать. При этом, с
учетом (14), входящие в (32)-(33) выражения в круглых скобках принимают вид:
будем пренебрегать. При этом, с
учетом (14), входящие в (32)-(33) выражения в круглых скобках принимают вид:
![]() ;
(34)
;
(34)
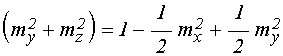 ;
(35)
;
(35)
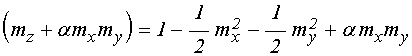 ;
(36)
;
(36)
![]() .
(37)
.
(37)
С использованием (29)-(31) и (34)-(37),
оставляя члены степеней не выше ![]() и
и ![]() , получаем слагаемые правых частей
уравнений (32)-(33):
, получаем слагаемые правых частей
уравнений (32)-(33):
![]()
![]() ; (38)
; (38)
![]() ;
(39)
;
(39)
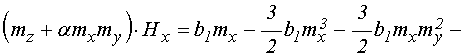
![]() ; (40)
; (40)
![]()
![]() . (41)
. (41)
Подставим (38)-(41) в (32)-(33),
а также учтем, что при реальных параметрах материала (например ЖИГ): ![]() ,
, ![]() , причем
, причем
![]() . То есть везде при умножении
. То есть везде при умножении ![]() на
на ![]() получаются
величины четвертого порядка малости, которые отбрасываем. При этом, учитывая,
что
получаются
величины четвертого порядка малости, которые отбрасываем. При этом, учитывая,
что ![]() , получаем:
, получаем:
![]() ;
(42)
;
(42)
![]() .
(43)
.
(43)
Это – два уравнения первого
порядка для компонент намагниченности ![]() ,
, ![]() , связанные с уравнением второго порядка (19)
для компоненты вспомогательной функции упругого смещения
, связанные с уравнением второго порядка (19)
для компоненты вспомогательной функции упругого смещения ![]() , определяющей основную компоненту
упругого смещения
, определяющей основную компоненту
упругого смещения ![]() через посредство формул (20) и
(21).
через посредство формул (20) и
(21).
6. Сведение двух уравнений первого порядка к одному уравнению второго порядка
Приведем теперь два уравнения
первого порядка для компонент намагниченности ![]() и
и ![]() к одному уравнению второго порядка для
компоненты
к одному уравнению второго порядка для
компоненты ![]() .
.
В уравнении (42) перенесем все слагаемые в левую часть, раскроем скобки и продифференцируем по времени:
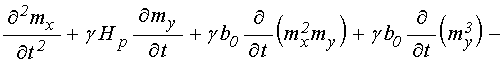
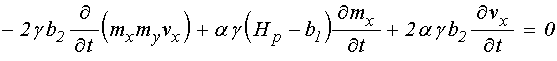 .
(44)
.
(44)
Раскрываем скобки при производных:
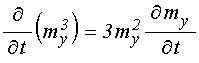 ;
(46)
;
(46)
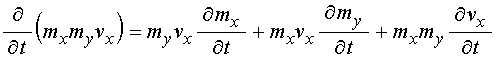 .
(47)
.
(47)
Подставляя производные (45)-(47) в
уравнение (44), меняя порядок слагаемых и выделяя производную ![]() , получаем:
, получаем:
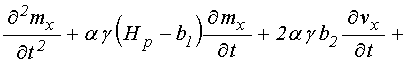
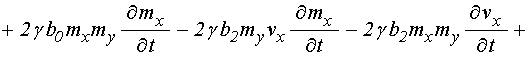
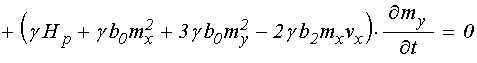 .
(48)
.
(48)
Подставляя производную ![]() в соответствии с (43) и оставляя члены не
выше третьего порядка малости, получаем:
в соответствии с (43) и оставляя члены не
выше третьего порядка малости, получаем:
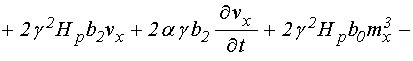
![]()
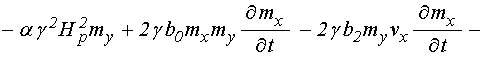
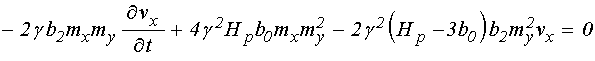 .
(49)
.
(49)
Это уравнение – для компоненты
намагниченности ![]() , однако в некоторых слагаемых
оно содержит компоненту
, однако в некоторых слагаемых
оно содержит компоненту ![]() , которая не позволяет
рассматривать это уравнение независимо от получаемого подобным путем уравнения
для
, которая не позволяет
рассматривать это уравнение независимо от получаемого подобным путем уравнения
для ![]() (здесь не приводим ввиду аналогичности). Развязать
эти уравнения можно в приближении круговой прецессии, реализованном далее.
(здесь не приводим ввиду аналогичности). Развязать
эти уравнения можно в приближении круговой прецессии, реализованном далее.
7. Приближение круговой прецессии
Предположим, что прецессия
намагниченности является круговой по правому кругу с частотой ![]() . Такое предположение справедливо, если в
плоскости пластины какое-либо нарушение симметрии (например анизотропия,
размагничивание или постоянное поле) отсутствует, то есть любые ориентации
намагниченности в плоскости пластины являются энергетически равноправными. В настоящей
задаче некоторое неравноправие может быть обусловлено магнитоупругим
взаимодействием, имеющим кубическую симметрию, однако контрольный численный
расчет по полным уравнениям (1)-(3), выполненный подобно проведенному в работе
[20], показывает, что даже при величине константы магнитоупругого
взаимодействия на порядок превышающий таковую для ЖИГ, прецессия остается
круговой с точностью до долей процента.
. Такое предположение справедливо, если в
плоскости пластины какое-либо нарушение симметрии (например анизотропия,
размагничивание или постоянное поле) отсутствует, то есть любые ориентации
намагниченности в плоскости пластины являются энергетически равноправными. В настоящей
задаче некоторое неравноправие может быть обусловлено магнитоупругим
взаимодействием, имеющим кубическую симметрию, однако контрольный численный
расчет по полным уравнениям (1)-(3), выполненный подобно проведенному в работе
[20], показывает, что даже при величине константы магнитоупругого
взаимодействия на порядок превышающий таковую для ЖИГ, прецессия остается
круговой с точностью до долей процента.
Таким образом, будем считать, что:
![]() ;
(50)
;
(50)
![]() ;
(51)
;
(51)
или в эквивалентном виде:
![]() ;
(52)
;
(52)
![]() ,
(53)
,
(53)
где ![]() –
амплитуда, для данного рассмотрения значения не имеющая, а
–
амплитуда, для данного рассмотрения значения не имеющая, а ![]() – частота собственных колебаний, в
линейном приближении [21] близкая к величине, свойственной случаю отсутствия
магнитоупругости [37]:
– частота собственных колебаний, в
линейном приближении [21] близкая к величине, свойственной случаю отсутствия
магнитоупругости [37]:
![]() .
(54)
.
(54)
Можно видеть, что в обоих случаях (50)-(51) и (52)-(53) выполняется соотношение:
Заметим, что поскольку частота (54)
свойственна только линейному режиму в отсутствие магнитоупругости [37], то возможное
изменение собственной частоты за счет нелинейности (нелинейная расстройка)
здесь не учитывается. то есть принятое предположение накладывает определенное
ограничение на амплитуду рассматриваемых здесь свободных колебаний. В случае установившихся
вынужденных колебаний прецессия происходит с частотой вынуждающей силы ![]() , поэтому вместо (54) надо брать частоту
этой силы (например, переменного поля), то есть вместо (55) надо использовать
формулу:
, поэтому вместо (54) надо брать частоту
этой силы (например, переменного поля), то есть вместо (55) надо использовать
формулу:
На данном этапе пока рассмотрим свободные
колебания, то есть ограничимся формулой (55), подставляя которую в (49) и
приводя подобные члены, получаем уравнение для свободных колебаний компоненты
намагниченности ![]() :
:
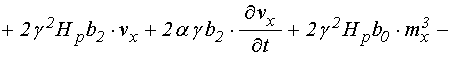
![]()
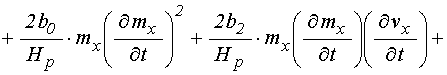
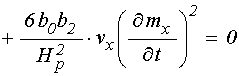 . (57)
. (57)
Это – уравнение второго порядка
для компоненты намагниченности ![]() в квадратичном
приближении, полностью отвязанное от подобного уравнения для
в квадратичном
приближении, полностью отвязанное от подобного уравнения для ![]() (тождественного полученному с точностью
до замены индексов
(тождественного полученному с точностью
до замены индексов ![]() ,
, ![]() ).
).
8. Уравнение для упругого смещения
Рассмотрим теперь уравнение (19)
для упругого смещения ![]() . Введем вспомогательные
обозначения:
. Введем вспомогательные
обозначения:
С этими обозначениями уравнение (19) принимает вид:
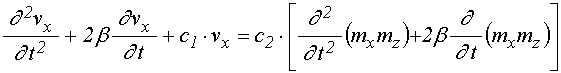 .
(60)
.
(60)
Раскрытие производных по
формулам, аналогичным (45)-(47), приводит к крайне громоздким выражениям.
Однако контрольный численный расчет по полным уравнениям (1)-(3), выполненный
аналогично проведенному в работе [20], при параметрах материала,
соответствующих ЖИГ, показывает, что правая часть уравнения (60) в линейном
режиме меньше левой приблизительно в 10 раз, а в сильно нелинейном – не менее
чем в 5 раз. Таким образом, входящие в правую часть члены третьего порядка
малости соответствуют относительно левой части четвертому порядку, то есть ими
в принятом приближении можно пренебречь. При этом входящую в правую часть
компоненту намагниченности ![]() можно не рассматривать
в квадратичном приближении вида (14), а просто положить равной единице. При
этом уравнение (60) принимает вид:
можно не рассматривать
в квадратичном приближении вида (14), а просто положить равной единице. При
этом уравнение (60) принимает вид:
Выражая вторую производную от
компоненты намагниченности ![]() в соответствии с (57)
и подставляя в (61), получаем:
в соответствии с (57)
и подставляя в (61), получаем:
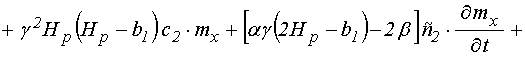
![]()
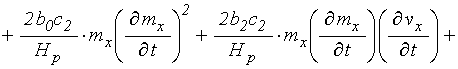
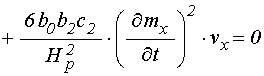 ,
(62)
,
(62)
Это – уравнение второго порядка
для компоненты редуцированной функции упругого смещения ![]() в
квадратичном приближении.
в
квадратичном приближении.
Уравнения (57) и (62) составляют искомую систему двух уравнений второго порядка для свободных колебаний намагниченности и редуцированного упругого смещения в квадратичном приближении.
9. Возбуждение переменным полем
Для рассмотрения вынужденных
колебаний будем полагать, что на систему действует синусоидальное переменное
поле круговой поляризации с частотой ![]() и амплитудой
и амплитудой ![]() , то есть:
, то есть:
![]() ;
(63)
;
(63)
![]() .
(64)
.
(64)
Согласно [21] (формула (19)), в рассматриваемой задаче возбуждение магнитных колебаний переменным полем описывается выражением:
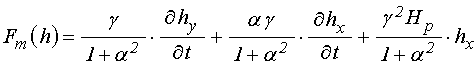 .
(65)
.
(65)
Выполненная в [21] численная
оценка показывает, что первые два слагаемых в правой части этой формулы меньше
третьего на три-пять порядков, то есть их можно не учитывать, в результате чего
при ![]() , получаем:
, получаем:
![]() .
(66)
.
(66)
Для описания вынужденных колебаний намагниченности это выражение надо подставить в правую часть уравнения (57).
Возбуждение упругих колебаний
происходит за счет связи с магнитными через магнитоупругое взаимодействие.
Такая связь осуществляется за счет правой части уравнения (61), куда входит
вторая производная от намагниченности. Подставляя таковую производную в
соответствии с уравнением (57), в правую часть которого подставлено вынуждающее
слагаемое вида (66), получаем в правой части уравнения (61) слагаемое, также
пропорциональное вынуждающему полю ![]() . Подробный вид правой
части получающегося уравнения для упругих колебаний приведен в работе [21] в
формуле (24). Однако очевидно, что упругие колебания непосредственно переменным
магнитным полем возбуждаться не могут, то есть наличие подобного слагаемого в
уравнении для упругости с физической стороны корректным не является. С
математической стороны получается как бы двукратный учет одного и того же
возбуждения переменным полем, действующим только на намагниченность. Чтобы избежать
такой некорректности, в правую часть уравнения (61) надо подставлять вторую производную
от намагниченности в виде, свободном от возбуждающего переменного поля. При
этом правая часть уравнения для упругости (62) остается равной нулю, а
возбуждение упругих колебаний осуществляется за счет слагаемых связи,
содержащих переменную намагниченность.
. Подробный вид правой
части получающегося уравнения для упругих колебаний приведен в работе [21] в
формуле (24). Однако очевидно, что упругие колебания непосредственно переменным
магнитным полем возбуждаться не могут, то есть наличие подобного слагаемого в
уравнении для упругости с физической стороны корректным не является. С
математической стороны получается как бы двукратный учет одного и того же
возбуждения переменным полем, действующим только на намагниченность. Чтобы избежать
такой некорректности, в правую часть уравнения (61) надо подставлять вторую производную
от намагниченности в виде, свободном от возбуждающего переменного поля. При
этом правая часть уравнения для упругости (62) остается равной нулю, а
возбуждение упругих колебаний осуществляется за счет слагаемых связи,
содержащих переменную намагниченность.
Замечание. Напомним
дополнительно, что при возбуждении переменным полем частоты ![]() , отличной от частоты свободных колебаний
, отличной от частоты свободных колебаний ![]() , вместо формулы (55) надо использовать (56),
однако пока положим, что частота возбуждения отличается от собственной не более
чем в пределах ширины резонансной кривой, то есть использование (55) будем считать
допустимым. Правомерность такого допущения будет проверена далее в разделе 19
на основе сравнения с решением полной системы (1)-(3).
, вместо формулы (55) надо использовать (56),
однако пока положим, что частота возбуждения отличается от собственной не более
чем в пределах ширины резонансной кривой, то есть использование (55) будем считать
допустимым. Правомерность такого допущения будет проверена далее в разделе 19
на основе сравнения с решением полной системы (1)-(3).
10. Система уравнений для вынужденных колебаний намагниченности и упругого смещения
В результате получаем следующую систему связанных уравнений для вынужденных колебаний намагниченности и упругого смещения в квадратичном приближении:
уравнение для намагниченности:
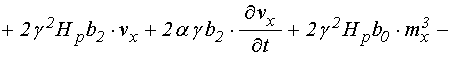
![]()
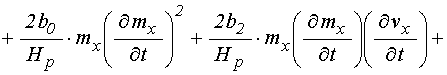
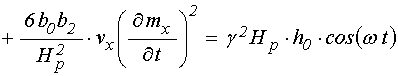 ; (67)
; (67)
уравнение для редуцированного упругого смещения:
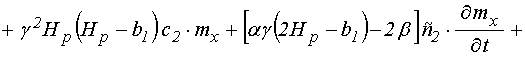
![]()
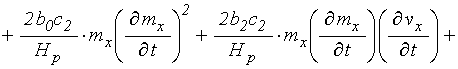
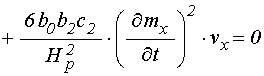 , (68)
, (68)
где ![]() ,
, ![]() и
и ![]() определяются
формулами (26)-(28), (58)-(59) и (6).
определяются
формулами (26)-(28), (58)-(59) и (6).
В линейном приближении эта система принимает вид:
уравнение для намагниченности:
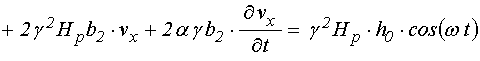 ; (69)
; (69)
уравнение для редуцированного упругого смещения:
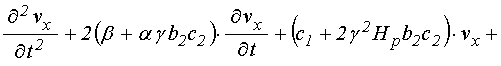
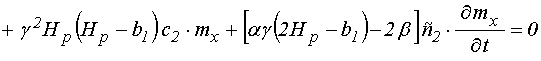 .
(70)
.
(70)
Можно видеть, что такая система с точностью до обозначений совпадает с полученной в работе [21] (формулы (19) и (24)).
Замечание. Поскольку за системой (69)-(70), соответствующей линейному приближению, укоренилось название «линеаризованной» [21], для удобства терминологии будем называть далее систему (67)-(68), полученную в квадратичном приближении, системой «квадрированной».
11. Проверка корректности линейного и квадратичного приближений
Рассмотрим степень приближения, обеспечиваемого как линеаризованной (69)-(70), так и квадрированной (67)-(68) системами по сравнению с исходной нелинейной системой (1)-(3).
На рис.2 показаны зависимости
поперечной компоненты намагниченности (а) и упругого смещения (б) от амплитуды
переменного поля при параметрах ЖИГ, принятых в работе [21]. Смещение ![]() получено из
получено из ![]() в
соответствии с формулой (21) при
в
соответствии с формулой (21) при ![]() . Кривые 1
соответствуют решению полной системы (1)-(3), кривые 2 – решению линеаризованной
системы (69)-(70), кривые 3 – решению квадрированной системы (67)-(68).
. Кривые 1
соответствуют решению полной системы (1)-(3), кривые 2 – решению линеаризованной
системы (69)-(70), кривые 3 – решению квадрированной системы (67)-(68).
Из рисунка видно, что как линеаризованная, так и квадрированная системы несколько завышают точные значения амплитуд намагниченности и смещения, причем для смещения это завышение выражено сильнее, чем для намагниченности. В то же время видно, что приближение, обеспечиваемое квадрированной системой, значительно лучше, чем приближение, даваемое линеаризованной системой.
Рис.2. Зависимости поперечной
компоненты намагниченности (а) и упругого смещения (б) от амплитуды переменного
поля. 1 – решение полной нелинейной системы (1)-(3); 2 – решение
линеаризованной системы (69)-(70); 3 – решение квадрированной системы (67)-(68).
На врезках – те же кривые в интервале переменного поля до 400 Э. Параметры материала
соответствуют ЖИГ (![]() ;
;![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ); а
также
); а
также ![]() ;
; ![]() ; частота
возбуждения:
; частота
возбуждения: ![]() .
.
Так линеаризованная система (69)-(70)
описывает точную картину до амплитуды переменного поля, равной 5 Э (то есть до ![]() ) с точностью порядка 10%, а для амплитуды
поля, равной 10 Э (до
) с точностью порядка 10%, а для амплитуды
поля, равной 10 Э (до ![]() ) – с точностью около 30%, после
чего ее приближение резко ухудшается.
) – с точностью около 30%, после
чего ее приближение резко ухудшается.
В то же время квадрированная
система (67)-(68) описывает амплитуду магнитных колебаний до амплитуды
переменного поля 100 Э (![]() ) с точностью порядка
3%, а для амплитуды поля 400 Э (
) с точностью порядка
3%, а для амплитуды поля 400 Э (![]() ) – до 5%. Та же
система описывает амплитуду упругих колебаний при амплитуде переменного поля 60
Э (
) – до 5%. Та же
система описывает амплитуду упругих колебаний при амплитуде переменного поля 60
Э (![]() ) с точностью 20%, при амплитуде 100 Э с
точностью 25%, а при амплитуде поля 400 Э – с точностью около двух раз.
) с точностью 20%, при амплитуде 100 Э с
точностью 25%, а при амплитуде поля 400 Э – с точностью около двух раз.
Таким образом, ограничиваясь
точностью описания упругих колебаний на уровне 20%, можно видеть, что
линеаризованная система допускает амплитуду переменного поля не более 0.05 от
намагниченности насыщения, что ограничивает углы прецессии на уровне ![]() , тогда как квадрированная система позволяет
рассматривать амплитуду переменного поля до 0.40 от намагниченности насыщения,
что обеспечивает углы прецессии до
, тогда как квадрированная система позволяет
рассматривать амплитуду переменного поля до 0.40 от намагниченности насыщения,
что обеспечивает углы прецессии до ![]() . Что касается
магнитных колебаний, то здесь возможности использования квадрированной системы
простираются до полей, превышающих намагниченность насыщения в несколько (не
менее трех) раз, что соответствует углам прецессии до 30-40 градусов. Столь
большие углы прецессии позволяют успешно использовать квадрированную систему
для описания многих нелинейных процессов с достаточно хорошим приближением.
. Что касается
магнитных колебаний, то здесь возможности использования квадрированной системы
простираются до полей, превышающих намагниченность насыщения в несколько (не
менее трех) раз, что соответствует углам прецессии до 30-40 градусов. Столь
большие углы прецессии позволяют успешно использовать квадрированную систему
для описания многих нелинейных процессов с достаточно хорошим приближением.
12. Уравнения движения в обобщенных обозначениях
Запишем (67)-(68) в обобщенных
обозначениях (для простоты записи индекс «![]() »
опускаем):
»
опускаем):
уравнение для намагниченности:
![]()
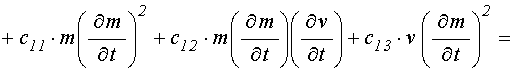
![]() ; (71)
; (71)
уравнение для редуцированного упругого смещения:
![]()
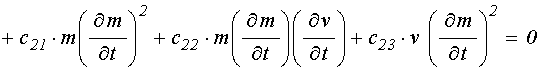 .
(72)
.
(72)
Здесь коэффициенты ![]() соответствуют линейному приближению [21],
коэффициенты
соответствуют линейному приближению [21],
коэффициенты ![]() – квадратичному приближению без
учета производных от переменных по времени и
– квадратичному приближению без
учета производных от переменных по времени и ![]() – квадратичному
приближению с учетом таких производных. Коэффициент
– квадратичному
приближению с учетом таких производных. Коэффициент ![]() соответствует
возбуждающей силе и присутствует только в первом уравнении, отражающем
колебания намагниченности, при этом возбуждение во втором уравнении, отражающем
упругие колебания, обеспечивается коэффициентами связи: в линейном приближении
соответствует
возбуждающей силе и присутствует только в первом уравнении, отражающем
колебания намагниченности, при этом возбуждение во втором уравнении, отражающем
упругие колебания, обеспечивается коэффициентами связи: в линейном приближении ![]() ,
, ![]() , в
квадратичном –
, в
квадратичном – ![]() ,
, ![]() .
.
13. Обобщенные коэффициенты
Обобщенные коэффициенты в уравнениях (71)-(72) имеют вид:
![]() ;
(74)
;
(74)
![]() ;
(75)
;
(75)
![]() ;
(76)
;
(76)
![]() ;
(77)
;
(77)
![]() ;
(78)
;
(78)
![]() ;
(79)
;
(79)
![]() ;
(80)
;
(80)
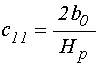 ;
(81)
;
(81)
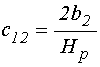 ;
(82)
;
(82)
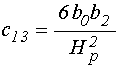 ;
(83)
;
(83)
![]() ;
(84)
;
(84)
![]() ;
(85)
;
(85)
![]() ;
(86)
;
(86)
![]() ;
(87)
;
(87)
![]() ;
(88)
;
(88)
![]() ;
(89)
;
(89)
![]() ;
(90)
;
(90)
![]() ;
(91)
;
(91)
![]() ;
(92)
;
(92)
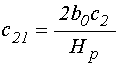 ;
(93)
;
(93)
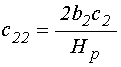 ;
(94)
;
(94)
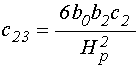 .
(95)
.
(95)
14. Обобщенные коэффициенты, выраженные через исходные параметры задачи
Подставляя в (73)-(95)
обозначения (26)-(28), (58)-(59), получаем обобщенные коэффициенты, выражение
через константы материала, постоянное поле и толщину пластины (обозначение ![]() для компактности записи сохраняем):
для компактности записи сохраняем):
![]() ;
(96)
;
(96)
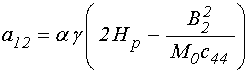 ;
(97)
;
(97)
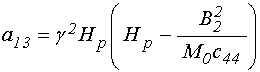 ;
(98)
;
(98)
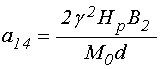 ;
(99)
;
(99)
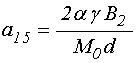 ;
(100)
;
(100)
![]() ;
(101)
;
(101)
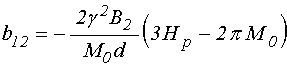 ;
(102)
;
(102)
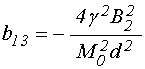 ;
(103)
;
(103)
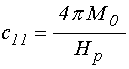 ;
(104)
;
(104)
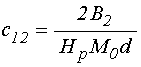 ;
(105)
;
(105)
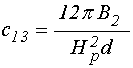 ;
(106)
;
(106)
![]() ;
(107)
;
(107)
![]() ;
(108)
;
(108)
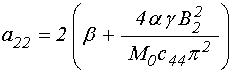 ;
(109)
;
(109)
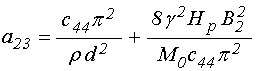 ;
(110)
;
(110)
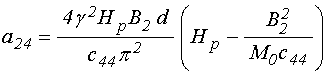 ;
(111)
;
(111)
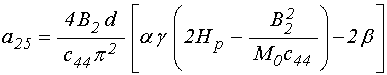 ;
(112)
;
(112)
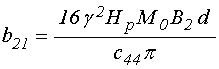 ;
(113)
;
(113)
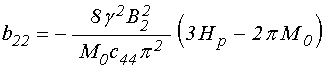 ;
(114)
;
(114)
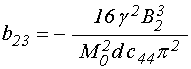 ;
(115)
;
(115)
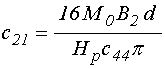 ;
(116)
;
(116)
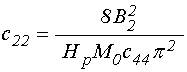 ;
(117)
;
(117)
 .
(118)
.
(118)
15. Полное упругое смещение
Система уравнений (71)-(72),
наряду с намагниченностью ![]() , определяет редуцированную
функцию упругого смещения
, определяет редуцированную
функцию упругого смещения ![]() . При этом полное
упругое смещение на поверхностях пластины определяется по формуле (21), которую
можно записать в виде:
. При этом полное
упругое смещение на поверхностях пластины определяется по формуле (21), которую
можно записать в виде:
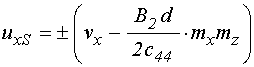 .
(119)
.
(119)
В квадратичном приближении (14), с учетом кругового характера прецессии (55), получаем:
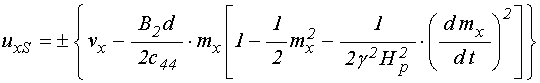 ,
(120)
,
(120)
или без индекса «![]() »:
»:
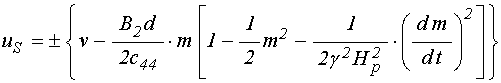 .
(121)
.
(121)
Замечание. Отметим, что
формулы (120)-(121) получены с помощью формулы (55), то есть для свободных
колебаний. В случае вынужденных колебаний надо пользоваться формулой (56).
Однако контрольный численный расчет при типичных параметрах ЖИГ показывает, что
при отклонении вынуждающей частоты ![]() от частоты собственной
от частоты собственной
![]() в пределах
в пределах ![]() 50%
замена формулы (55) на формулу (56) приводит к изменениям весьма незначительным,
менее 1%. Более того, при тех же параметрах величина первого слагаемого в
формуле (20) меньше величины второго на три порядка, то есть можно с точностью не
менее 1% полагать
50%
замена формулы (55) на формулу (56) приводит к изменениям весьма незначительным,
менее 1%. Более того, при тех же параметрах величина первого слагаемого в
формуле (20) меньше величины второго на три порядка, то есть можно с точностью не
менее 1% полагать ![]() . Заметим, что такое соотношение
получается при типичных параметрах ЖИГ и сильно зависит от величины константы
. Заметим, что такое соотношение
получается при типичных параметрах ЖИГ и сильно зависит от величины константы ![]() , то есть для других материалов возможность
взаимной замены формул (55) и (56) при выводе выражения для
, то есть для других материалов возможность
взаимной замены формул (55) и (56) при выводе выражения для ![]() требует непосредственной проверки.
требует непосредственной проверки.
16. Полный обобщенный вид связанной системы уравнений квадратичного приближения
Система уравнений (71)-(72) представляет собой частный вид более полной обобщенной симметричной системы:
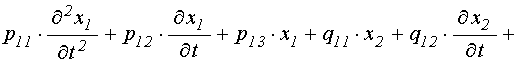
![]()
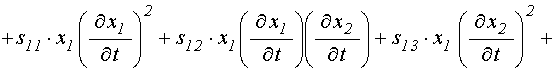
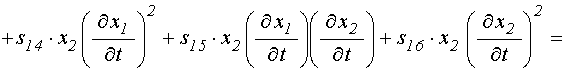
![]() ; (122)
; (122)
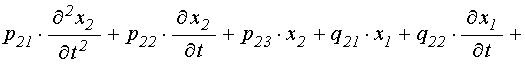
![]()
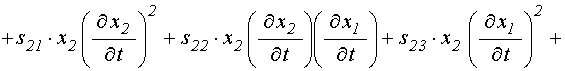
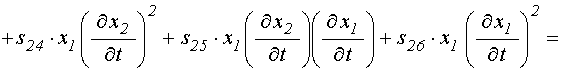
![]() . (123)
. (123)
Эти уравнения переходят одно в другое при замене индексов переменных и первых индексов коэффициентов «1» на «2» и обратно. Еще более полный вид подобной связанной системы должен включать в себя слагаемые, состоящие из произведений трех производных. Однако в решаемой здесь реальной задаче о вынужденных магнитоупругих колебаниях в ферритовой пластине такие слагаемые отсутствуют, поэтому на данном этапе не рассматриваются.
17. Численная оценка различных слагаемых в системе связанных уравнений
Вернемся к системе (71)-(72) и
рассмотрим ее структуру более подробно. Уравнения (71) и (72) содержат довольно
много слагаемых. Для того, чтобы выявить их роль в формировании колебаний
намагниченности и упругого смещения, оценим относительную величину отдельных
слагаемых для типичной ситуации возбуждения гиперзвуковых колебаний. Пусть параметры
материала соответствуют (ЖИГ): ![]() ;
; ![]() ;
; ![]() ;
; ![]() , параметры затухания:
, параметры затухания:![]() ;
; ![]() ,
толщина пленки:
,
толщина пленки: ![]() , поле
, поле ![]() ,
частота
,
частота ![]() (то есть
(то есть ![]() ). Выбранные
значения частоты и поля соответствуют возбуждению ферромагнитного и упругого
резонансов. Вспомогательные параметры (6), (26)-(28), (57)-(58) принимают
значения:
). Выбранные
значения частоты и поля соответствуют возбуждению ферромагнитного и упругого
резонансов. Вспомогательные параметры (6), (26)-(28), (57)-(58) принимают
значения: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Структура слагаемых уравнений (71)-(72)
представляет собой произведения коэффициентов ![]() ,
, ![]() ,
, ![]() на
переменные
на
переменные ![]() ,
, ![]() в той
или иной степени, умноженные на частоту
в той
или иной степени, умноженные на частоту ![]() в
первой или второй степени, получающуюся за счет производных (при временном
множителе типа
в
первой или второй степени, получающуюся за счет производных (при временном
множителе типа ![]() ).
).
Полученные таким образом абсолютные величины слагаемых уравнений (71)-(72) представлены в таблице 1 при различных значениях возбуждающего поля (знаки и наименования размерности в системе СГС (Гаусса) опущены для простоты записи).
Амплитуды переменных, полученные из разверток по времени при решении полной задачи (1)-(3) составляют:
при поле ![]() :
: ![]() ,
, ![]() ;
;
при поле ![]() :
: ![]() ,
, ![]() ;
;
при поле ![]() :
: ![]() ,
, ![]() ;
;
при поле ![]() :
: ![]() ,
, ![]() .
.
Такие значения полей выбраны,
исходя из того, что ![]() соответствует чисто линейному
режиму,
соответствует чисто линейному
режиму, ![]() соответствует слабо нелинейному режиму,
когда линейное приближение дает ошибку как по намагниченности, так и по
упругому смещению уже в два раза, тогда как квадратичное – по намагниченности
не более 2% и по упругому смещению менее 8%. Дополнительное удобство для
численного сравнения состоит в том, что при отношении амплитуд полей
возбуждения для этих двух режимов равном
соответствует слабо нелинейному режиму,
когда линейное приближение дает ошибку как по намагниченности, так и по
упругому смещению уже в два раза, тогда как квадратичное – по намагниченности
не более 2% и по упругому смещению менее 8%. Дополнительное удобство для
численного сравнения состоит в том, что при отношении амплитуд полей
возбуждения для этих двух режимов равном ![]() , отношение
амплитуд обоих видов колебаний при нелинейном режиме к тем же амплитудам при
линейном режиме составляет ровно 4 порядка. При этом отношение амплитуды магнитных
колебаний к амплитуде упругих в обоих режимах сохраняется равным
, отношение
амплитуд обоих видов колебаний при нелинейном режиме к тем же амплитудам при
линейном режиме составляет ровно 4 порядка. При этом отношение амплитуды магнитных
колебаний к амплитуде упругих в обоих режимах сохраняется равным ![]() .
.
Далее, поле ![]() выбрано как соответствующее сильно нелинейному
режиму, когда линейное приближение как по намагниченности, так и по упругому смещению
дает ошибку на порядок, тогда как квадратичное – по намагниченности менее 5% и
по упругому смещению – не более 25%.
выбрано как соответствующее сильно нелинейному
режиму, когда линейное приближение как по намагниченности, так и по упругому смещению
дает ошибку на порядок, тогда как квадратичное – по намагниченности менее 5% и
по упругому смещению – не более 25%.
Поле ![]() соответствует
еще более нелинейному режиму, когда линейное приближение как по
намагниченности, так и по упругому смещению дает ошибку на два порядка, тогда
как квадратичное – по намагниченности не более 5% и по упругому смещению –
всего около двух раз.
соответствует
еще более нелинейному режиму, когда линейное приближение как по
намагниченности, так и по упругому смещению дает ошибку на два порядка, тогда
как квадратичное – по намагниченности не более 5% и по упругому смещению –
всего около двух раз.
Таблица 1.
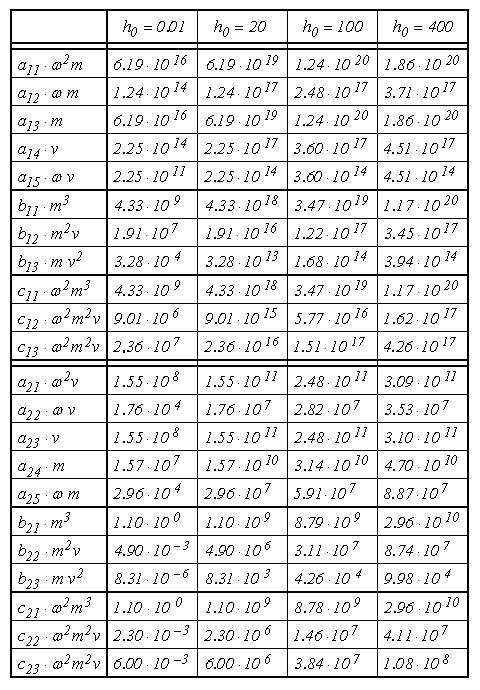
Из таблицы видно следующее. В
линейном режиме (![]() ) вклад от слагаемых с
коэффициентами
) вклад от слагаемых с
коэффициентами ![]() и
и ![]() меньше
основных слагаемых с коэффициентами
меньше
основных слагаемых с коэффициентами ![]() более чем на семь
порядков, то есть ими с весьма высокой точностью можно пренебречь. Связь обеспечивается
слагаемыми, пропорциональными первой степени переменных, то есть
более чем на семь
порядков, то есть ими с весьма высокой точностью можно пренебречь. Связь обеспечивается
слагаемыми, пропорциональными первой степени переменных, то есть ![]() и
и ![]() , тогда
как слагаемые, пропорциональные производным от переменных с
, тогда
как слагаемые, пропорциональные производным от переменных с ![]() и
и ![]() вносят
вклад, сравнимый со вкладом от параметров затухания с коэффициентами
вносят
вклад, сравнимый со вкладом от параметров затухания с коэффициентами ![]() и
и ![]() .
.
В слабо нелинейном режиме при ![]() вклад от слагаемых, пропорциональных
вклад от слагаемых, пропорциональных ![]() и
и ![]() ,
значительно возрастает и становится сравнимым со вкладом от основных слагаемых
,
значительно возрастает и становится сравнимым со вкладом от основных слагаемых ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
отставая всего на один-два порядка. Особенно заметным становится вклад от
слагаемых, пропорциональных третьей степени намагниченности с коэффициентами
,
отставая всего на один-два порядка. Особенно заметным становится вклад от
слагаемых, пропорциональных третьей степени намагниченности с коэффициентами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
составляя около 5%.
,
составляя около 5%.
В сильно нелинейном режиме при ![]() вклад от слагаемых, пропорциональных
вклад от слагаемых, пропорциональных ![]() и
и ![]() заметно
возрастает. Вклад от слагаемых, пропорциональных третьей степени
намагниченности, достигает 30% от вклада основных, а вклад от остальных
слагаемых остается меньше основного на 4-6 порядков.
заметно
возрастает. Вклад от слагаемых, пропорциональных третьей степени
намагниченности, достигает 30% от вклада основных, а вклад от остальных
слагаемых остается меньше основного на 4-6 порядков.
В особо сильно нелинейном режиме
при ![]() вклад от слагаемых, пропорциональных
вклад от слагаемых, пропорциональных ![]() и
и ![]() ,
возрастает еще более, по слагаемым с
,
возрастает еще более, по слагаемым с ![]() ,
, ![]() ,
, ![]() ,
, ![]() достигая 60%. Вклад от слагаемых,
пропорциональных
достигая 60%. Вклад от слагаемых,
пропорциональных ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() не
превышает 1%, однако становится сравнимым со вкладом от затухания
пропорциональным
не
превышает 1%, однако становится сравнимым со вкладом от затухания
пропорциональным ![]() и
и ![]() , тогда
как вклад от слагаемых, пропорциональных
, тогда
как вклад от слагаемых, пропорциональных ![]() и
и ![]() , остается крайне малым, меньше основного
на шесть порядков и вклада от затухания на три порядка.
, остается крайне малым, меньше основного
на шесть порядков и вклада от затухания на три порядка.
Таким образом, например, в
умеренно нелинейном режиме (![]() ) наряду с основными
) наряду с основными ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() , в
первую очередь надо учитывать только слагаемые, пропорциональные
, в
первую очередь надо учитывать только слагаемые, пропорциональные ![]() ,
, ![]() ,
, ![]() , а также
, а также ![]() ,
, ![]() ,
, ![]() . В
уравнении для упругого смещения заметную роль, сравнимую с ролью затухания,
может играть также слагаемое с коэффициентом
. В
уравнении для упругого смещения заметную роль, сравнимую с ролью затухания,
может играть также слагаемое с коэффициентом ![]() . В
результате система уравнений (71)-(72) принимает более простой укороченный вид:
. В
результате система уравнений (71)-(72) принимает более простой укороченный вид:
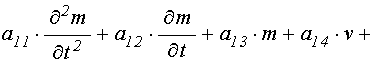
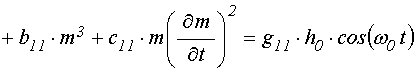 ;
(124)
;
(124)
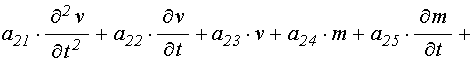
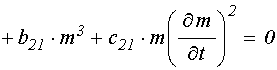 . (125)
. (125)
Замечание. Заметим, что выполненная оценка
слагаемых в уравнениях (71)-(72) проделана для частного случая параметров ЖИГ
при резонансных условиях. При других значениях параметров эти оценки могут быть
другими. Так, в работе [21] показано, что при достаточно большой константе
магнитоупругого взаимодействия ![]() преобладающую роль играют
слагаемые с коэффициентами
преобладающую роль играют
слагаемые с коэффициентами ![]() и
и ![]() , обеспечивающие связь осцилляторов через
производные. Именно эти слагаемые даже в линейном режиме позволяют определить
условия, приводящие к столь сильно нелинейному эффекту, как переориентация
вектора намагниченности от одного устойчивого положения к другому [36]. То есть,
во избежание ошибок, для каждого конкретной задачи надо проводить оценку слагаемых
в уравнениях (71)-(72) применительно к заданным условиям.
, обеспечивающие связь осцилляторов через
производные. Именно эти слагаемые даже в линейном режиме позволяют определить
условия, приводящие к столь сильно нелинейному эффекту, как переориентация
вектора намагниченности от одного устойчивого положения к другому [36]. То есть,
во избежание ошибок, для каждого конкретной задачи надо проводить оценку слагаемых
в уравнениях (71)-(72) применительно к заданным условиям.
18. Численный анализ ограничения амплитуды за счет кубической нелинейности
В работе [21] при рассмотрении линейного приближения показано, что в зависимости от величины параметров связи через производные возможны три режима вынужденных колебаний.
При малой величине связи амплитуда вынужденных колебаний после включения возбуждения сначала нарастает, а затем выходит на стационарный уровень по закону, соответствующему экспоненте с отрицательным показателем. При большой величине связи амплитуда вынужденных колебаний стремится к бесконечности по экспоненте с положительным показателем. Эти два режима разделены критической величиной связи (точкой бифуркации), при которой нарастание колебаний происходит линейно, то есть по экспоненте с нулевым показателем, причем критичность порога перехода от одного режима к другому по константе связи весьма высока и составляет не менее шести значащих цифр.
Как отмечалось в работе [21], режим экспоненциального нарастания колебаний соответствует бесконечному возрастанию их энергии, что в реальных системах недопустимо. То есть при достаточно высокой амплитуде колебаний должны работать механизмы ограничения. Одним из таких известных механизмов является нелинейная расстройка, при большой амплитуде приводящая к выводу системы из резонанса [22,23]. Рассмотрим, что добавляет к линейным явлениям, описанным в [21], нелинейность в квадратичном приближении.
Общие уравнения (71)-(72) содержат много слагаемых, роль которых в общем развитии колебаний, по-видимому, является различной. Однако, как показано в разделе 17, главную роль играют слагаемые, пропорциональные третьей степени намагниченности. Из классических представлений о колебаниях нелинейной системы с одной степенью свободы [22,23] следует, что ограничение амплитуды при резонансе происходит за счет расстроечного механизма, главную роль в котором играет нелинейность также кубического характера.
Поэтому пока пренебрежем ролью дополнительных механизмов и ограничим рассмотрение единственным слагаемым, соответствующим кубической нелинейности. При этом система уравнений (71)-(72) в обозначениях, подобных принятым в [21], сводится к следующей:
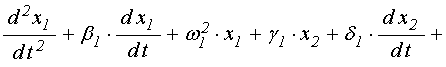
![]() ; (126)
; (126)
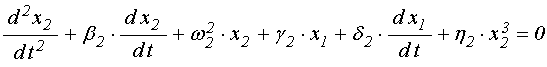 .
(127)
.
(127)
Здесь кубическая нелинейность введена в обоих уравнениях, что сделано для симметрии системы, обеспечивающей эквивалентность характера колебаний обоих осцилляторов. В реальном случае ЖИГ нелинейность упругого осциллятора отсутствует, то есть симметрия нарушена, что требует отдельного рассмотрения, здесь же ограничиваемся более простым симметричным случаем.
Развитие вынужденных колебаний во времени при различной величине связи и коэффициента кубической нелинейности иллюстрируется рис.3 (приведены эпюры для первого осциллятора, второй ведет себя аналогично).
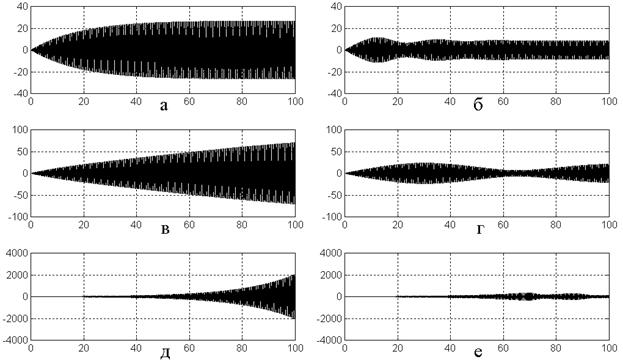
Рис.3. Развитие вынужденных колебаний во времени при
различной величине связи и коэффициента кубической нелинейности (первый
осциллятор). Параметры осцилляторов: ![]() ;
; ![]() ;
; ![]() ; параметры
возбуждения:
; параметры
возбуждения: ![]() ;
; ![]() .
Коэффициенты:
.
Коэффициенты:
а – ![]() ,
, ![]() ; б –
; б – ![]() ,
,
![]() ;
;
в – ![]() ,
, ![]() ; г –
; г – ![]() ,
, ![]() ;
;
д – ![]() ,
, ![]() ; е –
; е – ![]() ,
, ![]() .
.
Эпюры левого столбца на рис.3 представляют собой линейное приближение при различных величинах связи и повторяют таковые, приведенные в работе [21]. В правом столбце показано, как развиваются те же вынужденные колебания в условиях кубической нелинейности.
Из рисунка видно, что во всех
трех режимах кубическая нелинейность приводит к ограничению амплитуды
колебаний, что и является здесь главным результатом. Благодаря нелинейной
расстройке, установление колебаний происходит с биениями, проявляющимися в
модуляции амплитуды на рис.3б, 3г и 3е. При увеличении параметра нелинейности
период уменьшается. Так при ![]() (рис.3е) он
составляет
(рис.3е) он
составляет ![]() , при
, при ![]() период
составляет
период
составляет ![]() , при
, при ![]() (рис.3б)
период равен
(рис.3б)
период равен ![]() . Такое поведение периода биений
соответствует классическим представлениям [22,23].
. Такое поведение периода биений
соответствует классическим представлениям [22,23].
Следует отметить, что в случае ![]() (рис.3е) периоду биений в
(рис.3е) периоду биений в ![]() соответствуют два максимума при
соответствуют два максимума при ![]() и
и ![]() (второй
находится за правым краем рис.3е), наблюдаемый же на рис.3е максимум при
(второй
находится за правым краем рис.3е), наблюдаемый же на рис.3е максимум при ![]() является вторичным, отражающим довольно
сложный характер биений, в этом случае обусловленный, по-видимому, большой
величиной параметра связи
является вторичным, отражающим довольно
сложный характер биений, в этом случае обусловленный, по-видимому, большой
величиной параметра связи ![]() .
.
19. Амплитудно-частотные характеристики колебаний при квадратичном приближении
На рис.4 показаны амплитудно-частотные характеристики (АЧХ) магнитных (левый столбец) и упругих (правый столбец) колебаний при различных уровнях возбуждения.
Рис.4а,б соответствует линейному
режиму (![]() ). В этом случае резонансные кривые как
для магнитных (а), так и для упругих (б) колебаний полностью симметричны,
квадратичное приближение описывает полное решение с точностью не хуже 1%, кроме
ближайшей окрестности резонансной частоты
). В этом случае резонансные кривые как
для магнитных (а), так и для упругих (б) колебаний полностью симметричны,
квадратичное приближение описывает полное решение с точностью не хуже 1%, кроме
ближайшей окрестности резонансной частоты ![]() , где
точность составляет около 4%.
, где
точность составляет около 4%.
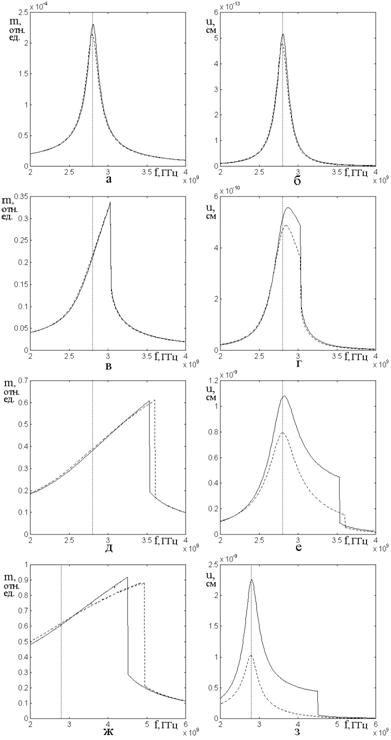
Рис.4. Амплитудно-частотные характеристики магнитных (левый столбец) и упругих (правый столбец) колебаний при различных уровнях возбуждения.
Сплошные линии – расчет по квадрированной системе (71)-(72). Пунктирные линии – расчет по полной системе (1)-(3). Вертикальная точечная линия соответствует резонансной частоте свободных колебаний. Уровни возбуждения:
а, б – ![]() (
(![]() ); в, г –
); в, г – ![]() (
(![]() );
);
д, е – ![]() (
(![]() ); ж, з –
); ж, з – ![]() (
(![]() ).
).
Параметры – аналогичные принятым для рис.2.
Рис.4в,г соответствует слабо
нелинейному режиму (![]() ). Резонансная кривая для
магнитных колебаний (в) принимает вид наклонного треугольника с крутым высокочастотным
спадом, что обусловлено классическим действием нелинейного расстроечного
механизма [22,23]. Максимум кривой соответствует началу крутого спада и
смещается относительно частоты свободных колебаний
). Резонансная кривая для
магнитных колебаний (в) принимает вид наклонного треугольника с крутым высокочастотным
спадом, что обусловлено классическим действием нелинейного расстроечного
механизма [22,23]. Максимум кривой соответствует началу крутого спада и
смещается относительно частоты свободных колебаний ![]() вверх
на
вверх
на ![]() . Квадратичное приближение соответствует
полному решению с точностью около 1%. Резонансная кривая для упругих колебаний
(г) расширяется, приобретая со стороны высоких частот крутой спад, смещенный
вверх на те же
. Квадратичное приближение соответствует
полному решению с точностью около 1%. Резонансная кривая для упругих колебаний
(г) расширяется, приобретая со стороны высоких частот крутой спад, смещенный
вверх на те же ![]() , на резонансной частоте
свободных колебаний
, на резонансной частоте
свободных колебаний ![]() имеется подъем, обусловленный
упругим резонансом магнитной пластины. Квадратичное приближение описывает
полное решение в окрестности резонансной частоты (
имеется подъем, обусловленный
упругим резонансом магнитной пластины. Квадратичное приближение описывает
полное решение в окрестности резонансной частоты (![]() ,
, ![]() ) с точностью около 12%, несколько превышая
точное решение. Вне этого интервала точность квадратичного приближения составляет
порядка 1%.
) с точностью около 12%, несколько превышая
точное решение. Вне этого интервала точность квадратичного приближения составляет
порядка 1%.
Рис.4д,е соответствует сильно
нелинейному режиму (![]() ). Магнитные колебания (д) по
прежнему представляют собой скошенный треугольник, причем частота спада
возрастает, согласно квадратичному приближению до
). Магнитные колебания (д) по
прежнему представляют собой скошенный треугольник, причем частота спада
возрастает, согласно квадратичному приближению до ![]() ,
согласно полному решению – до
,
согласно полному решению – до ![]() . В области вне спада
точность квадратичного приближения составляет около 2%. Кривая для упругих
колебаний (е) имеет такой же крутой спад на тех же частотах, что и магнитная,
однако резонанс на частоте
. В области вне спада
точность квадратичного приближения составляет около 2%. Кривая для упругих
колебаний (е) имеет такой же крутой спад на тех же частотах, что и магнитная,
однако резонанс на частоте ![]() выражен значительно
сильнее. Кривая квадратичного приближения проходит выше кривой полного, причем
точность квадратичного приближения в области резонанса близка к 30%, а вблизи
спада ухудшается до 50%.
выражен значительно
сильнее. Кривая квадратичного приближения проходит выше кривой полного, причем
точность квадратичного приближения в области резонанса близка к 30%, а вблизи
спада ухудшается до 50%.
Рис.4ж,з соответствует особо
сильно нелинейному режиму (![]() ). Характеристика для
магнитных колебаний (ж) наклоняется в сторону высоких частот еще больше, так
что частота спада по квадратичному приближению достигает
). Характеристика для
магнитных колебаний (ж) наклоняется в сторону высоких частот еще больше, так
что частота спада по квадратичному приближению достигает ![]() , а по полному решению –
, а по полному решению – ![]() . В области вне спада точность
квадратичного приближения составляет около 8%. На кривой для упругих колебаний
(е) крутой спад проявляется только в квадратичном приближении и приходится на
ту же частоту, что и магнитный –
. В области вне спада точность
квадратичного приближения составляет около 8%. На кривой для упругих колебаний
(е) крутой спад проявляется только в квадратичном приближении и приходится на
ту же частоту, что и магнитный – ![]() . Резонанс в области
. Резонанс в области ![]() при обоих решениях остается хорошо выраженным,
однако в квадратичном приближении его высота превышает высоту при полном решении
в 2,2 раза. В области частот выше резонансной точность квадратичного приближения
еще более падает, что обусловлено отсутствием крутого спада при полном решении.
при обоих решениях остается хорошо выраженным,
однако в квадратичном приближении его высота превышает высоту при полном решении
в 2,2 раза. В области частот выше резонансной точность квадратичного приближения
еще более падает, что обусловлено отсутствием крутого спада при полном решении.
Таким образом, приближенно можно
считать, что квадратичное приближение описывает магнитные колебания с точностью
не хуже 1% в поле до ![]() , до 2% в поле до
, до 2% в поле до ![]() и до 10% в поле до
и до 10% в поле до ![]() . То же приближение описывает упругие
колебания с точностью до 10% в поле до
. То же приближение описывает упругие
колебания с точностью до 10% в поле до ![]() , до
30% в поле до
, до
30% в поле до ![]() и до двух раз в поле до
и до двух раз в поле до ![]() , причем точность приближения при удалении
от резонансной частоты возрастает.
, причем точность приближения при удалении
от резонансной частоты возрастает.
Замечание. Как упоминалось в разделе 9, правомерность использования системы (71)-(72), при выводе которой использовалась формула (55), должна быть проверена при сравнении с полной системой (1)-(3). Можно полагать, что степень соответствия приведенных здесь АЧХ, рассчитанных по полной и квадрированной системам, в первую очередь вдали от частоты свободного резонанса, составляющая единицы и доли процента, служит для такой правомерности основанием вполне достаточным.
20. Оценка прикладных возможностей квадратичного приближения
С прикладной стороны представляет интерес оценить время счета и требуемые машинные ресурсы при использовании квадрированной системы (71)-(72) вместо полной (1)-(3). В настоящей работе при принятых параметрах для ЖИГ программа для расчета АЧХ в диапазоне от 2 до 6 ГГц с шагом в 10 МГц методом Рунге-Кутта четвертого порядка [38] по полной системе (1)-(3), написанная на языке «Фортран», составляла 490 строк и занимала объем около 12000 байт, при этом время расчета на компьютере с частотой 2.8 ГГц составляло 10-14 минут. Подобная программа для расчета по системе в квадратичном приближении (71)-(72) составляла 250 строк, занимала менее 6000 байт и имела время счета 7-9 секунд. Таким образом, расчет с помощью квадратичного приближения приводит к экономии машинных ресурсов в два раза и сокращению времени машинного счета на два порядка.
Заключение
В применении к задаче анализа работы магнитострикционного преобразователя СВЧ диапазона на частоте ферромагнитного резонанса рассмотрено возбуждение гиперзвуковых колебаний переменным магнитным полем в геометрии плоскопараллельной нормально намагниченной ферритовой пластины. Записаны уравнения движения вектора намагниченности и упругого смещения с граничными условиями и возбуждением переменным магнитным полем.
Для упрощения задачи рассмотрено квадратичное приближение по намагниченности с учетом кругового характера прецессии, в результате чего полная система, содержащая семь уравнений первого порядка и четыре граничных условия, сведена к квадрированной системе четырех уравнений первого порядка без граничных условий. Показано, что полученная ранее линеаризованная система является частным случаем полученной здесь квадрированной системы.
Введены эквивалентные параметры квадрированной системы, выраженные через параметры материала и геометрию исходной ферритовой пластины.
Записана полная система уравнений для квадратичного приближения в обобщенном симметричном виде, соответствующая модельной системе из двух связанных осцилляторов, нелинейность в которых описывается слагаемыми третьего порядка по намагниченности, упругому смещению и их производных.
На основе численного анализа соотношения составляющих эквивалентных параметров для реального случая железоиттриевого граната (ЖИГ), получены укороченные уравнения, содержащие только главные слагаемые, отвечающие за динамическое поведение системы. Показано, что главную роль играют слагаемые, пропорциональные третьей степени по намагниченности и произведению намагниченности на квадрат ее производной по времени.
Путем рассмотрения развития
колебаний во времени выполнен анализ приближения, обеспечиваемого
линеаризованной и квадрированной системами по сравнению с решением, обеспечиваемым
исходной нелинейной системой. Показано, что при описании упругих колебаний
на уровне точности 20% линеаризованная система является корректной на уровне
переменных полей не более 0.05 от намагниченности насыщения при углах прецессии
порядка ![]() , тогда как квадрированная система
сохраняет корректность вплоть до полей, составляющих 0.40 от намагниченности
насыщения, что соответствует углам прецессии до
, тогда как квадрированная система
сохраняет корректность вплоть до полей, составляющих 0.40 от намагниченности
насыщения, что соответствует углам прецессии до ![]() . По
магнитным колебаниям квадрированная система сохраняет точность 5% до полей,
превышающих намагниченность насыщения более чем в три раза, что соответствует
углам прецессии до
. По
магнитным колебаниям квадрированная система сохраняет точность 5% до полей,
превышающих намагниченность насыщения более чем в три раза, что соответствует
углам прецессии до ![]() .
.
На основе модельной системы связанных осцилляторов выполнен анализ нелинейности кубического характера. Выявлена роль кубической нелинейности, как главного фактора в ограничении экспоненциального роста амплитуды вынужденных колебаний, предсказанного линеаризованной системой по прохождении критической точки бифуркации. Показано, что ограничение амплитуды сопровождается биениями, вызванными нелинейной расстройкой.
Рассмотрены амплитудно-частотные характеристики магнитных и упругих колебаний при различных уровнях возбуждения. На основе их анализа показано, что вблизи резонанса квадратичное приближение при амплитуде переменного поля до 0.14 от намагниченности описывает магнитные колебания с точностью 1% и упругие с точностью 10%, при амплитуде 0.71 от намагниченности – магнитные – 2%, упругие – 30%, при амплитуде 2.86 – магнитные – 10% и упругие с точностью до двух раз, причем точность приближения при удалении от резонансной частоты возрастает.
Оценены прикладные возможности использования квадратичного приближения. Показано, что расчет с помощью квадратичного приближения приводит к экономии машинных ресурсов в два раза и сокращению времени машинного счета на два порядка.
Работа выполнена при финансовой поддержке РФФИ (грант №12-02-01035-а).
Литература
1. Физическая энциклопедия. Т.1. М.: Советская энциклопедия. 1988. Статья «Гиперзвук».
2. Физическая акустика. Под ред. Мэзона У., Терстона Р. Т.1-7. М.: Мир. 1966-1974.
3. Такер Дж., Рэмптон В., Гиперзвук в физике твердого тела. М.: Мир. 1975.
4. Поверхностные акустические волны. Под ред. Олинера А. М.: Мир. 1981.
5. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука. 1981.
6. Bleustein J.L. // Appl. Phys. Lett. 1968. V.13. P.412.
7. Гуляев Ю.В. // ПЖЭТФ. 1969. Т.9. С.63.
8. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.
9. Голямина И.П. // Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М., Наука, 1967.
10. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.
11. Ле-Кроу Р., Комсток Р. // В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.
12. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209.
13. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
14. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.
15. A.G. Temiryazev, M.P. Tikhomirova, P.E. Zilberman. // J. Appl. Phys. 1994. V.76. №12. P.5586.
16. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ. 1995. Т.108. №1. С.281.
17. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
18. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
19. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
20. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
21. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники. 2013. №11. (http://jre.cplire.ru/jre/nov13/3/text.pdf).
22. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.
23. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит. 2003.
24. Власов В.С., Шавров В.Г., Щеглов В.И. // Сб. тр. XXI Межд. конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2013. С.164.
25. Власов В.С., Шавров В.Г., Щеглов В.И. // Сб. тр. XXI Межд. конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2013. С.177.
26. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №1. С.84
27. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №6. С.719.
28. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №9. С.1120.
29. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.501.
30. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №8. С.806.
31. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №9. С.857.
32. Власов В.С., Котов Л.Н., Щеглов В.И. Нелинейная прецессия вектора намагниченности в условиях ориентационного перехода. Сыктывкар: ИПО СыктГУ. 2013.
33. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. М.: Наука. 1988.
34. Vlasov V.S., Kotov L.N., Asadullin F.F. // J. of Magnetism and Magnetic Materials. 2006.V.300. №1. P. e48-e51.
35. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. МГУ. 2007.
36. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689
37. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
38. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.