Анализ и минимизация аберраций в широкоугольных планарных зеркальных системах

УДК 629.396.67

АНАЛИЗ И МИНИМИЗАЦИЯ АБЕРРАЦИЙ В ШИРОКОУГОЛЬНЫХ ПЛАНАРНЫХ ЗЕРКАЛЬНЫХ СИСТЕМАХ

В. А. Калошин, Е. В. Фролова

Институт радиотехники и электроники им. В.А. Котельникова РАН

Статья получена 10 января 2014 г.

Аннотация. Представлены результаты исследования аберраций в планарных зеркальных системах. На основе метода трассировки и введенного критерия среднеквадратичной аберрации (СКА) предложен метод анализа и минимизации несимметричных аберраций в области фокусировки наклонных лучей. Получены асимптотические соотношения, характеризующие области параметров с минимальными аберрациями. Выполнено сравнение аберраций различных многолучевых планарных зеркальных систем: системы Кассегрена, системы Шварцшильда и однозеркальной системы с параболическим зеркалом по критерию СКА. Методом физической оптики рассчитаны зависимости коэффициента использования поверхности однозеркальной системы и системы Шварцшильда от угла отклонения луча.

Ключевые слова: планарные зеркальные системы, многолучевые антенны, система Кассегрена, система Шварцшильда, аберрации.

Abstract. The results of the study of aberrations in planar mirror systems are presented. Based on tracing method and imposed mean square aberration ( MSA ) a method for analyzing and minimizing asymmetrical aberrations in the focusing region oblique rays is proposed. Asymptotic relations that characterize the region of parameters with minimal aberrations have been obtained. The comparison of the aberrations in different multibeam planar mirror systems: Cassegrain systems, Schwarzschild system and single-dish system with a parabolic mirror was done using MSA. The efficiency dependence of a single-dish system and Schwarzschild system on angle of view was calculated using physical optics method.

Keywords: planar mirror systems, multi-beam antennas, Cassegrain system, Schwarzschild system, aberrations.

Введение

Планарные зеркальные системы (ПЗС) применяются в антенной технике в качестве одно- и многолучевых антенн с веерными диаграммами направленности [1], облучающих систем цилиндрических зеркал [1], а также в качестве диаграммообразующих схем линейных и планарных антенных решеток [2]. ПЗС строятся на основе планарных волноводов и могут выполняться в одном или нескольких слоях. В последнем случае обеспечивается отсутствие эффекта взаимного затенения, поскольку отраженные от зеркала волны распространяются в другом волноводе. Связь между волноводами происходит через щель (рис. 1,2). В работах [2-5] подробно анализировались двухслойные зеркальные системы, и было показано, что такие конструкции могут быть согласованы в широком диапазоне частот и углов падения волн, а фаза волны при переходе из одного слоя в другой слабо зависит от угла падения. Следовательно, на основе многослойных конструкций можно создавать ПЗС с отсутствием затенения, что важно использовании двухзеркальных систем с большим размером субрефлектора.

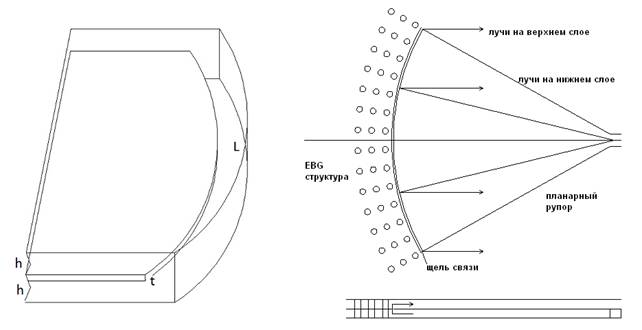
Рис.1 Рис.2

Как известно, основным фактором, ограничивающим сектор обзора зеркальных систем, являются аберрации [6-8]. Аберрации в однозеркальных и двухзеркальных системах описываются приближенными аналитическими формулами, полученными в рамках теории аберраций третьего порядка [6]. Эти формулы с успехом применяются при построении оптических систем, характеризующихся небольшими углами отклонения лучей (не превышающими несколько градусов) и большими продольными размерами оптической системы (по сравнению с поперечными). При увеличении угла отклонения луча или продольного размера системы классическая теории аберраций третьего порядка оказывается недостаточно для их адекватного описания. Формулы теории аберраций пятого порядка столь громоздки, что их сложно использовать для анализа и, особенно, для минимизации аберраций. Кроме того, если аберрации 5-го порядка велики, то необходимо учитывать и аберрации более высоких порядков, так как они становятся соизмеримыми [7]. При использовании зеркальных систем для построения многолучевых антенн и диаграммо-образующих схем в ММ и СБММ диапазонах представляет интерес получение больших углов обзора (несколько десятков градусов), а также возможность минимизации габаритов системы за счет уменьшения продольных размеров. В этом случае продольные размеры системы могут быть соизмеримы и даже меньше поперечных.

Цель работы – разработка методики анализа и минимизации аберраций , в том числе с учетом высших порядков, в широком диапазоне углов зрения и геометрических параметров различных ПЗС с использованием метода трассировки лучей. Отметим, что в планарных (двумерных) системах, в отличие от трехмерных, отсутствуют астигматизм, и аберрации связаны лишь с меридиональными лучами.

Методика работы основана на использовании трассировки лучей, широко применяемой при анализе зеркальных систем. Известно два варианта метода трассировки, отличающихся направлением хода лучей. В одном из вариантов, назовем этот вариант прямой трассировкой, рассматриваются лучи, выходящие из вынесенного из фокуса источника. Этот вариант часто используется совместно с методом Кирхгофа, в котором интегрируется полученное методом трассировки поле в апертуре главного зеркала и далее рассчитывается диаграмма направленности и коэффициент использования поверхности апертуры (КИП). При малых смещениях источника из фокуса распределение эйконала в апертуре главного зеркала двухзеркальной системы описывается формулами, полученными в [8]. Однако при увеличении величины смещения, необходимой для реализации больших углов зрения, точности этих формул оказывается недостаточно. При анализе и минимизации аберраций широкоугольных систем можно использовать метод трассировки лучей.

При электродинамической оптимизации системы определяются угол наклона, ширина диаграммы направленности, координат облучателя и геометрические параметры зеркал: расстояние между зеркалами, положение первичного фокуса и эквивалентное фокусное расстояние (в апланатической системе – фокальный радиус), обеспечивающие максимум КИПа при заданном отклонении луча. В связи с большим количеством параметров процесс оптимизации является трудоемким [9].

В оптике [6-7] принято использовать обратную трассировку, когда рассматриваются лучи, падающие на главное зеркало под углом к его оси. Эти лучи, пройдя оптическую систему, фокусируются в некоторой области, называемой областью рассеяния, формируя тот или иной вид каустики.

В данной работе на первом этапе мы будем исследовать аберрации методом обратной трассировки и при этом использовать понятия и термины оптической теории аберраций. На втором этапе будет введена величина средне- кадратичной аберрации, с использованием которой на третьем этапе будет проведено исследование и минимизация аберраций в системе Шваршильда за счет выбора оптимальных параметров. Электродинамическое моделирование с использованием аппретурного метода Кирхгофа будет использовано на четвертом этапе для оптимизации угла наклона, ширины диаграммы направленности и координат облучателя однозеркальной системы и апланатической системы Шварцшильда по критерию максимального КИПа в заданном секторе сканирования. Начальные значения этих параметров определяются на третьем этапе.

1. Виды аберраций в планарных зеркальных системах.

Рассмотрим вначале апланатическую систему Шварцшильда. Координаты образующих вспомогательного и главного зеркала двухзеркальной апланатической системы, обеспечивающих отсутствие комы 3-го порядка, определяются формулами [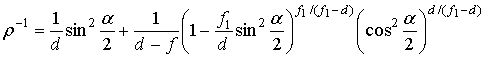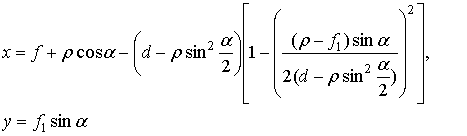1]:

(1)

где x, y, x₁ ,y₁ – декартовые координаты главного и вспомогательного зеркал, - фокальный радиус, d - расстояние между зеркалами, f - фокальный отрезок (расстояние от главного зеркала до первичного фокуса).

Далее будем использовать нормировку всех параметров системы на диаметр главного зеркала (в отличие от оптической теории, в которой принята нормировка на фокусное расстояние). При описании картины лучей, как это принято в оптике, будем называть луч, проходящий через центр главного зеркала, главным лучом, а область фокусировки лучей – пятном рассеяния [6].

Для иллюстрации возможных видов аберраций рассмотрим две апланатические системы с одинаковыми расстояниями между зеркалами d=0.5, различными фокальными отрезками и фокальными радиусами: 1 - f=0.3, =0.9; 2 - f=0, =0.52. Схемы трассировки лучей для угла зрения w=20° в этих системах изображены, соответственно, на рис. 3а, 3b.

Здесь и в дальнейшем, лучам, падающим на главное зеркало, отраженным от главного зеркала и затем отраженным от вспомогательного зеркала соответствуют линии разного цвета. Черным цветом изображен главный луч, значок ‘_*’ соответствует положению первичного фокуса. Как следует из рисункa, аберрации в апланатической системе могут иметь как несимметричный характер в виде “комы” (рис.3a), так и симметричный - в виде боковой сферической аберрации (рис.3b). В последнем случае каустика отраженных лучей имеет точку возврата. При изменении параметров зеркал в апланатической системе можно получить различные реализации несимметричных аберраций в пятне рассеяния.

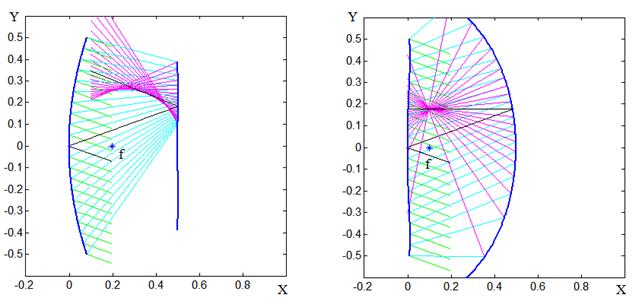
a) b)

Рис.3

Для корректного сравнения различных зеркальных систем определим эквивалентное фокусное расстояние , которое в апланатической системе равно фокальному радиусу , в однозеркальной системе – фокальному расстояние параболы F, в системе Кассегрена выражается через фокальное расстояние параболы F и эксцентриситет гиперболы в виде формулы:

, (2)

величины F и связаны с параметрами зеркальной сиcтемы: расстоянием между зеркалами d и фокальным отрезком f. Сравнение однозеркальной и двухзеркальных систем будем проводить при одинаковых эквивалентных фокусных расстояниях , а системы Кассегрена и Шварцшильда, кроме этого, – при одинаковых параметрах d и f.

На рис. 4а,b приведены результаты трассировки лучей в двухзеркальной системе Кассегрена (рис.4а) с параметрами: d=0.5, f=0.3, =0.9 и однозеркальной системе (рис.4b) c таким же фокальным расстоянием =0.9.

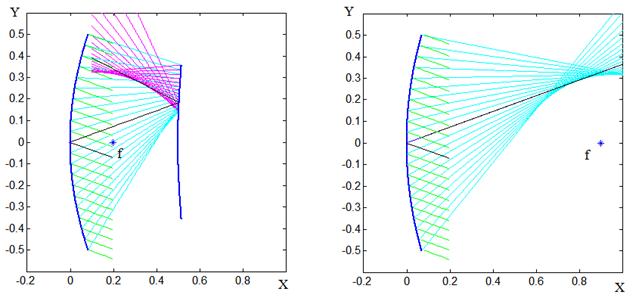
а) b)

Рис.4

Как видно из рис. 3,4 размеры пятна рассеяния в виде комы в трех различных системах могут быть соизмеримы.

Следует отметить, что для комы, формируемой зональными лучами, характерно увеличение ее размера с увеличением размера зоны на главном зеркале и максимальные аберрации наблюдаются для крайних лучей. Для пятна рассеяния, представленного на рис. 3b, зональные (в том числе и крайние) лучи могут пересекаться на главном луче. При наличии в пятне рассеяния аберраций высших порядков, точки пересечения образуют траекторию, которая может пересекать главный луч, вообще говоря, не один раз. Примеры траекторий приведены на рис.5 для системы с параметрами d=0.5, f=0.2, =1 и на рис.6 для d=0.5, f=0.05, =0.51. Аберрации такого вида нельзя оценивать по краевым лучам, как аберрацию “кома”, и следует ввести некоторый интегральный параметр, который позволит учитывать вклад множества зональных лучей [10].

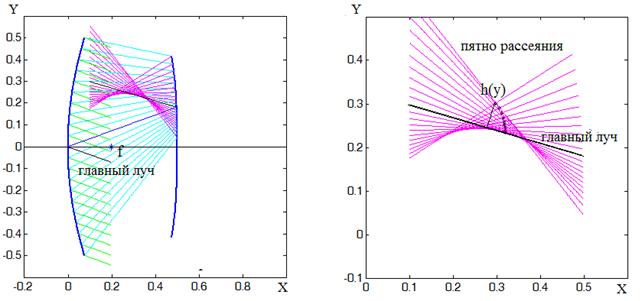
Рис.5

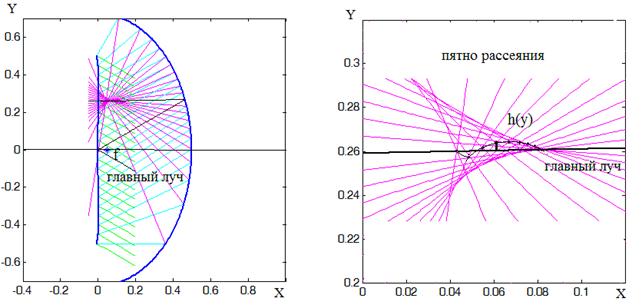
Рис.6

2. Среднеквадратичной аберрация.

Рассмотрим на примере однозеркальной системы (рис.7а) трассировку пары лучей, пересекающих образующую главного зеркала на одинаковом расстоянии от главного луча в точках с поперечными координатами ±y. Определим поперечную аберрацию этой пары зональных лучей h(y) в области фокусировки как расстояние от точки их пересечения до главного луча (см. рис.7b).

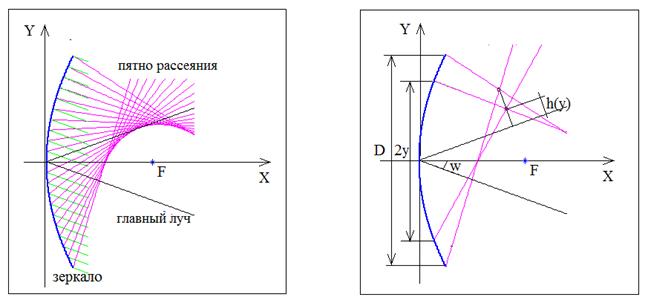
а) b)

Рис.7

Выберем в качестве интегрального параметра, характеризующего аберрации всех зональных лучей в пятне рассеяния среднеквадратичную аберрацию (СКА), определенную в виде :

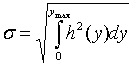(3)

где y_max=0.5 при принятой нормировке параметров.

Покажем, что, если в зеркальной системе преобладает кома третьего порядка (как в однозеркальной системе с параболическим зеркалом и системе Кассегрена), мера поперечных аберраций, определенная таким способом, приближенно равна радиусу комы. В теории аберраций третьего порядка [6] радиус комы определяется формулой:

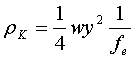(4)

Подставляя в соотношение (3) зависимость вида 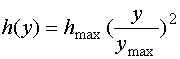, где максимальный размер аберрации , и интегрируя, получим:

(5)

Для комы пятого порядка, растущей пропорционально четвертой степени радиуса зоны главного зеркала , величина составляет примерно четверть от максимальной аберрации, повторяя при этом кубическую зависимость аберраций от угла зрения как .

Из формулы (3) также следует, что в случае симметричных относительно главного луча аберраций величина стремится к нулю, и, следовательно, этот параметр может быть использован для минимизации поперечных аберраций, а также для сравнения различных зеркальных систем по уровню аберраций.

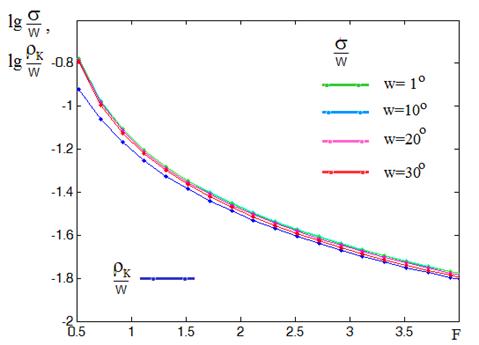
Рис.8

На рис. 8 приведены в сравнении зависимости радиуса комы третьего порядка, полученной по формуле (4) и величины СКА, полученной при трассировке лучей в параболическом зеркале, от фокусного расстояния параболы. Зависимости рассчитаны для углов наклона лучей w=1°, 10°, 20°, 30° и нормированы на угол w в первой степени. Из рисунка видно, что при фокусных расстояниях F>1 эти кривые близки как для малых, так и для больших углов. Для короткофокусного параболического зеркала (F<1) применение формулы (4) для радиуса комы третьего порядка неточно. Далее величина СКА будет использована для анализа аберраций и оптимизации параметров ПЗС с целью минимизации аберраций.

3. Анализ и минимизация аберраций по критерию СКА.

Для оценки влияния уровня аберраций на качество изображения в зеркальной системе необходимо сравнивать размер пятна рассеяния, определяемого в рамках геометрической оптики, с размером дифракционного пятна, пропорционального эквивалентному фокусному расстоянию и отношению длины волны к размеру главного зеркала . Для высокого качества системы радиус пятна рассеяния должен быть меньше дифракционного радиуса. Выполним нормировку величины аберраций на эквивалентный фокус . При этом уровень допустимых (нормированных) аберраций в зеркальной системе будет зависеть только от отношения (или от обратной величины – электрического размера зеркала ).

Перейдем к анализу зависимости СКА от параметров зеркал в однозеркальной и двухзеркальных системах Кассегрена и Шварцшильда. Выполнив трассировку лучей, получим зависимости СКА от эквивалентного фокуса при фиксированном расстоянии между зеркалами d=0.6 и фокальном отрезке f=0. Результаты расчета СКА для углов зрения 1° и 10° в виде зависимостей от приведены на рис.9, где кривые зеленого цвета относятся к однозеркальной системе, а кривые синего и красного цветов, соответственно, к системам Кассегрена и Шварцшильда.

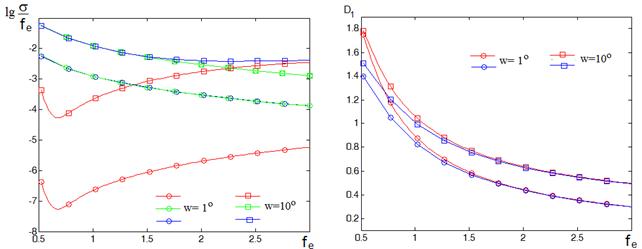
Рис.9 Рис.10

Как видно на рисунке, уровень аберраций в рассматриваемых зеркальных системах может быть соизмерим, хотя характер зависимостей при этом различается. В однозеркальной системе и системе Кассегрена аберрации уменьшаются с увеличением фокусного расстояния, а в апланатической системе при увеличении фокального радиуса аберрации растут и при некотором значении фокального радиуса становятся соизмеримы с аберрациям в системе Кассегрена. При этом они могут превышать аберрации в однозеркальной системе. Следует отметить, что анализ данных об уровне аберраций на рис. 9 необходимо проводить в совокупности с данными об относительном размере вспомогательного зеркала D₁, приведенными на рис. 10 (цвет кривых соответствует цветам на рис.9). Как видно на рис.10, с уменьшением эквивалентного фокусного расстояния в двухзеркальных системах увеличивается поперечный размер вспомогательного зеркала. Для апланатической системы это означает противоречие между требованием минимизации аберраций и ограничением на размер вспомогательного зеркала.

В дальнейшем ограничим поперечный размер вспомогательного зеркала D₁ с дополнительными участками образующей, необходимыми для перехвата наклонных лучей поперечным размером главного зеркала D.

При изменении параметров зеркал d и f характер зависимостей, приведенных на рис.9-10, принципиально не меняется. При этом следует добавить, что для апланатической системы зависимость 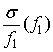всегда имеет минимум: либо локальный минимум при некотором оптимальном значении , либо минимум при минимально возможном фокальном радиусе f₁=0.5. В теории аберраций третьего порядка однозеркальная система и система Кассегрена имеют одинаковые аберрации [6]. При сравнении этих систем по критерию СКА на рис.9 видно, что в области малых F уровень аберраций в этих системах одинаковый, однако ростом F аберрации в однозеркальной системе убывают быстрее, чем в системе Кассегрена. Границей, при которой начинается различие, является значение эквивалентного фокусного расстояния, соответствующего плоскому вспомогательному зеркалу, когда . При этом значении f_e в системе Кассегрена происходит переход на другую ветвь гиперболы и вспомогательное зеркало из вогнутого становится выпуклым.

Для анализа аберраций при варьировании параметров в апланатической системе используем указанную выше особенность – существование минимума CKA при оптимальном значении фокального радиуса для каждой пары параметров d и f. Будем менять продольные размеры зеркальной системы в интересующем нас диапазоне от 0.2 до 1.2. При этом необходимо учитывать, что при положении фокуса за главным зеркалом, продольный размер системы характеризуется параметром . Результаты расчетов функции , полученные при трассировке лучей для угла наклона w=10, представлены на рис. 11-14. Распределение уровня аберраций в виде трехмерной поверхности при изменении параметров d, f приведено на рис.11, а при изменении параметров d и - на рис.12 – соответствующим цветом на плоскости. Рис.13 показывает соответствующие значения оптимального фокального радиуса, а рис. 14 – необходимый при этом относительный размер вспомогательного зеркала D₁/D.

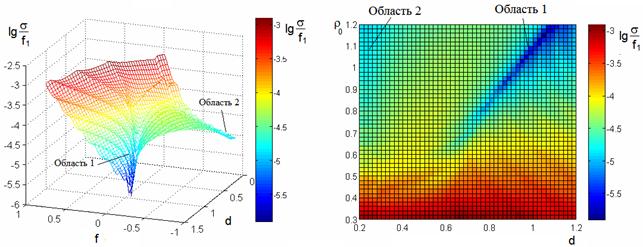
Рис.11 Рис.12

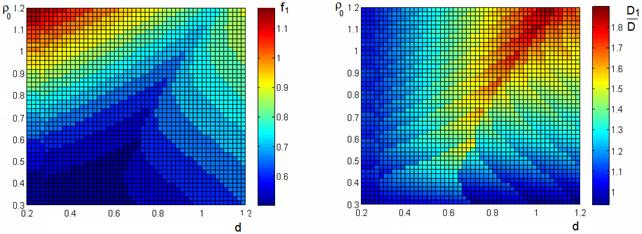
Рис.13 Рис.14

При анализе данных на рис. 11-14 прежде всего заметим, что уровень аберраций растет с уменьшением параметра для всех d, и область <0.4 соответствует максимальным аберрациям. При >0.6 выделяются две области минимальных аберраций: 1) d>0.6, 2) d<0.3. Для обеих этих областей характерно положение первичного фокуса за главным зеркалом f<0. Рассмотрим подробней эти две области.

1.Область d>0.6, >0.6.

Аберрации в этой области характеризуется существованием глубокого минимума функции вдоль линии, расположенной выше (см. рис.12). С ростом продольных размеров d, , и, соответственно, с увеличением оптимального эквивалентного радиуса f₁ вдоль этой линии аберрации уменьшаются (рис.13). Существенной особенностью этой области является большой поперечный размер вспомогательного зеркала (см. рис.14), необходимый для полного перехвата лучей в системе с оптимальным значением фокального радиуса.

Соотношения между параметрами зеркал в этой области минимальных аберраций можно аппроксимировать линейными функциями

, (6)

, (7)

(8)

На рис. 15 приведены зависимости (d) и f₁(d), полученные при трассировке лучей с углами наклона w=10°, 20°, 30°(кривые синего, зеленого и красного цвета, соответственно), в сопоставлении с аппроксимацими (6),(7) (линии черного цвета). Как видно из рисунка, приближенные формулы (6)-(8) применимы для оценки параметров в широком диапазоне углов зрения.

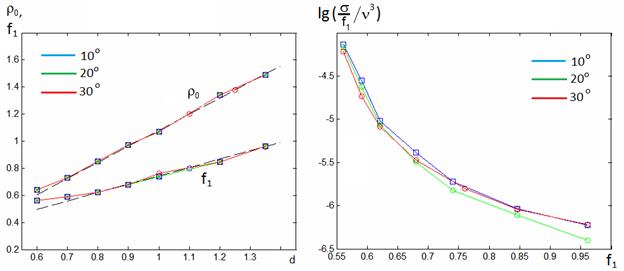
Рис.15 Рис.16

На рис. 16 показаны соответствующие зависимости 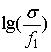от оптимального фокального радиуса f ₁ для угла w₀=10°. На этом же рисунке приведены аналогичные зависимости, полученные для углов w=20° и 30° градусов c нормировкой СКА на .

2.Область d<0.2, >0.6.

Назовем эту область параметров областью “тонких” зеркальных систем. С уменьшением расстояния между зеркалами в этой области аберрации уменьшаются. Минимальная толщина системы определяется условием – зеркала не должны пересекаться. Кроме того, возникает еще одно ограничение: при малых d не для всех значений параметров и f₁ существует решение задачи трассировки для крайних лучей.

Для определения зависимостей между оптимальными параметрами, характеризующими рассматриваемую область, выберем для примера расстояние между зеркалами d=0.12 и будем менять величину параметра .

На рис. 17 (цвет кривых соответствует цветам на рис.15-16) изображены зависимости оптимального фокального радиуса f₁ от продольного размера для трех значений угла наклона лучей 10°, 20°, 30°.

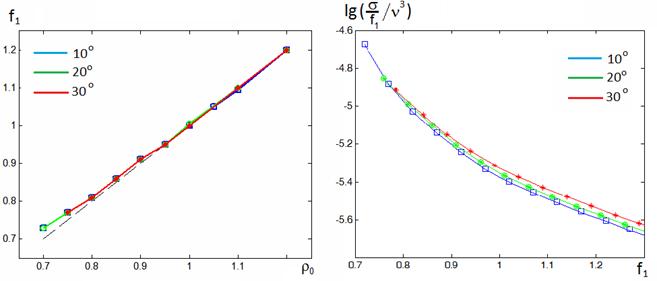
Рис.17 Рис.18

Эти зависимости так же, как в области 1, можно аппроксимировать линейной функцией

(9)

На рис. 18 представлены зависимости уровня аберраций 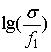от оптимального фокального радиуса f₁ для угла наклона лучей w_o=10° и нормированные кривые для углов 20° и 30° . Здесь, как и для кривых на рис. 16, выполнена нормировка СКА на .

Из данных на рис. 15-18 следует, что, как в области 1, так и в области 2 зависимость аберраций от угла зрения близка к кубической. На рис.19 представлен характерный вид образующих и ход лучей (при w=30°) в системе с параметрами, принадлежащими области 2 (d=0.12, f₁=0.9,=0.9). Для сравнения аберраций на рис. 20 приведена картина лучей в системе Кассегрена с эквивалентными параметрами.

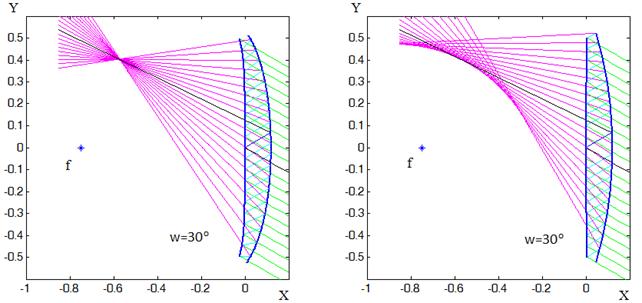
Рис.19 Рис.20

В заключение данного раздела отметим, что как соотношение (8), так и соотношение (9), отличаются от соотношения для идеального апланата (f₁/d ~ 1), приведенного в [1].

4. Исследование планарной апланатической системы с минимальными аберрациями методом интеграла Кирхгофа.

Как следует из предыдущего раздела, существуют две области параметров апланатических систем с малыми несимметричными аберрациями (с малым и большим расстоянием между зеркалами). В данном разделе мы исследуем характеристики систем с малым расстоянием между зеркалами, поскольку они обеспечивают малые потери из-за “промахивания” лучей. Из анализа аберраций в апланатических системах следует, что минимальным аберрациям соответствуют максимальный продольный размер , ограниченный допустимой величиной поперечного смещения источника dy=0.5 при оптимальном фокальном радиусе f₁_opt. Для дальнейшего анализа методом физической оптики была выбрана апланатическая система с минимальными значениями СКА и параметрами =0.87, =0.96, d=0.09 , образующие зеркал которой представлены на рис.21. На этом же рисунке изображена лучевая картина в этой системе для угла зрения 40°.

Расчеты зависимостей коэффициента использования поверхности (КИПа) от угла зрения были проведены апертурным методом Кирхгофа) при D/l=25 и D/l=100 . При вычислениях оптимизировались координаты, угол наклона и ширина диаграммы направленности источника.

На рис.22 приведены зависимости КИПа от угла отклонения луча для апланатической системы (кривые красного цвета).

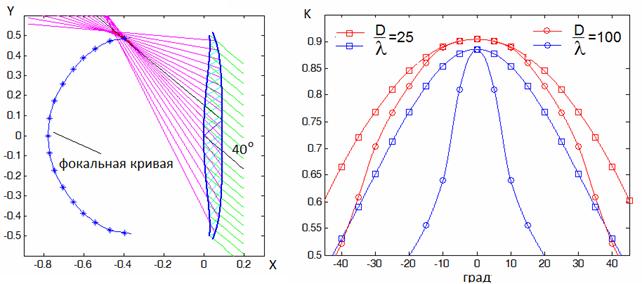
Рис.21 Рис.22

Для сравнения на рис. 22 синим цветом изображены зависимости КИПа однозеркальной системы с тем же продольным размером (F=0.87). Как видно на рисунке, углы зрения исследованных систем по уровню КИП=0.5 при D/l=100 составляют 42° и 20°, соответственно. При малых электрических размерах главного зеркала (D/l=25) преимущество двухзеркальной апланатической системы не столь значительно.

Работа поддержана грантом РФФИ №12-08-12003-офи_м.

Литература

1. Галимов Г.К. Апланаты, т.3, Апланатические телескопы и антенны: “Антенны-связь НПК”, 2011, 436 с.

2. Банков С.Е. Проектирование и экспериментальное исследование решетки щелевых излучателей. // РЭ, 2004, Т.49, №6, С. 701-706.

3. M. Ettorre and other, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, 2007,Vol.6, Dec. pp. 537-539.

4. Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.

5. Банков С.Е. Синтез зеркал с пространственной дисперсией коэффициента отражения // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL: http://jre.cplire.ru/jre/jan13/5/text.html.

6. Михельсон Н.Н. Оптические телескопы. Теория и конструкция, М., Наука, 1976, 510с.

7. Дубовик А.С., Апенко М.И., Дурейко Г.В. и др. Прикладная оптика. М. Недра, 1982, 612с.

8. Венецкий А.С., Калошин В.А. О распределении эйконала в апертуре двухзеркальной телескопической системы // РЭ, 2012,т.57, №9, с.1004-1011.

9. Калошин В.А., Фролова Е.В. Характеристики осесимметричных двухзеркальных апланатических антенн. “Антенны”, 2006, №7, С.45-51.

10. Банков С.Е., Калошин В.А., Фролова Е.В. Исследование и оптимизация планарной двухзеркальной системы Шварцшильда. Доклады I Всероссийской Микроволновой конференции, М. ИРЭ им. В.А.Котельникова РАН, 27-29 ноября 2013г.