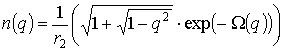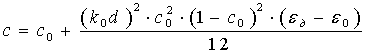УДК 621.396

ИССЛЕДОВАНИЕ ШИРОКОПОЛОСНЫХ ПЛАНАРНЫХ ЛИНЗ ЛЮНЕБУРГА

 

В. В. Ахияров ¹, В. А. Калошин ², Е. А. Никитин ^{2, 3}

¹ НИИ РЭТ МГТУ им. Н.Э. Баумана, ² ИРЭ им. В.А. Котельникова РАН, ³ МТУСИ

 

Статья получена 20 января 2014 г.

 

Аннотация. Проведено численное электродинамическое моделирование двух типов планарной металлодиэлектрической линзы Люнебурга: радиально-слоистой и на основе кольцевой диэлектрической EBG структуры. Моделирование проведено с использованием трех методов: параболического уравнения, интегрального уравнения и метода конечных элементов. Рассмотрены задачи излучения и дифракции плоской волны. Исследованы широкополосные свойства планарных линз Люнебурга.

Ключевые слова: Планарные линзы, линза Люнебурга, широкополосные антенны, интегральное уравнение, параболическое уравнение, метод конечных элементов.

Abstract. Numerical electromagnetic modeling of two types of metal-dielectric planar Luneburg lenses: a radially stratified and based on ring dielectric EBG structure have been made. Simulation is carried out using three methods: a parabolic equation, integral equations and finite element method. The problems of radiation and diffraction of a plane wave considered. The broadband properties of planar Luneburg lenses have been investigated.

Keywords: Planar lens, Luneburg lens, broadband antennas, integral equation, parabolic equation, finite element method.

 

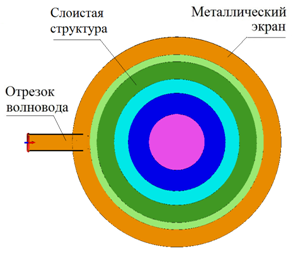
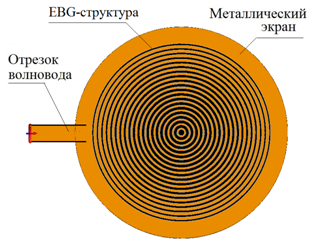
В данной работе тремя методами: параболического уравнения (ПУ), интегрального уравнения (ИУ), а также методом конечных элементов (МКЭ) проведено численное решение задач излучения и дифракции плоской волны для планарной линзы Люнебурга в виде радиально-слоистого диэлектрического диска (рис.1), а также в виде кольцевой диэлектрической EBG структуры (рис.2) в широкой полосе частот. Диэлектрические слои и диэлектрические кольца EBG структуры, а также питающий отрезок прямоугольного волновода расположены между двумя металлическими дисками (экранами) (рис.1,2). Прямоугольный волновод возбуждает в планарных волноводах, образованных экранами, ТЕМ моду. Поскольку ТЕМ мода не имеет отсечки и частотной дисперсии, следует ожидать, что линзы обладают широкополосными свойствами. Исследование этих свойств является главной задачей данной работы.

Практическая реализация непрерывного закона изменения коэффициента преломления от радиуса, т.е. синтез градиентной линзы в СВЧ и КВЧ диапазонах волн связана с большими сложностями. Поэтому ниже рассматриваются дискретные законы изменения n(r). Первый способ реализации такого закона – изготовление линзы Люнебурга из концентрических слоев с различной диэлектрической проницаемостью (рис.1), второй – использование кольцевой диэлектрической EBG структуры (рис.2). Преимущество второго способа реализации заключается в отсутствии необходимости использования диэлектриков с различными диэлектрическими проницаемостями.

 

Рис.1. Слоистая линза Люнебурга

Рис.2. EBG линза Люнебурга

 

Для численного моделирования диаметр линзы выбран равным 100 мм, толщина – 3,4 мм, диаметр экранов равен 118 мм.

Результаты численного моделирования исследуемых в работе линз c большим электрическим размером на частоте 35 ГГц приведены в [1], результаты численного исследования планарной линзы Люнебурга на основе кольцевой EBG структуры с малыми электрическими размерами приведены в работе [2]. Отметим, что планарная линза на основе кольцевой EBG структуры является частным случаем планарной металлодиэлектрической линзы Люнебурга на основе гофрированного диэлектрического диска, предложенной в [3]. Первые экспериментальные результаты для линзы Люнебурга на основе кольцевой EBG структуры представлены в [4]. Законы изменения толщины колец от радиуса для такой линзы в общем случае можно найти, используя обобщение решения задачи синтеза неоднородной анизотропной линзы с центральной симметрией [5] и формулы для компонентов тензора диэлектрической проницаемости плоскослоистой среды [6]. В случае поляризации электрического поля, ортогональной экранам, и возбуждения в планарном металлодиэлектрическом волноводе, образованного экранами, ТЕМ моды, внутри линзы распространяются «обыкновенные» лучи и для определения коэффициента преломления внутри линз обоих типов можно воспользоваться классическим решением Люнебурга-Моргана [7]. Для частного случая, когда один из фокусов находится на поверхности линзы, а другой – в бесконечности, решение для коэффициента преломления n в параметрической форме имеет вид

 

,                                  (1)

 

где

,                                           

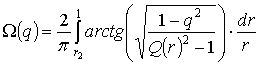– внутри оболочки (), r - нормированный радиус  – внутренний нормированный радиус оболочки,  – параметр.

         В случае отсутствия оболочки (r₂ =1) формула (1) переходят в классическое решение Люнебурга [8]:

 

                                                                         (2)

 

         Теория синтеза планарной линзы Люнеберга на основе кольцевой EBG  структуры в общем случае дана в [9]. В частном случае ТЕМ моды закон изменения толщины колец от радиуса определяется формулой:

 

                   (3)

 

где  - коэффициент заполнения, c₀ = (ε – ε₀)/(ε_д –ε₀) - та же величина в статическом приближении, d – период EBG структуры, a – толщина кольца, ε_д –относительная диэлектрическая проницаемость его материала, ε = n², ε₀ = 1. Для линзы без оболочки зависимость (3) сложно реализовать на практике, поскольку коэффициент преломления при приближении к границам линзы стремится к единице (2), а толщина колец - к нулю. Поэтому в данной работе рассматривается EBG линза с оболочкой. Коэффициент преломления оболочки n = 1.1, r₂ = 0.91.

В качестве слоистой линзы Люнебурга рассматривается диэлектрический диск из пяти концентрических слоев с различной диэлектрической проницаемостью, расположенный между двух экранов (рис.1). Законы изменения относительной диэлектрической проницаемости от радиуса для градиентной линзы, коэффициент преломления которой определен формулой (2) и исследуемой слоистой линзы Люнебурга, показаны на рис.3 сплошной и штриховой линией, соответственно.

EBG линза представляет собой структуру из 26 концентрических диэлектрических колец из полистирола (относительная диэлектрическая проницаемость ε_д = 2.56), расположенных между экранами с периодом 2 мм. Законы изменения коэффициентов преломления и заполнения планарной линзы Люнебурга на основе диэлектрической EBG структуры, рассчитанные по формулам (1) и (3),  показаны на рис.4, соответственно, сплошной и штриховой линиями.

 

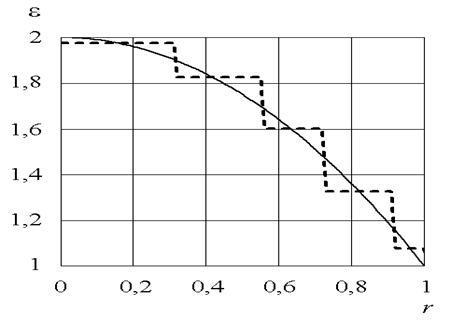
Рис.3. Закон изменения относительной диэлектрической проницаемости для градиентной (сплошная линия) и слоистой (штриховая линия) планарной линзы Люнебурга

 

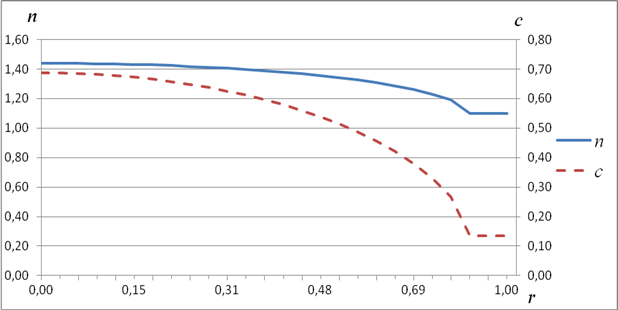
Рис.4. Закон изменения коэффициентов преломления n(r) и заполнения c(r) планарной линзы Люнебурга на основе EBG структуры

 

В основе моделирования описанных выше линз методом ИУ лежит сведение интегрального уравнения к системе линейных алгебраических уравнений, которая решается методом моментов, при численном решении методом конечных элементов используется вариационная постановка задачи. При использовании метода ПУ требуется решить уравнение для амплитуды поля u(x, z):

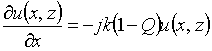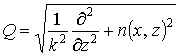,                 (4)

 

где x и z – соответственно продольная и поперечная координаты, ,  – показатель преломления.

Для среды с показателем преломления  используется приближенное представление дифференциального оператора Q в виде

      Q = Q^* + n(x,z) - 1                                                                  (5)

где

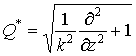                                                       (6)

 

оператор для свободного пространства [10]. С учетом (5) ПУ (4) можно представить в виде:

,                            (7)

 

который позволяет использовать эффективный алгоритм численного решения [11].

Для определения поля в дальней зоне вычисляется интеграл по координате z от полученного распределения ближнего  поля при фиксированном значении x = x₀

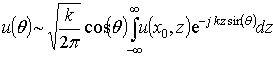   .                                         (8)

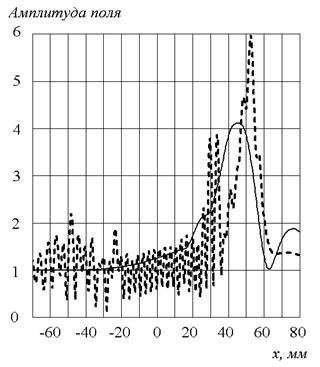
Для уточнения положения точки фокусировки была рассмотрена задача дифракции на линзе плоской волны. На рис.5а и 5б показано полученное распределение амплитуды поля в ближней зоне для слоистой и EBG линзы, при этом хорошо видна область локализации (фокусировки) поля, расчеты выполнялись методом ПУ. На рис. 6а, 6б показаны зависимости амплитуды поля с частотой  от продольной координаты x при для слоистой и EBG линзы, рассчитанные методом ПУ (сплошная линия) и ИУ (штриховая линия).

 

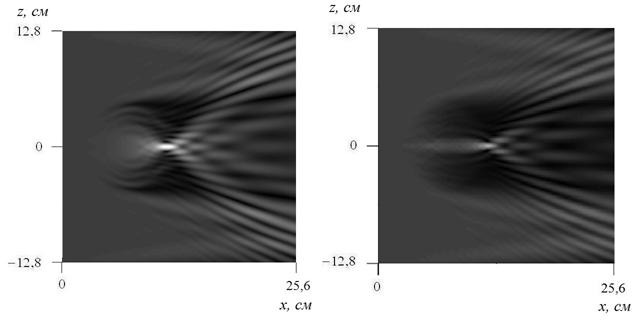
а)                                                                  б)

Рис.5. Распределение поля в ближней зоне при облучении линзы Люнебурга плоской волной (решение ПУ), частота .

а) слоистая линза, б) EBG-линза

 

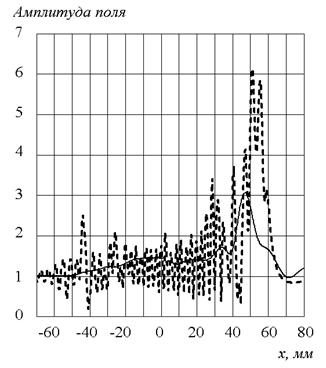
а)

б)

 

Рис.6. Изменение амплитуды поля вдоль диаметра линзы.

а) слоистая линза, б) EBG-линза

 

Результаты, полученные методами ИУ и ПУ для слоистой линзы, отличаются качественно. Определение точки фокусировки методом ПУ предсказывает ее положение внутри линзы, а методом ИУ – снаружи, амплитуды полей отличаются примерно на 2 дБ. Для EBG линзы метод ИУ дает положение точки фокусировки на границе линзы, что совпадает с геометрооптическим фокусом, решение ПУ приводит к его незначительному смещению внутрь линзы.

         Далее тремя методами решалась задача излучения при возбуждении планарной линзы Люнебурга прямоугольным волноводом сечением  на частоте . На рис.7 показано распределение амплитуды ближнего поля, полученное при решении скалярной задачи методом ПУ. На рис. 7а видна слоистая структура поля внутри линзы, связанная по-видимому с наличием скачков диэлектрической проницаемости на границах слоев. На рис.7б такой структуры не наблюдается.

 

       а)                                                                 б)

Рис.7. Распределение ближнего поля при возбуждении линзы Люнебурга

полем источника, расположенным в ее фокусе (решение ПУ),

частота . а) слоистая линза, б) EBG-линза

 

а)	б)	в)

 

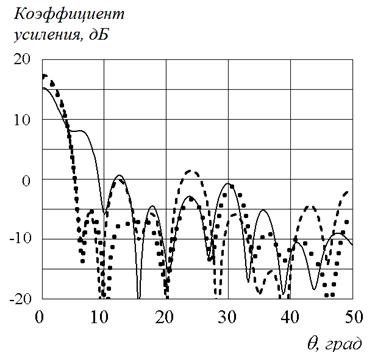
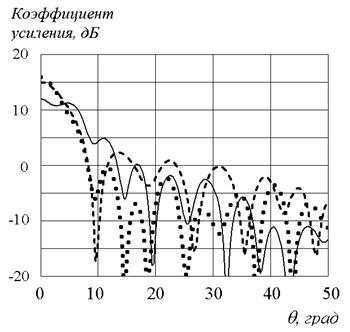
Рис.8. Диаграммы направленности слоистой линзы Люнебурга

при различном положении облучателя. Сплошная линия – решение ПУ, штриховая линия – МКЭ, пунктир – метод ИУ.

а) , б) , в)

 

На рис.8 представлены диаграммы направленности слоистой линзы для трех положений облучателя: открытый конец волновода расположен на расстоянии 1 мм от края линзы (рис.8а), помещен внутрь линзы на глубину 4 мм (рис.8б) и удален от ее края на 5 мм (рис.8в).

Приведенные на рис.8а результаты расчетов диаграммы направленности слоистой линзы Люнебурга были получены методами ИУ и ПУ, а также методом конечных элементов. Видно, что все три метода дают совпадающую ширину главного лепестка диаграммы направленности и угловое положение боковых лепестков, однако амплитуды боковых лепестков  существенно отличаются. Уже для первого бокового лепестка решение ПУ на 13 дБ превышает значение, которое было получено при решении методами ИУ и МКЭ. Меньшее значение коэффициента усиления и высокий уровень первого бокового лепестка, полученные при решении ПУ, обусловлены тем, что источник смещен из фокуса линзы, который был получен с использованием данного метода (рис.6а). Решения с использованием ИУ и МКЭ, отличаются, начиная со второго лепестка.

В случае, если источник расположен внутри линзы на расстоянии 4 мм от ее границы, коэффициенты усиления, полученные методами ИУ и ПУ, практически совпадают (рис.8б).

Сопоставление результатов, представленных на рис.8а –8в свидетельствует о том, что максимальное значение коэффициента усиления 17,5 дБ, полученное при решении ИУ и методом конечных элементов, наблюдается при , что примерно соответствует положению фокуса, которое было предсказано методом ИУ. Для метода ПУ максимальное значение коэффициента усиления 16 дБ достигается при , что соответствует фокусному расстоянию, которое было получено при использовании данного метода (рис.6а).

Это позволяет сделать вывод о том, что положение максимума поля, полученное при решении задачи дифракции плоской волны на линзе, в рамках одного метода (ИУ или ПУ) достаточно точно предсказывает положение облучателя. При этом строгое решение методом ИУ для EBG линзы дает совпадение дифракционного и геометрооптического фокусов.

 

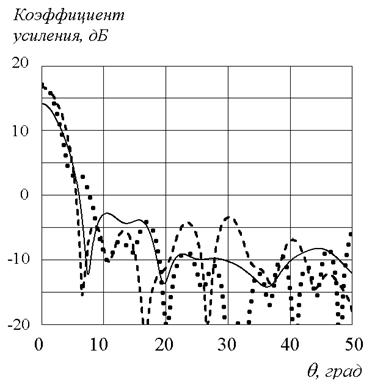
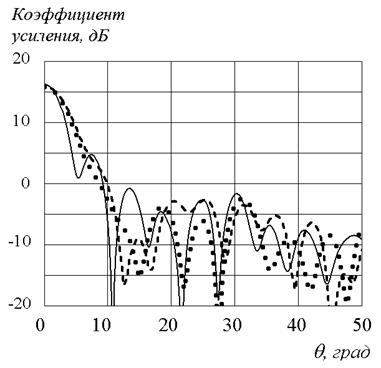
Рис.9. Диаграммы направленности планарной EBG-линзы Люнебурга.

Сплошная линия – решение ПУ, штриховая линия – МКЭ, пунктир – ИУ

 

На рис.9 представлены результаты расчетов диаграммы направленности EBG линзы, положение источника выбиралось на расстоянии  от центра линзы или 3 мм от ее внешнего кольца. Меньшее значение коэффициента усиления в направлении максимума излучения, полученное методом ПУ, обусловлено тем, что источник отклонен от положения фокуса, предсказанного в рамках данного метода (рис.6б).

На рис.10,11 представлены зависимости коэффициента усиления от частоты для двух рассмотренных типов линзы Люнебурга в диапазоне частот от 5 до 40 ГГц, полученные методом ИУ и МКЭ. Для исключения влияния облучателя на частотную зависимость коэффициента усиления линзы ширина широкой стенки прямоугольного волновода менялась с частотой, оставаясь равной  длины волны. Видно, что для слоистой линзы на частотах более 15 ГГц наблюдается очень хорошее соответствие результатов, полученных двумя различными методами, а для EBG линзы хорошее соответствие наблюдается во всем частотном диапазоне.

 

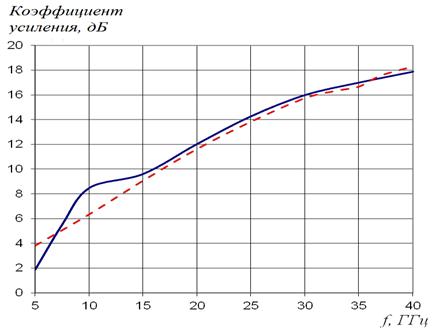
Рис.10. Зависимость коэффициента усиления слоистой линзы от частоты.

Сплошная линия – метод интегральных уравнений,

штриховая линия – метод конечных элементов

 

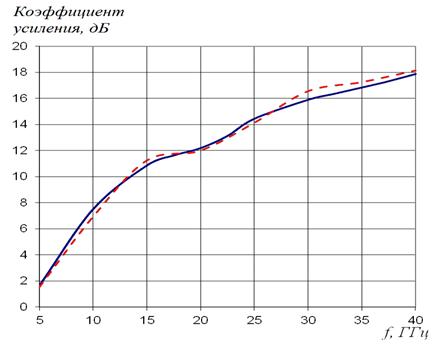
Рис.11. Зависимость коэффициента усиления EBG линзы от частоты.

Сплошная линия – метод интегральных уравнений,

штриховая линия – метод конечных элементов.

 

На рис.12,13 показаны соответствующие частотные зависимости коэффициента использования поверхности (КИП) апертуры.

 

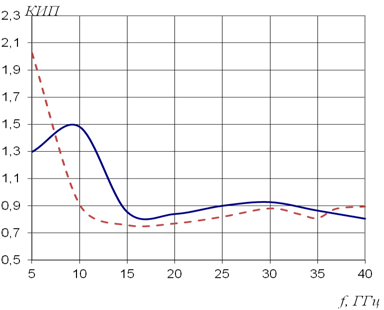
         Рис.12. Зависимость коэффициента усиления слоистой линзы от частоты.

Сплошная линия – метод интегральных уравнений,

штриховая линия – метод конечных элементов

 

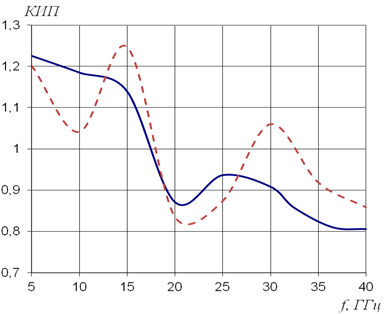
Рис.13. Зависимость коэффициента усиления EBG линзы от частоты.

Сплошная линия – метод интегральных уравнений,

штриховая линия – метод конечных элементов.

 

Сравнение представленных на рис.10-13 результатов показывает, что на частотах более 20 ГГц оба варианта планарной линзы Люнебурга в исследованном диапазоне волн имеют близкие значения коэффициента усиления и КИПа.

Следует отметить, что очень высокие значения величины КИПа в области низких частот связаны с маленьким электрическим размером апертуры линзы в Н плоскости.

По результатам работы можно сделать следующие выводы:

-планарные пятислойная и EBG линзы Люнебурга обладают хорошими частотными свойствами в исследованном диапазоне волн;

- решение задачи дифракции плоской волны позволяет предсказать оптимальное положение облучателя в рамках данного метода;

- метод интегрального уравнения и метод конечных элементов дают близкие значения для коэффициента усиления, ширины главного лепестка и уровня боковых лепестков;

- использование метода параболического уравнения позволяет правильно определить ширину главного лепестка ДН и положение боковых лепестков планарной линзы Люнеберга обоих типов.

 

Литература

1.     Ахияров В.В., Калошин В.А., Никитин Е.А., Моделирование планарной линзы Люнебурга, Труды I Всеросс. Микроволной конф., 2013., ноябрь, М. ИРЭ им. Котельникова РАН. С.393-396.

2.     Ашихмин А.В., Негробов В.В., Пастернак Ю.Г., Федоров С.М. Исследование конструкций сверхширокополосных излучающих структур на основе плоской линзы Люнеберга // Радиотехника. 2012, №5. С.14-17.

3.     Калошин В.А. Метод ключевых задач в асимптотической теории волноведущих и излучающих систем с кромками. Дисс. на соиск. уч. ст. докт. физ.- мат. наук, М., ИРЭ АН СССР, 1989 г.

4.     Калошин В.А. Многолучевые гибридные антенны // Труды междун. конф. Crimico-2002. Севастополь, сентябрь, 2002 г.

5.     Калошин В.А., Щербенков В.Я., Обобщение задачи Люнеберга для анизотропной среды // РЭ, 1973, т.18, №1, С.26-31.

6.     Калошин В.А., Стоянов С., Замедляющие свойства слоистых диэлектрических структур //РЭ. 1989, т.34, №12.С. 2640-2643.

7.     Morgan S.P., General Solution of the Luneberg Lens Problem // J. Appl. Phys. 1958, V.29, No. 9, P.1358.

8.     Luneburg R.K., Theory of Optics, Brown University, Providence, Rhode Island, 1944, P.189-213.

9.     Калошин В.А. Планарная линза Люнебурга на основе кольцевой EBG структуры, РЭ, 2014, (в печати).

10.  Levy М.F. Parabolic equation method for electromagnetic wave propagation. London. IEE, 2000, 336 p.

11.  Ахияров В.В. Решение задач дифракции методом параболического уравнения // Электромагнитные волны и электронные системы. 2012. №11. С.24-30.