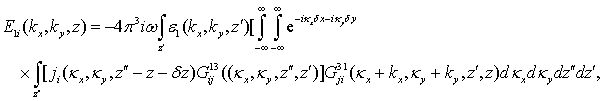УДК 621.371+537.87

ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ В ДИАГНОСТИКЕ

НЕОДНОРОДНЫХ СРЕД С ПРИМЕНЕНИЕМ ЛИНЗ ИЗ ЛЕВОСТОРОННЕГО МЕТАМАТЕРИАЛА¹

К. П. Гайкович

 Институт физики микроструктур Российской академии наук, г. Нижний Новгород

Нижегородский государственный университет им. Н.И. Лобачевского  

Статья получена 23 декабря 2014 г. 

Аннотация. Рассматриваются возможности диагностики диэлектрических неоднородностей в среде по данным измерений рассеянного поля над линзой из левосторонних метаматериалов. В работе развивается метод, основанный на решении обратной задачи рассеяния по многоуровневым измерениям двумерных распределений комплексных амплитуд электрического поля с помощью сканирующей системы источник-приемник. Выполнено численное моделирование восстановления трехмерной структуры распределенных диэлектрических неоднородностей (томографии) и восстановления формы поверхности сплошных объектов (компьютерной голографии).

Ключевые слова: неинвазивная диагностика, томография, голография, неоднородности диэлектрической проницаемости, линзы из левосторонних метаматериалов, обратная задача рассеяния.

Abstract: Possibilities of diagnostics of dielectric inhomogeneities in a medium by data of scattered field measurements above a lens of left-handed metamaterials are considered. In this paper, a method is developed based on the solution of inverse scattering problem by multilayer measurements of 2D distributions of complex amplitudes of electric field with a scanning source-receiver system. Numerical simulation of 3D structure retrieval of distributed dielectric inhomogeneities (of tomography) and of the surface shape retrieval of solid targets (of computer holography). 

Key words: noninvasive diagnostics, tomography, holography, inhomogeneities of permittivity, lens of left-handed metamaterials, inverse scattering problem.

 

1.     Введение

Как было показано в [1], слой метаматериала с отрицательным коэффициентом преломления (e = –1, m  = –1) – так называемая совершенная линза – обладает способностью фокусировать все компоненты поперечного спектра источника, включая ближнепольные, что приводит к возможности точного воспроизведения изображений двумерных объектов, расположенных в фокальной плоскости. Если излучение может проникать в неоднородности, расположенные за линзой, то сканирование источником зондирующего излучения, а, следовательно, и фокусом по другую сторону линзы открывает возможность нового вида томографии с субволновой разрешающей способностью – диагностики трехмерной диэлектрической структуры неоднородности по измерениям рассеянного ей излучения. Путем изменения расстояния источника до линзы толщиной d фокус может перемещаться за линзой в интервале d < z_f < 2d, что определяет глубину области зондирования.

Оказалось, однако, что реализовать на практике такие совершенные линзы весьма затруднительно, поскольку наличие в материале линзы даже минимального поглощения радикально ограничивают область субволновой фокусировки [2]. С точки зрения постановки обратной задачи рассеяния также имеются трудности. Во-первых, идеальную фокусировку зондирующего поля нарушает вторичное рассеяние поля в самой неоднородности, т.е. она имеет место только при решении задачи в борновском приближении; во-вторых, вблизи линии от фокуса к поверхности имеет место резкое нарастание поля вплоть до сингулярности, что с одной стороны нереалистично, а с другой – крайне трудно корректно учесть в алгоритме решения. Тем не менее, возможность решения такой идеализированной задачи была продемонстрирована в [3] в постановке, когда фокус перемещался в области под неоднородностью. Неоднородность при этом оказывалась в ближней зоне от фокуса, что позволило достичь субволновой разрешающей способности при численном моделировании алгоритма.

Левосторонние линзы из неидеального метаматериала, как оказалось, могут иметь свои практические преимущества. В этом случае оказывается возможным решать задачу в более реалистичной постановке, когда в зондируемой области имеется обычный фокус, который можно погружать в исследуемую неоднородность – что во многом компенсирует потерю субволновой фокусировки. Такие линзы было бы удобно использовать для зондирования не вполне плоских, но упругих сред – таких, как живые ткани или некоторые типы грунта, избавляясь от проблем, связанных с неровной границей. Задача в такой постановке была рассмотрена в [4], создан алгоритм и выполнено численное моделирование томографии с использованием «несовершенных» линз для неоднородностей в вакууме.

Целью данной работы является численное моделирование этого метода томографии для распределенных неоднородностей в диэлектрических средах, включая случай рассогласования линзы с внешней и внутренней сред с линзой по диэлектрическим параметрам, а также метода восстановления числовой формы поверхности сплошных диэлектрических объектов (компьютерной голографии), используя математически последовательный метод, предложенный в [5].

2.     Обратная задача рассеяния

Следуя [3], рассмотрим математическую постановку задачи. Пусть система источник-приемник расположены в среде 1 перед левосторонней линзой (слой 2), а зондируемая трехмерная неоднородность комплексной диэлектрической проницаемости e₁(r) расположена за линзой в среде 3. Зондирующее поле  в среде 3 определяется соответствующей функцией (тензором) Грина:

                                     ,                                   (1)

где  - распределение тока в источнике. Используя разложение (1) по плоским волнам [3], можно определить зондирующее поле в любой многослойной среде. В среде с неоднородностью полное поле может быть представлено в виде суммы зондирующего и рассеянного поля. Расчет поля в этом случае является достаточно сложной, но решаемой на современных компьютерах вычислительной задачей.

Для диагностики неоднородностей сканирование осуществляется на нескольких уровнях z, что позволяет менять глубину погружения фокуса линзы в зондируемую среду. Соответствующая обратная задача может решаться на основе трехмерного нелинейного интегрального уравнения 1-го рода, которое, как показано в [3], в борновском приближении можно свести к решению одномерного интегрального уравнения при условии фиксированного взаимного положения источника и приемника, характеризуемого вектором . При этом условии структура зондирующего поля инвариантна относительно поперечных перемещений такой системы при сканировании, а все наблюдаемые вариации принимаемого сигнала обусловлены только рассеянием на зондируемой неоднородности. Тогда двумерное фурье-преобразование исходного уравнения по поперечным координатам приводит к одномерному уравнению относительно глубинного профиля поперечного спектра неоднородности:

   (2)

где ,  - компоненты двумерного фурье-преобразования функции Грина G, которые определяют вклад j-й компоненты тока источника, расположенного в k-м слое, в i-ю компоненту поля в l-м слое. Эти функции для произвольной многослойной среды приведены в [3].

Таким образом, необходимо решить интегральное уравнении Фредгольма 1-го рода для каждой пары компонент поперечного спектра для определения вертикального профиля неоднородности в k-пространстве . Затем двумерное обратное преобразование Фурье дает искомое решение задачи томографии:

,                       (3)

Как показано в [3], в данном подходе возможна и некоторая коррекция решения за пределами борновского приближения.

Для решения этой некорректной задачи использовался алгоритм метода обобщенной невязки для комплекснозначных функций в гильбертовом пространстве (пространство Соболева), разработанный в [3]. На практике в анализе надо еще учесть аппаратную функцию приемно-передающей системы, как это было сделано в аналогичной с математической точки зрения задаче СВЧ подповерхностной томографии [5], что не меняет вид и метод решаемого уравнения.

Для сплошных внутренне однородных объектов, с которыми чаще всего приходится иметь дело на практике, достаточно решить задачу определения формы их поверхности, т.е. задачу компьютерной голографии. Из общих соображений ясно, что такое сильное ограничение способно привести к существенно более точному решению задачи. Для этого необходимо в алгоритм решения задачи можно внести дополнительную априорную информацию о постоянстве диэлектрических параметров внутри неоднородной области. Такой метод был предложен при решении задачи СВЧ подповерхностной голографии в [5,6]. Для его реализации можно непосредственно использовать решение (2) в k-пространствев предположении, что оно получено для объекта с известной постоянной внутренней комплексной диэлектрической проницаемостью. Если форму поверхности объекта в каждом сечении z можно задать в декартовой системе координат в виде двух функций  (см. на рис.1), то, выполнив фурье-преобразование по одной из переменных поперечного спектра k_y,

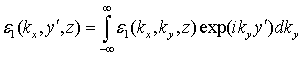,                             (4)

 

получаем (после замены ) комплексное трансцендентное уравнение

,                             (5)

 

решение которого для двух неизвестных x₁ и x₂ задает искомую форму поверхности объекта.

 

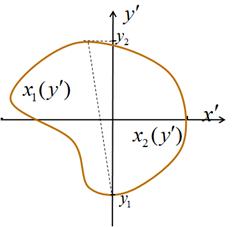
Рис.1. Граница сечения объекта при

 

Поскольку решение может быть получено при каждом значении k_x, уравнение (5) является переопределенным, и, следовательно, имеется возможность его оптимизации. Такой метод является математически последовательным, поскольку обратное преобразование Фурье решения в k-пространстве (3) не может точно воспроизвести скачок на границе объекта из-за известного эффекта Гиббса – даже не принимая во внимание неизбежное сглаживание границы при решении некорректной задачи.

 

3.     Результаты численного моделирования

Результаты численного моделирования рассматриваемого подхода к сканирующей многоуровневой томографии и голографии показали эффективность соответствующих алгоритмов.

Моделирование осуществлялось по замкнутой схеме: для заданных неоднородностей вычислялось поле рассеяния, на его значения набрасывалась случайная нормально распределенная погрешность с заданным уровнем в интегральной метрике L₂. Затем решалась обратная задача и полученное 3D распределение параметров неоднородностей сравнивалось с исходным.

На рис.2-4 показан пример томографии неоднородности в вакууме в условиях слабого рассогласования, связанного с наличием мнимой части комплексной диэлектрической проницаемости линзы [4] (результаты показаны в масштабе длины волны , показанной на рисунках стрелкой). Для восстановления трехмерного распределения неоднородности комплексной диэлектрической проницаемости e₁(r), которая моделировалась двумя гауссовыми распределениями (одинаковыми для действительной и мнимой части). При решения (2) использовались «данные измерений» x-компоненты рассеянного электрического поля на 6 уровнях z = z_i в плоскости x-y. Зондирующее поле задавалось источником  j(r²–r–dr) = j_zd (r² – r – dz)z₀. Задача решалась при уровне случайной гауссовой ошибки 5%. Характерные размеры неоднородностей несколько превышали длину волны, показанную на рисунке стрелкой. На рис.2 и далее распределения полей и диэлектрических параметров даны в относительном (к соответствующим максимальным значениям) масштабе, т.е. от 0 до 1.

 

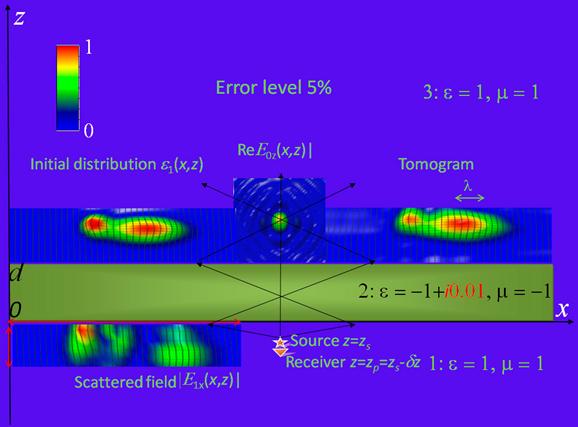
Рис.2. Численное моделирование томографии (вертикальное сечение через общий центр неоднородностей по y). Слой 1: слева в области, ограниченной стрелками – распределение амплитуды рассеянного поля; в центре – система источник-приемник. Слой 2: левосторонняя линза. Слой 3: слева исходное распределение реальной части комплексной диэлектрической проницаемости; в центре – распределение амплитуды зондирующего поля; справа – результат восстановления (томограмма).

 

На рис.2 можно видеть, что качество восстановления весьма неплохое (сходные результаты получены и для мнимой части комплексной диэлектрической проницаемости). На рис.3 показаны результаты решения обратной задачи для тех же неоднородностей, но расположенных ближе к поверхности линзы.

 

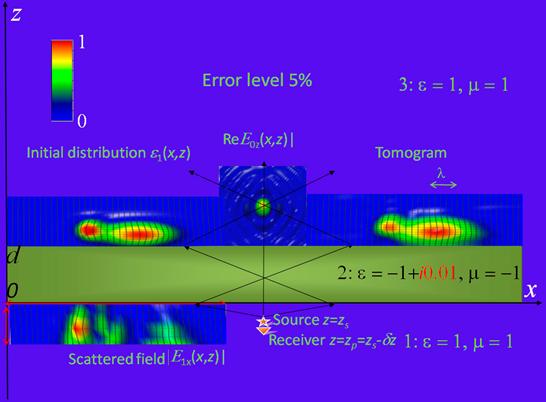
Рис.3. Численное моделирование томографии (вертикальное сечение). при уровне случайной ошибки данных 5%.

 

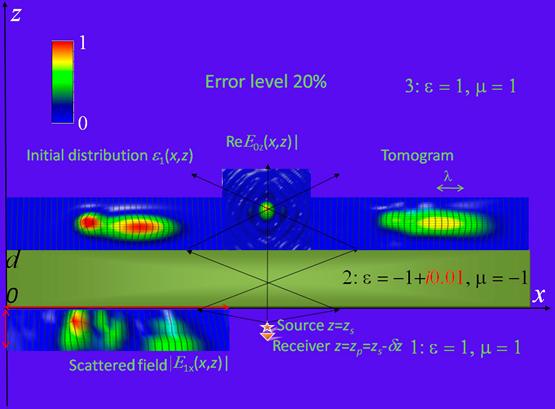
Рис.4. Численное моделирование томографии (вертикальное сечение) при уровне случайной ошибки данных 20%.

 

Влияние уровня ошибки данных на качество томографии можно оценить, сравнивая результаты на рис.2, полученные при 5% ошибке с результатами на рис.4 при ошибке 20%.

Более существенное рассогласование диэлектрических параметров сред и линзы приводит к отражениям на границах раздела сред и мультиплицированию фокуса. Пример моделирования томографии неоднородности в условиях, когда среда 3 с неоднородностями не согласована с линзой и по действительной и по мнимой части комплексной диэлектрической проницаемости, а среда 1 не согласована с измерительной системой по мнимой части представлен на рис.5. Поскольку длина волны в зондируемой среде уменьшается по сравнению с вакуумом, имеется возможность восстанавливать неоднородности с меньшими размерами.

 

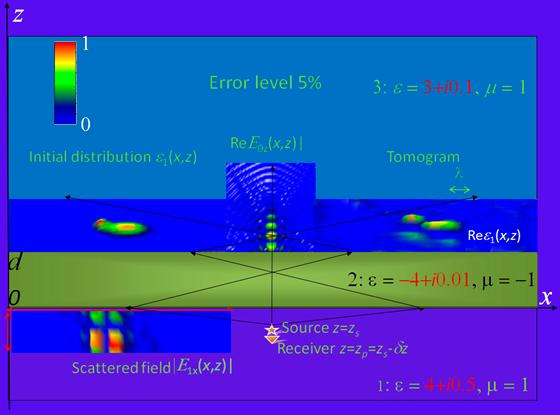
Рис.5. Численное моделирование томографии реальной части комплексной диэлектрической проницаемости
при отсутствии согласования сред с линзой.

 

Видно, что максимум зондирующего поля в данном случае расщеплен из-за отражения на границах раздела, но, тем не менее, основные детали неоднородной структуры воспроизводятся в целом правильно. Ниже восстановленного изображения можно видеть относительно слабо выраженные артефакты, связанные с влиянием вторичного рассеяния. На рис.6 представлено томографическое изображение мнимой части диэлектрической проницаемости этой неоднородности, которое значимых артефактов не содержит.

 

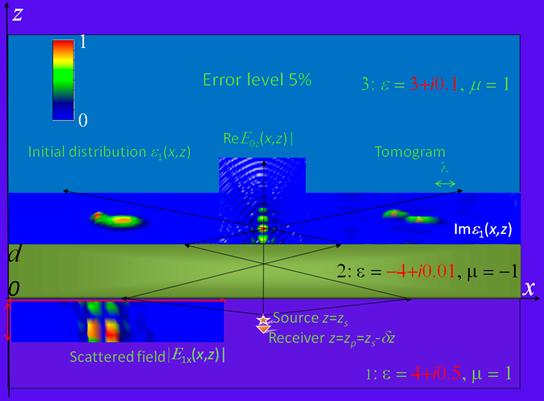
Рис.6. Численное моделирование томографии мнимой части комплексной диэлектрической проницаемости в несогласованных средах.

 

Анализ формы поверхности сплошного объекта в среде основан на решении уравнения (5), которое, в свою очередь, использует решение обратной задачи рассеяния (2) в k-пространстве. Пример восстановления поперечного спектра объекта в форме параллелепипеда с размерами 2,53,21,5 (в безразмерных единицах их отношения к длине волны) в среде 3 при z = z_max = d+1,5, основанного на решении (2), показан на рис.7 для параметров сред и линзы, тождественных представленным на рис.5,6.

 

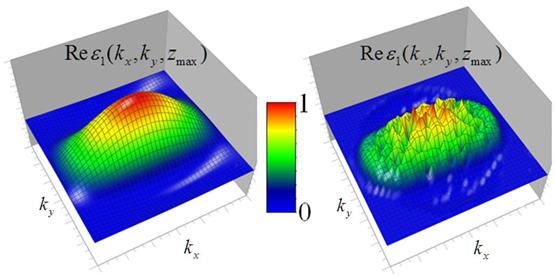
Рис.7. Решение обратной задачи рассеяния в k-пространстве для объекта в форме параллелепипеда. Сечение z = z_max. Слева – исходное распределение; справа – восстановленное при погрешности данных 5%.

 

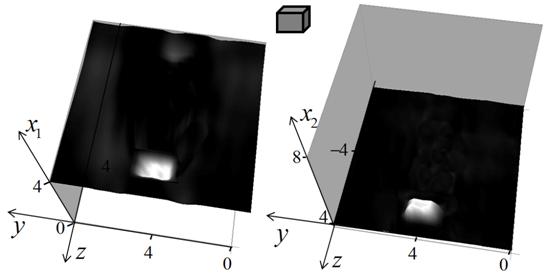
Рис.8. Численное моделирование голографии объекта в форме параллелепипеда, показанного на вставке.
Размеры по осям показаны в единицах длины волны.

 

С использованием решения (2) в уравнении (5), была восстановлена форма поверхности данного объекта, визуализированные изображения которой в виде двух функций  показаны на рис.8. Видно, что, несмотря на сложность зондирующего поля (см. на рис.5,6), голографические изображения подповерхностного объекта неплохо воспроизводят форму двух половин моделируемого объекта. В отличие от результатов томографии на рис.5, голографические изображения на рис.8 не содержат каких либо значимых артефактов.

Задачей дальнейших исследований является разработка методов решения обратной задачи за пределами применимости борновского приближения для случая сильных неоднородностей.

 

Исследования были выполнены при поддержке РФФИ, проекты № 13-07-97028_р_поволжье, а также программы ОФН РАН IV.13, а также частично поддержаны грантом Минобрнауки РФ (соглашение от 27 августа 2013г. № 02.В.49.21.0003 между МОН РФ и ННГУ).

 

Литература

1.     Pendry J.B. Negative refraction makes a perfect lens, Physical Review Letters, 2000, v. 85, No. 18, pp. 3966-3969.

2.     Ramakrishna S.A., Pendry J.B., Shurig E.D., Smith D.R. and Shultz S. Asymmetric lossy near-perfect lens, J. Mod. Opt., 2002, v. 49, No. 10 , pp. 1747-1762.

3.     Gaikovich K.P., Gaikovich P.K. Inverse problem of near-field scattering in multilayer media , Inverse Problems, 2010, v. 26, No. 12, pp. 125013 (1-17 pp.).

4.     Gaikovich K.P. Metamaterial lens tomography. Proceedings of 2011 13^th International Conference on Transparent Optical Networks (ICTON 2011, Stockholm, Sweden, June 26 – 30, 2011), pp. We.B2.1 (1-4).

5.     Gaikovich K.P., Gaikovich P.K., Maksimovitch Ye.S., Badeev V.A. Pseudopulse near-field subsurface tomography. Physical Review Letters, 2012, v. 108, No.16, pp. 163902 (1-5 pp.).

6.     Гайкович К.П., Максимович Е.С., Бадеев В.А. Микроволновая подповерхностная голография сплошных диэлектрических объектов. Журнал радиоэлектроники [электронный журнал], 2012, №6, с.1-15, http://jre.cplire.ru/jre/jun12/index.html.

¹ Данная статья является публикацией расширенного доклада на конференции «Радиолокация и радиосвязь» (ИРЭ им. В.А.Котельникова РАН, Москва, 21-25 ноября 2011 г.) – см. Труды конференции, с.271-275.