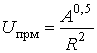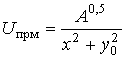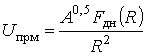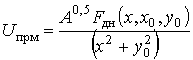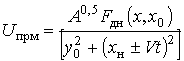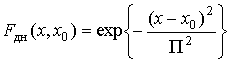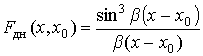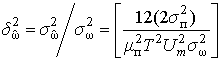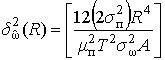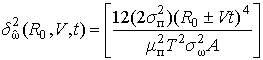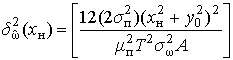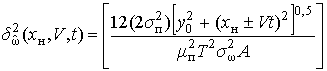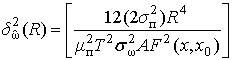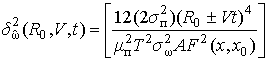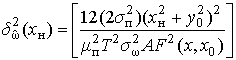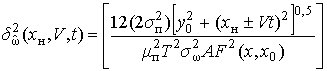"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2015

оглавление

УДК 681.3

Оценка погрешности измерения скалярного информационного параметра движущегося протяженного объекта на фоне аддитивных негауссовских помех

 

В. М. Артюшенко 1, В. И. Воловач 2

1 ГБОУ ВПО МО «Финансово-технологическая академия», г. Королев

2 ФГБОУ ВПО «Поволжский государственный университет сервиса», г. Тольятти

 

Статья получена 11 января 2015 г.

 

Аннотация. Показано, что в условиях небольших удалений лоцируемых объектов от радиолокационных измерителей систем ближней радиолокации характеристики обрабатываемого сигнала претерпевают значительные изменения в процессе движения объекта в зоне действия измерителя. Приведены  выражения для описания формы диаграммы направленности радиолокационного измерителя и проанализированы характеризующие ее зависимости. Определены погрешности измерения скалярного информационного параметра полезного сигнала, даны ее оценки на фоне аддитивной негауссовской помехи в условиях изменяющейся дальности с учетом влияния формы диаграммы направленности измерителя, а также в зависимости от характера движения лоцируемого объекта. В качестве скалярного информационного параметра рассматривается изменение частоты полезного сигнала, несущей информацию о скорости движения лоцируемого объекта. Показано, что учет негауссовского характера аддитивной помехи, воздействующей на измеряемые информационные параметры обрабатываемого сигнала, позволяет значительно повысить потенциальную точность измерителя.

Ключевые слова: радиолокационный измеритель, протяженный объект, скалярный информационный параметр, диаграмма направленности, аддитивная негауссовская помеха, отношение сигнал/помеха, погрешность измерения, скорость движения.

Abstract. It is shown that in the conditions of small deletions of located objects from  short-range radar characteristics of the processed signal significantдн change when the object moves within the range of the meter. The expressions for describing the shape of the radiation pattern of the radar meter are presented and analyzed. Measurement errors of scalar information parameter of useful signal is determined and the estimation of errors is given on the background of non-Gaussian additive noise in condition of the changing range, taking into account the radiation pattern shape meter, and depending on the nature of the movement of located object. The scalar information parameter is the frequency change of the useful signal, which carries information about the speed of movement of located object. It is shown that the inclusion of non-Gaussian nature of the additive noise which affects the measured information parameters of the processed signal, can significantly increase the potential accuracy of the meter.

Key words: radar meter, extended object, scalar information parameter, the radiation pattern, the additive Gaussian-noise ratio, signal to noise ratio, error of measurement speed.

Введение

В отличие от классической радиолокации, в которой вопросы измерения (оценки) параметров сигнала, несущих информацию о движении лоцируемых объектов (целей), подробно рассмотрены в различных источниках, например, в [1, 2], многие аналогичные аспекты, связанные с измерением параметров сигнала в системах ближней радиолокации (СБР) еще недостаточно изучены. Полезные сигналы в СБР содержат информацию о движении объектов, находящихся на относительно небольших расстояниях от радиолокационных измерителей (РИ), и имеют ряд специфических особенностей как теоретического, так и практического характера [3-5]. Например, в [3] показано, что в СБР характеристики обрабатываемого сигнала претерпевают значительные изменения в процессе движения объекта в зоне действия РИ. Помимо причин, подробно рассмотренных в [6-11], большую роль в этом играет процесс изменения дальности до лоцируемого объекта и, следовательно, изменения отношения сигнал/помеха (ОСП), а также форма диаграммы направленности (ДН) РИ.

1. Измерение параметров движения в условиях изменяющейся дальности

Назовем законом распределения дальности всякое соотношение, устанавливающее связь между возможными значениями удаления объекта от РИ и соответствующими вероятностями [4]. Очевидно, что этот закон определяется не только техническими характеристиками измерительного устройства, но также параметрами среды и характеристиками самого лоцируемого объекта [12].

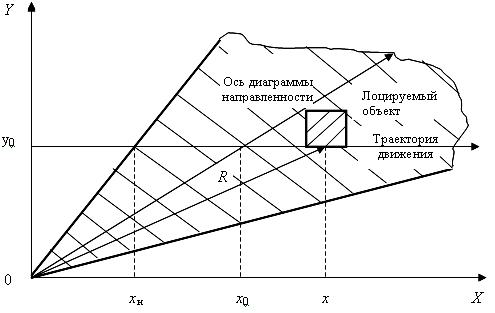
Рассмотрим далее преимущественно тот типичный случай, когда лоцируемый объект движется под углом к главной оси ДН антенны РИ (рис. 1), причем РИ расположен в начале системы координат. Воспользуемся введенными ранее [13] выражениями для описания формы ДН РИ, обозначив ее в полярной системе координат как функцию , где R – дальность до лоцируемого объекта, или в декартовой системе координат как функцию , где  – координаты пересечения главной оси ДН антенны с траекторией движения лоцируемого объекта, x – текущая координата объекта.

Отметим, что при движении лоцируемого объекта под углом к главной оси ДН антенны РИ целесообразно перейти к декартовой системе координат, в которой дальность до лоцируемого объекта в общем случае определяется выражением

.

В [13] приведен вывод выражений, позволяющих определить напряжение сигнала на входе приемника РИ, соответственно, в полярной и декартовой системах координат:

;       (1а),                            ,       (1б),

 

где А – коэффициент пропорциональности, выведенный в [13] из основного уравнения радиолокации и определяемый выражением:

,

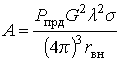в котором  – мощность передатчика, излучающего сигнал в сторону лоцируемого объекта, Вт; G2 – коэффициент усиления приемопередающей антенны; λ – длина волны излучаемого сигнала, м; σ – эффективная поверхность рассеяния (ЭПР) протяженного объекта, м; rвн – внутреннее сопротивление приемной антенны, Ом.

 

Рис. 1. Движение лоцируемого объекта в зоне действия РИ

 

Из (1б), в частности, следует, что по мере движения лоцируемого объекта в зоне действия РИ амплитуде обрабатываемого сигнала линейно зависит от координаты x. 

С учетом формы ДН выражения (1а) и (1б), соответственно, примут вид:

;       (2а),                       ,      (2б).

 

Рассмотрим законы распределения дальности. Опуская промежуточные рассуждения, приведенные в [3, 4], запишем выражения для определения величины  при условии, что  лоцируемый объект движется под углом к оси ДН [14]. В этом случае дальность до него будет определяться выражением:

,                                                         (3а)

где  – начальная координата объекта в момент вхождения в зону действия РИ.

С учетом скорости движения закон изменения дальности будет иметь вид:

,                                                   (3б)

где V – скорость движения лоцируемого объекта; t – время, в течение которого объект движется в зоне действия измерителя; (±) – знаки, учитывающие направление движения, (+) – объект удаляется, (–) – объект приближается.

В этом случае выражение (2б), учитывающее форму ДН РИ в декартовой системе координат примет вид:

.                                               (4)

На рис. 2 представлены кривые , полученные для (4) при y0 = 2 и V = 0, отражающая характер изменения величины амплитуды обрабатываемого сигнала с учетом формы ДН антенны РИ. Для учета формы ДН воспользуемся выражениями, приведенными в [13], которые позволяют получать требуемую точность расчетов при достаточной простоте.

Так, без учета влияния боковых лепестков ДН антенны хорошие результаты позволяет получить функция (рис. 2, а):

,                                  (5а)

где П – ширина ДН на уровне 0,707;

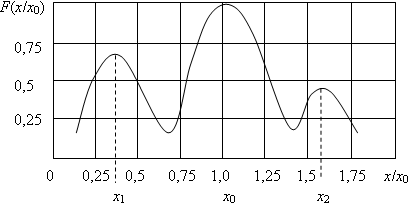
для учета реальной формы ДН антенны РИ используем функцию, учитывающую влияние боковых лепестков (рис. 2, б):

,                                    (5б)

где b – параметр, характеризующий ширину главного лепестка ДН антенны.

 

а)

б)

Рис. 2. Зависимости формы ДН  без учета влияния (а) и с учетом влияния (б) боковых лепестков ДН антенны РИ

 

Из рис. 2, а видно, что при описании ДН выражением (5а) форма кривой функции  имеет несимметричный куполообразный характер с максимумом при . Причем, правая сторона приведенной зависимости более пологая, чем левая [3].

При описании ДН выражением (5б) кривая  имеет три ярко выраженных максимума (рис. 2, б). Значение первого максимума несколько меньше максимального значения функции , но значительно больше величины третьего максимума .

Следует заметить, что представленные значения функции  в конкретных условиях практического использования РИ могут сильно отличаться от величин, рассчитанных по представленным формулам, поскольку на них будут оказывать влияние флюктуация параметров РИ, лоцируемых объектов, окружающей среды, среди которых, в первую очередь, следует обращать внимание на то или иное изменение т. н. определяющих факторов [13].

Проведение более точных расчетов требует тщательного учета характера условий работы РИ, степени их влияния на закон изменения распределения дальности до объекта, т. е. становится необходимым использовать вероятностно-статистические методы.

Отметим также, что при флюктуациях того или иного параметра, входящего в закон распределения дальности, как правило, необходимо произвести усреднение по этому параметру.

2. Погрешность измерения скалярного информационного параметра

Произведем оценку погрешности измерения скалярного информационного параметра на фоне аддитивной негауссовской помехи в условиях изменяющейся дальности.

На основании выше изложенного определим значения погрешности измерения (апостериорную дисперсию) параметров сигнала, несущих информацию о параметрах движения лоцируемого объекта [15] в зависимости от закона распределения дальности и формы ДН РИ в условиях воздействия аддитивной негауссовской помехи.

В качестве примера определим зависимость относительной погрешности измерения частоты w полезного сигнала

,

несущей информацию о скорости движения [16, 17], от закона распределения дальности до движущегося объекта.

Пусть оценка частоты осуществляется методом максимального правдоподобия, причем на сигнал воздействует негауссовская аддитивная помеха с независимыми значениями.

Воспользуемся результатами [3, 5] и запишем, что относительная погрешность измерения (оценки) частоты в этом случае будет равна:

,                                        (6)

где  – дисперсия оценки частоты полезного сигнала;  – дисперсия частоты полезного сигнала;  – дисперсия аддитивной негауссовской помехи;  – коэффициент, учитывающий отличие воздействующей аддитивной помехи от гауссовской; Т – время измерения; .

Воспользовавшись выражением (1а), перейдем к соотношению, описывающему относительную погрешность измерения частоты полезного сигнала, в зависимости от дальности до лоцируемого объекта:

.                                                 (7а)

Если лоцируемый объект движется со скоростью V вдоль оси главного лепестка ДН антенны РИ, то выражение (7а) примет вид:

,                                    (7б)

в котором учтено, что расстояние до объекта описывается выражением,  причем в начальный момент измерения параметров движения объекта дальность до него равна .

При движении объекта под углом к главной оси ДН относительная погрешность измерения частоты будет определяться:

.                                          (7в)

С учетом скорости движения выражение (7в), согласно (7б), запишется:

.                              (7г)

С учетом формы ДН антенны РИ  выражения для определения приведенной относительной погрешности частоты полезного сигнала (7а)–(7г) соответственно, запишутся в нижеследующем виде:

1) при движении объекта вдоль оси ДН:

,                                       (8а)

с учетом скорости движения лоцируемого объекта

;                                  (8б)

2) при движении объекта под углом к ДН в декартовой системе координат:

,                                      (8в)

с учетом скорости движения лоцируемого объекта

.                          (8г)

Таким образом, полученные выражения (7), (8) позволяют описывать относительную погрешность измерения частоты полезного сигнала в различных реальных условиях работы РИ.

Рассмотрим в качестве примера численную оценку величины относительной погрешности, описывающейся выражением (8в).

Обозначив через

,

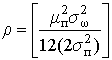играющее в рассматриваемом случае роль обобщенного ОСП, запишем (8в) в виде:

,                                            (9)

в котором

.

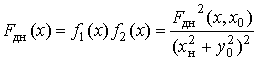Рассмотрим погрешность измерения частоты РИ, например, для случая учета влияния боковых лепестков ДН антенны измерителя. При этом, как было показано выше, функция, соответствующая выражению для , будет иметь три ярко выраженных локальных максимума (рис. 2, б). Величина максимумов боковых лепестков определяется ДН антенны РИ, а их асимметрия – геометрией решаемой задачи.

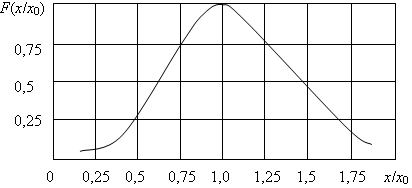
На рис. 3 представлены графики зависимостей  при A, , позволяющее оценить погрешности и точности измерения частоты обрабатываемого сигнала, которая, в свою очередь, несет информацию о скорости (ускорении) движения объекта в любой точке его траектории движения и  находящегося в зоне действия измерителя с учетом боковых лепестков ДН.

Из графиков рис. 3 и выражения (9) видно, что с увеличением значений A, ρ и T погрешность измерения уменьшается. Следует отметить, что к аналогичным выводам приводит и анализ соответствующих графиков, построенных без учета влияния боковых лепестков ДН.

Задаваясь допустимым уровнем погрешности , можно оценить интервал, на протяжении которого погрешность измерения не будет превышать заданной величины.

 

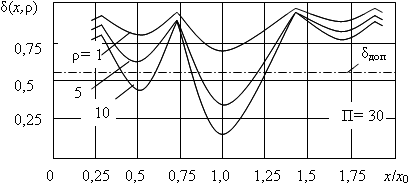
Рис. 3. Зависимости погрешности измерения частоты δ от ОСП  с учетом влияния боковых лепестков ДН антенны РИ

Заметим, что представленные графики построены в координатах, приведенных к величине x, где погрешность измерителя из-за его юстировки является минимальной.

Анализируя полученные зависимости, видно, что при неверной юстировке РИ из-за боковых лепестков ДН погрешность измерения может достигать очень больших значений, вплоть до 100%. Кроме того, может возникнуть ситуация, когда при определенном уровне заданной допустимой погрешности  боковой лепесток ДН начнет участвовать в процессе измерения частоты сигнала, отраженного от мешающего объекта, двигающегося рядом с лоцируемым. Для устранения этих явлений, следует осуществить точную юстировку ДН антенны РИ.

Следует отметить, что учет отличия воздействующей аддитивной помехи от гауссовской, определяемое коэффициентом  [5, 18], увеличивает обобщенное ОСП, что в свою очередь приводит, при прочих равных условиях работы РИ, к увеличению его потенциальной точности [5].

3. Выводы

Рассмотрены вопросы, связанные с оценкой погрешности измерения частоты сигнала, содержащей информацию о скорости движения лоцируемого объекта при работе радиолокационного измерителя на относительно небольших удалениях. Получены выражения, позволяющие определить погрешность измерения скорости движения протяженного объекта с учетом формы диаграммы направленности радиолокационного измерителя в условиях изменяющейся дальности на фоне воздействующих аддитивных негауссовских помех.

Показано, что при неправильной юстировке радиолокационного измерителя относительная погрешность измерения параметров движения протяженного объекта может достигать 100%. Учет негауссовского характера аддитивной помехи, воздействующей на измеряемые информационные параметры обрабатываемого сигнала, при всех прочих равных условиях работы радиолокационного измерителя позволяет значительно повысить его потенциальную точность.

Работа выполнена в рамках фундаментальной НИР, финансируемой из средств Минобрнауки РФ (Государственное задание на 2014 г., код 226).

Литература

1.     Теоретические основы радиолокации / Под ред. Я.Д. Ширмана. М.: Сов. радио, 1970. 560 с.

2.     Сосулин Ю. Г. Теоретические основы радиолокации и радионавигации: учеб. пособие для вузов. М.: Радио и связь, 1992. 304 с.

3.     Артюшенко В.М. Исследование и разработка радиолокационного измерителя параметров движения протяженных объектов. М.: ФГБОУ ВПО ФТА, 2013. 214 с.

4.     Воловач В.И. Методы и алгоритмы анализа радиотехнических устройств ближнего действия. М.: Радио и связь, 2013. 228 с.

5.     Артюшенко В.М. Обработка информационных параметров сигнала в условиях аддитивно-мультипликативных негауссовских помех. М.: ФГБОУ ВПО ФТА; изд-во «Канцлер», 2014. 298 с.

6.     Коган И.М. Ближняя радиолокация. М.: Сов. радио, 1973. 272 с.

7.     Артюшенко В.М., Воловач В.И. Анализ параметров спектра сигнала, отраженного от протяженного объекта // Приборостроение. 2012, т. 55, № 9. С. 62-67.

8.     Artyushenko V.M., Volovach V.I. Statistical Characteristics of Envelope Outliers Duration of non-Gaussian Information Processes // Proceedings of IEEE East-West Design & Test Symposium (EWDTS’2013). Rostov-on-Don, Russia, September 27–30, 2013. Kharkov: KNURE, 2013. P. 137-140.

9.     Артюшенко В.М., Воловач В.И., Иванов В.В. Статистические характеристики сигналов и помех в радиотехнических устройствах ближнего действия // Приборостроение. 2014, т. 57, № 7. С. 46-50.

10. Артюшенко В.М., Воловач В.И. Экспериментальное исследование параметров спектра доплеровского сигнала, отраженного от протяженного объекта // Прикаспийский журнал: управление и высокие технологии. 2012, № 3 (19). С. 17-24.

11.  Воловач В.И. Оценка потерь достоверности обнаружения радиотехническими устройствами обнаружения при неизвестной скорости движения обнаруживаемого объекта // Школа университетской науки: парадигма развития. 2013, № 1(8). С. 67-69.

12.  Артюшенко В.М., Воловач В.И. Особенности отражения зондирующих сигналов радиотехнических устройств обнаружения от протяженных объектов сложной формы // Школа университетской науки: Парадигма развития. 2012, № 2 (6). С. 42-46.

13.    Воловач В.И. Исследование плотности распределения вероятностей обнаружения объекта с учетом изменяющейся дальности // Известия вузов России. Радиоэлектроника. 2013, № 4. С. 71-75.

14.   Артюшенко В.М., Воловач В.И. Погрешность измерения скалярного информационного параметра на фоне аддитивной негауссовской помехи в условиях изменяющейся дальности // VIII Всероссийская конференция «Радиолокация и радиосвязь», 24-26 ноября 2014 г.,  Москва, ИРЭ им. В.А. Котельникова РАН. Москва, 2014. С. 108-112.

15. Артюшенко В.М., Воловач В.И. Выбор и обоснование моделей измеряемых параметров движения протяженных объектов // Школа университетской науки: парадигма развития. № 1(8), 2013. С. 109-114.

16. Artyushenko V.M., Volovach V.I. Threshold method of measurement of extended objects speed of radio engineering devices of short-range detection // Proceedings of IEEE East-West Design &Test Symposium (EWDTS’2014). Kiev, Ukraine, September 26–29, 2014.Kharkov: KNURE, 2014. P. 220-223.

17.  Артюшенко В.М., Воловач В.И. Пороговый способ измерения скорости протяженных объектов в зоне контроля радиотехнических устройств обнаружения ближней дальности // Журнал радиоэлектроники: электронный журнал. 2014, № 12. URL: http://jre.cplire.ru/jre/dec14/28/text.pdf

18.   Lu N.H., Eisenstein Bruce A. Detection of Weak Signals in Non-Gaussian Noise // IEEE Trans. Microwave Theory Tech. 1981, vol. IT-27, No. 6. P. 755-771.