| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2001 |  |
СПИРАЛЬНАЯ СТРУКТУРА
В АНТИФЕРРОМАГНЕТИКАХ
С МАГНИТОЭЛЕКТРИЧЕСКИМ ЭФФЕКТОМ
А .А. Халфина
Башкирский государственный университет
Получена 13 июля 2001 г.
Обсуждается возможность существования спиральной структуры в центроантисимметричных антиферромагнетиках. Показано, что такая структура обусловлена линейным неоднородным обменом и может быть индуцирована электрическим полем предпочтительно в материалах с малой анизотропией и большой величиной магнитоэлектрической восприимчивости.
Весьма распространенным
типом магнитного упорядочения в кристаллах является спиральная структура [1].
Микроскопическая теория спиральной структуры для обменной модели магнетика
хорошо разработана. Такая упорядоченность спинов является следствием разной
величины и знака обменных интегралов между атомами, принадлежащими к разным
атомным плоскостям. Часто период структуры несоизмерим с периодом
кристаллической решетки, и спираль можно рассматривать как длиннопериодическую
модуляцию ферромагнитной или антиферромагнитной структуры. В таком случае
уместно феноменологическое описание магнетика с учетом неоднородной части
обменной энергии [2]. Дзялошинским И.Е. впервые рассчитана модулированная
магнитная структура (ММС) одноосных антиферромагнетиков (АФМ) [3]. Показано,
что ММС обусловлена линейным по пространственным производным инвариантом лифшицевского
вида
![]() в
свободной энергии. Здесь
в
свободной энергии. Здесь
![]() – вектор антиферромагнетизма, ось
– вектор антиферромагнетизма, ось
![]() направлена вдоль оси
анизотропии. В работах [4, 5] обсуждается возможность индуцирования ММС
электрическим E и
магнитным H полями в
АФМ иной симметрии. Линейный неоднородный инвариант вида
направлена вдоль оси
анизотропии. В работах [4, 5] обсуждается возможность индуцирования ММС
электрическим E и
магнитным H полями в
АФМ иной симметрии. Линейный неоднородный инвариант вида
![]() , где
, где
![]() – вектор ферромагнетизма, допускает
магнитная симметрия центроантисимметричных антиферромагнетиков, которые
обладают магнитоэлектрическим эффектом [6–8]. Это обстоятельство позволяет
поставить задачу исследования специфической зависимости статических свойств ММС
и спектра линейных возбуждений от электрического поля.
– вектор ферромагнетизма, допускает
магнитная симметрия центроантисимметричных антиферромагнетиков, которые
обладают магнитоэлектрическим эффектом [6–8]. Это обстоятельство позволяет
поставить задачу исследования специфической зависимости статических свойств ММС
и спектра линейных возбуждений от электрического поля.
Рассмотрим двухподрешеточный
ромбоэдрический центроантисимметричный АФМ со структурой
![]() , которой, в частности, обладает
Cr2O3. Исходим из плотности свободной энергии
, которой, в частности, обладает
Cr2O3. Исходим из плотности свободной энергии
![]() ,
,
включающей магнитную, магнитоэлектрическую энергии и энергию электрической поляризации, каждая из которых имеет следующий вид [6–9]:
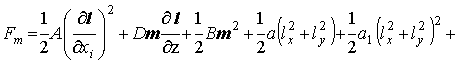
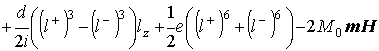 ,
,
![]() ;
;
![]() ,
,
![]() .
.
Здесь
![]() – константа однородного обмена,
– константа однородного обмена,
![]() –поперечная антиферромагнитная
восприимчивость, 2М0-намагниченность насыщения,
–поперечная антиферромагнитная
восприимчивость, 2М0-намагниченность насыщения,
![]() ,
,
![]() – константы квадратичного и линейного
неоднородного обмена,
– константы квадратичного и линейного
неоднородного обмена,
![]() –
постоянная кристаллической решетки,
–
постоянная кристаллической решетки,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – константы магнитной анизотропии;
– константы магнитной анизотропии;
![]() – тензор
магнитоэлектрического взаимодействия,
– тензор
магнитоэлектрического взаимодействия,
![]() ,
,
![]() – компоненты тензора электрической поляризуемости,
p – вектор поляризации.
– компоненты тензора электрической поляризуемости,
p – вектор поляризации.
Свободную
энергию в полях
![]() после
минимизации по p и m можно представить в виде
после
минимизации по p и m можно представить в виде
![]() , (1)
, (1)
![]() .
.
Здесь для краткости принято
![]() ,
,
![]() ,
,
![]() .
.
Пусть
![]() ,
,
![]() ,
,
![]() . Обычно ММС одномерна и волновой вектор спирали направлен
вдоль одной из кристаллографических осей. Поэтому рассмотрим случай одномерной неоднородности вдоль оси
z. Тогда плотность энергии (1) примет
вид:
. Обычно ММС одномерна и волновой вектор спирали направлен
вдоль одной из кристаллографических осей. Поэтому рассмотрим случай одномерной неоднородности вдоль оси
z. Тогда плотность энергии (1) примет
вид:
![]()
![]()
![]() , (2)
, (2)
где
![]() ,
,
![]() ,
,
![]() .
.
Задачу определения магнитной
структуры будем решать в одноосном приближении
![]() ,
, ![]()
![]() , которое обычно хорошо выполняется. Решением
уравнений Эйлера, определяющих однородное состояние
, которое обычно хорошо выполняется. Решением
уравнений Эйлера, определяющих однородное состояние
![]() ,
,
![]() в отсутствие поля E, являются две коллинеарные фазы:
в отсутствие поля E, являются две коллинеарные фазы:
1.
![]() , при
, при
![]() ,
,
![]() ,
,
2.
![]() , при
, при
![]() ,
,
![]() .
.
При
![]() условия устойчивости решений
перекрываются, в поле
условия устойчивости решений
перекрываются, в поле
![]() возможен фазовый переход первого рода
опрокидывания подрешеток.
возможен фазовый переход первого рода
опрокидывания подрешеток.
Исследуем неоднородное
состояние. Положим
![]() ,
,
![]() и для
простоты рассмотрим случай
и для
простоты рассмотрим случай
![]() , соответствующий полю фазового перехода
опрокидывания подрешеток. Уравнение Эйлера для энергии (2) по углу
, соответствующий полю фазового перехода
опрокидывания подрешеток. Уравнение Эйлера для энергии (2) по углу
![]() имеет первый интеграл
имеет первый интеграл
![]() . Свободная энергия (2)
в указанном приближении равна
. Свободная энергия (2)
в указанном приближении равна
где
![]() . Первый интеграл уравнения Эйлера для
функционала (3) запишем в виде
. Первый интеграл уравнения Эйлера для
функционала (3) запишем в виде
![]() – постоянная интегрирования. Уравнение (4)
имеет периодическое с периодом
– постоянная интегрирования. Уравнение (4)
имеет периодическое с периодом
![]() решение
решение
где
![]() – эллиптическая функция Якоби,
– эллиптическая функция Якоби,
![]() ,
,
![]() – полный эллиптический интеграл
первого рода.
– полный эллиптический интеграл
первого рода.
В силу малости магнитоэлектрической
восприимчивости АФМ
![]() (
(![]() ) будем считать, что
включение поля E не влияет на вид распределения l. Усреднив (2) по периоду структуры
согласно (5) с учетом (4), получим плотность энергии
) будем считать, что
включение поля E не влияет на вид распределения l. Усреднив (2) по периоду структуры
согласно (5) с учетом (4), получим плотность энергии
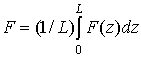 в виде:
в виде:
где
![]() – полный эллиптический интеграл II рода,
– полный эллиптический интеграл II рода,
![]() – характерное электрическое поле
неоднородного состояния системы. Для определенности положим
– характерное электрическое поле
неоднородного состояния системы. Для определенности положим
![]() , тогда минимуму (6)
соответствует значение
, тогда минимуму (6)
соответствует значение
![]() .
.
Постоянная интегрирования
уравнения Эйлера
![]() ,
а вместе с ней и период структуры L, определяется из условия минимума энергии (6) по
,
а вместе с ней и период структуры L, определяется из условия минимума энергии (6) по
![]() . Проанализируем два случая,
соответствующих предельным значениям
. Проанализируем два случая,
соответствующих предельным значениям
![]() и
и
![]() .
.
Используя разложения
![]() и
и
![]() [10] при малых
[10] при малых
![]() , имеем:
, имеем:
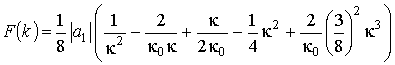 .
.
Условие
![]() удовлетворяется значением
удовлетворяется значением
![]() .
.
Тогда плотность энергии равна
В отсутствие поля E прирост энергии положителен, т.е.
неоднородное состояние энергетически невыгодно. Наличие поля E может привести к выгодности
неоднородного состояния, и тогда выражение (5) описывает ММС – модуляцию чисто
антиферромагнитного состояния
![]() или
или
![]() (спины вдоль 3z или 2х-осей). Прирост энергии (8) отрицателен при
(спины вдоль 3z или 2х-осей). Прирост энергии (8) отрицателен при
![]() , т.е.
длиннопериодическая (
, т.е.
длиннопериодическая (![]() )
ММС в рассматриваемых АФМ может возникнуть, только если поле Е превышает
пороговое значение Еп, величина которого вблизи спин-флоп
фазового перехода, как видно из (7), определяется константой анизотропии
четвертого порядка, антиферромагнитной и магнитоэлектрической восприимчивостями
и величиной параметра линейного неоднородного обмена. Отличие значения Еп
от результатов работ [4, 5] связано с тем, что инвариант
)
ММС в рассматриваемых АФМ может возникнуть, только если поле Е превышает
пороговое значение Еп, величина которого вблизи спин-флоп
фазового перехода, как видно из (7), определяется константой анизотропии
четвертого порядка, антиферромагнитной и магнитоэлектрической восприимчивостями
и величиной параметра линейного неоднородного обмена. Отличие значения Еп
от результатов работ [4, 5] связано с тем, что инвариант
![]() имеет существенно нелифшицевский
вид, а индуцирование ММС электрическим полем происходит через механизм
магнитоэлектрического взаимодействия. Период структуры
имеет существенно нелифшицевский
вид, а индуцирование ММС электрическим полем происходит через механизм
магнитоэлектрического взаимодействия. Период структуры
![]() ,
,
много больше постоянной
кристаллической решетки, например, для
![]() составляет
составляет
![]() .
.
В случае
![]() , минимум (6) достигается при
, минимум (6) достигается при
![]() , где
, где
![]()
![]() . Плотность полной энергии равна
. Плотность полной энергии равна
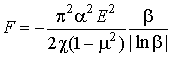 .
.
Структура энергетически выгодна при
![]() , т.е. начиная с полей
, т.е. начиная с полей
![]() .
.
Период структуры
![]() , величина
, величина
![]() , и теперь (5)
описывает периодическую структуру с чередованием широких участков однородной и
узких участков неоднородной намагниченности, похожую на доменную структуру, но
в отличие от обычной доменной структуры ММС энергетически выгодна.
, и теперь (5)
описывает периодическую структуру с чередованием широких участков однородной и
узких участков неоднородной намагниченности, похожую на доменную структуру, но
в отличие от обычной доменной структуры ММС энергетически выгодна.
Таким образом,
электрическое поле приводит к выгодности неоднородного состояния в центроантисимметричных
АФМ. В полях
![]() существует
длиннопериодическая ММС. С уменьшением поля структура становится похожей на
доменную структуру и затем ММС исчезает, система переходит в одно из однородных
состояний.
существует
длиннопериодическая ММС. С уменьшением поля структура становится похожей на
доменную структуру и затем ММС исчезает, система переходит в одно из однородных
состояний.
Неоднородную магнитную структуру можно рассматривать как застывшую спиновую волну, поэтому характеристики ММС можно получить изучая динамику системы. Функция Лагранжа исследуемого АФМ имеет вид [11]:
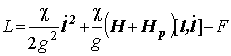 ,
,
где g – гиромагнитное отношение, а F определяется выражением (1).
В качестве основного состояния
выберем опрокинутую фазу
![]() ,
,
![]() , реализующуюся при условии
, реализующуюся при условии
![]() ,
,
![]() .
.
Линеаризованные уравнения
Лагранжа для распространяющихся вдоль
![]() малых отклонений
малых отклонений
![]() и
и
![]() от равновесных значений
от равновесных значений
![]() и
и
![]() следующие:
следующие:
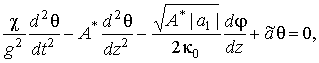
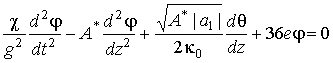 ,
,
Перейдя к компонентам Фурье
![]() ,
,
![]() ,
,
где ![]() – волновой вектор вдоль
– волновой вектор вдоль ![]() , получим дисперсионное
уравнение для определения частоты малых колебаний вектора l:
, получим дисперсионное
уравнение для определения частоты малых колебаний вектора l:
Решая (9), получим антиферромагнитную и квазиферромагнитную ветви колебаний с частотами
При
![]()
![]() ,
,
![]() , откуда следуют условия устойчивости
состояния
, откуда следуют условия устойчивости
состояния
![]() ,
,
![]() :
:
![]() ,
,
![]() .
.
На рисунке приведен закон
дисперсии (10) спиновых волн (пунктирная линия – антиферромагнитная ветвь,
сплошная – квазиферромагнитная) для значений поля E равных 0,
![]() ,
,
![]() ,
,
![]() – кривые 1, 2, 3, 4 соответственно.
– кривые 1, 2, 3, 4 соответственно.
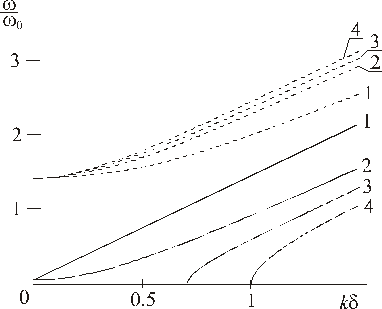
Частота квазиферромагнитной ветви колебаний при
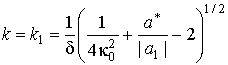
обращается в нуль, т.е. в интервале
(0,
![]() ) система
находится в основном неоднородном состоянии. В рассмотренном в статике случае
) система
находится в основном неоднородном состоянии. В рассмотренном в статике случае
![]()
и частота обращается в нуль в полях
![]() . Из выражения (5) в одногармоническом
приближении следует, что ее волновой вектор равен
. Из выражения (5) в одногармоническом
приближении следует, что ее волновой вектор равен
![]() . Из (11) при
. Из (11) при
![]() (
(![]() ) получаем то же значение волнового вектора
структуры, т.е. имеет место совпадение результатов статического и динамического
расчетов.
) получаем то же значение волнового вектора
структуры, т.е. имеет место совпадение результатов статического и динамического
расчетов.
Таким образом, проведенные исследования показывают,
что наличие линейного неоднородного инварианта
![]() в свободной энергии антиферромагнетиков с
центром антисимметрии приводит к выгодности неоднородного состояния. Появляется
возможность индуцирования спиральной структуры электрическим полем через
механизм магнитоэлектрического взаимодействия. Большая величина периода
структуры обусловлена малостью магнитоэлектрической восприимчивости
антиферромагнетиков.
в свободной энергии антиферромагнетиков с
центром антисимметрии приводит к выгодности неоднородного состояния. Появляется
возможность индуцирования спиральной структуры электрическим полем через
механизм магнитоэлектрического взаимодействия. Большая величина периода
структуры обусловлена малостью магнитоэлектрической восприимчивости
антиферромагнетиков.
Отметим, что в данной
работе рассмотрен только один класс магнитоэлектрических антиферромагнетиков –
![]() . Однако, пользуясь приведенной
в работе [12] таблицей тензоров магнитоэлектрических коэффициентов, можно
провести систематическое исследование всех антиферромагнетиков.
. Однако, пользуясь приведенной
в работе [12] таблицей тензоров магнитоэлектрических коэффициентов, можно
провести систематическое исследование всех антиферромагнетиков.
Автор выражает благодарность Шамсутдинову М.А. за полезное обсуждение работы.
Литература
1. Тябликов С.В. Методы квантовой теории магнетизма. М.: Наука, 1975. 527 с.
2. Изюмов Ю.А. // УФН. 1984. Т.144. №3. С.439–474.
3. Дзялошинский И.Е.// ЖЭТФ. 1964. Т.47. №3(9). С.992–1003.
4. Витебский И.М.// ЖЭТФ. 1982. Т.82. №2. С.57–361.
5. Барьяхтар В.Г., Яблонский Д.А.// ФТТ. 1982. Т.24. №8. С.2522–2524
6. Шавров В.Г.// ЖЭТФ. 1965. Т.48. С.1419–1426.
7. Шавров В.Г.// ФТТ. 1965. Т.7. С.328.
8. Фарзтдинов М.М. Физика магнитных доменов в антиферромагнетиках и ферритах. Наука. М. 1981. 156с.
9. Туров Е.А.// ЖЭТФ. 1993. Т.104. №5. С.3886–3896.
10. Янке Е. И др.// Специальные функции. Наука. М.: 1968, 344 с.
11. Халфина А.А., Харрасов М.Х., Шамсутдинов М.А. // ФТТ. 2001. Т.43, № 8. С.1478–1481.
12. Бучельников В.Д., Шавров В.Г.// ЖЭТФ. 1996. Т.109. №2. С.706–716.
Автор:
Халфина Аида Анваровна
Башкирский государственный университет, г.Уфа, ул. Фрунзе, 32
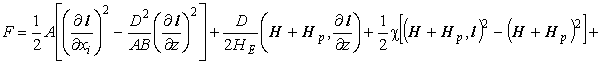
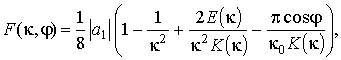 (6)
(6)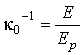 ,
,
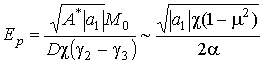 ,
,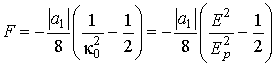 . (8)
. (8)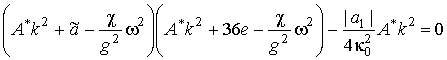 . (9)
. (9)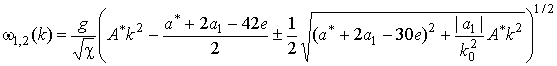 . (10)
. (10)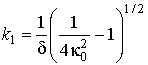 (11)
(11)