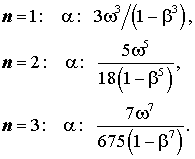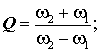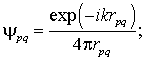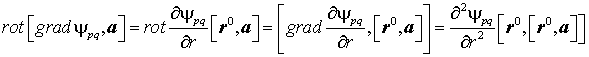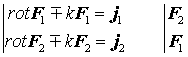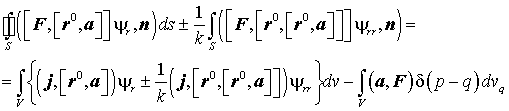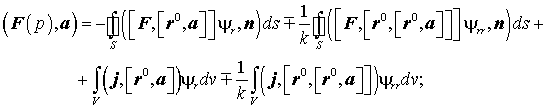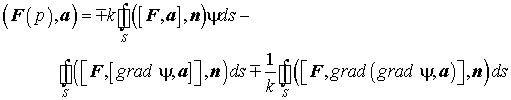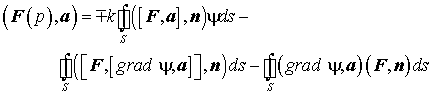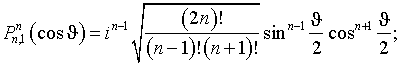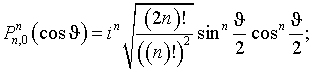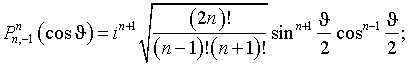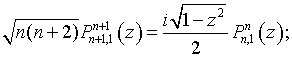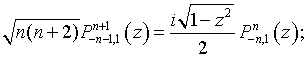ПРИМЕНЕНИЕ ВЕКТОРОВ ФАРАДЕЯ В ТЕОРИИ АНТЕНН
Б. Л. КоганОКБ МЭИ Федерального космического агентства
Получена 8 июля 2008 г.
Целью статьи является изложение метода решения задач теории антенн с использованием нестандартных векторов электромагнитного поля – векторов Фарадея, которые можно интерпретировать как носители радиоволн идеальной круговой поляризации. Векторы Фарадея применены к решению задач о кроссполяризационных искажениях, построению высокочастотной асимптотики дифракционных эффектов и вычислению потенциального усиления антенны заданных размеров, работающей в заданной частотной полосе.
1. Определение векторов Фарадея. Вектор Пойнтинга и условия излучения.
В данной статье обсуждается применение нестандартных векторов поля – векторов Фарадея, в задачах теории антенн. Для электромагнитного поля, удовлетворяющего системе уравнений Максвелла:
в линейной изотропной материальной среде с постоянными во времени параметрами векторы Фарадея определяются формулами:
импеданс среды
, как обычно, даётся выражением
. Для простоты предполагается, что параметры среды вещественные, поскольку в теории антенн задача излучения антенны в свободное пространство для нас является важнейшей.
С учётом замены (2) и обозначений
уравнения Максвелла принимают вид:
(квадратными скобками обозначено векторное произведение в 3-х мерном пространстве).
Второе слагаемое с изменённым порядком индексов вектора Фарадея в левой части уравнения (4) определяет взаимную связь между векторами
и
. Слагаемое взаимной связи по порядку величины (в смысле порядка дифференциального оператора) является младшим членом уравнения (в отличие от связи векторов
и
в старшем порядке системы уравнений Максвелла (1)). Из уравнения (4) следует, что в среде с пространственно-однородным импедансом (
) даже в случае пространственно-переменной скорости распространения электромагнитных волн, определяемой формулой:
, векторы
и
не взаимодействуют между собой. В этом случае система уравнений Максвелла с векторами поля, выраженными через векторы Фарадея, распадается на два независимых уравнения. Каждый вектор
и
описывает полное электромагнитное поле со своими источниками
и
, способное распространяться и излучаться.
Название: «векторы Фарадея», в честь корифея физики, впервые представившего себе электромагнитную волну, не является общепринятым, но используется в некоторых работах (например, [1]).
Уравнения Максвелла приводится к виду аналогичному (4) и в случае гармонической зависимости от времени электромагнитных колебаний. Будем предполагать, что зависимость от времени имеет вид:
. Обозначения для комплексных векторных амплитуд гармонических колебаний электромагнитного поля мы оставляем теми же, что и для векторов, зависящих от времени. Вид замен (2) и (3) при этом сохраняется, а система уравнений Максвелла для векторных амплитуд гармонических электромагнитных колебаний
с учётом обозначений
переходит в уравнение
В свободном пространстве в случае гармонической временной зависимости электромагнитных волн каждый из векторов
и
удовлетворяет своему дифференциальному уравнению
Для любого поля, имеющего структуру локально плоской волны, например, для уходящей волны в дальней зоне, каждый из этих векторов соответствует волне с идеальной круговой поляризацией, вектор
— с правой круговой, а вектор
— с левой. Совокупность двух векторов может представлять поле произвольной поляризации. Следует заметить, что сведение системы уравнений Максвелла к независимым уравнениям для векторов
и
возможно только в статическом случае, а применение векторов Фарадея позволяет перейти к двум независимым уравнениям электродинамики во многих задачах на всех частотах одновременно.
Касаясь энергетических соотношений, выпишем выражение для комплексного вектора Пойнтинга, совершив замену векторов поля (2) для случая гармонической зависимости от времени в стандартном выражении этого вектора.
Звёздочкой обозначен комплексно сопряжённый вектор. Так как для любого вектора
векторное произведение
чисто мнимое, первое слагаемое в правой части (8) всегда вещественно, второе же по своей структуре чисто мнимое. Чёткий физический смысл, связанный с потоком мощности излучения, имеет лишь вещественная (активная) часть комплексного вектора Пойнтинга. В формуле (8) она представлена суммой парциальных векторов Пойнтинга векторов Фарадея правой и левой поляризации. Таким образом, разноимённые векторы Фарадея независимы, а направленные мощности их излучения складываются по правилу сложения векторов. Интерпретация мнимой (реактивной) части комплексного вектора Пойнтинга не такая однозначная [2]. Если интересоваться возможностью обращения мнимой части в нуль, то из формулы (8) следует, что это происходит при коллинеарности векторов
и
, а также в случаях, когда хотя бы один из векторов Фарадея равен нулю.
Пример. Плоская электромагнитная волна.
Пусть
- декартова система координат,
- ортонормированный векторный базис в ней. Решение уравнения (7) в виде плоской волны, бегущей в сторону положительного направления оси z, для вектора Фарадея правой круговой поляризации ищем в виде:
. После подстановки этого выражения в (7) для вектора амплитуды
получим уравнение:
Вектор амплитуды определяется решением этого уравнения с точностью до постоянного множителя:
Для волны правой круговой поляризации, бегущей в противоположном направлении, решение будет комплексно сопряжённым:
Комплексный вектор Пойнтинга в первом случае равен
, а во втором
.
Рассмотренный пример плоской электромагнитной волны помогает выписать условия излучения на бесконечности для электромагнитного поля в форме векторов Фарадея. Для этих векторов удобно перейти от касательного к сфере векторного сферического базиса
к спиральному базису
по формулам:
Найдём связь между составляющими вектора в сферическом и спиральном базисах.
Из (9) и (10) следуют соотношения:
Уходящая на бесконечность локально плоская волна, подобно плоской, в спиральном базисе имеет лишь одну составляющую:
для вектора Фарадея правой поляризации и
для левой, поэтому условия излучения для векторов Фарадея имеют вид:
(Верхний знак относится к векторам Фарадея правой круговой поляризации).
2. Исторические замечания.
Возможность и преимущества замены векторов поля, при которой система уравнений Максвелла распадается на два независимых уравнения, были замечены очень давно. Самые старые библиографические ссылки указывают по этому поводу на работы Зильберштейна [3]. Эту замену в пионерских исследованиях групповых преобразований решений уравнений Максвелла использовал Г. Бейтмен [4]. В работах Бейтмена векторы Фарадея не имеют специфического названия и обозначаются всюду одинаково буквой
без нижнего индекса.
(Возможно, обозначение
у Бейтмена связано с именем Максвелла.) Бейтмен вводит эти векторы в более общей ситуации как в случае гармонической, так и произвольной зависимости от времени. Интерпретацию круговой поляризации волн этого типа Бейтмен не отмечает.
Отсутствие нижнего индекса в обозначениях Бейтмена связано с особенностью использованного им гиперкомплексного исчисления, которое он применяет при алгебраических вычислениях с векторами
. Дадим по этому поводу минимальные разъяснения, полезные для понимания способа введения векторов Фарадея в работе [4], а также аналогичных по смыслу векторов в [5]. Впрочем, математические подробности в двух последующих абзацах могут быть опущены без ущерба для понимания основного текста данной статьи.
Наряду с обычной единицей и мнимой единицей “i” Бейтмен вводит линейно независимую с ними единицу «неопределённого знака» “±1”, а в качестве скалярных множителей векторов поля рассматривает гиперкомплексные числа вида
где
- вещественные числа. Числа такого вида можно по обычным арифметическим правилам складывать, вычитать, умножать на произвольное комплексное число, делить на ненулевое комплексное число, а также коммутативно перемножать между собой. Правда, деление на числа вида (13) не всегда возможно, хотя Бейтмен об этом не пишет, избегая возможности сокращения на “множитель нуля”. (Легко проверить, что произведение ненулевых множителей
и
тождественно равно нулю. Эти множители называются множителями нуля). Числа вида (13) в вещественном случае были введены английским математиком Клиффордом. В русской математической литературе числа такого вида называют «двойными числами» [6]. При использовании данного гиперкомплексного исчисления два вектора поля
и
у Бейтмена представлены одним вектором
, а система двух уравнений Максвелла сводится к одному уравнению первого порядка относительно вектора
с гиперкомплексными коэффициентами вида (13).
В известных работах Л. Левина по решению волноводных задач электродинамики [5] в контексте с описанием электромагнитного поля в терминах векторов, подобных векторам Фарадея, применяется гиперкомплексное исчисление эквивалентное описанному выше. Но способ введения этого исчисления у Левина другой. В качестве новой образующей гиперкомплексных чисел вместо единицы неопределённого знака Левин вводит вторую мнимую единицу
, которая в обозначениях Бейтмена с использованием единицы неопределённого знака могла бы быть определена равенством
, а сама единица неопределённого знака могла бы быть выражена через произведение мнимых единиц
и
. Произведение
Левин выписывает при вычислениях, не обращая внимания на порядок сомножителей. Следовательно, используемое им гиперкомплексное исчисление также коммутативно. Он также избегает ситуации деления на множители нуля
или
, хотя нигде не упоминает об этом. (Гиперкомплексное исчисление Левина обозначениями напоминает кватернионы, но это совершенно разные математические объекты.)
В предлагаемой статье мы не применяем гиперкомплексного исчисления. Обозначение
используется для объединённой записи двух разных векторов Фарадея, знак «+» всегда относится к векторам Фарадея с правой круговой поляризацией, знак минус – к векторам с левой. При использовании
или
в качестве коэффициентов верхний знак относится к верхнему индексу вектора Фарадея. В некоторых случаях, когда это не вызывает недоразумений, индексы векторов Фарадея мы опускаем.
Электромагнитные поля со свойствами векторов Фарадея неоднократно исследовались и применялись в электродинамике и теории антенн. При этом замена векторов на новые производилась не всегда. В работах Рамзея [7] при исследовании электромагнитных полей со свойствами векторов Фарадея были сохранены классические обозначения.. Разработанную теорию Рамзей использовал при проектировании частотно независимых антенн. Известен ряд других работ, в которых используются векторы Фарадея или их обобщения для решения задач распространения радиоволн в более сложных материальных средах, например, киральных: [8], [9], [10], а также для анализа поляризации радиолокационных сигналов [11].
В [10] решения уравнений типа
называются «течениями Бельтрами». Действительно, выдающийся итальянский математик в поисках «механических» корней уравнений Максвелла в статье [12] исследовал класс течений жидкости, поле скоростей которой удовлетворяет уравнению (14), и указал на точную аналогию между характеристиками этих течений и параметрами формул Максвелла, описывающих действие электромагнитных сил. Но название «течения Бельтрами» не вполне правомерно, потому что Бельтрами не был первым исследователем таких течений жидкостей. За 8 лет до его публикации обстоятельную теорию вихревых течений жидкости, удовлетворяющей уравнению (14), разработал наш соотечественник казанский математик и механик И. С. Громека в диссертации [13]. В своей работе Громека сослался также на предшествующую статью американского математика [14], в которой тоже изучались некоторые свойства течений жидкости подобного вида.
Справедливости ради надо заметить, что диссертация Громеки была опубликована на русском языке и, по-видимому, осталась неизвестной за границей. Однако в статьях Бельтрами имеются ссылки на работы Лобачевского в том же издании (в Учёных записках Казанского университета). В 1868 г. Бельтрами опубликовал статью, получившую мировое признание, в которой впервые смоделировал геометрию ограниченного участка плоскости Лобачевского в евклидовом пространстве, заметив тождественность тригонометрических формул планиметрии Лобачевского и аналогичных формул внутренней геометрии псевдосферы - поверхности в евклидовом пространстве, геометрию которой исследовал другой российский математик - Ф.Г. Миндинг, профессор Дерптского университета.
Дифференциальное уравнение
, которому удовлетворяют векторы Фарадея, с математической точки зрения, не укладывается в стандартные схемы теории эллиптических и гиперболических задач. Корректные постановки краевых задач для этого уравнения исследованы Саксом Р.С. и обобщены в его диссертации: [15].
Коснёмся ещё одного важного вопроса. Введение новых обозначений и понятий в области знаний с устоявшимися обозначениями и терминологией часто и небезосновательно вызывает отторжение. Хотелось бы надеяться, что в данном случае этого не произойдёт. Введение векторов Фарадея (не новых, а давно забытых старых) во многом аналогично использованию в технике СВЧ наряду с понятиями токов и напряжений, понятий падающих и отражённых волн. Связанные с этим матрицы рассеяния не мешают использованию классических матриц, оперирующих понятием импеданса. Данная статья – это попытка показать, что использование в электродинамике наряду с классическими векторами
и
векторов Фарадея позволяет лучше понять математическую и физическую сущность уравнений Максвелла, применить в теории антенн другие методы, разработанные в течение 20 века в математике и математической физике.
Для удобства читателя в приложении 1 приведены формулировки общих соотношений электромагнитной теории, записанных в терминах векторов Фарадея и полезных в теории антенн, таких как лемма Лоренца, формула Стреттона-Чу, выражения для векторных потенциалов и полей элементарных источников. Некоторые из этих формул заимствованы из монографии Бейтмена [4].
3. О возбуждении кроссполяризованного излучения при рассеянии.
Векторы Фарадея
и
независимо возбуждаются и распространяются в свободном пространстве. Взаимное преобразование разноимённых векторов Фарадея, приводящее к появлению кроссполяризованной составляющей радиоволн круговой поляризации, происходит в соответствие с уравнениями (4), (6) при распространении радиоволн в сплошных неоднородных средах, а также на границах областей свободного пространства. Применение уравнений Максвелла в форме векторов Фарадея позволяет упростить нахождение элементов антенны или материальной среды, являющихся источниками возникновения поляризационных искажений.
Рассмотрим случай рассеяния радиоволн некоторой поверхностью, на которой касательные составляющие электрического и магнитного полей линейно и локально связаны между собой. В общепринятых обозначениях такая связь между касательными составляющими электрического и магнитного полей описывается с помощью матрицы поверхностного импеданса
:
где
- единичный вектор нормали, направленной из области, в которой происходит рассеяние, в сторону поверхности. Пусть эта поверхность облучается электромагнитной волной круговой поляризации. Каким условиям должна удовлетворять матрица поверхностного импеданса, чтобы при рассеянии не возникали кроссполяризационные искажения? В [16] сформулированы достаточные условия для этого:
где
— импеданс свободного пространства. Первое условие из (16) – это условие взаимности. Если оно нарушено, при каких-то вариантах возбуждения рассеивателя кроссполяризационные искажения обязательно возникнут. Достаточность условий (16) доказывается простой проверкой того, что после замены векторов поля
и
на векторы Фарадея краевое условие (15), в случае выполнения условий (16), распадается на два независимых краевых условия, одно из которых связывает между собой касательные составляющие вектора
, а другое -
. Наиболее важный частный случай соответствует реактивному импедансу. В этом случае условия (16) приводятся к известным [17] «балансным гибридным условиям»:
(17)
где
- собственные реактансы матрицы импеданса.
Условия (16) не являются необходимыми для того, чтобы кроссполяризационные искажения, вызванные отражением от поверхности с локальными краевыми условиями, не появились. Это связано с тем, что импедансные соотношения не охватывают предельных случаев (случаев обращения элементов матрицы импеданса в бесконечность). Чтобы охватить эти случаи нужно перейти от матрицы поверхностного импеданса к локально-поверхностной матрице рассеяния по известной формуле:
(18)
В формуле (18)
обозначает единичную матрицу в двумерном пространстве. Необходимые и достаточные условия отсутствия кроссполяризованной составляющей при рассеянии поверхностью рассматриваемого типа формулируются в терминах элементов двумерной матрицы рассеяния следующим образом:
Доказательство этого имеется в [18].
Импедансные границы, удовлетворяющие выписанным условиям, широко используются в технике проектирования гофрированных рупорных облучателей зеркальных антенн. Частными случаями условий (19), кроме балансных краевых условий, являются известные “soft’ и “hard” условия [19]. При условиях “soft’ и “hard” после приведения матрицы рассеяния к главным осям, один из диагональных элементов равен +1, другой -1, а их сумма равна нулю. Условия (19) охватывают также случаи частотно-зависимых краевых условий.
Выписанные условия характеризуют источники возникновения кроссполяризованного излучения, когда основное излучение поляризовано по кругу. Условия возникновения кроссполяризованного излучения для полей линейной или эллиптической поляризации формулируются более сложно и, дополнительно к выписанным, могут включать другие требования.
4. Применение векторов Фарадея при решении асимптотических и дифракционных задач.
В большинстве работ по построению высокочастотной асимптотики в задачах с геометрооптическими особенностями типа каустик, фокусов и полутеней используется скалярное приближение. Для векторного случая конкретного построения векторных асимптотик для уравнений Максвелла обычно не проводят, но при этом, как правило, утверждают, что принципиальных трудностей оно не вызывает. В тех случаях, когда векторное приближение всё же используется, обычно ограничиваются главным членом асимптотики, как это сделано в геометрической теории дифракции Келлера [20], см. также [21]. Всё это связано с тем, что в векторном случае формальные выкладки становятся существенно более громоздкими. Использование векторов Фарадея позволяет упростить формальные выкладки при построении асимптотического решения. Для нахождения вектора Фарадея достаточно решить одно векторное уравнение с производными 1-го порядка. Так, для представления полутеневой асимптотики поля, отражённого от рефлектора с криволинейной кромкой, можно использовать асимптотический векторный анзац — векторный аналог анзаца Боровикова [22]:
в котором
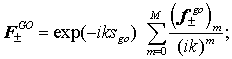
- интеграл Френеля,
- операция проектирования на направление кромки,
- эйконалы краевой и геометрооптической составляющих.
Асимптотический анзац (20) использован в [23] для нахождения в аналитической форме равномерной (по уровню поля, облучающего кромку,) асимптотики мощности, рассеянной кромкой контррефлектора зеркальной антенны. Согласно выведенным в [23] формулам, рассеянная мощность не обращается в нуль даже в случае, когда кромка контррефлектора облучается нулём диаграммы направленности облучателя. Обращение рассеянной мощности в нуль при облучении кромки нулём диаграммы направленности — это следствие ограничения первым приближением. Аналогичным образом может быть построена векторная асимптотика и в других задачах, в которых используется скалярная эталонная функция.
5. Сферические волны векторов Фарадея, выражение их через D-функции Вигнера. Компоненты «прямой» и «отражённой» волны.
Векторы Фарадея имеют интересную интерпретацию и оказываются полезными при решении задач в сферической системе координат. Вместо стандартного
- базиса при разложении касательных сферических составляющих векторов Фарадея естественным образом используется спиральный базис
(9). Для уходящей волны направление вращения одной из составляющих вектора Фарадея в спиральном базисе совпадает с направлением круговой поляризации этого вектора, а направление вращения другой противоположно. Вследствие этого каждая составляющая вектора Фарадея приобретает специфический физический смысл. Составляющая с согласованным направлением вращения обладает свойствами падающей волны, с противоположным вращением — отражённой волны, а радиальная составляющая ответственна за вихревые поля, направленные по касательной к сфере. Угловые зависимости сферических гармоник векторов Фарадея в спиральном базисе просто выражаются через известные D-функции Вигнера, введённые в 30-х годах 20 века в квантовой механике для формализации вычислений с векторными и тензорными физическими объектами. Для этих функций имеется хорошо разработанный математический аппарат, подробно описанный, например, в справочнике [24]. Среди D-функций Вигнера имеется серия гармоник с однонаправленным излучением, хорошо приспособленная для описания излучения направленных антенн. Структура разложения диаграмм направленности однонаправленных антенн по классическим
и
волнам сложнее.
Перейдём к выводу выражения для сферической гармоники электромагнитного поля в виде вектора Фарадея, удовлетворяющего на бесконечности условию излучения. Для этого воспользуемся стандартным выражением ротора векторного поля в сферической системе координат,
а затем построим на его основе аналогичное выражение ротора в спиральном базисе
векторные составляющие в котором связаны со сферическими составляющими по формуле [24]:
Будем искать решение уравнений Максвелла
в следующем виде:
В выражении (23) использовано обозначение D-функции Вигнера,
принятое в работах Гельфанда И.М., Шапиро З.Я.[25], и Виленкина [26]. В нашем случае верхний индекс
принимает целые положительные значения, второй нижний индекс
принимает лишь три значения
, соответствующие трём компонентам вектора в спиральном сферическом базисе трёхмерного пространства. Переменные
- обычные угловые переменные в сферической системе координат, угол
не входит в выражение (23), он соответствует вращению вектора поляризации. В справочнике [24] содержится подробная информация по поводу обозначений и определений D-функций Вигнера в различных литературных источниках. В приложении 2 приведены некоторые частные случаи и рекуррентные формулы для функций
.
После подстановки выражения (23) в уравнение Максвелла и применения рекуррентных соотношений для функций
:
(см. монографию [26]), получаем, что функция
есть решение сферического уравнения Бесселя
а функции
и
выражаются через функцию
с помощью дифференциальных операторов:
Для выполнения условий излучения решение сферического уравнения Бесселя выбирается в виде сферической функции Ханкеля второго рода. В результате получается следующее выражение сферической гармоники векторов Фарадея в спиральном базисе:
Некоторые частные случаи. Самые младшие гармоники при
описывают излучение элементарных источников круговой поляризации. При
это диполь круговой поляризации, ориентированный вдоль оси
, то есть, совокупность определённым образом сфазированных электрического и магнитного диполей, ориентированных вдоль этой оси. Поле такого диполя для вектора Фарадея правой круговой поляризации в спиральном базисе имеет следующий вид:
При
это элементы Гюйгенса круговой поляризации, направленные либо вдоль оси
, либо в противоположном направлении. Поле элемента Гюйгенса правой круговой поляризации, направленного вдоль оси
, в спиральном базисе имеет вид:
При
и любом
сферические гармоники векторов Фарадея формируют однонаправленное излучение (в сторону положительного направления оси
при
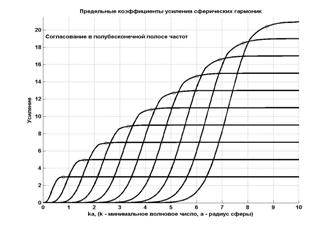
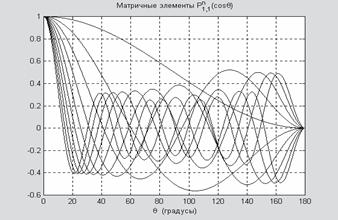
для векторов Фарадея правой круговой поляризации). На рис. 1 показаны графики функций
для первых десяти индексов
.
Рис.1 Однонаправленные сферические гармоники
Радиальные составляющие сферических гармоник как в спиральном базисе, так и для сферических
и
волн убывают на бесконечности как
. Касательные же составляющие ведут себя в
и
волнах и в спиральном базисе по-разному. Из четырёх касательных к сфере составляющих вектора
в
и
гармониках одна тождественно равна нулю, а три другие имеют порядок убывания
. То же относится и к касательным составляющим вектора
. В спиральном же базисе касательные составляющие, у которых направление вращения совпадает с направлением вращения вектора Фарадея, имеют порядок убывания
, а составляющие, направление вращения которых противоположно - порядок убывания
.
Чтобы прояснить физический смысл разной зависимости, вычислим вещественную часть радиальной составляющей вектора Пойнтинга и проинтегрируем её по поверхности сферы радиуса
, то есть, вычислим поток вектора Пойнтинга через поверхность сферы. Из (8) следует, что
Радиальная составляющая вектора Пойнтинга равна разности мощностей спиральных составляющих поля. Поток мощности одной составляющей направлен наружу, а другой внутрь сферы. При интегрировании квадратов модулей угловой части гармоник можно воспользоваться условиями ортогональности и нормировки D-функций Вигнера [24], [26], которые в нашем случае определяются соотношением:
В результате подстановки этого соотношения в поток мощности получим:
Для вычисления выражения в фигурных скобках воспользуемся связью между функциями Ханкеля первого и второго рода от вещественного аргумента и формулой для вронскиана:
В результате получаем, что поток вектора Пойнтинга через поверхность сферы радиуса
от этого радиуса не зависит и равен излучённой мощности гармоники, (что и следовало ожидать):
В то же время, мощность каждой спиральной составляющей от радиуса сферы зависит, причём, мощность составляющей, поток которой направлен наружу (для гармоник, удовлетворяющих условию излучения), всегда превышает мощность другой составляющей на постоянную величину излучённой мощности. Это похоже на соотношение мощностей падающей и отражённой волны в линии передачи, в данном случае, в сферическом волноводе. Исходя из энергетических соображений (26), можно определить «напряжения» падающей и отражённой волн в эквивалентной линии передачи для каждой гармоники в зависимости от радиуса следующими выражениями:
По мере увеличения радиуса «напряжение» падающей волны стремится к ненулевому пределу на бесконечности, а «напряжение» отражённой уменьшается как
. В дальней зоне устанавливается режим бегущей волны, который и определяет условие излучения. При фиксированном радиусе уровень обеих волн возрастает с увеличением номера гармоники.
Из характера убывания составляющих векторов Фарадея в дальней зоне следует, что диаграмма направленности определяется лишь одной составляющей,
для векторов Фарадея правой круговой поляризации и
- левой. Система функций
образует ортогональный базис [26] в пространстве квадратично интегрируемых функций на сфере вида:
.
При
вещественные части функций такого вида определяют векторную диаграмму направленности произвольной антенны правой круговой поляризации. Этими же свойствами обладает система функций
для векторных диаграмм направленности антенн левой круговой поляризации:
Полную векторную диаграмму направленности любой антенны можно представить в виде суммы таких функций. Таким образом, диаграмма направленности любой антенны может быть разложена в ряд по рассматриваемым системам функций. С помощью полученного ряда может быть восстановлено и полное поле на конечных расстояниях от источника излучения (конечно, в случае сходимости ряда в точке восстановления). Эта процедура аналогична использованию разложения полей в ряды по векторным сферическим функциям при проектировании зеркальных антенн и лучеводов, но существенно проще.
6. О «сверхусилении».
На основании полученных результатов, можно сделать качественные выводы относительно возможности эффективной концентрации излучения антенны в фиксированном направлении пространства. Любая сферическая гармоника каждого вектора Фарадея, удовлетворяющая условию излучения, содержит спиральную составляющую «падающей» волны, согласованную с направлением круговой поляризации, и «отражённой» волны с противоположным направлением спиральности. «Отражённая» волна уменьшает эффективность излучения тем больше, чем больше номер сферической гармоники и чем меньше расстояние от источника. Так как разноимённые векторы Фарадея являются решениями разных уравнений, а различные сферические гармоники энергетически независимы, погасить «отражённую» волну в пространстве, окружающем антенну, нечем. Чтобы излучение антенной сферической гармоники было эффективным, потери на отражение в рабочей полосе частот должны быть достаточно малыми. Следовательно, антенна должна выполнять функцию согласующего устройства излучаемых гармоник. А так как для физически реализуемого пассивного устройства без потерь возможности согласования в полосе частот ограничены, это накладывает физические ограничения на возможность эффективного излучения сферических гармоник по мере увеличения их номеров, а значит и на возможность роста усиления антенны ограниченного размера.
Здесь речь идёт не просто о согласовании входа антенны, а об эффективной трансформации подводимой к антенне мощности в излучённую волну. Если согласование входа антенны осуществлено, например, за счёт включения вентиля, отражённая волна поглотится в вентиле, но к.п.д. антенны при этом не увеличится. Следующий идеализированный пример показывает, что тот же результат может получиться при замене невзаимного согласующего элемента взаимным. В качестве антенны используем совокупность соосных электрического и магнитного диполей одинаковой длины. Как известно, поля излучения их ортогональны, а произведение входных импедансов не зависит от частоты и вещественно. Вследствие этого можно найти такой нормирующий импеданс, что нормированные входные импедансы электрического и магнитного диполей будут взаимно обратными функциями. Подключим эти антенны одинаковыми линиями передачи к выходу идеального 180-градусного моста со входным импедансом, равным нормирующему импедансу.
Рис. 2
Матрица рассеяния 180-градусного моста:
Мощность к антенне будем подводить через суммарный вход 1, а разностный вход 2 нагрузим на согласованную нагрузку. Из-за того, что коэффициенты отражения от рассматриваемых диполей равны по величине и противоположны по знаку, вся отражённая волна будет суммироваться в нагрузку, на вход 1 отражённая волна не попадёт, поэтому вход будет идеально согласован. Но это не добавит эффективности излучения. При малых по сравнению с длиной волны геометрических размерах диполей мощность отражённой волны будет составлять существенную долю подводимой мощности, а эффективность будет низкой. Таким образом, для обеспечения эффективности излучения антенна должна быть не просто согласованной, но согласованной с минимальными энергетическими потерями. В дальнейшем будет предполагаться, что согласующее устройство потерь не вносит. Потери в согласующем устройстве приведут к уменьшению усиления антенны.
Материал последующих разделов относится к теоретическому определению потенциальных ограничений физической возможности концентрации мощности излучения антенны ограниченных размеров, работающей в конечной (ненулевой) полосе частот. Напрямую, с использованием нестандартных векторов поля, за исключением мотивации, этот материал не связан.
Потенциально неограниченные возможности концентрации энергии излучения антенны сколь угодно малого размера были предсказаны в 1922 г. на основе анализа решений уравнений Максвелла шведским физиком Озееном [27].
(Карл Вильгельм Озеен больше известен как автор единственной номинации А. Эйнштейна на Нобелевскую премию, которая была поддержана Комитетом по Нобелевским премиям. Премия была присуждена знаменитому физику не как автору теории относительности, а как одному из создателей квантовой физики, объяснившему природу фотоэффекта с позиций квантовой теории.)
Несмотря на заманчивое предсказание возможности «сверхнаправленного излучения», дальнейшее развитие антенной техники показало, что практические возможности концентрации энергии излучения антенны ограничены. Антенны высокой направленности были реализованы лишь на оптических принципах, при которых усиление антенны ограничено функцией
. Термин «сверхусиление» относится к случаю, когда усиление антенны превышает это значение. Попытки дальнейшего увеличения усиления апертурных антенн и антенных решёток наталкивалось на технические трудности невозможности реализации сложных переменно-фазных распределений поля в апертуре с большими перепадами амплитуд, невозможности компенсации сильной взаимной связи близкорасположенных элементов антенной решётки. Препятствия хотя и были значительными, но оставалась надежда на их преодоление за счёт новых технологических достижений.
Непреодолимый на физическом уровне характер ограничения усиления антенны в зависимости от её размеров и полосы согласования, по-видимому, впервые чётко осознал Чу [28]. Он вычислил предельно достижимое усиление слабонаправленной антенны. Стало понятно, что усиление антенны любого размера не может быть сделано сколь угодно большим. Это привело к необходимости исключения из расчётных схем составляющих, имеющих признаки сверхнаправленности и сверхусиления. Так в работах по синтезу антенн и антенных решёток стали применять «ограничительные» функционалы, чтобы нереализуемые на практике варианты отсеивались уже на этапе оптимизации [29]. В работе Харрингтона [30] было постулировано простое эмпирическое правило, исключающее сверхнаправленность, которое констатировало невозможность эффективного излучения сферической гармоники, номер которой превышает «электрический» размер антенны
. Хотя эти приёмы были достаточно эффективными, предельно достижимые параметры антенн (за исключением «слабонаправленных») оставались неизвестными. При сохранении такого положения в теории антенн технический уровень создаваемых устройств на практике можно оценить только по сравнению с оптическим пределом. Признать такую ситуацию нормальной вряд ли возможно.
Теоретический анализ Чу относился к «слабонаправленным» антеннам, и максимальное внимание он уделил ограничениям по первой сферической гармонике. Чу связал ограничения эффективности антенн с возможностью компенсации реактивного импеданса сферических волн в пространстве, окружающем антенну. Он показал, что импеданс последовательности сферических волн совпадает с импедансом некоторой последовательности электрических лестничных цепей из емкостей и индуктивностей, нагруженных на импеданс свободного пространства. Для нахождения предельно реализуемой полосы согласования этих цепей Чу применил только что созданную теорию широкополосного согласования Фано [31], изложенную в его диссертации. В результате он показал, что максимально возможное усиление слабонаправленной антенны пропорционально кубу её диаметра при работе в некоторой полосе частот.
Вычисления ограничений полосы согласования или коэффициентов передачи сферических волн Чу осуществлял приближённо с заменой сложной лестничной схемы резонансным контуром. Он основывался при этом на том, что наибольшие ограничения исходят от одной из реактивностей в лестничной схеме. Параметры резонансного контура Чу выбирал, исходя из равенства энергии, «запасённой» в реактивностях сферической волны и резонансном контуре, и характеризовал величиной добротности
. В последующих работах других авторов по исследованию возможности реализации антенны со «сверхусилением» такое приближение использовалось повсеместно, за исключением строгого анализа ограничений, создаваемых первой сферической гармоникой, проведенного «по следам Чу» в работах некоторых авторов. Примечательно, что в обзорной статье Хансена [32] утверждалось, будто строгий анализ ограничений, создаваемых лестничными схемами Чу для гармоник выше первого порядка не имеет большого смысла из-за трудности анализа.
Несмотря на такой пессимистический прогноз и вопреки авторитетному мнению, вычисления со строгим анализом ограничений, создаваемых сферическими волнами в пространстве, окружающем антенну, не прекратились. Электрические цепи, связанные со сферическими гармониками, имеют характерную особенность – у них есть единственный нуль передачи высокой кратности на нулевой частоте. Кратность нуля передачи этих цепей на единицу превышает номер сферической гармоники. При создании метода определения предельной ширины полосы согласования антенны со сферическими гармониками эту особенность полезно учитывать. В [33] был предложен алгоритм решения задачи широкополосного согласования путём последовательного исключения нулей передачи или понижения их кратности. Предложенный алгоритм основан на методе Шура решения интерполяционной проблемы моментов. В качестве приложения метода была вычислена предельная полоса согласования по 1-й и 2-й сферическим гармоникам. Методика вычисления была достаточно громоздкой и неструктурированной, что мешало дальнейшему продвижению. Статья была опубликована в редком издании и осталась незамеченной. В [34] удалось построить алгоритм, специально приспособленный для анализа предельной полосы согласования электрических лестничных схем с единственным нулём передачи высокой кратности. Данным методом рассчитано предельно достижимое усиление антенны с заданной полосой согласования с учётом излучения первых 10-ти сферических гармоник. Возможности метода этим не исчерпываются. Далее даётся подробное изложение метода, предложенного в [34].
7. Математическая модель антенны, заключённой в сферу. Четырёхполюсники Чу. Узкополосное и широкополосное согласование. Максимизация усиления антенны.
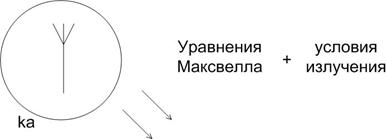
Исходным пунктом анализа максимально возможного усиления выбрана математическая модель антенны, предложенная Чу в [28] и показанная на рис.3.
Рис.3 Модель антенны, рассмотренная в работе [28].
Область пространства, занимаемого антенной, ограничена сферой радиуса
,
- волновое число. Электромагнитное поле вне сферы удовлетворяет уравнениям Максвелла и условиям излучения на бесконечности. Поле в области вне сферы можно разложить в ряд по сферическим гармоникам. Коэффициент отражения каждой сферической гармоники на поверхности сферы можно вычислить, исходя из выражений для амплитуд падающих и отражённых составляющих векторов Фарадея (28).
От этого выражения можно перейти к выражению
адмитанса
-й сферической гармоники по формуле:
.
В результате получается адмитанс, совпадающий с выражением адмитанса магнитной сферической гармоники
при
в работе Чу [28]:
,
Для электрических сферических гармоник
тем же выражением определяется импеданс
. Двойственные выражения импеданса и адмитанса сферических гармоник приводят к одним и тем же ограничениям полосы согласования.
Используя рекуррентные соотношения для сферических функций Бесселя, Чу получил разложение импеданса
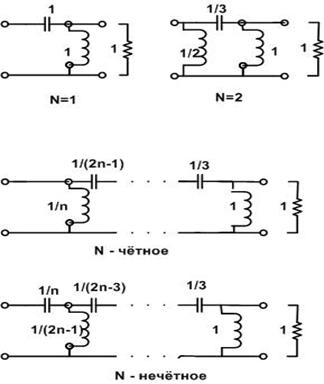
в цепную дробь (синоним – непрерывная дробь) и, тем самым, реализовал последовательность импедансов как последовательность электрических четырёхполюсников, нагруженных на единичный импеданс и изображённых на рис. 4.
Рис. 4. Четырёхполюсники Чу
Коэффициент передачи мощности
каждого четырёхполюсника равен коэффициенту излучения соответствующей сферической гармоники. Полный коэффициент усиления антенны при синфазном сложении гармоник можно вычислить с помощью ряда:
- комплексный коэффициент возбуждения сферической гармоники порядка
. Дифференцированием по
нетрудно показать, что максимальное значение усиления достигается при следующем соотношении:
В выражении (30) множитель
один и тот же для всех гармоник (множитель нормировки, не влияющий на усиление). Если все гармоники синфазны в направлении оси
, максимальное усиление даётся рядом:
Поскольку
- это коэффициент направленного действия сферической гармоники порядка
, излучающей в полярном направлении,
- это коэффициент усиления такой гармоники. Из выражения (31) следует, что максимальное усиление достигается при максимальных значениях коэффициентов передачи мощности
всех четырёхполюсников Чу.
Следует обратить внимание на различие значений коэффициентов направленного действия сферических гармоник в данной статье и в работе Чу [28]. Чу исследует характеристики сферических гармоник
и
волн. Максимальная направленность этих волн распределена в азимутальной плоскости по всем направлениям. Волны минимального порядка соответствуют элементарным диполям с коэффициентом направленного действия 1.5. Сферические гармоники, рассматриваемые в данной статье, образуются суперпозицией
и
волн. Среди этих гармоник всегда имеются однонаправленные. При
- это элемент Гюйгенса с коэффициентом направленного действия 3, вдвое превышающим направленность элементарных диполей. Направленность других гармоник также отличается не менее чем вдвое. Множитель 2 необходимо учитывать при сравнении результатов [28] и данной статьи.
Узкополосное согласование любого четырёхполюсника Чу на фиксированной частоте может быть осуществлено с помощью каскадно включённой схемы, состоящей из одного реактивного элемента и идеального трансформатора. Коэффициент передачи на этой частоте при достаточно точной реализации элементов и в отсутствии омических потерь будет близок к единице. Если такое согласование осуществить на одной фиксированной частоте для достаточно большого числа сферических гармоник, можно достичь любого, наперёд заданного, усиления. Таким образом, узкополосное согласование, нестеснённое технологическими ограничениями, может привести к неограниченному сверхусилению, предсказанному Озееном.
8. Задача широкополосного согласования четырёхполюсника Чу. Метод её решения с помощью цепных дробей. Теорема о возможности согласования четырёхполюсника Чу в заданной полосе частот.
Совершенно иная ситуация складывается, если антенна работает в реальной ненулевой полосе частот. В этом случае, согласно теории Фано [31], существуют физические ограничения уровня согласования, приводящие к ограничению уровня коэффициента передачи. Наша задача состоит в расчёте этих ограничений для четырёхполюсников Чу и применении результатов расчёта к вычислению ограничений коэффициента усиления по формуле (31).
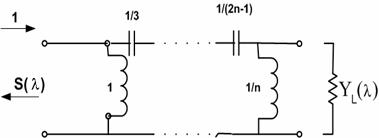
На рис. 5 показана схема четырёхполюсника Чу «со стороны бесконечности». На выходе четырёхполюсник нагружен на адмитанс антенны для сферической гармоники порядка
.
Рис. 5. Четырёхполюсник Чу, нагруженный на проводимость антенны.
Аргумент функций коэффициента отражения
и комплексной проводимости
- комплексная частотная переменная
, применяемая в электротехнике, её мнимая часть
- круговая частота. В терминах комплексной частоты
формулируются условия физической реализуемости функций
и
, которым, в конечном счёте, удовлетворяет конструкция антенны. Предполагается, что антенна является линейной, пассивной системой, с параметрами, не зависящими от времени, и удовлетворяющей принципу причинности. Применительно к функциям
и
условие причинности переходит в условие аналитической зависимости указанных функций от
в правой полуплоскости, а условие пассивности – в неравенства [35]:
Физически реализуемым устройствам отвечают только такие функции
и
, которые принимают вещественные значения на вещественной оси комплексной плоскости
,
- вещественные функции. Такие функции называются, соответственно, ограниченно-вещественными и положительно вещественными функциями.
При постановке задачи широкополосного согласования к коэффициенту отражения предъявляются требования по качеству согласования
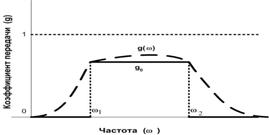
в заданной полосе частот. Функция
определяет заданные требования по коэффициенту передачи мощности (рис. 6).
Рис. 6. Частотные требования к коэффициенту передачи мощности.
Специфическая трудность решения задачи широкополосного согласования состоит в том, что, кроме условий физической реализуемости и требований к качеству согласования, функции коэффициента отражения и входного импеданса должны удовлетворять интерполяционным условиям в нулях передачи согласуемого устройства. Каждый четырёхполюсник Чу имеет единственный нуль передачи кратности
на нулевой частоте и, кроме того, является взаимным устройством. В этом случае, для формулировки интерполяционных условий проще всего воспользоваться разложением входной проводимости в цепную дробь:
Первые
коэффициентов цепной дроби не зависят от нагрузки
и однозначно определяются величинами реактивностей четырёхполюсников Чу (рис. 5),
-й коэффициент может зависеть от нагрузки, если нагрузка добавляет к реактивности
свою реактивность того же типа. В любом случае,
-й коэффициент дроби не может быть меньше соответствующей величины реактивности согласуемого четырёхполюсника. Характер приближения цепной дроби (34) её подходящими дробями в окрестности нуля передачи является асимптотическим. Для нахождения физически реализуемой проводимости нагрузки
, обеспечивающей согласование, по известной входной проводимости
необходимо и достаточно, чтобы разложение положительно вещественной функции
в цепную дробь удовлетворяло условию качества согласования и интерполяционным условиям. После определения
можно найти согласующий четырёхполюсник, как это сделано в работе Фано [31], применением процедуры Дарлингтона.
Решение интерполяционных задач в классах аналитических функций, в число которых входят ограниченно и положительно вещественные функции, имеет давнюю историю в математике, начавшуюся в 19 веке с работ П.Л.Чебышёва, А.А. Маркова и Т. Стильтьеса - это задачи типа проблемы моментов. В 20 столетии разработкой методов решения задач этого класса занималась целая плеяда выдающихся математиков, специалистов по функциональному анализу. С некоторыми их результатами можно ознакомиться по работам [36 - 38]. Строгий математический метод решения задачи широкополосного согласования экспериментально измеренного импеданса разработан Хелтоном У. [39], но применимость этого метода к исследуемой задаче сомнительна.
Условия разрешимости задач типа проблемы моментов обычно формулируются в виде условия положительной определённости некоторых матриц. Однако в простейшем случае единственного кратного нуля передачи на нулевой частоте условие разрешимости может быть сформулировано в виде условия положительности коэффициентов разложения в цепную дробь. Чтобы применить методы решения задач типа проблемы моментов к задаче широкополосного согласования, необходимо избавиться от несвойственного для интерполяционных задач требования к качеству согласования в виде неравенств (33). По этой причине, следуя [33], вводится функция:
которая является ограниченно вещественной функцией, не обращается в нуль в правой полуплоскости, а при подходе к мнимой оси обладает предельным свойством:
если частотная характеристика
- непрерывная функция.
Введём далее вспомогательный коэффициент отражения - ограниченно вещественную функцию
посредством отношения:
Интерполяционные условия (34) сформулированы применительно к функции входной проводимости, поэтому перейдём от вспомогательных функций
к функциям соответствующих вспомогательных проводимостей:
Функция вспомогательной проводимости
связана с проводимостями
и
выражением:
Из соотношений (36, 37) следует, что принадлежность функции
классу положительно вещественных функций обеспечивает автоматическое выполнение требований качества согласования. Чтобы поставить интерполяционную задачу относительно этой функции, достаточно перенести интерполяционные условия (34) на функцию
в соответствии с формулами (35) и (39).
Для получения численных результатов нужно конкретизировать требования к качеству согласования применительно к решаемой нами задаче вычисления предельного усиления антенны. Сигналы антенны проходят через все четырёхполюсники Чу, то есть, четырёхполюсники работают в единой полосе частот:
.
Достижение предельного усиления определяется возможностью согласования каждого четырёхполюсника Чу до максимального коэффициента передачи в этой полосе частот. Алгоритм существенно упрощается, если задаться частотной характеристикой допустимого коэффициента передачи (рис. 6) в виде предельной ступенчатой функции. В этом случае достаточно найти последовательность максимально возможных коэффициентов передачи сферических гармоник
, подстановка которых в формулу (31) позволит вычислить предельное усиление. Проводя интегрирование в формуле (35) для случая ступенчатой частотной характеристики, получим выражение для вспомогательного коэффициента отражения
в виде элементарной аналитической функции, определённой в плоскости комплексной частоты с двумя разрезами на мнимой оси частот в области рабочей полосы и в симметричной области отрицательных частот.
Функция
, определённая выражением (40), относится к классу ограниченно вещественных, однако некоторые свойства, описанные выше, нарушаются из-за её разрывного характера, а также из-за того, что вне рабочей полосы частот требования к качеству согласования не предъявляются. На краях разреза появляются точки ветвления, нарушается предельный переход в формуле (36), а также возможность применения на последнем этапе теоремы Дарлингтона. Тем не менее, при аппроксимации ступенчатой функции
рациональными все эти свойства сохраняются. Увеличение точности рациональной аппроксимации ступенчатой частотной характеристики позволит уменьшить погрешность аппроксимации величины максимально возможного коэффициента передачи до любого значения.
Согласно применяемой нами методике, перейдём от вспомогательной функции
к вспомогательной проводимости
по одной из формул (38).
Далее функции
и
нужно подставить в формулу (39), а полученную функцию
разложить в цепную дробь:
коэффициенты
разложения зависят от реактивностей соответствующего четырёхполюсника, а также от
, входящих в выражение (41). Нахождение вспомогательной проводимости
позволит получить решение нашей задачи широкополосного согласования, если первые
коэффициентов
цепной дроби будут положительны, а
-й коэффициент - неотрицательным.
Алгоритмически разложение
в цепную дробь легче всего получить, если в цепную дробь разложена функция
. Это разложение (в бесконечную цепную дробь) в явном виде может быть получено из разложений [40] типа разложений тангенса кратного угла, использовавшегося ещё Эйлером.
Сведения о сходимости этого разложения содержатся в приложении 3. Для нас важно, чтобы цепная дробь (43) сходилось к
в проколотой окрестности нуля передачи сферической гармоники
. Такая сходимость обеспечена.
Алгоритм получения коэффициентов
разложения (42) функции
в цепную дробь следующий:
- Выписываем рациональные выражения подходящих дробей
порядка разложений (34) и (43).
- Подставляем их в формулу (39).
- К полученному рациональному выражению применяем алгоритм Евклида (последовательное деление многочленов с остатком) для разложения в цепную дробь и получения выражений коэффициентов
.
Коэффициенты
зависят от
. При переходе от n-й сферической гармоники к (n+1)-й изменение значений элементов лестничной цепи (34) происходит по следующей схеме:
номер элемента
1
2
…
n
(n+1)
(n+2)
номер
гармоники
n
1
3
…
2n-3
n
(n+1)
1
3
…
2n-3
2n-1
(n+1)
Добавляется последний элемент, а предыдущий меняет своё значение. Такая же закономерность сохраняетсяи в коэффициентах
, поэтому при вычислениях достаточно ограничиться коэффициентами
и
.
(Символ
в (16) означает, что левая часть пропорциональна правой с положительным множителем.) Вычисление этих коэффициентов достаточно трудоёмко и осуществлено с использованием программного продукта “MAPLE”.
Решение нашей задачи основано на следующей теореме:
Пусть
- положительные числа
удовлетворяют системе неравенств:
- произвольная положительно-вещественная функция,
.
Тогда
1.
- положительно-вещественная функция,
2. Функция
- положительно-вещественная функция выходной проводимости четырёхполюсника Чу, то есть, существует положительно-вещественная функция нагрузки
, такая что
3. В полосе частот
коэффициент отражения
удовлетворяет неравенству:
.
Идея и некоторые элементы доказательства теоремы приведены в приложении 3.
9. Вычисление потенциального коэффициента усиления антенны как функции минимальной рабочей частоты.
Выписанная в условии 1 теоремы система неравенств образована многочленами от трёх переменных
,
, и
(с целыми коэффициентами). Для каждой гармоники необходимо найти функцию, удовлетворяющую всем неравенствам и определяющую наибольшее положительное значение
. При увеличении номера гармоники новыми неравенствами являются лишь два последних.
Заметим, что при
оба этих неравенства выполнены при всех значениях
. Следовательно, область положительности всех многочленов лежит между осью
и наименьшим положительным корнем каждого многочлена. При каждом
следует выбрать наименьший корень из корней двух многочленов. При этом оба неравенства будут выполнены, причём, одно из неравенств - в слабом смысле (больше или равно).
Чтобы конкретно сравнить силу неравенств в разных областях
, нужно воспользоваться методами качественного, асимптотического решения алгебраических уравнений высокой степени. Наглядный метод нахождения асимптотики корней алгебраических уравнений с двумя неизвестными был разработан ещё Ньютоном [41, 42]. Каждый многочлен от двух переменных – это сумма конечного числа одночленов вида
. Для множества всех одночленов данного многочлена с неравными нулю коэффициентами построим на плоскости систему точек с целочисленными координатами
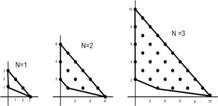
. Выпуклая оболочка этой системы точек называется многоугольником Ньютона. На рис. 7 показаны такие системы точек и их выпуклые оболочки для вторых многочленов из первых 3-х пар неравенств, определяемых многочленами (16).
Рис. 7. Многоугольники Ньютона
Стороны многоугольников, обращённые к началу координат, определяют асимптотику малых решений, внешняя сторона – асимптотику больших решений. Главные члены асимптотики определяются одночленами, соответствующими точкам, лежащим на сторонах многоугольника. Остальные одночлены оказывают тем меньшее влияние, чем дальше от рассматриваемой стороны многоугольника расположены соответствующие точки. Если в многочлене оставить только главные одночлены, а остальные отбросить, получим укороченное уравнение, определяющее главный член асимптотики решения. Для нижних сторон многоугольников, обращённых к началу координат, укороченные уравнения двучленные:
Их решения определяют главный член асимптотики
при малых значениях
:
(Кстати, асимптотика при
определяет знаменитую кубическую зависимость Чу.)
Из системы неравенств при
очевидно, а при остальных
можно доказать, что более сильные ограничения при малых значениях
дают решения вторых неравенств из выписанных пар.
Большим значениям
соответствуют внешние стороны многоугольников Ньютона, которые проходят через несколько точек рассматриваемого множества и наклонены под углом 45° к осям системы координат. Это означает, что главный член больших решений всех выписанных многочленов один и тот же:
. Чтобы определить, какое из неравенств пары сильнее, главного члена недостаточно. Нужно привлекать второй член асимптотического ряда Пюизё. Численные результаты показывают, что при больших значениях
более сильным всегда оказывается первое неравенство, которое и определяет соответствующую часть решения
. При значениях
, удовлетворяющим обоим уравнениям пары, оба неравенства равносильны. Если величины
превышают эти значения, для определения интересующего нас решения нужно численно решать первое уравнение пары, в противном случае – второе.
Выражение предельного коэффициента передачи можно получить из формулы (40).
Кривые предельных решений неравенств для 10-ти первых номеров сферических гармоник показаны на рис. 8. Значения коэффициентов передачи, согласно формуле (3), умножены здесь на (2n+1) – максимальный к.н.д. соответствующей сферической гармоники. На графике приведены только решения, отвечающие согласованию в полубесконечной полосе частот – случай
Кружками обозначены точки стыка разных алгебраических ветвей решений.
Рис. 8. Предельные усиления по отдельным гармоникам.
.
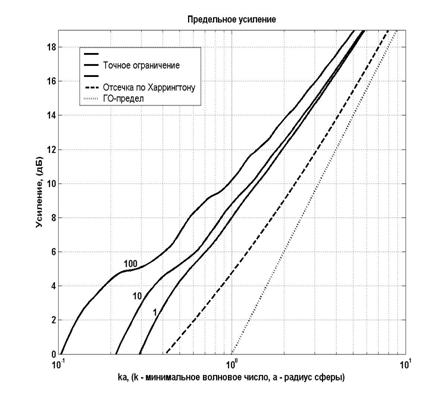
Для получения предельного усиления всей антенны необходимо сложить усиления по отдельным гармоникам, в соответствии с выражением (31). На рис. 9 показаны графики предельного усиления антенн в зависимости от
на нижней частоте полосы согласования. Три сплошные кривые соответствуют различным полосам согласования, параметризированным значениями добротности, определённой формулой:
(При обычно используемом определении добротность равна половине этой величины). При нашем определении добротность
отвечает полубесконечной полосе частот. Нижний график (точечный) – соответствует геометрооптическому пределу усиления:
Второй снизу пунктирный график соответствует предельному усилению, определяемому отсечкой Харрингтона [30]:
Рис. 9. Границы физически реализуемого усиления антенны.
Предельные ограничения усиления антенны при работе даже в самой широкой полосе частот (неограниченной сверху) превышают как предельное геометрооптическое усиление, так и усиление, определяемое отсечкой высших сферических гармоник по Харрингтону.
10. Заключение
Приведено определение векторов Фарадея, которые можно трактовать, как электромагнитные волны идеальной круговой поляризации. Даны примеры их применения в теории антенн: в задаче обеспечения отсутствия кроссполяризованного излучения при рассеянии, при вычислении векторных высокочастотных асимптотик в дифракционных задачах.
Исследована структура сферических волн векторов Фарадея в спиральном базисе. На основе этого исследования и теоретического анализа показано, что потенциальная возможность эффективной концентрации излучения антенны заданных размеров зависит от рабочей полосы частот, то есть, от информационной пропускной способности антенны. Ограничения усиления определяются фильтрующими свойсвами пространства, окружающего антенну. От конструкции антенны зависит возможность достижения предельных параметров. Предложен алгоритм вычисления предельного усиления антенны. Приведены численные результаты.
Приложения
10.1. Выражение основных электродинамических соотношений в терминах векторов Фарадея.
1. Векторный потенциал
Для свободного пространства
(П1.1)
векторы поля выражаются через векторный потенциал по формуле:
(П1.2)
В результате подстановки этого выражения в уравнение (П1.1) для векторного потенциала
получаем стандартное уравнение Гельмгольца:
. (П1.3)
с известным решением:
(П1.4)
в котором
- функция Грина:
а интегрирование распространяется по объёму, занимаемому токами.
2. Найдём выражение поля элементарного диполя с направлением вдоль вектора
:
Из формулы (П1.4) следует выражение для векторного потенциала диполя:
Подставляя это выражение в (П1.2), получим
(П1.5’)
или
(П1.5)
Преобразуем слагаемые с дифференциальными операторами:
(П1.6)
(П1.7)
Подставляя (П1.6), (П1.7) в (П1.5), получим:
Вне области, содержащей источник, первое слагаемое можно отбросить, получим следующее выражение для поля элементарного диполя:
(П1.8)
Вычислим выражение (П1.8), используя явный вид функции Грина
:
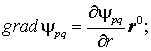
— единичный вектор, направленный от точки «истока»
к точке «наблюдения»
.
Получаем следующее окончательной выражение:
(П1.9)
3. Лемма Лоренца.
Пусть
и
— одноимённые векторы Фарадея, либо оба вектора правой поляризации, либо оба левой. Случай с двумя разноимёнными векторами Фарадея рассматривать бессмысленно, потому что они удовлетворяют разным уравнениям и не взаимодействуют между собой. Запишем уравнения Максвелла для векторов
и
:
Умножим скалярно первое уравнение на
, а второе на
и вычтем из первой строки вторую:
или
(П1.10’)
По теореме Гаусса-Остроградского получаем выражение леммы Лоренца:
(П1.10)
Здесь
— замкнутый объём с границей
,
— внешняя нормаль.
Используем лемму Лоренца для вывода выражения поля вне замкнутой поверхности через касательные составляющие поля на поверхности.
Положим в (П1.10):
— поле в объёме
— поле элементарного диполя,
— единичный вектор вдоль диполя.
точки
внутри объёма
.
Подставляя эти выражения в интегральное выражение леммы Лоренца, получаем:
или
Если источников поля
в объёме
нет, то выражение упрощается:
(П1.11)
Это выражение можно упростить дальше, выразив смешанные произведения.
,
— это касательные составляющие поля к поверхности
, которые можно обозначить как поверхностную плотность «тока»:
Подставляя эти выражения в (П1.11), получим выражение составляющих поля через поверхностный «ток»:
(П1.12)
В этом выражении вектор
— это вектор, на направление которого проектируется поле
в точке наблюдения
, единичный вектор
зависит от взаимного положения точек истока
и наблюдения
.
После вычисления производных получим:
(П1.12´)
Из выражения (П1.12´) следует формула для векторных составляющих поля в дальней зоне (диаграммы направленности):
(П1.13)
Векторы Фарадея в дальней зоне идеально поляризованы по кругу, поэтому в спиральном базисе диаграмма направленности каждого вектора Фарадея будет иметь лишь одну ненулевую составляющую. Спиральный базис вводится по правилу [24]:
С учётом этих соотношений поле в дальней зоне, выраженное через касательные составляющие поля на поверхности
, можно вычислить по формуле:
(П1.14)
Поле же другой спиральной составляющей убывает быстрее, чем
. Поэтому, для любого
и любого решения уравнений Максвелла вне гладкой ограниченной поверхности, удовлетворяющего условию излучения на бесконечности, касательные составляющие решения на поверхности удовлетворяют условию:
(П1.15)
4. Формула Стреттона - Чу.
В формуле Стреттона - Чу излученное поле выражается через касательные и нормальные составляющие поля на поверхности.
В формуле (П1.10) для леммы Лоренца выберем поле
в виде поля электрического диполя в форме (П1.5):
Получим выражение для поля в области, свободной от источников в виде:
Преобразуем последнее слагаемое, для этого воспользуемся тождеством:
,
а также тем, что для любого векторного поля
и любой замкнутой поверхности
,
а в области, где отсутствуют токи,
.
Тогда
или, после перестановки элементов смешанного произведения, получим:
(П1.16)
Это и есть формула Стреттона-Чу, выраженная в терминах векторов Фарадея.
10.2. Некоторые частные случаи и рекуррентные формулы для сферических функций
.
Матричные элементы неприводимых представлений группы вращений:
определены для значений индексов, удовлетворяющих неравенствам:
. (П2.1)
Индекс
в представлении векторных полей отвечает номеру векторной составляющей. Для электромагнитных полей круговой поляризации индекс
принимает значения 0 и ±1.
Для функций
справедливы следующие соотношения симметрии:
при
а также
Функции, отвечающие граничным значениям индексов в неравенстве (П2.1) имеют следующее явное представление:
Функции с индексами
выражаются с помощью одночленных рекуррентных формул:
Для выражения функций с индексами
справедливы двучленные рекуррентные соотношения:
Для всех остальных функций при увеличении индекса
на единицу применяется трёхчленная рекуррентная формула:
При соответствующих значениях индекса
трёхчленная формула переходит в двучленную и одночленную.
10.3. О разложении в бесконечную цепную дробь и доказательстве теоремы о предельном согласовании четырёхполюсника Чу.
Информацию относительно сходимости разложения функции
в бесконечную цепную дробь
можно найти в [43], или [44]. Функция
- аналитическая в комплексной плоскости
с двумя разрезами по мнимой оси, симметричными относительно начала координат. Разрезы соответствуют частотным областям, в которых требуемый коэффициент передачи мощности больше нуля. Края разрезов являются точками ветвления функции.
Сходимость бесконечной цепной дроби в области вне разрезов неравномерная, ухудшается при приближении к разрезам. Дробь типа (43) можно трансформировать (с сохранением скорости сходимости) [44] к виду, для которого справедлива теорема Ван Флека [43], утверждающая сходимость цепной дроби в симметричном угловом секторе в правой полуплоскости с вершиной в нуле и раствором меньше 180º. Численные расчёты подтверждают сходимость. В проколотом круге с центром в нуле и радиусом меньшем расстояния до разреза сходимость достаточно хорошая, значит, коэффициенты разложения
в цепную дробь хорошо описывают характеристики этой функции в окрестности нуля передачи исследуемых электрических цепей. А нам именно это и требуется, потому что мы хотим определить влияние нуля передачи на предельно достижимые коэффициенты передачи сферических гармоник.
Уровень сложности доказательства теоремы о предельном согласовании четырёхполюсников Чу зависит от рассматриваемого класса положительных вещественных функций. Доказательство сравнительно элементарное в случае рациональных функций. Чтобы можно было ограничиться этим случаем нужно, чтобы и требуемая частотная характеристика передачи мощности сферической гармоникой была рациональной. Но любая рациональная передаточная функция, общая для всех гармоник, заведомо не пропустит гармоники с более высоким номером, чем порядок рациональности передаточной функции. Следовательно, с рациональной передаточной функцией невозможно определить предельное усиление антенны достаточно большого размера. По этой причине в данной статье выбрана ступенчатая передаточная характеристика. Можно, конечно, использовать рациональную аппроксимацию ступенчатой передаточной функции, свою для каждого номера сферической гармоники. Это легко сделать с помощью баттервортовской или чебышёвской передаточных функций. В этом случае уравнения, определяющие предельно допустимую полосу согласования, усложнятся за счёт добавления параметров, характеризующих качество аппроксимации, однако принципиально такой подход возможен.
В данном приложении даётся доказательство применительно к рациональному случаю. Более тонкое математическое доказательство для случая самых общих положительных вещественных функций, определяемых интегральным критерием Неванлинны, здесь не приводится. Во-первых, идея доказательства в обоих случаях одна и та же, во-вторых, данная статья предназначена для инженеров. Кстати, если экономно определить промежуточный класс положительных вещественных функций, охватывающий рассматриваемый случай, и не выходить за его пределы, то можно ограничиться достаточно простым доказательством.
Отметим ещё один математический нюанс. Аналитические свойства передаточной функции наследуются импедансом согласующего устройства, соединённого с антенной. Аналитические свойства ступенчатой функции не соответствуют критерию Арова [45] применимости теоремы Дарлингтона. Поскольку целью данной работы не является конкретная реализация антенны с максимально возможным усилением, а только определение предельно допустимого усиления антенны, невозможность выделения согласующего устройства, нагруженного на единственный чисто активный импеданс, не препятствует достижению цели. Для конкретной реализации согласующих устройств, обеспечивающих оптимальную передачу сферических гармоник нужно пользоваться рациональной аппроксимацией характеристики передачи.
Переходим к доказательству теоремы о предельном согласовании четырёхполюсников Чу.
Первое утверждение теоремы следует из положительности коэффициентов
, неотрицательности коэффициента
, и положительной вещественности
. Здесь используется следующие свойства положительных вещественных функций: сумма двух положительно вещественных функций положительно вещественная, а обратная величина к положительной вещественной функции тоже является положительной вещественной функцией.
Первая часть 2-го утверждения о том, что функция
положительно вещественная, следует из положительной вещественности составляющих в правой части формулы и представления:
.
Вторая часть 2-го утверждения доказывается более сложно. То, что коэффициенты цепного разложения
совпадают с коэффициентами цепного разложения четырёхполюсника Чу следует из взаимной обратимости алгоритма преобразования их в коэффициенты цепного разложения функции
.
То, что остаточная функция
в представлении
- положительно вещественная следует из положительной вещественности
, а также того, что процедура последовательного отщепления реактивных импедансов с полюсом в нуле передачи не меняет значения активной части импеданса на оси частот
. Только доказательство этого утверждения требует более тонких математических рассуждений в общем случае нерациональных положительно вещественных функций.
Последнее утверждение теоремы следует из представления:
поскольку
является ограниченно вещественной функцией , полученной из положительно вещественной функции
по формуле
,
а
удовлетворяет требуемому неравенству по построению.
Литература
1. Meister E., Meister L., Quaternion Boundary Value Problems for Canonical Objects in Continuum Physics //Advances in Clifford Algebras, 2001. - 11(82), 231-246,
2. Вайнштейн Л.А., Электромагнитные волны. «Радио и связь», 1988
3. Silberstein L.// Ann. Phis., 1907. - 22, - 24,
4. Bateman H., The mathematical analysis of electrical and optical wave-motion, 1915 г. (Русский перевод: Бейтмен Г., Математическая теория распространения электромагнитных волн, 1958 г.)
5. Lewin L. Theory of waveguides, //London, Butterworth and Co Ltd., 1975. (Русский перевод: Левин Л., Теория волноводов, - М.: Радио и связь, 1981. – 311 с.)
6. Яглом И.М., Комплексные числа и их применение в геометрии, УРСС, 2004
7. Rumsey V.H. A New Way of Solving Maxwell’s Equations, IRE Transactions on Antennas and Propagation, 1961, Sept., 461-465
8. Третьяков С.А. Электродинамика сложных сред: киральные, биизотропные и некоторые бианизотропные материалы, //Радиотехника и электроника, 1994.- т.39, в.10, с.1457-1470
9. Шевченко В. В., Обратные волны в киральных средах и волноводах. Радиотехника и электроника, 2005, т.50, №11, с.1369-1373
10. Lakhtakia A. Beltrami fields in chiral media, //Singapore; River Edge, N.Y., World Scientific, 1994. – 535 p.
11. Козлов А.И., Логвин А. И., Сарычев В.А., Поляризация радиоволн, изд-во «Радиотехника», Кн. 1 (2005). Кн. 2 (2007)
12. Beltrami E., Considerazioni idrodinamiche,—Rendiconti del reale Instituto Lombardo, Milano, 1889, t.XXII, p. 121-130, см. также: “Opere Matematiche di Eugenio Beltrami”, Milano, 1920, T.IV, 87,300-309
13. И.С. Громека, Некоторые случаи движения несжимаемой жидкости,—Учёные записки Казанского университета, 1881, см. также: Собрания сочинений, Изд-во АН СССР, Москва, 1952, с. 76-148
14. Craig Th., On certain possible cases of steady motion in a viscous fluids.—American Journal of Mathematics, 1880, v.3, p.276
15. Сакс Р.С. Обобщённо эллиптические операторы и задачи математической физики. Автореферат диссертации на соискание учёной степени доктора физико-математических наук. – СПб. 1998. – 38 с.
16. Коган Б.Л., Об источниках кроссполяризованного излучения, Радиотехника и Электроника, 2004, том 49, №4, с.421-430.
17. H.C. Minnet, B. Mac A. Thomas, A Method of Synthesizing Radiation Pattern with Axial Symmetry, IEEE Transactions on Antennas and Propagation, 1966., - v. , Sept., p.654-656.
18. Коган Б.Л., Электромагнитные поля круговой поляризации, Докторская диссертация, 2004
19. P.-S. Kildal, Definition of artificially soft and hard surfaces in for electromagnetic waves, Electron. Lett., v.24, no.3, pp. 168-170, Feb. 4, 1988
20. Keller J.B. Geometrical theory of diffraction.—J. Opt. Soc. of Amer., 1962, v.52, № 2, p.116-130
21. Боровиков В.А., Кинбер Б.Е., Геометрическая теория дифракции, «Связь», 1978
22. Боровиков В. А., Краевые волны в задаче дифракции на криволинейной поверхности с ребром. Препринт ИПМ АН СССР, 1973, №63
23. Коган Б.Л., Асимптотическая оценка дифракционных потерь двухзеркальной антенны Кассегрена при низком уровне облучения края контррефлектора, Антенны, выпуск 2 (41), 1998
24. Д.А. Варшалович, А.Н. Москалёв, В. К. Херсонский: Квантовая теория углового момента. (аппарат неприводимых тензоров, сферические функции, 3nj-символы), «Наука», Ленинград, 1975 г.
25. Гельфанд И.М., Минлос Р.А., Шапиро З.Я., Представления группы вращений и группы Лоренца, 1958
26. Виленкин Н.Я., Специальные функции и теория представления групп, «Наука», ГРФМЛ, 1965
27. Oseen C.W. Die Einsteinsche Nadelstichstrahlung und die Maxwellschen Gleichungen. //Ann. Phys., 69, 202, 1922
28. Chu L.J. Physical Limitations of Omni-Directional Antennas//Journal of Applied Physics, 1948, 19, December, -1163-1175
29. Бахрах Л.Д., Кременецкий С.Д., Синтез излучающих систем, М., «Сов. радио», 1974 г.
30. Harrington R.F. On the Gain and Beamwidth of Directional Antennas.//IRE Transactions on antennas and propagations, 1958, July, 219-225.
31. Фано Р. Теоретические ограничения полосы согласования произвольных импедансов. Пер. с англ. – М.: Сов. радио, 1965, 70 с.
32. Hansen R.C. Fundamental Limitations in Antennas. //Proceedings of the IEEE, 1981, 69, No.2, February, -170-182
33. Коган Б.Л. Теория широкополосного согласования. //Сборник научно-методических статей по прикладной электродинамике, - М.: «Высшая школа», 1980.- в.3, - с. 162-182.
34. Коган Б.Л., Наибольшее усиление физически реализуемой антенны, «Антенны», в.2(105), 2006 г., с.4-12
35. Ефимов А.В., Потапов В.П. J-растягивающие матрицы-функции и их роль в аналитической теории электрических цепей. //Успехи математических наук, - 1973. – т. XXVII, -в. 1(169), - 65-130
36. Ахиезер Н.И. Классическая проблема моментов. – М.: Гос. изд. физ. – мат. лит., - 1961, -312 с.,
37. Крейн М.Г., Нудельман А.А. Проблема моментов Маркова и экстремальные задачи. – М.: Из-во Наука, ГРФ-МЛ, - 1973, - 552с.
38. Ковалишина И.В. Аналитическая теория одного класса интерполяционных задач. //Изв.АН СССР. Сер.мат. – 1983.-47, №3.-С.455-497
39. Helton J. W. Broadbanding:-Gain Equalization Directly From Data. //IEEE Tr. on circuits and systems, - 1981. - CAS-28, No.12, December, 1125-1137
40. Справочник по специальным функциям, под ред. М.Абрамовица и И.Стиган, M.: Наука, ГРФМЛ, 1979. – 830 c. (С.41, раздел 4.3.95)
41. Чеботарёв Н.Г. «Многоугольник Ньютона» и его роль в современном развитии математики.// «Исаак Ньютон», АН СССР, 1943, С.99-126,
42. Брюно А.Д. Локальный метод нелинейного анализа дифференциальных уравнений. –М.: Из-во Наука, 1979, 254 с.
43. Джоунс У., Трон В. «Напрерывные дроби: Аналитическая теория и приложения» , 1985
44. Буслаев В. И. «Введение в аналитическую теорию непрерывных дробей», 2006
45. Аров Д.З. Реализация матриц-функций по Дарлингтону. Изв. АН СССР, 37:6 (1973), 1299-1331.
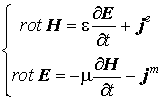 ,
(1)
,
(1)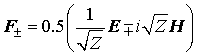 ,
(2)
,
(2)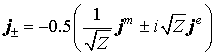 (3)
(3)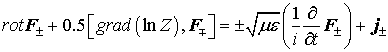
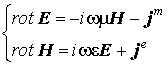 (5)
(5)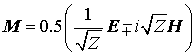 , (12)
, (12)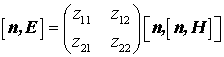 ,
(15)
,
(15)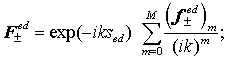
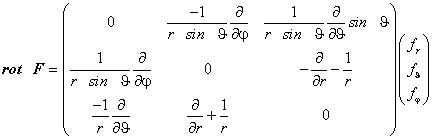 (21)
(21)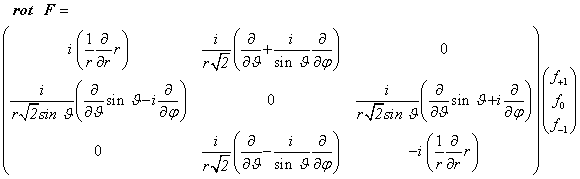 (22)
(22)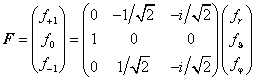
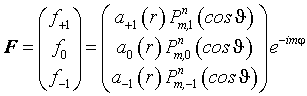 (23)
(23)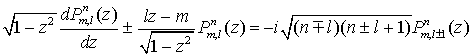
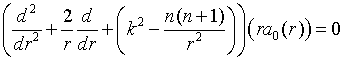
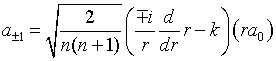
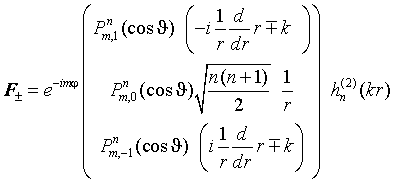 (24)
(24)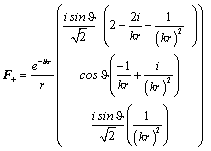
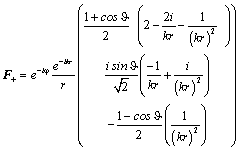
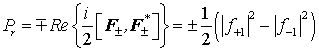 (25)
(25)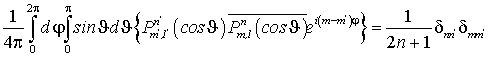
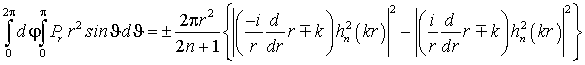 (26)
(26)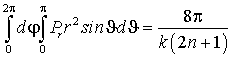 .
(27)
.
(27)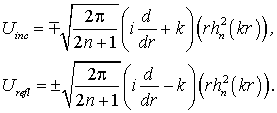 (28)
(28)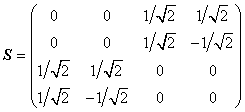
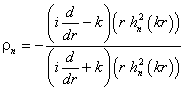
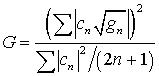 (29)
(29)
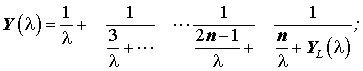 (34)
(34)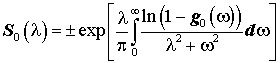
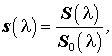 (37)
(37)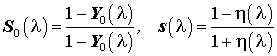 (38)
(38)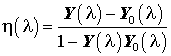 (39)
(39)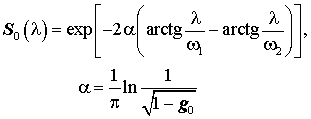
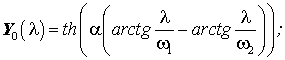 (41)
(41)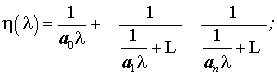 (42)
(42)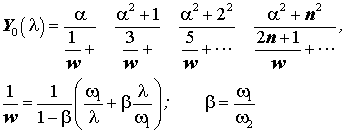 (43)
(43)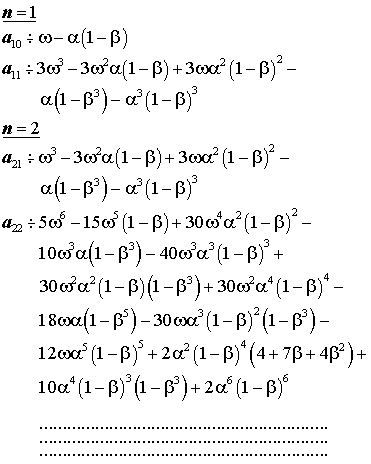
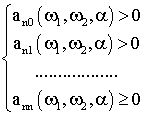
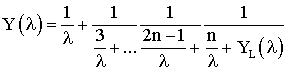
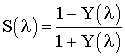
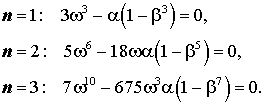 (45)
(45)