УДК: 537.876.23, 537.877, 621.3.09
МЕТОДЫ НЕЛИНЕЙНЫХ ВРЕМЯ-ЧАСТОТНЫХ ОТОБРАЖЕНИЙ
В АНАЛИЗЕ ФЛУКТУАЦИЙ ИНТЕНСИВНОСТИ ЛАЗЕРНОГО ПУЧКА
Т.И. Арсеньян, М.И. Бабанина, Н.А. Сухарева, А.П. Сухоруков
Физический факультет МГУ им. М.В.Ломоносова
Получена 26 июля 2013 г.
Аннотация. Представлены результаты нелинейного время-частотного анализа на основе отображения Вигнера-Вилли распределений интенсивности и их первых четырёх пространственных моментов для лазерного пучка, прошедшего модельную трассу. Обсуждаются свойства время-частотных карт, соответствующих разным режимам возмущения среды распространения, анизотропия и временные масштабы флуктуаций интенсивности. Экспериментально обнаружены астигматические искажения пучка, связанные с ветровой нагрузкой и дефокусировкой тепловой линзой.
Ключевые слова: открытые оптические каналы, дисторсия лазерного пучка, турбулентная среда, отображение Вигнера-Вилли, астигматические искажения.Abstract. Nonlinear time-frequency analysis was applied to the intensity fluctuations of a laser beam propagated through the model turbulent path. For this purpose the Wigner-Ville mapping of intensity distributions and their first four spatial moments were used. The characteristics of time-frequency maps corresponding to different modes of propagation channel are discussed as well as anisotropy and temporal scales of intensity fluctuations. The experiments on the model path revealed astigmatic distortions of the beam caused by the wind load and thermal lens defocussing.
Keywords: turbulent media, Wigner-Ville mapping, laser beam distortions, astigmatic distortions, FSO.
Введение
Динамика пространственных и временных искажений лазерного пучка при распространении в тропосфере – одна из классических задач, «точность решения» которой определяется прикладными акцентами использования открытых оптических каналов передачи данных. Основой теоретических моделей анализа распространения электромагнитного излучения в слабо возмущённом случайно-неоднородном тропосферном канале служит закон «двух третей» Колмогорова-Обухова, справедливый для условий слабых флуктуаций [1, 2]. На протяженных трассах влияние турбулентного канала выявило появление «сильных» флуктуаций [3].
Последние несколько лет активно развивается технология пространственно-временного кодирования оптических каналов, позволяющих компенсировать помехи на трассе при прогнозируемой статистике их возникновения [4, 5]. Выбор геометрии пространственного и временного разнесения парциальных приёмопередающих устройств основан на статистике помех, присущих квазистационарным режимам. К сожалению, отсутствуют модели нестационарных флуктуаций, позволяющие оценить влияния случайно-неоднородной атмосферы на сигнал [6].
Сложность анализа нестационарных флуктуаций связана, прежде всего, с их многообразием, требующим детального время-частотного контроля регистрируемого распределения поля. Традиционное разложение многокомпонентного сигнала в гармоническом базисе не предусматривает «вписывание» временной переменной в результирующий спектр и фактически не позволяет различать «порядок следования» компонент в сигнале. Методики анализа спектрограмм на основе укороченных Фурье-отображений ограничены по разрешающей способности, поскольку в отображении используются сопряженные компоненты [7]. Использование нелинейных отображений, относящихся к классу Коэна [8], позволяет достичь желаемого разрешения в актуальном диапазоне времени и частот специальным подбором ядра интегрального преобразования. Оценка информативности методов нелинейного время-частотного отображения выполнялась для серий экспериментальных выборок, полученных на тестовой трассе с управляемыми параметрами.
1. Нелинейные время-частотные отображения
Физически значимые параметры сигнала, как правило, заключены в его квадратичных формах (мощность, энергия). Следовательно, для оценки воздействия сигнала или уровня возбуждения системы, создающей сигнал, необходимо разработать аппарат время-частотного описания энергетических свойств сигнала. Энергетическое время-частотное распределение сигнала исходно строится на базе квадратичных форм как при частотном, так и при временном анализе. Независимо от вида представления рассматриваемого сигнала его полная энергия не должна измениться, следовательно, для любых типов базисов должно выполняться соотношение:
![]() , (1)
, (1)
здесь ![]() - исходный сигнал и его Фурье-отображение соответственно.
- исходный сигнал и его Фурье-отображение соответственно.
Подынтегральные выражения в (1) можно
интерпретировать как энергетическую плотность сигнала в данный момент времени
или на данной частоте. Естественным было бы определение ещё одной более
детальной энергетической характеристики сигнала x(t) - совместного
время-частотного распределения, описываемого плотностью распределения энергии ![]() и удовлетворяющего общему интегральному соотношению:
и удовлетворяющего общему интегральному соотношению:
![]() , (2)
, (2)
и двум маргинальным свойствам:
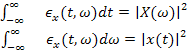 . (3)
. (3)
Представленные соотношения (2) и (3) непротиворечивы математически, но непригодны для сопряжённых переменных, точность измерения которых ограничена соотношением неопределённости:
![]() . (4)
. (4)
Для разрешения противоречия можно использовать квазивероятностное отображение Вигнера-Вилли (Wigner-Ville) [9, 10], которое может быть определено для исходного сигнала или его Фурье-отображения:
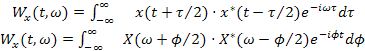 . (5)
. (5)
Разрешающая способность отображения Вигнера-Вилли значительно выше разрешения спектрограммы. В то же время для ряда областей время-частотной плоскости значения отображения Вигнера-Вилли становятся отрицательными, что противоречит интуитивно желаемому использованию распределения как вероятностного. Поскольку отображение Вигнера-Вилли строится на основе квадратичной функции от исходного сигнала, интерференционные процессы необходимо анализировать в приближении квадратичного принципа суперпозиции:
![]() , (6)
, (6)
где
Выражение (7) принято называть кросс-отображением Вигнера-Вилли [11]. Интерференционные компоненты в распределении формируются между «оригинальными» компонентами сигнала. Они осциллируют в направлении, перпендикулярном линии, соединяющей центры «оригиналов», с частотой, пропорциональной расстоянию между центрами «оригиналов». Проиллюстрируем утверждение на примере отображения Вигнера-Вилли для сигнала, составленного из двух атомарных компонент с разными частотами несущих и отстоящих друг от друга на заданный интервал времени:
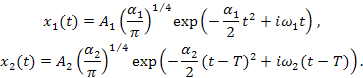
Собственные отображения и кросс-отображения получим после интегрирования в следующем виде:
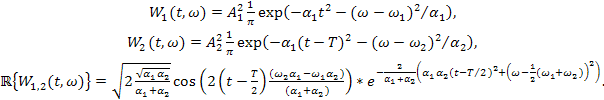
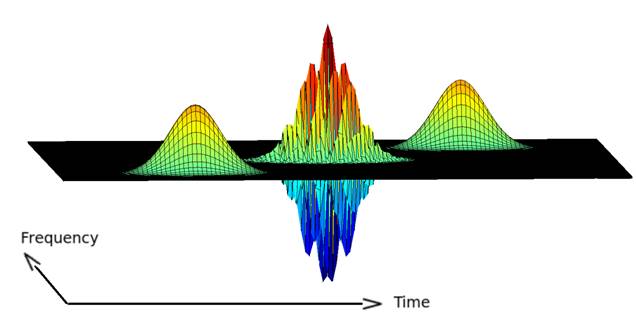
Иллюстрация вычисленного отображения представлена на рис.1, амплитуды парциальных сигналов и ширины гауссовских профилей полагались равными.
|
|
|
Рис.1. Карта отображения Вигнера-Вилли для суммы двух габоровских атомов. |
Физическая и математическая обоснованность время-частотного отображения Вигнера-Вилли могли бы сделать его мощным универсальным средством время-частотного анализа нестационарных сигналов. Однако интерпретация результатов анализа весьма затруднена прежде всего сильными интерференционными искажениями, требующими дополнительных критериев анализа наблюдаемых время-частотных карт. «Диалектическое противоречие» между высокой разрешающей способностью и проявлениями динамической квадратичной интерференции в отображении (7) можно компенсировать сглаживанием результирующего отображения с помощью дополнительных фильтров.
2. Отображение Вигнера для многокомпонентных сигналов
Пространственная неоднородность и нестационарность среды распространения лазерного пучка существенно нарушат исходную регулярную структуру волнового фронта и сформируют в зоне регистрации многокомпонентный сигнал. Решение задачи подавления интерференционных искажений следует проводить, не нарушая общего свойства отображения – ковариантности по отношению к смещению времени и частоты, позволяющей отнести отображение Вигнера-Вилли к классу Коэна [8, 12].
Интегральное определение функций класса Коэна вводится следующим образом:
где ![]() - функция параметризации. В ряде случаев удобнее работать
с Фурье-отображением функции параметризации и использовать иное представление
для функций класса Коэна:
- функция параметризации. В ряде случаев удобнее работать
с Фурье-отображением функции параметризации и использовать иное представление
для функций класса Коэна:
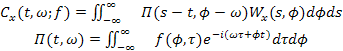 . (9)
. (9)
Как следует из (9), отображение Вигнера-Вилли принадлежит классу функций Коэна и создано с помощью единичной функции параметризации или двойной функции Дирака в Фурье-отображении:
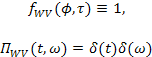 .
.
Управляя профилем функции параметризации отображения, можно получить практически весь набор энергетических время-частотных отображений, включая спектрограммы, псевдораспределения и ряд других правил отображения, отфильтровывающих интерференционные искажения время-частотной структуры сигнала. Так, для определения спектрограммы необходимо использовать в качестве функции параметризации отображение Вигнера-Вилли для оконной функции:
![]() . (10)
. (10)
В определении порядка регистрации спектрограммы предусмотрена работа только с профилем окна и временной апертурой. Для ряда задач создания новых время-частотных отображений разумно добавить дополнительную степень свободы в подбор функции параметризации и ввести дополнительное условие факторизации по аргументам:
![]() . (11)
. (11)
Подставив (11) в (8), получим выражение для сглаженного псевдораспределения Вигнера-Вилли:
![]() .
(12)
.
(12)
Подбор профилей временной и частотной выборки
проводится по критериям необходимого время-частотного разрешения и достаточного
подавления интерференционных компонент. Если в выражении (12) функцию ![]() заменить на функцию Дирака от
времени, получим псевдораспределение Вигнера:
заменить на функцию Дирака от
времени, получим псевдораспределение Вигнера:
![]() , (13)
, (13)
здесь ![]() - профиль окна. Псевдораспределение можно интерпретировать как
сглаживание исходного отображения с помощью частотного фильтра согласно
интегральному преобразованию:
- профиль окна. Псевдораспределение можно интерпретировать как
сглаживание исходного отображения с помощью частотного фильтра согласно
интегральному преобразованию:
![]() , (14)
, (14)
где ![]() - Фурье-отображение профиля окна
- Фурье-отображение профиля окна ![]() . Оконное преобразование в качестве
побочного эффекта позволяет избавиться от осциллирующих интерференционных
компонент вдоль оси времени. Оборотная сторона оконного преобразования – потеря
квазираспределением Вигнера-Вилли ряда свойств, присущих исходному отображению.
Так, для квазираспределения не справедливы маргинальные соотношения,
унитарность, частотная локализация.
. Оконное преобразование в качестве
побочного эффекта позволяет избавиться от осциллирующих интерференционных
компонент вдоль оси времени. Оборотная сторона оконного преобразования – потеря
квазираспределением Вигнера-Вилли ряда свойств, присущих исходному отображению.
Так, для квазираспределения не справедливы маргинальные соотношения,
унитарность, частотная локализация.
Сильной стороной рассматриваемого отображения для анализа флуктуационных процессов считается возможность детектирования нестационарных парциальных компонент сложного сигнала. Конкретные свойства компонент многокомпонентного сигнала, их частотная и временная локализация, модуляционные характеристики восстанавливаются однозначно после выбора опорного сигнала. Разделение компонент сигнала можно выполнить при условии относительно малой ширины полосы каждой из компонент по сравнению с разностью частот компонент. Например, для двухкомпонентного сигнала вида
![]()
разделение возможно, если справедливы неравенства
![]() .
.
Следует отметить ещё одну сложность интерпретации время-частотных карт многокомпонентных сигналов – нелокальность проявления «интерференционных возмущений» при динамической квадратичной интерференции (локализация во времени интерференционного сигнала не совпадает с локализацией интерферирующих), затрудняющую первичный отбор опорных сигналов.
3. Экспериментальный стенд и методика обработки видеоряда
Измерения проводились на специально созданной для моделирования открытого оптического канала установке, состоящей из источника излучения, трассы регулируемой длины с варьируемыми градиентами температур и средней скорости горизонтальных течений, широкоапертурного регистратора. Источником излучения служит твердотельный лазер, работающий на второй гармонике с длиной волны 532 нм. Излучение через систему линз, диафрагм и направляющих зеркал заводится в открытую с торцов цилиндрическую кювету длиной 1.5м. Зеркала, расположенные в торцах кюветы, позволяют прогонять пучок несколько раз через внутренний объём кюветы, наращивая эффективную длину трассы с шагом 1.3м. В нижней части кюветы расположена линейка нагревательных элементов, на боковых стенках находятся сопла, через которые внутрь кюветы компрессором закачивается воздух комнатной температуры. Аналогичная по геометрии (но не по параметрам) установка использовалась ранее в работе [13].
Градиент температур и неоднородность скорости формируют внутри кюветы турбулентные потоки, характеризующиеся флуктуациями показателя преломления различной интенсивности и масштаба. Длина рабочей трассы может варьироваться наклоном «гоняющих» зеркал и для представленных ниже выборок составляла 7м. Регистрация распределений интенсивности в поперечном сечении пучка выполнялась высокоскоростной камерой с частотой до 2.5кГц и разрешением 360х240 точек. Пространственная структура лазерного пучка на входе в кювету может меняться перестройкой системы линз и диафрагм, в обсуждаемых ниже случаях использовался пучок с относительно малым радиусом когерентности.
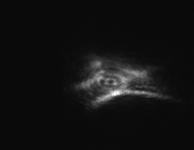
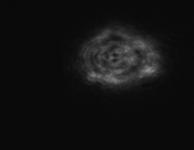
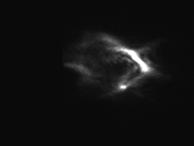
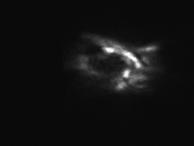
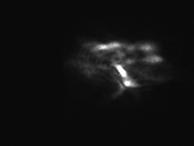
Исходная пространственная структура пучка, типичные распределения интенсивности для режимов с максимально доступным градиентом температуры и при максимальной скорости потока представлены на рис.2.
|
|
|
|
|
Рис.2 Сечение многомодового пучка в отсутствие градиентов (слева), при сильном градиенте скорости потока (в центре) и при градиенте температур (справа). |
||
Регистрация последовательности распределений интенсивности выполнялась с частотой следования 400 кадров/с, достаточной для временного разрешения модуляции интенсивности на частотах ниже 200 Гц. Интервал времени наблюдения для каждого из значений градиента температуры и скорости вводимого потока составлял не менее 20с, что обеспечивает длину выборки не менее 8000 кадров и позволяет обоснованно делать выводы о временных характеристиках регистрируемого распределения интенсивности.
Последовательность кадров с
заданным интервалом следования рассматривается как статистический ансамбль
реализаций состояния исследуемой системы. Каждая из реализаций описывается
дискретной функцией распределения интенсивности ![]() по координатам сетки регистрации, ось
X направлена вдоль вектора скорости воздушного потока, ось Y –
вдоль исходного градиента температуры. Пример трех последовательных реализаций
распределения интенсивности на регистрирующей матрице при максимально доступном
значении скорости потока и градиента температуры представлен на рис.3.
по координатам сетки регистрации, ось
X направлена вдоль вектора скорости воздушного потока, ось Y –
вдоль исходного градиента температуры. Пример трех последовательных реализаций
распределения интенсивности на регистрирующей матрице при максимально доступном
значении скорости потока и градиента температуры представлен на рис.3.
|
|
|
|
|
Рис.3 Примеры распределений интенсивности, разделенные интервалом времени 2.5мс. |
||
Пространственные искажения пучка, распространяющегося через случайно-неоднородную среду, характеризуются моментами функции распределения интенсивности первых четырех порядков, при этом дисперсия, асимметрия и эксцесс рассматривались как центральные моменты. Моменты в выбранной системе координат имеют две компоненты, в общем случае связанные друг с другом за счет геометрии вихревых потоков внутри трубы модельной трассы:
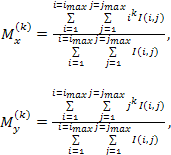 (15)
(15)
здесь k — порядок момента пространственного распределения интенсивности. Первые моменты соответствуют координатам «центра тяжести» при заданном распределении интенсивности, вторые центральные моменты характеризуют эффективные размеры эллипса, аппроксимирующего «рабочую зону» регистрируемого распределения интенсивности. Третий и четвертый моменты описывают асимметрию искажений профиля и статистику сильных возмущений структуры пучка.
Традиционно флуктуационные характеристики прошедших через случайную среду волн или пучков принято описывать через индекс мерцаний [14], определяемый следующим образом:
![]() (16)
(16)
Оценка среднего и квадрата среднего значения интенсивности в (16) проводится для эквидистантной временной выборки. На основе регистрируемых в экспериментах последовательностей кадров можно определить общий для полной апертуры регистрации и локальные (субапертурные) индексы мерцаний в приближении квазистационарности изучаемых случайных процессов. Пример геометрии размещения субапертур в зоне регистрации представлен на рис.4.
Симметрия расположения, число, линейные размеры и шаг размещения субапертур определяются типом решаемой задачи. Для анализа нестационарных свойств индекса мерцаний, непосредственно связанного с функцией когерентности четвертого порядка [15], может быть использован метод скользящего окна с временной апертурой, малой относительно характерного времени нестационарности и достаточной для набора статистики и определения локальной функции распределения вероятности регистрируемой интенсивности. Длительность статистически значимой выборки в определении индекса мерцаний для задач оптимизации открытых оптических каналов передачи данных должна быть согласована с характерными временами управляющих алгоритмов сеансов передачи данных.
4. Время-частотные карты «пространственных» моментов распределения интенсивности.
Ряд дискретных значений каждого из моментов пространственного распределения интенсивности может быть рассмотрен как нестационарный многокомпонентный случайный процесс, развивающийся под действием многих факторов. Классический метод фазового экрана при описании аберраций пучка с низкой степенью пространственной когерентности аппроксимирует среду распространения фазомодулирующей структурой с вариацией фазового набега в зависимости от координаты [16]. Выполним разложение фазового набега в ряд по пространственному аргументу, вводя векторные или тензорные (соответствующих порядков) коэффициенты разложения:
![]() , (17)
, (17)
здесь коэффициент G
характеризует мгновенный градиент показателя преломления, Q —
сферичность, A – астигматизм, ![]() – эксцесс возмущаемого экраном
волнового фронта.
– эксцесс возмущаемого экраном
волнового фронта.
Ориентации собственных осей тензоров второго и более высокого порядков выражения (17) зависят от геометрии течений и локальных градиентов температур, отношения соответствующих им радиусов случайным образом меняются во времени. Выбор декартовой системы координат при описании распределения в плоскости регистрации можно рассматривать как техническое приближение, связанное больше с методикой обработки изображения, нежели с симметрией физических процессов.
Для каждого кадра анализируемой выборки выполнялась процедура подавления шумов видеоматрицы, проводился контроль режима пересветки (выхода за пределы динамического диапазона регистратора) и вычислялись «мгновенные» значения четырёх моментов пространственной функции распределения интенсивности. Время-частотная карта высокого разрешения строилась на основе сглаженного квадратичного отображения Вигнера-Вилли для аналитического продолжения временного ряда (исключение из карты области отрицательных значений частот). Собственно предобработка исходного видеофайла, первичная фильтрация, контроль насыщения, шумоподавление, аналитическое продолжение и вычисление отображения выполнялись на базе библиотек пакета прикладных математических программ Scilab [17].
|
|
|
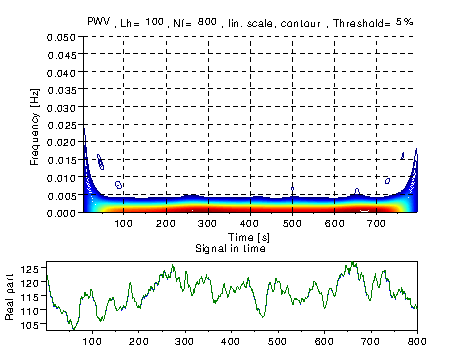
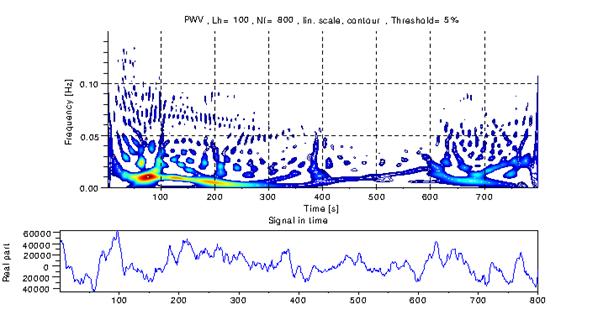
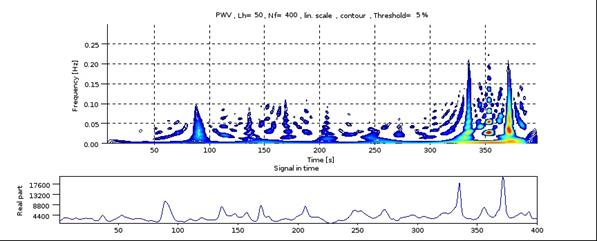
Рис.5а Время-частотная карта Y-компоненты момента первого порядка и временная развёртка обрабатываемого сигнала. |
Характерный вид время-частотных карт моментов первого, второго и третьего порядков порядков представлен на рис 5a-5с. При расчётах использовались значения, полученные для первых 800 кадров, что соответствует двухсекундной длительности. Представленные карты рассчитаны для смешанного режима «возбуждения» турбулентности при одновременном создании градиента температуры и горизонтальных потоков максимально доступной скорости, обеспечивающих сильную турбулентность в среде.
|
|
|
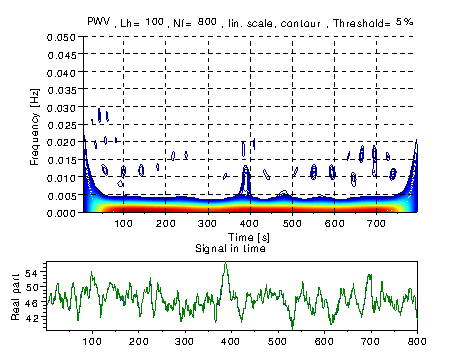
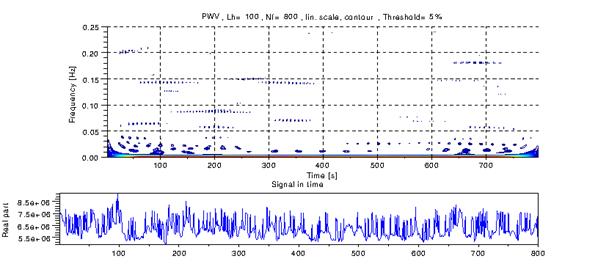
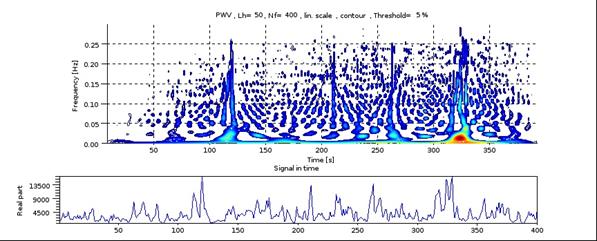
Рис.5b Время-частотная карта Y-компоненты момента второго порядка и временная развёртка обрабатываемого сигнала.
|
|
|
|
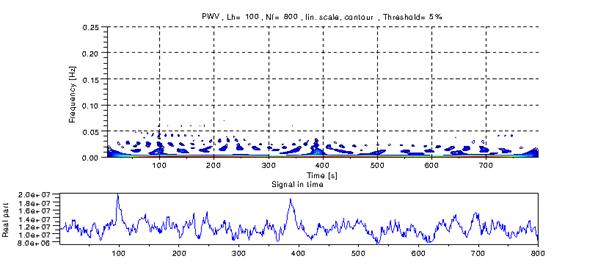
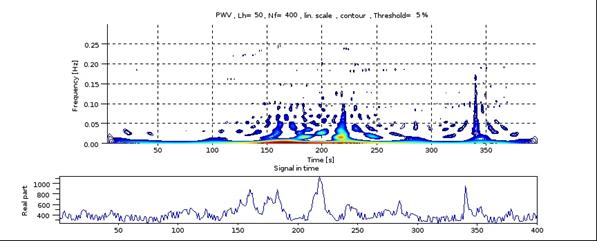
Рис.5c Время-частотная карта Y-компоненты момента третьего порядка и временная развёртка обрабатываемого сигнала. |
В режиме сильного «перемешивания» направления собственных осей тензоров второго и третьего порядков меняются с характерными временами распространения волн сжатия между стенками кюветы, «стирая» возможные различия время-частотных отображений для горизонтальной и вертикальной компонент. Иная картина на картах для моментов четвертого порядка (рис.6a и 6b).
|
|
|
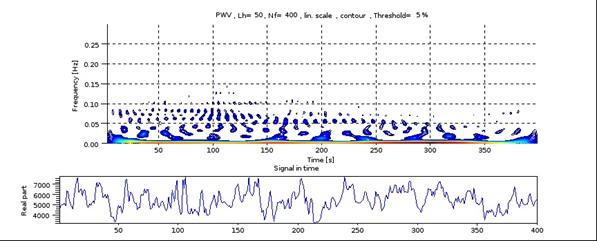
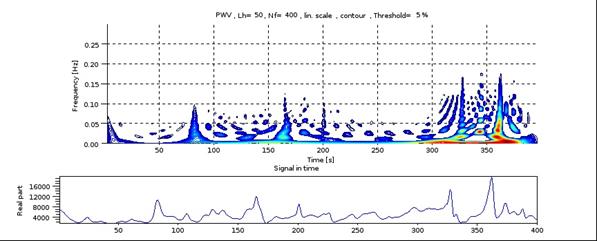
Рис.6a Время-частотная карта X-компоненты момента четвертого порядка и временная развёртка обрабатываемого сигнала.
|
|
|
|
Рис.6b Время-частотная карта Y-компоненты момента четвертого порядка и временная развёртка обрабатываемого сигнала. |
Следует отметить связь характерного частотного диапазона вариаций момента и его порядка, с возрастанием порядка момента поднимается верхняя граница значимого диапазона частот. Такое согласование хорошо объясняется в модели турбулентных течений на основе уравнения Навье-Стокса и цепочки уравнений Фридмана-Келлера [18, 19].
Как следует из первичного анализа время-частотных карт, наибольшее возмущение испытывает момент третьего порядка, характеризующий астигматизм пучка в зоне регистрации. Этот процесс крайне редко учитывается при проектировании регистрирующей системы открытых оптических каналов и требует специального внимания. Интересно наблюдаемое на картах компонент момента четвертого порядка явление «фильтрации» высокочастотных метастабильных компонент вдоль градиента температур.
5. Локальные флуктуации интенсивности и индекс мерцания
Пространственно-временное кодирование сигнала предполагает первичное расщепление пучка на группу отдельных сигнальных лучей (например, голографической решёткой) с последующей регистрацией элементов пространственного созвездия через многопозиционную апертуру. Искажения профиля пучка, описанные в предыдущем разделе, перейдут в глубокую стохастическую модуляцию интенсивности компонент сигнального созвездия. Для исследования закономерностей подобной модуляции и их связи с моментами функции распределения интенсивности была выполнена обработка последовательности кадров с наложением многопозиционной прямоугольной маски (субапертурной матрицы), захватывающей актуальную область приёма пучка (рис.4).
Шаг, число элементов и линейные размеры отдельного элемента выбирались, исходя из характерных геометрических параметров промышленных приёмопередатчиков для открытых оптических каналов. Рассмотрим три варианта регистрации суммарного потока, попадающего в зону регистрации:
– одиночная апертура максимального размера, гарантированно захватывающая весь пучок (220пт.х220пт.),
– девятипозиционная маска 3x3 с шагом 30пт и размерами одного элемента 10пт.х10пт,
– предельный случай девятипозиционной маски 3x3 с шагом 60пт и размерами одного элемента 1пт.
В таблице 1 представлены значения индекса мерцаний для двадцатисекундной выборки при трёх различных режимах – только нагреве, при наличии потока и смешанном режиме. Индекс мерцания при полном захвате сечения близок к нулю, что закономерно для пучков с низкой пространственной когерентностью. Расщепление пучка несколькими субапертурами выявляет неоднородность и анизотропность мерцания в различных зонах наблюдения.
|
Тип апертуры |
Градиент температуры |
Внешний поток |
Градиент температуры + Внешний поток |
|||||||||||||||||||||||||||
|
220x220pt |
0.0012 |
0.0016 |
0.0017 |
|||||||||||||||||||||||||||
|
Девятипо-зиционная
10x10pt |
|
|
|
|||||||||||||||||||||||||||
|
Девятипо-зиционная
1x1pt |
|
|
|
|||||||||||||||||||||||||||
|
Таблица. 1. Индексы мерцаний для трёх различных условий распространения пучка. |
||||||||||||||||||||||||||||||
Как следует из результатов, в условиях эксперимента мерцание в основном связано с присутствием внешнего потока, собственно градиент температур относительно слабо возмущает среду распространения.
Время-частотные карты для «мгновенного» значения интенсивности рассмотрим только для центрального элемента, несущего основную нагрузку в устройствах передачи данных (рис.7).
|
|
|
|
|
|
|
Рис.7 Время-частотные карты для односекундной выборки при нагреве (верхний), под воздействием потока (средний) и под воздействием обоих факторов (нижний). |
Наблюдаемые на время-частотных картах рис.7 короткоживущие возмущения могут быть связаны с локальными вихревыми структурами, создаваемыми восходящим потоком при неоднородном нагреве или вводимым извне потоком [20, 21].
Анизотропия перераспределения глубины флуктуаций интенсивности в плоскости регистрации пучка в модельном эксперименте, связанная с геометрией ввода потока (в используемой системе координат – слева) наглядно отображается на картах диагональных элементов субапертурной матрицы ({1,3} и {3,1} на рис.8).
|
|
|
|
|
Рис.8. Время-частотные карты для односекундной выборки под воздействием потока для диагональных элементов {1,3} (верхний) и {3,1} (нижний). |
Время-частотная структура карт на рис.8 близка, однако следует отметить более чем шестнадцатикратное различие масштаба значений суммарной интенсивности, регистрируемой на {3,1} относительно {1,3} элементах апертурной матрицы, что хорошо согласуется со значениями индекса мерцаний (таб.1).
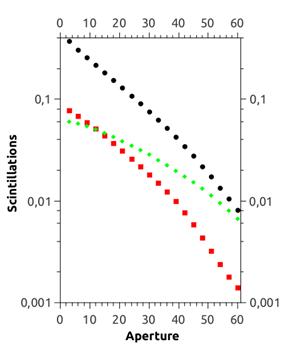
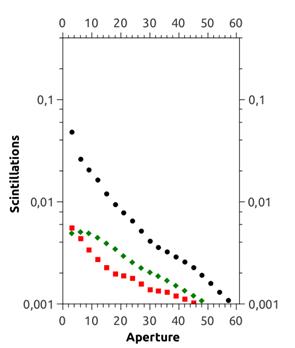
Закономерности изменения индекса мерцаний, среднего значения регистрируемой мощности излучения в зависимости от положения и линейных размеров апертуры принципиальны для проектирования приёмопередающей аппаратуры, поскольку профиль апертуры следует согласовывать с ожидаемыми типами дисторсии пучка. Пример зависимости индекса мерцаний от линейных размеров трех типов апертур – щелевой вертикальной, щелевой горизонтальной и квадратной – для среды под воздействием нагрева или внешних воздушных течений представлен на рис.9.
|
|
|
|
Рис.9. Изменение индекса мерцаний интенсивности с ростом апертуры приёмника для трассы с внешним потоком (слева) и нагревом (справа). Квадратная апертура — черные круги, вертикальная щель — красные квадраты, горизонтальная щель — зелёные ромбы. |
|
Характер зависимостей, представленных на рис.9, определяется геометрией вносимых возмущений и подтверждает значимую анизотропию дисторсии пучка. Различный ход зависимости индекса мерцаний для горизонтально ориентированный щелевой апертуры при возмущении среды потоком и градиентом температуры может быть связан с преимущественно периферийными флуктуациями интенсивности в первом случае, и «дыханием» пучка под действием «тепловой линзы» во втором [22]. Однако во всех случаях можно говорить о динамической стохастической анизотропии искажений, которая характеризуется в равной мере время-частотными распределениями и средними по ансамблю параметрами.
Заключение
Открытый оптический канал – анизотропная квазистационарная среда с высоким уровнем рефракционных искажений вдоль направления доминирующего потока. Вид флуктуаций интенсивности однозначно связан с типом «порождающего фактора» и может быть положен в основу детектирования и прогнозирования «сноса» пучка при одноапертурной регистрации.
Использованная в экспериментах трасса распространения – тестовая для отладки методики контроля состояния пучка. Представленные серии выполнены для пучка с малым радиусом пространственной когерентности, что существенно упрощает интерпретацию результатов. Повышение пространственной когерентности пучка приведёт к интерференционным искажениям исходного профиля интенсивности и увеличит уровень помех в оптическом канале.
Результаты нелинейного время-частотного анализа структуры пространственно-временных возмущений распределения интенсивности могут быть положены в основу модели мультипликативных помех для открытых оптических каналов передачи данных. Представленная методика анализа перспективна для широкого класса нестационарных сигналов.
Литература
1. Татарский В.И. Распространение волн в турбулентной атмосфере, – Москва: Наука, 1967
2. Larry C. Andrews, Ronald L. Phillips. Laser beam propagation through random media. - 2nd ed. SPIE Press, Bellingham, Washington , 2005
3. Семенов А.А., Арсеньян Т.И. Флуктуации электромагнитных волн на приземных трассах. – М. : Наука. 1978.
4. Claude Oestges and Bruno Clerckx MIMO Wireless Communications. From real-world propagation to space–time code design – : Elsevier. 2007
5. Mohsen Kavehrad, Jarir Fadlullah, and Zeinab Hajjarian «MIMO FSO Communications in Cloud and Turbulence» [Электронный ресурс]. URL:
http://dx.doi.org/10.1364/LSC.2011.LTuC3, 2011
6. Т.И. Арсеньян, П.В. Короленко Оптика случайно-неоднородных сред и проблемы распространения лазерного излучения в тропосфере. - М.: Физический факультет МГУ, 2001
7. Antonia Papandreou-Suppappola Applications in time-frequency signal processing, : CRC Press LLC . 2003
8. Cohen Leon. Time Frequency Analysis: Theory and Applications, : Prentice Hall; 1994
9. L. Cohen, «A critical review of the fundamental ideas of joint time-frequency distributions», // IEEE Proc. Int. Symp. on Circuits and Systems, vol. 1, pp. 28-33,1986
10. L. Cohen, «On a fundamental property of the Wigner distribution» // 7IEE Trans. Acoust, Speech, Signal Processing, vol. 35, pp. 559-561,1987
11. L. Cohen, «What is a Multicomponent Signal?» // Proc. IEEE ICASSP- 92, vol. 5, pp. 113-116,1992
12. L. Cohen «Time-Frequency Distributions - A Review» // Proc. of the IEEE, vol. 77, pp. 941-981,1989
13. Арсеньян Т.И., Зотов А.М., Короленко П.В., Маганова М.С., Таначев И.А. «Об устойчивости фрактальных свойств лазерного излучения в турбулентных средах» // Оптика океана и атмосферы, т.19, № 12, 2006. C. 1013-1015.
14. Charles L. Rino The Theory of Scintillation with Applications in Remote Sensing : John Wiley & Sons, Inc., Hoboken, New Jersey. , 2011
15. Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику часть II. – М.: Наука. Главн. ред. Физико-математической литературы, 1978.–463с
16. Кандидов В.П., Чесноков С.С., Шленов С.А. «Компьютерное моделирование формирования изображения протяженного объекта в турбулентной атмосфере. Часть I» // Оптика атмосферы и океана, т. 11, №4, с.401-405, (1998).
17. [Электронный ресурс]. URL: http://www.scilab.org
18. Ландау, Л. Д., Лифшиц, Е. М., Гидродинамика. — Издание 4-е, стереотипное.. — М.: Наука, 1988
19. Фрост У., Турбулентность. Принципы и применения, Мир, М., 1980
20. В.Ф. Копьев, С.А. Чернышев «Колебания вихревого кольца, возникновение в нём турбулентности и генерация звука» // УФН. 2000. Т.70. No7. Стр.713-742
21. Fedor V. Shugaev, Evgeni N. Terentiev, Ludmila S. Shtemenko, Oksana A. Nikolaeva, Oxana A. Solenaya «Laser beam propagation through an ensemble of vortex rings in air» // Proc. SPIE 8535, Optics in Atmospheric Propagation and Adaptive Systems XV, 85350G (November 8, 2012); doi:10.1117/12.974548
22. John W. Strohbehn «The feasibility of laser experiments for measuring atmospheric turbulence parameters» // Journal of Geophysical Research Volume 71, Issue 24, pages 5793–5808, 15 December 1966.